Real-Time IoMT-driven Optimisation for Large-Scale Home Health Care

Planning

Seyedamirhossein Salehiamiri

, Richard Allmendinger

and Arijit De

Alliance Manchester Business School, University of Manchester, Manchester, M15 6PB, U.K.

Keywords:

Home Health Care, Internet of Medical Things, Computational Intelligence, Care Planning.

Abstract:

The number of home caretakers is rising rapidly due to an increasing number of elderly people, recent pan-

demics, and the advancement of home health care facilities. Wearable medical devices and the Internet of

Medical Things (IoMT) help health care managers monitor patients in real-time and provide remote medical

care. This reduces home visits and helps Home Health Care (HHC) companies plan their resources. The paper

addresses the HHC planning problem of allocating the optimal number of experts to patients while minimising

the delay in visiting the patient, matching medical expertise with patient needs, and identifying the patient’s

visit sequence. To tackle this, a new mixed-integer mathematical problem is proposed to reduce the total visit

time for patients. This paper makes three key contributions towards tackling this plan, including (i) providing

a formal deﬁnition of the problem and putting it in context with related work, (ii) proposing multiple problem

instances varying in complexity, and (iii) an initial analysis of several heuristics and an exact solver (CPLEX)

on these problem instances. The results indicated that the application of computational intelligence combined

with IoMT can reduce patient visitation time signiﬁcantly in a daily plan and therefore lead to 3.7 percent

improved care for HHC patients.

1 INTRODUCTION

Supply chain management is an important component

of sustainable development and plays a key role in

optimising various systems. The Home Health Care

(HHC) system has recently attracted the attention of

various systems and settings since it deals with hu-

man lives and supply chain considerations (Reddy

et al., 2022). Inefﬁciencies in home health care sys-

tems and their supply chain operations have signiﬁ-

cant impacts on human lives worldwide. In the con-

text of home health care, research has shown that

nurses spend a considerable amount of time on non-

clinical supply chain duties, indicating inefﬁciencies

in the system (De Vries and Huijsman, 2011; Vervoort

et al., 2021). This system could save a human life, es-

pecially when patients with traumatic diseases need

timely and justiﬁed services from the comfort of their

homes (Nikzad et al., 2021). Hence, efﬁcient use of

supply chain networks (including expert home carers,

patients, and HHC organisations) could improve the

https://orcid.org/0000-0001-5980-8192

https://orcid.org/0000-0003-1236-3143

https://orcid.org/0000-0002-0361-5911

effectiveness of HHC systems, since the daily demand

for home care is increasing.

Nowadays, patient monitoring and care are crucial

to recovery. Some organisations offer real-time pa-

tient monitoring and data recording by employing ap-

plications to both reduce their costs and face the chal-

lenges of meeting the growing demands of patients.

Technologies used to monitor patients with HHC

have shown signiﬁcant beneﬁts in reducing mortal-

ity rates (Polisena et al., 2010). Athelas is a lead-

ing provider of patient monitoring systems (Athelas,

2003). Patients carry sensitive data about their health,

which requires more layers of protection. Therefore,

a new form of IoT (Internet of Things) for health care

has emerged: IoMT (Internet of Medical Things). If

any results are beyond the normal range, the patient

immediately receives an alert from the nursing staff

for further follow-up medical treatments (Dwivedi

et al., 2022).

The motivations behind using the IoMT concept

are to perform real-time patient monitoring and plan

patient visits. A real-time device is attached to the pa-

tient’s body according to their chronic diseases. This

device not only monitors patients daily, but can also

perform certain health care activities, such as remote

Salehiamiri, S., Allmendinger, R. and De, A.

Real-Time IoMT-driven Optimisation for Large-Scale Home Health Care Planning.

DOI: 10.5220/0012938900003837

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 72-83

ISBN: 978-989-758-721-4; ISSN: 2184-3236

monitoring of the patient’s heart rate and administer-

ing certain types of medicine. In contrast to earlier re-

search on HHC supply chain network planning (see,

e.g., (Ait Haddadene et al., 2019; Goodarzian et al.,

2021; Fathollahi-Fard et al., 2022)), IoMT responds

quickly to changes in the schedule and can resched-

ule the current plan as needed.

The contributions of the study include a new math-

ematical model considering allocating skill-based

nurses to HHC patients based on different service

menu, developing multiple metaheuristic algorithms

suitable to solve the problem, and considering real-

time changes to verify the applicability of the IoMT

plan.

Therefore, in this study, a methodology for IoMT

wearable devices is ﬁrst proposed. The problem aims

to assign an optimal number of experts to various pa-

tients requiring service while minimising the total vis-

itation time, determining the daily plan and visitation

intervals. The term “threshold intervention level” is

used to identify patients with conditions of the high-

est severity. Finally, several metaheuristics that de-

pend on different concepts are adapted to the prob-

lem and benchmarked on several realistic problem in-

stances that vary in complexity.

The proposed mathematical problem considers

various inputs and settings, such as using con-

straints considering the patient’s time window, mul-

tiple choices to assign nurses, the Patient’s Service

Menu (PSM), and the uncertain nature of the pro-

posed IoMT plan. In contrast to previous studies,

each patient has its own unique time window for the

visit and requires speciﬁc services among the range

of services. First, we adapt the well-established Sim-

ulated Annealing (SA) and Particle Swarm Optimisa-

tion (PSO) to tackle the problem and serve as base-

lines. We then introduce a new co-evolutionary Parti-

cle Swarm Optimisation (CPSO) algorithm to explore

if a more sophisticated approach translates into better

performance (measured in terms of solution quality).

Several problem instances, varying in size, are intro-

duced to validate the performance of the three search

algorithms and an exact solver (CPLEX).

The organisation of the paper is as follows. The

next section provides the reader with a comprehen-

sive literature review of related works. The proposed

IoMT methodology and mathematical modelling are

presented in Section 3. Section 4 includes the opti-

misation strategy and the experimental results of the

metaheuristics. Finally, Section 6 concludes the paper

and discusses future work.

2 LITERATURE REVIEW

The research ﬁeld on HHC management is not new.

However, there is a growing trend in HHC research

to consider decision-making and management science

approaches.Most HHC supply chain papers have fo-

cused on creating a strategic framework. According

to (Landers et al., 2016), 52 percent of patient trans-

actions are conducted online, virtual or through an

app. As a result, more studies are needed to ﬁll this

gap and address the transition from traditional care to

HHC. This section represents an overview of the rel-

evant literature on HHC followed by a discussion of

research gaps in HHC.

Routing and Scheduling Problems. Most cur-

rent studies in the ﬁeld of HHC supply chain net-

work design employ new algorithms or introduce new

methodologies to solve their proposed mathematical

modelling. The study of Fard et al. (Fathollahi-Fard

et al., 2018) addressed a green HHC vehicle rout-

ing problem by using a mixed-integer linear program-

ming model to reduce expenses and green emissions.

Using the Lagrangian relaxation procedure, Decerle

et al. (Decerle et al., 2018) solved HHC routing and

scheduling for many time windows using a memetic

algorithm. The results of the problems were promis-

ing. Shi et al. (Shi et al., 2019) proposed a ro-

bust optimisation problem for an HHC plan and com-

pared the results in a deterministic setting. Math-

ematical programming was used to minimise vehi-

cle route logistics expenses per visitation. Bahadori

et al. (Bahadori-Chinibelagh et al., 2022) addressed

multi-depot routing programming for HHC optimi-

sation to reduce transportation costs. The study as-

sumed that routing rates must be limited. The model

was ﬂexible and effective under different conditions

due to two constructive algorithms. The scheduling

of HHC staff under uncertain conditions was inves-

tigated in (Restrepo et al., 2020). The objective was

to minimise work shift costs by achieving optimal al-

location, reducing shift-changing penalties, and ex-

pecting recourse. Having an optimised routing and

scheduling plan can be most beneﬁcial when having

access to the required resources. Therefore, alloca-

tion models are needed to overcome problems such as

nurse workloads, time window, and fair distribution

of resources. However, assigning the optimal number

of resources based on the patient’s condition has been

overlooked.

Allocation Problems. The use of location-allocation

problems can be seen in the design of recent HHC

supply chain networks. For instance, in (Rodriguez-

Verjan et al., 2018; Lin et al., 2018) a location-

allocation problem is proposed to both locate the

Real-Time IoMT-driven Optimisation for Large-Scale Home Health Care Planning

HHC centres and reduce the total cost of resources

and facilities. The authors used mixed-integer lin-

ear programming, as in (Xiao et al., 2018), to ad-

dress the HHC problem. However, the utilised time

window is not able to address real-time changes as

it is assumed to be ﬁxed. The application of location-

allocation problems is quite limited in the literature of

HHC. In addition, allocating nurses to patients based

on the PSM is ignored in this sense.

Metaheuristics for HHC Applications. The appli-

cation of metaheuristics has been highlighted in pre-

vious studies. Erdam et al. (Erdem and Koc¸, 2019)

addressed HHC patients with electronic vehicle rout-

ing challenges and their limitations. The problem was

to optimise travel time and the number of nurses. In

the analysis, metaheuristics based on genetic algo-

rithms and variable neighbourhood search performed

better. Other studies (eg (Decerle et al., 2019b; De-

cerle et al., 2019a)) considered using metaheuristics

such as non-dominated sorting genetic algorithm II

(NSGA-II) and an evolutionary approach like multi-

directional local search (MDLS) to optimise working

time and quality of service, respectively.

Bi-objective programming could reduce routing

time and reduce costs in an HHC system, according

to (Khodabandeh et al., 2021). The epsilon-constraint

method veriﬁes the results of the problem. In (Er-

dem and Koc¸, 2022) a hybrid algorithm is proposed

to address the problem of HHC with electronic ve-

hicles. Promising results were reported for complex

routing problems. In (Xiang et al., 2023) a routing

and scheduling HHC problem that accounts for the

patient’s preference was considered. The cost ob-

jective is minimised using hybrid NSGA-II, which

proved to be better than the e-constraint method.

In summary, there is a research gap in that the ap-

plication of IoMT and real-time changes has not yet

been considered in the existing literature (Fikar and

Hirsch, 2017; Emiliano et al., 2017; Dwivedi et al.,

2021). This study ﬁrst proposes a dynamic and real-

time plan using IoMT in a smart platform environ-

ment to enable online and instant decision-making

during an unexpected patient emergency scenario.

Previous studies insisted on routing and scheduling,

such as (Di Mascolo et al., 2021), or deﬁned a new so-

lution strategy to address HHC problems, such as (Liu

et al., 2021). Only a few studies have used an alloca-

tion strategy to assign the optimal number of nurses

to each patient. Furthermore, this work is the ﬁrst to

propose (and account for in optimisation) a combina-

tion of different time windows, patient service menus,

and service levels for experts.

3 FORMAL PROBLEM

DEFINITION

HHC monitors and improves patient care using med-

ical records, such as age, sex, symptoms, vital signs,

trauma, and others. HHC technologies, including

wearable devices, allow real-time patient monitor-

ing, medical data storage, and remote care (McGillion

et al., 2020). Therefore, HHC resources are allocated

when needed and patients are served more efﬁciently.

Each patient starts the day with the expectation of cer-

tain services. The HHC sector has many experts that

can be assigned to these patients, but each expert can

only provide speciﬁc medical care.

In summary, the proposed methodology has the

following steps:

• Phase one - System installation: The phase is

centred on using the HHC system with IoMT,

which calls for the mobilisation of actual indus-

try 4.0 systems—computers, software, and wear-

ables—for patient programming, monitoring, and

analysis.

• Phase two - Diagnosis: Wearable Internet of

Things (IoMT) devices can diagnose symptoms,

monitor patient status, and provide remote med-

ical treatment, therefore saving time and money.

They are able to forecast when to intervene and

alert medical staff before the patient’s condition

deteriorates. A speciﬁed Threshold Intervene

Level (TIL) enables the wearable device to proac-

tively assess and store real-time patient conditions

in a cloud-based data centre. With expert des-

ignations for every patient, this system uses past

data, real-time diagnosis, and patient observation

to identify and forecast urgent conditions.

• Phase three - Provide healthcare: Depending on

TIL, the IoMT wearable devices distinguish be-

tween patient severity levels. The technology

tracks and saves real-time data if the level is less

than TIL. Patients can also push a button to re-

quest assistance if it goes beyond TIL, and an ex-

perienced home health carer is dispatched.

Considering the proposed methodology, IoMT in

HHC is a network of connected devices in which

patient monitoring is done using secured network

based on internet. This provides online and instant

monitoring of each patient. On the other hand,

TIL is a critical parameter in which determines the

health condition of each patient separately. IoMT

and TIL are interconnected in the proposed HHC

problem since IoMT alerts the HHC staff based

on instant changes of patient’s condition given

the TIL level. Current study only focuses on the

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

scheduling aspect of the HHC as the main prob-

lem that HHC companies dealing with specially in

Canada. Therefore, this study considers schedul-

ing for the HHC patient without taking into ac-

count machine learning or triggering mechanism.

However, these will be a part of future develop-

ment of the current study. Given the current nature

of the problem and considering the IoMT changes

in a real-time manner, this setup can be utilised

in US and UK considering their challenges in the

HHC sector (Statista, 2020).

The objective of the HHC planning problem is to

assign experts to HHC patients based on their ser-

vice requirements. Patients expect the HHC system

to provide home medical care, and accordingly the

HHC manager matches experts who possess a par-

ticular medical expertise with patients requiring that

speciﬁc medical care. In other cases, interventions

such as prompt visits to patients in extreme cases are

allocated by the HHC system. The HHC system pro-

vides remote medical care in speciﬁc cases, thereby

reducing patient visit costs and time.

Following discussions with carers and medics, we

have developed the following (formal) problem state-

ment to capture the essence of the problem: In this

problem, two factors determine the number of home

health carers to be assigned per day based on the pa-

tient’s service requirement and time window. The ob-

jective is to reduce the visitation time associated with

the experts serving the patients. It should be noted

that the assignment of experts takes place only if they

have the required skills to serve patients. In addition,

only a limited number of resources are available each

day. Therefore, based on the structure of the proposed

HHC, the following assumptions can be considered:

• Each patient has a speciﬁc service menu that must

be served during the day.

• Only one expert home carer must be assigned to

each patient.

• An expert would be assigned to a patient only if

the person has the required medical skill to serve

the patient.

• An expert is sent to a patient only if the threshold

severity level goes beyond the real-time severity

level.

• The number of experts available is ﬁxed and lim-

ited each day.

Table 1 provides an overview of the problem pa-

rameters: Lim

is based on time and signiﬁes the

travel time that has to be bounded due to the suppo-

sitions of the problem. Furthermore, INT

deﬁnes the

Table 1: Problem parameters and deﬁnitions.

Notations Deﬁnition

e = 1,.. . ,E Set of expert home caregivers

i, j,h = 1,... , P Set of patients

k = 1, . .. , K Set of all periods (days)

ϕ = 1, ... , j Set of all visits

Parameters Deﬁnition

TrT

i, j

Travel time visits of patients i and j

ViT

The time duration in which patient i must be visited

PT The penalty time

The earliest visit of patient i

The latest visit of patient i

The total number of experts

The skill of the expert caregiver e to visit patient i

Lim

Distance parameter to limit the travel time

max

Maximum available time for expert home caregivers

The real-time severity level of patient i

INT

≥ λ

,1 Otherwise, 0

V B A very big number (without dimension)

Variables Deﬁnition

e,i, j,k

1, if expert home caregiver e is assigned to patient j

after visiting patient i in period k

e,i

Starting time of in-home patient i for visitation

e,i,k

The arrival time of an expert home caregiver e

threshold intervention level of the patient by a num-

ber (derived from the IoMT system and wearable de-

vices in real-time). If its value goes above λ

, an ex-

pert must be sent to visit the patient. Considering 1,

the proposed objective function and constraints of the

HHC problem can be expressed as below:

MinZ =

∑

e∈E

∑

i∈P

∑

j∈P−i

∑

k∈K

e,i, j,k

∗ (TrT

i, j

+ViT

) +

∑

e∈E

∑

i∈P

e,i

(1)

Equation 1 deﬁnes the objective function, which

minimises visit time based on the patient’s time win-

dow. Expert home carers must adhere to the patient’s

schedule.

e, j,k

≤ LV

∀e ∈ E, j ∈ P,k ∈ K (2)

≤ AT

e, j,k

∀e ∈ E, j ∈ P,k ∈ K (3)

Constraints 2– 3 highlight that the unique time

window for a patient needs to be taken into consider-

ation while performing the allocation of HHC experts

to the respective patient.

∑

e∈E

∑

i∈P

∑

j∈P−i

∑

k∈K

e,i, j,k

= Ne

∀e ∈ E,i ∈ P,k ∈ K

(4)

∑

e∈E

∑

e,i, j,k

∗ SE

≥ 1 ∀ j ∈ P − i,k ∈ K (5)

Constraint 4 requires all skilled expert workers to

organise and comply with expert plan visits. Whilst

Constraint 5 ensures that all skilled home carers are

Real-Time IoMT-driven Optimisation for Large-Scale Home Health Care Planning

assigned based on their competence and the PSM.

e,i,k

+ViT

+ TrT

i, j



e,i, j,k

− 1



∗V B ≤ AT

e, j,k

∀e ∈ E,i ∈ P,k ∈ K

(6)

e, j,k

− AT

e,i,k

−ViT

≤ Lim



1 − A

e,i, j,k



∗V B

∀e ∈ E,i ∈ P,k ∈ K

(7)

e,i,k

+ViT

+ TrT

i,0

≤ DU

max

∀e ∈ E,i ∈ P,k ∈ K

(8)

Constraint 6 determines the time it takes an expe-

rienced home carer to reach a patient requiring medi-

cal service. It is necessary to divide expert home car-

ers by time gap to assign them to patient homes. Thus,

expert home carers must maintain a time between vis-

its. It must be noted that this is not a routing constraint

and it only divides experts using time; Constraint 7

accounts for this. Constraint 8 requires expert home

carers to work a certain number of hours each day.

∑

e∈E

∑

i∈ϕ

e,i, j,k

∑

e∈E

∑

j∈ϕ

e, j,h,k

∀k ∈ K,h ∈ ϕ (9)

∑

′

∈E

′

∑

i∈ϕ

′

,i, j,k

∑

′

∈E

∑

h∈P

′

, j,h,(k+1)

∀k ∈ K,i, j ∈ P

(10)

Here, the set ϕ = {0,1,... ,n + m} is deﬁned to

show the total number of visits n and visit breaks

from one home to another m. If we consider pa-

tients from the set {0,1,.. ., i, j, h,..., m}, it is impor-

tant for an expert home carer to ﬁnish his/her work

at a patient’s home before visiting another patient.

Hence, Constraint 9 is utilised to overcome this is-

sue. Constraint 10 is shaped to ensure the continuity

of the assigned home care to all the expert home care-

givers.Once an expert is assigned and served a patient,

it must continue the service to other patients if possi-

ble.

∑

i∈P

e,i,0,k

= 1 ∀e ∈ E, k ∈ K (11)

∑

J∈P

e,0, j,k

= 1 ∀e ∈ E, k ∈ K (12)

e,1

∑

i∈P

∑

j∈P

TrT

0,1

∗A

e,0,1,k

∗INT

∀i, j = 1 (13)

e,i, j,k

∈ {0, 1} ∀e ∈ E, ∀i, j ∈ P,k ∈ K (14)

e,i,k

≥ 0 ∀e ∈ E, ∀i ∈ P, k ∈ K (15)

Constraints 11– 12 ensure that experts must return

to the HHC centre after visiting their patients. Con-

straint 13 deﬁnes the start time of the plan. Finally,

Constraints 14– 15 indicate binary and non-negative

decision variables, respectively.

The following methodology addresses real-time

changes in the proposed HHC planning problem:

First, the model initialises by setting the values of

TrT

i, j

, ViT

, PT , EV

, LV

, Lim

, and DU

max

. In each

search, it sets i = P if INT

≥ λ

. The model is then

optimised based on λ

to achieve an efﬁcient assign-

ment. However, if λ

changes, the problem sets i = P

and e = E to their new values. Then the input value

of the model will be updated and solved.

4 EXPERIMENTAL SETUP

This section motivates and deﬁnes the experimental

setup pertaining to optimisation algorithms, their pa-

rameter settings, and test problems as used for the

subsequent experimental study.

4.1 Optimisation Strategies

To tackle the IoMT-based HHC planning problem

proposed in Section 3, we consider four different

algorithms: two established metaheuristics used as

a baseline, Simulated Annealing (SA) and Particle

Swarm Optimisation (PSO); a more recent method,

Co-evolutionary PSO (CPSO), used to understand if

we can achieve improved performance; ﬁnally, an ex-

act optimizer, CPLEX, will be used to understand the

applicability and limits of exact optimisation to the

problem.

We would expect the exact solver to do well on

small and medium-sized versions of the problem but

to be computationally intractable for larger problems,

providing a sweet spot for metaheuristics. The imple-

mentation of algorithms, test problems, and visualisa-

tions can be downloaded at xxx.

SA and PSO Algorithms.The complexity of prob-

lems in the HHC domain means that there is scope

for the application of metaheuristics (Liu et al., 2021;

Hiermann et al., 2015; Goodarzian et al., 2021).

We consider the application of two well-known and

widely used algorithms to solve problems of the type

considered here, SA and PSO (Kennedy and Eberhart,

1995). SA has shown to be a promising approach for

discrete mathematical problems (Yuan et al., 2009),

while PSO was originally proposed for continuous

problems but has been adapted to different types of

problems since then. In our case, each discrete vari-

able is represented by a binary string, which means

that our PSO algorithm searches over a binary space.

In solving the problem, these algorithms use the same

approach to create an initial solution. The results of

these two metaheuristics are then compared with the

The link will be made available upon acceptance of the

paper.

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

baseline using the GAMS CPLEX solver in terms of

the improved performance of the proposed HHC plan.

Penalization is used as the constraint-handling strat-

egy with the penalty term simply counting the number

of violated constraints; more advanced strategies are

part of future research.

CPSO Algorithm. CPSO (He and Wang, 2007) is

a multi-population version of classic PSO aimed at

tackling complex multi-modal problems more efﬁ-

ciently. This is addressed for the ﬁrst time in (He

and Wang, 2007). CPSO uses multiple populations of

particles, allowing the algorithm to explore the search

space more thoroughly and ﬁnd a better balance be-

tween exploitation and exploration. The chromosome

design is shown below:

According to Figure 1, a chromosome represents

a set of patients who must be served by an expert with

a corresponding service level. This will form a set of

patients (P) followed by experts (E), in which they

must be served according to their service menu (S).

To form this, a heuristic method based on the stair-

case method is applied using the north-west corner.

Based on this method, suppliers (experts) and cus-

tomers at demand points (patients) form a matrix in

which their demands must be met given their required

services (Holmberg and Ling, 1997). This method

guarantees the feasibility of the HHC plan and as-

signs each expert to a patient based on their daily

needs (Bazaraa et al., 2011). Therefore, multiple rows

are formed based on the total number of patients and

experts in the HHC, as shown in Figure 1. To simplify

services and differentiate them, services 1 through 3

are denoted by A,B, and C. Consequently, a corre-

sponding value of 0 and 1 is assigned to show whether

a patient needs a certain service or not (for example,

AB equals (1,1,0), showing that the patient requires

services one and two). Based on the north-west corner

method, experts are assigned to patients to fully meet

their demands. The north-west corner method works

as follows: A matrix is created in which rows respon-

sible for experts and columns are responsible for pa-

tients. each cell of the matrix represents the allocation

of experts to patients. The method begins with the

north-west corner of the matrix and allocates the units

as much as possible, then it moves to the next row, this

process is continues until the resources are exhaust in

each row and assignments are done. Given an hour to

complete each task, the assigned patients and their re-

quired time for treatment form the right-hand side of

the expert column. Finally, the assignment of each ex-

pert is shown. Once allocated (red brackets) using the

north-west corner, the required skills are assigned and

therefore deducted from the PSM. This process will

continue until every patient has an assigned expert to

visit.

Figure 1: Representation of chromosome and allocation of

experts using heuristic staircase method (P: Patients; E: Ex-

perts; PSM: Patient’s Service Menu (a tuple consisting of 0

and 1 digit, representing three services); EE: Expert’s Ex-

pertise, (eight patients, four experts, and three services)).

Table 2: Parameter setting for SA, PSO, and CPSO algo-

rithms.

Alg. Parameter Setting

SA Maximum iteration MaxIt 100

Sub iteration SubIt 50

Initial Temperature 15000

Rate of reduction 0.99

PSO & Population size N 100

CPSO Interia weight W 1

Weight Damping Ratio W damp 0.99

Accelaration coefﬁcient c

1.3

Accelaration coefﬁcient c

1.3

Internal swarm value (CPSO) w

0.22

External swarm value (CPSO) w

0.42

4.2 Test Problems

To better understand the complexity of the problem

and the performance of the solution methods, we

propose case studies (problem instances) of varying

problem sizes and parameter values, including small,

medium, and large problems; in practice, this could

translate to HHC services of varying size (eg due to

geographical differences) (AlayaCare, ). In addition,

the following setting in Table 2 is used for algorithm

parameters:

SA uses a reduction rate of 0.99. The reduction

rate signiﬁes the reduced value of the initial tempera-

ture (15000) in each iteration. In each iteration, a new

solution is found and if the new solution is inferior to

the best solution, then it will be retained as the best so-

lution discovered. Otherwise, exp(−δ/temperature)

is solved, where δ is the difference between the cur-

rent solution and the best solution. The parameters

values are derived from (Kirkpatrick et al., 1983)

as one of the best practices for this problem. For

the CPSO algorithm, the settings have been taken

from (Kou et al., 2009). It must be noted that, to

consider the same condition when evaluating the pro-

posed metaheuristics, the number of function evalua-

tions is set to 1000 as stopping criteria.

The values of the problem parameters can vary

within a range in practice; however, following (Alay-

Real-Time IoMT-driven Optimisation for Large-Scale Home Health Care Planning

aCare, ) we set the parameters as follows: TrT

i, j

= 25,

= 18, ViT

= 65, Lim

= 75, PT = 300, DU

max

45, EV

= 10, and λ

is veriﬁed by our IoMT. The ex-

perimental study presented in the next section will ini-

tially use these settings to evaluate the performance of

each metaheuristic used.

5 EXPERIMENTAL RESULTS

This section evaluates the proposed HHC network for

different problem sizes using various parameter val-

ues and settings. Table 3 displays the mean of the best

objective score (BOS), computational time, and the

standard deviation over 50 runs of the solution meth-

ods. For CPLEX we use the lower bound obtained by

using GAMS.

Table 3 Column 1 contains the problem instance’s

identiﬁer, in which the ﬁrst number is patients, the

second and third are the number of internal and ex-

ternal experts, and the fourth number is the number

of required services. Column 2 presents the lower

bounds for the problem instances that arise from solv-

ing the model using the CPLEX solver in GAMS.The

best results over 50 trials of each algorithm is taken.

The CPU time is in seconds, and the mean standard

deviation is the amount of variation between prob-

lem solutions. It is observed that CPLEX was able

to solve the problem with up to 45 patients, 15 in-

ternal and 8 external caregivers within the time limit

of 7200 seconds. No signiﬁcant improvement was

observed by increasing the time limit or employing

additional RAM and CPU (the initial computation is

performed on Windows OS 10, 16 Gigabyte RAM,

and 4 Gigabyte GPU). However, SA was able to solve

the problem faster, especially for larger problems.

PSO needed more CPU time and achieved a lower

BOS when compared to SA. However, in the case

of CPSO, the results are more promising. For prob-

lems in which 15 and 10 internal and external home

caregivers we employed to serve 35 and 45 patients,

CPSO showed better results compared to both SA and

PSO. Moreover, the mean CPU time to ﬁnd the best

solution and the standard deviation for CPSO is sig-

niﬁcantly shorter compared to the SA algorithm.

Figure 2 shows the variance of the BOS obtained

in 50 runs for the metaheuristics (CPLEX is determin-

istic). For small problems (Samples 1-4) (Figure (a)),

both the SA and CPSO algorithm work well in terms

of the optimal solution. Furthermore, PSO presented

a good solution and, with a slight difference, placed it-

self after SA and CPSO. For medium-sized problems

(Samples 5-10) (Figure (b)), the SA algorithm is sta-

tistically the best performing algorithm among meta-

(a)

(b)

(c)

Figure 2: Box plot of the different metaheuristics (a) small

(Samples 1-4), (b) medium (Samples 5-10), (c) large (Sam-

ples 11-16).

heuristics and in some samples close to the CPLEX

results. It is interesting to note that the CPSO algo-

rithm provides the second-best solution. However, for

large problems (Samples 11-16) (Figure (c)), CPSO is

able to obtain a good objective function solution with

a relatively lower standard deviation value compared

to SA and PSO. It might be noted that the CPSO takes

slightly higher computational time than SA and PSO,

due to the additional operators which CPSO employs

for obtaining a good solution in every test run. The

additional operators helps to obtain a better solution

in every test run, and hence the standard deviation is

higher for 50 trials compared to SA and PSO. In three

larger problem instances, CPLEX was unable to ob-

tain a result in the given 7200 seconds (as indicated

by ‘-’ in the table). Also, the convergence plot in

Figure 3 indicates that all algorithms have a similar

convergence behaviour with SA converging slightly

faster than others.

The current study uses three metaheuristics, which

are compared in a paired fashion, and performance

outputs do not follow a normal distribution. There-

fore, we can use the Friedman’s test (Marusteri and

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

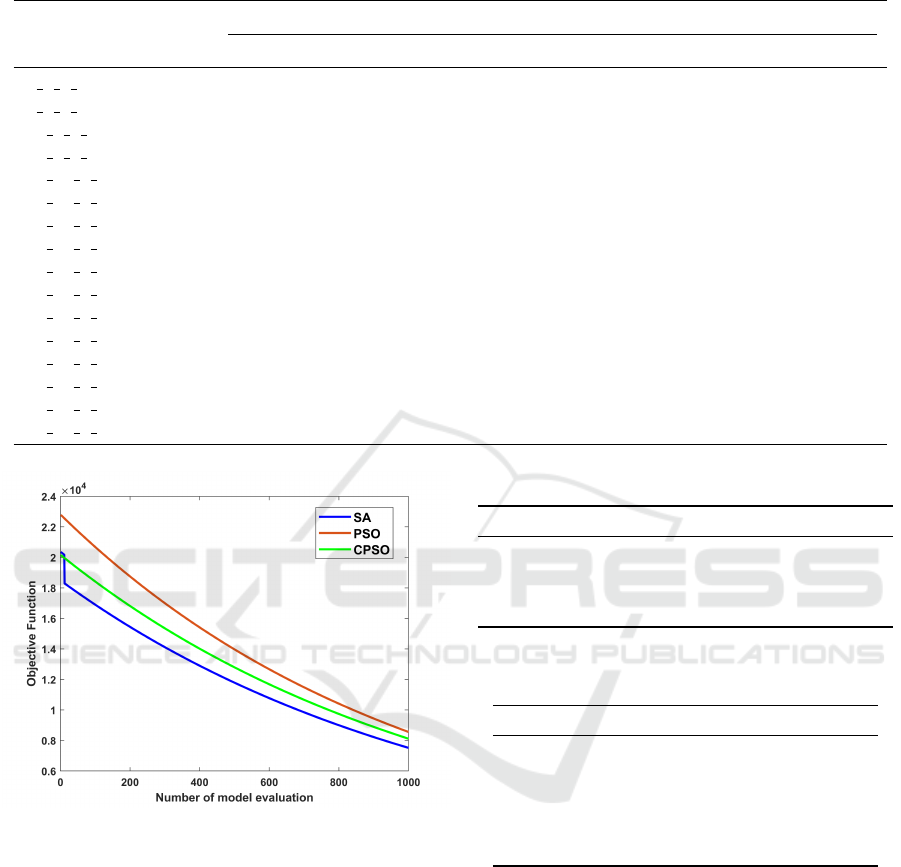
Table 3: Summary of the average result obtained from different algorithms for set

instance over 50 runs (Instance ID,

respectively: Number of patients, internal experts, external experts, required services; CPLEX: The lower bound from GAMS;

BOS: Best objective score; Std.dv: The standard deviation; Time: Computational time in seconds.)

Instance ID CPLEX SA PSO CPSO

BOS Std.dv Time BOS Std.dv Time BOS Std.dv Time

6 2 2 5 311.2 323.2 1.1 25.3 323.7 4.1 32.5 317.7 4.8 24.1

6 3 3 5 331.4 350.6 2.2 37.3 359.9 2.1 41.1 353.8 2.6 35.1

10 2 2 5 350.3 363.7 4.2 39.6 374.8 4.3 51.1 369.4 5.4 40.1

10 3 3 5 371.4 380.1 2.8 35.3 382.8 5.1 64.1 368.7 9.9 38.1

15 10 5 5 2264.8 2149.5 51.4 437.7 2252.9 26.4 512.6 2248.1 11.5 412.7

15 15 8 5 2353.9 2333.2 45.1 354.5 2395.1 27.4 408.9 2357.8 35.6 418.1

25 10 5 5 2430.8 2437.8 46.7 323.4 2467.4 47.5 503.2 2458.3 52 400.4

25 15 8 5 2562.6 2568.4 38.3 447.7 2588.9 26.9 506.7 2586.5 27.9 423.1

35 10 5 5 2704.2 2718.3 17.9 444.2 2759.8 40.8 478.8 2757.1 37.6 443.1

35 15 8 5 2956.5 2965.9 52.2 451.3 2990.4 51.9 504.3 2962.8 55.3 521.1

45 10 5 5 8099.1 6237.1 59.4 439.6 6280.1 87.9 401.5 6285.9 72.6 420.8

45 15 8 5 - 6132.3 101.6 455.6 6143.1 96.9 549.3 6142.8 105.4 513.5

65 10 5 5 10033.3 6830.7 34.7 424.5 6882.1 38.7 554.2 6876.6 32.5 418.4

65 15 8 5 - 6822.5 49.1 490.3 6891.1 58.8 497.5 6932.3 47.7 478.1

85 10 5 5 19092.8 7023.1 97.5 486.2 7307.1 47.7 507.3 7300.6 52.1 462.9

85 15 8 5 - 7838.4 50.3 438.5 7903.9 89.7 472.5 7907.2 44.9 487.1

Figure 3: Convergent level of the metaheuristic algorithms

based on objective function and number of model evaluation

for large (85-15-8-5 problem).

Bacarea, 2010) to determine whether there are statisti-

cally signiﬁcant differences among the performances

of these algorithms. Table 4 shows the result of the

Friedman’s test for the metaheuristics considering the

large problem (to evaluate the performance of the al-

gorithms in real-world-size problems), which had the

greatest impact on algorithm performance, consisting

of 85 patients, 15 internal and 8 external experts, with

a signiﬁcance level equal to 0.05. Since the p − value

is less than the signiﬁcance level, the result implies

that there is a signiﬁcant difference in the perfor-

mance of these algorithms.

Table 4: Friedman’s ANOVA for signiﬁcance level 0.05.

Source SS df MS Chi-sq Prob>Chi-sq

Columns 171.04 2 85.52 48.87 2.44526e-11

Interaction 98.96 48 2.0617

Error 167.5 75 2.2333

Total 437.5 149

Table 5: Sensitivity analysis on PSM (Before the IoMT

plan).

Scenario A (Before) Visit time

Before any changes (A-a) 734

Changes four hours before IoMT plan starts (A-b) 734

Changes three hours before IoMT plan starts (A-c) 760

Changes two hours before IoMT plan starts 760

Changes one hour before IoMT plan starts 760

Changes one hour without IoMT plan 789

5.1 A More in Depth Analysis of a

Single Case Study

The HHC centre service menu is shown in Table 6.

In addition, Expert’s skills can be summarised as fol-

lows: Expert 1 (S1,S2,S4), Expert 2: (S2,S4,S5), Ex-

pert 3: (S1,S2,S3,S4), Expert 4: (S2,S3,S4,S5), Ex-

pert 5: (S5), Expert 6: (S1-S5), Expert 7: (S2,S4,S5),

Expert 8: (S5), Expert 9: (S1,S2,S3,S4), Expert 10:

(S1-S5). S1-S5 deﬁnes their ability to perform a ser-

vice.

Table 6 assumes that patients (1–15) are chosen

from a group of patients with INT

≥ λ

. The real-life

Real-Time IoMT-driven Optimisation for Large-Scale Home Health Care Planning

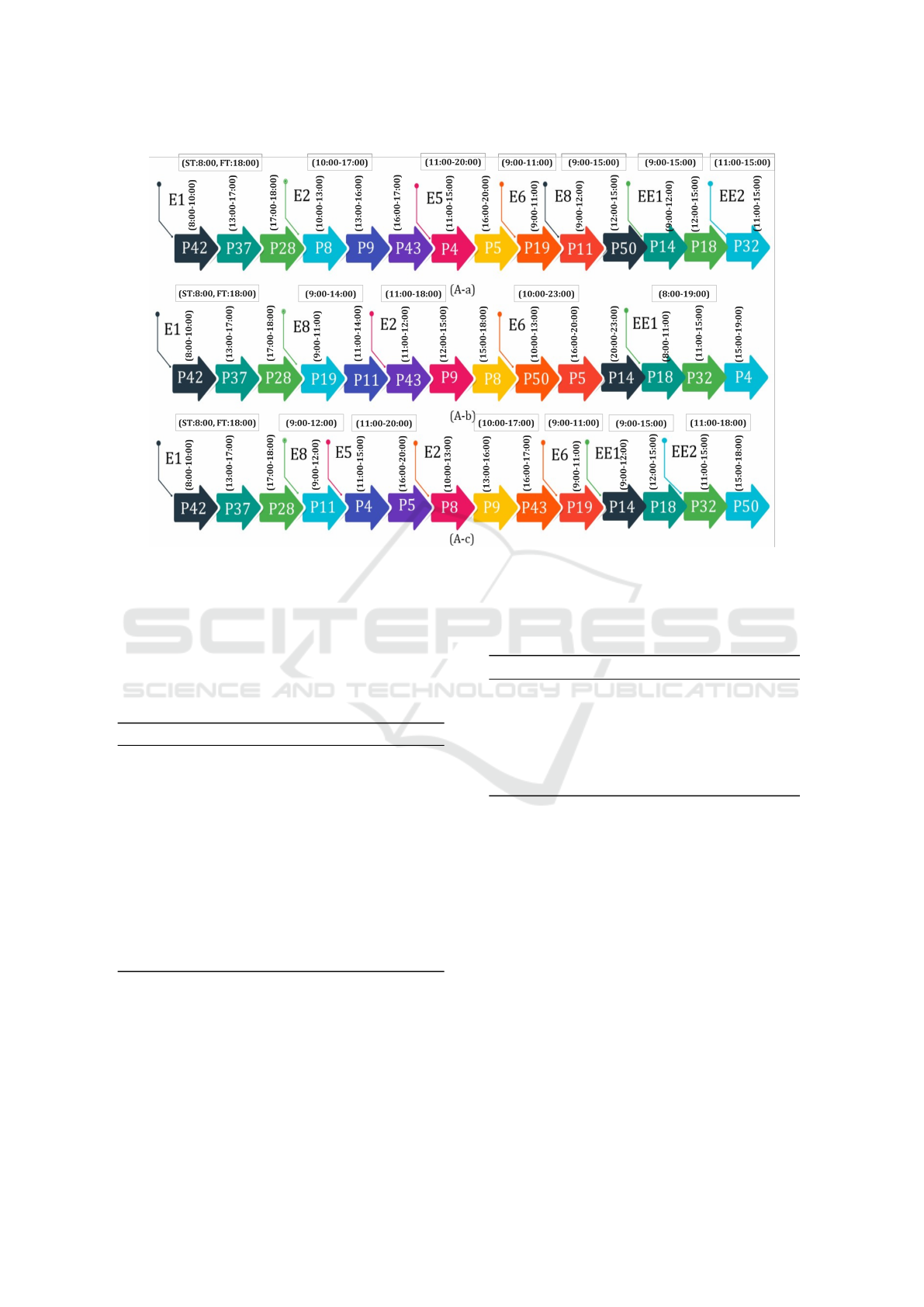
Figure 4: Patient’s visitation sequence and assignments of experts to patients in scenario A; A-a: Before any change; A-b:

Changes four hours before the start of IoMT plan; A-c: Changes three hours before the start of IoMT plan (E: Internal experts;

EE: External experts; P: Patients; ST: Start time; FT: Finish time).

experience of similar HHC companies (AlayaCare, )

combined with available resources motivated this ar-

ticle to use current settings.

Table 6: PSM; P:Patients; S: Services; λ: Current condition

of each patient.

ID λ S1 S2 S3 S4 S5 Time Window

P1 0.86 1 1 0 1 0 (11:00-16:00)

P2 0.95 0 0 1 1 0 (16:00-22:00)

P3 0.92 1 1 1 0 1 (10:00-15:00)

P4 0.99 1 0 1 1 0 (9:00-22:00)

P5 0.94 0 0 0 0 1 (9:00-17:00)

P6 0.78 0 0 1 0 0 (9:00-15:00)

P7 0.99 0 0 0 1 0 (15:00-19:00)

P8 0.78 0 1 1 0 0 (9:00-12:00)

P9 0.93 0 0 0 0 1 (13:00-16:00)

P10 0.82 0 0 1 1 0 (11:00-21:00)

P11 0.98 0 1 0 1 0 (13:00-20:00)

P12 0.95 1 0 0 1 0 (8:00-19:00)

P13 0.78 1 0 0 1 0 (11:00-20:00)

P14 0.76 0 0 1 1 0 (10:00-21:00)

P15 0.84 0 1 0 0 1 (13:00-22:00)

Using the large problem settings and CPSO algo-

rithm, the scheduling plan and optimal solutions are

presented in Table 7. It shows the expert’s alloca-

tion to the patients alongside their intervals. In ad-

dition, the visitation time of each expert for the entire

day (including start and ﬁnish times for each expert;

10 experts, 15 patients, and 5 services) is provided.

Table 7: The IoMT plan and assignment of experts for E:10,

P:15, and S:5.

Assignments Visitation Intervals

Expert 9 (11:00-16:00) P1 → P13

Expert 6 (10:00-18:00) P3 → P2

Expert 3 (9:00-12:00) P4

Expert 10 (9:00-18:00) P5 → P8 → P11 → P12 → P14

Expert 4 (9:00-13:00) P6 → P10

Expert 2 (15:00-20:00) P7 → P15

Expert 7 (13:00-14:00) P9

Given the skill level and time window of both patients

and experts, it is clear that expert 10 visits most of the

patients, while other experts are only eligible to visit

either one or two patients within the considered plan.

5.2 Sensitivity Analyses Based on IoMT

Real-Time Changes

The proposed IoMT plan considers three phases, in-

cluding service installation, diagnosis, and perform-

ing home care for patients. System installation is per-

formed using wireless wearable sensors and the con-

dition of the patients is monitored in real time. The

plan is dynamically responsive to changes and offers

a new plan rapidly when a change occurs. Here, sce-

nario A is deﬁned as follows: In scenario A, we con-

sider that a change has occurred in the PSM before the

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

plan starts. In this scenario, it is assumed that patient

4 (P4) has changed their service plan from (10110)

to (11110), which means that this patient changed his

services from services 1, 3, and 4 to services 1, 2, 3,

and 4 before the start of the IoMT plan.

Based on Figure 4 and Table 5, the sensitivity

analysis is conducted on the original plan, consider-

ing the change in PSM for patient 4. Changes are ob-

served four to one hour before the IoMT plan starts. In

addition, the original plan (A-a), changes four hours

before the start of the IoMT plan (A-b), changes three

hours before the start of the IoMT plan (A-c), changes

two hours before the start of the IoMT plan, and

changes one hour before the start of the IoMT plan

are identiﬁed in this table. Four hours before the plan

starts, the assignments are distributed with more ﬂex-

ibility and a reduction in total visitation time is ob-

served. Last but not least, the problem shows a 3.7

percent difference from the original IoMT plan, con-

sidering one hour before changes and no IoMT plan

is implemented ((788-760)/760=0.037).

By tightening this time to three and two hours,

fewer options remain to assign experts to care for pa-

tients; therefore, an increase in total visitation time

is predictable (see Figure 4 (A-b)). Here, the model

avoided ignoring patient 11 and tried to assign it to

an expert. Since the model assigned E8 to this patient

in Figure 4 (A-c), the patients previously assigned to

internal experts now must be assigned to external ex-

perts for visitation; therefore, an increase in total vis-

itation time has occurred here. One hour before the

start of the IoMT plan, the total visitation time re-

mains constant since there is no ﬂexibility to change

the sequence of assignments based on the patient’s

service menu and time window. It is observed from

this ﬁgure that even a slight change in PSM can ulti-

mately result in allocation of different experts or util-

isation of more external experts, which may result in

an increase in the total number of visitation hours in a

daily HHC plan. Another interesting point to mention

here is the CPSO’s role to respond (re-solve) the prob-

lem when having immediate changes. The algorithm

updates the input according to the current changes

and solves the new problem in the least possible time.

This shows the adaptability and responsiveness of the

proposed algorithm and the suggested IoMT plan to

any real-time changes.

6 CONCLUSIONS AND FUTURE

WORK

The proposed IoMT methodology controls, monitors

and records the real-time condition of patients. A

structured plan by IoMT is suggested to assign the

optimal number of experts to a set of available home

carers. Real-time monitoring of a patient’s condition

is a crucial tool for HHC managers to identify current

and real-time conditions and decide accordingly how

to react. If changes occur before the plan, the changes

can be made only three hours in advance. However,

applying instant changes is more challenging during

the ﬁnal hours, when many patients are scheduled to

be visited by experts.

The experiments carried out revealed that the

HHC planning problem is difﬁcult due to the large

number of variables and constraints. In addition, us-

ing multiple metaheuristics allowed us to evaluate the

efﬁciency of the methods under various conditions

and settings. SA and CPSO both proved to be ef-

ﬁcient when faced with medium-sized problems. In

terms of dealing with large problems, CPSO has been

statistically proven to be better. In terms of objective

function of the problem, both SA and CPSO have sim-

ilar results, with SA slightly working better; however,

by the means of the overall time spent to reach their

best solutions, CPSO performed better when CPLEX

was bound to 7200 seconds in large-size problems.

This result can be meaningful, especially when work-

ing with patients with more serious symptoms.

The current results of the problem enable man-

agers to make better decisions in severe conditions.

Considering real-time changes, it adds another layer

of credibility and reliability among the patients and

the HHC’s medical staff. This study sets the ground-

work for future research to evaluate optimal experts

for the IoMT plan. Future work will look at ﬁnd-

ing a more efﬁcient way to optimise the HHC prob-

lem. In addition, the mathematical formulation can

be extended to include external experts, risk-related

elements, and algorithm’s parameter adjustments.

REFERENCES

Ait Haddadene, S. R., Labadie, N., and Prodhon, C. (2019).

Bicriteria vehicle routing problem with preferences

and timing constraints in home health care services.

Algorithms, 12(8):152.

AlayaCare, H. H. C. A. personal communication.

Athelas (2003). Digital tools made for modern healthcare

organisations. http://https://www.athelas.com/.

Bahadori-Chinibelagh, S., Fathollahi-Fard, A. M., and

Hajiaghaei-Keshteli, M. (2022). Two constructive

algorithms to address a multi-depot home health-

care routing problem. IETE Journal of Research,

68(2):1108–1114.

Bazaraa, M. S., Jarvis, J. J., and Sherali, H. D. (2011). Lin-

Real-Time IoMT-driven Optimisation for Large-Scale Home Health Care Planning

ear programming and network ﬂows. John Wiley &

Sons.

De Vries, J. and Huijsman, R. (2011). Supply chain man-

agement in health services: an overview. Supply chain

management: An international journal, 16(3):159–

165.

Decerle, J., Grunder, O., El Hassani, A. H., and Barakat, O.

(2018). A memetic algorithm for a home health care

routing and scheduling problem. Operations research

for health care, 16:59–71.

Decerle, J., Grunder, O., El Hassani, A. H., and Barakat, O.

(2019a). A hybrid memetic-ant colony optimization

algorithm for the home health care problem with time

window, synchronization and working time balancing.

Swarm and Evolutionary Computation, 46:171–183.

Decerle, J., Grunder, O., El Hassani, A. H., and Barakat,

O. (2019b). A memetic algorithm for multi-objective

optimization of the home health care problem. Swarm

and evolutionary computation, 44:712–727.

Di Mascolo, M., Martinez, C., and Espinouse, M.-L.

(2021). Routing and scheduling in home health care:

A literature survey and bibliometric analysis. Com-

puters & Industrial Engineering, 158:107255.

Dwivedi, R., Mehrotra, D., and Chandra, S. (2021). Poten-

tial of internet of medical things (iomt) applications

in building a smart healthcare system: A systematic

review. Journal of oral biology and craniofacial re-

search.

Dwivedi, R., Mehrotra, D., and Chandra, S. (2022). Poten-

tial of internet of medical things (iomt) applications

in building a smart healthcare system: A systematic

review. Journal of oral biology and craniofacial re-

search, 12(2):302–318.

Emiliano, W., Telhada, J., and do Sameiro Carvalho, M.

(2017). Home health care logistics planning: a review

and framework. Procedia Manufacturing, 13:948–

955.

Erdem, M. and Koc¸, C¸ . (2019). Analysis of electric vehi-

cles in home health care routing problem. Journal of

Cleaner Production, 234:1471–1483.

Erdem, M. and Koc¸, C¸ . (2022). Home health care and dialy-

sis routing with electric vehicles and private and pub-

lic charging stations. Transportation Letters, pages

1–16.

Fathollahi-Fard, A. M., Hajiaghaei-Keshteli, M., and

Tavakkoli-Moghaddam, R. (2018). A bi-objective

green home health care routing problem. Journal of

Cleaner Production, 200:423–443.

Fathollahi-Fard, A. M., Hajiaghaei-Keshteli, M., Tavakkoli-

Moghaddam, R., and Smith, N. R. (2022). Bi-level

programming for home health care supply chain con-

sidering outsourcing. Journal of Industrial Informa-

tion Integration, 25:100246.

Fikar, C. and Hirsch, P. (2017). Home health care routing

and scheduling: A review. Computers & Operations

Research, 77:86–95.

Goodarzian, F., Abraham, A., and Fathollahi-Fard, A. M.

(2021). A biobjective home health care logistics con-

sidering the working time and route balancing: a

self-adaptive social engineering optimizer. Journal

of Computational Design and Engineering, 8(1):452–

474.

He, Q. and Wang, L. (2007). An effective co-evolutionary

particle swarm optimization for constrained engineer-

ing design problems. Engineering applications of ar-

tiﬁcial intelligence, 20(1):89–99.

Hiermann, G., Prandtstetter, M., Rendl, A., Puchinger, J.,

and Raidl, G. R. (2015). Metaheuristics for solv-

ing a multimodal home-healthcare scheduling prob-

lem. Central European Journal of Operations Re-

search, 23(1):89–113.

Holmberg, K. and Ling, J. (1997). A lagrangean heuristic

for the facility location problem with staircase costs.

European journal of operational research, 97(1):63–

74.

Kennedy, J. and Eberhart, R. (1995). Particle swarm opti-

mization. In Proceedings of ICNN’95-international

conference on neural networks, volume 4, pages

1942–1948. IEEE.

Khodabandeh, P., Kayvanfar, V., Raﬁee, M., and Werner,

F. (2021). A bi-objective home health care routing

and scheduling model with considering nurse down-

grading costs. International Journal of Environmental

Research and Public Health, 18(3):900.

Kirkpatrick, S., Gelatt Jr, C. D., and Vecchi, M. P.

(1983). Optimization by simulated annealing. science,

220(4598):671–680.

Kou, X., Liu, S., Zhang, J., and Zheng, W. (2009). Co-

evolutionary particle swarm optimization to solve

constrained optimization problems. Computers

& Mathematics with Applications, 57(11-12):1776–

1784.

Landers, S., Madigan, E., Leff, B., Rosati, R. J., Mc-

Cann, B. A., Hornbake, R., MacMillan, R., Jones, K.,

Bowles, K., Dowding, D., et al. (2016). The future of

home health care: a strategic framework for optimiz-

ing value. Home health care management & practice,

28(4):262–278.

Lin, C.-C., Hung, L.-P., Liu, W.-Y., and Tsai, M.-C.

(2018). Jointly rostering, routing, and rerostering for

home health care services: A harmony search ap-

proach with genetic, saturation, inheritance, and im-

migrant schemes. Computers & Industrial Engineer-

ing, 115:151–166.

Liu, W., Dridi, M., Fei, H., and El Hassani, A. H. (2021).

Hybrid metaheuristics for solving a home health care

routing and scheduling problem with time windows,

synchronized visits and lunch breaks. Expert Systems

with Applications, 183:115307.

Marusteri, M. and Bacarea, V. (2010). Comparing groups

for statistical differences: how to choose the right sta-

tistical test? Biochemia medica, 20(1):15–32.

McGillion, M., Ouellette, C., Good, A., Bird, M., Henry,

S., Clyne, W., Turner, A., Ritvo, P., Ritvo, S., Dvirnik,

N., et al. (2020). Postoperative remote automated

monitoring and virtual hospital-to-home care system

following cardiac and major vascular surgery: user

testing study. Journal of Medical Internet Research,

22(3):e15548.

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

Nikzad, E., Bashiri, M., and Abbasi, B. (2021). A

matheuristic algorithm for stochastic home health care

planning. European Journal of Operational Research,

288(3):753–774.

Polisena, J., Tran, K., Cimon, K., Hutton, B., McGill, S.,

Palmer, K., and Scott, R. E. (2010). Home telemoni-

toring for congestive heart failure: a systematic review

and meta-analysis. Journal of telemedicine and tele-

care, 16(2):68–76.

Reddy, K. N., Kumar, A., Choudhary, A., and Cheng, T. E.

(2022). Multi-period green reverse logistics network

design: An improved benders-decomposition-based

heuristic approach. European Journal of Operational

Research.

Restrepo, M. I., Rousseau, L.-M., and Vall

ee, J. (2020).

Home healthcare integrated stafﬁng and scheduling.

Omega, 95:102057.

Rodriguez-Verjan, C., Augusto, V., and Xie, X. (2018).

Home health-care network design: Location and con-

ﬁguration of home health-care centers. Operations re-

search for health care, 17:28–41.

Shi, Y., Boudouh, T., and Grunder, O. (2019). A robust op-

timization for a home health care routing and schedul-

ing problem with consideration of uncertain travel and

service times. Transportation Research Part E: Logis-

tics and Transportation Review, 128:52–95.

Statista (2020). Home health care demand.

Vervoort, D., Guetter, C. R., and Peters, A. W. (2021).

Blockchain, health disparities and global health. BMJ

Innov, 7(2):506–514.

Xiang, T., Li, Y., and Szeto, W. Y. (2023). The daily

routing and scheduling problem of home health care:

based on costs and participants’ preference satisfac-

tion. International Transactions in Operational Re-

search, 30(1):39–69.

Xiao, L., Dridi, M., and El Hassani, A. H. (2018). Math-

ematical model for the home health care scheduling

and routing problem with ﬂexible lunch break require-

ments. IFAC-PapersOnLine, 51(11):334–339.

Yuan, X., Nie, H., Su, A., Wang, L., and Yuan, Y. (2009).

An improved binary particle swarm optimization for

unit commitment problem. Expert Systems with ap-

plications, 36(4):8049–8055.

Real-Time IoMT-driven Optimisation for Large-Scale Home Health Care Planning