Cardiovascular Disease Prediction Based on Machine Learning

Zhangyu Fan

1a*

, Bohao Liu

and Xiao Yan

School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou, 350108, China

School of Computer Science and Technology, Harbin Engineering University, Harbin, 150000, China

School of Computer Science and Technology, Beijing Jiaotong University, Wei Hai, 264400, China

Keywords: Cardiovascular Diseases (CVD), Machine Learning, Decision Tree Model, Correlation.

Abstract: In recent years, the incidence and mortality rates of cardiovascular diseases (CVD) have been increasing

globally, showing characteristics of high prevalence, hospitalization, and mortality. Due to the multiple

factors that contribute to CVD and the high cost of treatment, it is difficult for people to prevent and detect it

in a timely manner. In this paper, the dataset of CVD from Kaggle is utilized to analyze and compare the

factors that contribute to CVD using correlation analysis. After feature selection, six machine learning models,

including regression models, decision tree models, random forest models, gradient boosting decision tree

models, XGBoost models, and deep neural network models, are compared to find the model with the highest

comprehensive efficiency in terms of accuracy, precision, recall, and other aspects as the prediction model.

The results show that among various influencing factors, age, creatine phosphokinase levels, and troponin

levels have a significant impact on CVD, and the decision tree model performs the best in CVD prediction.

1 INTRODUCTION

Cardiovascular diseases (CVD) refer to diseases that

affect the heart, blood vessels, and other organs such

as the kidneys, eyes, and brain. CVD includes various

conditions (Swathy and Saruladha, 2022). According

to literature (Roth GA, 2019), the incidence and

mortality rates of CVD have been continuously

increasing globally. From 1990 to 2019, the number

of people affected by CVD has risen from 271 million

to 523 million, while the number of deaths has

increased from 12.1 million to 18.6 million,

accounting for one-third of the global total deaths.

The estimated cost of CVD treatment is expected to

rise from 863 billion US dollars in 2010 to 1,044

billion US dollars in 2030 (Mela A, 2020). Due to the

high prevalence, hospitalization rate, disability rate,

and mortality rate of CVD, early detection is of great

significance in reducing disability and mortality.

Research shows that the total cost (direct and indirect)

of cardiovascular diseases ranged from 34.9 billion

zlotys (8.2 billion euros) to over 40.9 billion zlotys

(9.6 billion euros) between 2015 and 2017 (Mela A,

https://orcid.org/0009-0009-3883-1903

https://orcid.org/0009-0008-4448-6571

https://orcid.org/0009-0001-1406-4158

2020). The exact causes of cardiovascular diseases

are still not clear, but the probability of developing

CVD involves multiple factors, with prominent

factors being high blood pressure, high cholesterol,

diabetes, age, family history, etc. (Swathy and

Saruladha, 2022). Analyzing the impact of these

factors on cardiovascular diseases through data

analysis is crucial in providing preventive measures

and timely detection for treatment (Venkatesh, 2024).

Machine learning, as a data exploration method,

can uncover hidden relationships between various

factors that are difficult for humans to observe and

effectively intervene in cardiovascular diseases

(Manikandan, 2024). In this study, we utilize an

existing dataset from Kaggle to conduct a deep-level

analysis of the data and explore the influence of

different variables through correlation analysis. After

feature selection, we compare six machine learning

(ML) models, including regression models, decision

tree models, random forest models, gradient boosting

decision tree models, XGBoost models, and DNN.

Through iterative learning, we aim to improve

accuracy and precision, and find the most suitable

404

Fan, Z., Liu, B. and Yan, X.

Cardiovascular Disease Prediction Based on Machine Learning.

DOI: 10.5220/0012939000004508

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Engineering Management, Information Technology and Intelligence (EMITI 2024), pages 404-411

ISBN: 978-989-758-713-9

machine learning model for predicting cardiovascular

diseases, thus enhancing the prediction rate of CVD.

2 METHOD

In this study, the dataset underwent initial

preprocessing. Subsequently, various machine

learning models, including regression models,

decision tree models, random forest models (RF),

gradient boosting decision tree models (GBDT),

XGBoost models, and deep neural network models

(DNN), were constructed and trained to yield

corresponding results for subsequent analysis.

2.1 Data Preprocessing

Before constructing and training the cardiovascular

disease prediction model, data preprocessing is

essential (Pavithra et al., 2023). Since the utilized

dataset lacks missing values and qualitative attributes,

there is no need for a data cleaning procedure.

However, considering the relevance to the labels used

for prediction, feature selection is performed using

the correlation coefficient method.

In the construction of the DNN, the impact of the

dataset's scale on the model's performance cannot be

ignored. Therefore, Min-Max scaling is introduced

here to transform the dataset. This tool scales each

feature independently to a specified range, typically

between 0 and 1, using the following formula:

x_new = (x - x_min) / (x_max - x_min) (1)

Apart from data scaling, the original dataset is

commonly divided into a training set (70%) and a test

set (30%).

2.2 Model Selection and Construction

In this study, we opt to implement several ensemble

learning models for regression tasks to predict

cardiovascular diseases. Leveraging the advantages

of combining multiple machine learning algorithms,

ensemble learning models can achieve greater

predictive performance than using any individual

algorithm alone. Ensembles are composed of

numerous individual learners termed base learners,

which are typically created by fundamental learning

algorithms such as decision trees and neural

networks. Based on the differences in the methods for

generating base learners, current ensemble learning

models can be broadly categorized into two types:

Boosting and Bagging. Boosting sequentially

generates individual learners with strong correlations,

while Bagging, the method adopted by random

forests, independently generates individual learners

in parallel. In this paper, we select XGBoost, GBDT,

and RF as typical ensemble learning models.

To compare and further analyze model

performance, this paper also constructs several

classical machine learning models. Representing

traditional machine learning models, linear regression

and decision trees are chosen as benchmark models.

Additionally, a DNN is established for predicting

cardiovascular-related diseases.

2.2.1 Linear Regression

For a given dataset, the objective of linear regression

is to fit a linear model where the coefficients

minimize the sum of squared residuals between the

actual values and the predicted values.





𝑥



, 𝑦







𝑥



, 𝑦





,…,



𝑥



, 𝑦







𝑥





𝑥



, 𝑥



,…,𝑥







, 𝑦



∈𝑅𝑤 =



𝑤



, 𝑤



,…,𝑤





(2)

Mathematically, this problem can be formalized as:

min



∥𝑋𝑤−𝑦∥



(3)

𝑋=

⎝

⎛

𝒙





𝒙





⋮⋮

𝒙





⎠

⎞

, 𝑦

𝑦



𝑦



⋮

𝑦



 (4)

2.2.2 Decision Tree

Decision trees make decisions based on a tree-like

structure, starting from the root node and branching

along partition attributes until reaching a leaf node.

As a non-parametric supervised technique, decision

trees are widely applied in supervised machine

learning (Contractor, 2023). In this study, the

partition attribute chosen is the CART Gini

coefficient.

CART considers the problem from a statistical

modeling perspective. Unlike information theory,

which measures purity with information entropy,

statistical modeling requires sampling. If the results

of two samples are the same, they are considered

"pure." The following formula reflects the probability

of randomly drawing two examples with inconsistent

categories from the data set D. If p





equals p





, the

probabilities of the two examples are consistent, and

Gini(D) (with different probabilities) is smaller,

indicating a purer dataset:

Gini (𝐷)=1−

∑

||



𝑝





(5)

Cardiovascular Disease Prediction Based on Machine Learning

405

Similarly, with many nodes, each node has

different weights:

𝐺𝑖𝑛𝑖



𝑛𝑑𝑒𝑥(𝐷, 𝑎)=

∑

||



∣

∣

||

𝐺𝑖𝑛𝑖

(

𝐷



)

(6)

Select the attribute from the candidate set that

minimizes the Gini coefficient after partitioning.

2.2.3 RF

RF is an advanced ensemble learning model and an

extension of Bagging, running by generating a large

number of decision trees during training. The RF

algorithm introduces additional randomness by

searching for the maximum attribute from a random

subset of features during the node-splitting process.

When it comes to predicting for regression tasks, RF

takes the average of the predictions from all

individual decision trees.

One significant advantage of Random Forest is its

capability to estimate the relative importance of each

feature. Technically, the importance of a variable

used for prediction is calculated as the sum of the

weighted impurity reductions for all nodes t used in

the forest, averaged over all trees (for) in the forest:

𝐼𝑚𝑝 𝑋



=





∑





∑

∈



𝟏

(

𝑗



= 𝑗

)



𝑝(𝑡)𝛥𝑖

(

𝑠



, 𝑡

)



(7)

where 𝑝(𝑡) is the proportion of samples reaching

node 𝑡, 𝑗



is the identifier for the variable used to

split node 𝑗



, and Δ𝑖

(

𝑠



, 𝑡

)

is the weighted impurity

reduction.

2.2.4 XGB and GBDT

XGB stands for "eXtreme Gradient Boosting," and it

is an scalable distributed machine learning system

based on GBDT. While Random Forest is an

extension of Bagging, Gradient Boosting is an

extension of Boosting, combining weak models to

generate an overall powerful model. The GBDT

model trains a collection of decision trees iteratively.

In each iteration, it fits the residual of the previous

model to the subsequent model, and the final

prediction is the weighted sum of predictions from all

trees. XGBoost was developed to enhance the

performance and computational speed of machine

learning models. It is a highly accurate and scalable

implementation of GBDT, gaining significant

popularity.

Given the Heart Disease Classification Dataset,

where tree ensemble methods use an additive function

to predict results:

𝐷= (𝑥



, 𝑦



), (𝑥



, 𝑦



), ⋯,(𝑥



, 𝑦



), 𝑥



(𝑥



, 𝑥



, ⋯, 𝑥



)



, 𝑦



∈𝑅 (8)

𝑦



= 𝜑(𝑥



∑

𝑓



(𝑥



)





, 𝑓



∈𝐹 (9)

where 𝐹 is the regression tree space.

The regularization objective function for the

XGBoost model is:

𝐿(𝜑)=

∑

𝑙(𝑦



, 𝑦



)





∑

𝛺(𝑓



)



(10)

2.2.5 DNN

DNN is a typical deep learning model consisting of

multiple layers of neurons. Neural networks are

composed of an input layer, one or more hidden

layers, and an output layer. The input layer receives

data, the hidden layers transform the data, and the

output layer is responsible for generating predictions

(Javed, 2022). In this experiment, a DNN with two

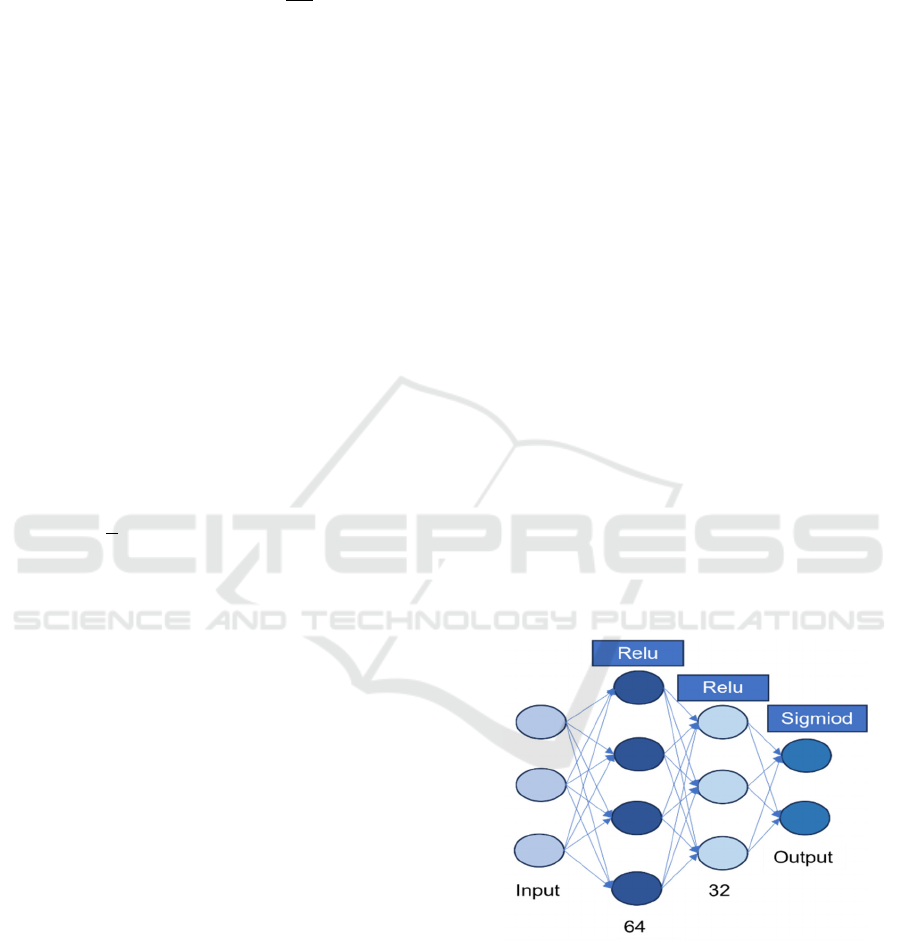
hidden layers is constructed, as shown in Figure 1.

For regression, the output layer in the neural network

has only one neuron.

Each neuron in the network receives input signals

from the neurons in the previous layer through

weighted connections. It then compares the weighted

sum of the received signals with a threshold. The

output signal is generated using an activation

function. Utilizing the error BP algorithm, which

adjusts weights to minimize prediction errors, the

network is trained (Jain, 2022).

Figure 1: Deep neural

network

structure diagram

(Photo/Picture credit :Original).

In the hidden layers, the activation function

utilized is the Rectified Linear Unit (ReLU) function.

ReLU (𝑥)=

𝑥𝑥0

0 𝑥0

= 𝑚𝑎𝑥(0, 𝑥).

(11)

EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence

406

The ReLU function applies element-wise non-

linear transformations to the input, enhancing the

neural network's non-linear features and aiding in

better feature learning.

2.3 Evaluation Metrics

The metrics used for model evaluation are AUC,

accuracy, recall, precision, and F1-score.

2.3.1 AUC (Area Under the Curve)

AUC is a metric used to evaluate model performance

in binary classification problems, especially in cases

of sample imbalance. A higher AUC, closer to 1,

indicates better model performance.

2.3.2 Accuracy

Accuracy measures the proportion of correctly

predicted samples out of the total number of samples.

The accuracy calculation formula is:

Accuracy =

Number of Correct Predictions

Total Number of Predictions

(12)

2.3.3 Precision1 (Precision for the Positive

Class)

Precision1 represents the proportion of true positive

predictions among all samples predicted as positive

(class 1). The formula for precision1 is:

Precision1 =

True Positives1

True Positives1+False Positives1

(13)

Where True Positives1 is the number of samples

correctly predicted as positive, and False Positives1

is the number of negative samples incorrectly

predicted as positive.

2.3.4 Recall1 (Recall for the Positive Class)

Recall1 indicates the proportion of true positive

predictions among all actual positive samples. The

formula for recall1 is:

Recall1 =

True Positives1

True Positives1+False Negatives1

(14)

Where True Positives1 is the number of samples

correctly predicted as positive, and False Negatives1

is the number of positive samples incorrectly

predicted as negative.

2.3.5 F1-Score

F1-Score is a metric that combines precision and

recall, commonly used for evaluating model

performance in binary classification problems. The

F1-Score is the harmonic mean of precision and

recall.

The F1-Score for the positive and negative classes

is calculated as follows:

𝑓1 −𝑠𝑐𝑜𝑟𝑒 1=

×  × 

Precision 1+ Recall1

(15)

𝑓0 −𝑠𝑐𝑜𝑟𝑒 0=

×  × 

Precision 0+ Recall0

(16)

3 EXPERIMENTAL SETUP AND

RESULTS

3.1 Dataset Overview

This article utilized the Heart Disease Classification

Dataset sourced from Kaggle (Contractor, 2023). The

dataset consists of 1319 samples with nine fields,

where 8 fields are used for input and 1 field is used

for output (As shown in Table 1).

Table 1: Description of

Attributes in the Dataset.

Attributes Description

age The age of the subjects

ende

The

ende

of the sub

ects

impluse

The heart rate of the subjects

pressurehight

The systolic blood pressure of the

sub

ects

pressurelow

The diastolic blood pressure of the

sub

ects

glucose

The blood glucose level of the

subjects

The creatine kinase of the sub

ects

tro

onin The tro

onin of the sub

ects

class

Whether the subjects suffer from

heart disease

Cardiovascular Disease Prediction Based on Machine Learning

407

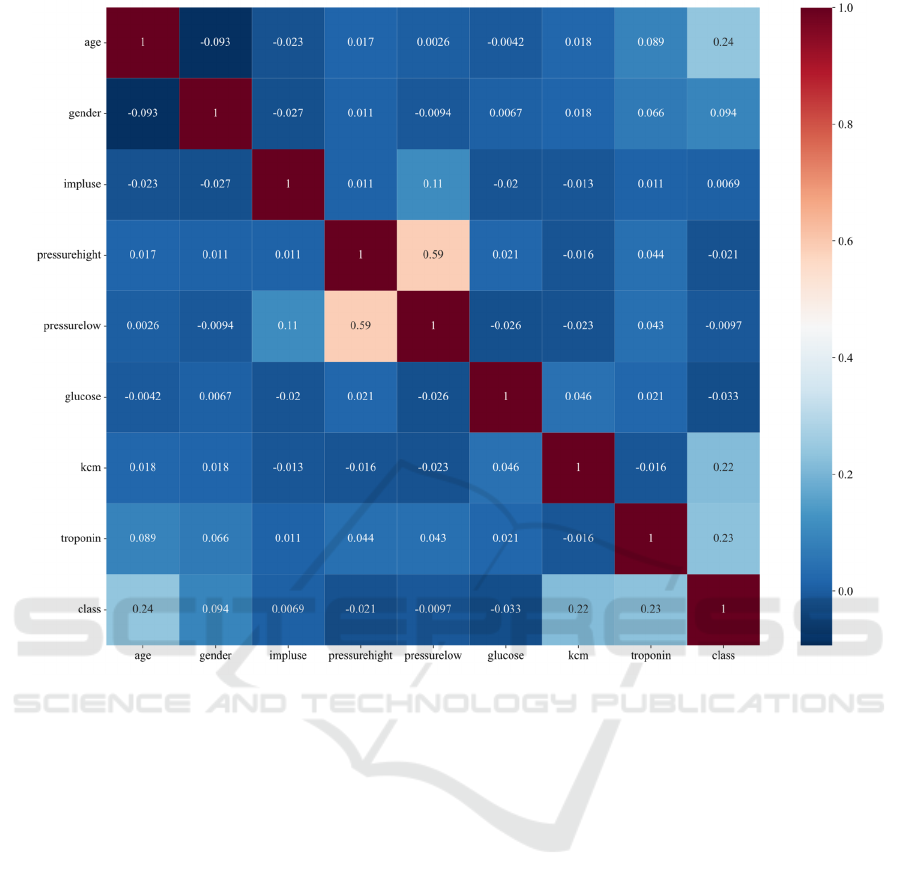
Figure 2: Correlation heatmap (Photo/Picture credit: Original) .

We also utilized a heatmap to delve deeper into

the correlations among all attributes, hoping to

identify factors related to the occurrence of heart

disease (Figure 2). According to the heatmap, no

significant linear relationships were found among the

features. Upon observation, it was noted that the

factors of age, kcm, and troponin exhibited relatively

high correlations, all exceeding 0.2.

3.2 Experimental Settings

In this study, all models were implemented in a

Python 3.7.11 environment, including the Pandas,

Scikit-Learn, TensorFlow, and XGBoost packages.

The hardware configuration comprised an AMD

Ryzen 9 6900HX with Radeon Graphics (16 CPUs),

3.3GHz.

3.3 Model Evaluation

In all models, as predicted, the LR model performed

the worst in all aspects due to the lack of clear linear

relationships in the model.DT and RF both

demonstrated satisfactory results in all aspects, with

DT performing the best among all evaluation metrics.

Under the f1-score0 metric, DT outperformed RF by

0.95%, possibly due to the lack of clear linear

relationships in the dataset. GBDT and XGBoost

exhibited insufficient accuracy compared to other

models, possibly due to large deviations between

residual estimates and actual values. Additionally, the

DNN algorithm also demonstrated higher accuracy

but took the longest time to execute (Figure 3 and

Figure 4).

EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence

408

Figure 3: The accuracy and Area Under the Curve (AUC) metrics under different methods (Photo/Picture

credit :Original).

Figure 4: The f1-score0 and f1-score1 metrics under different

methods (Photo/Picture credit :Original).

Figure 5: Pearson correlation

representation

(Photo/Picture credit: Original).

3.4 Exploration of Feature Importance

Common correlation coefficients in statistics include

Spearman correlation, Pearson correlation, and rank

correlation. Pearson correlation is suitable for

analysing the correlation of continuous variables. If

two variables are positively correlated, the closer they

are to a positive correlation, the closer the magnitude

of their changes is to a linear value approaching 1.

Conversely, if two variables are negatively correlated,

the closer the magnitude of their changes is to -1, the

closer the Pearson correlation coefficient is to -1. The

formula for calculating the Pearson correlation

coefficient is as follows:

𝛾=

∑

(





)(







)



∑

(





)



∑

(







)



(17)

The Pearson correlation coefficient, initially designed

by statistician Karl Pearson, is a statistical indicator

that measures the degree of linear dependence

between variables, ranging from -1 to +1, reflecting

the direction and extent of the trend in changes

between two variables (Javed, 2022,Wang, 2024 ).

According to Figure 5, the three most important

features are age, kcm, and troponinn. The following

content will explain this result further. From Figure 6,

it can be observed that the incidence of cardiovascular

disease is relatively low between ages 0 and 40,

increases gradually between ages 40 and 80, and

peaks around age 60

As shown in Figure 7, when kcm

Cardiovascular Disease Prediction Based on Machine Learning

409

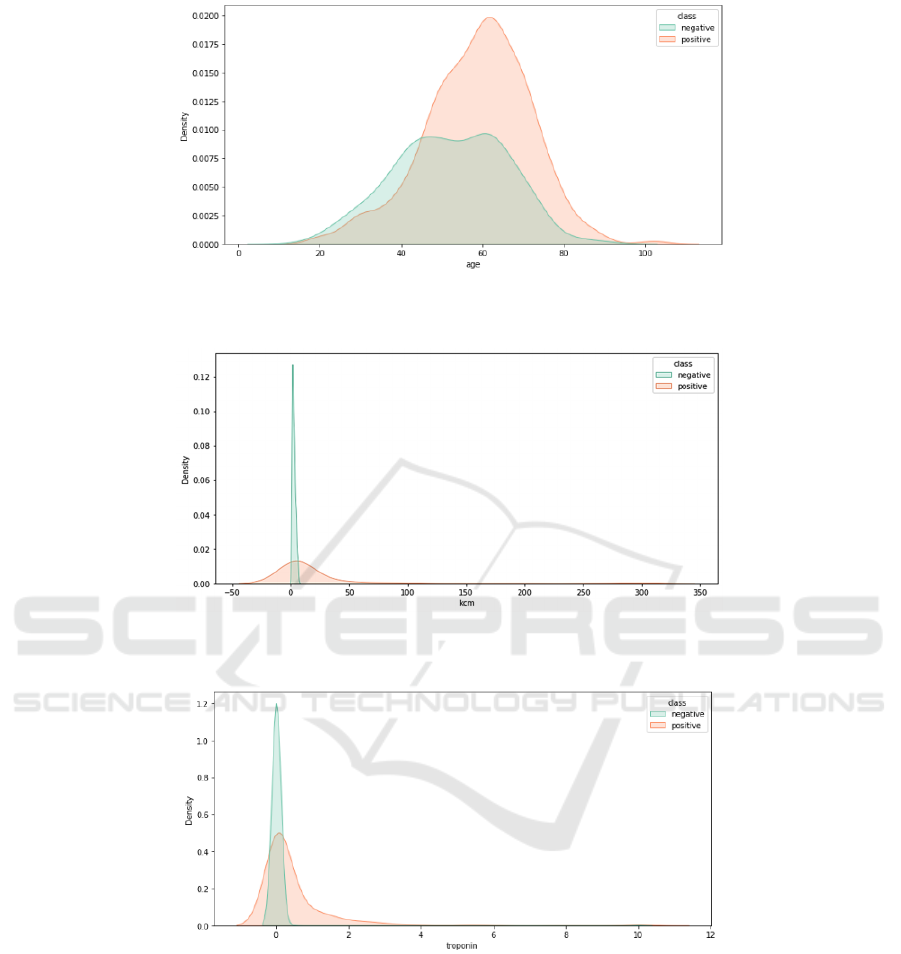
Figure 6: Comparison of cardiovascular disease incidence rates across different age groups

(Photo/Picture credit:

Original)

Figure 7: Impact of CK-MB (KCM) values on the incidence of cardiovascular disease (Photo/Picture credit:

Original).

Figure 8: Impact of troponin levels on the incidence of cardiovascular disease age (Photo/Picture credit:Original).

values are between 0 and 10, the incidence of

cardiovascular disease is relatively low (Rahadian,

2023). Based on Figure 8, when levels of troponin are

low (less than 0.25), the incidence of cardiovascular

disease is relatively low.

4 CONCLUSIONS

In summary, this study utilizes machine learning and

deep neural network approaches to identify various

factors related to the onset of cardiovascular diseases

for prevention and prediction purposes. The models

used in the experiments include Linear Regression,

Decision Tree, Random Forest, Gradient Boosting

Decision Tree, XGBoost, and Deep Neural Networks.

After comparing the precision, accuracy, and recall

rates of these models, the Decision Tree machine

learning method performed the best in all aspects,

with accuracy of 0.9924, AUC of 0.9953, f1-score0 of

EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence

410

0.9902, and f1-score1 of 0.9938. Therefore, the

Decision Tree model is chosen for more accurate

prediction of cardiovascular disease onset. Through

correlation analysis, it was found that age, kcm, and

troponin are highly correlated with the onset of heart

disease. Individuals over 40 years old, with kcm over

10, and troponin levels over 0.25 are at a higher risk

of developing the disease. These individuals should

undergo further examinations for preventative

measures against cardiovascular diseases.

Future research could incorporate additional

factors for analysis, such as smoking history, Insulin

resistance (IR)，family history of heart disease, and

integrate electrocardiograms and other imaging for

further analysis. Utilizing larger datasets for testing

could enhance prediction accuracy. Collaboration

with medical institutions to obtain more realistic

clinical data could identify the most significant

influencing factors, aiding in the timely detection of

cardiovascular disease precursors, prompt medical

intervention, and reducing the disability and mortality

rates associated with cardiovascular diseases.

AUTHORS CONTRIBUTION

All the authors contributed equally and their names

were listed in alphabetical order.

REFERENCES

Contractor D., 2023. Heart Disease Classification Dataset.

Kaggle https://www.kaggle.com/datasets/bharath011

/heart-disease-classification-dataset

Jain, A., Kumar, A., Susan, S. (2022). Evaluating Deep

Neural Network Ensembles by Majority Voting Cum

Meta-Learning Scheme. In: Reddy, V.S., Prasad, V.K.,

Wang, J., Reddy, K.T.V. (eds) Soft Computing and

Signal Processing. Advances in Intelligent Systems and

Computing, vol 1340. Springer, Singapore.

https://doi.org/10.1007/978-981-16-1249-7_4

Javed A, Muhammad A, Md Tabrez Nafis, M. Afshar Alam,

2022. A systematic review on machine learning

approaches for cardiovascular disease prediction using

medical big data, Medical Engineering & Physics,

Volume 105.

Kosmas CE, Bousvarou MD, Kostara CE,

Papakonstantinou EJ, Salamou E, Guzman E. Insulin

resistance and cardiovascular disease. Journal of

International Medical Research. 2023;51(3).

doi:10.1177/03000605231164548

Manikandan G., Pragadeesh B., Manojkumar V.,

Karthikeyan A.L., Manikandan R., Gandomi Amir H.,

Classification models combined with Boruta feature

selection for heart disease prediction, Informatics in

Medicine Unlocked, Volume 44, 2024, 101442,

Mela A, Rdzanek E, Poniatowski Ł A, et al. 2020.

Economic costs of cardiovascular diseases in Poland

estimates for 2015- 2017 years. Frontiers in

Pharmacology, 11:1231.

Pavithra V, Jayalakshmi V, 2023, Hybrid feature selection

technique for prediction of cardiovascular diseases,

Materials Today: Proceedings, Volume 81, 336-340.

Rahadian H., Bandong S., Widyotriatmo A., Joelianto E.,

2023. Image encoding selection based on Pearson

correlation coefficient for time series anomaly

detection, Alexandria Engineering Journal, Volume 82,

304-322,

Roth GA, Mensah GA, Johnson CO, et al., 2019. Global

burden of cardiovascular diseases and risk factors,

1990-2019. Journal of the American College of

Cardiology, 76(25):2982-3021.

Swathy M., Saruladha K., 2022, A comparative study of

classification and prediction of Cardio-Vascular

Diseases (CVD) using Machine Learning and Deep

Learning techniques, ICT Express, 8, 1, 109-116.

Venkatesh C., Prasad B.V. V. S., Khan M., Chinna Babu J.,

Venkata Dasu M., 2024. An automatic diagnostic model

for the detection and classification of cardiovascular

diseases based on swarm intelligence technique,

Heliyon, 10 (3).

Wang S, Shui F, Stratford T. , 2024. Modelling nonlinear

shear creep behaviour of a structural adhesive using

deep neural networks (DNN), Construction and

Building Materials, Volume 414.

Cardiovascular Disease Prediction Based on Machine Learning

411