Deep Learning and Multi-Objective Evolutionary Fuzzy Classifiers:
A Comparative Analysis for Brain Tumor Classification in MRI Images
Giustino Claudio Miglionico
1
, Pietro Ducange
1
, Francesco Marcelloni
1
and Witold Pedrycz
2
1
Department of Information Engineering, University of Pisa, Largo Lucio Lazzarino 1, 56122 Pisa, Italy
2
Department of Electrical and Computer Engineering, University of Alberta, Edmonton, Canada
Keywords:
Brain Tumor Classification, Explainable Artificial Intelligence, Deep Learning Learning, Fuzzy Rule-Based
Classifiers, Multi-Objective Fuzzy Systems.
Abstract:
This paper presents a comparative analysis of Deep Learning models and Fuzzy Rule-Based Classifiers
(FBRCs) for Brain Tumor Classification from MRI images. The study considers a publicly available dataset
with three types of brain tumors and evaluates the models based on their accuracy and complexity. The
study involves VGG16, a convolutional network known for its high accuracy, and FBRCs generated via a
multi-objective evolutionary learning scheme based on the PAES-RCS algorithm. Results show that VGG16
achieves the highest classification performance but suffers from overfitting and lacks interpretability, making it
less suitable for clinical applications. In contrast, FBRCs, offer a good balance between accuracy and explain-
ability. Thanks to their straightforward structure, FRBCs provide reliable predictions with comprehensible
linguistic rules, essential for medical decision-making.
1 INTRODUCTION
The use of Machine Learning (ML) and Artificial
Intelligence (AI) for Magnetic Resonance Imaging
(MRI) scan analysis is revolutionizing the tools sup-
porting physicians for brain cancer detection, diagno-
sis, and prognosis. This disease affects approximately
24,000 people annually in the U.S.
1
and 22,000 peo-
ple in Europe
2
. With around 18,000 and 17,000
deaths per year in the U.S. and in Europe, respec-
tively, these advanced diagnostic tools are crucial for
improving accuracy and timeliness in patient treat-
ment (Khalighi et al., 2024).
The first generation of methods for automatic
medical image analysis was based on classical ML
models. Currently, Deep Learning (DL) models have
become the state-of-the-art approach because of their
ability to automatically learn complex features from
raw image data (Zhou et al., 2023). Convolutional
neural networks (CNNs), in particular, have shown re-
markable performance in accurately classifying brain
tumor images, often surpassing traditional ML meth-
ods (Al-Zoghby et al., 2023). However, despite their
high accuracy, DL models are often criticized for be-
ing “black boxes” with limited transparency, in a field
1
https://seer.cancer.gov/statfacts/html/brain.html
2
https://ecis.jrc.ec.europa.eu
where the decision-making process is as important as
the accuracy of the prediction (Hulsen, 2023). As a
result, proposals in the specialized literature are pre-
sented to make medical decision-making question-
able, understandable, and explainable to the different
stakeholders. As discussed in (Wang et al., 2024), the
transparency and explainability requirements are fun-
damental due to the critical and high-risk nature of
AI-based medical imaging applications.
To address the explainability requirements, post-
hoc techniques have been developed to provide in-
sights into the predictions made by DL models
(Van der Velden et al., 2022). Methods such as
saliency maps , Grad-CAM, and SHAP are commonly
used to highlight the regions of an image that most
influence the model’s decision. However, post-hoc
explanations are often approximations that may not
fully capture the model’s reasoning process, and they
can be computationally intensive, adding complexity
to the analysis pipeline.
Alternatively, tools such as radiomics (Saidak
et al., 2024), that extracts quantitative features from
medical images, can be used in combination with
interpretable by-design classifiers, such as decision
trees (Du et al., 2023). However, radiomics-based
models still require careful design and feature selec-
tion, which can be laborious and time-consuming.
108
Miglionico, G., Ducange, P., Marcelloni, F. and Pedrycz, W.
Deep Learning and Multi-Objective Evolutionary Fuzzy Classifiers: A Comparative Analysis for Brain Tumor Classification in MRI Images.
DOI: 10.5220/0012940500003886
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Explainable AI for Neural and Symbolic Methods (EXPLAINS 2024), pages 108-115
ISBN: 978-989-758-720-7
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

Fuzzy rule-based classifiers (FRBCs) are capable
of meeting the demands of explainability and trans-
parency in critical health applications (Cao et al.,
2024), since they utilize a set of human-readable rules
to make decisions. Compared to DL models with
post-hoc explainability methods, FRBCs are simpler,
faster to generate, and involve fewer parameters, es-
pecially if combined with radiomics features (Zhang
et al., 2022).
One advanced approach in the realm of FR-
BCs is represented by Multi-Objective Evolutionary
Fuzzy Classifiers (MOEFCs) (Antonelli et al., 2016).
MOEFCs deal with FRBCs designed using a Multi-
objective evolutionary learning (MOEL) scheme to
generate models characterized by good trade-offs be-
tween accuracy and interoperability.
This paper presents an experimental analysis com-
paring a DL model with FRBCs, generated by us-
ing PAES-RCS, in brain tumor classification (BTC)
from MRI scans. As regards the PAES-RCS method,
we discuss its advantages in generating models that
are almost as accurate as those generated using DL.
Moreover, we argue on the fact that the FBRCs gen-
erated by PAES-RCS not only offer competitive clas-
sification performance but also provide superior inter-
pretability and transparency than DL models, making
them a valuable tool in the clinical decision-making
process.
The rest of the paper is organized as follows: in
Section 2 we review the most recent state-of-the-art
on ML and DL models used for brain tumor image
classification. In Section 3 we describe the archi-
tecture of the DL model adopted in the experimen-
tal analysis and we introduce MOEFCs. Section 4
presents a comprehensive overview of the dataset in-
volved in the experiments and shows details on how
radiomic features are extracted from MRI brain im-
ages included in the dataset that we selected for our
experimental analysis. Section 5 argues on the ex-
periments and presents a detailed description of the
achieved results, focusing on accuracy metrics and
model complexity. Finally, Section 6 offers some con-
cluding remarks.
2 RELATED WORK
Over the last years, methods based on DL have been
the most adopted ones for dealing with brain tu-
mor classifications from MRI images , (Kaifi, 2023).
Most of them consider Convolutional Neural Net-
works (CNNs), which are well known for their ability
to perform automatic feature extraction (Al-Zoghby
et al., 2023).
When dealing with DL , authors mainly consider
two general approaches, with or without a prelimi-
nary segmentation step (Muhammad et al., 2020). Re-
cent works (Ghamry et al., 2023), (Unde and Rathore,
2024), directly adopt DL models, such as VGG16,
AlexNet, ResNet50, and R-CNN . On the contrary,
the authors of the works (Akter et al., 2024) and
(Khan et al., 2023), first adopt a segmentation stage
based on U-Net model and Fuzzy C-Means, respec-
tively. Then, a DL model, such as VGG and Efficient-
Net, is applied considering the segmented portion of
the image as an input.
To ensure some degree of explainability, the au-
thors of (Maqsood et al., 2022) and (Chmiel et al.,
2023) adopted a post-hoc procedure to derive an ex-
plicator for the classification decision. Specifically,
the authors considered Grad-CAM technique to iden-
tify regions of the MRI image that contribute sig-
nificantly to the final prediction of different types
of CNNs, such as VGG16, ResNet50, and Efficient-
NetB7.
In addition to DL approaches, traditional ML
models, such as decision trees and support vector ma-
chines, have also been employed for BTC (Muham-
mad et al., 2020). To use these models, it is necessary
to manually extract features from the images. In (De-
cuyper et al., 2018), a CNN is used for feature extrac-
tion, which is then combined with a Random Forest
classifier. In contrast, in (Cho et al., 2018), qualita-
tive radiomic features are extracted and then used as
inputs of ML classifiers such as logistic regression,
support vector machine, and random forest.
Few works discuss the use of fuzzy classifiers for
BTC. Specifically, in (Kalam et al., 2023) authors pro-
pose the use of the well-known Adaptive Neuro Fuzzy
Inference System (ANFIS) adapted for classification
tasks. Both papers leverage the ANFIS model for
classifying segmented portions of the MRI. To this
aim, radiomic features are extracted from the seg-
mented images. It is worth noting that although AN-
FIS belongs to the category of interpretable models by
design, its level of interpretability is much lower than
that of MOEFC. Indeed, frequently the integrity of the
fuzzy partitions is compromised, especially due to the
high overlapping of the fuzzy sets. Moreover, ANFIS
considers all rules to make inferences, instead of just
one as in the case of FRBCs generated with PAES-
RCS. Thus, ANFIS local interpretability, namely the
capability of explaining the decision taken for a spe-
cific input, may be compromised, especially if the rule
base contains several rules.
Deep Learning and Multi-Objective Evolutionary Fuzzy Classifiers: A Comparative Analysis for Brain Tumor Classification in MRI Images
109

3 PRELIMINARIES
3.1 Workflow of the Traditional BTC
The methodology commonly adopted in CAD sys-
tems for brain tumor classification using MRI, de-
tailed in (Muhammad et al., 2020), involves the steps
discussed in the following.
The first two steps regards the acquisition and data
collection of brain images using different MRI scan-
ning sequences. The preprocessing stage improves
image quality with noise reduction and intensity cor-
rection techniques.
Segmentation is a critical step to identify regions
of interest (ROIs) in the image, namely suspicious ar-
eas of brain tumor. ROIs can be detected manually
by experienced radiologist or automatically by using
specific algorithms or AI models.
Once the ROIs have been segmented, various
types of features may be extracted. Usually quanti-
tative values, such as radiomics features, describing
morphological and geometrical aspects may be ex-
tracted from the image. When dealing with DL mod-
els feature extraction is automatically carried out by
the convolutional layers. However, these features, are
not easy to interpret.
Feature selection and dimensionality reduction
stages involve techniques for enhancing model per-
formance by reducing overfitting, improving compu-
tational efficiency, and highlighting the most relevant
features, thereby potentially increasing the accuracy
and interpretability of the model.
The classification stage may involve both super-
vised or unsupervised models, for categorizing the
segmented image into malignant or benign lesions
or to distinguish the tumor among different types or
gravity levels.
Finally, the CAD system may provide a possible
brain tumor diagnosis and tumor grade classification,
presenting the results visually to facilitate clinical in-
terpretation.
3.2 VGG Models for Image
Classification
The DL model that we adopted in our experimental
analysis is the VGG16 network. It has been designed
and developed by the Visual Geometry Group (VGG)
of the University of Oxford (Simonyan and Zisser-
man, 2014). It has been recently experimented for
addressing the BTC task in (Muhammad et al., 2020).
In this study, the VGG16, appropriately modified for
dealing with the specific dataset, achieved the best re-
sults among other DL models in BTC tasks in seg-
mented MRIs. It is worth noticing that in our exper-
imental analysis, we adopted the same dataset used
in (Muhammad et al., 2020) and discussed in Section
4. We built our specific BTC model from an VGG16
network pre-trained on the ImageNet dataset and pub-
licly available in the TorchVision library
3
and prop-
erly fine tuned on the selected dataset.
3.3 Multi-Objective Evolutionary Fuzzy
Classifiers
Over the past decades, Multi-Objective Evolution-
ary Algorithms (MOEAs) have been extensively em-
ployed to design the architecture of FRBCs. The com-
bination of MOEAs and FRBCs led to the so-called
MOEFCs (Antonelli et al., 2016).
We recall that an FRBC comprises a rule base
(RB), a database (DB) and an inference engine for the
classification. The RB is composed by linguistic if-
then rules: the antecedent part of each rule includes
fuzzy conditions. These conditions, contained in the
DB, are defined for each input variables by properly
partitioning them with fuzzy sets. In this work, the
output of the FRBC is generated by using the max-
imum matching inferencing method: the rule which
is fired the most by an input pattern provides the es-
timated class. Details on fuzzy rules and inference
methods can be found in (Antonelli et al., 2016).
In our experimental analysis, we adopted the
Pareto Archived Evolution Strategy (PAES) for Rule
and Condition Selection (RCS) method as MOEL
scheme for concurrently learning the RB and the DB
of a set of FRBC. PAES-RCS generates a set of
FRBC characterized by different trade-off between
accuracy and complexity. PAES-RCS has been suc-
cessfully experimented in (Antonelli et al., 2016) for
classification tasks with tabular datasets. The adopted
MOEL scheme starts from a set of candidate rules
generated by using the multi-way fuzzy decision tree
for classification tasks described in (Segatori et al.,
2018). Once generated the initial set of candidate
rules, the evolutionary process will select only the
most relevant ones, along with their most relevant
conditions. Simultaneously, the algorithm tunes the
strong fuzzy partitions that define the DB by apply-
ing a lateral displacement of the core. The optimiza-
tion is guided by two conflicting objective functions,
namely the Total Rule Length (TRL) and the accu-
racy computed in terms of classification rate. At the
end of the evolutionary process, an approximation of
the Pareto Front is achieved. Details on chromosome
coding, crossover and mutation operators, the scheme
3
https://pytorch.org/vision/stable/index.html
EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods
110

of PAES-RCS, and the parameters to set for running
the algorithm can be found in (Antonelli et al., 2016).
4 DATASET DESCRIPTION &
FEATURE EXTRACTIONS
In our experimental analysis, we considered the
“Brain Tumor Public Data Set” introduced in (Cheng
et al., 2015) that includes T1-weighted and Contrast-
Enhanced MRI images of 233 patients, retrieved from
two different hospitals in China between 2005 and
2010. It consists of 3064 imaging sections or slices.
Each image has a size of 512 x 512, a thickness from
6 to 1 mm, and a space between sections of 6 mm,
and can be associated with one of the following la-
bels: meningioma (708 images), glioma (1426 im-
ages), and pituitary tumor (939 images). The tumor
area is segmented by three experienced radiologists.
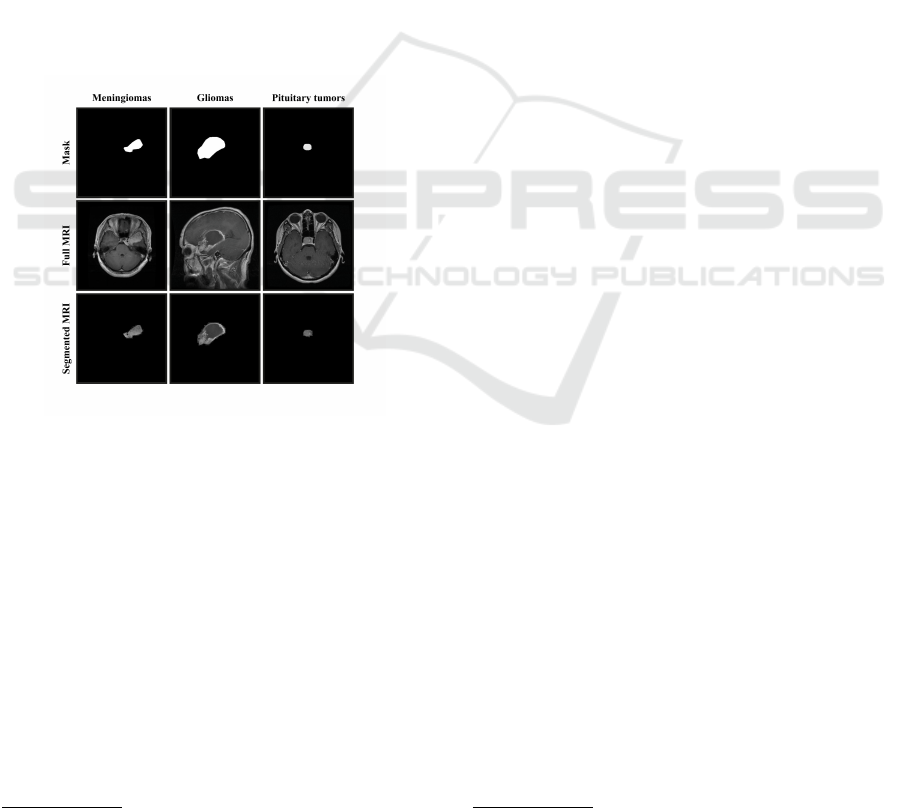
An example of an MRI image and tumor mask is
shown in Figure 1.
Figure 1: Images of brain tumors from the public dataset.
The first row presents the segmentation masks, the second
row shows the complete images, and the last row illustrates
the segmented tumors.
To provide images as inputs of FRBCs, we need
to transform them into numerical vectors. To this
aim, we use radiomics algorithms that describes im-
age characteristics such as pixel intensities, relation-
ships, shapes, and textures (Bera et al., 2022).
In this work, we adopted the pipeline for ex-
tracting radiomic features proposed in (Carr
´
e et al.,
2020). We used PyRadiomics
4
, a flexible open-source
Python library, to extract a number of features from
MRI images. Adhering to the guidelines of the Imag-
ing Biomarker Standardization Initiative (Zwanen-
burg et al., 2020), PyRadiomics ensures standardiza-
tion and reproducibility of radiomic features extracted
4
https://pyradiomics.readthedocs.io/en/latest
from medical images. Specifically, Z-Score normal-
ization, combined with absolute discretization, was
used for the extraction of radiomic features. The ex-
tracted features include: first-order features, such as
the mean, standard deviation, skewness, and kurto-
sis of pixel values; second-order features, such as
the gray-level co-occurrence matrix, which measures
the frequency of pixel pairs with specific gray val-
ues; and higher-order features, such as the gray-level
run-length matrix and the gray-level size zone matrix,
which assess the length of pixel sequences and the
size of homogeneous gray-level zones, respectively.
A total of 110 features were extracted from each
ROI of the MRI images. A decision tree-based proce-
dure was adopted for feature selection using the same
cross-validation scheme discussed in Section 5. The
15 most relevant features were selected. The selected
features are described in Table 1.
5 EXPERIMENTAL ANALYSIS
5.1 Experimental Setup
In our analysis, we adopted a five-fold cross-
validation procedure. During the creation of the folds,
attention was focused on two crucial aspects: each
fold contains images from distinct groups of patients
and images of the same patient are not included in
different folds.
To handle the insufficient number of data for
network model identification, we used the transfer
Learning technique, discussed in (Muhammad et al.,
2020): the final convolutional set of layers, the fully
connected layers, and the softmax layer were fine-
tuned, while the other layers were kept frozen. The
fine-tuning was conducted by showing the network
with the images of segmented regions of tumor tissue.
No augmentation techniques were employed. VGG16
network fine-tuning sessions lasted 50 epochs, em-
ploying a validation mechanism to prevent overfitting
and selecting the optimal set of weights. The batch
size was set to 32, the maximum learning rate factor
to 0.001, and the optimizer used was Adam.
When running PAES-RCS, we considered the tab-
ular dataset of images described in the radiomic fea-
tures space outlined in Section 4. We adopted a pub-
licly available PAES-RCS implementation
5
. The val-
ues of the parameters used for running PAES-RCS are
the same than the ones in (Antonelli et al., 2016).
Some parameters, namely C
R
and C
T
, underwent a
tuning procedure to achieve an optimal balance be-
5
https://github.com/GionatanG/skmoefs
Deep Learning and Multi-Objective Evolutionary Fuzzy Classifiers: A Comparative Analysis for Brain Tumor Classification in MRI Images
111

Table 1: Selected Feature Descriptions.
No. Feature Name Description
X
1
Skewness Measures the asymmetry of the distribution of gray levels in the image.
X
2
Maximum Maximum pixel value in the original image.
X
3
Contrast Quantifies the contrast based on the gray level co-occurrence matrix.
X
4
Mean Mean pixel value in the original image.
X
5
Minimum Minimum pixel value in the image.
X
6
Small Dependence High Gray Level Emphasis Emphasizes small dependencies with high gray levels.
X
7
10th Percentile The 10th percentile of gray levels in the image.
X
8
Range Range between the maximum and minimum pixel values in the image.
X
9
Root Mean Squared The square root of the mean of squared gray level values.
X
10
Gray Level Non-Uniformity Measures the non-uniformity of gray levels based on the gray level de-
pendence matrix.
X
11
Large Dependence Low Gray Level Emphasis Emphasizes large dependencies with low gray levels.
X
12
Median Median pixel value in the image.
X
13
Kurtosis Measures the “peakedness” of the distribution of gray levels.
X
14
Long Run High Gray Level Emphasis Emphasizes long runs with high gray levels in the gray level run length
matrix.
X
15
Energy Sum of squared gray level values, representing the energy of the image.
tween exploring and exploiting the solution space,
taking into account the dataset’s distinctive features
for brain cancer classification.
5.2 Results and Discussions
As regards PAES-RCS, for each fold we run ten tri-
als (each with a different seed of the random number
generator). For each fold and each trial of the cross-
validation we generated an approximation of the opti-
mal Pareto front. We report the average results, con-
sidering 50 trials in total, in terms of classification
performance and model complexity, of three repre-
sentative solutions. As discussed in (Antonelli et al.,
2016), we sorted the FRBCs in each Pareto front ap-
proximation in ascending order of accuracy. Then, we
extracted the First (the most accurate and the less ex-
plainable), the Median, and the Last solution (the less
accurate and the most explainable).
5.2.1 Classification Performance Analysis
Table 2 presents the mean and standard deviation of
the accuracy achieved by each model, along with pre-
cision, recall, and F1-score metrics for each class.
It is easy to notice that VGG16 achieves the high-
est average values of accuracy both on the training
and test set. However, it suffers the most from over-
fitting.
Glioma is the tumour that is best recognised by all
models. Indeed, the VGG16 model achieves an F1-
score of 84% on the test set. In comparison, the First,
Median, and Last FRBCs attain, respectively, 86%,
83%, and 72%. For meningiomas, VGG16 achieves
an F1-score of 65%, while the First, Median, and
Last FRBCs accomplish 65%, 62%, and 46%, respec-
tively. For pituitary tumors, VGG16 attains an F1-
score of 86%, whereas the First, Median, and Last
FRBCs achieve, respectively, 72%, 68%, and 50%.
In a nutshell, for Meningioma and Glioma tumors,
the First and Median FRBCs perform similarly to
VGG16. As regards Pituitary tumor, VGG16 out-
performs all three FRBCs. However, in this class,
VGG16 achieves an F1-score of 99% on the training
set, which drops to 86% on the test set suggesting that
the model suffers from overfitting, likely due to the
underrepresentation of the Pituitary tumor class in the
training data.
5.2.2 Complexity Analysis
Table 3 presents the mean and standard deviation of
some complexity metrics for each model. Specifi-
cally, for all models, we show the total number of pa-
rameters (NP), the model weight in terms of memory
occupancy in kBs, and the number of input variables
F. As regards the FRBCs, we also show the TRL and
the total number of rules in the RB (M). We recall that
PAES-RCS performs also feature selection during the
optimization process, thus the total number of input
variables considered in the FRBCs in the Pareto front
approximation may be lower than 15, i.e. lower than
the number of features that we extracted and selected
using the procedure described in Section 4.
The total number of parameters NP for represent-
ing an FRBC is the sum of the parameters of its DB,
equal to the total number of real numbers adopted for
representing all the fuzzy sets of each input variable
(in our case 3), and of its RB, equal to the total num-
ber of conditions in the antecedents and the total num-
ber of class labels of each rule. Thus, the value of NP
can be calculated as follows:
NP = F ×
F
∑
f =1
T
f
× 3 + T RL + M (1)
EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods
112

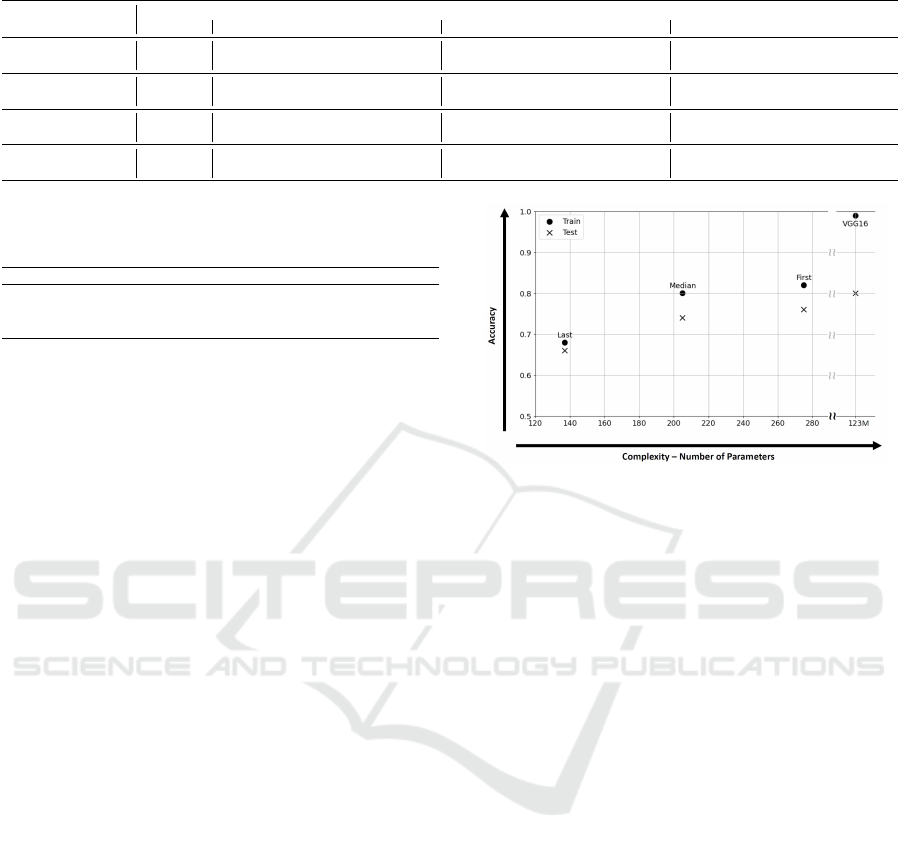
Table 2: Average performance results achieved by PAES-RCS and VGG16.
Model Accuracy
Meningioma Glioma Pituitary Tumor
Precision Recall F1-score Precision Recall F1-score Precision Recall F1-score
FRBC-First
Train 0.83 ± 0.02 0.76 ± 0.05 0.73 ± 0.05 0.75 ± 0.03 0.87 ± 0.03 0.92 ± 0.03 0.89 ± 0.02 0.80 ± 0.03 0.76 ± 0.06 0.78 ± 0.03
Test 0.78 ± 0.04 0.65 ± 0.09 0.64 ± 0.12 0.65 ± 0.09 0.82 ± 0.04 0.90 ± 0.04 0.86 ± 0.03 0.75 ± 0.08 0.69 ± 0.09 0.72 ± 0.07
FRBC-Median
Train 0.79 ± 0.03 0.74 ± 0.06 0.68 ± 0.07 0.70 ± 0.04 0.84 ± 0.04 0.90 ± 0.03 0.87 ± 0.03 0.77 ± 0.05 0.72 ± 0.09 0.74 ± 0.05
Test 0.75 ± 0.05 0.62 ± 0.11 0.59 ± 0.13 0.62 ± 0.10 0.81 ± 0.04 0.87 ± 0.07 0.83 ± 0.04 0.72 ± 0.11 0.66 ± 0.10 0.68 ± 0.08
FRBC-Last
Train 0.65 ± 0.09 0.69 ± 0.14 0.49 ± 0.22 0.52 ± 0.19 0.71 ± 0.11 0.83 ± 0.05 0.76 ± 0.06 0.68 ± 0.15 0.51 ± 0.22 0.54 ± 0.16
Test 0.63 ± 0.10 0.51 ± 0.22 0.44 ± 0.23 0.46 ± 0.19 0.69 ± 0.10 0.82 ± 0.22 0.72 ± 0.14 0.68 ± 0.19 0.47 ± 0.24 0.50 ± 0.18
VGG16
Train 0.99 ± 0.00 0.99 ± 0.01 1.00 ± 0.00 0.99 ± 0.01 1.00 ± 0.00 1.00 ± 0.00 1.00 ± 0.00 0.99 ± 0.01 1.00 ± 0.00 0.99 ± 0.01
Test 0.80 ± 0.00 0.69 ± 0.09 0.63 ± 0.06 0.65 ± 0.06 0.83 ± 0.05 0.85 ± 0.04 0.84 ± 0.02 0.84 ± 0.04 0.87 ± 0.07 0.86 ± 0.03
Table 3: Average complexity results achieved by PAES-
RCS and VGG16.
Model NP Weight (kB) TRL M F
FRBC-First 309.42 ± 58.48 13.59 ± 0.07 125.06 ± 46.34 21.16 ± 7.43 10.88 ± 0.85
FRBC-Median 235.32 ± 70.26 11.36 ± 0.03 72.54 ± 49.67 12.48 ± 8.09 10.02 ± 1.24
FRBC-Last 138.82 ± 24.26 4.05 ± 0.03 17.02 ± 9.69 3.30 ± 1.61 7.90 ± 1.18
VGG16 123M ± 0.0 540471.00 - - 16
where F is the number of the input variables of
the FRBC, T
f
is the number of fuzzy sets adopted for
each input variable X
f
, T RL is the total number of
parameters considered in the RB and M is the number
of rules in the RB .
As shown in Table 3, FRBC models have sig-
nificantly fewer parameters than the VGG16 model.
In particular, the average number of parameters
of FRBC-First, FRBC-Median, and FRBC-Last is
300.42, 235.32, and 183.82, respectively. In con-
trast, VGG16 has 123 million parameters, so it has
a higher complexity that can have an impact both on
the computational resources required for training and
inference and on the suffering from overfitting. We
verified that the fine-tuning process of VGG16 takes
around 26 minutes on the hardware previously dis-
cussed. In comparison, PAES-RCS takes only around
2 minutes and the radiomic feature extraction process
takes around 6 minutes. Table 3 also shows that the
complexity of the model in terms of NP is closely re-
lated to the weight of the model. Indeed, FRBC mod-
els are lightweight, while VGG16 has a substantially
larger memory footprint making FRBC models more
suitable for deployment on devices with limited mem-
ory resources.
5.2.3 Accuracy-Complexity Tradeoff Analysis
Figure 2 presents a projection in the accuracy and
complexity (expressed in terms of NP) plane of the
mean values associated with the FRBCs generated by
PAES-RCS and the VGG16 network. Each model is
depicted by a point, illustrating the trade-off between
accuracy and complexity.
Using the notion of non-dominance, adopted in
multi-objective optimization, none of the models
dominates the others. This means that all models rep-
resent a different trade-off between the accuracy and
Figure 2: Performance-complexity trade-offs of the models
obtained on the ”Brain Tumor Public Data Set” dataset.
the complexity. It is worth to notice that, while dif-
ferences in the accuracy dimension are on the same
order of magnitude, the overall complexity of the FR-
BCs is four orders of magnitude smaller than the one
of VGG16. Moreover, on the one hand, FRBC-First
demonstrates competitive classification performance
compared to the VGG16, achieving an average over-
all accuracy of 78%, only 2 percentage points lower
than the VGG16. On the other hand, the FRBC-
Median represents an excellent compromise between
accuracy and explainability. The TRL is reduced from
125 to 72, the number of rules from 21 to 12, and it in-
curs only a 4% decrease in accuracy compared to the
FRBC-First. Finally, The FRBC-Last represents the
most interpretable solution, reducing the TRL from
125 to 17 and the number of rules from 21 to 3, but
its precision is 11 percentage points lower than the
FIRST solution, resulting in an overall accuracy of
63%. This solution is particularly suitable when hav-
ing a highly interpretable model is a mandatory re-
quirement, even if it means sacrificing some accuracy.
5.2.4 Some Discussions the Explainability of
Fuzzy Rules
In Fig. 3 we show some examples of fuzzy rules ex-
tracted from the RB of an FRBC-First, picked from
one of the Pareto front approximations generated by
PAES-RCS. The linguistic rules are formulated in
terms of the optimized strong fuzzy partitions of each
Deep Learning and Multi-Objective Evolutionary Fuzzy Classifiers: A Comparative Analysis for Brain Tumor Classification in MRI Images
113

input variable. Each variable has been described us-
ing 5 fuzzy set labeled as follows: VL (very low), L
(low), M (medium), H (high), and VH (very high).
We verified that, at the end of the optimization pro-
cess, the fuzzy partitions still maintain a good level
of integrity in terms of ordering, coverage, and distin-
guishability.
It is worth to notice that the RB of the chosen
FRBC-first is very compact and the rules include a
reduced number of conditions. Indeed, the average
rule length of the entire RB is equal to 6.0. This
aspect also supports the high explainability level of
the generated FRBCs. Indeed, the lower the number
of conditions in each rule, the higher the local ex-
plainability of the decision associated with a specific
rule. In conclusion, the extracted rules are highly in-
terpretable and easy-to-understand by humans. In the
example, R
3
, if activated, explains that an image has
been classified as Meningioma because the value of
the intensity of most of the pixel(information related
to X
4
and X
12
)) is high (prevalence of white level) and
the ROI is averagely jagged (information related to
X
6
and X
10
). In contrast, the deep neural network
structure of VGG16 makes it difficult to explain in-
dividual predictions or understand the contribution of
specific input variables without the a posterior ap-
plication of sophisticated tools and techniques, such
as layer-wise relevance propagation or saliency maps
(Mandloi et al., 2024). It is worth highlighting that,
as regards FRBCS generated by PAES-RCS, no ex-
tra computation, such as in the post-hoc explainabil-
ity procedure adopted for DL models, is necessary.
Indeed, FRBCs are interpretable by design and all the
elements necessary for the explanations are already
available in the DB and in the RB.
R
1
: IF X
1
is M AND X
2
is H AND X
7
is M AND
X
8
is L AND X
12
is M THEN Class is Glioma
R
2
: IF X
4
is H AND X
6
is L AND X
12
is H
THEN Class is Pituitarytumor
R
3
: IF X
4
is H AND X
6
is M AND X
10
is M AND
X
12
is H THEN Class is Meningioma
Figure 3: Some examples of fuzzy rules extracted from an
FRBC-first.
6 CONCLUSION
In this paper, we presented a comparative analysis
between two different types of artificial intelligence
models for approaching the BTC task from MRI
images. Specifically, we considered Deep Learn-
ing models and FBRCs. We carried out an exper-
imental campaign considering a publicly available
dataset composed by MRI images including 3 dif-
ferent types of brain tumors. The comparison was
performed along the accuracy and the complexity of
the models. We considered the VGG16 convolutional
network and FBRCs based on the PAES-RCS algo-
rithm. VGG16 directly takes the MRI image in input,
whereas FBRCs take a representation of the image ex-
pressed in terms of quantitative features extracted us-
ing the radiomics methodology.
Results have shown that even though VGG16
achieves the highest classification performance, it suf-
fers from overfitting, its architecture is very com-
plex, characterized by 123 millions of parameters,
and the lack of transparency and interpretability lim-
its its clinical applicability. In contrast, PAES-RCS
has generated a set of FRBCs characterized by differ-
ent trade-offs between accuracy and complexity. The
most complex FRBCs, composed by hundreds of pa-
rameters and able to provide explanations in terms
of simple linguistic rules, are characterized by a low
loss of classification performance in comparison with
VGG16.
Despite the promising results, there exist several
directions for future research. In particular, it is nec-
essary to improve the feature selection process to en-
hance interpretability and make the explanations more
intuitive. In addition, exploring advanced data aug-
mentation and re-balancing techniques could reduce
the overfitting issues and improve the classification
performance of the different classification models,
particularly for the recognition of underrepresented
classes.
ACKNOWLEDGEMENTS
This work has been partly funded by the Italian Min-
istry of University and Research in the framework of
the FoReLab project.
REFERENCES
Akter, A., Nosheen, N., Ahmed, S., Hossain, M., Yousuf,
M. A., Almoyad, M. A. A., Hasan, K. F., and Moni,
M. A. (2024). Robust clinical applicable CNN and
u-net based algorithm for MRI classification and seg-
mentation for brain tumor. Expert Systems with Appli-
cations, 238:122347.
Al-Zoghby, A. M., Al-Awadly, E. M. K., Moawad, A.,
Yehia, N., and Ebada, A. I. (2023). Dual deep
EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods
114

CNN for tumor brain classification. Diagnostics,
13(12):2050.
Antonelli, M., Ducange, P., Lazzerini, B., and Marcel-
loni, F. (2016). Multi-objective evolutionary design of
granular rule-based classifiers. Granular Computing,
1:37–58.
Bera, K., Braman, N., Gupta, A., Velcheti, V., and Mad-
abhushi, A. (2022). Predicting cancer outcomes with
radiomics and artificial intelligence in radiology. Na-
ture reviews Clinical oncology, 19(2):132–146.
Cao, J., Zhou, T., Zhi, S., Lam, S., Ren, G., Zhang, Y.,
Wang, Y., Dong, Y., and Cai, J. (2024). Fuzzy infer-
ence system with interpretable fuzzy rules: Advancing
explainable artificial intelligence for disease diagno-
sis—a comprehensive review. Information Sciences,
662:120212.
Carr
´
e, A., Klausner, G., Edjlali, M., Lerousseau, M.,
Briend-Diop, J., Sun, R., Ammari, S., Reuz
´
e, S., Al-
varez Andres, E., Estienne, T., et al. (2020). Stan-
dardization of brain MR images across machines and
protocols: bridging the gap for MRI-based radiomics.
Scientific reports, 10(1):12340.
Cheng, J., Huang, W., Cao, S., Yang, R., Yang, W.,
Yun, Z., Wang, Z., and Feng, Q. (2015). En-
hanced performance of brain tumor classification via
tumor region augmentation and partition. PloS one,
10(10):e0140381.
Chmiel, W., Kwiecie
´
n, J., and Motyka, K. (2023). Saliency
map and deep learning in binary classification of brain
tumours. Sensors, 23(9):4543.
Cho, H.-h., Lee, S.-h., Kim, J., and Park, H. (2018). Classi-
fication of the glioma grading using radiomics analy-
sis. PeerJ, 6:e5982.
Decuyper, M., Bonte, S., and Van Holen, R. (2018). Binary
glioma grading: radiomics versus pre-trained cnn fea-
tures. In Medical Image Computing and Computer As-
sisted Intervention–MICCAI 2018: 21st International
Conference, Granada, Spain, September 16-20, 2018,
Proceedings, Part III 11, pages 498–505. Springer.
Du, P., Wu, X., Liu, X., Chen, J., Chen, L., Cao, A., and
Geng, D. (2023). The application of decision tree
model based on clinicopathological risk factors and
pre-operative mri radiomics for predicting short-term
recurrence of glioblastoma after total resection: a ret-
rospective cohort study. American Journal of Cancer
Research, 13(8):3449.
Ghamry, F. M., Emara, H. M., Hagag, A., El-Shafai, W.,
El-Banby, G. M., Dessouky, M. I., El-Fishawy, A. S.,
El-Hag, N. A., and El-Samie, F. E. A. (2023). Efficient
algorithms for compression and classification of brain
tumor images. Journal of Optics, 52(2):818–830.
Hulsen, T. (2023). Explainable artificial intelligence (XAI):
Concepts and challenges in healthcare. AI, 4(3):652–
666.
Kaifi, R. (2023). A review of recent advances in brain tumor
diagnosis based on AI-based classification. Diagnos-
tics, 13(18):3007.
Kalam, R., Thomas, C., and Rahiman, M. A. (2023). Brain
tumor detection in MRI images using adaptive-anfis
classifier with segmentation of tumor and edema. Soft
Computing, 27(5):2279–2297.
Khalighi, S., Reddy, K., Midya, A., Pandav, K. B., Madab-
hushi, A., and Abedalthagafi, M. (2024). Artificial
intelligence in neuro-oncology: advances and chal-
lenges in brain tumor diagnosis, prognosis, and pre-
cision treatment. NPJ Precision Oncology, 8(1):80.
Khan, M. A., Khan, A., Alhaisoni, M., Alqahtani,
A., Alsubai, S., Alharbi, M., Malik, N. A., and
Dama
ˇ
sevi
ˇ
cius, R. (2023). Multimodal brain tumor
detection and classification using deep saliency map
and improved dragonfly optimization algorithm. In-
ternational Journal of Imaging Systems and Technol-
ogy, 33(2):572–587.
Mandloi, S., Zuber, M., and Gupta, R. K. (2024). An
explainable brain tumor detection and classification
model using deep learning and layer-wise relevance
propagation. Multimedia Tools and Applications,
83(11):33753–33783.
Maqsood, S., Dama
ˇ
sevi
ˇ
cius, R., and Maskeli
¯
unas, R.
(2022). Multi-modal brain tumor detection using
deep neural network and multiclass SVM. Medicina,
58(8):1090.
Muhammad, K., Khan, S., Del Ser, J., and De Albuquerque,
V. H. C. (2020). Deep learning for multigrade brain
tumor classification in smart healthcare systems: A
prospective survey. IEEE Transactions on Neural Net-
works and Learning Systems, 32(2):507–522.
Saidak, Z., Laville, A., Soudet, S., Sevestre, M.-A., Con-
stans, J.-M., and Galmiche, A. (2024). An MRI ra-
diomics approach to predict the hypercoagulable sta-
tus of gliomas. Cancers, 16(7):1289.
Segatori, A., Marcelloni, F., and Pedrycz, W. (2018). On
distributed fuzzy decision trees for big data. IEEE
Transactions on Fuzzy Systems, 26(1):174–192.
Simonyan, K. and Zisserman, A. (2014). Very deep con-
volutional networks for large-scale image recognition.
arXiv preprint arXiv:1409.1556.
Unde, M. and Rathore, A. S. (2024). Brain mri image anal-
ysis for alzheimer’s disease diagnosis using mask r-
cnn. International Journal of Intelligent Systems and
Applications in Engineering, 12(13s):137–149.
Van der Velden, B. H., Kuijf, H. J., Gilhuijs, K. G., and
Viergever, M. A. (2022). Explainable artificial in-
telligence (xai) in deep learning-based medical image
analysis. Medical Image Analysis, 79:102470.
Wang, A. Q., Karaman, B. K., Kim, H., Rosenthal, J.,
Saluja, R., Young, S. I., and Sabuncu, M. R. (2024).
A framework for interpretability in machine learning
for medical imaging. IEEE Access.
Zhang, Y., Yang, D., Lam, S., Li, B., Teng, X., Zhang,
J., Zhou, T., Ma, Z., Ying, T.-C., and Cai, J. (2022).
Radiomics-based detection of covid-19 from chest X-
ray using interpretable soft label-driven TSK fuzzy
classifier. Diagnostics, 12(11):2613.
Zhou, S. K., Greenspan, H., and Shen, D. (2023). Deep
learning for medical image analysis. Academic Press.
Zwanenburg, A., Valli
`
eres, M., Abdalah, M. A., Aerts,
H. J., Andrearczyk, V., Apte, A., Ashrafinia, S.,
Bakas, S., Beukinga, R. J., Boellaard, R., et al. (2020).
The image biomarker standardization initiative: stan-
dardized quantitative radiomics for high-throughput
image-based phenotyping. Radiology, 295(2):328–
338.
Deep Learning and Multi-Objective Evolutionary Fuzzy Classifiers: A Comparative Analysis for Brain Tumor Classification in MRI Images
115