EMG-Based Shared Control Framework for Human-Robot
Co-Manipulation Tasks
Francesca Patriarca
a
, Paolo Di Lillo
b
and Filippo Arrichiello
c
Department of Electrical and Information Engineering, University of Cassino and Southern Lazio,
Via G. Di Biasio 43, 03043 Cassino (FR), Italy
Keywords:
Physical Human-Robot Interaction, Human-Robot Collaboration, Shared Control.
Abstract:
The paper presents a shared control architecture designed for human-robot co-manipulation tasks, that allows
the human to switch among robot’s operational modes through surface electromyography (sEMG) signals
from the user’s arm. A support vector machine (SVM) classifier is employed to process the raw EMG data to
identify two classes of contractions that are fed into a finite state machine algorithm to trigger the activation
of different sets of admittance control parameters corresponding to the envisaged operational modes. The
proposed architecture has been experimentally validated using a Kinova Jaco
2
manipulator, equipped with
Force/Torque sensor at the end-effector, and with a user wearing Delsys Trigno Avanti EMG sensors on the
dominant upper limb.
1 INTRODUCTION
Collaborative robotics involves robotic systems inter-
acting directly with humans in a shared workspace to
complete tasks together, combining the versatility and
decision-making capabilities of human workers with
the precision, strength, and repeatability of robots
and improving task quality and productivity. Intuitive
user interfaces, advanced sensors, and control sys-
tems are crucial for smooth cooperation and safe op-
eration close to humans (Villani et al., 2018). Unlike
industrial robots, collaborative robots (cobots) dy-
namically adapt to people and objects that enter their
workspace (Matheson et al., 2019), without the need
for physical barriers, making them suitable for var-
ious applications like logistics, assembly, and med-
ical procedures (Sladi
´
c et al., 2021). However, de-
veloping effective human-robot teams presents chal-
lenges such as robots situational awareness, clear
communication protocols, and ensuring safety with-
out limiting robot’s speed or motion (Sharifi et al.,
2022). To address these challenges, shared control,
which involves both the robot and the human as ac-
tive parts in the control loop (Abbink et al., 2018),
has emerged as a promising solution in collaborative
robotics by enabling smoother interactions and im-
a
https://orcid.org/0009-0005-5849-6162
b
https://orcid.org/0000-0003-2083-1883
c
https://orcid.org/0000-0001-9750-8289
Figure 1: The scenario shows the experimental setup in
which a human operator performs a co-manipulation task
wearing four EMG sensors and using a Jaco
2
manipulator.
proving task efficiency and safety. To achieve this,
impedance/admittance control strategies can be em-
ployed for controlling robots to behave as virtual dy-
namic systems with adjustable impedance parame-
ters (Cacace et al., 2019). This allows the robot to
adapt its compliance and motion synchronization ca-
pabilities to better interact with their environment (Fi-
46
Patriarca, F., Di Lillo, P. and Arrichiello, F.
EMG-Based Shared Control Framework for Human-Robot Co-Manipulation Tasks.
DOI: 10.5220/0012943600003822
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 2, pages 46-53
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

cuciello et al., 2015). The rates of change of inter-
action force and human arm admittance parameters
can be used to modify the variable admittance param-
eters (Wang and Zhao, 2023); while predicting human
motion trajectories enables robots to anticipate move-
ments and adapt accordingly, optimizing task comple-
tion (Losey and O’Malley, 2018). In order to estimate
user movement intentions, surface electromyography
(sEMG) sensors, which capture muscle electrical ac-
tivity, are essential (Grafakos et al., 2016). These
sensors help to adapt virtual online damping, leading
to the integration of EMG signals with adaptive ad-
mittance control in robotic manipulation, skill learn-
ing, and rehabilitation devices (Gonzalez-Mendoza
et al., 2022). Integration of human motion predic-
tion, adaptation algorithms, and virtual guidance also
enhances the quality of assistance (Li et al., 2022),
as demonstrated in applications like exoskeleton con-
trol (Zhuang et al., 2021). Furthermore, the sEMG
signals also play a crucial role in encoding stiffness
and movement patterns to improve robotic skill learn-
ing and adaptive behavior (Zeng et al., 2021).
This paper presents a shared control architecture
for human-robot co-manipulation tasks that allows the
human operator to dynamically change the robot’s op-
erational mode using sEMG signals from the user’s
arm and hand. These signals are classified by a Sup-
port Vector Machine (SVM) (Hearst et al., 1998)
algorithm, which detects various contractions and
movements. The output of the classifier is then fed
into a finite state machine algorithm, which adjusts
the parameters of a variable admittance controller to
allow for better human-robot interaction. Since the
dynamic behavior of the manipulator is not unique,
managing different types of interactions in a unified
way ensuring optimal co-manipulation experiences is
not easy. Key factors in determining admittance pa-
rameters include the robot’s compliance with forces
applied by human, the fluidity and intuitiveness of
the manual driving experience, and the speed and ac-
curacy of task execution. Lower damping improves
maneuverability but can cause instability or inaccu-
racy, while higher damping enhances precision but
reduces compliance, making co-manipulation more
difficult and slower. Using sEMG signals to adjust
admittance parameters is a novel approach that en-
sures stable robot behavior, contrasting with previ-
ous methods relying on heuristics (Ferraguti et al.,
2019) or specific stable region of parameters for spe-
cific interaction (Ficuciello et al., 2015). Wrench sen-
sor readings make complex to distinguish intentional
operator’s gestures from unintentional collisions be-
cause the user holds the end-effector after the sen-
sor that can not detect the forces between the contact
point and the environment if the forces are exerted
by the user; while integrating musculoskeletal activ-
ity allows to recognize such interactions that would
be indistinguishable otherwise.
The paper presents a shared control architecture
that dynamically changes the variable admittance
controller parameters based on the operator’s EMG
signals to enhance precision in task performance by
reducing downtime, improving human-robot interac-
tions for a more intuitive co-manipulation experi-
ence. The approach’s effectiveness and robustness
have been experimentally validated with a user wear-
ing four sEMG sensors on his/her dominant upper
limb and using a 7DOF manipulator equipped with
a Force/Torque sensor for admittance control, despite
not being torque-controlled.
2 SHARED CONTROL
ARCHITECTURE
The proposed architecture includes two possible op-
erational modes:
• Low-Damping mode: hand-guidance of the end-
effector in the free space to allow the operator to
move the end-effector, e.g., to reach a workpiece;
• High-Damping mode: hand-guidance of the end-
effector near a surface or a workpiece to perform
operations such as welding or painting.
To achieve this, the gains of the admittance con-
troller of the manipulator are changed between two
sets corresponding to each operational mode. A fi-
nite state machine algorithm handles the switching
between these sets based on the movements or con-
tractions of the operator’s arm, which are recognized
through an EMG-based classifier.
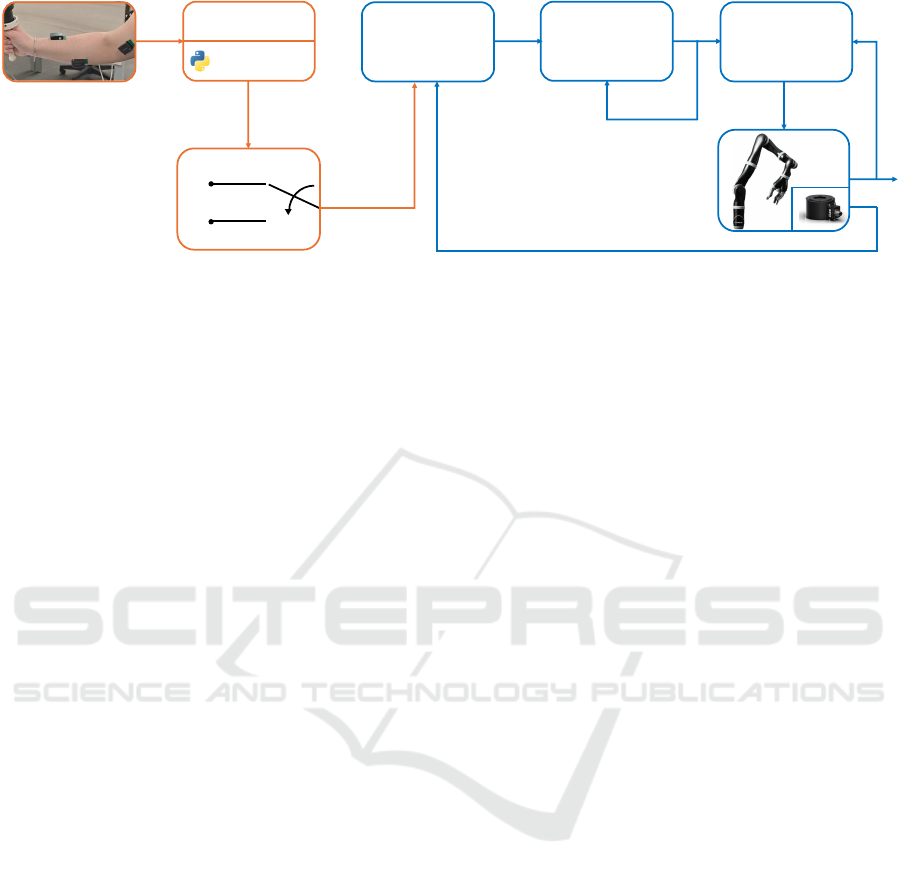
Figure 2 shows the block diagram of the entire
shared control architecture. The High-level layer in-
cludes all the functional blocks that generate specific
sets of admittance gains, while the Low-level layer in-
cludes all the blocks that concern the motion control
of the manipulator. The raw EMG signals go as in-
put to a SVM classifier that recognizes two possible
classes of motions/contractions of the operator. The
finite state machine algorithm receives this informa-
tion and it sets the admittance gains based on the oper-
ational mode; then, an admittance controller (Di Lillo
et al., 2021) outputs a desired trajectory for the end-
effector, which is finally tracked by computing the
needed joint velocity with an inverse kinematics al-
gorithm (Di Lillo et al., 2023). In the following sec-
tions, details about all the functional blocks are given
in a bottom-up order.
EMG-Based Shared Control Framework for Human-Robot Co-Manipulation Tasks
47

A
D
n
L
C
I
K
g
h
l
m
k
e
f
a
b
d
z
c
High-Level
Layer
Low -level
Layer
F
E
P
G
P
Figure 2: Proposed shared control architecture. The High-Level layer is responsible for the EMG signal acquisition and
classification. Then, the recognized class is used into a finite-state machine algorithm that outputs a set of admittance gains.
The Low-Level layer is responsible for the motion control of the manipulator, and it employs a variable admittance controller,
an inverse kinematics algorithm and a joints controller.
3 LOW-LEVEL LAYER
The low-level layer implements the robot control al-
gorithm and consists of three blocks: i) the joints con-
troller, that generates actual joint velocity commands
based on joint encoder readings and the inverse kine-
matics controller output; ii) the inverse kinematics
controller, which computes the desired joint velocities
that make the end-effector track the desired trajectory;
and iii) the variable admittance controller, that modi-
fies the input reference trajectory for the end-effector,
using wrench sensor readings, to achieve a desired dy-
namic behavior, and outputs a new desired trajectory
for the end-effector.
3.1 Inverse Kinematics and Joints
Controller
Considering a serial manipulator with n Degrees of
Freedom (DOFs), the state of the system is described
by the vector q
q
q = [q
1
, q
2
, ·· · , q
n
]
T
∈ R
n
, which con-
tains the joint positions. Define the vector that gathers
the end-effector configuration as x
x
x =

p
p
p
T
o
o
o
T

T
∈ R
7
,
where p
p
p = [p
x
, p
y
, p
z
]
T
∈ R
3
represents the coordi-
nates of the end-effector expressed in the arm base
frame, while o
o
o = [o
x
, o
y
, o
z
, o
w
]
T
∈ R
4
is the quater-
nion that expresses the orientation of the end-effector
with respect to the arm base frame. The velocity
of the end-effector can be described by the vector
v
v
v =

˙
p
p
p
T
ω
ω
ω
T

T
∈ R
6
, where
˙
p
p
p = [ ˙p
x
, ˙p
y
, ˙p
z
]
T
∈ R
3
and
ω
ω
ω = [ω
x
, ω
y
, ω
z
]
T
∈ R
3
represent the end-effector lin-
ear and angular velocities, respectively. The differ-
ential relationship between the end-effector velocity
and the joint velocity vector
˙
q
q
q = [ ˙q
1
, ˙q
2
, ·· · , ˙q
n
]
T
can
be expressed as v
v
v = J
J
J
˙
q
q
q, where J
J
J ∈ R
6×n
is the robot
Jacobian matrix.
Assuming a redundant manipulator, i.e. n > 6, and
the availability of a desired end-effector trajectory ex-
pressed as:
x
x
x
d
=

p
p
p
d
o
o
o
d

∈ R
7
v
v
v
d
=

˙
p
p
p
d
ω
ω
ω
d

∈ R
6
a
a
a
d
=

¨
p
p
p
d
α
α
α
d

∈ R
6
,
(1)
where x
x
x
d
represents the desired position and quater-
nion, v
v
v
d
gathers the desired linear and angular ve-
locities and a
a
a
d
represents the desired linear and an-
gular accelerations. The desired joint velocity that
makes the end-effector track the desired trajectory can
be computed by resorting to the Closed-Loop Inverse
Kinematics (CLIK) algorithm:
˙
q
q
q
d
= J
J
J
†
(v
v
v
d
+ K
K
K
ik
˜
x
x
x) , (2)
where J
J
J
†
is the Moore-Penrose pseudoinverse of the
Jacobian matrix, K
K
K
ik
∈ R
6×6
is a positive-definite ma-
trix of gains and
˜
x
x
x is the error vector, defined as:
˜
x
x
x =

˜
p
p
p
˜
o
o
o

=

p
p
p
d
− p
p
p(q
q
q
d
)
o
o
o
−1
d
⋆ o
o
o(q
q
q
d
)

∈ R
6
, (3)
where
˜
p
p
p and
˜
o
o
o are the position and quaternion errors,
respectively, q
q
q
d
is the vector of desired joint position
obtained by numerically integrating the desired joint
velocity vector
˙
q
q
q
d
, p
p
p(q
q
q
d
) and o
o
o(q
q
q
d
) are the position
and orientation of the end-effector obtained by con-
sidering q
q
q
d
as joint positions in the direct kinematics
computation.
Finally, the desired joint velocity vector is passed
to the joints controller, which computes the actual
command to send to the manipulator by resorting to
a proportional controller including a feedforward ac-
tion as:
˙
q
q
q
r
=
˙
q
q
q
d
+ K
K
K
jc
˜
q
q
q , (4)
where K
K
K
jc
∈ R
n×n
is a positive-definite matrix of gains
and
˜
q
q
q = q
q
q
d
− q
q
q is the joint position error computed
with respect to the actual readings of the joint en-
coders.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
48

3.2 Admittance Control
The admittance controller aims to assign a virtual dy-
namics to the manipulator, characterized by a desired
mass, damping, and stiffness. More in detail, assum-
ing to have a wrench sensor mounted on the wrist of
the manipulator and to have a certain reference tra-
jectory for the end-effector, the desired end-effector
trajectory must have the following dynamics:
K
K
K
m
˜
a
a
a
r,d
+ K
K
K
d
˜
v
v
v
r,d
+ K
K
K
k
˜
x
x
x
r,d
= h
h
h , (5)
where the positive-definite matrices:
K
K
K
m
=

K
K
K
p
m
O
O
O
3×3
O
O
O
3×3
K
K
K
o
m

(6)
K
K
K
d
=

K
K
K
p
d
O
O
O
3×3
O
O
O
3×3
K
K
K
o
d

(7)
K
K
K
k
=

K
K
K
p
k
O
O
O
3×3
O
O
O
3×3
K
K
K
o
k

, (8)
represent the virtual mass, damping, and stiffness,
respectively, where the position K
p
(·)
and orientation
K
K
K
o
(·)
gains are highlighted, h
h
h =

f
f
f
T
µ
µ
µ
T

T
∈ R
6
is the
vector stacking the linear force and moments mea-
sured by the wrench sensor, and:
˜
x
x
x
r,d
=

˜
p
p
p
r,d
˜
o
o
o
r,d

=

p
p
p
r
− p
p
p
d
o
o
o
−1
r
⋆ o
o
o
d

(9)
˜
v
v
v
r,d
= v
v
v
r
− v
v
v
d
(10)
˜
a
a
a
r,d
= a
a
a
r
− a
a
a
d
, (11)
are the operational space configuration, velocity and
acceleration errors computed between the reference
and the desired trajectories. The desired acceleration
in output from the admittance controller can be com-
puted by folding Eqs (9)-(11) in Eq. (5) and rearrang-
ing the terms, obtaining:
a
a
a
d
= K
K
K
−1
m
[K
K
K
m
a
a
a
r
+ K
K
K
d
˜
v
v
v
r,d
+ K
K
K
k
˜
x
x
x
r,d
− h
h
h] . (12)
The desired end-effector velocity v
v
v
d
and configura-
tion x
x
x
d
to be tracked by the inverse kinematics con-
troller in Eq. (2) can then be obtained by numerical in-
tegration of the desired acceleration. It is worth notic-
ing that the virtual mass, damping and stiffness can be
varied, obtaining a variable admittance controller.
Each one of the operational modes listed in Sec. 2
has a corresponding set of admittance gains that ad-
just the robot’s behavior to successfully execute them.
In detail, with reference to Eqs. (6)-(8), when in Low-
Damping mode the K
K
K
k
gain is set to O
O
O
6×6
to allow
the operator to freely change the end-effector posi-
tion and orientation. The matrix K
K
K
p
d
is set as K
K
K
p
d
=
diag{k
p
d,low
, k
p
d,low
, k
p
d,low
}, with low element k
p
d,low
to
assure smooth teleoperation to the user; similarly,
for the orientation, the matrix K
K
K
o
d
is set as K
K
K
o
d
=
diag{k
o
d,low
, k
o
d,low
, k
o
d,low
}, with low element k
o
d,low
.
Regarding the virtual mass, the matrix K
K
K
p
m
is set to
diag = {k
p
m,low
, k
p
m,low
, k
p
m,low
}, while the matrix K
K
K
o
m
is
set to diag = {k
o
m,low
, k
o
m,low
, k
o
m,low
}.
When in High-Damping mode the K
K
K
k
gain
is still set to O
O
O
6×6
, while K
K
K
p
d
is set as K
K
K
p
d
=
diag{k
p
d,high
, k
p
d,high
, k
p
d,high
} with high element k
p
d,high
to ensure slow and precise movements, for ex-
ample when painting a thin element. Regard-
ing the orientation, the matrix K
K
K
o
d
is set as K
K
K
o
d
=
diag{k
o
d,high
, k
o
d,high
, k
o
d,high
}, with high element k
o
d,low
.
Finally, the virtual mass, the matrix K
K
K
p
m
is set to
diag = {k
p
m,high
, k
p
m,high
, k
p
m,high
}, while the matrix K
K
K
o
m
is set to diag = {k
o
m,high
, k
o
m,high
, k
o
m,high
}.
4 HIGH-LEVEL LAYER
The high-level layer is composed of three main func-
tional blocks: i) the EMG sensors, ii) the operator’s
motion classifier, and iii) the finite state machine al-
gorithm.
4.1 EMG Signal Analysis
Electromyography (EMG) signals, produced by mus-
cle contractions and relaxations, are detected us-
ing surface or needle-based electrodes, and need to
be amplified and filtered to remove noise. In this
works EMG signals are used to detect muscle activ-
ity and patterns. The proposed solution refers to a
Support Vector Machine classifier, a common super-
vised learning algorithm for classification tasks, that
processes features extracted from EMG signals seg-
mented into time windows (or epochs), specifically
using three commonly time-domain features: Root
Mean Square (RMS), Mean Absolute Value (MAV)
and Average Amplitude Change (AAC) (Li et al.,
2022).
To train the SVM classifier, a dataset of feature
vectors with associated class labels, obtained with a
predetermined acquisition procedure, is used. The
SVM algorithm learns a decision boundary to sep-
arate different classes by finding an optimal hyper-
plane in the feature space, governed by two main hy-
perparameters: the regularization parameter C, which
prevents overfitting by limiting misclassification, and
γ, which determines how much far points influence
the hyperplane calculation. During the training, the
SVM adjusts the parameters by solving a quadratic
programming problem to identify the support vectors,
i.e., the points closest to the decision boundary.
EMG-Based Shared Control Framework for Human-Robot Co-Manipulation Tasks
49

In the proposed scenario, the classifier is trained
to discriminate between two classes: free (movements
made by the operator in various directions with mini-
mal resistance) and contraction (generated by the op-
erator by tightening his hand).
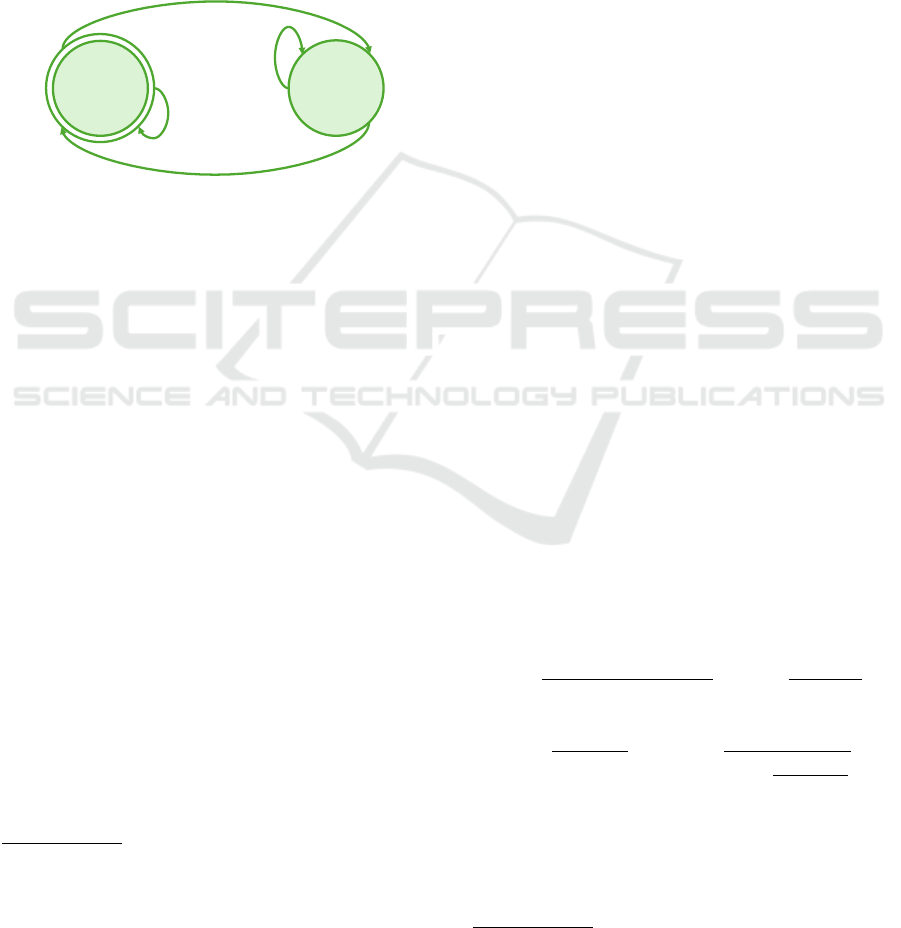
4.2 Finite State Machine
The two classes in output from the SVM classifier are
fed into a finite state machine algorithm to automati-
cally switch between the operational modes, as shown
in Figure 3.
C
m
c
u
F
m
f
f
Figure 3: Finite State Machine.
In detail, the system starts in Low-Damping mode;
when the operator executes the contraction class for at
least 1.5s, the state switches to High-Damping mode,
corresponding to a set of admittance gains that allow
the operator to move the end-effector to follow a pre-
defined path, without touching it, with lower speed
and higher accuracy due to the increased damping.
By generating the contraction class for at least 3s, the
state returns to the Low-Damping mode, in which the
operator can move the end-effector more easily and
faster towards the starting point to execute the path
again.
5 EXPERIMENTAL VALIDATION
5.1 Experimental Setup
To validate the effectiveness of the proposed shared
control architecture, experiments of human-robot co-
manipulation tasks were conducted using a 7DOF Ki-
nova Jaco
2
manipulator
1
equipped with a Bota Sys-
tems Rokubimini force/torque sensor
2
. Four non-
invasive Delsys Trigno Avanti active sensors
3
with a
frequency of 1.78 kHz were placed on the dominant
1
https://www.kinovarobotics.com/product/gen2-robots
2
https://www.botasys.com/force-torque-sensors/rokubi
3
https://delsys.com/trigno-avanti/. These sensors have
an integrated pre-amplification circuit to reduce input noise
and do not require amplifying and filtering signals.
arm of the human operator. Following Seniam guide-
lines
4
, they were put on the biceps and triceps brachii,
flexor carpi radialis and extensor carpi ulnaris mus-
cles, as much as possible in the center of muscles.
The streaming of EMG data was done through a
Python GUI on a Windows PC, while the control soft-
ware and the SVM classifier, developed using Python
and the Scikit-learn library (Kramer, 2016), were im-
plemented in the ROS (Robotic Operating System)
framework running on Linux. To allow the two work-
stations to communicate TCP/IP sockets were used.
5.2 Training and Test of the Classifier
To train the SVM classifier described in section 4.1,
EMG signals from a human operator’s arm were
recorded while performing specific movements or
contractions interacting with a manipulator. Two in-
teractions were considered for data collection: in the
first, the robot’s behavior was made compliant, using
the Low-Damping mode parameters, and the operator
moved the end-effector in random directions to col-
lect data related to the free class; in the second, the
robot had a rigid behavior, obtained by referring to
a standard position controller, and the operator tight-
ened the hand on the end-effector handle to collect
data related to the contraction class. A Matlab GUI
told the operator which movements or contractions to
perform and automatically labeled the data to obtain
two datasets: one for training and one for testing the
classifier. For each of the four EMG sensors, three
time-domain features were extracted, resulting in a
12-element feature vector, with an associated class la-
bel. The SVM model is trained using the hyperpa-
rameters in Table 1. The confusion matrix for binary
problems, where the rows represent the expected class
distribution and the columns the predicted distribution
by the classifier, was used to evaluate classifier perfor-
mance and to compute class metrics such as Accuracy,
Precision, Recall, and F1-score, yielding the follow-
ing indexes:
A =
T P
T P + T N +FP + FN
P =
T P
T P + FP
R =
T P
T P + FN
F1 =
T P
T P +
FN + FP
2
where T P, T N, FP and FN are true posi-
tives/negatives and false positives/negatives taken
from the binary problem confusion matrix, respec-
tively. True positives and negatives are the correctly
4
http://seniam.org
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
50

identified positive/negative classes, while false pos-
itives and negatives are the incorrectly classified val-
ues. The accuracy measures how many instances were
correctly classified, the precision measures the accu-
racy of the positive predictions, the recall is the ratio
of positive instances that are correctly detected, and
the F1-score is the harmonic mean of precision and
recall.
In the on-line use of the classifier, the statistical
mode of the predicted classes calculated over the last
1.5s is sent to the finite state machine to increase the
robustness in terms of misclassifications.
5.3 Experimental Results
To validate the overall architecture by triggering all
the envisioned state transitions, a series of experi-
ments were performed in which a subject
5
(female,
aged 29) wearing EMG sensors had to guide the robot
end-effector several times along a predefined path, as
if she were performing a painting operation on a thin
element, as shown in Figure 1. The path consists of a
cylindrical filament whose shape is similar to a square
wave. The user repeated the designed experiment 15
times to test the reproducibility of the approach.
Table 1: Experimental parameters used in the proposed ar-
chitecture.
Control parameters
Parameter Value Description
K
K
K
ik
diag{20 I
I
I
3
, 15 I
I
I
3
} Inverse kinematics gain
K
K
K
jc
diag{3 I
I
I
4
, 2 I
I
I
3
} Joints controller gain
k
p
d,low
40 Low-damping position gain
k
o
d,low
2 Low-damping orientation gain
k
p
m,low
3 Low-mass position gain
k
o
m,low
0.1 Low-mass orientation gain
k
p
d,high
120 High-damping position gain
k
o
d,high
4 High-damping orientation gain
k
p
m,high
5 High-mass position gain
k
o
m,high
0.1 High-mass orientation gain
Classifier parameters
Parameter Value Description
C 1 Regularization parameter
γ ’scale’
6
Parameter of a Gaussian Kernel
Kernel ’RBF’ Kernel used in the SVM Classifier
5
The experiments were taken in accordance with the
Declaration of Helsinki, the protocol has been approved by
the Research Ethics Committee at the university where the
study is conducted and the subject gave informed consent.
6
’scale’ is a parameter calculated as 1 divided by the
product of the features number and the variance of the fea-
ture vector.
Table 1 shows the parameters for the con-
trollers and the classifier used in the experiments,
where all the admittance parameters were experi-
mentally determined; while a video showing the
experiments is provided at the following link:
https://youtu.be/93u5i8HmsPY.
M
98.2% 1.8%
0.0% 100.0%
F C
f
c
Figure 4: The confusion matrix obtained after training the
classifier.
In the following, the results of the classifier perfor-
mances and the experimental execution are discussed.
In particular, the confusion matrix is shown in Fig-
ure 4, while Table 2 contains the classifier indexes.
All performance indexes exceed 99%, as indicated in
the confusion matrix, which has only 1.8% of mis-
classifications for contraction class. This means that,
in addition to the high classification performance at-
tested by the high accuracy value, the number of false
positives is also very low. The precision and recall
also indicate a solid balance confirmed by the F1-
score, whose value is close to the accuracy. Thus, the
numerical results attest a reliable and accurate classi-
fication capability, also supported by the use of only
two classes.
Table 2: Table containing performance evaluation metrics.
Accuracy (%) Precision (%) Recall (%) F1-Score (%)
99.20 99.28 99.12 99.19
Figure 5 shows the path followed by the end-
effector during one of the experiments performed, in-
cluding the start and end points. Two different col-
ors were used to highlight the path followed by the
manipulator, depending on the corresponding active
operational mode: green and blue paths correspond
to Low-Damping and High-Damping modes, respec-
tively. The user drives the end-effector near the be-
ginning of the filament to be followed, generates the
contraction class for 1.5s to switch to High-Damping
mode, and moves the end-effector along the filament
without touching it using the free class. By generat-
ing contraction for at least 3s, the user switches the
FSM back to Low-Damping mode and quickly moves
the end-effector back to start point with the free class
(as can be seen by the green edge connecting the ends
of the blue lines). Then, the user generates contrac-
EMG-Based Shared Control Framework for Human-Robot Co-Manipulation Tasks
51

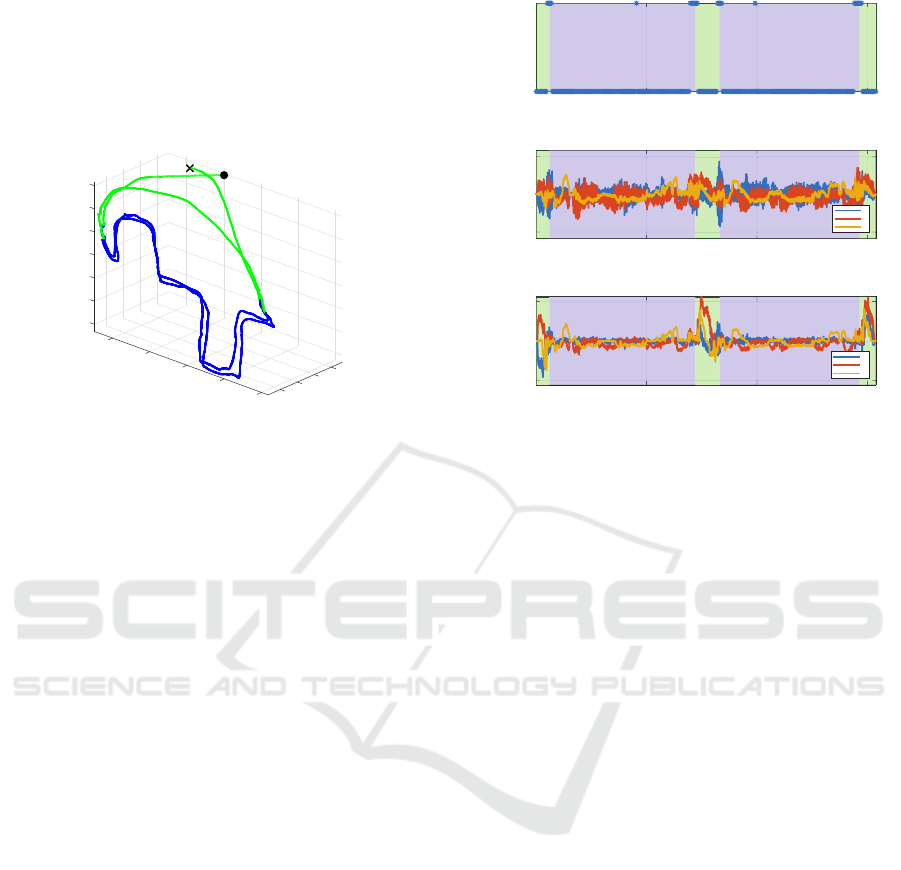
tion for 1.5s, returning the FSM to High-Damping
mode, and uses the free class to follow the filament
again; in fact, there are two blue lines in the shape
of a square wave. Finally, the user switches the FSM
back to Low-Damping mode using contraction for 3s
and moves the manipulator to the endpoint.
0.1
0.15
0.2
-0.1
0.25
z
0.3
S
0.35
E
-0.2
0.4
p
y
-0.3
-0.25
-0.3
x
-0.4
-0.35
-0.4
-0.5
Figure 5: The path followed by the manipulator’s end-
effector in one of the experiments performed. The path is
highlighted with two colors based on the two operational
modes: Low-Damping mode is marked in green and High-
Damping mode is highlighted in blue.
The user was able to complete the experiment
without difficulty by easily changing the operational
modes, as outlined in the NASA-TLX questionnaire
she completed.
Figure 6 shows the time evolution of the classifier
output, the force measured by the F/T sensor, and the
linear velocity of the manipulator’s end-effector. Sim-
ilarly to what was highlighted in the performed path,
the colors green and blue indicate the Low-Damping
and High-Damping modes, respectively. In particu-
lar, Figure 6a shows the time evolution of the classi-
fier output, which provides information about how it
was able to distinguish between free and contraction
classes. The classifier output determines the transition
between the control modes, as highlighted by the dif-
ferent colored areas; in fact, after the first 6s (or after
83s) in which the operator is in free class, she gen-
erates contraction for 1.5s and the FSM switches to
High-Damping mode; the FSM remains in the same
state until the operator stops following the filament;
then, the operator generates a 3s contraction (after 72
or 146s) and the FSM returns to Low-Damping mode.
Instead, the time evolution of the force and linear ve-
locity of the end-effector are shown in Figures 6b and
6c, respectively. The velocity increases significantly
in the green areas, corresponding to a mode with low
damping values, compared to the blue areas where,
since the damping is higher, the manipulator becomes
less compliant and moves more slowly during the co-
manipulation.
0 50 100 150
t
f
c
e
0 50 100 150
t
-10
0
10
N
F
x
y
z
0 50 100 150
t
-0.1
0
0.1
l
V
X
Y
Z
Figure 6: Experimental results: a) EMG Classifier Output;
b) Force measured by the F/T sensor; c) End-Effector Lin-
ear Velocity. The different colored areas on all graphs cor-
respond to the two different control modes: green and blue
represent the Low-Damping and the High-Damping modes,
respectively.
Oscillations in the force trend also increase in the
green areas corresponding to Low-Damping, espe-
cially when the user generates the contraction class to
switch modes. In the transition from Low-Damping
to High-Damping this happens because, before the
transition occurs, the force sensor perceives the user’s
hand as a rigid external environment; while in the
transition from High-Damping to Low-Damping the
operator does not stop contracting immediately after
the transition because of his reflexes, and the lower
damping is not sufficient to reduce the oscillations due
to residual contractions.
6 CONCLUSIONS
In this work, a shared control architecture is proposed
that allows changing the admittance parameters of a
manipulator using sEMG sensors in a human-robot
co-manipulation scenario. A dedicated classifier rec-
ognizes the human movements and contractions to
switch among two sets of admittance parameters cor-
responding to two robot behaviors. The robustness
of the approach is validated using a Jaco
2
manipula-
tor and four Trigno Avanti EMG sensors through a
series of experiments. The interaction with external
environment can produce oscillations that can cause
resonance phenomena (known in the literature), espe-
cially when the robot comes into contact with more
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
52

rigid environments. Future work will be devoted to
analyze these phenomena in order to extend this ap-
proach to more complex scenarios where both human-
robot and robot-environment interactions are consid-
ered. This will require an increase in the number of
operational modes to handle complex scenarios and,
consequently, the introduction of a greater number of
classes from EMG signals.
ACKNOWLEDGEMENTS
The research leading to these results has re-
ceived funding from Project COM
3
CUP
H53D23000610006 funded by EU in NextGen-
erationEU plan through the Italian “Bando Prin
2022 - D.D. 104 del 02-02-2022” by MUR, from
H2020-ICT project CANOPIES (Grant Agree-
ment N. 101016906), and by Project “Ecosistema
dell’innovazione - Rome Technopole” financed by
EU in NextGenerationEU plan through MUR Decree
n. 1051 23.06.2022.
REFERENCES
Abbink, D. A., Carlson, T., Mulder, M., de Winter, J. C. F.,
Aminravan, F., Gibo, T. L., and Boer, E. R. (2018). A
topology of shared control systems—finding common
ground in diversity. IEEE Transactions on Human-
Machine Systems, 48(5):509–525.
Cacace, J., Caccavale, R., Finzi, A., and Lippiello, V.
(2019). Variable admittance control based on virtual
fixtures for human-robot co-manipulation. In 2019
IEEE International Conference on Systems, Man and
Cybernetics (SMC), pages 1569–1574.
Di Lillo, P., Simetti, E., Wanderlingh, F., Casalino, G., and
Antonelli, G. (2021). Underwater intervention with
remote supervision via satellite communication: De-
veloped control architecture and experimental results
within the dexrov project. IEEE Transactions on Con-
trol Systems Technology, 29(1):108–123.
Di Lillo, P., Vito, D. D., and Antonelli, G. (2023). Merging
global and local planners: Real-time replanning algo-
rithm of redundant robots within a task-priority frame-
work. IEEE Transactions on Automation Science and
Engineering, 20(2):1180–1193.
Ferraguti, F., Talignani Landi, C., Sabattini, L., Bonfe, M.,
Fantuzzi, C., and Secchi, C. (2019). A variable admit-
tance control strategy for stable physical human–robot
interaction. The International Journal of Robotics Re-
search, 38(6):747–765.
Ficuciello, F., Villani, L., and Siciliano, B. (2015). Variable
impedance control of redundant manipulators for intu-
itive human–robot physical interaction. IEEE Trans-
actions on Robotics, 31(4):850–863.
Gonzalez-Mendoza, A., Quinones-Uriostegui, I., Salazar-
Cruz, S., Perez Sanpablo, A. I., L
´
opez, R., and
Lozano, R. (2022). Design and implementation of a
rehabilitation upper-limb exoskeleton robot controlled
by cognitive and physical interfaces. Journal of Bionic
Engineering, 19.
Grafakos, S., Dimeas, F., and Aspragathos, N. (2016). Vari-
able admittance control in pHRI using EMG-based
arm muscles co-activation. In 2016 IEEE Interna-
tional Conference on Systems, Man, and Cybernetics
(SMC), pages 001900–001905.
Hearst, M. A., Dumais, S. T., Osuna, E., Platt, J., and
Scholkopf, B. (1998). Support vector machines. IEEE
Intelligent Systems and their applications, 13(4):18–
28.
Kramer, O. (2016). Scikit-learn. Machine learning for evo-
lution strategies, pages 45–53.
Li, J., Li, G., Chen, Z., and Li, J. (2022). A novel emg-
based variable impedance control method for a tele-
operation system under an unstructured environment.
IEEE Access, 10:89509–89518.
Losey, D. P. and O’Malley, M. K. (2018). Trajectory defor-
mations from physical human–robot interaction. IEEE
Transactions on Robotics, 34(1):126–138.
Matheson, E., Minto, R., Zampieri, E. G. G., Faccio, M.,
and Rosati, G. (2019). Human–robot collaboration in
manufacturing applications: A review. Robotics, 8(4).
Sharifi, M., Zakerimanesh, A., Mehr, J. K., Torabi,
A., Mushahwar, V. K., and Tavakoli, M. (2022).
Impedance variation and learning strategies in hu-
man–robot interaction. IEEE Transactions on Cyber-
netics, 52(7):6462–6475.
Sladi
´
c, S., Lisjak, R., Runko Luttenberger, L., and Musa,
M. (2021). Trends and progress in collaborative robot
applications. Politehnika, 5:32–37.
Villani, V., Pini, F., Leali, F., and Secchi, C. (2018). Survey
on human–robot collaboration in industrial settings:
Safety, intuitive interfaces and applications. Mecha-
tronics, 55:248–266.
Wang, C. and Zhao, J. (2023). Based on human-like vari-
able admittance control for human–robot collabora-
tive motion. Robotica, 41(7):2155–2176.
Zeng, C., Yang, C., Cheng, H., Li, Y., and Dai, S.-
L. (2021). Simultaneously encoding movement and
sEMG-based stiffness for robotic skill learning. IEEE
Transactions on Industrial Informatics, 17(2):1244–
1252.
Zhuang, Y., Leng, Y., Zhou, J., Song, R., Li, L., and
Su, S. W. (2021). Voluntary control of an an-
kle joint exoskeleton by able-bodied individuals and
stroke survivors using emg-based admittance control
scheme. IEEE Transactions on Biomedical Engineer-
ing, 68(2):695–705.
EMG-Based Shared Control Framework for Human-Robot Co-Manipulation Tasks
53