Solving Multi-Agent Pathﬁnding with Stochastic Local Search SAT

Algorithms

Max Frommknecht

and Pavel Surynek

Faculty of Information Technology, Czech Technical University in Prague, Th

akurova 9, Prague, Czechia

ﬁ ﬁ

Keywords:

Multi Agent Path Finding, SAT, SAT Solver, Local Search, Initial Assignment, Conﬂict-Driven Clause

Learning.

Abstract:

This paper explores the suitability of Stochastic Local Search (SLS) solvers for Multi-Agent Pathﬁnding

(MAPF) translated into the SAT domain. Traditionally, SAT encodings of MAPF have been tackled using

Conﬂict-Driven Clause Learning (CDCL) solvers, but this work investigates the potential of SLS solvers, par-

ticularly ProbSAT, in solving MAPF under the makespan objective. By employing the MDD-SAT approach

and comparing the performance of ProbSAT against the Glucose 4 CDCL solver, the effects of eager and lazy

encodings are evaluated, as well as the beneﬁt of providing initial variable assignments. Results show that

ProbSAT can effectively solve MAPF instances, especially when initial assignments based on agents’ shortest

paths are provided. This study suggests that SLS solvers can compete with CDCL solvers in speciﬁc MAPF

scenarios and highlights future research directions for optimizing SLS performance in MAPF.

1 INTRODUCTION

Multi-agent pathﬁnding (MAPF) is to compute paths

without collisions for multiple agents, from their

starting positions to their goals in a shared envi-

ronment. Managing multiple entities within a con-

strained space is a fundamental problem for many ar-

tiﬁcial intelligence and robotics applications, such as

automated warehouse logistics, autonomous vehicles

and digital entertainment (Stern et al., 2019). Single-

agent pathﬁnding has been solved optimally with the

A* algorithm (Hart et al., 1968) which therefore lends

itself as a reliable basis for many MAPF algorithms.

Optimal path planning for multiple agents is an NP-

Hard problem, presenting signiﬁcant computational

challenges(Yu and LaValle, 2013a)(Surynek, 2010).

Many different approaches exist to solve the MAPF

problem, some guarantee optimal solutions while oth-

ers sacriﬁce optimality for performance, prominent

ones are:

Sub-Optimal Solvers: These methods are often efﬁ-

cient and fast but have no guarantee that the solution

is optimal. There are sub-optimal search-based algo-

rithms like Hierarchical Cooperative A*, which plans

the path of each agent consecutively based on a prior-

https://orcid.org/0009-0008-1202-3599

https://orcid.org/0000-0001-7200-0542

ity heuristic and reserves its locations at certain times

so others will not occupy them (Silver, 2005).

Rule-based algorithms rely on speciﬁc instruc-

tions for speciﬁc circumstances like Push-and-Swap

which uses the ”push”-rule to guide agents towards

their goal until a conﬂict arises, which triggers the

”swap”-rule that resolves the conﬂict by swapping the

positions of the agents according to pre-speciﬁed in-

structions (Luna and Bekris, 2011).

It is also possible to combine these two ap-

proaches in algorithms like Flow Annotation Replan-

ning (FAR) which imposes different ﬂows of direc-

tion on parts of the grid space, similar to road net-

works. This limits the state space in which a path is

planned for each Agent individually. Conﬂicts that

arise are handled locally following a heuristic (Wang

et al., 2008).

Optimal Solvers: While being slower and only able

to handle relatively small numbers of agents, these al-

gorithms can guarantee that a found solution is opti-

mal. Usually, the optimality of these solvers is with

respect to the sum of cost objective, which is the

total cost of the paths of all agents (Standley and

Korf, 2011) or the makespan objective, which is the

cost of the longest path among all agents (Surynek,

2014). There are A*-based algorithms that extend A*

to the multi-agent scenario and make them feasible by

limiting the branching factor or by decomposing the

Frommknecht, M. and Surynek, P.

Solving Multi-Agent Pathﬁnding with Stochastic Local Search SAT Algorithms.

DOI: 10.5220/0012944800003822

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 67-78

ISBN: 978-989-758-717-7; ISSN: 2184-2809

MAPF problem into smaller ones that can be solved

independently (Standley, 2010) (Wagner and Choset,

2015).

Conﬂict-based search (CBS) can use any optimal

single agent pathﬁnder like A* to ﬁnd individual paths

for all agents, conﬂicts in the solution are added as

constraints to prevent conﬂicts of the individual paths

in the next iteration until there are no conﬂicts left

(Sharon et al., 2015). There are improved CBS vari-

ants that incorporate changes like merging agents into

meta agents and restarting the search, preferring cer-

tain types of conﬂicts, bypassing conﬂicts by trying

a quick ﬁx procedure or incorporating an admissible

heuristic, these additions make the algorithm signif-

icantly more efﬁcient (Boyarski et al., 2015) (Felner

et al., 2018).

Increasing Cost Tree Search (ICTS) stores all

shortest paths for each individual agent in multi-value

decision diagrams (MDD) (Srinivasan et al., 1990) all

MDDs together are viewed as on node in the cost tree.

The cross-product of the MDDs is searched to ﬁnd

a solution without conﬂicts. If none is found, new

nodes are created in each of which one agent’s short-

est path and with this its MDD’s length is increased

by one until a node is created from which a solution

can be obtained (Sharon et al., 2013).

Reduction-based approaches translate MAPF to

another domain of problems and search for a so-

lution for it with a solver designed for that do-

main. Mapf has been translated to many domains the

most prominent of which is Constraint Programming

(CP) which includes Boolean Satisﬁability (SAT)

(Surynek, 2016), picat (Bart

ak et al., 2017), SAT

modulo theory (SMT) (Surynek, 2019b), Answer Set

Programming (ASP) (Erdem et al., 2013) and network

ﬂow problems (Yu and LaValle, 2013b).

None of these methods, whether optimal or sub-

optimal is the deﬁnite best approach for all circum-

stances (Felner et al., 2017). It remains to be a topic

of exploration.

2 RELATED WORK

2.1 MAPF SAT

This work explores the translation of MAPF into the

SAT domain under the makespan objective, to ﬁnd

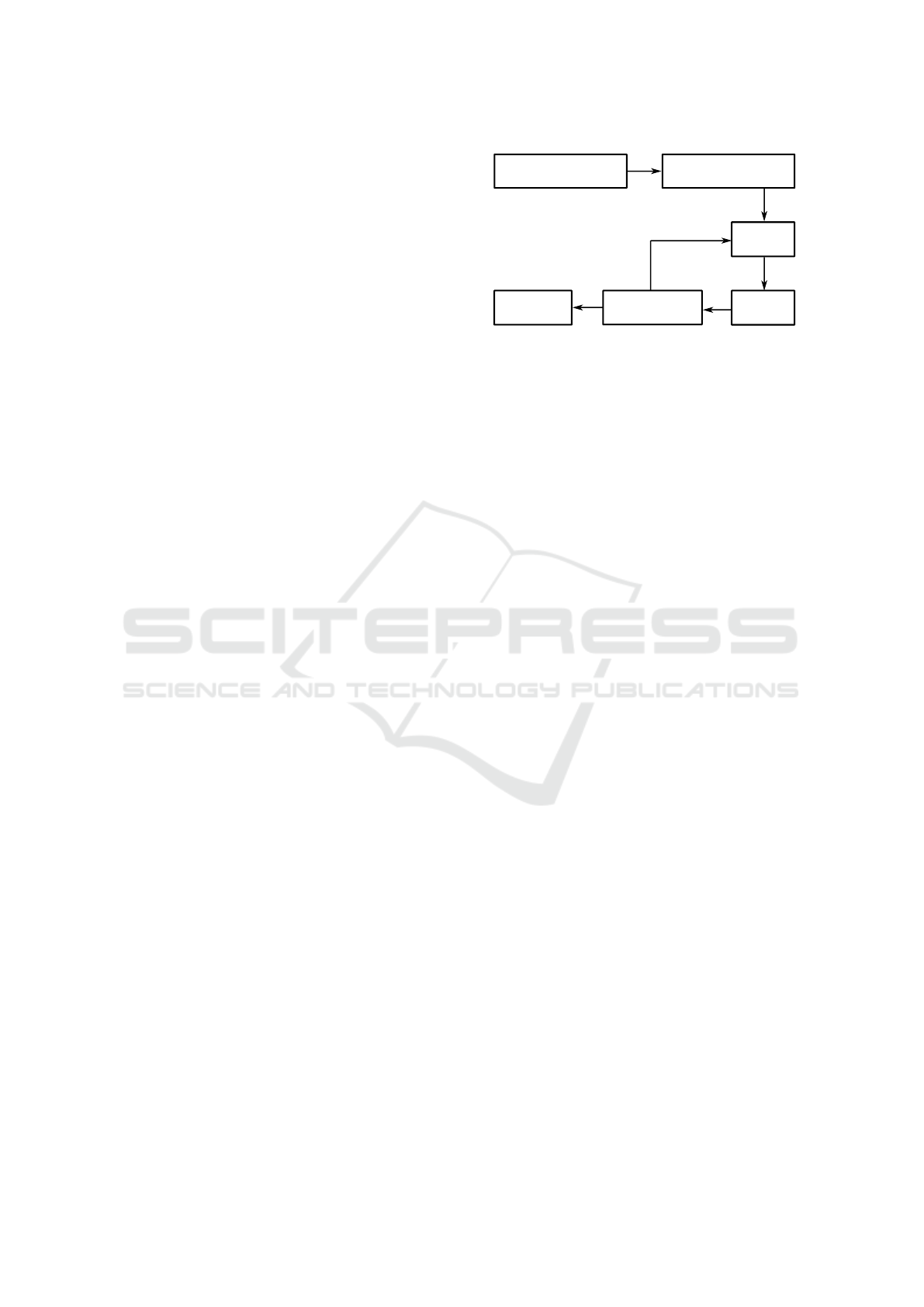
optimal solutions as shown in ﬁgure 1. There are dif-

ferent methods to translate MAPF into a conjunctive

normal form (CNF) formula. The classic approach

to translating a grid world is to use directed acyclic

Time Extension Graphs (TEG) which represent all

MAPF Instance

MDD's

CNF

SAT-Solver

Solution

min Makespan

Makespan+1

Figure 1: Framework for MAPF-SAT.

positions for each timestep for one agent. To trans-

late MAPF into a CNF formula one needs:

• Time-Position variables for all positions at all

times, which are true if the agent occupies a posi-

tion at a certain timestep and false if the agent is

elsewhere. These can be obtained by combining

a TEG for each agent, each vertex gets assigned

one boolean variable.

• Constraints to ensure the agent starts and ends at

the speciﬁed positions.

• Position constraints to ensure each agent is only

at one vertex during each time step.

• Movement constraints to ensure agents move

alongside edges.

• Conﬂict constraints to prevent collisions, adding

one speciﬁc clause for all possible collisions that

only allows one of the colliding agents to be at a

certain vertex

This quickly amounts to a very large number of vari-

ables and clauses. A more efﬁcient approach is MDD-

SAT (Surynek et al., 2016) which uses MDDs to store

all possible shortest paths for all agents individually.

Under the sum of cost objective MDDs only con-

tain positions for each timestep that are on one of

the shortest paths from the start to the goal of an

agent. Under the makespan objective, the length of

all agent’s paths is equal to the length of the longest

shortest path of all agents. This makes them much

smaller than TEGs while also reducing the number

of needed collision clauses immensely. While TEGs

of agents share all vertices and thus all vertices at ev-

ery timestep need a collision clause, MDDs often only

overlap partially. So the number of possible collisions

is reduced not only by the difference in possible po-

sitions but also by less overlap between the represen-

tations of agents. MDD-SAT can be further enhanced

to prevent edge conﬂicts, that is when two agents

traverse the same edge at the same time (Surynek,

2019a). Encoding all conﬂict constraints is also re-

ferred to as eager encoding. Another way to signiﬁ-

cantly decrease the number of clauses in a CNF is to

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

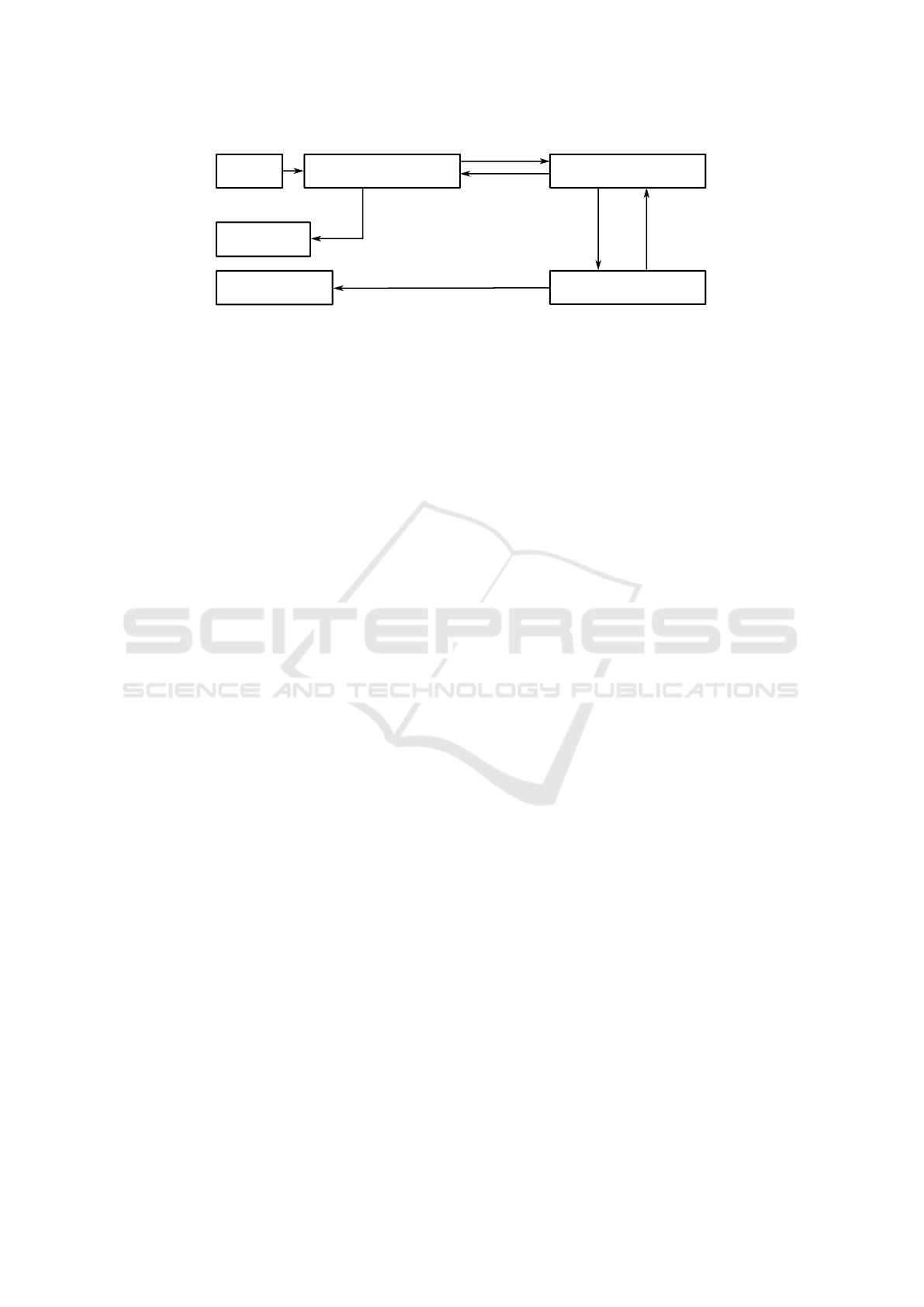
CNF

Unit Propagation

Conflict Analysis

No Conflict

Top level Conflict

All Variables set

Choose Variable

Conflict Backtrack

Solution

Unsatisfiable

Figure 2: Framework for CDCL Solvers.

omit all collision constraints and add them ”lazily”.

After a solution for the CNF is obtained it is checked

for collisions for which constraints are added to the

CNF until a solution without collisions is found. This

is referred to as lazy encoding, which only arrives at

the full (eager) encoding in the worst case and often

ﬁnds a solution much earlier (Surynek et al., 2019).

2.2 Stochastic Local Solvers

A popular alternative to Conﬂict-Driven Clause

Learning (CDCL) shown in ﬁgure 2 solvers are

stochastic local search (SLS) solvers shown in ﬁg-

ure 3. SLS solvers operate by assigning all variables

randomly and then ﬂipping single variables to im-

prove the current assignment locally until the CNF is

solved or a pre-speciﬁed amount of maximum ﬂips is

reached. If no solution is found the solver is restarted

until a pre-speciﬁed amount of maximum restarts is

reached (Biere et al., 2009). Which variable to ﬂip

is the crucial decision. GSAT either changes a vari-

able that will improve the current assignment so that

more clauses are satisﬁed or with a certain proba-

bility ﬂips a random variable (Selman et al., 1993).

WalkSAT improved upon this design, it randomly se-

lects an unsatisﬁed clause and ﬂips one of its vari-

ables. This ’makes’ the clause satisﬁed, however, it

may ’break’ another clause that also holds this vari-

able. The variable that ’breaks’ the least clauses is

chosen to be ﬂipped. If there is a choice that breaks

no other clauses it is always taken. Otherwise, half

of the time a random variable is ﬂipped instead of the

one with the least ’breaks’ (Kautz and Selman, 1996).

The Sparrow solver introduced a novel probabilis-

tic variable selection method and an adaptive noise

mechanism, enhancing its ability to escape local min-

ima and explore the search space more effectively. It

combined these innovations with sophisticated clause

weighting and hybrid heuristics, leading to signiﬁ-

cant performance improvements on industrial bench-

marks.(Balint and Fr

ohlich, 2010).

Preprocessing techniques (PPTs), when appro-

priately parameterized, can signiﬁcantly enhance

the performance of both SLS and CDCL solvers.

Bounded variable elimination (BVE) is a particularly

effective technique, but optimal conﬁgurations for

preprocessing differ between SLS and CDCL solvers

(Balint and Manthey, 2013).

ProbSAT elegantly simpliﬁes this choice by se-

lecting a random clause and assigns a probability

for each of its variables to be ﬂipped. Balint and

Sch

oning propose two different functions, based on

the make- and break-value of a variable as well as a

break (cb) and a make (cm) constant, to compute this

probability. One function takes the constants to the

power of the make- and break-values which is called

Exponential Function. The other function takes the

make- and break-values to the power of the constants

which is called Polynomial Function. Both functions

divide the make-result by the break-result. The op-

timal constants can be ﬁne-tuned for speciﬁc prob-

lems. In their experiments, they discover that the

make-result is of little impact and functions that only

use the break-result perform just as well. A higher

cb-value makes the algorithm more greedy(Balint and

Sch

oning, 2012).

Further improvements in SLS solvers for uniform

k-SAT with long clauses include XOR caching, in-

corporating multi-level break-values and improved

clause selection heuristics (Balint et al., 2014). Balint,

Biere, Fr

ohlich, and Sch

oning recommend using

brake2 values (cb2) and the XOR implementation for

structured problems, but to use the XOR caching only

for problems with shorter clause length (k < 7) be-

cause its efﬁciency in random SAT instances seems to

be in inverse proportional to k. Furthermore, the cb2

values can be computed much more efﬁciently when

no XOR caching is implemented. For clause selection

in structured problems, the PBFS scheme is recom-

mended. YalSAT employs a diverse set of ProbSAT

algorithms, each incorporating various combinations

of advanced improvements. These algorithms are se-

lected randomly when the solver restarts to enhance

the overall efﬁciency and effectiveness of the solver

which did well in SAT competitions (Biere, 2014)

(Biere, 2017).

Solving Multi-Agent Pathﬁnding with Stochastic Local Search SAT Algorithms

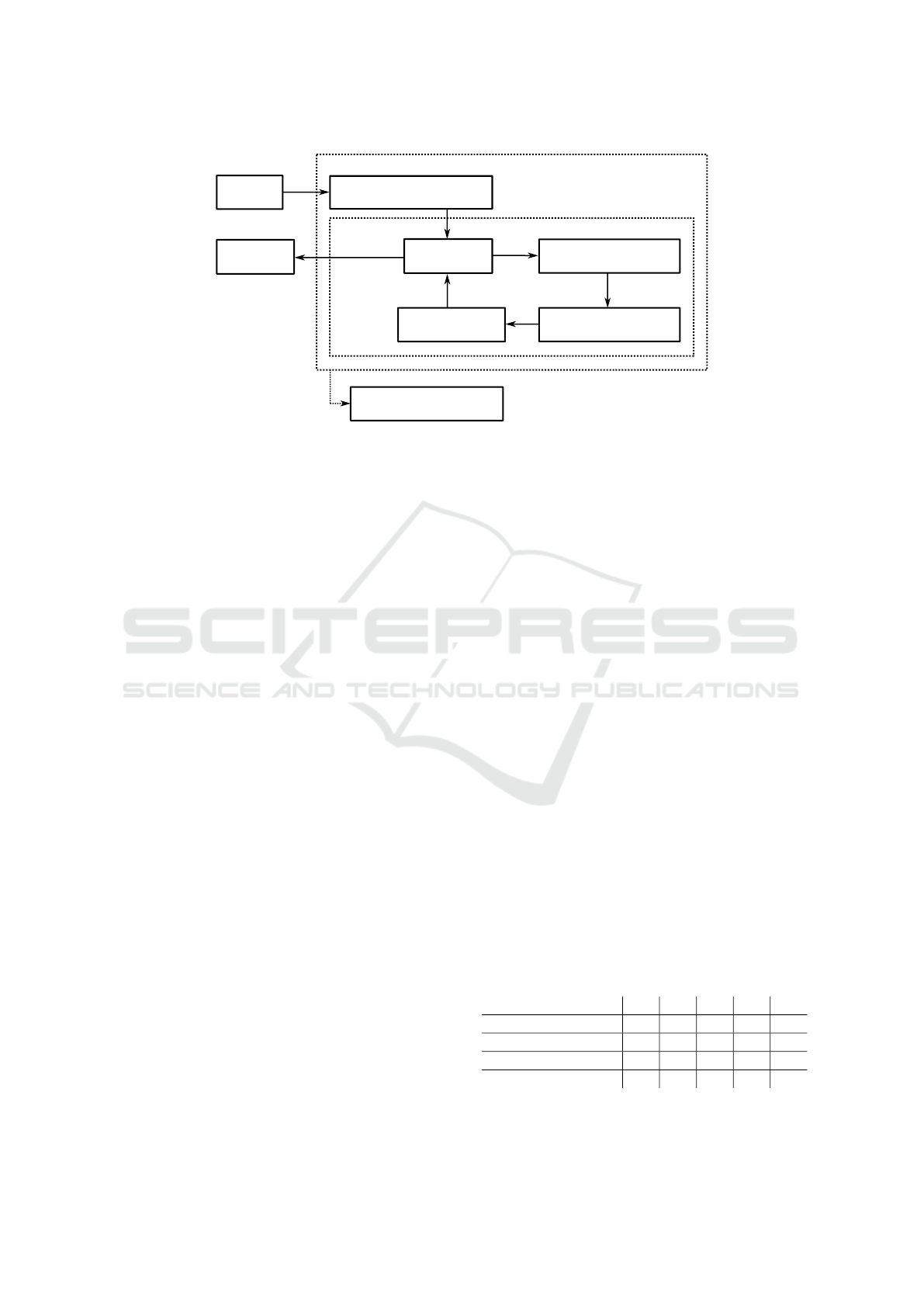
Clause Selection

Variable Selection

Flip Variable

Satisfied?

No Solution found

CNF

For Max-Tries

Assign all Variables

For Max-Flips

Solution

Yes

Figure 3: Framework for SLS Solvers.

The efﬁciency of SLS solvers is impacted by the

random initialization of all variables at the start. NLo-

calSAT uses a Neural Network to predict a solution

for the CNF. This solution does not solve the CNF but

can serve as the SLS solver’s starting point. On aver-

age 88% of the initial assignment was already correct.

Using this ’smart guess’ as an initial assignment is of-

ten signiﬁcantly better than a random assignment, the

closer the initialization is to the solution the easier it

is for the solver to ﬁnd a solution (Zhang et al., 2020).

3 CONTRIBUTION

This work explores if SLS-solvers are suitable for

the MAPF problem. To the author’s awareness, the

MAPF-SAT approach has only been used in combi-

nation with CDCL-solvers. SLS-solvers and CDCL-

solvers for MAPF-SAT are compared in combination

with the MDD-SAT approach (Surynek et al., 2016)

under the makespan objective. The effects of lazy and

eager encodings on the performance are also exam-

ined. Furthermore aiding the solver with a meaning-

ful initial assignment of variables is explored. The

assignment is computed by translating sampled paths

from the MDDs for all agents.

4 METHOD

For the comparison of SLS and CDCL solvers, the

ProbSAT (Balint and Sch

oning, 2012) algorithm was

chosen for its simplicity and Glucose 4.0 (Audemard

et al., 2013) was selected as a fair comparison as

it is a performant solver that was published around

the same time as ProbSAT. Glucose 4.0 is heavily

based on MiniSAT 2.2 (E

en and S

orensson, 2003).

Both Solvers were tested with ﬁve different variants

shown in table 1. Variants include eager (V 1, V 2)

and lazy encodings (V 3, V 4, V 5). Both encodings are

tested with and without an initial assignment to aid the

solver. When a lazy encoding is used with an initial

assignment (V 4, V5) conﬂict constraints for all vertex

collisions of the sampled paths are added to the CNF,

this is not necessary for the eager encoding (V 2) be-

cause the CNF already contains conﬂict clauses that

prevent all possible vertex collision. Update Assign-

ment in table 1 is only relevant for the lazy encoding,

it indicates that after a solution is found by the SAT-

solver which contains conﬂicts a new assignment is

generated based on the solution (V 3, V 4), if no new

initial assignment is provided (V 5) the initial assign-

ment is used again.

Additionally, for the ProbSAT solver, an alterna-

tive initial assignment that sets all variables negative

was tested. When no initial assignment is provided

and no new initial assignment is generated after a so-

lution with conﬂicts is found, the solver will most

likely ﬁnd a new solution that is completely different

from the previous one. Early tests often needed many

iterations to arrive at a solution without conﬂicts. The

idea is to reﬁne the encoding for one solution, if the

solver is restarted and comes up with a different solu-

tion it takes a lot of additional iterations.

Table 1: Algorithm Variants.

V 1 V 2 V 3 V 4 V 5

Eager Encoding ✓ ✓ - - -

Lazy Encoding - - ✓ ✓ ✓

Initial Assignment - ✓ - ✓ ✓

Update Assignment - - ✓ ✓ -

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

4.1 Implementaion

The algorithm 1 was implemented in Python. For

the CDCL SAT solver, PySAT was used which pro-

vides efﬁcient Python wrappers for the code of CDCL

solvers originally implemented in the C/C++ lan-

guages (Ignatiev et al., 2018).

4.1.1 Hyperparameters and Versions of

ProbSAT

For the local SAT solver, brake-only ProbSAT was

chosen, as the make-value for this solver proved to be

of little impact compared to the brake-value (Balint

and Sch

oning, 2012). No optimal brake-constant (cb)

value for MAPF-SAT is known and it probably varies

with the size of the statespace. Therefore the cb-

values derived by Balint and Sch

oning from experi-

ments with k-SAT, which are dependent on the max-

imum clause size (k), were used. Whether the poly-

Table 2: cb values for different k.

k ≤ 3 4 5 6 ≥ 7

oldcb 2.06 2.85 3.7 5.1 5.4

newcb 2.06 3.0 3.88 4.6 4.6

nomial or exponential function of the ProbSAT algo-

rithm is better suited for MAPF-SAT is also unknown

but it was shown that for smaller maximum clause

lengths (k ≤ 4) the polynomial function worked better

and for larger ones the exponential function worked

better (Balint and Sch

oning, 2012). Thus unless the

MAPF instance is very small the exponential function

with the highest cb value is chosen. The original ver-

sion of this algorithm that does not use the make value

and is written in the C language was obtained from

GitHub (Adrian Balint, 2022). This version from

2012 comes with the ’old cb’ values shown in table 2

and uses Pseudo Depth First Search (PDFS) for clause

selection, it will be referred to as old-ProbSAT. PDFS

improves on random clause selection by iterating over

the list of unsatisﬁed clauses, selecting the clause at

index j%m (% = modulo), where j is the number of

ﬂips and m is the highest index of the list of unsatis-

ﬁed clauses. It is not clear why exactly this performs

much better but it is probably related to incorporating

the ﬂips into the decision and it might select clauses

more evenly. A newer version from 2014 that imple-

ments the possibility of using XOR caching of brake

values, computation of a second brake value with a

second brake constant (cb2 = 1), and reﬁned newcb

values shown in table 2 (Balint et al., 2014). This

version was also used by NlocalSAT (Zhang et al.,

2020). The newer version will be referred to as new-

ProbSAT.

These versions were modiﬁed to be able to in-

corporate an initial assignment of variables. Further-

more, additional timers were implemented to obtain

the time it took to ﬁnd a solution or terminate. The

Maximum number of ﬂips before a restart was conﬁg-

ured to 10000000, with the maximum number of tries

set to 1000. In later tests, the maximum tries were

set to 100 or 10 to reduce the run time for instances

without a solution.

4.1.2 Creating the CNF with MDDs

The makespan was determined by comparing the

length of all the shortest paths of all agents. To be

able to create the MDDs a distance matrix was cre-

ated for each agent using the Dijkstra algorithm which

holds the distance from all vertices to the goal. The

MDDs were created with the distance matrices, the

starting points, and the makespan by evaluating dur-

ing each timestep which neighbouring positions of

reached vertices can still reach the goal in the remain-

ing time.

The CNF was created by adding one variable for

each node in the MDDs, representing all possible

agent positions on the shortest paths to the goal. For

each layer (timestep) in the MDDs, one clause was

added that constrained the agent to be at one of the

valid positions at that timestep. This also ensures

agents start at the start and ﬁnish at the goal since

the ﬁrst and last layers of the MDDs only hold the

start and the goal respectively. Movement constraints

were added to ensure each agent only moves from one

node to its children nodes in the MDD, which can in-

clude the same position if there is sufﬁcient time to

still reach the goal if the agent waits. For the ea-

ger encoding, all possible conﬂicts were determined

by computing the overlap of the MDDs, and conﬂict

constraints were added for all overlapping nodes.

4.1.3 Initial Assignments

Initial assignments for the ProbSAT solver are cre-

ated by sampling paths from all agent’s MDDs and

translating them to a solution of the CNF, assigning

all variables representing the paths as true and all oth-

ers as false. Initial assignments for the Glucose are

also called assumptions and will be part of the solu-

tion the solver ﬁnds. It is necessary to only supply a

partial assignment that leaves room for the solver to

ﬁnd a valid solution. This was achieved by ﬁrst sam-

pling paths from the MDDs which are then checked

for collisions. For each found collision the path of

one or both agents of each collision can be excluded,

resulting in a partial assignment that has no conﬂicts.

It was ﬁrst decided to only exclude one agent’s path

Solving Multi-Agent Pathﬁnding with Stochastic Local Search SAT Algorithms

per collision to aid the solver more. This sometimes

caused the solver to not ﬁnd a solution with the ini-

tial makespan because the assumptions were too strict

and led to an unnecessary increase in the makespan.

Thus for later tests, it was decided to exclude all paths

of agents involved in collisions from the assumption

assignment.

The solution a solver which is working with a lazy

encoding needs to be checked for collisions. If any

are found constraint clauses to prevent these colli-

sions are added to the CNF and the solver runs again.

Either with the same initial assignment or with an up-

dated version. The Glucose solver always requires to

exclude the paths of agents involved in newly found

collisions from it assumptions to be able to ﬁnd a so-

lution with the new constraints. The update Assign-

ment version of the algorithms constructs a new initial

assignment from the latest solution instead of always

working with the same assignment which was com-

puted from by sampling paths from the MDDs.

Data: MAPF problem: set of starts and goals,

grid map

Result: Shortest paths for each set of starts and

goals

Makespan = length of the longest shortest path

across all agents ;

Solution found = False;

while not Solution found do

MDDs = Create MDDs from paths with

length of Makespan;

CNF = Create CNF from MDDs ;

if Initial Assignment then

Initial Assignment(MDDs);

check for collisions;

Add collisions constraints to CNF;

end

Solution found = SAT-Solver(CNF);

check solutions for collisions;

while Solution contains collisions do

Add Collision constraints to CNF ;

if Update Initial Assignment then

new Initial Assignment(solution)

end

Solution found = SAT-solver(CNF) ;

check solutions for collisions;

end

Makespan ++;

end

Algorithm 1: SAT solver with lazy encoding.

4.2 Benchmarks

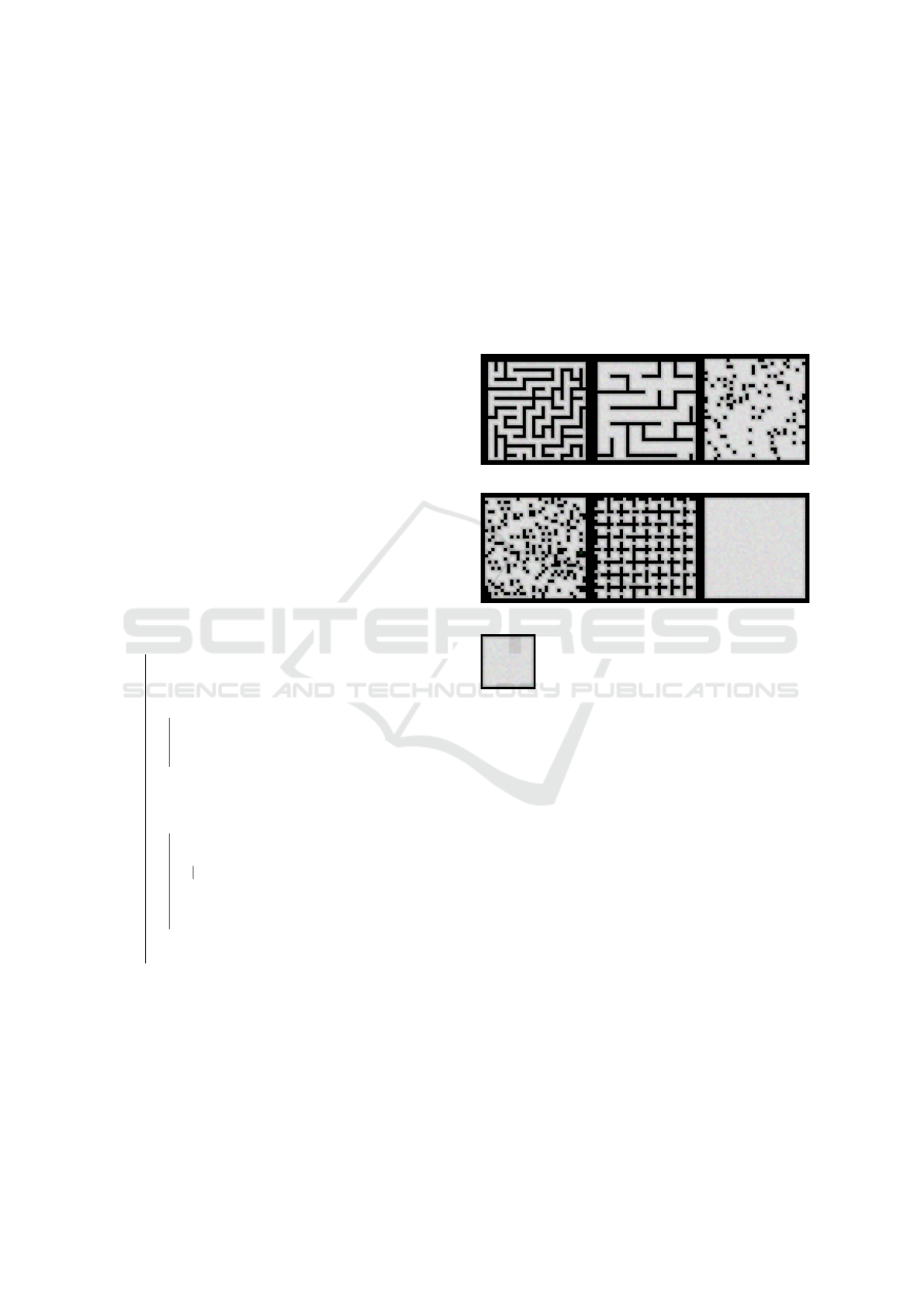
The Sat Solvers were compared on the maps ’empty-

16-16’, ’empty-32-32’, ’maze-32-32-2’, ’maze-

32-32-4’, ’random-32-32-10’, ’random-32-32-20’,

’room-32-32-4’ which are published on movin-

gai.com in the benchmark section (Stern et al., 2019).

Six of the maps shown in ﬁgure 4 have a grid size of

32x32 and one has a grid size of 16x16. For each map,

movingai.com also provides 25 even and 25 random

scenarios with starts and goals for agents. All algo-

rithm variants were tested on all maps with 10 agents

100 times. 10 sets of starts and goals for the agents

were obtained from the ﬁrst 10 even scenarios of each

map. This amounts to 700 tests for every variant of

all algorithms.

maze-32-32-2 maze-32-32-4 random-32-32-10

random-32-32-20 room-32-32-4 empty-32-32

empty-16-16

Figure 4: The Benchmark Maps of movingai.

4.3 Hardware

The algorithm was run in Visual Studio Code on

a Framework Laptop 13 with a 13th Gen Intel(R)

Core(TM) i7-1360P processor and 32GB SO-DIMM

DDR4 Synchronous 320 working memory.

5 RESULTS

In only two of the 700 tests that were carried out for

each variant of each solver, it was not possible to

ﬁnd a solution with the initial makespan, which led

the ProbSAT solvers to run through all of their ﬂips

(10000000) for each of their tries until they reached

their max tries. These two tests were excluded from

the data analysis for all solvers because they heavily

skew the means for ProbSAT. During all other tests,

the ProbSAT solvers found a solution on the ﬁrst try,

in the two tests in which the makespan needed to be

increased the ProbSAT algorithms also only needed

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

one try after the increase was made. Originally the

max tries parameter was set to 1000 in later experi-

ments it was reduced to 100 and eventually reduced

to 10 but could have been set to 1 too as that would

have been sufﬁcient in this dataset.

The assumptions provided for the Glucose solver

initially only excluded one agent’s path of each col-

lision that was found in the initial assignment, this

proved rather restrictive as the Glucose solver was un-

able to ﬁnd a solution with the initial makespan for 50

out of the 700 tests. Relaxing the initial assumptions

by excluding all paths of agents which are involved in

a collision prevented these increases in makespan.

5.1 Creation of MDDs

MDDs were always created in the same way for both

solvers across all variants. The mean creation time

was 0.3736s (std= 0.4770s). The faster creation only

took 0.0045s while the longest took 7.4262s. The

time it takes to create a MDD is proportional to the

makespan (mean:52.68, std:24.36) which had a mini-

mum of 11 and a maximum of 114.

5.2 Comparing Eager and Lazy

Encoding

Creating eager and lazy CNF encodings from the

MDDs involved a mean of 58553 variables (std =

37831), the smallest CNF consisted of only 1190 vari-

ables while the biggest consisted of 185539. Eager

encodings had a mean of 7238475 clauses (std =

6547660, min = 11726, max = 47621632) while lazy

encodings had a mean of 7174070 (std = 6491100,

min = 11124, max = 47234525). The lazy encod-

ing was computed in a mean time of 16.0434s (std =

18.5569s) while it took an average of 17.0622s (std =

19.1832s) to compute the eager encoding, the lazy

encoding was computed signiﬁcantly(p = 3.252e

−5

)

faster than the eager encoding by approximately one

second. This gives a headstart to variants V 3, V 4 and

V 5.

5.3 Solver Comparison

The upper part of table 3 depicts the mean number

of operations the variants (see table 1) of all tested

solvers needed to arrive at a valid solution. For Glu-

cose4 these operations consist of the decisions and

the propagations together, which are also shown sepa-

rately in table 4 in the appendix. The number of oper-

ations for ProbSAT is the number of ﬂipped variables.

The lower part of table 3 shows the mean cpu-time

the solvers needed to compute a solution. The run-

time and number of operations for V1 and V2 were

obtained from single runs, while the entries of the

variants V3, V4 and V5 are the sum of multiple runs,

where each run reﬁned the CNF by adding found col-

lisions until a valid solution was found.

Glucose V2 exhibited the fastest solving time,

whereas ProbSAT (oldcb, cb2) V2 required the fewest

operations.

5.3.1 Number of Operations

Differences Between Solvers: An ANOVA test fol-

lowed by Tukey’s HSD post hoc signiﬁcance test with

a signiﬁcance Niveau of 0.05% showed a signiﬁcant

difference between the number of operations of the

Glucose4 solver and all ProbSAT solvers.

Differences Between Variants: Testing for signiﬁ-

cant differences between the variants regarding solver

operations revealed two signiﬁcantly different groups,

V1, V3 and V2, V4, V5. A follow-up test in each of

these groups found no signiﬁcant difference between

V1 and V3, no signiﬁcant differences between V2 and

V4 but a signiﬁcant difference between V5 and V2 as

well as between V5 and V4.

Differences Between All Instances: An ANOVA test

followed by Tukey’s HSD post hoc signiﬁcance test

with a signiﬁcance niveau of 0.05% revealed that the

number of operations are signiﬁcantly different be-

tween Glucose and all ProbSAT versions and between

most Variants. No signiﬁcant difference was found

across the different versions of ProbSAT in the vari-

ants V1, V2, V3 V4 and V5, also no signiﬁcant dif-

ference between variants V1 and V3, as well as no

signiﬁcant difference between V2, V4 and V5 (for

ProbSAT) was found. Furthermore, there was no sig-

niﬁcant difference between Glucose4 V4 and V5.

5.3.2 Runtimes

Differences Between Solvers: An ANOVA test fol-

lowed by Tukey’s HSD post hoc signiﬁcance test with

a signiﬁcance niveau of 0.05% showed a signiﬁcant

difference between the solving times of the Glucose4

solver, the newProbSAT solvers and the oldProbSAT

solvers, but no signiﬁcant differences between old and

new cb values. No signiﬁcant differences between

the newProbSAT versions suggest that the inﬂuence

of the cb2 parameter is very small.

Differences Between Variants: An ANOVA test fol-

lowed by Tukey’s HSD post hoc signiﬁcance test with

a signiﬁcance niveau of 0.05% found no signiﬁcant

differences between the variants V 4 and V 5. There

were signiﬁcant differences between all other vari-

ants.

Solving Multi-Agent Pathﬁnding with Stochastic Local Search SAT Algorithms

Table 3: Runtimes and operations of different solvers.

Solver Operations V 1 V 2 V 3 V 4 V 5

Glucose 4 115933.63 8240127 188023.93 159542.32 152200.24

ProbSAT (newcb,cb2) 28573.17 10.67 28577.42 10.59 14.00

ProbSAT (oldcb,cb2) 28572.66 10.20 28577.41 10.45 14.58

ProbSAT (newcb,nocb2) 28573.17 10.68 28577.42 10.25 14.01

oldProbSAT (oldcb) 28634.05 10.57 28638.58 10.33 14.10

oldProbSAT (newcb) 28634.34 10.49 28638.59 10.81 14.67

Solver Times [s]

Glucose 4 0.0234 0.0233 0.0378 0.0385 0.0350

ProbSAT (newcb,withcb2) 0.0930 0.0447 0.1265 0.0486 0.0488

ProbSAT (oldcb,withcb2) 0.0909 0.0424 0.1227 0.0467 0.0469

ProbSAT (newcb, nocb2) 0.0914 0.0430 0.1242 0.0466 0.0462

oldProbSAT (oldcb) 0.1126 0.0292 0.1211 0.0312 0.0318

oldProbSAT (newcb) 0.1138 0.0292 0.1217 0.03187 0.03186

Differences Between All Instances: An ANOVA test

followed by Tukey’s HSD post hoc signiﬁcance test

with a signiﬁcance niveau of 0.05% revealed three

signiﬁcantly different groups of solver times. The ﬁrst

group includes all Glucose4 variants and the variants

V2, V4 and V5 of the oldProbSAT, the second group

includes all ProbSAT V3 versions and the oldProb-

SAT V1 versions and the third group includes all new-

ProbSAT V1 versions. Since there were a lot of tests

carried out Tukey’s HSD post hoc is rather restric-

tive as it adjusts for the number of carried out tests.

Thus three more signiﬁcance tests were carried out,

one in each of the three found groups. Only the test

in the ﬁrst group revealed signiﬁcant differences be-

tween the following subgroups: Glucose V1 and V2,

Glucose V3 and V4, and oldProbSAT V2, V4, V5,

Glucose V5.

5.4 Alternative Initial Assignment

The alternative initial assignment which set all vari-

ables to negative also referred to as zero initialization

was only tested with some solver versions of ProbSAT

V2, V4 and V5 and are shown in table 4 in the ap-

pendix. This form of the initial assignment was very

helpful to the solver, decreasing the needed operations

and CPU time immensely but the performance with it

was still signiﬁcantly worse compared to the initial

assignment based on the shortest paths.

6 DISCUSSION

The results demonstrate that SLS solvers, speciﬁcally

ProbSAT, are viable alternatives to CDCL solvers like

Glucose 4.0 for solving the MAPF problem under the

makespan objective.

6.1 Initial Assignments

One key ﬁnding is the signiﬁcant performance im-

provement when initial variable assignments based on

agents’ shortest paths are provided. This suggests that

the quality of initial assignments is crucial for the ef-

ﬁciency of SLS solvers in this domain.

While the ProbSAT algorithms performed much

better when given an initial assignment the Glucose4

algorithm does not show a huge beneﬁt. When their

number of operations is examined closer (see table 4)

it reveals that in variants V1 and V2, the number of

decisions decreases while the number of propagations

remains the same, this suggests that for computation

time the propagations are more relevant compared to

the decisions. The results also suggest that updating

the initial assumptions for the Glucose solver based

on found solutions leads to a slight decrease in per-

formance while sticking with the same initial assump-

tions and only excluding paths of agents involved in

collisions does perform slightly better. However us-

ing relaxed assumptions can theoretically still prevent

the solver from ﬁnding a solution, which can be pre-

vented by decreasing the number of assumptions to

zero before an increase in makespan is carried out.

Providing an initial assignment for the ProbSAT al-

gorithms that represents the latest found solution with

collisions decreases the needed number of operations

slightly compared to always using the same initial as-

signment. This effect is more apparent when exam-

ining the number of operations for the zero initialisa-

tion where the number of operations was reduced by

approximately 65%. While the zero initialization is a

signiﬁcant improvement over no initialization it per-

forms worse compared to the initialization based on

the shortest paths. However, it is an alternative that

needs less computation compared to the shortest path

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

Table 4: Operations and Runtimes of different solvers.

Solver V 1 V 2 V 3 V 4 V 5

Glucose4 Decisions 57490.87 23958.51 76533.57 43373.08 47648.82

Glucose4 Propagations 58442.76 58442.76 111490.36 116169.24 104551.42

ZeroInit operations

ProbSAT (newcb,cb2) - 539.3879 - 546.2040 1588.4741

ProbSAT (oldcb,cb2) - 539.1465 - 546.1868 1521.0201

oldProbSAT (oldcb) - 539.1264 - 545.7845 1514.1178

ZeroInit Times [s]

ProbSAT (newcb,cb2) - 0.0532 - 0.0985 0.1490

ProbSAT (oldcb,cb2) - 0.0673 - 0.1110 0.1809

oldProbSAT (oldcb) - 0.0330 - 0.0643 0.0879

initialization, which might be relevant if more agents

are deployed or when bigger maps are used.

6.2 Lazy and Eager Encoding

Another ﬁnding is that lazy encodings are computed

more rapidly than eager encodings. While solvers of-

ten have to run multiple times with the lazy encoding

leading to longer solving times compared to the ea-

ger encoding, they are still faster since the time saved

during the computation of the encoding exceeds the

extra solving time. The most performant variants are

V4 and V5, which do not signiﬁcantly differ in com-

putation time.

6.3 Solver Performance

Overall the fastest observed performances were the

oldProbSAT versions V4 and V5 as well as the Glu-

cose4 V5, as there was no signiﬁcant difference be-

tween their computation times, ProbSAT can solve

the MAPF problem just as well as Glucose 4 on the

examined maps when the makespan did not need to

be increased. For the cases when the makespan does

need to be increased, it is crucial to have the smallest

possible amount of maxTries and maxFlips, while the

observed performance suggests that maxTries can be

set to 1 the optimal number of ﬂips is not easy to de-

cide but should probably be based on the number of

variables and clauses of the CNF.

It is also astonishing how few operations the Prob-

SAT solver needs when an initial assignment, based

on the shortest paths of the agents, is provided. There

is also a not signiﬁcant but slight difference between

old and new cb values, which suggests that a greed-

ier algorithm might need fewer operations. Using a

cb2 value did not have a signiﬁcant effect. The older

implementation of ProbSAT is more performant with

an initial assignment but less performant without it

compared to the newer implementation. They make

no signiﬁcantly different amount of ﬂips, jet the old

version is signiﬁcantly faster.

6.4 Future Research Directions

Optimization of Initial Assignments: With an ini-

tial assignment the problem does not seem so hard

anymore as the number of operations becomes very

few for the ProbSAT algorithms. The initial as-

signments based on sampled shortest paths from the

MDDs worked well but all paths are chosen randomly.

This might be improved by guiding the sampling of

the initial paths preventing agents from entering the

same regions if possible and thereby preventing some

collisions as agents occupy different parts of the map.

Including Edge Conﬂicts: The presented algorithm

does not detect edge conﬂicts, which means agents

are allowed to swap positions. This can be solved by

including edges in the MDD encodings and handling

them like additional positions. Alternatively, it is also

possible to use the current vertex encodings and check

for edge conﬂicts in the solution. If any occur special

edge conﬂict clauses, to prevent a position swap, can

be added to the CNF.

Scaling to Larger Problems: It would be valuable

to investigate how the performance of SLS solvers

with different hyperparameters and the initial assign-

ments scales with larger maps and a greater number

of agents.

6.4.1 Parameter Tuning

The cb parameters for ProbSAT used in this study

were tuned based on uniform k-SAT instances (Balint

and Sch

oning, 2012) (Balint et al., 2014). There was

no signiﬁcant difference between the tested cb val-

ues. However, there are probably more optimal set-

tings for MAPF-SAT. The slight difference in perfor-

Solving Multi-Agent Pathﬁnding with Stochastic Local Search SAT Algorithms

mance with the old and the new cb values suggests

that being greedier might be more beneﬁcial in com-

bination with an initial assignment.

Determining that there is no solution with the ini-

tial makespan and deciding to increase it is crucial

and can be done by the ProbSAT solver in a reason-

able time if the maxTries and maxFlips are adjusted

to be as little as possible. More exploration in sce-

narios that are not solvable with the initial makespan

is needed to form a better understanding of feasible

settings for the maxTries and maxFlips parameters al-

though the results of this study suggest a maxTries

value of 1 is sufﬁcient with a relatively large number

of maxFlips and the tested cb values.

An interesting approach would be to reduce the

number of ﬂips to very few and try to ﬁnd a solu-

tion with a high cb value at ﬁrst and to decrease the

cb value while increasing the number of ﬂips during

consecutive tries.

6.4.2 Exploration of Different Algorithms

Extending the study to other SLS solvers and to other

objectives like the sum of cost objective, which ex-

pands the MDDs individually, could provide a more

comprehensive understanding of the strengths and

limitations of SLS solvers in MAPF. An interesting

addition to the ProbSAT solver is the xor caching of

brake values, which was found to be too costly for

bigger clauses (k > 6), but Balint, Biere, Fr

ohlich, and

Sch

oning suggest a hybrid solution that performs xor

caching for clauses of length 3 or less but does not for

longer ones. They also suggest clause weights as one

way to improve the quality of clause selection heuris-

tics (Balint et al., 2014).

Hybrid Solvers: Another promising avenue of re-

search combines CDCL and local solvers into hy-

brid solvers which outperform most other solvers that

solely rely on one of the two paradigms (Cai and

Zhang, 2021). In the 2020 SAT competition all win-

ning solvers of the Main track periodically schedule

runs of a SLS solver and import statistical informa-

tion generated in unsuccessful SLS runs to reconﬁg-

ure weights in their branching heuristics (Froleyks

et al., 2021).

Neural Networks: The usage of Neural Networks

(NNs) proved beneﬁcial for the NlocalSAT algorithm

to ﬁnd meaningful initial assignments for SLS solvers

(Zhang et al., 2020). NNs have also been used for

CDCL solvers and are utilizable for performance im-

provements (Selsam et al., 2018) (Li and Si, 2022).

6.5 Limitations

Benchmarks: The study was conducted on a spe-

ciﬁc set of benchmark maps, which do not cover the

full spectrum of MAPF problem instances encoun-

tered in practical applications. Future work should

include a wider variety of MAPF instances, such as

those with different grid sizes, obstacle densities, and

agent counts.

Computational Resources: The experiments were

run on a single type of hardware. Performance eval-

uations on different hardware conﬁgurations would

provide a more generalizable understanding of the

solvers’ efﬁciency and how performance scales with

computational power and memory availability.

Implementation Constraints: While the solvers

were implemented in C++, the overarching algorithm

was implemented in Python, which may not be the

most efﬁcient programming language for this pur-

pose. Implementing the algorithms in a more perfor-

mant language like C++ could yield different results.

7 CONCLUSION

This study has shown that SLS solvers, particu-

larly ProbSAT, are capable of effectively solving the

MAPF problem under the makespan objective. The

key ﬁnding is that providing meaningful initial as-

signments signiﬁcantly boosts the performance of

SLS solvers, bringing them on par with CDCL solvers

like Glucose 4.0 in speciﬁc scenarios. This insight

opens up new avenues for research and development

in the ﬁeld of MAPF. These are the contributions of

this study to the Field:

• Introduction of SLS Solvers to MAPF: It was

demonstrated that SLS solvers are viable options

for MAPF, adding them to the range of tools avail-

able for researchers and practitioners.

• Insights into Initial Assignments: Providing a

meaningful initial assignment that serves as a

starting point which is already closer to a solu-

tion can greatly enhance the performance of SLS

solvers.

• Lazy Encoding Efﬁciency for SLS Solvers:

Lazy encodings are faster to compute than eager

encodings and should be preferred when working

with SLS solvers, despite the need for multiple

solver runs.

In conclusion, this study provides a foundational ex-

ploration into the viability of SLS solvers for MAPF,

highlighting the importance of initial assignments and

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

suggesting several promising directions for future re-

search. By improving and extending the use of SLS

solvers, we can enhance the efﬁciency and scalability

of MAPF solutions, beneﬁting a wide range of practi-

cal applications.

ACKNOWLEDGEMENTS

This research has been supported by GA

CR - the

Czech Science Foundation, grant registration number

22-31346S.

REFERENCES

Adrian Balint, M. S. (2022). ProbSAT: an efﬁcient im-

plementation of a variant of the probsat solver pre-

sented in: ”choosing probability distributions for

stochastic local search and the role of make ver-

sus break” by adrian balint, uwe sch

oning. GitHub:

https://github.com/adrianopolus/probSAT.

Audemard, G., Lagniez, J.-M., and Simon, L. (2013). Im-

proving glucose for incremental sat solving with as-

sumptions: Application to mus extraction. In Interna-

tional conference on theory and applications of satis-

ﬁability testing, pages 309–317. Springer.

Balint, A., Biere, A., Fr

ohlich, A., and Sch

oning, U. (2014).

Improving implementation of sls solvers for sat and

new heuristics for k-sat with long clauses. In Theory

and Applications of Satisﬁability Testing–SAT 2014:

17th International Conference, Held as Part of the Vi-

enna Summer of Logic, VSL 2014, Vienna, Austria,

July 14-17, 2014. Proceedings 17, pages 302–316.

Springer.

Balint, A. and Fr

ohlich, A. (2010). Improving stochastic lo-

cal search for sat with a new probability distribution.

In Theory and Applications of Satisﬁability Testing–

SAT 2010: 13th International Conference, SAT 2010,

Edinburgh, UK, July 11-14, 2010. Proceedings 13,

pages 10–15. Springer.

Balint, A. and Manthey, N. (2013). Boosting the perfor-

mance of sls and cdcl solvers by preprocessor tuning.

In POS@ SAT, pages 1–14.

Balint, A. and Sch

oning, U. (2012). Choosing probability

distributions for stochastic local search and the role

of make versus break. In International Conference

on Theory and Applications of Satisﬁability Testing,

pages 16–29. Springer.

Bart

ak, R., Zhou, N.-F., Stern, R., Boyarski, E., and

Surynek, P. (2017). Modeling and solving the multi-

agent pathﬁnding problem in picat. In 2017 IEEE 29th

International Conference on Tools with Artiﬁcial In-

telligence (ICTAI), pages 959–966. IEEE.

Biere, A. (2014). Yet another local search solver and

Lingeling and friends entering the SAT Competition

2014. In Balint, A., Belov, A., Heule, M., and

arvisalo, M., editors, Proc. of SAT Competition 2014

– Solver and Benchmark Descriptions, volume B-

2014-2 of Department of Computer Science Series of

Publications B, pages 39–40. University of Helsinki.

Biere, A. (2017). Cadical, lingeling, plingeling, treengeling

and yalsat entering the sat competition 2018. Proceed-

ings of SAT Competition, 14:316–336.

Biere, A., Heule, M., and van Maaren, H. (2009). Handbook

of satisﬁability, volume 185. IOS press.

Boyarski, E., Felner, A., Stern, R., Sharon, G., Betza-

lel, O., Tolpin, D., and Shimony, E. (2015). Icbs:

The improved conﬂict-based search algorithm for

multi-agent pathﬁnding. In Proceedings of the In-

ternational Symposium on Combinatorial Search, vol-

ume 6, pages 223–225.

Cai, S. and Zhang, X. (2021). Deep cooperation of cdcl

and local search for sat. In Theory and Applications

of Satisﬁability Testing–SAT 2021: 24th International

Conference, Barcelona, Spain, July 5-9, 2021, Pro-

ceedings 24, pages 64–81. Springer.

en, N. and S

orensson, N. (2003). An extensible sat-solver.

In International conference on theory and applica-

tions of satisﬁability testing, pages 502–518. Springer.

Erdem, E., Kisa, D., Oztok, U., and Sch

uller, P. (2013).

A general formal framework for pathﬁnding problems

with multiple agents. In Proceedings of the AAAI Con-

ference on Artiﬁcial Intelligence, volume 27, pages

290–296.

Felner, A., Li, J., Boyarski, E., Ma, H., Cohen, L., Kumar,

T. S., and Koenig, S. (2018). Adding heuristics to

conﬂict-based search for multi-agent path ﬁnding. In

Proceedings of the International Conference on Au-

tomated Planning and Scheduling, volume 28, pages

83–87.

Felner, A., Stern, R., Shimony, S., Boyarski, E., Golden-

berg, M., Sharon, G., Sturtevant, N., Wagner, G., and

Surynek, P. (2017). Search-based optimal solvers for

the multi-agent pathﬁnding problem: Summary and

challenges. In Proceedings of the International Sym-

posium on Combinatorial Search, volume 8, pages

29–37.

Froleyks, N., Heule, M., Iser, M., J

arvisalo, M., and Suda,

M. (2021). Sat competition 2020. Artiﬁcial Intelli-

gence, 301:103572.

Hart, P. E., Nilsson, N. J., and Raphael, B. (1968). A for-

mal basis for the heuristic determination of minimum

cost paths. IEEE transactions on Systems Science and

Cybernetics, 4(2):100–107.

Ignatiev, A., Morgado, A., and Marques-Silva, J. (2018).

PySAT: A Python toolkit for prototyping with SAT or-

acles. In SAT, pages 428–437.

Kautz, H. and Selman, B. (1996). Pushing the envelope:

Planning, propositional logic, and stochastic search.

In Proceedings of the national conference on artiﬁcial

intelligence, pages 1194–1201.

Li, Z. and Si, X. (2022). Nsnet: A general neural probabilis-

tic framework for satisﬁability problems. Advances

in Neural Information Processing Systems, 35:25573–

25585.

Solving Multi-Agent Pathﬁnding with Stochastic Local Search SAT Algorithms

Luna, R. and Bekris, K. E. (2011). Push and swap: Fast co-

operative path-ﬁnding with completeness guarantees.

In IJCAI, volume 11, pages 294–300.

Selman, B., Kautz, H., et al. (1993). Domain-independent

extensions to gsat: Solving large structured satisﬁabil-

ity problems. In IJCAI, volume 93, pages 290–295.

Selsam, D., Lamm, M., B

unz, B., Liang, P., de Moura,

L., and Dill, D. L. (2018). Learning a sat

solver from single-bit supervision. arXiv preprint

arXiv:1802.03685.

Sharon, G., Stern, R., Felner, A., and Sturtevant, N. R.

(2015). Conﬂict-based search for optimal multi-agent

pathﬁnding. Artiﬁcial intelligence, 219:40–66.

Sharon, G., Stern, R., Goldenberg, M., and Felner, A.

(2013). The increasing cost tree search for opti-

mal multi-agent pathﬁnding. Artiﬁcial intelligence,

195:470–495.

Silver, D. (2005). Cooperative pathﬁnding. In Proceedings

of the aaai conference on artiﬁcial intelligence and in-

teractive digital entertainment, volume 1, pages 117–

122.

Srinivasan, A., Ham, T., Malik, S., and Brayton, R. K.

(1990). Algorithms for discrete function manipu-

lation. In 1990 IEEE international conference on

computer-aided design, pages 92–93. IEEE Computer

Society.

Standley, T. (2010). Finding optimal solutions to coopera-

tive pathﬁnding problems. In Proceedings of the AAAI

conference on artiﬁcial intelligence, volume 24, pages

173–178.

Standley, T. and Korf, R. (2011). Complete algorithms for

cooperative pathﬁnding problems. In IJCAI, pages

668–673. Citeseer.

Stern, R., Sturtevant, N., Felner, A., Koenig, S., Ma, H.,

Walker, T., Li, J., Atzmon, D., Cohen, L., Kumar, T.,

et al. (2019). Multi-agent pathﬁnding: Deﬁnitions,

variants, and benchmarks. In Proceedings of the In-

ternational Symposium on Combinatorial Search, vol-

ume 10, pages 151–158.

Surynek, P. (2010). An optimization variant of multi-robot

path planning is intractable. In Proceedings of the

AAAI conference on artiﬁcial intelligence, volume 24,

pages 1261–1263.

Surynek, P. (2014). Compact representations of coopera-

tive path-ﬁnding as sat based on matchings in bipartite

graphs. In 2014 IEEE 26th International Conference

on Tools with Artiﬁcial Intelligence, pages 875–882.

IEEE.

Surynek, P. (2016). Makespan optimal solving of coopera-

tive path-ﬁnding via reductions to propositional satis-

ﬁability. arXiv preprint arXiv:1610.05452.

Surynek, P. (2019a). Conﬂict handling framework in gen-

eralized multi-agent path ﬁnding: Advantages and

shortcomings of satisﬁability modulo approach. In

ICAART (2), pages 192–203.

Surynek, P. (2019b). Multi-agent path ﬁnding with continu-

ous time viewed through satisﬁability modulo theories

(smt). arXiv preprint arXiv:1903.09820.

Surynek, P., Felner, A., Stern, R., and Boyarski, E. (2016).

Efﬁcient sat approach to multi-agent path ﬁnding un-

der the sum of costs objective. In Proceedings of the

twenty-second european conference on artiﬁcial intel-

ligence, pages 810–818.

Surynek, P., Kumar, T. S., and Koenig, S. (2019). Multi-

agent path ﬁnding with capacity constraints. In AI* IA

2019–Advances in Artiﬁcial Intelligence: XVIIIth In-

ternational Conference of the Italian Association for

Artiﬁcial Intelligence, Rende, Italy, November 19–22,

2019, Proceedings 18, pages 235–249. Springer.

Wagner, G. and Choset, H. (2015). Subdimensional expan-

sion for multirobot path planning. Artiﬁcial intelli-

gence, 219:1–24.

Wang, K.-H. C., Botea, A., et al. (2008). Fast and memory-

efﬁcient multi-agent pathﬁnding. In ICAPS, volume 8,

pages 380–387.

Yu, J. and LaValle, S. (2013a). Structure and intractabil-

ity of optimal multi-robot path planning on graphs. In

Proceedings of the AAAI Conference on Artiﬁcial In-

telligence, volume 27, pages 1443–1449.

Yu, J. and LaValle, S. M. (2013b). Multi-agent path plan-

ning and network ﬂow. In Algorithmic Foundations of

Robotics X: Proceedings of the Tenth Workshop on the

Algorithmic Foundations of Robotics, pages 157–173.

Springer.

Zhang, W., Sun, Z., Zhu, Q., Li, G., Cai, S., Xiong,

Y., and Zhang, L. (2020). Nlocalsat: Boosting lo-

cal search with solution prediction. arXiv preprint

arXiv:2001.09398.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics