Epidemic Impact of Temporary Large People Mass Fluxes: The

COVID-19 and the Jubilee 2025 Reference Case

Paolo Di Giamberardino

and Daniela Iacoviello

Department of Computer, Control and Management Engineering Antonio Ruberti, Sapienza University of Rome, Italy

{paolo.digiamberardino, daniela.iacoviello}@uniroma1.it

Keywords:

Epidemic Spread, COVID–19, Multigroup Interactions, Population Flows, Jubilee 2025.

Abstract:

In the paper, the problem of the interaction between two separated population is considered when an infectious

disease is presented. An asymmetric behaviour is studied, with one smaller population receiving a people ﬂow

from a second more numerous one. For each of them, the different conditions with respect to the epidemic

status are considered as well as different numbers of ﬂowing individuals. The reference case in mind is the

possible COVID-19 epidemic during the next Jubilee 2025, where a very large amount of pilgrims are expected

to come in Italy and, mainly, in Rome, with numbers comparable with the usual living population. A theorical

study about the effects on the equilibria conditions, completed with a numerical analysis of different possible

scenarios, is reported in the paper, showing that it must be expected a sensible increment of the number of

infected individuals.

1 INTRODUCTION

The analysis of epidemic spread over a population

has been widely addressed, (Daley and Gani, 1999;

Martcheva, 2015), introducing compartmental mod-

els with increasing number of compartments as the

complexity of the epidemic dynamics required: SIR

(Di Giamberardino and Iacoviello, 2017), SIS, SEIR

(Casagrandi et al., 2006) and others, whose names are

given by the initials of the compartments names: Sus-

ceptible, Infected, Recovered, Exposed, and so on.

Following the particular characteristics of the epi-

demic modeled, higher dimensional models have

been introduced. This has happened in the very re-

cent years for the study of the COVID–19, being

important to distinguish level of infections, different

contagious ways, response to contagious, illness epi-

logue, in view of ﬁnding effective containment solu-

tions (Iranzo and P

erez–Gonz

alez, 2021).

Advanced modeling of COVID-19 addressed also

the dynamics of interactions between homogeneous

groups of individuals in the same population (Contr-

eras et al., 2020), clustered by age (Di Giamberardino

et al., 2020; Yue et al., 2023), by work, by fragility

due to co–morbidities, etc.

A further interactions in the epidemic modeling,

https://orcid.org/0000-0002-9113-8608

https://orcid.org/0000-0003-3506-1455

analysis and control is among populations: mobil-

ity of infected people contributes to the virus spread.

Mobility from and to Wuhan have been addresses

since the beginning of the infection (Ng et al., 2020),

and then studied for different populations or sub-

populations interactions (Di Giamberardino et al.,

2021b).

In this paper, a slightly different point of view is

assumed in the analysis of multi-group interactions:

the unidirectional people motion from one population

to another and the analysis of the effect on the receiv-

ing population only. The phenomena addressed are

all those situations in which the number of individ-

uals in one population in some quite long (months)

time periods suddenly increase doubling or more the

number of individuals. This is usually the situation of

some holiday places that in particular periods of the

year host a number of guests much higher than the

usual population. However, although the relative in-

crement is quite sensible, the absolute values are quite

contained.

A similar effect with much higher numbers is ex-

pected for the next Jubilee 2025, during which Italy,

but in particular Rome, will be interest by the pres-

ence of a very high number of pilgrims/tourists, num-

bers almost comparable with the population of the

city.

This event is then assumed as a case study in the

analysis of the effects of large ﬂuxes of individuals

Di Giamberardino, P. and Iacoviello, D.

Epidemic Impact of Temporary Large People Mass Fluxes: The COVID-19 and the Jubilee 2025 Reference Case.

DOI: 10.5220/0012945400003822

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 567-578

ISBN: 978-989-758-717-7; ISSN: 2184-2809

567

towards a population from outside regions, assumed

behaving like a second population.

The paper is organized as follows. Section 2 is

devoted to address the SEIR model adopted, recalling

dynamic characteristics in terms of equilibria and sta-

bility, and according to classical epidemic indicators

like the reproduction number. Then, the model un-

der study, which includes the population ﬂux and the

source second population dynamics, is introduced and

described in section 3. The full dynamics is studied in

Section 4 for what concerns new equilibria and their

stability, while in Section 5 the transient evolutions in

function of characteristic parameters of the infection

are presented, described and analyzed. A concluding

Section 6 summarizes the main results and introduces

the ongoing and the next steps of the present research.

2 THE MATHEMATICAL MODEL

For sake of simplicity, the epidemic modeling is per-

formed referring to the SEIR model, the most generic

one able to include also an incubation period which

can reduce the effects of possible infected mobility

limitations.

2.1 First Population: Recalls on SEIR

Model

The situation described takes into consideration one

population with an epidemic steady state condition,

which can be the epidemic free situation or the en-

demic one if the infection is already present in the

country. These two possibilities are obtained starting

from the equations

= −β

− µ

+ N

(1)

= β

− δ

− µ

(2)

= δ

− γ

− µ

(3)

= γI

− µ

(4)

This is a classical SEIR model, where the dynam-

ics of the Susceptible (S), Exposed (E), Infected (I)

and Removed (R) individuals of a population inter-

ested by an infection is modeled; they correspond, re-

spectively, to the healthy individuals that can be in-

fected, the infected but not yet infectious persons, the

infected individuals and the healed ones respectively.

The parameters describe the infection rate β, the death

rates µ

∗

, the incubation time

, the average healing

time

and the newborn individuals N. The subscript

”1” denoted the ﬁrst system here introduced, in view

of the description in next Section 3.

For such a system it is well known that there are

two equilibrium points: the epidemic free one

1,e







1,e



















(5)

and the endemic condition

1,e







1,e













(δ

+µ

)(γ

+µ

)

(δ

+µ

)

−

(γ

+µ

)

(δ

+µ

)(γ

+µ

)

−

(δ

+µ

)(γ

+µ

)

−







(6)

While the ﬁrst point always exists, for P

1,e

the con-

dition

≥

(δ

+ µ

)(γ

+ µ

)

(7)

must be satisﬁed in order to have all the state compo-

nents non negative.

At steady state, the disease condition clearly de-

pends on the stability of the two equilibrium points. In

order to obtain the conditions of the stability, a local

study can be performed starting from the computation

of the Jacobian for (1)–(4) evaluated in each equilib-

rium point, corresponding to the dynamic matrix of

the linear approximation of the nonlinear dynamics.

For the Jacobian, one has

J =





−β

−µ

0 −β

−δ

−µ

0 δ

−γ

−µ

0 0 γ

−µ





(8)

Setting, for shortening the expressions length,

1,1

= (δ

+ µ

); m

2,1

= (γ

+ µ

) (9)

and evaluating (8) at P

1,e

, matrix

J(P

1,e

) =







−µ

0 −β

0 −m

1,1

0 δ

−m

2,1

0 0 γ

−µ







(10)

is obtained. Stability can be deduced looking at its

eigenvalues. Two of them are λ

= −µ

and λ

−µ

, strictly negative by parameters deﬁnition. For

the remaining two, the roots of the polynomial

+ (m

1,1

+ m

2,1

)λ + m

1,1

2,1

− β

(11)

must be computed. The condition for local asymp-

totic stability is the negativeness of all the eigenvalues

and in this case it holds true once

1,1

2,1

− β

> 0 (12)

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

568

that can be rewritten putting in evidence the epidemic

transmission factor,

1,1

2,1

Nδ

(13)

For the second equilibrium point, the local dynam-

ics is described by the matrix

J(P

1,e

) =







−

1,1

2,1

0 −

1,1

2,1

1,1

2,1

− µ

−m

1,1

2,1

0 δ

−m

2,1

0 0 γ

−µ







Here the negative eigenvalue λ

= −µ

is imme-

diately obtained. For the other three ones, the roots of

the polynomial

+ a

λ + a

(14)

must be studies, with

βN

1,1

2,1

+ m

1,1

+ m

2,1

=β

1,1

+ m

2,1

1,1

2,1

=β

− µ

1,1

2,1

A necessary condition to have all the roots with nega-

tive real part is the positiveness of all the coefﬁcients,

in this case

1 −

1,1

2,1

> 0 ⇔ β

1,1

2,1

(15)

to be compared with the equilibrium point existence

condition (7).

Making use fo the Routh-Hurwitz criterion, neces-

sary and sufﬁcient conditions for negativeness of the

roots are

> 0, a

− a

> 0 (16)

The ﬁrst coincides with the necessary condition

(15), the second is always veriﬁed. For the third, one

has to check if

− a



2,1

1,1



βN

1,1

2,1

+ m

1,1

+ m

2,1



− (β

− µ

1,1

2,1

) > 0

Easy computations give

(β

)

1,1

+ m

2,1

1,1

2,1

+ β

1,1

+ m

2,1

)

1,1

2,1

− β

+ µ

1,1

2,1

> 0

showing a second order inequality

(

1,1

2,1

)

1,1

+ m

2,1

)

1,1

2,1



1,1

+ m

2,1

)

− m

1,1

2,1



+ µ

1,1

2,1

> 0 (17)

with respect to the term

1,1

2,1

put in evidence. Since

1,1

2,1

)

−m

1,1

2,1

= m

1,1

2,1

1,1

2,1

> 0

(18)

then, with respect to the quantity

1,1

2,1

(19)

it is easy to verify, without any computation, that the

inequality (17) is satisﬁed for all

1,1

2,1

if the roots

and r

are complex (with negative real part), or for

1,1

2,1

< −r

∪

1,1

2,1

> −r

(20)

with r

> r

> 0, if they are real. Recalling that con-

dition (15) can be rewritten as

1,1

2,1

> µ

(21)

it is possible to conclude that the equilibrium point

1,e

is stable (locally asymptotically) if (21), coinci-

dent with the existence condition (7), holds.

2.1.1 The Reproduction Number

For this population, it is possible to evaluate the basic

reproduction number R

(van den Driessche, 2017)

as well as the reproduction number under endemic

conditions, R

. The approach followed is the clas-

sical next generation matrix computation (Ledzewicz

and Schattler, 2011), whose spectral radius is the re-

production number estimation. To this aim, the par-

tial dynamics with direct infection and propagation is

taken









−



(δ

+ µ

−δ

+ (γ

+ µ



=F − V (22)

and the local approximating matrices

F =

∂F

∂(E,I)



0 β

0 0



(23)

V =

∂V

∂(E,I)



1,1

−δ m

2,1



(24)

Epidemic Impact of Temporary Large People Mass Fluxes: The COVID-19 and the Jubilee 2025 Reference Case

569

are computed, making use also of substitutions (9).

From these, through their evaluation in the conditions

under analysis and computing the spectral radius of

−1

, one has

=σ



−1





1,e

=σ



0 β

0 0



1,1

2,1

1,e

=σ

δβ

1,1

2,1

βS

2,1

0 0

1,1

2,1

(25)

= σ



−1





1,e

1,1

2,1

= 1 (26)

In the transient conditions, the current reproduc-

tion number R

can be considered

(t)

1,1

2,1

(27)

The reproduction numbers are indexes usually

adopted to characterise the spread of the epidemic:

if R

< 1, the infections asymptotically vanishes; it

corresponds to the stability condition of the epidemic

free equilibrium point. If R

> 1, the epidemics is

spreading, with the number of infected individuals al-

ways different from zero. If R

= 1, the endemic equi-

librium is the current situation, with constant non null

infected individuals present, with severity of the con-

ditions depending on the infection factor β

. Clearly,

if R

= 1, R

> 1. Both these two parameters refer

to steady state conditions. The current reproduction

number R

follows the same conditions but it is re-

ferred to the time varying situation.

3 THE INCOMING POPULATION

FLUX

The population referred in the previous Section is as-

sumed subject to a high intense people incoming ﬂux

for a time period sufﬁciently high to participate to the

infection process.

In a ﬁrst approximation, an average epidemic con-

dition for incoming individuals is assumed, so that it

is possible to consider one unique source for popula-

tion transfer without dividing them according to dif-

ferent countries with non homogeneous conditions.

The full population source of the incoming ﬂux can

be described by a second SEIR model, and the pop-

ulation variation can be modelled as an increment of

each class of the population in (1)–(4) given by a frac-

tion of the external people.

In order to introduce the population variation, the

external averaged source of incoming people is here

represented as a second SEIR model; also the incom-

ing population is subject to the same epidemic spread

but with different conditions, being possible to have a

better or a worst behaviour of the disease.

The result is the same as (1)–(4), but with different

parameters and number of individuals in the classes

= −β

− µ

+ N

(28)

= β

− δ

− µ

(29)

= δ

− γ

− µ

(30)

= γ

− µ

(31)

For such a system, the same computations per-

formed for the dynamics 1 are possible, showing that

the two equilibrium points are P

2,e

and P

2,e

, whose

expressions are the same as (5) and (6) respectively,

with subscript 2 instead of 1. Analogously, the stabil-

ity conditions (13) and (7) holds, with the substitution

of the subscript. Finally, also the reproduction num-

bers, here denoted by adding superscript ”2” (R

, R

and R

), have the same expressions.

Assume a permanent uniform ﬂux of people going

from system 2 to system 1 and then coming back, with

a time limited permanence but sufﬁciently long to be

fully involved in the epidemic evolution of system 1;

this means that after a few days, a steady state condi-

tion is reached and a ﬁrst approximated model can be

given, for the population 1 under incoming, assuming

that the total number of each class members becomes

S = S

+ α

; E = E

+ α

;

I = I

+ α

; R = R

+ α

so that

= S − α

; E

= E − α

;

= I − α

; R

= R − α

Actually, assuming four different fractions α

charac-

terising each class may be a too generic position. It

is assumed here for sake of generalization, but some

particular cases will be discussed in the sequel.

The new total population dynamics is then mod-

elled by

S = −β

SI − µ

S + N

+ α

+α

S + α

I − α

(α

+ β

+α

(µ

− µ

(32)

E = β

SI − m

1,1

E − α

S − α

+α

+ α

+α

1,1

− m

2,1

(33)

I = δ

E − m

1,2

I − α

+ α

+α

1,2

− m

2,2

(34)

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

570

R = γ

I − µ

R − α

+ α

+α

(µ

− µ

(35)

The full model is then represented by equations

(32)–(35) along with (28)–(31).

4 ANALYSIS OF THE DYNAMICS

Formally, using a compact notation





(36)

with all the consequent meanings of the use of super-

script and subscript, if the dynamics of the ﬁrst popu-

lation (1)–(4) is denoted by

˙x

= f

) (37)

while the dynamics of the second one (28)–(31) is ex-

pressed by

˙x

= f

) (38)

a ﬂux from the second population to the ﬁrst can

be modelled introducing ¯x

= x

+ αx

as the new

augmented state of the ﬁrst dynamics; consequently,

¯x

= x

−αx

= (1 −α)x

denotes the decreased pop-

ulation of the second system. Note that α ∈ R if all

= α, while α = diag{α

} in case of different val-

ues of α

. Assume, without lost of generality in the

results, the case of α ∈ R to simplify the expressions.

Otherwise, (1 − α)

−1

should replace

1−α

. The full

dynamics is then

¯x

= ˙x

+ α ˙x

= f

) + α f

)

= f

( ¯x

− αx

) + α f

( ¯x

+ αx

)

= f

( ¯x

−

(1 − α)

¯x

) + α f

(

(1 − α)

¯x

)

(α; ¯x

, ¯x

)

¯x

=(1 − α) ˙x

= (1 − α) f

(

(1 − α)

¯x

)

(α; ¯x

)

The new equilibrium points ¯x

and ¯x

can be com-

puted from

( ¯x

−

(1 − α)

¯x

) + α f

(

(1 − α)

¯x

) = 0 (39)

(1 − α) f

(

(1 − α)

¯x

) = 0 (40)

The second equation gives

(1 − α)

¯x

= P

2,e

⇒ ¯x

= (1 − α)P

2,e

(41)

where P

2,e

can be P

2,e

or P

2,e

, according to the system

conditions; by substitution in the ﬁrst one,

( ¯x

− αP

2,e

) = 0 (42)

allowing to ﬁnd

¯x

− αP

2,e

= P

1,e

⇒ ¯x

= P

1,e

+ αP

2,e

(43)

with P

1,e

with the same deﬁnition as P

2,e

above.

Stability of the four possible equilibria can be

studied making reference to the Jacobian matrix

J =

∂

(α; ¯x

, ¯x

)

∂ ¯x

∂

(α; ¯x

, ¯x

)

∂ ¯x

∂

(α; ¯x

)

∂ ¯x





∂ f

( ¯x

−

(1−α)

¯x

)

∂ ¯x

∂ f

( ¯x

−

(1−α)

¯x

)

∂ ¯x

+ α

∂ f

(

(1−α)

¯x

)

∂ ¯x

0 (1 − α)

∂ f

(

(1−α)

¯x

)

∂ ¯x





(44)

In detail, component–wise, computations of (44) give

∂ f

( ¯x

−

(1−α)

¯x

)

∂ ¯x

∂ f

)

∂x



=( ¯x

−

(1−α)

¯x

)

∂ f

( ¯x

−

(1−α)

¯x

)

∂ ¯x

+ α

∂ f

(

(1−α)

¯x

)

∂ ¯x

= −

(1 − α)

∂ f

)

∂x



=( ¯x

−

(1−α)

¯x

)

(1 − α)

∂ f

)

∂x

)



(1−α)

¯x

)

= (1 − α)

∂ f

(

(1−α)

¯x

)

∂ ¯x

∂ f

)

∂x



(1−α)

¯x

)

The evaluations at any equilibrium point give

∂ f

)

∂x



=((P

1,e

+αP

2,e

)−

(1−α)

(1−α)P

2,e

)

∂ f

)

∂x



1,e

(45)

= −

(1 − α)

∂ f

)

∂x



1,e

(1 − α)

∂ f

)

∂x

)



2,e

(46)

∂ f

)

∂x



2,e

(47)

Thanks to the block triangular structure, it is pos-

sible to verify that after the people ﬂow from the sec-

ond population to the ﬁrst, at steady state each popu-

lation remains in its previous status of epidemic free

or endemic conditions.

Epidemic Impact of Temporary Large People Mass Fluxes: The COVID-19 and the Jubilee 2025 Reference Case

571

However, in case of motion of individuals, they

sum to the already present ones and, moreover, they

act as an initial perturbation producing a transient

evolution which depend on the R

of the hosting

population. The new equilibrium points take into

account the ﬂux, decreasing for the second system

( ¯x

= (1 − α)P

2,e

) while increasing for the ﬁrst one

( ¯x

= P

1,e

+ αP

2,e

). Since the equilibrium changes,

some consequences are expected for the reproduction

number too.

4.1 Effects on the Reproduction

Number

The computation of the new reproduction number fol-

lows the approach already used in Section 2 but mak-

ing use of the the new dynamics (32)–(35), in partic-

ular the (E,I) part of the dynamics (33) and (34)

E = β

SI − m

1,1

E − α

S − α

+α

+ α

+α

1,1

− m

2,1

(48)

I = δ

E − m

2,1

I − α

+ α

+α

1,2

− m

2,2

(49)

Following the previous computations, the F and V

are deﬁned as

F =





(50)

V =



1,1

E + α

S + α

I − α

−δ

E + m

2,1

I + α





−α

− α

1,1

− m

2,1

−α

− α

1,2

− m

2,2



(51)

and consequently

F =



0 β

0 0



¯x

V =



1,1

−δ

2,1



¯x

−1

1,1

2,1

+ δ



2,1

−α

1,1



¯x

−1

1,1

2,1

+ δ



S β

1,1

0 0



¯x

and its spectral radius, tanks to the matrix structure, is

given by



−1



1,1

2,1

+ δ



¯x

(52)

The four cases of equilibrium conditions must be

considered. For the ﬁrst system, the basic repro-

duction number is obtained evaluating in ¯x

= ¯x

1,e

+ αP

2,e

both the epidemic free (5) and endemic

(6) conditions for the second system.

For the ﬁrst case,

1,e

+ α

2,e

)

1,1

2,1

+ δ

2,e

(53)

while for the second one

1,e

+ α

2,e

)

1,1

2,1

+ δ

2,e

(54)

In both cases a consistency condition is veriﬁed, since



α=0



α=0

(55)

The effect of the people ﬂux can be observed in

the dependency of

from the α

2,e

and

from

the α

2,e

; while the pre existing status is unchanged,

so that if the system is in epidemic free condition, it

will always be in the same condition, the increment of

population produces a change in the epidemic spread

capabilities changing the reproduction number wors-

ening it. In particular, note that

lim

→+∞

= lim

→+∞

= 1 (56)

that is asymptotically the behaviour in any case tends

to be equivalent to an endemic condition.

On the other hand, if the ﬁrst system is in endemic

conditions, as previously computed, in absence of ﬂux

= 1 (57)

is obtained evaluating the next generation matrix in

the endemic equilibrium point.

Under the people motion, two possible cases are

addressed: the second system is in epidemic free con-

dition, so that S

= S

2,e

, or in endemic status, so that

= S

2,e

; the new expressions for the reproduction

numbers are obtained evaluating the spectral radius

of the next generation matrix in such two cases:

1,e

+ α

2,e

)

1,1

2,1

+ δ

2,e

(58)

and

1,e

+ α

2,e

)

1,1

2,1

+ δ

2,e

(59)

In order to study the effects of the incoming ﬂux,

expression (58) can be rewritten as

1 +

2,e

1,e

1 +

2,e

1,e

= 1 ∀α

≥ 0 (60)

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

572

making use of the identity (26); the same holds for

expression (59).

This result proves that the modiﬁed dynamics re-

mains in endemic conditions, changing the equilib-

rium point, that is the number of infected individuals

at steady state according to the new equilibrium point.

A deeper analytical analysis involves large and

meaningless expressions. However, to face the prob-

lem, some assumptions can be introduced to simplify

the model without lost of generality. A ﬁrst hypothe-

sis assumed is that the initial conditions for both the

original (population 1) and the external (population

2) systems are at one of their steady state conditions.

With the addition of the observation that the fractions

are very low, when cases as the reference one are

addressed, it is possible to assume that the ﬂux is a

very small perturbation for system 2 and its steady

state condition does not vary. One of the main con-

sequences is that in system (28)–(31), the variables

, E

, I

and R

can be assumed constant and equal

to P

2,e

if the external population is assumed epidemic

free, or by P

2,e

if the endemic condition is the case.

A last hypothesis is the uniformity of the ﬂux in the

sense that no selection is performed on the basis of

the epidemic status and then the fractions α

can be

assumed all equal and denoted by α.

In the present analysis, once that the asymptotic

behaviour is deﬁned, it is important to evaluate also

the transients.

This analysis is performed by means of numerical

simulation addressing the different combinations dis-

cussed above with different levels of epidemic spread.

5 NUMERICAL ANALYSIS

In this section numerical simulations are carried on

in order to put in evidence the transient behaviour for

each case of populations conditions. They all are per-

formed starting from the new equilibrium points as

computed in previous Section and applying a small

perturbation.

The choice of the parameters are performed to re-

spect the reference case, but clearly qualitative results

can be applied to any populations combinations.

So, for the ﬁrst system, the following parameters

in Table 1 have been chosen

to best ﬁtting with Italian case (Di Giamberardino

et al., 2021a) in a SEIR model. Different values for

are assumed in the four simulation cases to change

the possible combination of epidemic conditions.

The second system has been chosen with similar

characteristics of system 1 except for the number of

individuals, assumed a little more than 10 times the

Table 1: Parameters values for system 1.

Parameter Value

1.69 · 10

1/3

1/10

= µ

2.81 · 10

−5

2 ∗ 2.81 · 10

−5

ﬁrst. The idea is to simulate Europe vs. Italy, but also

in this case a simple change of values let the model be

adaptable to any conditions. Also for this system, the

Table 2: Parameters values for system 2.

Parameter Value

2 · 10

1/3

1.2 ∗ (1/10)

= µ

0.8 ∗ 2.81 · 10

−5

2 ∗ 2.81 · 10

−5

values of β

is assumed in next Subsections according

to the epidemic characteristics under analysis.

The time scale is one day and the simulations have

been performed over two years (730 days) to show

the effects over the ﬁrst year of interest and to stress

the transient characteristics of the infection evolution

according to the stability conditions veriﬁed.

Although the actual case study proposed, people

ﬂux in Italy (Rome) during the Jubilee 2025, should

consider two populations with endemic characteris-

tics, this case will be addressed after the analysis of

the behaviours in the other three possible combina-

tions.

5.1 Both Population in Epidemic Free

Equilibrium Conditions

In this case, the two populations are assumed to be

both in epidemic free conditions. The ﬁrst one is char-

acterised by a basic reproduction number R

= 0.85,

with an infection factor β

= 1.5 10

−9

. The results

of a ﬁrst set of simulations are reported in Figure 1,

where a factor R

= 0.81, with a infection parame-

ter β

= 1.1 10

−10

, has been assumed for the second

systems. Three different ﬂux intensities are tested:

α = 0.01, a low ﬂux, corresponding, with the present

numbers, to an increment of about 10% of living pop-

ulation, α = 0.1, a ﬂux corresponding about to double

the living population, and α = 0.99, for an evaluation

of asymptotic behaviours, with a population which in-

creases ten time the usual number.

It is possible to note that the epidemic free asymp-

totic condition assures that the number of infected

Epidemic Impact of Temporary Large People Mass Fluxes: The COVID-19 and the Jubilee 2025 Reference Case

573

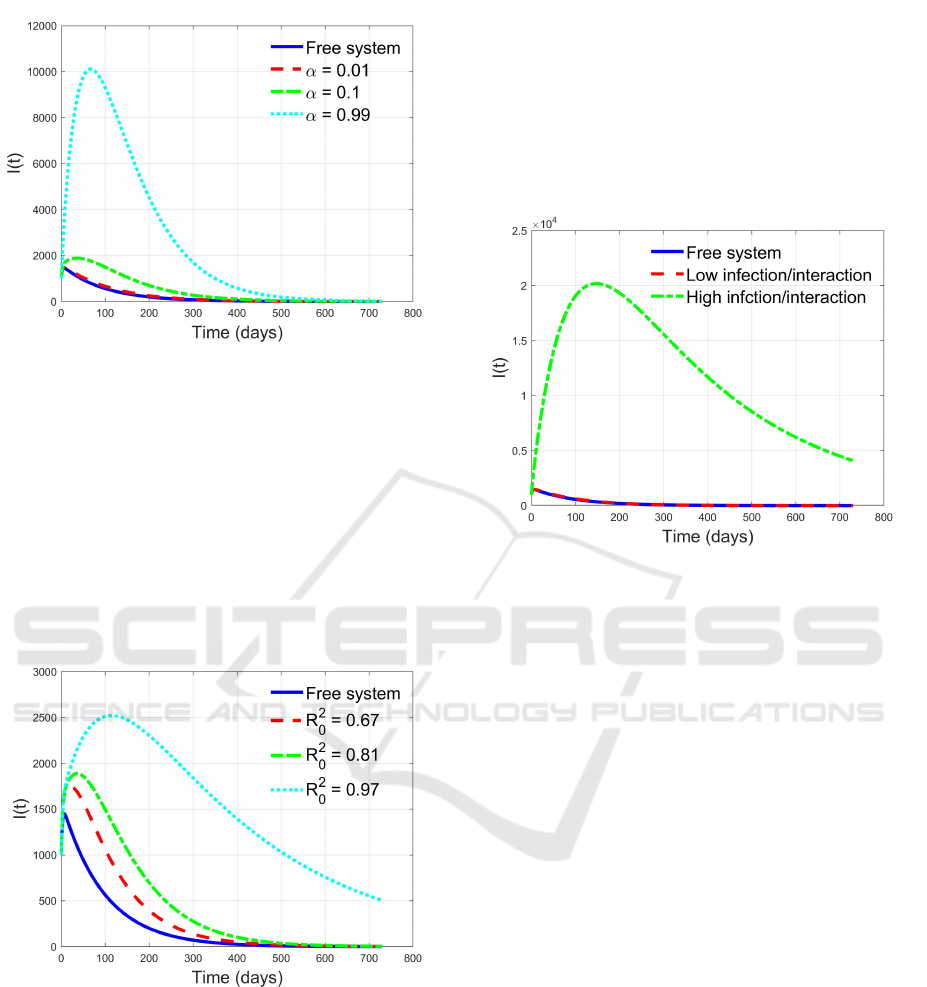
Figure 1: Time history of I(t) in epidemic free cases for

different ﬂux intensities.

goes to zero as time passes, but the peak value, as

well as the time in which the number is sensibly high,

become greater as the ﬂux increments.

A different analysis is reported in Figure 2, where

under an average ﬂux (α = 0.1), three reproduction

number values for the incoming population are taken,

still remaining in the epidemic free conditions. So

= 0.9 10

−10

, β

= 1.1 10

−10

and β

= 1.3 10

−10

are assumed, yielding to R

= 0.67, R

= 0.81 and

= 0.97 respectively.

Figure 2: Time history of I(t) for medium income ﬂux

α = 0.1 from population with different basic reproduction

numbers

Also in this case, the lower is the stability con-

dition R

, the higher are the amplitude and the time

length of the transient. An interesting observation is

that while from a qualitative point of view a small

worsening of the medical situation can be expected,

the results here presented show that the intensity of

such a worsening can be higher than expected.

The extremes of the possible behaviours are sum-

marised in Figure 3 where the best and the worst sit-

uations are reported. The ﬁrst one is referred to the

minimum ﬂux (α = 0.01) from a population with low

reproduction number (R

= 0.67), while for the sec-

ond one a very high ﬂux (α = 0.99) from population

with a high reproduction number (R

= 0.97) is con-

sidered. The peak value and the time length of high

value are proportionally very high.

Figure 3: Time history of I(t) for the lowest and the high-

est dangerous situation according to the choice of epidemic

characteristics and population ﬂow.

5.2 Epidemic Free Receiving Population

from One in Endemic Condition

This set of simulations has the goal to evaluate if and

how an epidemic free population can be affected by

a ﬂux from a population where the epidemics is in

an endemic condition. In all the simulations, for the

ﬁrst population, a value of R

= 0.85 has been chosen,

corresponding to a β

= 1.510

−9

. The ﬁrst set of sim-

ulations, analogously to the previous case, has been

performed assuming the same different rates of ﬂux:

α = 0.01, a low ﬂux, α = 0.1, a ﬂux corresponding

about to double the living population, and α = 0.99,

for an evaluation of asymptotic behaviours. The re-

sults are reported in Figure 4, showing a sensible con-

tribution to the worsening of the epidemic in terms

of number of infected individuals even for medium

ﬂuxes.

It is intuitive that different levels of stability,

equivalent to different R

values, for the receiving

epidemic free population produce variations in the

number of infected individuals I

. This is a condition

that the hosting population can evaluate regardless the

infection conditions of the incoming people.

On the other hand, it can be more useful and inter-

esting to evaluate how much the epidemic conditions

of the source population, denoted by the values of R

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

574

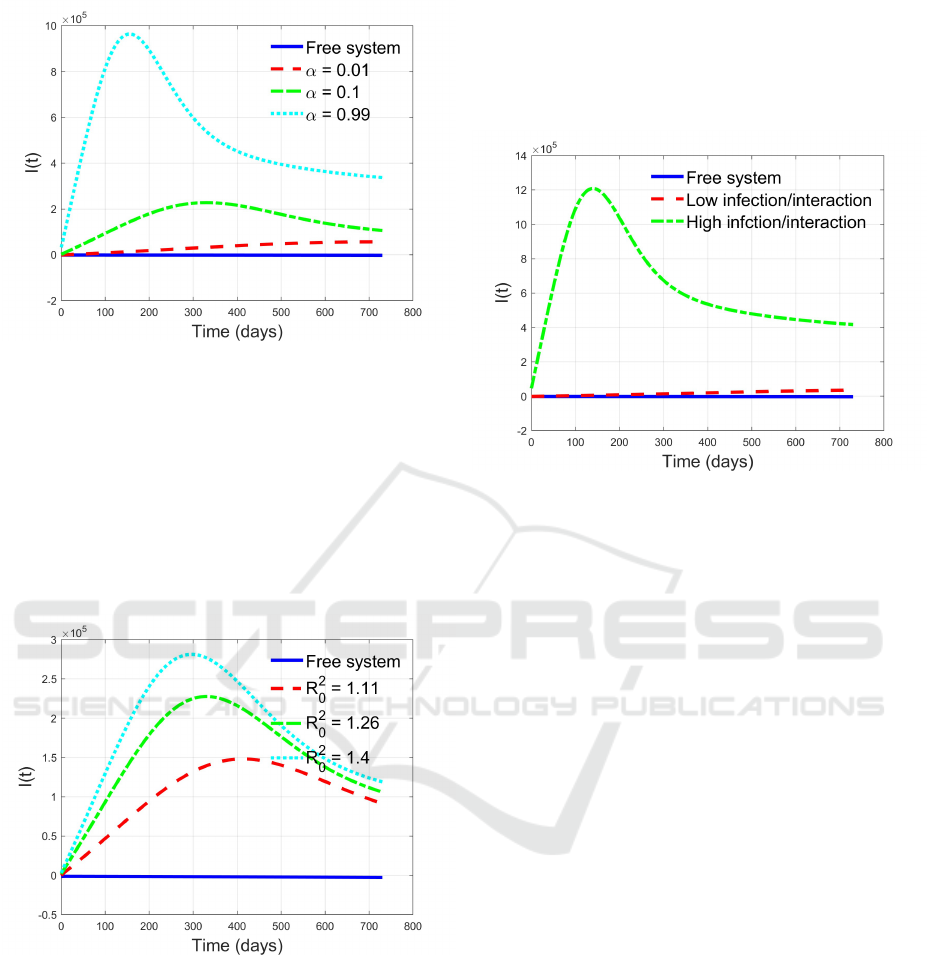
Figure 4: Time history of I(t), in case of epidemic free pop-

ulation with ﬂux from one with endemic conditions, for dif-

ferent incoming intensities.

can affect the dangerousness of the ﬂux with respect

to the receiving population for prevention purposes.

In Figure 5, the results of a set of simulations in

which the ﬂux rate is kept constant and equal to the

median value α = 0.1, the reproduction number of the

population 1 is ﬁxed to R

= 0.85 while the R

has

changed, with values R

= 1.11, R

= 1.4 and R

1.4.

Figure 5: Time history of I(t) for medium income ﬂux

α = 0.1 from population with different basic reproduction

numbers.

In Figure 5 it is evidenced that the contribution of

the epidemic condition of the external population 2 is

in a worsening of the receiving population, but specif-

ically concentrated in the transient with the behaviour

that tends to became equally dangerous at the end of

the second year.

An overall evaluation of the effects on the incre-

ment of infected individuals in amplitude and in time

length is reported in Figure 6, where the lowest effect,

with the minimum ﬂow (α = 0.01) and minimum in-

fection rate (β

= 1.5 10

−10

, that is R

= 1.11), and

the highest contribution, for high ﬂow (α = 0.99) and

high β

= 1.9 10

−10

= 1.4), are reported com-

pared with the absence of ﬂow.

Figure 6: Time history of I(t) for the lowest and the high-

est dangerous situation according to the choice of epidemic

characteristics and population ﬂow.

5.3 Flow from Epidemic Free to

Endemic Populations

The case here considered seems the less dangerous

among the ones studied, since the incoming popu-

lation has the best situation with respect to the epi-

demics, being in epidemic free condition. This status

is modelled assuming β

= 1.1 10

−10

, corresponding

to R

= 0.81.

The effects of different ﬂows and different contact

rates for the ﬁrst population are analysed. In Figure

7 the reproduction number for the ﬁrst system is set

to R

= 1.42, corresponding to β

= 2.5 10

−9

, for the

second one is set to R

= 0.81, for β

= 1.1 10

−10

while the moving population is quantiﬁed by α =

0.01, α = 0.1 and the asymptotic α = 0.99. The re-

sult is that also this case presents a sensible level of

dangerousness, making worse and worse the infected

situation as the ﬂow increases, despite the health situ-

ation of the incoming individuals.

The dual situation is reported in Figure 8, where

with a ﬁxed medium value for the ﬂow, different re-

production number values for the second system are

set, still remaining in the epidemic free condition

< 1): R

= 0.67, R

= 0.81 and R

= 0.97,

given by choosing β

= 0.910

−10

, β

= 1.110

−10

and

= 1.3 10

−10

respectively.

Looking at the plots in Figure 8, even in healthy

situation for incoming people, the infected individuals

more or less double with a quite long transient.

Epidemic Impact of Temporary Large People Mass Fluxes: The COVID-19 and the Jubilee 2025 Reference Case

575

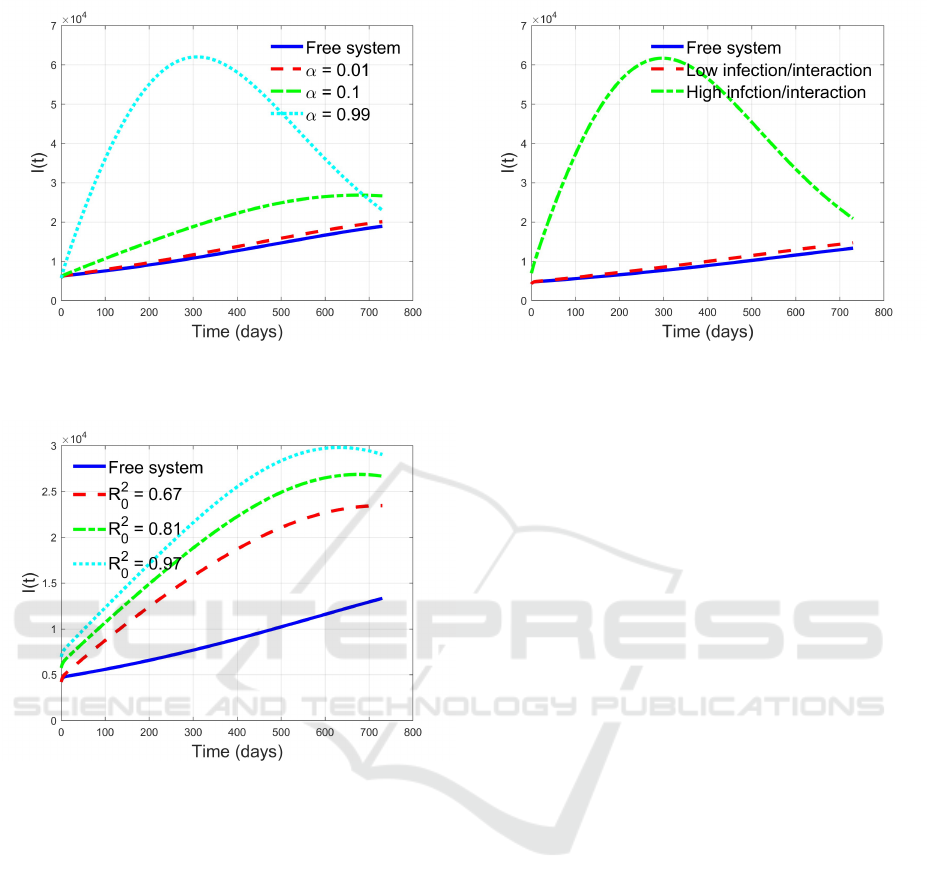
Figure 7: Time history of I(t), in case of population with

endemic conditions receiving income people from one in

epidemic free status, for different ﬂux intensities.

Figure 8: Time history of I(t) for medium income ﬂux

α = 0.1 from population with different basic reproduction

numbers.

Lastly, also in this case an estimation of the bound

interval between the best condition (low ﬂux and low

infection rate) and the worst one (high ﬂux, high in-

fection rate), is reported in Figure 9, which put in ev-

idence the possibility of a great worsening of the dis-

ease situation in terms of number of infected individ-

uals, with a peak about at the end of the ﬁrst year.

5.4 Flow from Endemic to Endemic

Populations

The present situation all over the world with respect

to any known infection with large diffusion, includ-

ing COVID–19, is represented by the presence of the

virus with a stable limited number of infected indi-

viduals at a physiological level. That is, the endemic

condition can be assumed, with different values for

Figure 9: Time history of I(t) for the lowest and the high-

est dangerous situation according to the choice of epidemic

characteristics and population ﬂow.

the equilibrium point according to local characteriza-

tion of the parameters. So, this is the real situation

that will be faced in the reference case studied.

However, since the actual conditions in terms of

infection situation at the beginning of the event con-

sidered, more or less the end of the present year

(2024), following the previous analysis, a (small)

range of possible infection rates has to be considered,

both for the receiving population 1 and for the incom-

ing population 2.

Then, the effect of the intensity of the people

ﬂow α is considered in a ﬁrst set of simulations in

which the reproduction numbers for the two systems

are varied: R

= 1.25 and R

= 1.11 for Figure 10,

= 1.25 and R

= 1.4 for Figure 11, R

= 1.59 and

= 1.11 for Figure 12 and R

= 1.59 and R

= 1.4

for Figure 13. While the qualitative variations seem

similar, it is clear comparing Figures 10 and 12 with

Figures 11 and 13 that, despite the variation of the R

is almost the same for both the systems, the effect of

variation of the second system produces a doubling in

the effect on the infected increment.

The same considerations can be deduced from

Figure 14 where, for α = 0.1, the two plots associated

with the higher value for R

show a double number

of infected individuals with respect to the lower ones,

quite independently from the R

The comparison between the behaviour with the

lowest infection values and ﬂow and the highest ones,

corresponding to the best and the worst conditions in

the range here studied, is reported in Figure 15, when

it is possible to understand that it must be expected a

possible sensible increment of individuals that require

medical support, with a peak of ten times the usual

number of patients and the low decrement towards the

new equilibrium condition.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

576

Figure 10: Time history of I(t) for R

= 1.25 and R

1.11, under different ﬂux intensities.

Figure 11: Time history of I(t) for R

= 1.25 and R

= 1.4,

under different ﬂux intensities.

Figure 12: Time history of I(t) for R

= 1.59 and R

1.11, under different ﬂux intensities.

Figure 13: Time history of I(t) for R

= 1.59 and R

= 1.4,

under different ﬂux intensities.

Figure 14: Time history of I(t) for medium income ﬂux α =

0.1: effects of different combinations of basic reproduction

numbers.

Figure 15: Time history of I(t) for the lowest and the high-

est dangerous situation according to the choice of epidemic

characteristics and population ﬂow.

Epidemic Impact of Temporary Large People Mass Fluxes: The COVID-19 and the Jubilee 2025 Reference Case

577

6 CONCLUSIONS AND FUTURE

WORK

In the paper the analysis of the effects of a temporary

increment of a population on the epidemic character-

istics and on the increment of the number of infected

individuals. The ﬂux is assumed coming from a sec-

ond population with its own infection status. A SEIR

model is assumed for describing both the population,

being important to put in evidence the effects on the

infected individuals only. Steady state conditions are

initially considered, with the analysis carried out an-

alytically, giving the conditions for having the classi-

cal epidemic free or endemic status, along with their

stability conditions. A reference to the reproduction

number has been also addressed to evaluate the epi-

demic spread conditions.

While at steady state it is easy to evaluate the ef-

fects of the people ﬂux, being the new equilibria the

combinations of the previous ones, a different ap-

proach has been used to study the transients, trying to

quantify the effects in terms of increment of infected

individuals in population 1. This analysis has been

performed in a numerical way, studying the effects of

the possible different contributions of the people vari-

ation and of the epidemic status of the populations to

the worsening of the infection conditions. Numeri-

cally, the case study in mind has been the analysis of

the possible epidemic effects of the Jubilee 2025 on

the Italian or, suitably scaled, Roman situation during

the year of intense pilgrim/tourists income.

The main result is that it would be necessary to

considered a sanitary prevention plan for an effec-

tive approach to the effects of the disease contain-

ment. Moreover, these considerations can be ex-

tended, qualitatively, to any infectious illness: im-

proving the analytical aspects it is possible to address

a more general class of infections and different pop-

ulations, being possible to extend the results, suitably

scaled, also to several different case like high density

touristic places. Moreover, a more speciﬁc analysis

of how and how much these fast increments of pop-

ulations can affect the infection rate β is going to be

faced.

REFERENCES

Casagrandi, R., Bolzoni, L., Levin, S., and Andreasen, V.

(2006). The SIRC model and inﬂuenza. A. Mathe-

matical Biosciences, 200:152–169.

Contreras, S., Villavicencio, H., Medina-Ortiz, D., Biron-

Lattes, J., and Olivera-Nappa, A. (2020). A multi-

group seira model for the spread of covid-19 among

heterogeneous populations. Chaos, Solitons and Frac-

tals, 136.

Daley, D. J. and Gani, J. (1999). Epidemic Modelling: An

Introduction. Cambridge Studies in Mathematical Bi-

ology. Cambridge University Press.

Di Giamberardino, P., Caldarella, R., and Iacoviello, D.

(2021a). A control based mathematical model for

the evaluation of intervention lines in COVID-19 epi-

demic spread: The Italian case study. Symmetry,

13(5).

Di Giamberardino, P. and Iacoviello, D. (2017). Optimal

control of SIR epidemic model with state dependent

switching cost index. Biomedical Signal Processing

and Control, 31.

Di Giamberardino, P., Iacoviello, D., Albano, F., and

Frasca, F. (2020). Age based modelling of sars-cov-2

contagion: The italian case. pages 274–279.

Di Giamberardino, P., Iacoviello, D., Papa, F., and Sinis-

galli, C. (2021b). A data-driven model of the covid-19

spread among interconnected populations: epidemio-

logical and mobility aspects following the lockdown

in italy. Nonlinear Dynamics, 106(2):1239–1266.

Iranzo, V. and P

erez–Gonz

alez, S. (2021). Epidemiological

models and covid-19: a comparative view. Hist Philos

Life Sci., 43(3).

Ledzewicz, U. and Schattler, E. (2011). On optimal sin-

gular controls for a general SIR-model with vaccina-

tion and treatment. Discrete and continuous dynami-

cal systems, pages 981–990.

Martcheva, M. (2015). An introduction to mathemati-

cal epidemiology. Text in Applied Mathematics 61,

Springer.

Ng, O., Marimuthu, K., Chia, P., Koh, V., Chiew, C., and

et al. (2020). SARS-CoV-2 infection among trav-

elers returning from wuhan, china. N Engl J Med.,

382(15):1476–1478.

van den Driessche, P. (2017). Reproduction numbers of

infectious disease models. Infectious Disease Mod-

elling, 2:288–303.

Yue, Y., Tan, Y., and Tang, S. (2023). Stability analysis of

the covid-19 model with age structure under media ef-

fect. Computational and Applied Mathematics, 42(5).

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

578