BVE + EKF: A Viewpoint Estimator for the Estimation of the Object’s

Position in the 3D Task Space Using Extended Kalman Filters

Sandro Costa Magalhães

1,2 a

, António Paulo Moreira

1,2 b

, Filipe Neves dos Santos

1 c

and Jorge Dias

3,4 d

INESC TEC, Porto, Portugal

FEUP, Porto, Portugal

ISR, University of Coimbra, Coimbra, Portugal

KUCARS, Khalifa University, Abu Dhabi, U.A.E.

Keywords:

Viewpoint Selection, 3D Position Estimation, Pose Estimation, Statistics, Kalman Filter, Active Perception,

Active Sensing.

Abstract:

RGB-D sensors face multiple challenges operating under open-ﬁeld environments because of their sensitivity

to external perturbations such as radiation or rain. Multiple works are approaching the challenge of perceiving

the three-dimensional (3D) position of objects using monocular cameras. However, most of these works focus

mainly on deep learning-based solutions, which are complex, data-driven, and difﬁcult to predict. So, we

aim to approach the problem of predicting the three-dimensional (3D) objects’ position using a Gaussian

viewpoint estimator named best viewpoint estimator (BVE), powered by an extended Kalman ﬁlter (EKF).

The algorithm proved efﬁcient on the tasks and reached a maximum average Euclidean error of about 32 mm.

The experiments were deployed and evaluated in MATLAB using artiﬁcial Gaussian noise. Future work aims

to implement the system in a robotic system.

1 INTRODUCTION

Agriculture is a critical sector that has been facing

several difﬁculties over time. That constraints are

well-designed by several organizations, such as the

United Nations (UN) in the objectives for sustain-

able development (ODS) (General Assembly, 2015).

However, their solution is still a challenge.

The increased food demand promoted by the pop-

ulation growth (FAO, 2023) and labor shortage re-

quire improved and efﬁcient agricultural technologies

that may speed up the execution of farming tasks.

Monitoring and harvesting are some tasks that may

beneﬁt from robotization in the area.

Autonomous robots require robust perception sys-

tems to detect and identify fruits and other agricul-

tural objects. Several works use RGB-D

cameras to

see the objects and infer their three-dimensional (3D)

https://orcid.org/0000-0002-3095-197X

https://orcid.org/0000-0001-8573-3147

https://orcid.org/0000-0002-8486-6113

https://orcid.org/0000-0002-2725-8867

Red, green, blue and depth sensor

position (Kumar and Mohan, 2022; Magalhães et al.,

2022). However, RGB-D sensor can malfunction un-

der open-ﬁeld environments due to external interfer-

ences (Kumar and Mohan, 2022; Gené-Mola et al.,

2020; Ringdahl et al., 2019), such as radiation or rain.

To overcome this challenge, several works designed

solutions to infer the position of the objects from

monocular sensors. The most common systems are

based on deep learning to infer the six-dimensional

(6D) or 3D pose of objects (Li et al., 2023; Parisotto

et al., 2023; Chang et al., 2021; Wang et al., 2021)

or estimate their depth (Ma et al., 2019; Birkl et al.,

2023). Deep learning deploys, although complex, al-

gorithms that are very data-dependent, usually super-

vised, and hard to predict and modify.

Despite the tendency for deep-learning solutions,

we still can use Bayesian algorithms to infer the 3D

position of objects. In previous work, (Magalhães

et al., 2024) designed the MonoVisual3DFilter to es-

timate the position of objects using histogram ﬁlters.

However, the algorithm still requires the manual def-

inition of viewpoints to estimate the position of the

fruits.

Magalhães, S., Moreira, A., Santos, F. and Dias, J.

BVE + EKF: A Viewpoint Estimator for the Estimation of the Object’s Position in the 3D Task Space Using Extended Kalman Filters.

DOI: 10.5220/0012945800003822

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 2, pages 157-165

ISBN: 978-989-758-717-7; ISSN: 2184-2809

157

Therefore, in this work, we challenge to identify a

mechanism that can autonomously infer the 3D posi-

tion of fruits without the demand for manually deﬁn-

ing viewpoints.

We approach our question with the challenge of

autonomously identifying the position of fruits, such

as tomatoes, in the tomato plant for precision moni-

toring or harvesting tasks. We assume the system has

a manipulator with a monocular camera conﬁgured in

an eye-hand manner.

In the following sections, this article explores the

proposed solution. The section 2 details the im-

plementation of the best viewpoint estimator (BVE)

mate the 3D position of the objects in the tasks space.

This section also deﬁnes some experiments to evalu-

ate the algorithm. The section 3 illustrates the results

for the various experiments and some algorithm limi-

tations. Finally, section 4 concludes and summarizes

this study and introduces future work.

2 MATERIALS AND METHODS

2.1 BVE

A statistical optimization approach guides towards a

solution for this problem. The observation of a fruit

from a viewpoint has an associated observation error.

The goal is to identify a subsequent viewpoint that

minimizes this error. Thus, the problem is the mini-

mization of a loss function related to the intersection

of Gaussians distributions (1), where N

(µ

,Σ

) de-

notes a Gaussian distribution. The index i ∈N corre-

sponds to each observation viewpoint.

N(µ

,Σ

) = N

(µ,Σ

) ·. . . ·N

(µ,Σ

) (1)

The Gaussian distribution’s product (1) presents

signiﬁcant computational complexity. Nevertheless,

(Petersen and Pedersen, 2012) posits that we can de-

compose the product of Gaussians into two distinct

equations—addressing the mean values and the co-

variance. Because we expect the fruit to remain

stopped while hung on the tree, this solution proposes

that the position of the tomato, k , remains invariant,

thus µ

= k . Hence, we simplify the optimization

problem to (2).

= (Σ

−1

+ ... + Σ

−1

)

−1

(2)

The observation noise covariance is predomi-

nantly a characteristic intrinsic to the camera. Con-

sequently, the camera’s covariance Σ

remains con-

stant within the camera’s frame, C. The movement of

the camera to different poses, c , changes the observa-

tion noise in the ﬁxed world frame W . So, the model

requires an observation covariance matrix expressed

within the main frame W (3) to correlate the multi-

ple observations. The matrix R

represents a rota-

tion matrix that delineates the relationship between

the camera’s frame C and the main frame W .

= R

⊺

(3)

In concluding the initial problem deﬁnition, we

should recognize that the covariance matrix under-

goes modiﬁcation with each iteration of the algorithm

as a consequence of the computations performed in

equations (2) and (3). To generalize the system’s ini-

tial conditions, a generic covariance matrix, Σ

, is

considered. This matrix represents the culmination of

all previous intersections of covariance matrices up to

the point k −1.

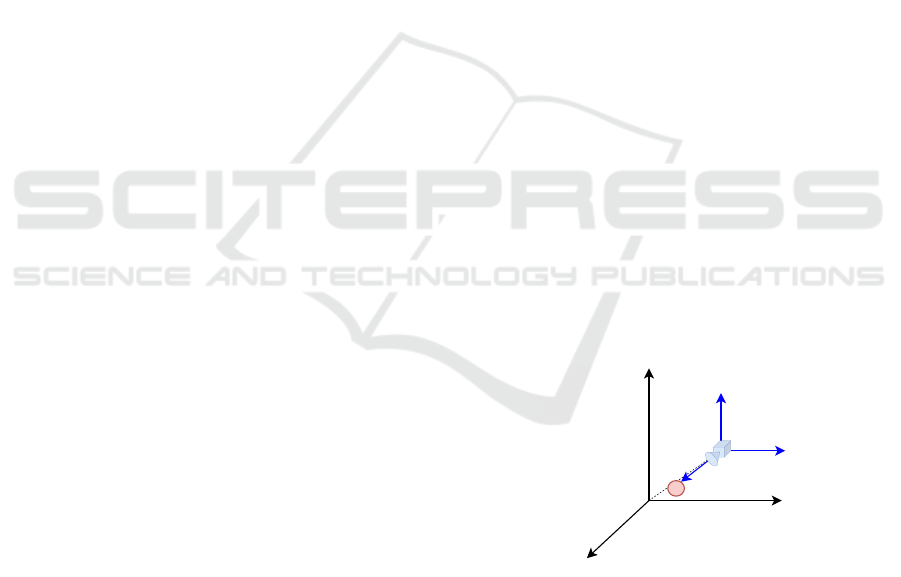
2.1.1 Deﬁnition of the Rotation Matrix

The observation covariance matrix Σ

is initially de-

ﬁned into the camera’s frame. We can convert data

between frames using homogeneous transformations,

namely rotation matrices, because the translation is

irrelevant. Figure 1 illustrates a possible generic re-

lationship between frames. The camera’s frame, de-

noted as Ox

, is centered at the sensor, and the

axis indicates the camera’s viewing direction. For

simplicity, we assume that y

is always parallel to the

plane deﬁned by

. This simpliﬁcation is possi-

ble because the covariance matrix is ideally symmet-

rical in the x

axis, and the other axis’s orientation is

irrelevant.

Figure 1: Deﬁnition of the camera’s frame and the main

frame.

Given the fruit position’s estimation in the main

frame,

k , e

denotes the unit vector of x

axis (4),

where c is the camera’s position. We can deﬁne the

camera frame’s axes in the main frame through (5),

(6), and (7). The rotation matrix R

that relates the

camera frame to the main frame is obtained from (8).

In (8), e

, e

, and e

are the unit vector of x

, and z

, respectively.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

158

k −c

k −c ||

(4)





⊺

(5)



−x



⊺

(6)

×y

(7)

(8)

2.1.2 Deﬁnition of the Objective Function

We aim to minimize a function related to the product

of Gaussian distributions (2). This endeavor requires

a loss function directly contingent upon the Gaussian

intersection. The optimizer predicates a scalar output

from the loss function we designed as a dispersion

dependency.

For each observation, (9) characterizes the inter-

section of two covariance matrices in a ﬁxed main

frame. The computation of this intersection necessi-

tates the calculation of three inverse matrices, which

is a computationally demanding operation.

= (Σ

−1

+ Σ

−1

)

−1

(9)

We reduced the number of these operations

through the precision matrix (P = Σ

−1

). Then, the

precision’s concentration (c = det((P))) translates the

matrix into a scalar. So, we can deﬁne the objec-

tive function as the dispersion (

/c), because, accord-

ing to the properties of the determinants, det(P

−1

) =

det(P )

−1

. Due to the low magnitude of the loss func-

tion, we scaled the dispersion into the logarithmic

scale (10). P and Σ

are dependent on

c , the next

estimated position of the camera, which we aim to

optimize.

f (

c ) = −ln(det(Σ

−1

+ Σ

−1

)) (10)

Alternatively to the loss function 10, we can min-

imize the absolute maximum eigen value of the co-

variance matrix if we have enough computing power

to compute (9). While using this loss function, we

should remember that it is highly non-linear and

whose derivative function varies at each step because

of the maximum function.

f (

c ) = max(|eig(Σ

)|) (11)

We can use optimization algorithms operating

with non-linear restrictions and loss functions to solve

the problem using both functions. For the current

analysis, we opted to use an interior-point algorithm

(Nocedal et al., 2014), already implemented in MAT-

LAB’s optimization toolbox(The MathWorks, Inc.,

2024).

We also intend to effectively drive the camera to

the objects to perform tasks, while estimating the po-

sition of the fruit. Towards that, we added an ad-

ditional component to the loss function (13). The

act(i,a,b) is a sigmoid activation function (12). The

sigmoid activates the additional component, forcing

the camera to approximate the object. In the activa-

tion function (12), a and b are control parameters that

set its aggressiveness and its set point (i.e., the value

of the function for act(·) = 0.5), respectively; i is the

iteration number of the procedure. Through this strat-

egy, we can activate gradually the Euclidean error to

the fruit according to the evolution of the estimation

procedure.

act(i,a,b) =

1 + e

−a·(i−c)

(12)

c ) = f (

c ) + act(i,a,b) ·||

k −

c || (13)

2.1.3 Deﬁnition of the Restrictions

The proposed algorithm can effectively estimate the

best camera poses that maximize the observability of

the fruits. However, some restrictions should be im-

plemented to match the environment and hardware

constraints. So, we deﬁned that the selected poses

must be inside the working space of a 6 DoF

ma-

nipulator. A spheric model simpliﬁes this workability

restriction. Considering a manipulator with a working

space centered in m and with a radius r

, in meters,

the camera’s pose

c must be inside (14). We only es-

timate the center position of the fruit but mislead its

volume. An additional condition forces the camera to

be outside the fruit space. Thus, considering an aver-

age fruit radius r

, centered in k , the camera’s pose

has to comply with (15).

(

c −m) ·(

c −m)

⊺

−r

≤ 0 (14)

−(

c −

k ) ·(

c −

k )

⊺

+ r

≤ 0 (15)

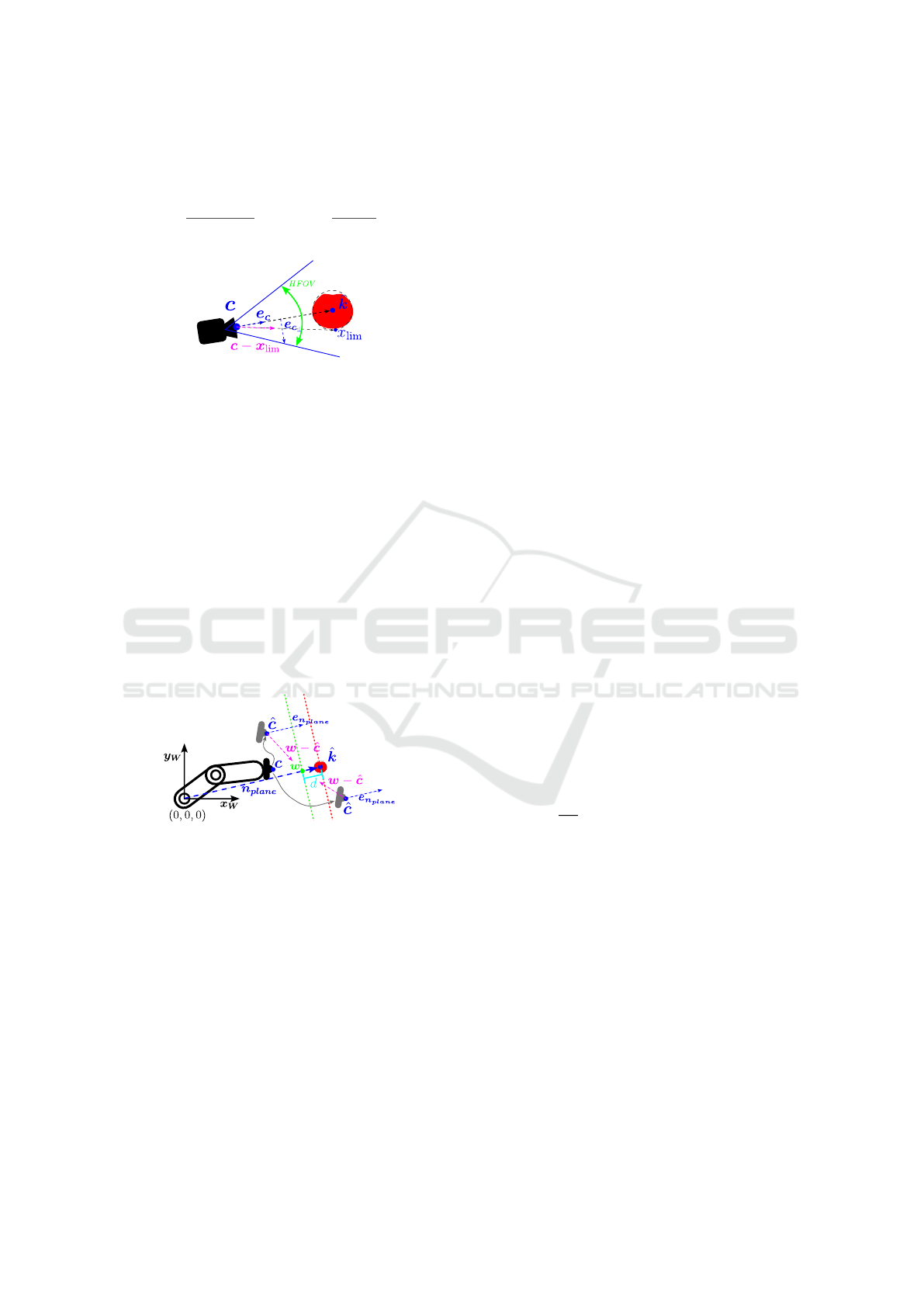
The camera’s orientation is also relevant to ensure

it looks towards the fruit. The algorithm only focuses

in estimating the best position for the camera, but also

the orientation of it should be constrained, ensuring

the camera is looking towards the fruits. The camera

has a conical vision proﬁle. So, we constrained the

fruits to be inside the camera’s ﬁeld of view, with a

conical shape, (19) and ﬁgure 2, where HFOV is the

angle of the horizontal ﬁeld of view of the camera in

radians.

k −

c ||

(16)

Degrees of freedom

BVE + EKF: A Viewpoint Estimator for the Estimation of the Object’s Position in the 3D Task Space Using Extended Kalman Filters

159

⊥



−e

c,2

c,1

c,3



⊺

(17)

lim

k + r

·e

⊥

(18)

0 ≥

lim

−

||x

lim

−

c ||

·e

−cos



HFOV



(19)

Figure 2: Restriction—fruit inside the camera’s ﬁeld of

view.

In a tomato greenhouse, where plants are aligned

in rows, the robot must avoid crossing these rows to

prevent damage. These rows make a wall of uncross-

able tomato plants. Avoiding crossing the designed

walls is managed by deﬁning a restriction (22), mod-

elling the plant rows as a planar boundary to keep the

robot on one side, set at a distance d meters from the

fruit, as illustrated in the ﬁgure 3. The plane’s orien-

tation is determined by the normal unit vector e

plane

which represents the normal vector n

plane





⊺

(20)

w =

k −d ·e

plane

(21)

0 ≥e

plane

·(

c −w ) (22)

trees

plane

Figure 3: Restriction—camera cannot cross the fruits’ trees.

In addition to the previous restrictions, we de-

signed extra ones based on the manipulator’s spe-

ciﬁc features. These ensure that only valid poses are

selected, making the kinematics computable, which

varies with the manipulator’s kinematics.

The previously designed constraints are very spe-

ciﬁc and complex for the designed target. Conduct-

ing essays with simpliﬁed algorithms should be ad-

vantageous in understanding the beneﬁts and the lim-

itations of a more complete scene design. So, we

also conducted experiments with simpliﬁed restric-

tions, considering just one: the distance between the

camera and the fruit, denoted as l

dist

in (23).

dist

−ε < ||

c −

k || < l

dist

+ ε (23)

2.2 Fruit Pose Estimation Using the

EKF

The BVE computes the best observability viewpoints

but does not estimate the 3D position of the objects.

Based on an initial rough estimation of the position of

the fruit, the EKF can provide iterative reﬁnement of

the objects’ position.

To ensure a good correct operation of the EKF,

the camera should move smoothly while looking at

the fruit to correct the fruit position estimation itera-

tively. So, an additional restriction is implemented to

the BVE to ensure that the camera moves to the next

best viewpoint in a radius of r

meters, (24).

k +1

−c

||−r

< 0 (24)

The EKF is divided into two main steps: the pre-

diction phase and the correction phase. The fruit po-

sition is continuously estimated during prediction, at-

tending dynamics and predictive movement. At the

correction phase, the fruit is observed by a dedicated

sensor, and so its position is corrected according to

the measurements performed.

Prediction. During the prediction phase, we esti-

mate the fruit’s position, attending to its zero dynam-

ics. The EKF should expect the fruit to not move. So,

the predicted position of the fruit is the same as the

previous one (25). Besides, the EKF also has to prop-

agate the covariance estimation error (26).

k |k −1

= f (

k −1|k −1

k −1

) = I ·

k −1

(25)

k |k −1

·P

k |k −1

·F

⊺

= P

k |k −1

(26)

∂ f

∂ x



k −1|k−1

= 1 (27)

Correction. Assuming that the camera always ob-

serves the fruit, the EKF always has a correction

phase after a prediction phase. During this phase,

the EKF corrects the estimation of the fruit’s position

(35), acknowledging the measures obtained from the

camera to the sensor (28). The EKF uses the same

rough initial estimation method based on the fruit’s

average size and the camera’s distortion. The cor-

rection phase also corrects the covariance propagation

error (33). In these equations,

x is the estimated po-

sition of the fruit for each instance, and ε is a random

noise variable added to create noise for the simulated

environment (under real conditions, this value is real-

istically measured and should be ignored).

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

160

k |k −1

) =||

k −1

−c || (28)

=||k −c ||+ ε ·

√

(29)

=∇h(

k |k −1

) =

k −1

−c

k −1

−c ||

(30)

k |k −1

·H

⊺

·(H

·P

k |k −1

·H

⊺

+ R

)

−1

(31)

=σ

(32)

k |k

=(I −K

·H

) ·P

k |k −1

(33)

−h(

k |k −1

) (34)

k |k

k |k −1

+ K

(35)

2.3 Experiments

Multiple essays were made under a simulation context

in MATLAB to validate the designed algorithms. We

deployed an iterative protocol that adds restrictions to

the optimizer. That helps to understand the limitations

with the increase of the optimization difﬁculties. Bel-

low, we systematize the different experiments and the

restrictions considered for each one. Mind that in all

cases, the BVE always considers the restriction (24)

in r

of 0.2 m. The EKF uses a near-realistic covari-

ance matrix for the camera’s observations of the fruit,

corresponding to a diagonal matrix and a bigger ob-

servation variance in the xx axis.

E1. For this experiment, we used the loss function

(10) and restricted the BVE’s behavior with lim-

ited the position of the camera l

dist

of (1.0 ±

0.1) m to the fruit, (23).

E2. In this experiment, we repeated the previ-

ous essay, but we also considered the restric-

tion (14) that assures that the camera is in-

side the manipulator’s working space, consider-

ing the Robotis Manipulator-H with its center m



0 0 0.159



⊺

m and a maximum range r

0.645 m.

E3. In this experiment, we consider the loss function

(10) and the restrictions (14), (15) with the aver-

age tomato size r

, and (19).

E4 This experiment considers the restrictions and the

loss function of E3 and adds the restriction (22),

considering d = 0.1 m;

E5. This experiment repeats the previous experiment,

adding the kinematics constraints, ensuring that

the camera’s pose is always a valid pose for the

manipulator;

E6. Repeats the experiment E1, considering the loss

function (11), based on the minimization of the

maximum covariance, instead of the dispersion-

based loss function (10);

E7. Repeats the experiment E2, considering the loss

function (11);

E8. Repeats the experiment E3, considering the loss

function (11);

E9. Repeats the experiment E4, considering the loss

function (11); and

E10. Repeats the experiment E5, considering the loss

function (11).

We executed the simulation code for 100 runs for

each of these experiments. In each run, we consider

a random position for the tomato k , k

∈ [−1,1] m,

and a random initial position for the camera c ,c

∈

[−2,2] m. The initial estimation of the fruit was ini-

tialized in its real position k added by a random bias

between [−0.15;0.15] m for each axis.

We assessed the algorithm’s performance using

the mean absolute percentage error (MAPE) (36),

mean absolute error (MAE) (37), root mean square er-

ror (RMSE) (39), and mean square error (MSE) (38).

MAPE (µ

) =

N ·M

∑



i j

−

i j



×100

∀j ∈ N : {1..M} (36)

MAE (µ

) =

N ·M

∑

|µ

i j

−

i j

∀j ∈ N : {1..M} (37)

MSE (µ

) =

N ·M

∑

(µ

i j

−

i j

)

∀j ∈ N : {1..M} (38)

RMSE (µ

) =

N ·M

∑

(µ

i j

−

i j

)

∀j ∈ N : {1..M} (39)

3 RESULTS AND DISCUSSION

The BVE powered with EKF can effectively estimate

the fruits’ position while using a monocular camera.

We organized ten experiments, as described in the

section 2.3. Table 1 reports the average errors for

the different experiments. Figure 4 illustrates sam-

ple paths produced by the optimizer for experiments

E2, E5, E7, and E10.

Analyzing the table 1, we verify that simpler and

more ﬂexible restrictions result in smaller estimation

errors. However, discarding E1, all the experiments

conducted in similar estimation errors with an Eu-

clidean error of about 30 mm, if considering the loss

BVE + EKF: A Viewpoint Estimator for the Estimation of the Object’s Position in the 3D Task Space Using Extended Kalman Filters

161

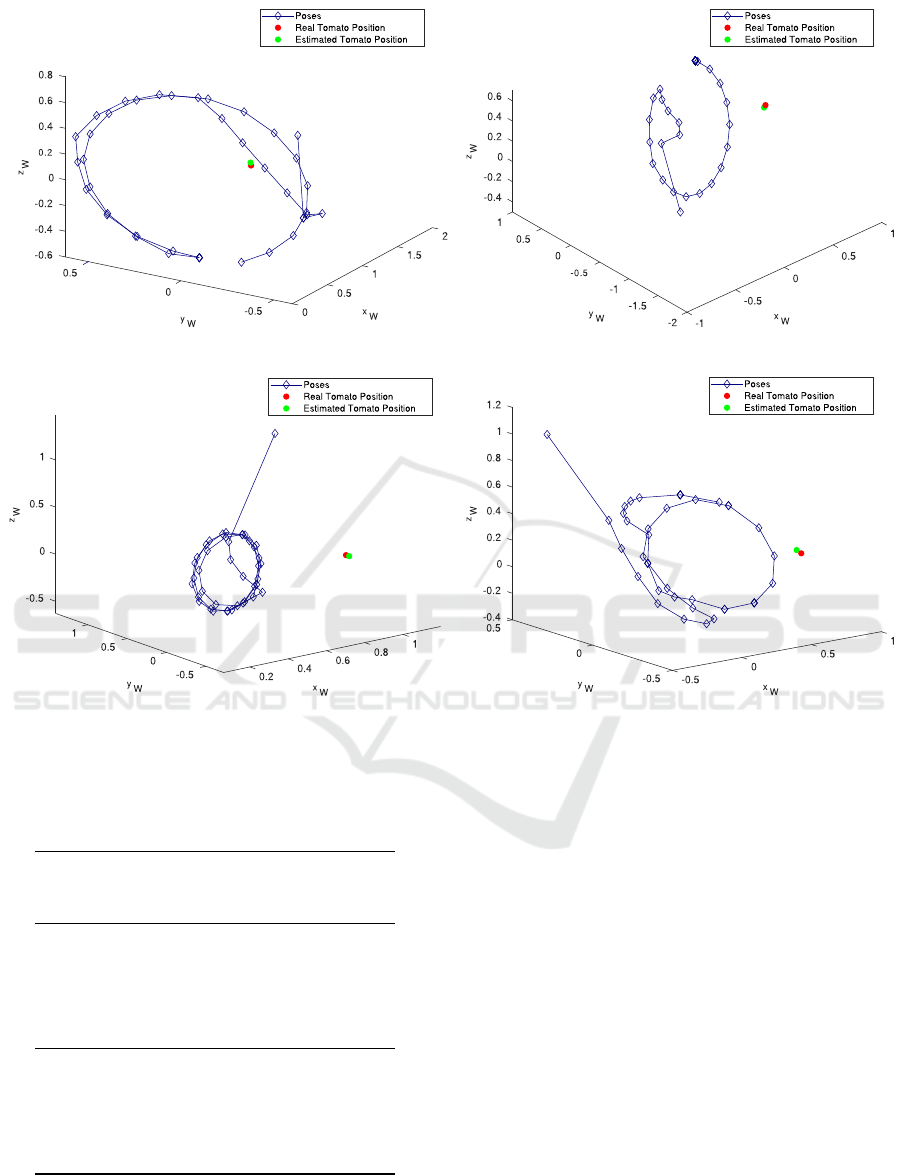
(a) E2 (b) E7

Figure 4: Sample paths generated by the different experiments to assess the fruit’s position. Light blue – poses; red – real

fruit position; green – estimated fruit position.

Table 1: Error computations to the centre estimation using

the BVE and the EKF.

MAPE

(%)

MAE

(mm)

RMSE

(mm)

MSE

(mm)

E1 5.12 37.1 15.5 241.64

E2 12.86 52.5 25.5 650.47

E3 8.64 53.8 28.1 790.79

E4 11.65 57.2 29.1 848.40

E5 10.62 60.9 31.2 971.44

E6 32.38 53.5 26.3 689.63

E7 14.79 53.1 24.7 612.17

E8 12.62 48.0 21.2 447.57

E9 10.44 53.0 23.4 548.17

E10 20.06 62.3 31.3 982.65

function (10). Despite constraining, the BVE + EKF

can perform similarly while increasing the constrain-

ing difﬁculty. Differently, the loss function 11 has a

more progressive behavior, having better results than

(10) for less constraining restrictions.

In a general evaluation, we can conclude that us-

ing a differentiable loss function (experiments E1 to

E5) such as the dispersion (10) brings advantages over

a none differentiable loss function (experiments E6

to E10) such as (11), which depends on a maximum

operation. Besides, empirical analysis of the perfor-

mance of both loss functions under the same condi-

tions concludes that the dispersion loss function was

also faster to compute because it has one less inver-

sion matrix to calculate. Simpler and less restrictive

conditions deliver lower errors while estimating the

position of the fruits once the camera has more free-

dom to navigate around the region of interest. In both

strategies, the BVE tends to plan an approximated cir-

cular path in the case where the algorithm is free to

design its path to the most restricted cases (Figures

4). These circular paths do not always happen in the

same plan but in various plans, even transversal ones.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

162

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

Initial deviation error to real position (m)

0.01

0.02

0.03

0.04

0.05

0.06

0.07

0.08

Error

RMSE

MSE

MAE

(a) E1

0 0.1 0.2 0.3 0.4 0.5

Initial deviation error to real position (m)

0.02

0.04

0.06

0.08

0.1

0.12

0.14

Error

RMSE

MSE

MAE

(b) E6

0 0.1 0.2 0.3 0.4 0.5

Initial deviation error to real position (m)

0.05

0.1

0.15

0.2

0.25

Error

RMSE

MSE

MAE

0 0.1 0.2 0.3 0.4 0.5 0.6

Initial deviation error to real position (m)

0.05

0.1

0.15

0.2

0.25

Error

RMSE

MSE

MAE

(d) E10

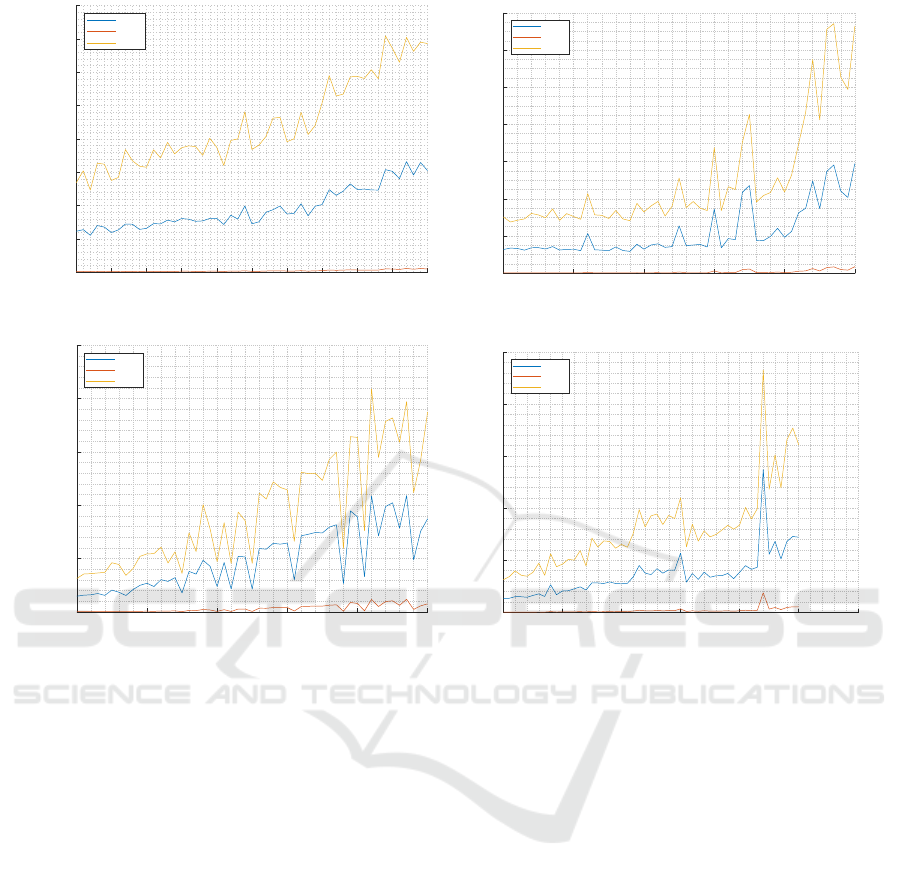
Figure 5: Average error for the recoverability of the loss functions for the BVE + EKF considering different initial estimation

errors. Blue – RMSE; red – MSE; yellow – MAE.

For some applications, such as precise and care-

ful fruit picking with cutting tools, the reported esti-

mation errors may not be small enough. To improve

the error, the system should apply strategies and algo-

rithms that reduce the covariance. Freer systems also

prove to have smaller errors because of the liberty of

the algorithm to choose the best observation positions.

Besides, implementing historical knowledge should

optimize innovation and promote the acquisition of

new scene perspectives.

The previous conclusions are enough to under-

stand the performance of both models but do not allow

us to understand their limitations and recovery capac-

ity. So, we also performed a recoverability analysis

for the loss function to approximate the fruit’s posi-

tion correctly. To achieve this aim, we made multiple

essays for estimating the real position of the fruits,

considering an initial estimation error between 0 m to

0.5 m in steps of 1 cm. We considered ten simula-

tions for each initial estimation error and computed

the average result. Figure 5 illustrates the average er-

rors, given the initial conditions for experiments E1

and E5.

From these experiments, we can conclude that

both loss functions perform similarly under the most

complex and demanding restrictions. Still, the algo-

rithm can tolerate bigger initial estimation errors by

using the dispersion minimization loss function (10).

Besides, this loss function is also easier to compute,

and the next viewpoint is estimated quickly and eas-

ily.

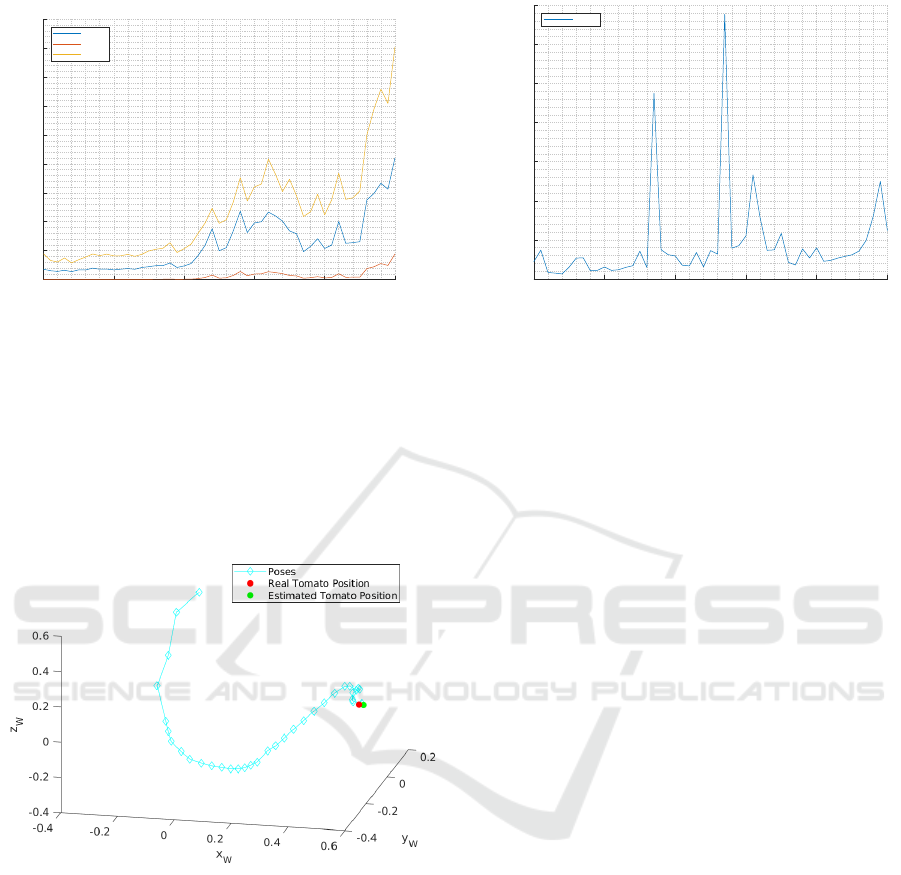
As has been observed, the algorithm is effective in

searching for the best viewpoint to estimate the posi-

tion of the fruits. However, task execution is also rel-

evant to ensure the sensory apparatus moves toward

the object. The algorithms can approximate the ob-

ject in a two-step procedure: positioning the fruit and

moving to it. However, using a properly designed loss

function such as (13), the BVE + EKF algorithms can

iteratively reﬁne the fruit’s position while moving to-

wards it. Figure 7 illustrates a possible path to move

the sensors from the starting pose to the object, con-

BVE + EKF: A Viewpoint Estimator for the Estimation of the Object’s Position in the 3D Task Space Using Extended Kalman Filters

163

0 0.1 0.2 0.3 0.4 0.5

Initial deviation error to real position (m)

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

Error

RMSE

MSE

MAE

(a) Error

0 0.1 0.2 0.3 0.4 0.5

Initial deviation error to real position (m)

100

150

200

250

300

350

Error (%)

MAPE

(b) MAPE

Figure 6: Average Error and MAPE for the recoverability of the loss functions for the BVE + EKF considering different initial

estimation errors for the loss function (13) and the restrictions such as in E5. On left (blue – RMSE; red – MSE; yellow –

MAE); On Right (blue – MAPE).

sidering the restrictions E5. This scheme shows that

the algorithm tends to have a circular path while cor-

recting the fruit’s position.

Figure 7: Sensor approximation’s path using the loss func-

tion (13) and the restrictions such as in E5. Light blue –

poses; red – real fruit position; green – estimated fruit posi-

tion.

Similar to the previous examples, we also per-

formed a recoverability analysis of the algorithm run-

ning the loss function (13). The behavioral results are

illustrated in ﬁgure 6 plots. The algorithm tends to

perform worse and accumulate more errors for this

function. Here, we can rely on an initial estimation

error until about 15 cm. Initial estimation errors big-

ger than that will result in a ﬁnal signiﬁcant estimation

error.

4 CONCLUSIONS

The robotization of agricultural ﬁelds is an approach

that can help to overcome some current societal chal-

lenges, such as labor shortages in the ﬁeld or im-

proved crops. However, that requires the implementa-

tion of robust 3D or 6D perception systems indepen-

dent of depth sensors because of their sensibility to

external perturbances.

To approach the problem, we studied a Gaussian-

based solution to minimize the observation covari-

ance over the fruits, which we called BVE. We pow-

ered the BVE with an EKF that iteratively approxi-

mates the position of the fruits. The essay was de-

ployed and tested in mathematical simulation over

MATLAB. We designed two loss functions to opti-

mize the resulting observability error: a covariance

dispersion-based function and the maximum variance

of the covariance matrix. The system reached reason-

able results with average Euclidean errors lower than

31.2 mm. A more distinctive analysis concludes that

the maximum covariance function is more sensitive to

restrictions, so a lower error with fewer constraining

restrictions. On the other hand, the dispersion-based

function is empirically faster to compute and more ro-

bust.

Additional evaluations were conducted to assess

the algorithm’s robustness to different initial condi-

tions, which show that both loss functions perform

similarly. A variant loss function that drives the sen-

sor to the object proves the robot can perform both

tasks simultaneously.

Future work should focus on developing the sys-

tem in a robotic system under controlled environ-

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

164

ments. Besides using EKF, other equivalent algo-

rithms may be tested, such as the Unscented Kalman

Filter (UKF). Additional improvements may also be

studied, such as implementing historical knowledge

that promotes the selection of newer innovative poses.

ACKNOWLEDGEMENTS

This work is ﬁnanced by National Funds through

the FCT – Fundação para a Ciência e a Tec-

nologia, I.P. (Portuguese Foundation for Science

and Technology) within the project OmicBots,

with reference PTDC/ASP-HOR/1338/2021

(DOI:10.54499/PTDC/ASP-HOR/1338/2021).

Sandro Costa Magalhães is granted by the Por-

tuguese Foundation for Science and Technology

(FCT) through the ESF integrated into NORTE2020,

under scholarship agreement SFRH/BD/147117/2019

(DOI:10.54499/SFRH/BD/147117/2019).

REFERENCES

Birkl, R., Wofk, D., and Müller, M. (2023). MiDaS v3.1 –

a model zoo for robust monocular relative depth esti-

mation.

Chang, J., Kim, M., Kang, S., Han, H., Hong, S., Jang,

K., and Kang, S. (2021). GhostPose: Multi-view Pose

Estimation of Transparent Objects for Robot Hand

Grasping. In 2021 IEEE/RSJ International Conference

on Intelligent Robots and Systems (IROS). IEEE.

FAO (2023). FAOSTAT Statistical Database. 2024-05-21.

General Assembly (2015). Transforming our world: the

2030 Agenda for sustainable development. Resolution

A/RES/70/1.

Gené-Mola, J., Llorens, J., Rosell-Polo, J. R., Gregorio, E.,

Arnó, J., Solanelles, F., Martínez-Casasnovas, J. A.,

and Escolà, A. (2020). Assessing the performance of

RGB-D sensors for 3D fruit crop canopy characteriza-

tion under different operating and lighting conditions.

Sensors-basel., 20(24):7072.

Kumar, M. S. and Mohan, S. (2022). Selective fruit harvest-

ing: Research, trends and developments towards fruit

detection and localization – a review. Proceedings of

the Institution of Mechanical Engineers, Part C: Jour-

nal of Mechanical Engineering Science, 237(6):1405–

1444.

Li, F., Vutukur, S. R., Yu, H., Shugurov, I., Busam,

B., Yang, S., and Ilic, S. (2023). NeRF-

Pose: A First-Reconstruct-Then-Regress Approach

for Weakly-supervised 6D Object Pose Estimation. In

2023 IEEE/CVF International Conference on Com-

puter Vision Workshops (ICCVW), pages 2115–2125.

Ma, X., Wang, Z., Li, H., Zhang, P., Ouyang, W., and

Fan, X. (2019). Accurate monocular 3D object de-

tection via color-embedded 3D reconstruction for au-

tonomous driving. In 2019 IEEE/CVF International

Conference on Computer Vision (ICCV), pages 6850–

6859, Seoul, Korea (South). IEEE.

Magalhães, S. A., Moreira, A. P., dos Santos, F. N., and

Dias, J. (2022). Active perception fruit harvesting

robots — a systematic review. Journal of Intelligent

& Robotic Systems, 105(14).

Magalhães, S. A. C., dos Santos, F. N., Moreira,

A. P., & Dias, J. M. M. (2024). MonoVi-

sual3DFilter: 3D tomatoes’ localisation with monoc-

ular cameras using histogram ﬁlters. Robotica, 1–20.

doi:10.1017/S0263574724000936

Nocedal, J., Öztoprak, F., and Waltz, R. A. (2014). An in-

terior point method for nonlinear programming with

infeasibility detection capabilities. Optim. Methods

Softw., 29(4):837–854.

Parisotto, T., Mukherjee, S., and Kasaei, H. (2023).

MORE: simultaneous multi-view 3D object recogni-

tion and pose estimation. Intelligent Service Robotics,

16(4):497–508.

Petersen, K. B. and Pedersen, M. S. (2012). The Matrix

Cookbook. Version 20121115.

Ringdahl, O., Kurtser, P., and Edan, Y. (2019). Performance

of RGB-D camera for different object types in green-

house conditions. In 2019 European Conference on

Mobile Robots (ECMR), pages 1–6, Prague, Czech Re-

public. IEEE.

The MathWorks, Inc. (2024). MATLAB 9.14.0.2206163

(R2023a).

Wang, H., Dong, L., Zhou, H., Luo, L., Lin, G., Wu, J., and

Tang, Y. (2021). YOLOv3-litchi detection method of

densely distributed litchi in large vision scenes. Math.

Probl. Eng., 2021:1–11.

BVE + EKF: A Viewpoint Estimator for the Estimation of the Object’s Position in the 3D Task Space Using Extended Kalman Filters

165