Augmented Feasibility Maps: A Simultaneous Approach to Redundancy

Resolution and Path Planning

Marc Fabregat-Ja

1 a

, Adri

an Peidr

1 b

, Esther Gonz

alez-Amor

, Mar

ıa Flores

1 c

and

Oscar Reinoso

1,2 d

Instituto de Investigaci

on en Ingenier

ıa de Elche, Universidad Miguel Hern

andez, Avda. Universidad s/n, Elche, Spain

ValgrAI: Valencian Graduate School and Research Network of Artiﬁcial Intelligence, Cam

ı de Vera s/n, Valencia, Spain

{mfabregat, apeidro, esther.gonzaleza, m.ﬂores, o.reinoso}@umh.es

Keywords:

Redundancy Resolution, Path Planning, Feasibility Maps, Redundant Manipulators, Obstacle Avoidance.

Abstract:

Redundant robotic manipulators are capable of performing complex tasks with an unprecedented level of

dexterity and precision. However, their redundancy also introduces signiﬁcant computational challenges, par-

ticularly in the realms of redundancy resolution and path planning. This paper introduces a novel approach to

simultaneously address these challenges through the concept of Augmented Feasibility Maps, by integrating

task coordinates as decision variables into the traditional feasibility maps. We validate the AFM concept by us-

ing Rapidly-Exploring Random Trees to explore the maps, demonstrating its efﬁcacy in simulations of various

dimensionalities. The method is capable of incorporating kinematic constraints, such as obstacle avoidance

while adhering to joint limits.

1 INTRODUCTION

Kinematically redundant robots have more degrees of

freedom n (DoF) than the dimension m of the primary

or main task that they must perform. For example, a

3-DoF planar manipulator that must control the posi-

tion coordinates p

and p

of its gripper in the plane

has one degree of redundancy, as it would sufﬁce to

have 2 DoF to complete this task. Kinematic redun-

dancy increases the versatility of robotic manipulators

because the excess of r = n − m degrees of freedom

can be leveraged to satisfy secondary goals or con-

straints in addition to the main task, e.g., minimiza-

tion of torques or energy consumption, or avoidance

of singularities or obstacles, etc. (Peidro and Haug,

2023). However, this comes at the expense of a higher

computational complexity, because their inverse kine-

matic problem (IKP), i.e., the problem of computing

the joint displacements that allow the manipulator to

place its gripper at the desired position, admits in-

ﬁnitely many different solutions. Deciding which one

of these inﬁnite solutions should be picked to com-

plete its task is the problem of redundancy resolution.

https://orcid.org/0009-0002-4327-0900

https://orcid.org/0000-0002-4565-496X

https://orcid.org/0000-0003-1117-0868

https://orcid.org/0000-0002-1065-8944

Typically, the problem of redundancy resolution is

solved for a given desired trajectory of the kinematic

variables that deﬁne the task of the robot, which we

denote by x. For a speciﬁed x(t), with 0 < t < t

, a

redundancy resolution algorithm should provide the

time history q(t) of all n joint displacements (or co-

ordinates) of the manipulator, considering the inﬁni-

tude of solutions that exist for each t, as well as any

existing constraints or secondary goals. Methods to

solve this problem can be classiﬁed into velocity-

based methods and position-based.

Velocity-based methods operate with the veloc-

ity relationship between task and joint coordinates:

x = J

q, where J is the non-square n × m Jacobian

matrix. This velocity equation is the basis of pseu-

doinverse and optimization approaches to redundancy

resolution, which obtain

q and integrate it. Pseudoin-

verse methods (Whitney, 1969) solve joint velocities

q = J

†

x plus an additional nullspace term that op-

timizes secondary goals without affecting the main

task (Kazemipour et al., 2022), where (·)

†

denotes the

Moore-Penrose pseudoinverse. Optimization meth-

ods minimize programs to ﬁnd the optimal value of

q, where the velocity equation

x = J

q is included as

an equality constraint, avoiding inversion (Zanchettin

and Rocco, 2017). The main advantage of velocity-

based methods is their simplicity and compatibility

with real time, but they usually provide only locally

166

Fabregat-Jaén, M., Peidró, A., González-Amorós, E., Flores, M. and Reinoso, Ó.

Augmented Feasibility Maps: A Simultaneous Approach to Redundancy Resolution and Path Planning.

DOI: 10.5220/0012946000003822

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 2, pages 166-173

ISBN: 978-989-758-717-7; ISSN: 2184-2809

optimal trajectories, may suffer from non-holonomy

and singularities (when pseudoinverting), and may

fail to accurately satisfy constraints that, like colli-

sions, are deﬁned better at position level than at ve-

locity level (Peidro and Haug, 2023).

These limitations are alleviated by position-based

methods, which operate directly at conﬁguration

level. Solving redundancy at position level means

obtaining all the solution sets of the space of joint

coordinates q that yield a desired task value x.

Generically, these solution sets are manifolds called

self-motion manifolds (Burdick, 1989). By scanning

all self-motion manifolds for a given x, it is possible

to ﬁnd the q

∗

that globally optimizes secondary crite-

ria, allowing for globally-optimal solutions to the re-

dundancy problem. This, however, can be a costly ap-

proach, as computing the self-motion manifolds can

be rather computationally expensive (Albu-Sch

affer

and Sachtler, 2023). A similar approach is offered

by the Feasibility Maps (FMs) (Wenger et al., 1993;

Reveles et al., 2016), which represent all feasible val-

ues of a set of r redundant variables for each instant t

of the trajectory, and allow for planning trajectories in

these maps avoiding obstacles and singularities while

globally optimizing other criteria.

Independently of the taken approach, it may occur

that the desired task trajectory x(t) is unfeasible. This

happens when the solution set of the IKP becomes

empty due to singularities, joint limits or collisions,

which materialize as external boundaries or internal

barriers of the workspace of the manipulator (Peidro

et al., 2018). When this happens, the manipulator can-

not complete its task regardless of the method used.

To avoid this, in this paper we propose a method

to simultaneously solve the redundancy problem and

the path planning problem, where the latter consists

in ﬁnding a feasible task trajectory x(t) that allows

the manipulator to reach a speciﬁed goal x

respecting

the considered constraints. To achieve this, we begin

with the idea of FMs as in (Fabregat-Jaen et al., 2023),

which represent all feasible values of the redundant

coordinates at each instant of the trajectory, but, as a

novelty, we augment these maps by considering also

the task coordinates as decision variables whose time

evolution must also be determined.

This paper is organized as follows. First, Section

2 deﬁnes the Augmented Feasibility Maps (AFM).

Next, Section 3 presents a method based on Rapidly-

Exploring Random Trees (RRT) to explore the AFM

and connect the initial state of the robot to the desired

goal x

through a path that is asymptotically optimal.

Section 4 illustrates the method with one and two de-

grees of redundancy. Finally, conclusions and future

work are discussed in Section 5.

2 AUGMENTED FEASIBILITY

MAPS

Consider a manipulator whose joint conﬁguration is

given by q = [q

, q

, . . . , q

]

, where n represents

DoF. Its forward kinematics can be expressed as a

function that maps the n-dimensional joint space to

the m-dimensional task space:

x = f(q), (1)

where x = [x

, x

, . . . , x

]

denotes the m task coordi-

nates.

In order to determine the IK, (1) should ideally

be inverted to obtain an expression for q as a func-

tion of x (i.e., q = f

−1

(x)). Nevertheless, deriving

a universal IK function is often unfeasible, even for

non-redundant manipulators (where n = m), due to

the forward kinematics function generally being non-

bijective, rendering the IK mapping multi-valued.

The concept of aspects helps interpret this phe-

nomenon. In (Borrel and Li

egeois, 1986), an aspect is

deﬁned as a connected set of points in the joint space

where the Jacobian matrix remains full rank. As such,

aspects delineate subsets of the joint space wherein

the manipulator can move without encountering sin-

gularities. By deﬁnition, a transition between aspects

is marked by a singularity, at which point the Jaco-

bian matrix loses rank. For manipulators that must

pass through singularities to change posture, the IKP

yields a unique solution for each aspect. In this case,

an IK function g(·) can be deﬁned for each aspect,

mapping each task point to a unique joint position.

Multi-valuedness is further aggravated for redun-

dant manipulators (where n > m), as there exist in-

ﬁnitely many joint conﬁgurations that can reach a

given task space point. The degree of redundancy r,

that characterizes a robot and task combination, is de-

ﬁned as r = n − m. In this context, the use of an aug-

mented task space, which incorporates r additional

dimensions to encode the redundancy, has been pro-

posed as a means to simplify the IKP. The augmented

task space is deﬁned as:



, q



(2)

where q

corresponds to the additional r-dimensional

vector that virtually removes the redundancy. The

components of q

must be independent of every other

component of x

, and can be chosen arbitrarily, but

usually correspond to a subset of joint coordinates or

a differentiable function of them.

In (P

amanes G et al., 2002), the authors studied

the effect that the extra dimensions of the augmented

task space had on the Jacobian matrix. Given that the

rows corresponding to q

induced new singularities, a

Augmented Feasibility Maps: A Simultaneous Approach to Redundancy Resolution and Path Planning

167

new set of aspects were produced, which were named

extended aspects. Therefore, depending on the selec-

tion of q

, the number of extended aspects and their

domain can vary.

The augmented task space allows for the deﬁnition

of a unique augmented IK function g

(·) that maps ev-

ery augmented-task-space point to a unique joint con-

ﬁguration that lies in a certain extended aspect:

q = g

) (3)

However, rather than a single ﬁxed task point, the

IKP is often posed as the tracking of a task trajectory.

Such trajectory x(t) can be parameterized by an arc-

length parameter t (hereafter referred to as time for

simplicity). In this situation, the set of joint conﬁg-

urations that successfully track the trajectory can be

gathered in an (r + 1)-dimensional space, where one

of the dimensions of this space is time t, whereas the

other r dimensions are the q

coordinates. This con-

ceptual space is referred to as feasibility map (FM),

a term introduced in (Wenger et al., 1993). A feasi-

bility map FM is deﬁned as the set of points in the



t, q



space for which the augmented IKP yields a

real solution that satisﬁes additional kinematic con-

straints (e.g., joint limits or obstacles), i.e.:

FM =







q = g

), x



x(t)



, q∈Q



(4)

where Q denotes the joint-space subset that satisﬁes

the kinematic constraints. Note that, for a speciﬁed

task trajectory x(t), and a given choice of q

, there

exist as many FMs as extended aspects, and each

FM corresponds to a different augmented IK func-

tion g

(·) that maps the augmented task space to joint-

space points within that extended aspect.

Figure 1(a) shows an example of an FM for a 2-

DoF manipulator with a 1-dimensional task, hence re-

dundancy r = 1, resulting in a 2D map. Note that the

feasible space corresponds to the uncolored region, as

the colored regions represent subsets that do not sat-

isfy the kinematic constraints. Speciﬁcally, the red re-

gions correspond to conﬁgurations that lead to a colli-

sion with an obstacle, while the purple regions corre-

spond to conﬁgurations that yield complex solutions

for the IKP.

In particular, this example corresponds to the ma-

nipulator depicted in Figure 2, which has two joints

q = [q

, q

]

and a task x = p

, with forward kine-

matic function p

= sin(q

) + sin(q

+ q

). The task

trajectory is p

(t) = −6.662t

+ 8.162t − 1.5 with

t ∈ [0, 1], and the choice of redundant parameters is

= q

, hence x

= [p

, q

]

. The augmented IK

function (3) in this example is:

q =



+ σ



− arcsin(p

(t) − sin q

)



− q



(5)

which has two solutions (i.e., extended aspects) if an-

gles are constrained to the range [−π, π] rad, corre-

sponding to the two possible values of σ = ±1. This

yields two possible feasibility maps; Fig 1(a) shows

the one corresponding to σ = −1. The FM shown in

Fig 1(a) is obtained by sweeping plane (t, q

) between

ranges 0 < t < 1 and −π < q

< π with a given dis-

crete step, and for each point (t, q

), q is computed

using (5). If the computation of q yields non-real

solutions (i.e., |p

− sin q

| > 1), the corresponding

point (t, q

) is marked in purple. If it produces colli-

sions with the ellipse shown in Figure 2, it is marked

in red. Otherwise, it is left uncolored, indicating that

the solution is feasible, i.e., it belongs to F M .

FMs have been employed in the literature to ad-

dress the redundancy resolution problem, which in-

volves the selection of the redundant parameters q

that fulﬁll a speciﬁed task x while optimizing a cer-

tain criterion and satisfying the kinematic constraints.

For instance, a modiﬁed RRT algorithm that explores

FMs for online redundancy resolution is proposed in

(Fabregat-Jaen et al., 2023). Another example is (Fer-

rentino and Chiacchio, 2020), where the authors com-

pute every FM and employ them to globally address

the redundancy resolution problem through an ex-

haustive search across the combined maps. Nonethe-

less, these methods rely on a predeﬁned task tra-

jectory x(t), potentially resulting in unfeasible joint-

space motions if the task trajectory is not properly de-

signed, accounting for the kinematic constraints, sin-

gularities or internal barriers of the robot’s workspace

(Peidro et al., 2018).

For example, consider the FM shown in Figure

1(a). Assuming that the initial conﬁguration of the

manipulator corresponds to the FM point A = (t =

0, q

= −2), any valid trajectory that fulﬁlls the de-

sired task x(t) should connect A with any valid point

of the vertical line t = 1, e.g., FM point B. The trajec-

tory T shown in Figure 1(a) accomplishes this (note

that T wraps around q

because −π can be identiﬁed

with +π). However, if we forbid angular wrapping by

setting joint limits, the only way to connect A with

any point satisfying t=1 is by traversing the narrow

corridor encircled by N. If the desired task trajectory

x(t) was slightly perturbed, it may occur that the red

and purple regions near N touch each other, eliminat-

ing the corridor and making it impossible to reach

t = 1 from A unless angular wrapping is permitted,

thus rendering the desired task trajectory x(t) unfeasi-

ble. To avoid unfeasible task trajectories, in this paper

we will only specify the desired ﬁnal value for x in-

stead of specifying its trajectory x(t), and we will in-

corporate the task variables into the feasibility maps

in order to ﬁnd their time history at the same time

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

168

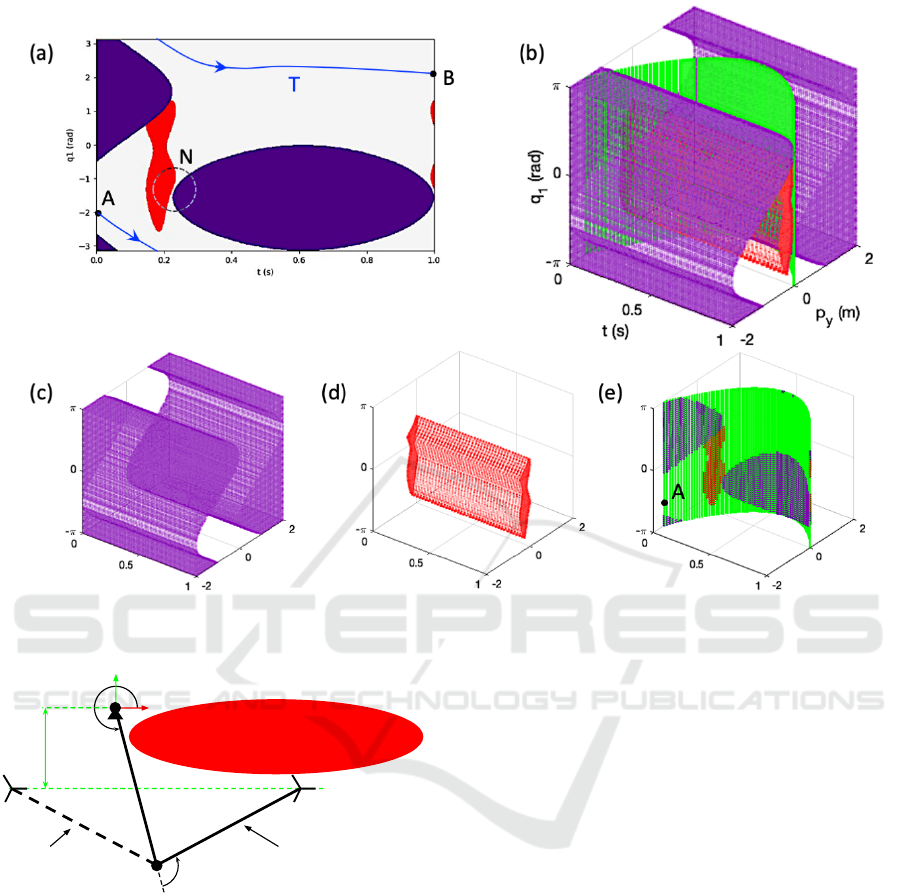
Figure 1: (a) Example of an FM for r = 1. (b) AFM that includes the task coordinate (p

). (c) Region of non-real solutions.

(d) Region of collisions. (e) Parabolic sheet corresponding to the task p

= −6.662t

+ 8.162t − 1.5.

σ = +1

σ = -1

Figure 2: 2-DoF manipulator with an elliptical obstacle.

that the motion of q

is determined, simultaneously

solving the path planning of x(t) and the redundancy

resolution.

To achieve this, we propose extending the concept

of FMs to augmented feasibility maps (AFMs), which

incorporate the task trajectory into the FM deﬁnition.

An AFM is deﬁned as:

AFM =







q = g

), x





, q∈Q



(6)

To illustrate this idea, consider the same exam-

ple of Figure 2, but instead of specifying the time

history of the task p

(t), we specify only its ﬁnal

value p

(1) = 0. If p

can be freely varied, it can

be included as an additional dimension in the FM, re-

sulting in a 3D map (t, p

, q

) of feasible conﬁgura-

tions, shown in Figure 1b. This map includes three

objects that, for clarity, have been represented sepa-

rately in Figures 1c-e. Firstly, Figure 1c shows some

purple surfaces that enclose three-dimensional vol-

umes made of conﬁgurations that, when substituted

in (5), yield non-real solutions of q. Secondly, the

red surfaces shown in Figure 1d enclose conﬁgura-

tions for which the end-effector of the manipulator

penetrates the elliptical obstacle. Finally, the green

surface shown in Figure 1e is a parabolic sheet de-

ﬁned parametrically as: {(t, p

, q

) | 0 < t < 1, p

−6.662t

+ 8.162t − 1.5, −π < q

< π}. This sheet

represents the task trajectory that was speciﬁed in the

previous example, and Figure 1e includes the inter-

sections between this sheet and the purple and red for-

bidden regions. In fact, the projection of this sheet on

plane (t, q

) yields the conventional FM depicted in

Figure 1a.

Note that, if we do not specify the task trajectory

(t), the conﬁguration of the robot is not constrained

to move along the parabolic sheet, being able to move

freely along the three-dimensional feasible space that

is free from non-real solutions and collisions. This

Augmented Feasibility Maps: A Simultaneous Approach to Redundancy Resolution and Path Planning

169

increases the chances of ﬁnding a task trajectory that

successfully connects point A to any feasible point

of the goal set, which is the vertical line deﬁned as:

{

(t, p

, q

) | t = 1, p

= 0, −π < q

< π

}

Generalizing the previous example, we propose a

method to solve the motion of redundant manipula-

tors to reach a goal task point x

in time t

. This

deﬁnes a goal set as an r-dimensional subset of the

AFM where the coordinates t and x are ﬁxed to their

goal values (i.e., t = t

and x = x

), and the remaining

dimensions of q

are free to vary. The method ex-

plores the free space of the augmented space (t, x, q

)

to ﬁnd a feasible trajectory connecting the initial con-

ﬁguration of the manipulator to the goal set, simulta-

neously solving path planning (i.e., time history of the

task x) and redundancy resolution (i.e., q

). The pro-

posed method, which performs online, is described in

the following section.

Other works have proposed concurrently ad-

dressing both problems, albeit through different ap-

proaches. In (Tassi et al., 2021), a method based on

hierarchical quadratic programming is proposed to ef-

fectively augment the decision variables of the opti-

mization problem with the task trajectory. The au-

thors of (Zhou et al., 2023) propose a two-stage ap-

proach. First, an RRT is built by sampling points in

the task space. In the second stage, for each sam-

pled RRT node, self-motion manifolds are calculated,

and a joint trajectory is derived based on an exhaus-

tive search that evaluates an averaged performance in-

dex (e.g., reciprocal condition number) along each se-

quence of self-motion manifolds.

3 EXPLORING AFMs VIA RRT

The proposed method is based on the RRT algorithm.

Particularly, we employ the RRT* variant (Karaman

and Frazzoli, 2011), which is an extension that guar-

antees asymptotic optimality. In this section, we

present the modiﬁcations required to adapt the RRT*

algorithm to explore AFMs. Algorithm 1 outlines the

method. The general structure of the RRT* algorithm

is maintained, with the main difference being the spe-

ciﬁc deﬁnition of the procedures.

The ﬁrst line of Algorithm 1 initializes the tree T

with a root node n

= s

, where s

is the initial state

of the robot. We deﬁne a state as a point in the AFM

space s =



t, x

, q



, while a node n is an element of

the tree T that contains a stored state s, and a pointer

to its parent node n

parent

. The main loop of the algo-

rithm is then entered, where T is expanded N times.

In each iteration, a random state s

rand

is sampled

Algorithm 1: RRT** algorithm.

1 Initialize tree T with root node n

= s

2 for i = 1 to N

3 s

rand

← SAMPLESTATE(α, x

)

4 n

near

← NEARESTNODE(s

rand

, T )

5 n

new

← STEER(n

near

, s

rand

, ∆s)

6 if FEASIBLECONNECTION(n

near

, n

new

)

7 N ← NEIGHBORS(n

new

, T , r)

8 n

parent

← BESTPARENT(N , n

new

)

9 Add n

new

to T with parent n

parent

10 T ← REWIRE(T , N , n

new

)

11 P ← BESTPATH(T )

from the AFM space (line 3). The SAMPLESTATE

function generates a random state in the domain of

the AFM. The t dimension of the AFM is constrained

to the interval [0, t

], where t

is the user-deﬁned du-

ration of the trajectory. The x domain is deﬁned by a

prior workspace analysis of the robot, and q

is con-

straint by the joint limits. To guide the exploration

towards the goal x

, samples are drawn from the goal

set (which depends on x

) with probability α, which

normally ranges from 0.05 to 0.2 (i.e., at most, 20%

of the samples generated in line 3 of Algorithm 1 will

belong to the goal set).

In line 4, NEARESTNODE ﬁnds the node n

near

the tree T that is closest to s

rand

. The distance metric

is given by a cost function deﬁned by the user. For in-

stance, the cost function could be the weighted norm

of the differences between the states:

c(s

, s

) =

− s

)

W (s

− s

) (7)

where W is a positive-deﬁnite diagonal matrix that

weights the dimensions of the AFM space, due to the

non-homogeneous units of the different coordinates

of s. The weights can be used to prioritize the mini-

mization of certain dimensions over others. One im-

portant aspect of the NEARESTNODE function is that

it must consider the time dimension t when computing

the distance between states. Since the time is strictly

monotonically increasing, only the states with a time

value less than that of s

rand

are considered.

The STEER function (line 5) generates a new state

new

by moving an incremental distance ∆s from n

near

towards s

rand

. The ∆s parameter is a user-deﬁned con-

stant that determines the step size of the exploration.

The function is exempliﬁed in Figure 3(a), where n

new

is generated by moving from n

near

towards s

rand

with

a step size of ∆s.

Next, the FEASIBLECONNECTION function (line

6) determines if the connection between n

near

and

new

is feasible (red segment in Figure 3(a)). This

function evaluates if the segment between the two

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

170

states satisﬁes the kinematic constraints, i.e., conﬁgu-

rations are real and collision-free. If the connection is

feasible, the algorithm proceeds to the two character-

istic steps of the RRT* algorithm: the selection of the

parent node and the rewiring of the tree.

In line 7, the NEIGHBORS function computes the

set of nodes N in the tree T that are within a radius

r from n

new

. In Figure 3, the set of neighbors N are

represented by the nodes within the purple circle, of

radius r, centered at n

new

. Then, the BESTPARENT

function (line 8) selects the best parent node n

parent

from N . The best parent is the one that minimizes

the cost function deﬁned in (7) for the entire path from

the root node n

to n

new

, routing through n

parent

. The

path and its cost can be computed by backtracking

from n

new

to its parent node, and so on until the root

node is reached, accumulating the cost of each seg-

ment during the process. The tree is then updated

by adding n

new

as a child of n

parent

(line 9). In Fig-

ure 3(b), the node n

new

is connected to its best parent

parent

(purple segment), instead of the parent n

near

that the original RRT would choose (red segment).

rand

new

STEER

Δs

new

near

parent

REWIRE

(a)

(b)

Figure 3: Procedures of the RRT* algorithm.

Finally, the REWIRE function in line 10 updates

the tree T by performing a local analysis of the neigh-

borhood of n

new

. The same set of neighbors N as in

BESTPARENT is employed, but the roles are swapped.

In this case, the function evaluates if the path from the

root node to each neighbor in N can be improved by

routing through n

new

. If the path is improved for any

neighbor, the parent of such neighbor is updated to

new

, and the tree is restructured accordingly. This

process is illustrated in Figure 3(b).

Once the main loop is completed, the BESTPATH

function (line 11) is called to extract the best path P

from the tree T . Calculating the cost in a similar way

to the BESTPARENT and REWIRE functions, every

path from the root node to each node that lies in the

goal set is evaluated, and the best path P is selected.

Due to the nature of the RRT* algorithm, the re-

turned path presents discontinuous velocities, as well

as inﬁnite accelerations at the node points. To address

this issue, a post-processing step is required to smooth

the path. We propose employing a cubic b-spline in-

terpolation to generate a smooth trajectory that con-

nects the nodes of the path. Similarly to (Fabregat-

Jaen et al., 2023), a series of intermediate control

points are generated between each pair of consecutive

nodes, and the b-spline is ﬁtted to these points (see

Figure 4). However, instead of deﬁning a ﬁxed num-

ber of control points per segment, we propose em-

ploying the value of ∆s as the distance between con-

trol points. Since the values of ∆s are small, the re-

sulting b-spline will not deviate signiﬁcantly from the

original path, i.e., there is little risk that the smoothed

path becomes unfeasible due to invading forbidden re-

gions, while ensuring a smooth trajectory.

Δs

Figure 4: B-Spline interpolation (orange) of the original

path (black) along the blue control points.

4 SIMULATIONS

In this section, we present results of the proposed

method for different combinations of manipulators

and tasks. The simulations are conducted in an In-

tel Core i7-9700F CPU @ 3.00GHz with 32 GB of

RAM, running Ubuntu 24.04. The code is imple-

mented in Python 3.12.

4.1 2-DoF Robot, 1-Dimensional Task

The ﬁrst example corresponds to the same scenario

considered in the ﬁrst experiment of (Fabregat-Jaen

et al., 2023). It consists of a 2-DoF planar ma-

nipulator and a 1-dimensional task, shown in Figure

2. However, instead of tasking the manipulator with

tracking a predeﬁned trajectory, only the ﬁnal task

point is speciﬁed, and corresponds to the p

coordi-

nate of the end-effector being equal to 0 at t

= 1 (see

green line at Figure 5(b)). The kinematic constraints

are deﬁned by the joint limits q

∈ [−π, π]rad ∀i ∈

{1, 2}, and an elliptical obstacle that the end-effector

must avoid (red ellipse in Figures 2 and 5(b)), deﬁned

by the equation

−1.1)

+0.2)

0.25

≤ 1. Both links

of the manipulator l

and l

have a length of 1m. We

selected q

as the single redundant parameter in q

For this example, we set the RRT* parameters as

Augmented Feasibility Maps: A Simultaneous Approach to Redundancy Resolution and Path Planning

171

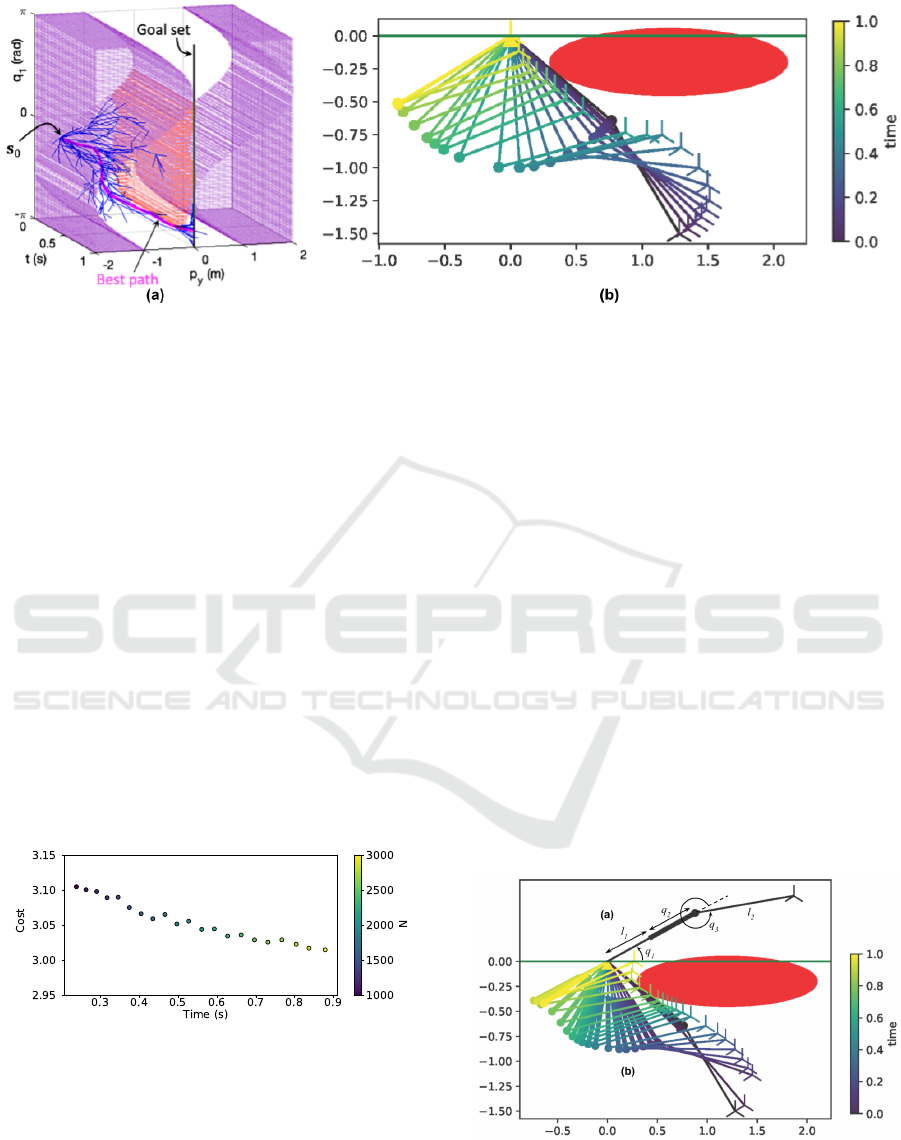
Figure 5: (a) AFM and RRT solution for a 2-DoF manipulator and a 1-dimensional task. (b) Corresponding robot motion.

follows: ∆s = 0.2, r = 0.4, α = 0.2 and N = 1000.

The cost function corresponds to the one deﬁned in

(7), with W = I.

Figure 5(a) illustrates the AFM for the imposed

constraints and an executed RRT* tree that explores

the AFM. The same color code as in the FMs in Sec-

tion 2 is employed. In addition, the best path com-

puted is plotted in green, and its corresponding robot

motion is represented in Figure 5(b) for different time

values. It is worth remarking that the AFM is illus-

trated only for visual purposes, as the method does

not require the computation of the AFM.

In addition, in Figure 6, we present a graph that

shows the execution times of the RRT* algorithm, as

well as the cost of the solution, averaged over 100

runs, for different values of the number of iterations

N. As expected, the execution times proportionally

increase with the number of iterations. As for the cost

of the solution, although some variability is observed,

the values seem to follow a decreasing trend as the

number of iterations increases.

Figure 6: Execution time versus cost of the solution for 21

different values of N, averaged over 1000 runs.

4.2 3-DoF Robot, 1-Dimensional Task

Finally, we consider an RPR (Revolute-Prismatic-

Revolute) planar manipulator (shown in Figure 7(a))

and a 1-dimensional task, which produces redundancy

r = 2 and a 4-dimensional AFM. The same ﬁnal task

value and kinematic constraints as in the previous

example are considered. However, in order to in-

crease the complexity of the problem and showcase

the method’s efﬁciency, we consider that the entire

manipulator must avoid the obstacle, rather than just

the end-effector. For this purpose, we have employed

the HPP-FCL library (Pan et al., 2024) to evaluate the

collisions between the manipulator and the obstacle.

The new prismatic joint coordinate q

is restricted to

∈ [0, 1]m, and its value extends the length of the

ﬁrst link of the manipulator. The redundant param-

eter vector is composed of the ﬁrst revolute and the

prismatic coordinates: q

= [q

, q

]

The same RRT* parameters as for the previous

experiment are used, which are: ∆s = 0.2, r = 0.4,

α = 0.2, N = 1000 and W = I.

Since the corresponding AFM is 4-dimensional, it

is not possible to visualize it directly. Therefore, we

only present different time values of the robot motion

in Figure 7(b). The average execution time for 100

runs is 97.3ms, demonstrating the method’s efﬁciency

in solving the problem, even when considering whole-

body collisions and a higher-dimensional AFM.

Figure 7: (a) RPR manipulator. (b) Algorithm solution.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

172

5 CONCLUSIONS

In this paper, we have proposed a method to solve

the motion of redundant manipulators to reach a goal

task point in a given time. The method is based on the

RRT* algorithm, which is adapted to explore AFMs,

which incorporate the task trajectory into the feasibil-

ity analysis. The proposed method is capable of si-

multaneously solving path planning and redundancy

resolution, and it is demonstrated to be efﬁcient in

two examples of planar manipulators with different

degrees of redundancy. The method overcomes the

limitations of previous works that require a predeﬁned

task trajectory, which may not be always feasible.

In the future, we will implement direct compar-

isons with other methods that address the redundancy

resolution and path planning problem, such as the hi-

erarchical quadratic programming method proposed

in (Tassi et al., 2021) and the two-stage approach pro-

posed in (Zhou et al., 2023). In addition, the inher-

ent ﬂexibility of the RRT algorithm will allow our

method to incorporate non-holonomic constraints, as

well as dynamic constraints, since the time dimension

is taken into account in the AFM space.

Additional future work should focus on extend-

ing the method to higher dimensionalities, as well as

incorporating dynamic constraints and obstacles that

move in time. Moreover, the method could be ex-

tended to consider every AFM that corresponds to dif-

ferent extended aspects. Finally, the method should

be tested in real robotic systems to evaluate its perfor-

mance in practical scenarios.

ACKNOWLEDGEMENTS

Work supported by project PID2020-116418RB-

I00 and grant PRE2021-099226, funded by

MCIN/AEI/10.13039/501100011033 and the ESF+.

REFERENCES

Albu-Sch

affer, A. and Sachtler, A. (2023). Redundancy

resolution at position level. IEEE Transactions on

Robotics.

Borrel, P. and Li

egeois, A. (1986). A study of multiple

manipulator inverse kinematic solutions with applica-

tions to trajectory planning and workspace determi-

nation. In Proceedings. 1986 ieee international con-

ference on robotics and automation, volume 3, pages

1180–1185. IEEE.

Burdick, J. W. (1989). On the inverse kinematics of re-

dundant manipulators: Characterization of the self-

motion manifolds. In Advanced Robotics: 1989: Pro-

ceedings of the 4th International Conference on Ad-

vanced Robotics Columbus, Ohio, June 13–15, 1989,

pages 25–34. Springer.

Fabregat-Jaen, M., Peidro, A., Gil, A., Valiente, D., and

Reinoso, O. (2023). Exploring feasibility maps for

trajectory planning of redundant manipulators using

rrt. In 2023 IEEE 28th International Conference

on Emerging Technologies and Factory Automation

(ETFA), pages 1–8. IEEE.

Ferrentino, E. and Chiacchio, P. (2020). On the optimal

resolution of inverse kinematics for redundant manip-

ulators using a topological analysis. Journal of Mech-

anisms and Robotics, 12(3):031002.

Karaman, S. and Frazzoli, E. (2011). Sampling-based algo-

rithms for optimal motion planning. The international

journal of robotics research, 30(7):846–894.

Kazemipour, A., Khatib, M., Al Khudir, K., Gaz, C., and

De Luca, A. (2022). Kinematic control of redundant

robots with online handling of variable generalized

hard constraints. IEEE Robotics and Automation Let-

ters, 7(4):9279–9286.

amanes G, J. A., Wenger, P., and Zapata D, J. L. (2002).

Motion planning of redundant manipulators for spec-

iﬁed trajectory tasks. Advances in Robot Kinematics:

Theory and Applications, pages 203–212.

Pan, J., Chitta, S., Pan, J., Manocha, D., Mirabel, J., Car-

pentier, J., and Montaut, L. (2024). HPP-FCL - An

extension of the Flexible Collision Library.

Peidro, A. and Haug, E. J. (2023). Obstacle avoidance in

operational conﬁguration space kinematic control of

redundant serial manipulators. Machines, 12(1):10.

Peidro, A., Reinoso, O., Gil, A., Mar

ın, J. M., and Paya,

L. (2018). A method based on the vanishing of

self-motion manifolds to determine the collision-free

workspace of redundant robots. Mechanism and Ma-

chine Theory, 128:84–109.

Reveles, D., Wenger, P., et al. (2016). Trajectory planning

of kinematically redundant parallel manipulators by

using multiple working modes. Mechanism and Ma-

chine Theory, 98:216–230.

Tassi, F., De Momi, E., and Ajoudani, A. (2021). Aug-

mented hierarchical quadratic programming for adap-

tive compliance robot control. In 2021 IEEE interna-

tional conference on robotics and automation (ICRA),

pages 3568–3574. IEEE.

Wenger, P., Chedmail, P., and Reynier, F. (1993). A global

analysis of following trajectories by redundant manip-

ulators in the presence of obstacles. In [1993] Pro-

ceedings IEEE International Conference on Robotics

and Automation, pages 901–906. IEEE.

Whitney, D. E. (1969). Resolved motion rate control of ma-

nipulators and human prostheses. IEEE Transactions

on man-machine systems, 10(2):47–53.

Zanchettin, A. M. and Rocco, P. (2017). Motion planning

for robotic manipulators using robust constrained con-

trol. Control Engineering Practice, 59:127–136.

Zhou, Z., Zhao, J., Zhang, Z., and Li, X. (2023). Motion

planning method of redundant dual-chain manipula-

tor with multiple constraints. Journal of Intelligent &

Robotic Systems, 108(4):69.

Augmented Feasibility Maps: A Simultaneous Approach to Redundancy Resolution and Path Planning

173