Model-Free versus Model-Based Reinforcement Learning for
Fixed-Wing UAV Attitude Control Under Varying Wind Conditions
David Olivares
1,2 a
, Pierre Fournier
1 b
, Pavan Vasishta
2 c
and Julien Marzat
1 d
1
DTIS, ONERA, Universit
´
e Paris-Saclay, 91123 Palaiseau, France
2
AKKODIS Research, 78280 Guyancourt, France
Keywords:
Reinforcement Learning, Unmanned Aerial Vehicle, Fixed-Wing Unmanned Aerial Vehicle, Attitude Control,
Wind Disturbances.
Abstract:
This paper evaluates and compares the performance of model-free and model-based reinforcement learning for
the attitude control of fixed-wing unmanned aerial vehicles using PID as a reference point. The comparison
focuses on their ability to handle varying flight dynamics and wind disturbances in a simulated environment.
Our results show that the Temporal Difference Model Predictive Control agent outperforms both the PID con-
troller and other model-free reinforcement learning methods in terms of tracking accuracy and robustness over
different reference difficulties, particularly in nonlinear flight regimes. Furthermore, we introduce actuation
fluctuation as a key metric to assess energy efficiency and actuator wear, and we test two different approaches
from the literature: action variation penalty and conditioning for action policy smoothness. We also evaluate
all control methods when subject to stochastic turbulence and gusts separately, so as to measure their effects on
tracking performance, observe their limitations and outline their implications on the Markov decision process
formalism.
1 INTRODUCTION
Robotic controllers must act according to their state
and environment. In the context of fixed-wing un-
manned aerial vehicles (FWUAV) flight, modeling the
aircraft and its interactions with the environment is a
challenging task for two reasons.
First, the aerodynamic forces exhibit different dy-
namic regimes that depend on the attitude of the
FWUAV. On one hand, low attitude angles near the
equilibrium state present relatively simple dynam-
ics often approximated by formulating hypotheses on
their linearity and independent coupling of the con-
trolled axes. On the other hand, high attitude angles
lead the FWUAV to encounter complex aerodynam-
ics where lift and drag behave nonlinearly and also
exhibit important cross-couplings between axes.
A second source of complexity lies in FWUAVs
potentially evolving in disturbed environments. These
disturbances are the result of unpredictable meteoro-
a
https://orcid.org/0009-0001-5021-3042
b
https://orcid.org/0000-0002-0209-2901
c
https://orcid.org/0000-0002-2976-8457
d
https://orcid.org/0000-0002-5041-272X
logical phenomena such as turbulence and wind gusts.
As a result, effectively modeling FWUAVs’ aerody-
namics is often a tedious task required to design Con-
trol Theory (CT)-based controllers.
A solution could come from Reinforcement
Learning (RL) to alleviate the burden of system mod-
eling by using data to approximate these models ei-
ther implicitly (model-free RL) or explicitly (model-
based RL).
Model-free RL (MF-RL) control for attitude con-
trol of a quadrotor UAV is presented as outperform-
ing the widely used PID in (Koch et al., 2019). Sim-
ilar conclusions are drawn by (Song et al., 2023b)
for acrobatic high-speed UAV racing. For FWUAVs,
MF-RL was introduced as a robust control approach
to deal with turbulence (Bøhn et al., 2019). As
for model-based RL (MB-RL), it showed recent
breakthroughs by outperforming MF-RL algorithms
in highly complex dynamical environments such as
games, locomotion and manipulation tasks (Hafner
et al., 2023; Hansen et al., 2024). We identify a gap
in literature for MB-RL applied to UAV flight: most
recent works focus on MB-RL’s sample efficiency for
learning flying policies (Becker-Ehmck et al., 2020;
Lambert et al., 2019) and do not evaluate the perfor-
Olivares, D., Fournier, P., Vasishta, P. and Marzat, J.
Model-Free versus Model-Based Reinforcement Learning for Fixed-Wing UAV Attitude Control Under Varying Wind Conditions.
DOI: 10.5220/0012946600003822
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 79-91
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
79

mance of latest MB-RL algorithms. While not be-
ing the focus of our study, MB-RL often incorporates
concepts from Control Theory (CT) which can miti-
gate the blackbox aspect of MF-RL (by adding a plan-
ning step) and could be an additional benefit of this
class of methods. Our work aims to evaluate the ben-
efits of RL methods, in particular MB-RL versus MF-
RL, for attitude control of a FWUAV under varying
specific conditions (wind disturbances).
We focus on the attitude control problem, where
the controller has to track reference attitude angles for
roll and pitch. First, we choose state-of-the-art MF-
RL methods such as Proximal Policy Optimization
(PPO) and Soft Actor Critic (SAC). Second, we select
Temporal Difference Model Predictive Control (TD-
MPC), a MB-RL method that mixes concepts from
RL such as temporal difference learning and concepts
from CT for predictive planning. Finally, we include
a PID controller as a reference point, because of its
very wide use in UAV attitude control.
Our contributions are as follows:
• We propose the first application of a recent MB-
RL method (TD-MPC) to FWUAV attitude con-
trol under varying wind conditions.
• Our comparison provides insights for FWUAV
practitioners on the current state-of-the-art RL al-
gorithms with respect to the industry standard
PID.
• We exhibit TD-MPC’s superiority for pure refer-
ence tracking in the case of nominal wind condi-
tions (no turbulence and no gusts), most notably
on hard attitude angle references.
• We improve this analysis with two additional
studies:
– A secondary metric for actuation fluctuation
shows that RL, be it model-free or model-
based, struggles to produce smooth action out-
puts. We evaluate two methods from the litera-
ture to deal with this issue.
– In the presence of wind perturbations and when
evaluated specifically on this aspect, the gains
of RL methods appear more limited than sug-
gested by previous work (Bøhn et al., 2019).
• For replicability and facilitating comparison
among contributors, we release our code for the
RL-compatible simulation framework
1
based on
the open-source flight simulator JSBSim (Berndt,
2004) and the control algorithms
2
presented in
this work.
1
https://github.com/Akkodis/FW-JSBGym
2
https://github.com/Akkodis/FW-FlightControl
2 RELATED WORKS
Learning-based methods appear as a promising tool
to achieve nonlinear and perturbation resilient con-
trollers for UAVs. An example of learning with CT
is the field of adaptive control, which now includes
learning-based approaches where a neural network
learns a model of the problematic part of the dy-
namics (disturbances, modeling errors) and uses it as
a feed-forward component inside a classical control
controller (Shi et al., 2019; Doukhi and Lee, 2019;
Shi et al., 2021). These studies displayed encourag-
ing results for jointly using a learned model of the un-
known dynamics together with a mathematical model
of the known nominal dynamics.
2.1 Reinforcement Learning Control of
UAVs
However, when the nominal dynamics are not given,
RL has proven to be a powerful choice for learn-
ing controllers without any prior knowledge of the
system. It has shown impressive results for deci-
sion making in games (Mnih et al., 2013; Schrit-
twieser et al., 2020) and in robotics (Hansen et al.,
2024; Hafner et al., 2023) such as dexterous robotic
hand manipulation (Andrychowicz et al., 2020) or
quadruped locomotion (Lee et al., 2020; Peng et al.,
2020) and can be classified into model-free and
model-based approaches. Since rotary-wing and
fixed-wing UAVs share similarities, methods applica-
ble to one may transfer effectively to the other.
2.1.1 Model-Free RL
In model-free RL (MF-RL), the agent learns to take
actions through trial and error without learning or us-
ing an explicit model of the environment’s dynamics.
For rotary-wing UAVs, MF-RL has been applied as
a flight controller for waypoint navigation (Hwangbo
et al., 2017) and the recent work of (Koch et al., 2019)
has applied various RL algorithms in order to learn
attitude control policies outperforming their base-
line PID controller counterpart. A proof-of-concept
Deep Deterministic Policy Gradient (DDPG) agent
has demonstrated encouraging attitude control perfor-
mance despite exhibiting steady state errors (Tsour-
dos et al., 2019). Recent work has highlighted the
benefits of RL for trajectory tracking over classical
two-stage controllers (a high-level stage for trajectory
planning and a lower-level stage for attitude control)
(Song et al., 2023b). The authors concluded that the
cascading of two control loops splits the overall way-
point tracking objective into two sub-objectives lead-
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
80

ing to suboptimal solutions, whereas RL can optimize
the higher-level waypoint objective directly.
For FWUAVs, experiments have been conducted
in the context of high performance control in a com-
bat environment of an F-16 fighter jet (De Marco
et al., 2023). RL has also been studied for addressing
specific problems on civil aircraft (Liu et al., 2021),
where the authors used vision-based observations to
achieve takeoff under crosswind conditions. A study
(Bøhn et al., 2019) compared RL and PID attitude
controllers under wind disturbances and both meth-
ods achieved similar performance, paving the way
for the deployment of a RL control law in a real
FWUAV (Bøhn et al., 2023). The former (Bøhn et al.,
2019) demonstrated PPO’s resilience to stochastic
turbulence in simulation and the latter demonstrated
SAC as a data-efficient algorithm for real-world de-
ployment of the RL attitude controller. We use those
two works as starting points and extend the analysis
with a MB-RL method (TD-MPC) and under an addi-
tional disturbance source: wind gusts.
2.1.2 Model-Based RL
Model-based RL (MB-RL) is a branch of RL where
the agent, through trial and error too, separately learns
a model of the environment and an action planning
strategy from this model. MB-RL is often more sam-
ple efficient, requiring fewer training episodes than
MF-RL algorithms to converge. This observation
was exploited in (Becker-Ehmck et al., 2020) where
the authors trained a controller for waypoint naviga-
tion of a rotary-wing UAV, directly in the real world.
(Lambert et al., 2019) present a sample efficient MB-
RL method for hovering control using a “random-
shooter” MPC for simulating candidate trajectories
obtained with a learned-model of the dynamics. A
higher-level trajectory tracking off-line MB-RL con-
troller is presented by (Liang et al., 2018), lever-
aging data trajectories obtained on multiple UAVs.
Current MB-RL literature for UAVs emphasizes MB-
RL’s sample efficiency for learning flying policies, yet
does not assess the performance of the latest MB-RL
algorithms. Moreover, we found no studies regarding
MB-RL applied to FWUAV flight under varying wind
conditions. With the present paper, we intend to ex-
tend the existing literature by evaluating the benefits
of MF-RL versus MB-RL for this specific setting.
3 UAV MODEL
3.1 Kinematics
The studied FWUAV is the Skywalker x8 as in (Bøhn
et al., 2019). The FWUAV is modeled as a rigid-body
mass m with inertia matrix I. According to (Beard and
McLain, 2012), the following kinematic equations ap-
ply to the positions p = [x, y, z]
T
and the orientation q:
˙
p = R
n
b
(q)v (1)
˙
q =
1
2

0 −ω
T
ω −S(ω)

q (2)
where R
n
b
is the rotation matrix from the body frame
{b} attached to the FWUAV center of gravity to the
inertial {n} North-East-Down (NED) world frame,
while v = [u, v, w]
T
and ω = [p, q, r]
T
are the linear
and angular body velocities respectively and S is the
skew-symmetric matrix.
The linear and angular velocities v and ω expres-
sions are derived from the Newton-Euler equations of
motion:
m
˙
v + ω × v = R
n
b
(q)
T
mg
n
+ F
prop
+ F
aero
(3)
I
˙
ω + ω ×Iω = M
prop
+ M
aero
(4)
Where g
n
is the force of gravity in the inertial frame.
The other terms, F
aero
and M
aero
are the aerodynam-
ical forces and moments while F
prop
and M
prop
are
the propulsion forces and moments.
3.2 Aerodynamic Forces and Moments
3.2.1 Wind Disturbances
v
b
r
is the velocity of the FWUAV with respect to the
relative wind as:
v
b
r
= v
b
g
−v
b
w
(5)
with v
b
g
the velocity vector of the aircraft relative to
the ground and v
b
w
the wind speed in the body frame.
The wind speed can be decomposed into two parts: a
steady ambient wind component v
n
w
s
expressed in the
inertial frame and a stochastic process v
b
w
g
represent-
ing wind turbulence expressed in the body frame.
v
b
w
= R
b
n
(q)v
n
w
s
+ v
b
w
g
=


u
r
v
r
w
r


(6)
Similarly, the angular rate relative to the air comprises
two terms: the nominal angular rate of the FWUAV
ω
b
and the additional turbulent angular rates ω
b
w
:
ω
b
r
= ω
b
−ω
b
w
=


p
r
q
r
r
r


(7)
Model-Free versus Model-Based Reinforcement Learning for Fixed-Wing UAV Attitude Control Under Varying Wind Conditions
81

The stochastic processes modeling the additional tur-
bulence correspond to white noise passed through fil-
ters given by the Dryden spectrum model (Beard and
McLain, 2012; mil, 1980). The airspeed V
a
, angle of
attack α and sideslip angle β are defined as:
V
a
=
q
u
2
r
+ v
2
r
+ w
2
r
(8)
α = tan
−1

u
r
w
r

, β = sin
−1

v
r
V
a

(9)
3.2.2 Aerodynamic Model
The flying wing Skywalker x8 is not equipped with a
rudder. The available control surfaces only consist in
aileron and elevator deflection angles, δ
a
and δ
e
, and
a throttle command δ
t
. The translational aerodynamic
forces F
aero
are the drag D, the lateral force Y and the
lift L. They are expressed in the wind frame and can
be expressed in the body frame as:
F
aero
= R
b
w
(α, β)


− D
Y
− L


(10)


D
Y
L


=
1
2
ρV
2
a
S


C
D
(α, β, q
r
, δ
e
)
C
Y
(β, p
r
, r
r
, δ
a
)
C
L
(α, q
r
, δ
e
)


(11)
Typically, these nonlinear forces are described by
C
D
, C
Y
, C
L
. They consist in a set of coefficients de-
termined by computational fluid dynamics simula-
tions and/or experimental wind tunnel data. The ex-
pressions of the aerodynamic moments M
aero
can be
found following the same logic:
M
aero
=
1
2
ρV
2
a
S


bC
l
(β, p
r
, r
r
, δ
a
)
cC
m
(α, q
r
, δ
e
)
bC
n
(β, p
r
, r
r
, δ
a
)


(12)
where ρ is the air density, V
a
the nominal airspeed, S
the wing area, b the wingspan and c the aerodynamic
chord. The aerodynamic coefficients and geometric
parameters of the x8 FWUAV are taken from (Gryte
et al., 2018).
3.2.3 Propulsion Forces and Moments
The propeller of the x8 FWUAV is located at the back
of the airframe and aligned with the body frame’s
x-axis such that F
prop
= [T
p
, 0, 0]
T
. In the current
simulation, a simplified model of the engine and the
propeller is used, which provides a linear relation
T
p
= Cδ
t
between the thrust force T
p
and the δ
t
throt-
tle command given in the [0, 1] interval, with C = 5.9.
3.3 Actuator Dynamics and Constraints
Input commands in the simulator are normalized
in the range [−1, 1] for control surface deflections
(δ
a
, δ
e
) and between [0, 1] for the throttle δ
t
. Fol-
lowing (Bøhn et al., 2019), the aileron and eleva-
tor dynamics are described by rate-limited and satu-
rated second-order transfer functions with natural fre-
quency ω
0
= 100 and damping ζ =
1
√
2
. The control
surface deflection angles and rates are limited to ±30
◦
and ±200
◦
/s. The throttle dynamics are modeled by a
first-order transfer function, with gain K = 1 and time
constant T = 0.2.
4 CONTROL METHODS
In this study the controller’s task is to track desired
states φ
d
and θ
d
for the attitude roll and pitch angles φ
and pitch θ of the aforedescribed FWUAV when sub-
ject to various wind disturbances. Following (Bøhn
et al., 2023), the airspeed remains controlled by a PI
controller driving the throttle command δ
t
to maintain
a nominal airspeed, with the gains tuned as in (Bøhn
et al., 2019): k
p
V
= 0.5 and k
i
V
= 0.1. This airspeed PI
controller is common to all the following controllers.
This choice was motivated by the fact that when cer-
tain references are generated, the desired pitch can
contradict the desired airspeed, e.g. low desired air-
speed and nose down desired pitch. In a case where
one would control the desired altitude, the outer loop
would give coherent desired states to the inner atti-
tude control loops, but this is beyond the scope of the
present work.
4.1 PID Control
PID control is a widely used controller for UAV atti-
tude control because of its ease of use and is therefore
considered as a reference point in the RL literature
for UAV control (Bøhn et al., 2019; Bøhn et al., 2023;
Koch et al., 2019; Lambert et al., 2019). We fine-
tuned the PID gains given by (Bøhn et al., 2019) to
better suit our simulated loops in nominal conditions
i.e. with no wind disturbances, with the gains pre-
sented in Table 1.
Table 1: PID controller parameters.
Parameter Value Parameter Value
k
pφ
1.5 k
pθ
−2
k
iφ
0.1 k
iθ
−0.3
k
dφ
0.1 k
dθ
−0.1
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
82

4.2 Reinforcement Learning (RL)
Control
In RL, the control problem is formulated as that of
finding an optimal action strategy in an environment
modeled as a Markov Decision Process (MDP) (Sut-
ton and Barto, 2018) comprised of:
• A set of actions a ∈ A, here the same as in the
roll and pitch PID loops with the superscript c de-
noting a commanded position of the aileron and
elevator, a = (δ
c
a
, δ
c
e
).
• A set of states s ∈ S, based on (Bøhn et al., 2023):
– the attitude angles: roll φ and pitch θ;
– the airspeed V
a
;
– the angular rates ω
b
r
= [p
r
, q
r
, w
r
]
T
;
– the angle of attack α and the angle sideslip β;
– the roll and pitch errors:
e
φ
= φ
d
−φ
e
θ
= θ
d
−θ
(13)
– the roll and pitch integral errors:
I
e
∗
= I
e
∗
+ e
∗
·dt, ∗ = {φ, θ}, dt = 0.01 (14)
where dt is the simulation period, also equal to
the control rate. The integral error is reset at the
beginning of each episode or target change.
– The last action taken by the agent: δ
c
a|
t−1
and
δ
c
e|
t−1
.
• A transition function T , defining a distribution
over the next states given a current state and ac-
tion: P(s
t+1
|s
t
, a
t
) = T (s
t
, a
t
).
• A scalar reward function R
t
, outputting a score,
rewarding the agent for good actions and penaliz-
ing bad ones, that shapes the agent’s task.
The reward function has been adapted from (Bøhn
et al., 2019) as follows:
R
φ
= clip

|φ −φ
d
|
ζ
φ
, 0, c
φ

R
θ
= clip

|θ −θ
d
|
ζ
θ
, 0, c
θ

R
t
= −(R
φ
+ R
θ
)
ζ
φ
= 3.3, ζ
θ
= 2.25, c
φ
= c
θ
= 0.5
(15)
where ζ
∗
are scaling coefficients to take into account
the differences between roll and pitch error ranges,
each reward component is clipped to 0.5 so the mini-
mal total reward equals to -1.
RL algorithms aim to discover the best map-
ping π from a state to an action (control law), in
the RL literature, referred as the optimal policy
(π
∗
), and defined as the policy leading to trajectories
τ = (s
0
, a
0
, s
1
, a
1
, ...) that maximize the expected dis-
counted sum of accumulated rewards:
π
∗
= argmax
π
E
τ∼π
"
∞
∑
t=0
γ
t
R
t
(s
t
, a
t
)
#
(16)
with γ being the discount factor.
This policy, often represented by an artificial neu-
ral network (ANN) with learnable parameters Θ,
serves as a nonlinear controller.
4.2.1 Model-Free RL: PPO & SAC
We choose Proximal Policy Optimization (PPO)
(Schulman et al., 2017) and Soft Actor-Critic (SAC)
(Haarnoja et al., 2018) to represent the MF-RL end
of the control spectrum because of their state-of-the-
art performance for robotic applications with continu-
ous action spaces. Moreover, SAC’s choice was moti-
vated by its similar policy update to the mixed method
used in this work (TD-MPC).
4.2.2 Model-Based Method: TD-MPC
Temporal Difference Model Predictive Control (TD-
MPC) (Hansen et al., 2022) is an MB-RL, mixed con-
trol method combining an explicit dynamics model
and a terminal value function learned by using Tem-
poral Difference learning in an RL setting. We use its
latest implementation from (Hansen et al., 2024).
Trainable Models. TD-MPC learns a Task-Oriented
Latent Dynamics (TOLD) model, comprised of sev-
eral MLPs (Multi-Layer Perceptrons) with trainable
parameters Θ. They aim at modeling certain func-
tions, most notably: the agent’s dynamics, the reward
function R
Θ
, the Q-value function Q
Θ
and the policy.
During training, a trajectory of prediction horizon H
is sampled from a replay buffer in an off-policy RL
fashion. Using this sampled trajectory, the TOLD
model is trained by optimizing a loss function in-
cluding: the reward prediction function, the dynamics
model and a Bellman error component for Q
θ
. The
policy is learned by maximizing a similar objective to
the SAC algorithm (Haarnoja et al., 2018).
Planning. TD-MPC uses a control-theory basis
for planning, utilizing Model Predictive Path Inte-
gral (MPPI) (Williams et al., 2015). MPPI is a
sampling-based model-predictive control (MPC) al-
gorithm iteratively learning the parameters of a mul-
tivariate Gaussian distribution using importance sam-
pling. First, TD-MPC simulates candidate trajecto-
ries Γ by sampling a mixture of trajectories of horizon
H by querying both the Gaussian distribution and the
Model-Free versus Model-Based Reinforcement Learning for Fixed-Wing UAV Attitude Control Under Varying Wind Conditions
83

learned policy function π
Θ
for actions and by recur-
sively predicting next states using the learned dynam-
ics model. One of TD-MPC’s key idea is to use the
learned Q-value function Q
Θ
to give an estimation of
the terminal value when computing a trajectory’s to-
tal return φ
Γ
. Here, Q
Θ
gives an estimate of the value
of the trajectory beyond the horizon limit, emulating
infinite-horizon MPC.
φ
Γ
≜ E
Γ
[γ
H
Q
Θ
(z
H
, a
H
)
| {z }
Terminal value
estimated by Q
Θ
+
H−1
∑
t=0
γ
t
R
Θ
(z
t
, a
t
)
| {z }
Total return of the
candidate trajectory over
the time horizon H
] (17)
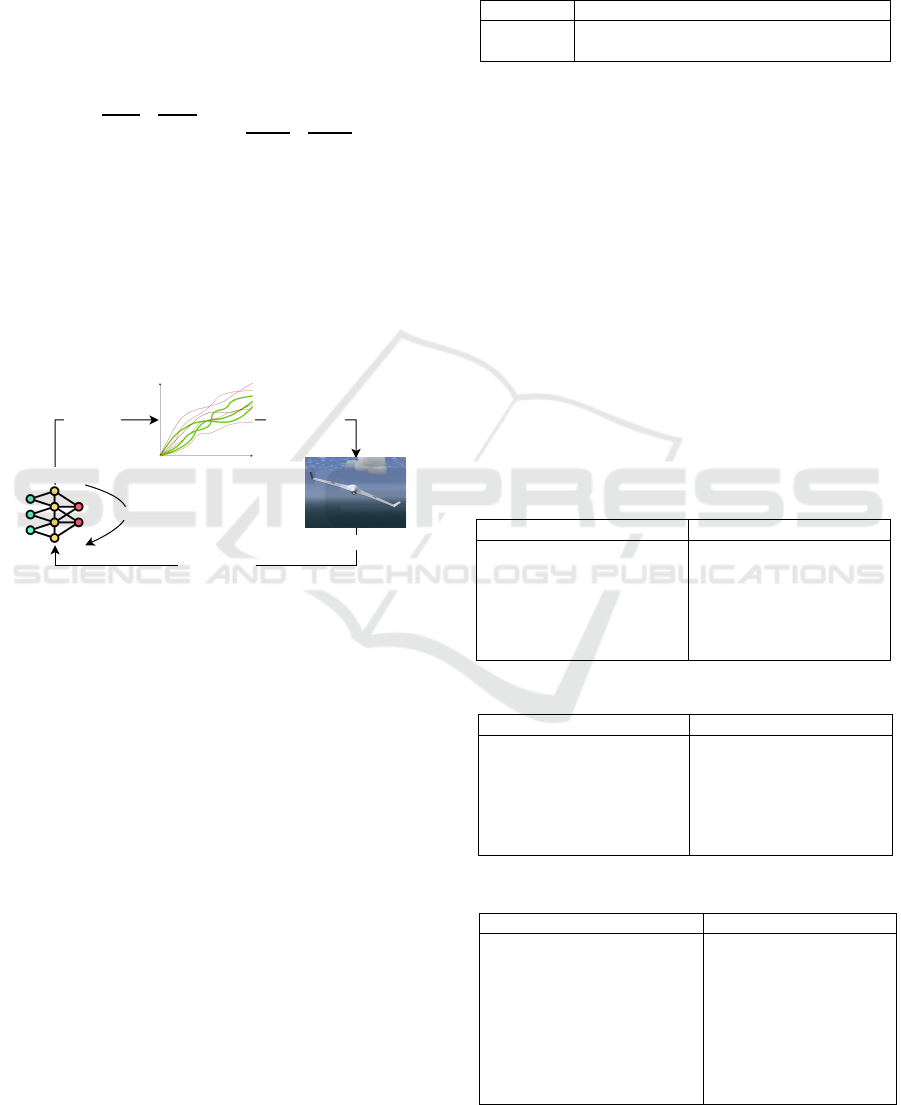
As illustrated in Figure 1, after taking the trajec-
tories with the best return, MPPI computes the ac-
tion Gaussian parameters update by using importance
sampling, see (Hansen et al., 2022). The action Gaus-
sian is then sampled and the first action is sent to the
actuators, as in receding-horizon MPC.
Apply the action
State & Reward
Environment
Trajectories
Simulation
TOLD
Training
Select action from
the best trajectories
Figure 1: TD-MPC Control Block Diagram. 1) The trained
TOLD model is used for simulating candidate trajectories
and estimating their return. 2) Using importance sampling
update an action Gaussian distribution and sample it. 3)
Sample an action from the action distribution and apply it.
5 EXPERIMENTAL SETUP
5.1 Simulation
We conducted our experiments in the JSBSim flight
simulator (Berndt, 2004) because of its ability to han-
dle fixed-wing aircraft flight dynamics and to model
all the studied wind disturbances: constant wind,
wind gusts and stochastic turbulences. JSBSim was
preferred over the PyFly simulator presented in (Bøhn
et al., 2019) because of its wide use in the aerospace
open-source and research communities and its built-
in wind gust generation (Moallemi and Towhidnejad,
2016; Mathisen et al., 2021; De Marco et al., 2023).
We are interested in separating the performance of
the studied control methods between linear and non-
linear regimes. Therefore, we introduce a classifica-
tion of attitude angle references in Table 2, with nom-
inal and hard levels representing linear and nonlinear
regions of the state space respectively.
Table 2: References classification.
Difficulty Roll(°) Pitch(°)
Nominal [−45, 45] [−25, 25]
Hard [−60, −45] ∪[45, 60] [−30, −25] ∪[25, 30]
5.2 Implementation Details
For the optimization algorithms, we used the
CleanRL PPO & SAC implementations (Huang et al.,
2022) with the parameters presented in Tables 3 & 4.
We used the most recent implementation of TD-MPC,
TD-MPC2 (Hansen et al., 2024) with the parameters
specified in Table 5.
We trained the RL agents for 375 episodes of
2000 timesteps each, i.e. 20 seconds of flight time
at 100 Hz. At the start of every episode, we initialize
the FWUAV at 600 m above sea level, with a nomi-
nal speed of 17 m/s and roll, pitch, yaw {φ, θ, ψ} = 0.
We compute the mean and standard error of the mean
over 5 runs for each metric. Training was conducted
on a RTX A6000 with 48GB of memory.
Table 3: PPO Parameters.
Parameter Value Parameter Value
LR 3e-4 Entropy coef 1e-2
Parallel envs 6 Value fn coef 0.5
Rollout steps 2048 Total timesteps 750k
Discount factor γ 0.99 Minibatches 32
GAE λ 0.95 Batch size 12228
PPO clip 0.2
Table 4: SAC Parameters.
Parameter Value Parameter Value
Buffer size 1e6 Q-net LR 1e-3
Discount factor γ 0.99 π update freq 2
Q
targ
smoothing τ 5e-3 Q
targ
update freq 1
Batch size 256 Total timesteps 750k
Seed steps 5000 Noise clip 0.5
Policy LR 3e-4 Entropy reg 0.2
Table 5: TD-MPC Parameters.
Parameter Value Parameter Value
Buffer size 1e6 Total timesteps 750k
Discount factor γ 0.99 Temporal coef 0.5
Target smoothing τ 0.01 MPPI Iterations 6
Batch size 256 MPPI Samples 512
Seed steps 10 000 MPPI Elites 64
LR 3e-4 MPPI π Trajs 24
Reward coef 0.1 Horizon 3
Value coef 0.1 Temperature 0.5
Consistency coef 20
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
84

6 RESULTS AND DISCUSSIONS
Our first experiment aims at comparing RL agents in
nominal, non-disturbed conditions and with respect
to reference tracking only (Section 6.1.1). We also
show that RL agents tend to converge towards policies
that produce oscillating actions, and we evaluate two
strategies to mitigate the issue (Section 6.1.2). Then
we study the impact of turbulence and wind gusts
separately on each algorithm performances (Section
6.2) and provide a deeper discussion of the results
(Section6.3).
6.1 Nominal Wind Conditions
This section focuses on evaluating all 4 controllers
under nominal wind conditions i.e. no wind, no turbu-
lence and no wind gusts. Agents are trained and tested
with these wind settings and across the two reference
difficulty levels from Table 2.
6.1.1 Base RL Algorithms
The results from Table 6 confirm that PID is a strong
baseline in nominal conditions, with only TD-MPC
from RL algorithms performing slightly better. On
the contrary, under more nonlinear dynamics forced
by hard references, all RL methods clearly outper-
form PID, with a significant advantage of TD-MPC
over PPO and SAC. Figure 4 illustrates TD-MPC’s
better hard reference tracking compared to PPO.
Overall TD-MPC displays moderate to strong gains
over all methods across both dynamics regimes.
6.1.2 RL Policies and High Action Oscillation
The RL literature usually focuses on performance
metrics only (Koch et al., 2019; Hansen et al., 2022),
but for true robotic applications, we practitioners
must also make sure to minimize wear and tear as well
as energy consumption. This can only be done by
monitoring actuation solicitation and thus we incor-
porate in our evaluation an actuation fluctuation (Act
Fluct) metric, following (Song et al., 2023a):
ξ(π) =
1
2
∑
j∈[a,e]
1
E
E
∑
n=1
"
1
T
T
∑
t=1
|δ
j|
t
−δ
j|
t−1
|
#
(18)
It incentivizes the minimization of the distance be-
tween two consecutive actuator positions (δ
a
or δ
e
).
Table 7 shows that high performances of RL meth-
ods come at the cost of strongly oscillating actions.
In fact, RL can lead to bang-bang control, where the
learned optimal policy consists in alternating abruptly
between actions far from each other in the action
space (Seyde et al., 2021). To mitigate this issue, we
evaluate two oscillation regulation methods from the
literature.
Action Variation Penalty (AVP). Adding an AVP in
the reward function is a common way of addressing
the bang-bang policy problem. Hence, we modify
the base reward of Equation 15 and propose adding
a simple additional reward component R
δ
, similar to
(Bøhn et al., 2019) for penalizing abrupt changes of
consecutive actions, forming the reward function de-
noted R
AV P
:
R
δ
= clip
1
2
∑
j∈[a,e]
|δ
c
j|
t
−δ
c
j|
t−1
|
ζ
δ
, 0, c
δ
!
δ
c
a|
t−1
R
AV P
= −(R
φ
+ R
θ
+ R
δ
)
ζ
φ
= 3.3, ζ
θ
= 2.25, ζ
δ
= 2
(19)
We separately tuned the c
∗
clipping coefficients of
the AVP reward function for each RL method, giving
c
φ
= c
θ
= 0.25 and c
δ
= 0.5 for TD-MPC and SAC.
However, such a tuning led PPO not converging to a
successful flying policy, therefore we found an appro-
priate tuning for this method as c
φ
= c
θ
= 0.45 and
c
δ
= 0.1.
Conditioning for Action Policy Smoothness
(CAPS). Another candidate to mitigate this behavior
is the Conditioning for Action Policy Smoothness
(CAPS) loss (Mysore et al., 2021). CAPS is added
to the policy loss and prevents the emergence of
non-smooth action policies by applying temporal and
spatial regularization:
L
CAPS
(π
Θ
) = λ
TS
·L
TS
(π
Θ
) + λ
SS
·L
SS
(π
Θ
)
L
TS
(π
Θ
) = ∥π
Θ
(s
t
) −π
Θ
(s
t+1
)∥
2
L
SS
(π
Θ
) = ∥π
Θ
(s
t
) −π
Θ
( ˆs
t
)∥
2
, ˆs
t
∼ N (s
t
, 0.01)
(20)
The time-only version of the CAPS loss is used to
enforce temporal smoothness (with λ
T S
= 0.05) while
leaving room for high reactivity in the state space.
Results. Table 7 exhibits the consistent improve-
ment of the action fluctuation metric across all MF-
RL agents with CAPS. For RMSE tracking perfor-
mance, Table 7 confirms that TD-MPC remains better
than PID and MF-RL agents.
As for action regulation methods, we observe that
action regulation methods remain algorithm depen-
dent. Table 7 shows that the AVP reward function
has a strong effect on actuation fluctuation, reducing
it by at least an order of magnitude for TD-MPC and
SAC. Conversely, AVP for PPO shows a drastic in-
crease in actuation fluctuation, which highlights the
difficult task of tuning the reward function with the
goal of combining a lower actuator fluctuating flying
policy. In fact, one tuning of AVP can work for certain
Model-Free versus Model-Based Reinforcement Learning for Fixed-Wing UAV Attitude Control Under Varying Wind Conditions
85

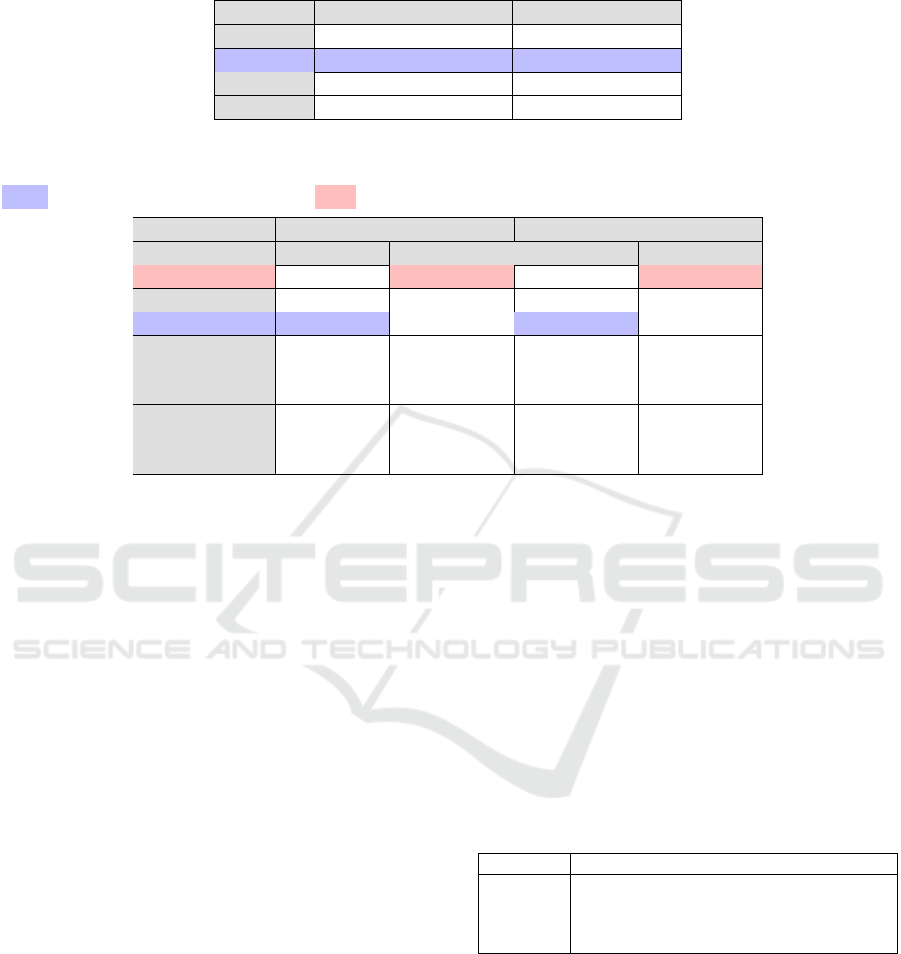
Table 6: Nominal Atmosphere. Average of roll and pitch tracking RMSE, over all reference difficulty levels. Best scores are
highlighted in blue.
Agent Nominal Refs (x10
−2
) Hard Refs (x10
−2
)
PID 4.20 20.10
TD-MPC 3.81 ± 0.10 9.10 ± 0.69
PPO 5.29 ± 0.12 15.78 ± 2.48
SAC 6.64 ± 0.83 11.15 ± 0.65
Table 7: Nominal Atmosphere + Actuation Regulation (through AVP or CAPS). Average of roll - pitch tracking errors and
aileron - elevator action fluctuation, over all reference difficulty levels. Bold values are the best score among one agent type.
Blue : best RMSE score across all agents. Red : best Actuator Fluctuation score across all agents.
Nominal Refs (x10
−2
) Hard Refs (x10
−2
)
Agent RMSE Act Fluct RMSE Act Fluct
PID 4.20 0.07 20.10 0.17
TD-MPC 3.81 ± 0.10 4.37 ± 0.48 9.10 ± 0.69 6.02 ± 0.59
TD-MPC AVP 3.58 ± 0.01 0.54 ± 0.02 8.09 ± 0.03 0.60 ± 0.02
PPO 5.29 ± 1.20 1.98 ± 0.58 15.78 ± 2.48 5.54 ± 0.93
PPO CAPS 5.05 ± 1.50 1.47 ± 0.27 19.17 ± 4.68 4.56 ± 0.60
PPO AVP 5.78 ± 2.10 13.78 ± 3.16 13.80 ± 0.82 13.48 ± 2.50
SAC 6.64 ± 0.83 10.07 ± 1.12 11.15 ± 0.65 12.00 ± 0.71
SAC CAPS 6.79 ± 0.74 0.53 ± 0.27 12.28 ± 1.17 1.44 ± 0.55
SAC AVP 6.54 ± 0.75 0.50 ± 0.18 15.14 ± 3.39 1.20 ± 0.32
algorithms such as SAC and TD-MPC and give an un-
derperforming PPO agent requiring a specific tuning.
CAPS appears to be a better action regulation method
for MF-RL methods because of its consistency with
a single tuned parameter λ
T S
= 0.05. As an exam-
ple, Figure 5 outlines CAPSs’ action smoothing for
SAC through a trajectory plot. As a result, the CAPS
method has been retained for the following ablations.
Despite showing great results for MF-RL methods,
CAPS is not directly applicable to TD-MPC because
it only regularizes its learned policy prior, while TD-
MPC never directly outputs an action by sampling this
prior. Indeed, we found in additional experiments that
applying CAPS led to learning a smooth action policy
prior but did not guarantee smooth actions after the
planning step.
6.2 Wind Disturbances
Aerial robotics present challenging environmental
conditions which add a layer of complexity for con-
trol systems. This section focuses on studying the
impact of such conditions on our four controllers of
interest. Wind disturbances are divided into two sub-
categories: stochastic turbulence modeled by proba-
bilistic dynamics and wind gusts consisting in unpre-
dictable and sudden changes in dynamics. Agents are
tested and trained under stochastic turbulence in Sec-
tion 6.2.1 and wind gusts in Section 6.2.2 separately.
The parameters for turbulence and gusts are drawn
uniformly along the values reported in Table 8. This
classification of constant winds is only used for eval-
uation. During training, constant wind magnitudes
are uniformly sampled from the continuous interval
[0, 23] m/s. Constant wind and wind gusts directions
with respect to the NED inertial frame are also sam-
pled uniformly in the [−1, 1] interval.
To better isolate the effects of each disturbance
from the effects of hard attitude angle reference track-
ing, the agents were trained and tested only for the
nominal attitude reference angle range from Table 2.
Table 8: Wind Disturbance Severity Levels (m/s). The clas-
sification for constant wind and gust magnitudes is taken
from (Bøhn et al., 2019). ”Turbulence W20” is a predefined
parameter in JSBSim Dryden model turbulence classifica-
tion (Berndt, 2004).
Constant Wind Turbulence W20 Gust
OFF 0 0 0
Light 7 7.6 7
Moderate 15 15.25 15
Severe 23 22.86 23
6.2.1 Stochastic Turbulence
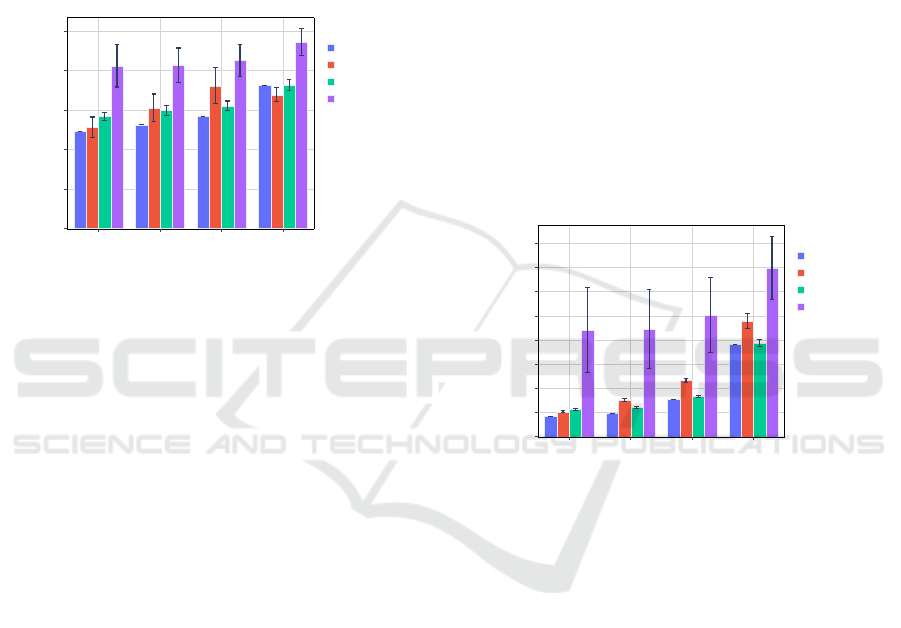
As explained in Section 3.2.1, turbulence is simu-
lated as a stochastic process applying linear and an-
gular forces to the FWUAV. On one side, Figure 2
outlines SAC’s underperforming across all turbulence
levels. On the other side, TD-MPC shows good per-
formance, reaching the same levels of performance as
PID and PPO. We observe that the severity of wind
disturbance dominates over the choice of algorithm
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
86

to predict the final performances. In contrast to Sec-
tion 6.1.1, where TD-MPC showed a clear advan-
tage on deterministic nonlinear dynamics for track-
ing high attitude reference angles, here its learned dy-
namics model seems here to have difficulty captur-
ing the stochastic turbulent dynamics of this scenario,
and can only resort to learning an “on-average” ro-
bust policy. To the best of our knowledge, TD-MPC
has not been applied to environments with stochastic
dynamics and adapting TD-MPC to stochastic envi-
ronments remains an open problem.
OFF Light Moderate Severe
0
0.02
0.04
0.06
0.08
0.1
Agents
PID
TD-MPC AVP
PPO CAPS
SAC CAPS
Turb Level
AVG RMSE
Figure 2: Stochastic Turbulences + Action Regulation. Av-
erage tracking RMSE on nominal reference difficulty.
6.2.2 Wind Gusts
In our simulated environment, wind gusts are trig-
gered twice per episode at timesteps 500 and 1500.
Gusts are parameterized with a startup duration (time
for reaching maximum wind speed) of 0.25 s, a steady
duration (time span where the wind stays at maximal
magnitude) of 0.5 s, and an end duration (time for the
gust to disappear) of 0.25 s. The startup and end tran-
sients are modeled as a smooth cosine function. The
magnitude level of the gust is determined by its max-
imum wind speed and follows Table 8.
The results presented in Figure 3 point that
SAC significantly underperforms relative to the other
agents and TD-MPC slightly underperforms PPO and
PID. To explain these observations, we emit the hy-
pothesis that such a disturbance alters the MDP for-
malism into a Partially Observable Markov Decision
Process (PO-MDP). In fact, an MDP is comprised of
a transition function P(s
t+1
|s
t
, a
t
) = T (s
t
, a
t
) which
does not exist at every point in time in the case of un-
predictable gusts. From a formal point of view, while
hard references simply lead to a more complex tran-
sition function, wind gusts actually make it impos-
sible to rigorously define such a transition function.
Wind information is hidden from the agent which can-
not anticipate wind variations, thus conducing to state
aliasing (McCallum, 1996). In fact, unpredictable
gusts lead to the following situation: for two sepa-
rate experiments, for a given common state, taking
the same action could lead to two different next states.
Recurrent Neural Networks have been presented as a
good baseline for solving PO-MDPs (Ni et al., 2022;
Asri and Trischler, 2019) and could be applied to all
the RL methods presented in the present article.
RL methods learn the transition function either
explicitly in the case of model-based RL (TD-MPC)
or implicitly in the case of model-free RL (PPO and
SAC). Due to state aliasing, opposite updates of the
function approximators occur at the onset of a wind
gust. To explain PPO’s better performance compared
to its RL counterparts (SAC and TD-MPC), a second
hypothesis could be PPO’s clipping of the policy loss
(Schulman et al., 2017). Motivated by limiting too
large policy updates that could lead to a bad policy
where it can be hard to recover from, this conserva-
tive policy update could protect the PPO agent from
the contradictory updates when subject to wind gusts.
OFF Light Moderate Severe
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Agents
PID
TD-MPC AVP
PPO CAPS
SAC CAPS
Gusts Level
AVG RMSE
Figure 3: Wind Gusts + Action Regulation. Average track-
ing RMSE on nominal reference difficulty.
6.3 Discussions
TD-MPC’s Superiority for Nonlinear Regimes.
The superior results of TD-MPC under nonlinear dy-
namics are consistent with the reported superior per-
formance of TD-MPC over other MF-RL methods
for complex nonlinear manipulation and locomotion
tasks (Hansen et al., 2022; Hansen et al., 2024). It
solidifies the hypothesis that mixed control, combin-
ing learning an explicit model of the system dynamics
and leveraging it for planning with terminal value esti-
mation, can result in improved tracking performance
for a wide range of attitude angles. It also suggests
that learning an implicit representation of the dynam-
ics limits the ability of MF-RL agents to deal with dif-
ferent dynamic regimes when trained simultaneously
on nominal and hard regimes.
Wind Disturbances. We also evaluated the control
methods under wind disturbances of different nature.
Model-Free versus Model-Based Reinforcement Learning for Fixed-Wing UAV Attitude Control Under Varying Wind Conditions
87

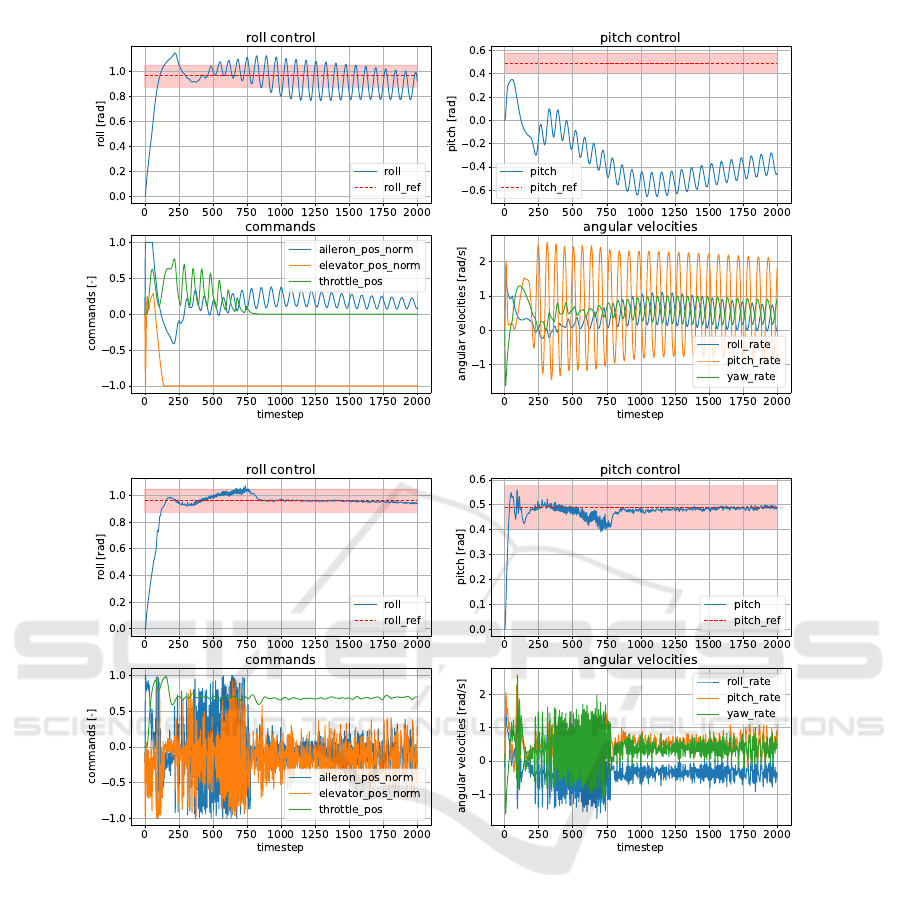
(a) PPO.
(b) TD-MPC.
Figure 4: TD-MPC’s Superiority for Hard References: PPO vs TD-MPC. Red dashed lines are the references: Roll = 55
◦
,
Pitch = 28
◦
. The red area around the reference line corresponds to ±5
◦
error bounds.
Both studies revealed that with the exception of SAC
underperforming, the severity of turbulences domi-
nates over the choice of algorithm to predict final per-
formances. As previously stated, hard references only
consist in a harder-to-model nonlinear MDP transition
function. We hypothesized that turbulence and gusts
transform the MDP formalism into a non-stationary
PO-MDP and we observe that not all perturbations
affect with equal magnitude how well the MDP for-
malization fits the environment conditions. The tur-
bulence study presented in Section 6.2.1 suggest that
turbulence can be dealt with more simply than gusts
because there exists a time-averaged MDP close to
the true MDP that RL algorithms fall back into by de-
fault. However, gusts present a multi-modal problem
(nominal mode and gust mode) by making it impossi-
ble to strictly define a transition function which could
be detrimental in the learning phase as presented in
Section 6.2.2. Therefore, we conclude that training
agents with various of perturbations is not enough to
ensure robustness and generalization and that differ-
ent types of perturbations may require different types
of approaches. The multi-model MDP framework
could be investigated for this purpose (Steimle et al.,
2021).
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
88

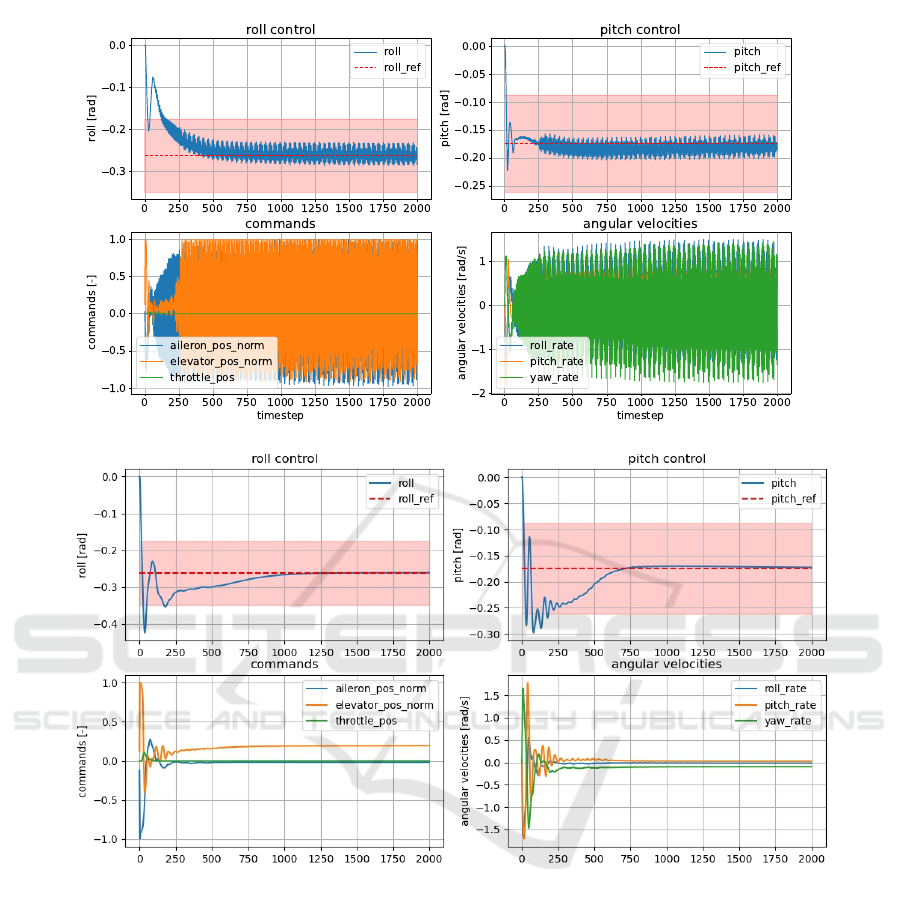
(a) Base SAC.
timestep
timestep
(b) SAC + CAPS.
Figure 5: Mitigating Highly Action Oscillating Policy: SAC vs SAC + CAPS. Red dashed lines are the references: Roll =
−15
◦
, Pitch = −10
◦
. The red area around the reference line corresponds to ±5
◦
error bounds.
7 CONCLUSIONS AND
PERSPECTIVES
We proposed an in-depth study of different RL con-
trollers with the aim of comparing model-free and
model-based RL approaches. TD-MPC, an MB-RL
method with algorithmic elements from CT and RL,
yielded the best performance in nominal wind condi-
tions. Its superiority especially shined for hard ref-
erences and demonstrated its ability to perform well
for deterministic nonlinear dynamics across the entire
state-space. We attribute such results to TD-MPC’s
learning of an explicit dynamics model jointly used
with predictive planning. We evaluated these con-
trol methods under various wind perturbations and
found that, aside from SAC underperforming, turbu-
lence severity significantly impacts final performance
more than the choice of algorithm.
We identified high actuation fluctuation as an im-
portant drawback of RL methods. Since this metric
is is key in robotics, we applied and tested counter-
Model-Free versus Model-Based Reinforcement Learning for Fixed-Wing UAV Attitude Control Under Varying Wind Conditions
89

measures, namely: action variation reward penalty
(AVP) for all methods and regularization of the ac-
tor network through CAPS for the MF-RL methods.
As a result, we retained CAPS as action regulation
method due to its consistency and ease of tuning
across all MF-RL agents. Another path to smooth ac-
tions for TD-MPC (for which CAPS is not applicable)
is MoDeM-v2 (Lancaster et al., 2023) which aims at
learning safe policies by biasing the initial data dis-
tribution towards a desired behavior, in our case an
action smooth controller.
We identify several future research directions:
one could focus on experimenting with probabilistic
models for TD-MPC in order to better capture the
stochasticity of turbulence dynamics, thus formulat-
ing a more rigorous transition function that outputs
a probability distribution. For both gusts and turbu-
lence, RL algorithms with recurrent networks appear
to be a good starting point (Ni et al., 2022; Asri and
Trischler, 2019) to solve PO-MDPs. One could also
use ideas from robust-RL to achieve disturbance re-
siliency of RL controllers (Hsu et al., 2024). Other
directions include learning-based adaptive control as
a field of potential mixed control methods (Shi et al.,
2019; Doukhi and Lee, 2019), where a closed form
of the nominal dynamics is used together with a feed-
forward component of the unknown, disturbance dy-
namics predicted by a learned model.
REFERENCES
(1980). Flying qualities of piloted airplanes, military spec-
ification. Technical report, MIL-F-8785C.
Andrychowicz, O. M., Baker, B., Chociej, M., Jozefowicz,
R., McGrew, B., Pachocki, J., Petron, A., Plappert,
M., Powell, G., Ray, A., et al. (2020). Learning dex-
terous in-hand manipulation. The International Jour-
nal of Robotics Research, 39(1):3–20.
Asri, L. E. and Trischler, A. (2019). A study of state aliasing
in structured prediction with RNNs. arXiv preprint
arXiv:1906.09310.
Beard, R. W. and McLain, T. W. (2012). Small Unmanned
Aircraft: Theory and Practice. Princeton University
Press.
Becker-Ehmck, P., Karl, M., Peters, J., and van der Smagt,
P. (2020). Learning to fly via deep model-based rein-
forcement learning. arXiv preprint arXiv:2003.08876.
Berndt, J. (2004). JSBSim: An open source flight dynam-
ics model in C++. In AIAA Modeling and Simulation
Technologies Conference and Exhibit, page 4923.
Bøhn, E., Coates, E. M., Moe, S., and Johansen, T. A.
(2019). Deep reinforcement learning attitude control
of fixed-wing UAVs using proximal policy optimiza-
tion. In International Conference on Unmanned Air-
craft Systems (ICUAS), pages 523–533.
Bøhn, E., Coates, E. M., Reinhardt, D., and Johansen, T. A.
(2023). Data-efficient deep reinforcement learning
for attitude control of fixed-wing UAVs: Field exper-
iments. IEEE Transactions on Neural Networks and
Learning Systems.
De Marco, A., D’Onza, P. M., and Manfredi, S. (2023).
A deep reinforcement learning control approach for
high-performance aircraft. Nonlinear Dynamics,
111(18):17037–17077.
Doukhi, O. and Lee, D. J. (2019). Neural network-
based robust adaptive certainty equivalent controller
for quadrotor UAV with unknown disturbances. Inter-
national Journal of Control, Automation and Systems,
17(9):2365–2374.
Gryte, K., Hann, R., Alam, M., Roh
´
a
ˇ
c, J., Johansen, T. A.,
and Fossen, T. I. (2018). Aerodynamic modeling of
the Skywalker x8 fixed-wing unmanned aerial vehi-
cle. In International Conference on Unmanned Air-
craft Systems (ICUAS), pages 826–835.
Haarnoja, T., Zhou, A., Abbeel, P., and Levine, S. (2018).
Soft actor-critic: Off-policy maximum entropy deep
reinforcement learning with a stochastic actor. In In-
ternational Conference on Machine Learning, pages
1861–1870. PMLR.
Hafner, D., Pasukonis, J., Ba, J., and Lillicrap, T. (2023).
Mastering diverse domains through world models.
arXiv preprint arXiv:2301.04104.
Hansen, N., Su, H., and Wang, X. (2024). TD-MPC2:
Scalable, robust world models for continuous control.
In International Conference on Learning Representa-
tions (ICLR).
Hansen, N., Wang, X., and Su, H. (2022). Temporal differ-
ence learning for model predictive control. In Inter-
national Conference on Machine Learning.
Hsu, H.-L., Meng, H., Luo, S., Dong, J., Tarokh, V., and
Pajic, M. (2024). REFORMA: Robust reinforcement
learning via adaptive adversary for drones flying un-
der disturbances. In 2024 IEEE International Confer-
ence on Robotics and Automation (ICRA).
Huang, S., Dossa, R. F. J., Ye, C., Braga, J., Chakraborty,
D., Mehta, K., and Ara
´
ujo, J. G. (2022). CleanRL:
High-quality single-file implementations of deep re-
inforcement learning algorithms. Journal of Machine
Learning Research, 23(274):1–18.
Hwangbo, J., Sa, I., Siegwart, R., and Hutter, M. (2017).
Control of a quadrotor with reinforcement learning.
IEEE Robotics and Automation Letters, 2(4):2096–
2103.
Koch, W., Mancuso, R., West, R., and Bestavros, A.
(2019). Reinforcement learning for UAV attitude con-
trol. ACM Transactions on Cyber-Physical Systems,
3(2):1–21.
Lambert, N. O., Drew, D. S., Yaconelli, J., Levine, S., Ca-
landra, R., and Pister, K. S. (2019). Low-level con-
trol of a quadrotor with deep model-based reinforce-
ment learning. IEEE Robotics and Automation Let-
ters, 4(4):4224–4230.
Lancaster, P., Hansen, N., Rajeswaran, A., and Kumar,
V. (2023). MoDem-V2: Visuo-motor world mod-
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
90

els for real-world robot manipulation. arXiv preprint
arXiv:2309.14236.
Lee, J., Hwangbo, J., Wellhausen, L., Koltun, V., and Hut-
ter, M. (2020). Learning quadrupedal locomotion over
challenging terrain. Science robotics, 5(47).
Liang, X., Zheng, M., and Zhang, F. (2018). A scalable
model-based learning algorithm with application to
uavs. IEEE control systems letters, 2(4):839–844.
Liu, F., Dai, S., and Zhao, Y. (2021). Learning to have a
civil aircraft take off under crosswind conditions by
reinforcement learning with multimodal data and pre-
processing data. Sensors, 21(4):1386.
Mathisen, S., Gryte, K., Gros, S., and Johansen, T. A.
(2021). Precision deep-stall landing of fixed-wing
uavs using nonlinear model predictive control. Jour-
nal of Intelligent & Robotic Systems, 101:1–15.
McCallum, A. K. (1996). Reinforcement learning with se-
lective perception and hidden state. University of
Rochester.
Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,
Antonoglou, I., Wierstra, D., and Riedmiller, M.
(2013). Playing Atari with deep reinforcement learn-
ing. arXiv preprint arXiv:1312.5602.
Moallemi, M. and Towhidnejad, M. (2016). B-737 autopilot
design and implementation for simulated flight man-
agement system. In Proceedings of the 49th Annual
Simulation Symposium, pages 1–7.
Mysore, S., Mabsout, B., Mancuso, R., and Saenko, K.
(2021). Regularizing action policies for smooth
control with reinforcement learning. In IEEE In-
ternational Conference on Robotics and Automation
(ICRA), pages 1810–1816.
Ni, T., Eysenbach, B., and Salakhutdinov, R. (2022). Re-
current model-free RL can be a strong baseline for
many pomdps. In International Conference on Ma-
chine Learning, pages 16691–16723. PMLR.
Peng, X. B., Coumans, E., Zhang, T., Lee, T.-W., Tan, J.,
and Levine, S. (2020). Learning agile robotic loco-
motion skills by imitating animals. arXiv preprint
arXiv:2004.00784.
Schrittwieser, J., Antonoglou, I., Hubert, T., Simonyan,
K., Sifre, L., Schmitt, S., Guez, A., Lockhart, E.,
Hassabis, D., Graepel, T., et al. (2020). Mastering
Atari, Go, Chess and Shogi by planning with a learned
model. Nature, 588(7839):604–609.
Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and
Klimov, O. (2017). Proximal policy optimization al-
gorithms. arXiv preprint arXiv:1707.06347.
Seyde, T., Gilitschenski, I., Schwarting, W., Stellato, B.,
Riedmiller, M., Wulfmeier, M., and Rus, D. (2021). Is
bang-bang control all you need? solving continuous
control with bernoulli policies. Advances in Neural
Information Processing Systems, 34:27209–27221.
Shi, G., Azizzadenesheli, K., O’Connell, M., Chung, S.-J.,
and Yue, Y. (2021). Meta-adaptive nonlinear control:
Theory and algorithms. Advances in Neural Informa-
tion Processing Systems, 34:10013–10025.
Shi, G., Shi, X., O’Connell, M., Yu, R., Azizzadenesheli,
K., Anandkumar, A., Yue, Y., and Chung, S.-J. (2019).
Neural lander: Stable drone landing control using
learned dynamics. In International Conference on
Robotics and Automation, pages 9784–9790.
Song, X., Duan, J., Wang, W., Li, S. E., Chen, C., Cheng,
B., Zhang, B., Wei, J., and Wang, X. S. (2023a). Lip-
sNet: a smooth and robust neural network with adap-
tive Lipschitz constant for high accuracy optimal con-
trol. In International Conference on Machine Learn-
ing, pages 32253–32272. PMLR.
Song, Y., Romero, A., M
¨
uller, M., Koltun, V., and Scara-
muzza, D. (2023b). Reaching the limit in autonomous
racing: Optimal control versus reinforcement learn-
ing. Science Robotics, 8(82).
Steimle, L. N., Kaufman, D. L., and Denton, B. T. (2021).
Multi-model Markov decision processes. IISE Trans-
actions, 53(10):1124–1139.
Sutton, R. S. and Barto, A. G. (2018). Reinforcement learn-
ing: An introduction. MIT press.
Tsourdos, A., Permana, I. A. D., Budiarti, D. H., Shin, H.-
S., and Lee, C.-H. (2019). Developing flight con-
trol policy using deep deterministic policy gradient.
In IEEE International Conference on Aerospace Elec-
tronics and Remote Sensing Technology (ICARES).
Williams, G., Aldrich, A., and Theodorou, E. (2015).
Model predictive path integral control using covari-
ance variable importance sampling. arXiv preprint
arXiv:1509.01149.
Model-Free versus Model-Based Reinforcement Learning for Fixed-Wing UAV Attitude Control Under Varying Wind Conditions
91