Testing Emergent Bilateral Symmetry in Evolvable Robots with Vision
Michele Vannucci
1 a
, Satchit Chatterji
2 b
and Babak H. Kargar
1 c
1
Vrije Universiteit Amsterdam, The Netherlands
2
University of Amsterdam, The Netherlands
Keywords:
Evolution, Robotics, Symmetry.
Abstract:
Bilateral symmetry is a prominent characteristic in the animal kingdom and is linked to evolutionary advan-
tages such as cephalization. This study investigates whether integrating vision into modular evolvable robots
influences bilateral symmetry development for a targeted locomotion task. Through simulation, we found that
vision did not significantly increase our measure of symmetry in the robots, which predominantly evolved
into ‘snake-like’ morphologies (with only one limb extending from the head). However, vision capability was
observed to accelerate the convergence of the evolutionary process in some conditions. Our findings suggest
that, while vision enhances evolutionary efficiency, it does not necessarily promote symmetrical morphology
in modular robots. Further research directions are proposed to explore more complex environments and alter-
native symmetry measures.
1 INTRODUCTION
One of the most prominent features of terrestrial life
is symmetry. Notably, a large swathe of life falls un-
der the clade Bilateria, consisting of organisms that
majorly exhibit bilateral symmetry. However, the ori-
gin and usefulness of such symmetry is highly de-
bated within biology (Møller and Thornhill, 1998;
Toxvaerd, 2021; Holl
´
o, 2015). It has been argued (e.g.
in Finnerty, 2005) that bilateral symmetry is closely
tied to the property of cephalization, that is, an organ-
ism having a distinct head and tail. Having a head
with a concentration of perceptual organs (such as
eyes, ears and a mouth) lends itself to improved self-
perception of direction, as a front, back, left and right
(also often up and down) can be defined with respect
to the head. As a result, it was suggested by Finnerty
(2005) that developing directionality along an axis of
bilateral symmetry allows for better locomotion.
With respect to perceptual benefits as a result of
cephalization, vision is an important one. In a num-
ber of contexts such as depth perception, low descrip-
tional complexity and redundancy, bilateral symmetry
provides a selection bias to animals with vision (Tox-
vaerd, 2021; Johnston et al., 2022). In contrast to this,
there exist organisms with sight that are asymmetric
a
https://orcid.org/0009-0008-1838-0562
b
https://orcid.org/0009-0003-8648-1158
c
https://orcid.org/0000-0003-4841-0597
(such as various species of flat fish) – however, their
embryos are nevertheless symmetric, suggesting that
they evolved from bilaterally symmetric ancestors to
cover specific ecological niches (Friedman, 2008).
It is thus natural to ask to what extent (if at all)
bilateral symmetry lead to the perceptual benefits of-
fered by cephalization, and whether perception in turn
influenced symmetry. Though this is difficult to test
in the real world, it may be studied in simulated envi-
ronments with a population of embodied organisms
affected by evolutionary algorithms. Notably, the
field of evolutionary robotics provides a framework
where both the morphology (the ‘body’) and the con-
trol architecture (the ‘brain’) of each organism may
be evolved simultaneously in a physical or simulated-
physical environment (Eiben and Smith, 2015).
In this paper, we attempt to characterize the influ-
ence of directed vision in evolvable robots in a simu-
lated environment with a targeted locomotion task in
terms of the bilateral symmetry of their bodies. We
hypothesize that the addition of vision capability will
have a significant positive impact on the symmetry of
the evolved robots.
2 BACKGROUND
To empirically assess our hypothesis we run the evo-
lutionary process and physical simulations making
96
Vannucci, M., Chatterji, S. and Kargar, B.
Testing Emergent Bilateral Symmetry in Evolvable Robots with Vision.
DOI: 10.5220/0012947400003837
In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 96-107
ISBN: 978-989-758-721-4; ISSN: 2184-3236
Copyright © 2024 by Paper published under CC license (CC BY-NC-ND 4.0)

use of Revolve2 (Computational Intelligence Group,
2023; Hupkes et al., 2018), a collection of Python
packages used for researching evolutionary algo-
rithms and modular robotics. We first briefly discuss
about the robots themselves and some specifics about
how they are generated. Next, we discuss the targeted
locomotion task that the robots would evolve to opti-
mize, and then the specifics of the evolutionary pro-
cess utilized. Finally, we discuss how symmetry is
currently defined in the context of modular robots.
2.1 Modular Evolvable Robots
Several studies have previously described modular
robots in detail (e.g. the Revolve paper, Hupkes et al.
2018) and likewise evolvable morphologies and con-
trollers (Miras et al., 2018, 2020a). Lan et al. (2021)
provide a clear description of past studies in the field
and experiments with a directed locomotion task.
In Lan et al. (2021) the controller is learned sec-
ondly to the recombination of the body, during a
stage, namely ”infancy”, that precedes the ”mature”
life, in which the phenotype is ultimately evaluated
for selection. In contrast, in our experiment both the
controller and the robot body are recombined at the
same time. This happens through the HyperNEAT
(Stanley et al., 2009) algorithm before each new gen-
eration, meaning that the robot doesn’t learn during
the simulation, and is evaluated only one time at end
of its life. This algorithm as been shown to work well
on evolving modular robots controllers as far back as
2010 (Haasdijk et al., 2010).
Our robot has three types of modules: the core,
active hinges and brick modules. Both the controller
and the body genotypes are developed through a com-
positional pattern-producing network (CPPN), that is
evolved with HyperNEAT as already mentioned. This
method of separating the components of the robot
genotype in two parts has been already covered in past
research as in Jelisavcic et al. (2019) for which Fig-
ure 1 is illustrative.
Figure 1: The complete architecture of the learning system.
Image reprinted from Jelisavcic et al. (2019).
• The body is represented as a tree structure that
starts from the core and new modules are recur-
sively attached based on the orientation of the par-
ent on the empty sides. The CPPN takes as input
the position of the potential children modules de-
fined in a three-dimensional grid space, and the
length of the shortest path of the node to the core.
The output is the node type, which can also be
empty, terminating the branch, and how it should
be oriented. This results in a three-dimensional
robot.
• The controller phenotype is developed based on
the underlying morphology of the robot, using
a technique that has been proven working with
modular robots on different kinds of tasks by past
studies (De Carlo et al., 2020; Lan et al., 2021).
The final controller is a central pattern genera-
tor network (CPG) which has, for each joint/hinge
i, three neurons x
i
, y
i
(connected bidirectionally),
and o
i
, which has one in-going connection from
x
i
. The cyclical connection between the x and y
neurons allow the periodical propagation of the
signal, while the o neuron provides the output
controlling the one degree of freedom joint with
a value in the range [−1.0, 1.0]. To propagate to
all parts of the robot information about the other
joints all the x neurons have a bidirectional con-
nection between each other with weights w
x
j
x
i
and
w
x
i
x
j
, where i and j are two different hinges. Fig-
ure 2 gives an example representative illustration.
All the weights are learned and computed by the
CPPN that takes as input a 8-dimensional vector,
three dimensions each for the position of the first
and second neuron respectively and one dimen-
sion each that encodes their type (x, y or o).
Figure 2: Example CGP controller of a robot with 8 active
hinges. Image reprinted from Lan et al. (2021).
2.2 Targeted Locomotion
The goal of any evolutionary algorithm across genera-
tions is the optimization of a function that individuals
in a generation are evaluated against. In our experi-
ment, we begin by placing the modular robot at the
origin of a 3D environment and evaluate it based on
how far it is to a predetermined target
⃗
t = (x
t
,y
t
) on
Testing Emergent Bilateral Symmetry in Evolvable Robots with Vision
97

the ground at the end of the simulation (i.e. after a
certain number of timesteps in simulated time). This
target is the same for all individuals in the popula-
tion of the same generation so they may be compared.
The fitness function is set simply to the negative of the
Euclidean distance from the final location of the core
of the robot with respect to this target. Thus the algo-
rithm aims to maximize the following function for the
robots R with final core location
⃗
loc
R
= (x
R
,y
R
):
f (R) = −|
⃗
loc
R
−
⃗
t| (1)
= −
q
(x
R
−x
t
)
2
−(y
R
−y
t
)
2
(2)
Note that while the core of the robot technically
has a 3D location (with a potentially non-zero height),
the above equation simplifies this by using the projec-
tion of its position onto the xy-plane.
We also experimented using the squared distance,
as it can provide higher evolutionary pressure in the
first few generations, but we empirically concluded
that this is helpful only in the first part of the evolu-
tion process, as it accelerates the improvement of the
first generations but stagnates later – after around 100
generations the robots would reach the same fitness
plateau as the ones evolved with the regular distance
metric. Thus, for simplicity, we opted for Equation 1.
2.3 The Evolutionary Process
In this section, we describe techniques used for each
phase of the evolutionary algorithm. This is a brief
summary of a fairly common method, and we direct
the readers to Eiben and Smith (2015) and Hupkes
et al. (2018) for more thorough descriptions.
2.3.1 Initialization
The µ ∈N CPPN genotypes of the first generation are
initialized as empty, after which the HyperNEAT mu-
tation is applied 5 times to introduce initial diversity.
In this phase the robots of the starting generation are
also evaluated to assign them fitness values to kick-off
the iterative evolution process.
2.3.2 Parent Selection
λ ∈ N pairs of parents are selected randomly over the
µ members of the current generation. This allows the
selection pressure to be localized only in the later sur-
vivor selection phase.
2.3.3 Mutation and Crossover
Mutation and crossover are run (in that order) over all
the pairs of selected parents using the HyperNEAT al-
gorithm already mentioned, and the specific hyperpa-
rameters used are detailed in Section 3.2. This phase
creates λ offsprings.
2.3.4 Evaluation
In this phase λ simulations are run in parallel to eval-
uate the newly generated offsprings using the fitness
function described in Equation 1. More specifics on
the physics simulations will follow in Section 3.
2.3.5 Survivor Selection
In this phase we use (µ + λ) selection (Eiben and
Smith, 2015, sec. 5.3.2), as we select µ robots from
the union set of the current generation and the off-
springs. In this phase, tournament selection is per-
formed with k sampled individuals.
2.3.6 Termination Criteria
After each new generation is created, steps 2.3.2 to
2.3.5 are repeated. The termination criteria is set
to a predetermined maximum number of generations
G
max
.
2.4 Symmetry
Miras et al. (2020b) define an approximation of bilat-
eral symmetry along two axes with respect to the the
core of a 2D robot (Equation 3),
Z = max(z
v
,z
h
) (3)
The values z
v
and z
h
represent the symmetry values
along the vertical (x) and horizontal (y) axes respec-
tively when seen from a top-down view.
In our case, since the robot body develops itself
in three-dimensional space, instead of calculating the
symmetry with respect to one-dimensional axes, we
do it with respect to the x-z and the y-z planes, which
generalize the symmetry values defined above for a
3D robot placed on the x-y plane (i.e. parallel to the
floor). Given that the position of the core of some
robot is located at (x
c
,y
c
,z
c
), the planes of symmetry
to compute z
x-z
and z
y-z
are defined as x = x
c
and y =
y
c
respectively. Finally the symmetries are calculated,
with a score in the interval [0, 1], ignoring the modules
on the plane of symmetry (where the “spine” of the
robot is) with an analogous equation to Equation 3:
Z
3D
= max(z
x-z
,z
y-z
) (4)
Closely related to the method by Miras et al. (2020b),
we count the number of connected modules on one
side of each respective plane that has a mirrored
module on the other side, and multiply this by two.
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
98

Finally, we divide this value by the total number of
modules compared. The modules that lie on each re-
spective plane are not considered in this computation
as well.
3 METHODS
The code
1
was implemented in Python 3.10 making
use of the already meantioned Mujoco-based library
Revolve2 (Computational Intelligence Group, 2023)
pre-release version v0.4.0-beta2. This was the base of
our implementation, from the evolutionary algorithm
to physics simulation of the modular robots. The fit-
ness function used is Equation 1 as discussed previ-
ously, while the symmetry measure (Equation 4) was
also collected at the end of each generation for every
individual. Significant additional contributions with
respect to our experiments are discussed below.
3.1 Vision-Augmented Steering
A fundamental aspect of our research is the addition
of visual perception to the robot controller that, in
its default implementation, does not possess a vision
component. The latter is needed to implement what
we refer to as the ‘steering behavior’ of the robot
within this paper. To achieve this, we added a Mu-
joco camera in the environment with its position and
orientation locked to that of the core (i.e. the robot
always looks ‘forward’ with respect to its core).
To connect the camera input to the controller we
adapted a technique introduced in Luo et al. (2022)
that consists of directly altering the CPG output val-
ues based on a measure of the error angle θ between
the target direction and the robot direction. In Luo
et al. (2022) θ was calculated directly using the co-
ordinates of the target and the robot. However, in
our case, it is done creating a mask onto the cam-
era image to detect the red sphere object that repre-
sents the target. This is done with a boolean con-
dition on every pixel of an input frame, defined as
M
x,y
= (G
x,y
< 100) ∧ (R
x,y
> 100) ∧ (B
x,y
< 100),
where G
x,y
, R
x,y
and B
x,y
are the intensity values of
the green, red and blue RGB channels respectively for
the pixel positioned at coordinate (x,y) (the origin is
placed at the top left of the image). Subsequently,
we compute the mean x and y values for pixels where
the condition is satisfied to get the position (x
s
,y
s
) of
the center of the portion of the sphere in the camera
frame. θ and g are then calculated as:
1
The code can be found at https://github.com/
satchitchatterji/OriginOfSymmetry
θ =
w
cam
2
−x
s
(5)
g(θ) =
w
cam
2
−|θ|
w
cam
2
n
(6)
Where w
cam
is the width of the camera image in
pixels and n is a parameter that we set to 7 (value
taken from Luo et al., 2022). Since θ is a value in the
range [0,
w
cam
2
], g will be in the range [0,1]. Finally,
g is directly applied as a factor to the output o
i
of the
neuron for joint i, depending on where the joint of the
robot is with respect to its core. If the joint is on the
left side of the body, it uses the formula:
o
i
=
(
g(θ) ·o
i
if θ < 0
o
i
if θ ≥ 0
Thus, it is slowed down when the target is on the right
side of the robot’s visual field (θ < 0). Analogously,
if i is on the right hand-side of the robot the following
formula is applied:
o
i
=
(
o
i
if θ < 0
g(θ) ·o
i
if θ ≥ 0
This method doesn’t necessarily benefit every possi-
ble robot, but it is expected that the ones that take
advantage of it would emerge through selection.
3.2 Hyperparameter Selection
Table 1: Hyperparameter selection for targeted locomotion
task. The “Selection Set” refers to the list of hyperparam-
eter options tested for that variable. The variables selected
for the full experiment are in bold.
Hyperparameter Selection Set
Population size (µ) {100}
Offspring size (λ) {50}
Num. of generations (G
max
) {50,100,200}
Brain mutation rate (p
brain
) {0.9,0.15,0.2}
Body mutation rate (p
body
) {0.9,0.15,0.2}
Tournament size (k) {3,6}
Firstly, population size and offsprings size (µ and λ)
were fixed to 100 and 50 respectively, as they are rea-
sonable amounts that have already been proven work-
ing for similar tasks (for example, Luo et al., 2022).
We also trialed higher numbers, but the improvements
in fitness weren’t significant enough to justify the in-
crease in computation time.
Secondly, the number of generations G
max
was set
to 200 to assure that the convergence was reached be-
fore the end of the experiment as we saw in pilot ex-
periments that this would happen around the 100th
generation for a population size of 100.
Testing Emergent Bilateral Symmetry in Evolvable Robots with Vision
99

Subsequently, the final parameters that we se-
lected were the HyperNEAT mutation values and the
tournament size k. Since our HyperNEAT implemen-
tation has over 30 parameters we focused only on the
overall mutation rate for “brain” and “body” sepa-
rately (p
body
and p
brain
), while keeping the remain-
ing values as those that can be found in the default
Revolve implementation. Finally, p
body
, p
brain
and
k were selected simultaneously through grid search,
considering both scenarios where the camera func-
tionality was activated or deactivated. More details
on this sweep can be found in Appendix A. All the
hyperparameters we opted for can be found in Table
1.
3.3 Experimental Conditions
All robots are initially placed at coordinate (0, 0, 0).
Three target conditions were selected for the final ex-
periment, each placed at z = 1:
• The first condition, T
1
, is where the target for all
individuals was placed at the coordinate (5,5), i.e.
in front and to the right of the robot.
• In the second condition, T
2
, the target was placed
at the coordinate (0,
√
50), right in front of the
robot and at the same distance as in T
1
to ensure
just comparisons between conditions.
• Finally, the third condition, T
3
, consisted of cycli-
cally changing the target in after each generation
from (i) the left of the robot, (−5, 5), (ii) straight
ahead, (0,
√
50), and (iii) to the right (5,5). Gen-
eration 0 had the same target as generation 3 (to
the left); generation 1 had the same as generation
4 (in front); generation 2 had the same as gener-
ation 5 (to the right), and so on. All robots in a
single generation were tasked with reaching the
same target. Therefore, under this condition, the
robot should be able to reach the target regardless
of its location to optimize fitness.
Each condition has two sub-conditions, the case
where the robot has vision and the one where it
doesn’t. Each condition was tested at least 10 times
in total (5 times per sub-condition).
4 RESULTS
The code was run on a Mac Pro with an M2 chipset.
A single generation with steering took about 30 sec-
onds with a population size of 100. No-steer runs took
about 20 seconds with the same configuration.
In the remainder of this section, we present ag-
gregated results concerning the training (Section 4.1)
and behaviors exhibited (Section 4.2) by the evolved
robots, exploring how those may affect the primary
hypothesis that vision influences symmetry (Sec-
tion 4.3). We also present an additional post hoc result
about the speed of convergence of the evolutionary al-
gorithm in this task (Section 4.4). For completeness,
we present graphs which aggregate the maximum fit-
nesses and symmetries per generation in Appendix C,
though for our analysis, Figure 4 suffices (portraying
the means of the same).
4.1 Fitness
To test our hypothesis properly we first needed the
robots to reach the target consistently. This was en-
abled by the hyperparameter tuning process detailed
in Section 3.2. In the the left column of Figure 4 we
compare how the two types of robot, with vision and
without, perform across the generations for all three
conditions in order for the main experiments.
We can see that for conditions T
2
ad T
3
(Figures
4c and 4e) the robots with steering functionality con-
verge to an optimal fitness (around zero) faster than
those without across multiple experiments. We dis-
cuss this further in Section 4.4.
This trend isn’t that clear for condition T
1
(Figure
4a), but still holds when we aggregate all three condi-
tions together. This can be explained by the fact that
for T
2
, the optimal final position is (0,
√
50), while
for T
3
the one that leads, on average, to best the fit-
ness, is located on the Fermat point (Weisstein, 2003)
of the triangle generated by the three targets, which
is (0,
√
50). This means that, for both conditions, the
robot needs to go straight, which is easier. We didn’t
expect this behavior – the robots, even with vision,
get stuck on the local optima. This is illustrated in the
next section.
4.2 Paths
Since the fitness trend and manually looking at the
videos from the robot’s perspective wasn’t sufficient
to have a clear overview of the robots’ behavior in-
side the simulation, we generated graphs displaying
the paths taken by a sample of robots within the same
generation. In Figures 3a and 3b we can see how they
evolve between generation 50 and 150 for condition
T
1
, while in Figures 3c and 3d we have the same com-
parison for condition T
3
.
Under condition T
1
the robots improve their fit-
ness by moving straight ahead, further on at genera-
tion 150 they appear to have learned how to navigate
to the target on the right, displayed with a green cross.
On the other hand, for condition T
3
the robots, en-
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
100

(a) Condition T
1
, generation 50 (b) Condition T
1
, generation 150
(c) Condition T
3
, generation 50 (d) Condition T
3
, generation 150
Figure 3: Example paths (grey lines) without steering functionality. For T
1
(top), the target is shown by the red cross. For
T
3
, (bottom) the 3 cyclically changing target are shown as red, blue and green crosses respectively. Condition T
2
(with the
target being the green cross) shows similar paths to T
3
and is excluded here for the sake of brevity. Grey arrows represent
the intermediary 2D orientations of the robot’s core, and red arrows show the final orientations. The green path shows one of
the robots with the best fitness, and the dotted orange line is the path of one of the robots with the best fitness (there may be
multiple individuals with the same fitness and/or symmetry in one generation).
dowed with vision capability, seem to reach the Fer-
mat point quickly as already at generation 50 they are
in its close vicinity, we observed a similar behavior
for robots without vision. We can’t say confidently
that the robots are taking advantage of the camera to
move towards the target. Looking at the paths we can
confirm that, even when provided with the steering
behavior, they merely go towards the Fermat point.
Nevertheless, this doesn’t explain why the plots of
the mean fitness don’t have steeper dips, as the targets
(−5,5) and (5, 5) are more than 5 units away from the
Fermat point, while the mean fitness decreases only
by ≈ 0.5. We are unsure of why this happens.
4.3 Main Result: Symmetry & Vision
Looking at the graphs for condition T
2
and T
3
(Fig-
ures 4d and 4f), it is evident that, according to our
measure of symmetry, as the robots adapt and their fit-
ness values increase, the symmetry shrinks to 0. This
is slightly different for condition T
1
(Figure 4b) for
which there is no rapid convergence trend as some ex-
periments did not produce a robot capable of reaching
the target.
As shown in the right column of Figure 4, we
see that the experiments dependably create robots
that are not symmetric with or without vision.
We compare the mean of the symmetries of the
generations over all the runs for each experimental
condition for the steer and no-steer robots using a
Mann-Whitney U test. This results in p >> 0.05,
even approaching p = 1 for T
2
and T
3
. This test was
used as the assumptions of the standard t-test cannot
be verified (notably, the normality test and the low
sample size). Furthermore, the symmetry values
themselves approach zero (testing the hypothesis
that the symmetries are non-zero results in p → 1 as
generations increase for T
2
and T
3
). Thus, we fail
to reject our null hypothesis that robots with vision
evolve to be more symmetric than those without.
Testing Emergent Bilateral Symmetry in Evolvable Robots with Vision
101

(a) Fitness results for condition T
1
. (b) Symmetry results for condition T
1
(c) Fitness results for condition T
2
. (d) Symmetry results for condition T
2
(e) Fitness results for condition T
3
. (f) Symmetry results for condition T
3
Figure 4: Mean of (mean fitnesses per generations, left) and mean of (mean symmetries per generations, right) over all runs
for robots with steering behavior (blue) and without (red). The x-axis is the generation index and the y-axis is the fitness
according to Equation 1 (left) or 3D symmetry according to Equation 4 (right). The shadows represent standard error.
4.4 Additional Result: Rate of
Convergence
Finally, we demonstrate the improvement of conver-
gence for robots augmented with vision. Since we
could not find a standard way to quantify the speed of
convergence, we first aggregated each population to a
mean fitness value, then grouped all experiments ac-
cording to whether the robots had steering or not. We
then applied a Mann-Whitney U test to see whether
having vision significantly makes a difference in the
fitness means across generations. This test was used
as the assumptions of the standard t-test could not be
justified. The results can be seen in Figure 5. We note
significant differences (p << 0.05) in a large portion
of generations in condition T
3
from generation 30 to
around generation 130 (with the lowest p ≈ 0.0002).
Looking at the training graph in Figure 4e, we see that
the convergence graphs between the steer and no-steer
conditions deviate significantly between these gener-
ations, meaning the robots that have vision converge
to a solution with the same fitness as those that don’t,
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
102

but faster.
For condition T
2
, although we can visually see
faster convergence for robots with vision, this is not
reflected in the Mann-Whitney U tests: the p-value
approaches p = 0.05 but never crosses it, and thus
there is no significant difference for any generation.
Lastly, the p-values for T
1
are relatively large, (the
lowest p-value ≈ 0.155), and thus the convergence
rates are not significantly different at all.
5 DISCUSSION
This paper demonstrates first steps in attempting to
verify if vision may affect symmetry in evolvable
modular robots. Although we did not find significant
results, it must be recognized that this paper is a small
slice of possible experiments in this vast area. Here,
we reflect on various aspects of this paper and direc-
tions in which future research may venture.
5.1 Robot Morphology and Symmetry
After failing to reject our initial null hypothesis about
the effect of vision on symmetry (Section 4.3), we
dug deeper to find out what kinds of robots the exper-
iments were actually producing. When examining the
bodies of the robots, we noticed an interesting trend.
The morphologies of the robots all tended towards
a core with a long line of active hinges, as seen in
Figure 6. We offer a straightforward explanation for
this phenomenon, derived from observing simulation
videos. The evolutionary algorithm determined that
this was the most efficient anatomy as it enabled the
robots to execute one or more large jumps, propelling
them towards the target more rapidly. This is also
confirmed by the path plots (Figure 3) which illustrate
the robots’ seemingly random orientations during
intermediate states as they rotate while jumping. In
Section 5.2 we suggest how this could be avoided
using a different fitness function. These findings, in
addition to Equation 4, explain why the symmetries
of the evolved robot population (in the right column
of Figure 4) tended to go to zero.
In a sense we can argue that the evolved robots are
symmetrical, perhaps trivially so (as, for example, a
worm is considered bilaterally symmetric in biologi-
cal literature). Thus, it is possible that the current def-
inition of symmetry as per Miras et al. (2020b) and
Equation 4 is either insufficient or inadequate to be
used when comparing evolvable robots to real evolu-
tion. An alternative may be to take all modules into
account when computing symmetry (instead of ignor-
ing those that lie on the plane of symmetry) or to use
an alternative measure such as the symmetry of the
planar images of the robots. Additionally, there exist
animals in nature with other forms of symmetry (no-
tably rotational symmetry), and thus an analogue may
be useful in the context of evolvable robotics too.
5.2 Further Developments
In conclusion, as already suggested, a number of as-
pects of this research could be developed further for
future studies, a selection of possible improvements
include:
• More Detailed Hyperparameter Selection: A
large majority of our hyperparameters were cho-
sen based on other papers (notably Miras et al.,
2018 and Luo et al., 2022) that have been shown
to work in tasks similar to ours. However, with the
additonal element of vision, the optimal hyperpa-
rameters may not be the same as theirs. Though
we did do some tuning, a fuller search (requiring
substantial compute) may be needed to explore
this topic fully.
• More Efficient Computation: One of the chal-
lenges faced during this project was the fact
that running the experiments was often time-
consuming and not cross-platform. Thus, for
a more complete experiment (especially those
that aim to do a fuller hyperparameter selec-
tion sweep), we suggest finding ways to make
this computation faster and more robust. We at-
tempted to work towards this by heuristically min-
imizing the simulation time of the environment
for each robot, and though it showed promising
results, we did not have time to fully flesh this out.
A description of this can be found in Appendix B.
• Fitness Function: The fitness function defined
previously (Equation 1) was kept simple in or-
der not to have too many confounding variables in
our analysis. Thus, the simplest fitness for a tar-
geted locomotion task is the Euclidean distance
between the target and the final robot position.
However, future studies may augment this to in-
clude other aspects of movement, such the length
and shape of the full path to the target or the orien-
tation of the robot’s core, as was done in Luo et al.
(2022). This could force the robots to reach the
target through a more rectilinear and natural loco-
motion. That, in turn, could lead to more bilateral
morphologies that differ from those described in
Section 5.1.
• Symmetry: As discussed earlier, the symmetry
measure adapted from Miras et al. (2020b) may
Testing Emergent Bilateral Symmetry in Evolvable Robots with Vision
103

(a) Results for condition T
1
. (b) Results for condition T
2
(c) Results for condition T
3
Figure 5: Mann-Whitney U test across each generation to compare the means of fitnesses for robots with steering vs no steering
behaviour. The y-axis is log-scaled for clarity, and the dotted line represents the standard significance level of p = 0.05. Note
that in the T
2
condition, the significance reference line is too low to be displayed. The shaded area represents the portion of
the graph that lies under p = 0.05. Refer to Section 4.4 for details.
Figure 6: Most common robot morphology evolved at con-
vergence in all experiments. Each 1×1 box is a single mod-
ule: the yellow voxel represent the core, and the red voxels
represent active hinge modules.
not cover all aspects of visual and biological sym-
metry. Thus, a variety of alternatives may need
to be developed to verify their usefulness and to
allow a fairer comparison with biological organ-
isms. Additionally, nature shows other pattern
types such as fractals, which may be interesting
to study in the context of larger evolvable robots.
• Other Morphological Measures: In addition to
symmetry, other morphological measures may be
interesting to study as vision is incorporated, for
example, balance, or the number of limbs. Kargar
et al. (2021) and Miras et al. (2018) list a number
of measures in this direction.
• Vision Implementation: Our implementation of
vision follows Luo et al. (2022), as the target in-
formation extracted from the video is used di-
rectly to influence the outputs for the joints in the
controller network. Though this worked for their
needs, it does introduce bias for the simplicity of
the model and a new hyperparameter (with respect
to Equation 6). Thus, given enough computing
resources, it may be more natural for a system
to evolve end-to-end, i.e. the camera feed is used
as an input to the controller network, with which
it may gain useful information about its environ-
ment. For example, depending on the task, this
may be in the form of a bag-of-words histogram or
even a convolutional neural network (being care-
ful of its inductive bias of translational invariance)
that is pre-trained or co-evolved with the robot’s
brain and body.
• More Complex Tasks/Environments: The task
of targeted locomotion is fairly simple, and was
chosen indeed for its simplicity. However, this
may have been the cause of the rejection of the
null hypothesis in this paper – perhaps the envi-
ronment was too simple for there to be a signif-
icant advantage of having vision and of develop-
ing symmetry. A different task (such as survival
or balance), or more complex environments (ele-
ments of non-stationarity or partially-observable
states) may lead to a fairer test of the hypothesis.
• Studying the Effect of Vision on Convergence:
Although we cannot gather much evidenced for
the effect of vision on symmetry, we uncovered
an interesting trend in Section 4.4 that robots with
vision may converge quicker than those without.
Thus, using this work as a jumping off point, it
may be beneficial for future research to study this
in more detail, and verify which tasks and envi-
ronments also produce this trend.
REFERENCES
Computational Intelligence Group, V. U. A. (2023). Re-
volve2. https://github.com/ci-group/revolve2. Version
used: 0.4.2.
De Carlo, M., Zeeuwe, D., Ferrante, E., Meynen, G., Ellers,
J., and Eiben, A. (2020). Robotic task affects the
resulting morphology and behaviour in evolutionary
robotics. In 2020 IEEE symposium series on compu-
tational intelligence (SSCI), pages 2125–2131. IEEE.
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
104

Eiben, A. E. and Smith, J. E. (2015). Introduction to evolu-
tionary computing. Springer.
Finnerty, J. R. (2005). Did internal transport, rather than
directed locomotion, favor the evolution of bilateral
symmetry in animals? BioEssays, 27(11):1174–1180.
Friedman, M. (2008). The evolutionary origin of flatfish
asymmetry. Nature, 454(7201):209–212.
Haasdijk, E., Rusu, A. A., and Eiben, A. E. (2010). Hy-
perneat for locomotion control in modular robots.
In Evolvable Systems: From Biology to Hardware:
9th International Conference, ICES 2010, York, UK,
September 6-8, 2010. Proceedings 9, pages 169–180.
Springer.
Holl
´
o, G. (2015). A new paradigm for animal symmetry.
Interface focus, 5(6):20150032.
Hupkes, E., Jelisavcic, M., and Eiben, A. E. (2018). Re-
volve: a versatile simulator for online robot evolu-
tion. In Applications of Evolutionary Computation:
21st International Conference, EvoApplications 2018,
Parma, Italy, April 4-6, 2018, Proceedings 21, pages
687–702. Springer.
Jelisavcic, M., Glette, K., Haasdijk, E., and Eiben, A.
(2019). Lamarckian evolution of simulated modular
robots. Frontiers in Robotics and AI, 6:9.
Johnston, I. G., Dingle, K., Greenbury, S. F., Camargo,
C. Q., Doye, J. P., Ahnert, S. E., and Louis, A. A.
(2022). Symmetry and simplicity spontaneously
emerge from the algorithmic nature of evolution.
Proceedings of the National Academy of Sciences,
119(11):e2113883119.
Kargar, B. H., Miras, K., and Eiben, A. (2021). The effect of
selecting for different behavioral traits on the evolved
gaits of modular robots. In ALIFE 2021: The 2021
Conference on Artificial Life. MIT Press.
Lan, G., De Carlo, M., van Diggelen, F., Tomczak, J. M.,
Roijers, D. M., and Eiben, A. E. (2021). Learning
directed locomotion in modular robots with evolvable
morphologies. Applied Soft Computing, 111:107688.
Luo, J., Stuurman, A. C., Tomczak, J. M., Ellers, J., and
Eiben, A. E. (2022). The effects of learning in mor-
phologically evolving robot systems. Frontiers in
Robotics and AI, 9:797393.
Miras, K., De Carlo, M., Akhatou, S., and Eiben,
A. (2020a). Evolving-controllers versus learning-
controllers for morphologically evolvable robots. In
Applications of Evolutionary Computation: 23rd Eu-
ropean Conference, EvoApplications 2020, Held as
Part of EvoStar 2020, Seville, Spain, April 15–17,
2020, Proceedings 23, pages 86–99. Springer.
Miras, K., Ferrante, E., and Eiben, A. E. (2020b). Envi-
ronmental influences on evolvable robots. PloS one,
15(5):e0233848.
Miras, K., Haasdijk, E., Glette, K., and Eiben, A. E. (2018).
Search space analysis of evolvable robot morpholo-
gies. In Applications of Evolutionary Computation:
21st International Conference, EvoApplications 2018,
Parma, Italy, April 4-6, 2018, Proceedings 21, pages
703–718. Springer.
Møller, A. P. and Thornhill, R. (1998). Bilateral symmetry
and sexual selection: a meta-analysis. The American
Naturalist, 151(2):174–192.
Stanley, K. O., D’Ambrosio, D. B., and Gauci, J. (2009).
A hypercube-based encoding for evolving large-scale
neural networks. Artificial life, 15(2):185–212.
Toxvaerd, S. (2021). The emergence of the bilateral symme-
try in animals: A review and a new hypothesis. Sym-
metry, 13(2):261.
Weisstein, E. W. (2003). Fermat points. https://mathworld.
wolfram.com/FermatPoints.html.
APPENDIX
A Hyperparameter Selection
Analysis
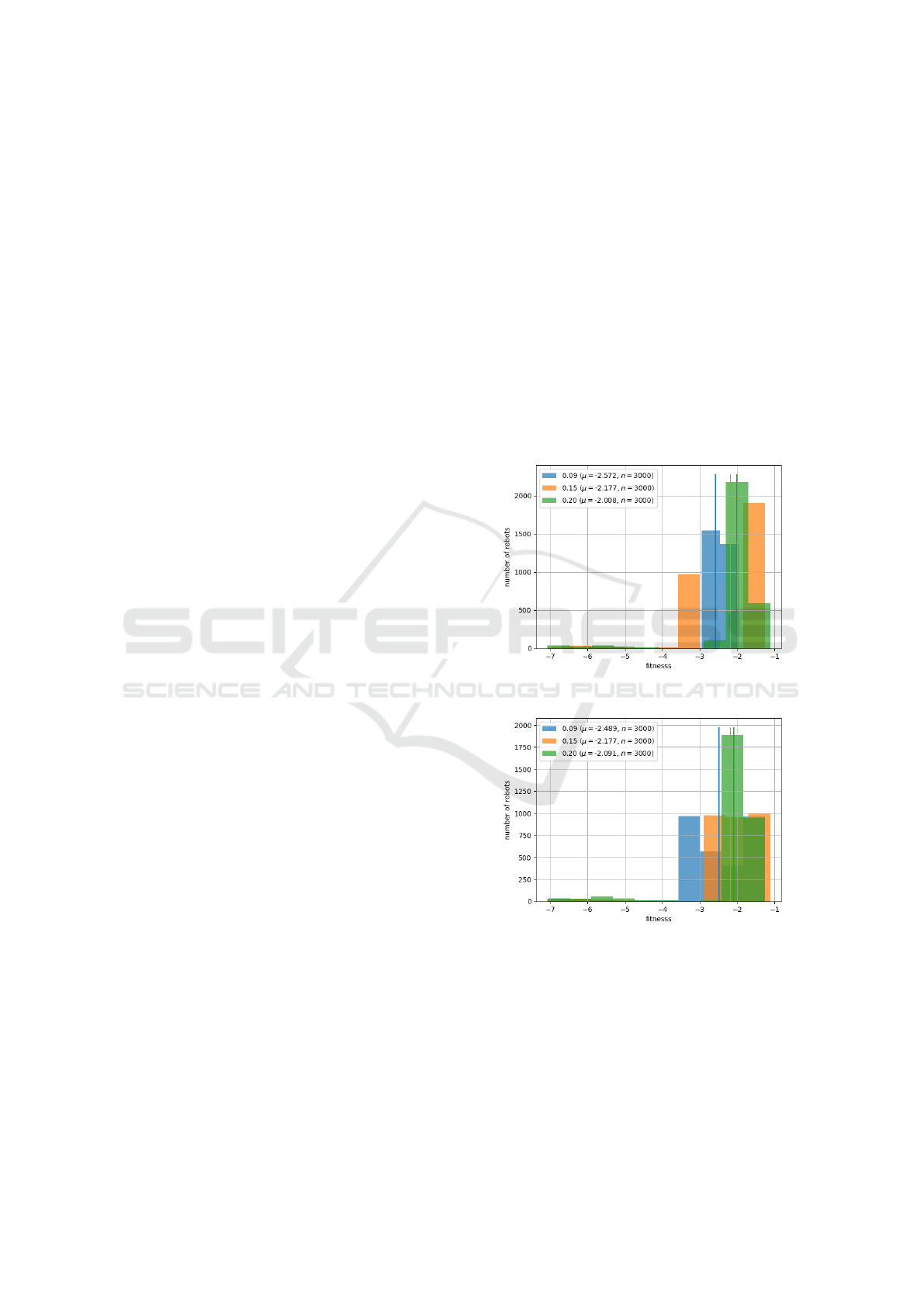
(a) Fitness distributions for different values of
body mutation rates (p
brain
).
(b) Fitness distributions for different values of
brain mutation rates (p
brain
).
Figure 7: Comparing distributions of robots fitnesses of last
generations over 30 experiments, while controlling, with
grid search, for k and vision capability, given different val-
ues of mutation rates. n = µ ∗30.
While for the tournament size parameter k we
saw some clear improvement in convergence using
a higher value of 6 instead of 3, for the overall mu-
tation rates of the “brain” and “body” genotypes we
Testing Emergent Bilateral Symmetry in Evolvable Robots with Vision
105

(a) Fitness results for condition T
1
. (b) Symmetry results for condition T
1
(c) Fitness results for condition T
2
. (d) Symmetry results for condition T
2
(e) Fitness results for condition T
3
. (f) Symmetry results for condition T
3
Figure 8: Mean of (max fitnesses per generations, left) and mean of (max symmetries per generations, right) over all runs
for robots with steering behavior (blue) and without (red). The x-axis is the generation index and the y-axis is the fitness
according to Equation 1 (left) or 3D symmetry according to Equation 4 (right). The shadows represent standard error.
didn’t have conclusive results that would make us lean
more towards a singular option. Because of this, for
both genotypes, we chose the median of the values
experimented during grid search. In Figure 7a and 7b
we compare the distributions via histograms of the fi-
nesses attained in the hyperparameter selection task
(targeted locomotion with the target at (5, 5)). The
analysis indicates that variations in this parameter do
not significantly lead to better performances, thus mo-
tivating our decision.
B Terminating Simulations Early
With the aim of saving computation time, we ex-
perimented with prematurely stopping simulations,
specifically targeting those where the robots failed to
make sufficient progress towards the target beyond a
certain threshold. This was motivated by the fact that
we noticed how, especially in the first 40 generations,
many robots weren’t moving towards the correct di-
rection or weren’t moving at all. Thus, it may be use-
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
106

ful to use the first few seconds of the robot’s life as a
heuristic to terminate its simulation earlier. This was
achieved by defining a minimum velocity v
min
and
calculating the distance traveled towards the target at
time t as:
s
t
= d
o
+ f
t
(7)
Where d
o
is the Euclidean distance between the ori-
gin (where the robot is generated) and the target, and
f
t
, which is negative, is the value of the fitness func-
tion at time t. Finally, s
t
has to satisfy the following
condition to avoid the termination of the simulation:
s
t
≥ v
min
·t ·
p
i
gen
(8)
where i
gen
is the generation index that goes between 0
and G
max
. We multiply by
p
i
gen
to increase the value
for higher generations as we assume that the robots
are slowly performing better and we can expect higher
standards of performance.
We empirically observed our computation time for
100 generations of 100 individuals being decreased
by a factor of ≈ 3 as many simulations were killed
especially in the first few generations. This reduc-
tion is particularly impactful, given that a single run
of this type originally took ≈ 25 minutes. However,
the mean fitness appeared to be marginally decreased
by ≈ 0.2. Since computation efficiency was not the
main focus of the research, we decided to abandon
this method for the time being. Nevertheless, this ap-
proach could be developed further in future research
for any task, and an improved strategy we suggest
would be to adjust the threshold for the minimum
speed based on the current average performance and
the standard deviation within the population.
C Mean of Maximum Results per
Generation
Figure 8 shows the relevant figures of the means of
(max fitnesses per generations, left) and means of
(max symmetries per generations, right) over all runs
for robots with steering behaviour and without.
Testing Emergent Bilateral Symmetry in Evolvable Robots with Vision
107