Grammatical Evolution of Synthesizable Finite State Machine-Based
Behavioural Level Hardware Description Language Codes
Bilal Majeed
1 a
, Jack McEllin
1 b
, Rajkumar Sarma
1 c
, Ayman Youssef
2 d
,
Douglas Mota Dias
3 e
and Conor Ryan
1 f
1
BDS Labs, Dept. of CSIS, University of Limerick, Limerick, Ireland
2
Dept. of Computers and Systems, Electronics Research Institute, Cairo, Egypt
3
Department of Computer Science & Applied Physics, Atlantic Technological University, Galway, Ireland
Keywords:
Evolvable Hardware, Grammatical Evolution, Synthesizable Sequential Logic Circuits, Hardware Description
Language Design, Electronic Design Automation.
Abstract:
The importance of designing efficient and accurate digital circuits has grown due to the widespread use of
wearable, ready-made, and custom electronic products. These digital circuits are typically sequential and de-
signed using synthesizable Hardware Description Languages (HDLs) that can be translated into hardware. A
large part of this exercise comprises designing synthesizable HDLs for sequential circuits, which are challeng-
ing to design and test, thus requiring much time for the engineers to construct them. This paper proposes using
Grammatical Evolution (GE) to evolve the synthesizable HDL codes for sequential circuits on the behavioural
or algorithmic level in SystemVerilog. The codes evolved in this work are of JK-Flip Flop (JK-FF), 3-bit Up-
Down Counter (UDC), and 8-Floor Elevator (8FE), all from the perspective of Finite State Machines (FSMs).
Circuits such as 3-bit UDC and JK-FF are the basic blocks in many circuits in the industry, while 8FE is a
real-life example mimicking 3-bit UDC but with a few practical exceptions. All circuits are evolved using two
types of grammars. The G1 Type Grammar evolves parts of the code, while the more powerful and generic
G2 Type Grammar evolves the full HDL codes for these sequential circuits. The GE-based evolution of these
synthesizable design codes using both types of grammar achieves a success rate of over 86% for all circuits.
Moreover, all the solution circuits evolved with the best achieved success score under the respective hyper-
parameter settings for G1 and G2 Type Grammar are synthesised, and their synthesis reports are compared
against the synthesis reports of Gold (human-designed) circuits. The synthesis is performed using Cadence
Genus at Generic Process Design Kit (GPDK) 45, 90, and 180 nm technology libraries. The synthesis results
show that machine-generated designs often perform as well as or better than human-designed circuits.
1 INTRODUCTION
The foundation of contemporary electronics is digital
circuits, which enable the processing and modifica-
tion of digital signals. In contrast to continuous levels
in analog circuits, binary digits (‘0’ and ‘1’) represent
discrete levels in digital circuits. Logic gates such as
AND, OR, and NOT, which carry out logical opera-
tions on binary inputs, are the essential components of
a
https://orcid.org/0000-0001-7528-275X
b
https://orcid.org/0000-0002-0187-9614
c
https://orcid.org/0000-0002-5551-1006
d
https://orcid.org/0000-0001-6145-4071
e
https://orcid.org/0000-0002-1783-6352
f
https://orcid.org/0000-0002-7002-5815
digital circuits. Combining these gates results in more
sophisticated circuits that may execute various com-
puting functions, including flip-flops, registers, and
arithmetic units. Because of their binary structure,
digital circuits are very dependable in various appli-
cations, from microprocessors and memory modules
in computers to microcontrollers in everyday devices.
Digital circuits are divided into two main cat-
egories depending on their structure and function:
combinational and sequential. Digital circuits that
rely only on the current input values for their out-
put are known as combinational circuits. Past inputs
and outputs are neither stored nor remembered. The
circuit’s logical functions combine the current inputs
to produce the output. The logic gates noted above
are the basic building blocks of combinational circuits
222
Majeed, B., McEllin, J., Sarma, R., Youssef, A., Dias, D. and Ryan, C.
Grammatical Evolution of Synthesizable Finite State Machine-Based Behavioural Level Hardware Description Language Codes.
DOI: 10.5220/0012948300003837
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 222-233
ISBN: 978-989-758-721-4; ISSN: 2184-3236
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

(AND, OR, NOT, etc.). Boolean functions are imple-
mented via the connections between these gates.
Unlike combinational circuits, sequential circuits
feature memory components, implying that the cir-
cuit’s outputs depend on the present inputs and their
past states. These circuits can retain data and make
decisions depending on previous inputs. Key com-
ponents of sequential circuits include flip-flops and
latches. By storing binary data, these memory com-
ponents enable the circuit to maintain state informa-
tion across time. Sequential circuits are mainly rep-
resented as FSMs to show the data flow of the cir-
cuit through the state transitions depending on the
current state and/or the change in inputs of the cir-
cuit. This way of representing the sequential circuits
is suggested since it shows how these circuits should
behave at each clock cycle according to the current
state of the FSM (Morris and Ciletti, 2007).
Most common sequential circuits include memory
units such as Flip Flops, counters (which can count up
or down or both), and registers. Out of these circuits,
JK-FF and 3-bit UDC are evolved in this work. A JK-
FF is a type of bistable multivibrator, a fundamental
building block in digital electronics used for storing
and transferring binary data. The JK-FF is a refine-
ment of the SR (Set-Reset) Flip-Flop and eliminates
the ambiguous state found in SR Flip-Flops (Morris
and Ciletti, 2007). 3-bit UDC is a digital sequential
circuit that counts up (‘0’ to ‘7’) or down (‘7’ to ‘0’)
in binary, based on the control input. When operating
as an Up counter, it starts from ‘0’ and counts up to
‘7’, then wraps around back to ‘0’ to begin again. As
a Down counter, it starts from ‘7’ and counts down to
‘0’, then wraps around back to ‘7’ to start anew.
The 8FE circuit evolved in this work is a practi-
cal example of a counter-like machine used to control
the lift/elevator system, yet it is complex to design
and hard to evolve. It mimics the 3-bit UDC with the
practical exception of being unable to wrap around at
Floor-0 or Floor-7. So, each clock cycle can move up
one floor, down one floor, or stay on the same floor,
depending on the control input. Unlike a 3-bit UDC
jumping directly from ‘0’ to ‘7’, it cannot leap di-
rectly from Floor-0 to Floor-7 or vice versa.
FSMs are essential for modeling behavior and
managing states based on inputs in sequential circuit
design. There are two types of FSM: Mealy machines,
where outputs depend on both the current state and
inputs, and Moore machines, where outputs depend
only on the current state. Moore machines typically
require more states than Mealy machines (Klimovich
and Solov’ev, 2010). The JK-FF is implemented us-
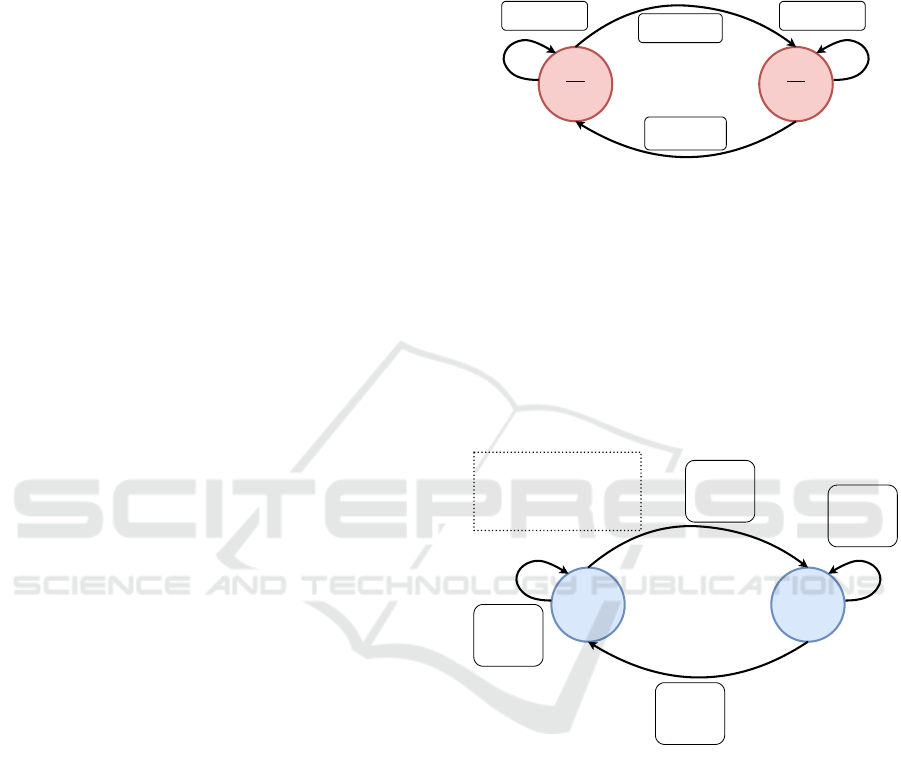
ing a Moore machine, as shown in Figure 1. Flip-flops
are not typically represented as FSMs; if needed, they
are represented as Moore machines since Mealy ma-
chines maintain a single state. A single-state FSM
lacks dynamic behavior crucial for modeling state
changes based on input events.
S0
q = 0
S1
q =1
jk = 10, 11
jk = 01, 11
jk = 00, 01 jk = 00, 10
Figure 1: Moore FSM of JK-FF.
The FSMs of the 3-bit UDC and 8FE evolved in
this paper are Mealy machines and are shown in Fig-
ure 2 and Figure 3, respectively. Typically, these ma-
chines would have eight states each, but their FSMs
are optimized to generate a compact and optimized
system in terms of HDL code. Since 8FE cannot jump
directly from Floor-0 to Floor-7 or from Floor-7 to
Floor-0, it is shown in Figure 3 that at each state, it is
working on two inputs, one of which is keeping track
of the current floor where the elevator is standing.
S0 S1
State Transition Label's
Order:
sel (input) / q +/-
1(output)
1 (Down)
/
q-1
1 (Down)
/
q-1
0 (Up)
/
q-1
0 (Up)
/
q-1
Figure 2: Mealy FSM of 3-bit UDC.
HDLs are specialized programming languages
that model and describe digital circuits and systems.
Modern circuits are built, with very few exceptions,
using HDLs rather than logic gates; this relation-
ship is analogous to that between high-level program-
ming languages and assemblers. These languages of-
fer a greater abstraction than typical programming
languages, giving engineers a systematic and dis-
ciplined means to represent digital circuits’ timing,
structure, and behavior. Verilog (Ciletti, 2010) and
VHDL (Navabi, 2007) are the two most popular
HDLs. Verilog is renowned for its straightforward,
C-like syntax, which makes it comparatively sim-
ple to learn, but VHDL is verbose and provides a
more explicit way to express hardware elements. Sys-
Grammatical Evolution of Synthesizable Finite State Machine-Based Behavioural Level Hardware Description Language Codes
223

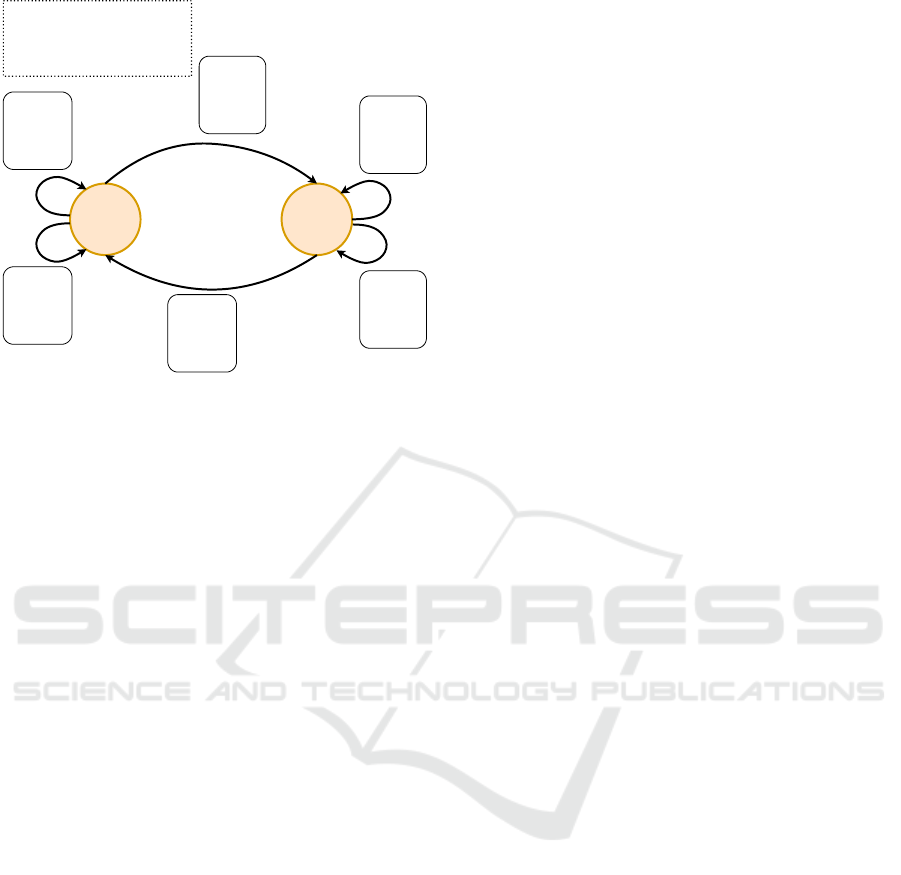
S0 S1
State Transition Label's
Order:
[sel (input)], q (input) / [q +/-
0/1 (output)]
0 (Up),
q<7
/
q+1
0 (Up),
q>=7
/
q
0 (Up),
q<7
/
q+1
1 (Down),
q>0
/
q-1
1 (Down),
q>0
/
q-1
1 (Down),
q<=0
/
q
Figure 3: Mealy FSM of 8FE.
temVerilog (Spear, 2008) is another widely used HDL
that enables engineers to use complicated testbench
topologies and random stimuli in simulation to vali-
date the design, thus working as both a Hardware Ver-
ification Language (HVL) and an HDL, which is why
it is used here for the evolution of the circuits.
Logic synthesis follows the generation of HDL
code for circuits. The HDL code offers a high-
level abstraction of the circuit at the Register Transfer
Level (RTL). During logic synthesis, this description
is converted into an equivalent gate-level netlist of
registers and/or Boolean equations, representing the
circuit’s logical structure.
Logic synthesis is typically performed using tools
like Genus by Cadence (Cadence, 1998). These tools
analyse HDL code and optimise it for performance,
area, and power consumption. Logic synthesis also
considers technology parameters, like transistor sizes,
based on the target manufacturing process and en-
vironmental requirements. A logically perfect cir-
cuit from functional simulators may become non-
synthesizable (cannot be implemented on a chip) if
it does not use synthesizable HDL constructs, such
as consistent use of blocking (=) and non-blocking
(<=) HDL assignments in sequential code. Issues
can be more complex, so it’s crucial to create synthe-
sizable code, as synthesis follows creating logically
correct code.
Artificial Intelligence (AI), particularly Machine
Learning (ML), has shown promising capabilities
in automatic problem-solving across various fields,
leading to its growing application in circuit design.
In Electronic Design Automation (EDA) tools, which
are crucial for designing electronic circuits, some can
automatically generate specific circuit parts. Cur-
rently, ML-based systems like Solido (Solido, 2005),
and synthetic intelligence tools like Eagle (Eagle,
1988) and Kicad (Kicad, 1992), exist. However, these
systems cannot generate entire circuits and are pri-
marily used for designing specific components only.
Search-based methods from the field of Evolution-
ary Computation (EC), such as Genetic Algorithms
(GA) (Mirjalili, 2019), Genetic Programming (GP)
(Koza, 1992), Evolutionary Strategies (ES) (Rudolph,
2012), and GE (Ryan et al., 1998) have shown mas-
sive success in automatically generating parts or com-
plete circuits. The field of study that focuses on the
use of EC for the automatic generation of electronics
is called Evolvable Hardware (EH). GE is used here
since it is, so far, best to evolve the sequential cir-
cuits’ hardware on a behavioural level in HDL due to
its ability to evolve behavioural level code with a great
success rate (Majeed. et al., 2023) and does not suffer
from issues such as the problem of closure, which GP
does even if we use grammar-based GP.
2 RELATED WORK ON
SEQUENTIAL CIRCUIT
EVOLUTION
The first work was presented on the evolution of se-
quential circuits by (Hemmi et al., 1996) where a se-
quential adder was evolved using Production Genetic
Algorithm (PGA) (Mizoguchi et al., 1994), a unique
type of GA specially designed for EH and which used
the production rules written in the form of Backus
Naur Form (BNF). The designers called this an HDL
grammar since it was designed to evolve circuits in
HDL. Their mapping process differs from GE, al-
though it also employs BNF grammars.
Next, two more sequential circuits, a modulo-
6 counter and the ISCAS’89 benchmark circuit
named lion, were evolved using Developmental
Cartesian Genetic Programming (DCGP) (Shanthi
et al., 2005). Cartesian Genetic Programming (CGP)
(Miller, 2011), which was initially designed to evolve
gate-level combinational circuits, is an evolutionary
algorithm that represents programs or circuits as di-
rected acyclic graphs, providing a flexible and effi-
cient way to encode and manipulate solutions to vari-
ous problems. DCGP is an enhanced form of CGP,
which uses two levels of evolution. The first level
identifies the best solution in the search space with the
most negligible hazards. Three types of hazards could
be found here: static hazard, which occurs when a sig-
nal changes twice in a row while it should change only
once; dynamic hazard, which occurs when a signal
changes several times in a row while it should change
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
224

only once; and functional hazard, which usually oc-
curs when two inputs change simultaneously. The
second level of evolution aims to eliminate any such
pending hazards. Involving two evolutionary stages,
the proposed work cannot provide an end-to-end auto-
matic system to generate problem-specific sequential
circuits.
(Liang et al., 2009) presented a 3-stage decom-
position system for the evolution of complex sequen-
tial circuits where the sequential circuit is decom-
posed into state decomposition, input decomposition,
and output decomposition. Each stage is separately
evolved using ES. They have evolved a series of se-
quential logic circuits from the Microelectronics Cen-
ter of North Carolina (MCNC) benchmark library.
However, they evolved the circuits at the gate level,
which is not scalable to complex and large circuits.
Additionally, no circuits were evolved using single-
stage direct evolution, unlike in this work.
In another work, a 7-bit sequence signal generator
was evolved (Zhiwu et al., 2011) using a fully con-
nected feed-forward neural network, where gates such
as XOR and NAND served as basic modules, and
then the primary circuits were built on top of them.
This work used the GA to evolve this neural network
through which the signal generator was created.
Over time, (Xiong and Rafla, 2009), (Tao et al.,
2012), (Majeed. et al., 2023), and (Majeed et al.,
2023) presented their work on the automatic gener-
ation of Sequence Detectors (SDs) through evolution-
ary methods. SDs are crucial in digital systems and
can be used to trigger alarms when sensing a specific
sequence. They are also used to detect the specific
sequence of events and keep track of them. Of these
works, only our previous works (Majeed. et al., 2023)
and (Majeed et al., 2023) evolved the circuits at the
behavioural level, while all others evolved them at the
gate level.
No previous work has attempted to evolve FFs
from the perspective of an FSM. However, FFs are
the modules for many EA- or other ML-based sequen-
tial circuit designs and synthesis since they are the
essential memory elements in any sequential circuit.
It makes them equally important to be evolved since
they can save area, power, delay, and, most impor-
tantly, the design time and effort for complex circuits
if evolved than using a human-designed or hardcoded
module.
In (Manovit et al., 1998), the gate level code of
the FSM of a 3-bit UDC (mentioned as Reversible 8-
counter in their work) along with some other sequen-
tial circuits such as a serial adder and frequency di-
vider was evolved, presented with enhanced correct-
ness (Chongstitvatana and Aporntewan, 1999). It was
evolved online on an Field Programmable Gate Array
(FPGA) (Aporntewan and Chongstitvatana, 2001) us-
ing a GA. In a later work, another 3-bit Up counter
was evolved at the gate level using GA (Soliman and
Abbas, 2004). They evolved it using two different
techniques; in the first round, they evolved just the
combinational part, while the entire sequential circuit
evolved in the second. No counter in these works has
evolved on a behavioural level from the perspective of
an FSM, which means that, specifically, an FSM has
not evolved.
The work shown in (Lucas and Reynolds, 2003)
evolves the transition matrix of an elevator using ES
and shows that their work outperforms the Evidence-
Driven State Merging (EDSM) algorithm, which is
considered a premium FSM learning algorithm. An
FSM was evolved in (Tsarev and Egorov, 2011) using
a genetic algorithm that caters to control the doors
of an elevator system. This FSM has three states,
five different kinds of inputs, two outputs, and seven
transitions. However, this work does not evolve any
gate or behavioural level code for this FSM. Multiple
works are shown for either run-time or offline ML-
based fault diagnosis of elevator systems such as (Bao
et al., 2012) and (Zhang et al., 2022). Also, many
works are shown on either manual or automatic opti-
mization of elevator control and performance, such as
(Markon et al., 2006) and (Pham et al., 2015). How-
ever, no work has automatically generated either the
gate level or behavioural level code for the elevator
FSM through evolution or any other method.
In this work, we propose the GE-based evo-
lution of the synthesizable behavioural level HDL
codes of the FSMs of three crucial sequential cir-
cuits named JK-FF, 3-bit UDC, and 8FE using spe-
cially designed training and test data sets (explained
in Section 4). To the authors’ knowledge, this is
the first work to evolve these sequential circuits us-
ing GE. In addition, all the circuits in this work
are evolved using single-stage evolution on the be-
havioural level, so none of the Divide-and-Conquer
techniques, such as Bidirectional Incremental Evo-
lution (BIE) (Kalganova, 2000), or any Generalised
Disjunction Decomposition (GDD) (Stomeo et al.,
2006) are used in this work. This work emphasises
evolving the behavioural-level code and not the gate-
level code due to the scalability issues faced in gate-
level codes while designing a complex system. De-
signing complex circuits using gate-level codes at one
stage becomes almost impossible due to the expo-
nential growth of gate-level instances with increased
complexity in digital circuits. Such lengthy gate-level
codes are too challenging to handle when fixing bugs
and making modifications.
Grammatical Evolution of Synthesizable Finite State Machine-Based Behavioural Level Hardware Description Language Codes
225

3 GRAMMATICAL EVOLUTION
GE (Ryan et al., 1998) employs BNF grammars to
map genotypes to phenotypes. BNF is a formal no-
tation used to describe the syntax of programming
languages, data structures, and communication pro-
tocols. It provides a way to express the rules for the
structure of a language in a precise and unambigu-
ous manner. In BNF, a language is defined through
a series of production rules, each specifying how
a particular syntactic element can be composed of
other elements. Utilizing context-free grammar, GE
evolves structures/objects in any programming lan-
guage. Successful applications include combinational
(Youssef et al., 2021) and sequential circuit design
(Majeed. et al., 2023), symbolic regression (Ali et al.,
2021), and classification (Murphy et al., 2021). GE
can generate HDL codes for circuits, enabling analy-
sis of efficiency and power/hardware usage.
BNF grammars consist of a four-tuple <
N, T, P, S >. That is a set of non-terminals N, which
act as placeholders that can be expanded into other
symbols. T represents the set of terminal symbols,
which are the concrete symbols or tokens of the lan-
guage and cannot be further expanded. P is a set of
production rules (also called rules) that replace a N
with another N or T . Finally, S is the starting symbol,
which is a specific N from which the mapping starts.
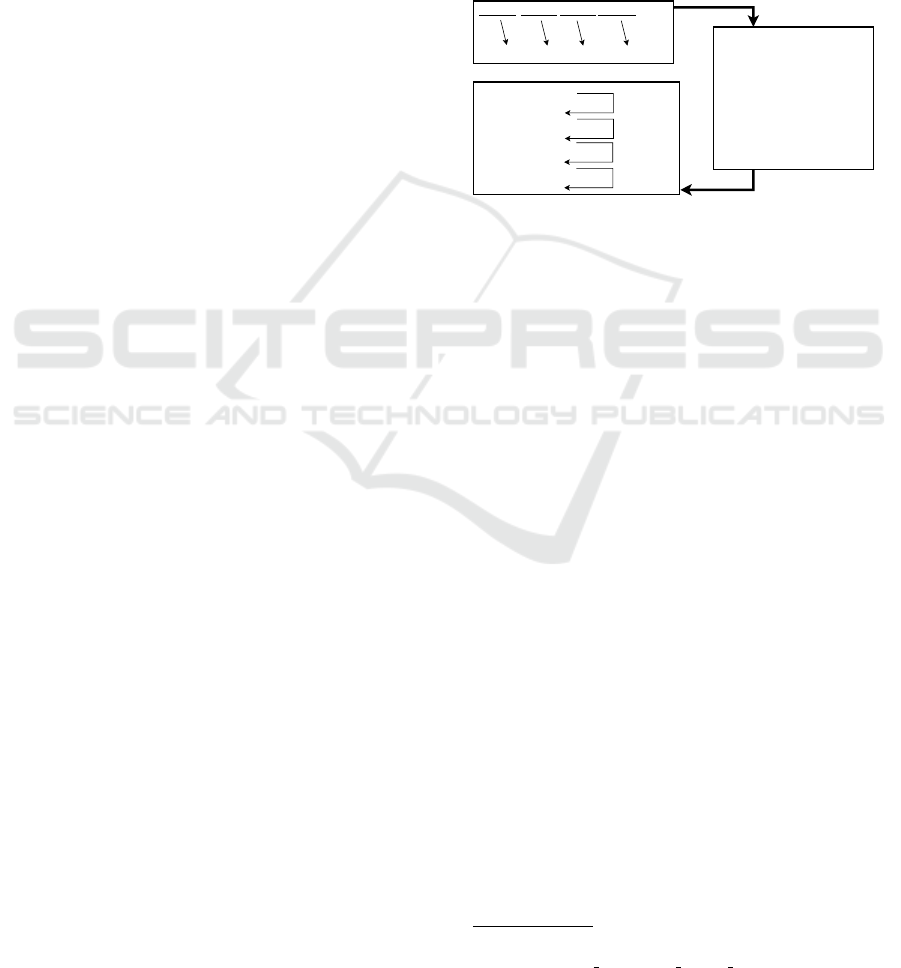
We have three rules in the example shown in Fig-
ure 4 where N are the grammar parts found on either
side of equality, which can be further mapped to a
symbol, such as <var> (on the RHS of the first P
and the LHS of the third P in the example), which is
further mapped to T . In contrast, T , as mentioned be-
fore, cannot be further mapped and appears only on
the right side, e.g., ‘!’ and ‘ & ’ in the RHS of the sec-
ond P. In the example shown here, leftmost <exp> in
the first P serves as S.
The example shown in Figure 4 illustrates the
genotype to phenotype mapping at the gate level
for HDL circuit design. Each 8-bit chunk, such as
‘00101000’, is converted to the respective decimal,
‘40’ in this case, and decimal values expand the P of
grammar until expressions with only T are reached.
The example depicts logic gate generation between
input variables x and y, yielding AND, OR, and NOT
gates as options. It can be seen that starting from the
first rule, a modulus of ‘40’ is computed with ‘2’ since
there are only two options available in that rule on the
RHS separated by ‘|’. As a result of ‘40%2’ equal
to ‘0’, the first option available on the RHS of that
rule is selected. Now, suppose this selected option is
comprised of more than one N. In that case, the left-
most will be expanded first, and to expand that N, the
modulus of the following decimal (coming from the
next chunk of 8-bits) will be computed with the num-
ber equal to the available options on the RHS of the
rule used to map this N. This process continues un-
til an expression has only T in it. Note that the NOT
gate, denoting inversion, can only be applied to a sin-
gle variable (e.g., !x). The final expression in this ex-
ample implies an OR gate between the circuit’s input
variables, x and y, with a detailed explanation avail-
able for this example in our previous work (Majeed.
et al., 2023).
00101000 01110110 01111100 10001001 .............
     40     118     124      137 .............
Binary String
 <exp> ::= <var <op> <var>
           | <op> <var>

  <op>  ::= "&"
     | "|"
    | "!"
  <var>  ::= "x"
    | "y"
(0)
(1)
(0)
(1)
(2)
(0)
(1)
BNF Grammar
(A)
(B)
(C)

 <exp>
 <var> <op> <var>
   x  <op> <var>
  x    |  <var>
   x    |    y
40 % 2 = 0
118 % 2 = 0
124 % 3 = 1
137 % 2 = 1
Mapping
Figure 4: Genotype to phenotype mapping in GE.
4 TRAINING AND TEST
DATASET GENERATION
The data set used in this work comprises specialized
exhaustive training cases where the system is set to
a specific state of its FSM and then examined sepa-
rately for random and shuffled as well as a minimal
required combination of all the inputs. For example,
in the case of the 8FE, the system is set to its first
state (S0) and then checked for the random inputs
such as [0101101001xx1010] (shown in the data set
diagram given in the Supplementary Material (SM)
1
where ‘0’ reflects move up a floor, ‘1’ reflects move
down a floor, and ‘x’ reflects stay on the same floor).
After a reset of the whole system, the system is again
set to S0 and checked for a minimum and in-lined re-
quired combination to complete a clockwise and anti-
clockwise cycle such as [0000x0001111x111], which
checks its whole cycle from Floor-0 to Floor-7 and
then back to Floor-0 from Floor-7. The inputs shown
as ‘x’ check the system for unfortunate conditions
where the input system can fail or if the system is in
the idle state. In such a case, the elevator will stay on
the same floor, or for this kind of input, the counter
will stay in the same state until reset is applied. The
same approach is used for the training data set of 3-
bit UDC. The training data set of JK-FF is different
1
Supplementary Material: https://github.com/
bmmajeed/Basic Sequential CKTS ECTA24
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
226

since we take its initial state from the training case as
well, but we cover all the maximum input combina-
tions according to the values of ‘j’ and ‘k’, which are
40 in total (shown in Table 1). However, taking the
maximum input combinations for the other two cir-
cuits is impossible since they involve random inputs,
including ‘x’, to mimic their real-life usage.
According to the minimum requirement of the
training dataset, the number of used training/test cases
and the length of each case are shown in Table 1 for
JK-FF, 3-bit UDC, and 8FE, respectively. Note that
for all three circuits, as shown in Table 1, the length of
the training vector is one bit larger than the test vector
since we are not setting the system to a specific state
in the test dataset. This extra bit is only used for the
exhaustive training of the system, so it can be trained
practically to take a perfect start from any state at any
time.
Table 1: Size and length of train/test data set used for evo-
lution.
Circuits
No. of Train/
Test Vectors
Each Vector’s
Length in bits
Training Test
JK-FF 40 5 4
UCD 80 6 5
8FE 128 6 5
The advantage of this approach can be seen in the
results in Table 3 and Table 4, which show that all
solutions evolved using the training data set perform
excellently on the unseen test data set, which has the
same structure but does not have the one bit used to
set the system at a specific state only for training. It
is a significant step forward compared to the results
shown in the complex sequential circuits’ FSM evo-
lution given in our previous works (Majeed. et al.,
2023) and (Majeed et al., 2023), where the perfect
success rate on the test dataset was never achieved for
sequential circuits’ evolution.
5 EXPERIMENTS AND RESULTS
5.1 Experimental Setup, Tools, and
Evolutionary Parameters
Each of the three circuits is evolved using two
different BNF grammars, G1 Type Grammars and
G2 Type Grammars, which present constrained (G1
Type Grammars) and unconstrained spaces (G2 Type
Grammars). G1 Type Grammars evolve five parts of
the HDL sequential code: the present state, input vari-
ables, input values, output values, and the next state
.
.
<set_state> ::=
"if (state_in || !state_in)
state = state_in;
else \n\t\t\t
state = state;"
<states_block> ::=
"if (state == "<states>")
begin
q = "<values>";"
<conditional> "end"
.
.
<conditional> ::=
"if ("<vars>" == "<values>")
state = "<states>";
else
state = "<states>";"
.
.
<vars> ::= "j" | "k"
<states> ::= "S0" | "S1"
<values> ::= "0" | "1"
Figure 5: BNF grammar having full structure of the HDL
code for FSM to evolve the current state, input variables,
input values, output values, and the next state of JK-FF.
of the system. The G1 Type Grammars used for JK-
FF (Figure 5) show that the structure of nested if-
else statements in this grammar is given to the sys-
tem to implement the FSM, and the specified bits are
evolved. This grammar is used to evolve JK-FF, but
the same structure and approach are used to evolve
the 3-bit UDC and 8FE. G2 Type Grammars are much
more general grammars that evolve the entire if-else
code structure from scratch.
In both grammars, <set state> is used to set the
system at a specific state (discussed in detail in Sec-
tion 4) after each reset, and then the system starts
from there by giving the values of ‘j’ and ‘k’ as in-
puts. Note that after taking the input, ‘0’ or ‘1’ for
the current state (‘state-in’) from the first training case
and setting the system to that state, this input is set
to ‘x’ (don’t care) in all the remaining training cases
until the next reset of the system since this input is
just used in first clock cycle to put the system in that
specific state. The mapping in both grammars starts
from <states block> where it can be seen in Figure 5
that the structure of if else-if is hardcoded in G1 Type
Grammars. At the same time, the conditionals of if
and else-if, which are values of the current states, and
the input variables (‘j’ and ‘k’) and input values (‘0’
Grammatical Evolution of Synthesizable Finite State Machine-Based Behavioural Level Hardware Description Language Codes
227

.
.
<states_block> ::= <if> <else> | <if> <else_ifs> <else>
<else_ifs> ::= <else_if> | <else_if> <else_ifs>
<if> ::= "if ("<lhs1>" == "<rhs>") begin"
<op_options> "
end" |
"if ("<lhs1>" == "<rhs>") begin"
<op_options>
<states_block> "
end"
.
.
<op_options> ::= <lhs2>" <= "<rhs>";" | <lhs2>" <= "<rhs>";"
<lhs2>" <= "<rhs>";"
<lhs1> ::= "j" | "k" | "q" | "state"
<lhs2> ::= "q" | "state"
<rhs> ::= "0" | "1" | "S0" | "S1" | "j" | "k" | "q"
Figure 6: BNF grammar evolving the HDL code’s full structure in addition to the current state, input variables, input values,
output values, and the next state for an FSM of JK-FF.
and ‘1’) are evolved. In addition, the values of output
‘q’ and the next state are also evolved using G1 Type
Grammars.
In contrast, using G2 Type Grammars, the system
evolves its whole nested if else-if structure and the
appropriate conditionals and assignments, as seen in
Figure 6. <rhs>, which represents the RHS of con-
ditionals of if and else-if as well as of assignments
coming from <op options>, is the same wherever it
is applied. However, the LHS is not the same and is
divided in <lhs1> and <lhs2>. <lhs1> is used in the
conditionals where ‘j’ and ‘k’ can come on the LHS
of assignment since we are evaluating their value, but
they cannot become a part of <lhs2> since they are
defined as inputs and cannot be assigned as outputs
of the circuit. If a circuit tries to do so, the system
gives a syntax error and discards the phenotype. In
contrast, <rhs> holds all the values and variables that
can fit everywhere on the RHS of any assignment or
conditional. Since all three FSMs evolved here have
two states only, the RHS is happy to use the values of
‘S0’ and ‘S1’ as 1-bit ‘0’ and 1-bit ‘1’ (can be seen in
Figure 9). If we use the same production rule in some
more complex systems, which involve more than two
states, then it might not take the state parameter hav-
ing a 2-bit value of ‘11’ at the RHS when LHS is de-
fined to have a 1-bit value only.
To evolve the HDL codes for JK-FF, 3-bit UDC,
and 8FE, an experimental setup was used, combining
libGE (a C++ library for GE mapping) with Icarus
Verilog, a simulator for Verilog/SystemVerilog, to
evaluate the individuals. All experiments were run
on a Dell OptiPlex 5070 Desktop computer compris-
ing a single unit RAM of 16 GB, 1 TB HDD, and 256
GB SSD. It has a 64-bit quad-core 9th generation i7
processor with a 12MB cache processor.
For all the experiments, the evolutionary parame-
ters which are kept the same are shown in Table 2. All
experiments with the G1 Type Grammars use a popu-
lation size of 100, and this parameter is only increased
when required to get a better success rate for the 8FE,
as shown in Table 3.
Table 2: Evolutionary parameters.
Parameter Value
No. of Runs 30
Initialisation Sensible
Crossover Probability 0.9 (One Point)
Mutation Probability 0.01
Parent Selection Tournament
Elitism Yes
Due to the ample search space of G2 Type Gram-
mars, a larger population size of 1000 was used. Ta-
ble 4 shows that JK-FF did not evolve even with
this population size, so the maximum generations and
population size were increased where required. For
all the circuits, the maximum generations in the ini-
tial experiments using G1 Type Grammars were set
to 30. In contrast, for experiments using G2 Type
Grammars, this value was set to 60 and only increased
where the error bars on the resulting graph showed
room for significant improvement. In Table 3 and Ta-
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
228

ble 4, the blue colour indicates the success rate on the
training data set out of 30 runs, while the bold green
colour indicates the success rate on the test data set
out of the perfect solutions captured on the training
data set.
For all the experiments with both types of gram-
mar, a success rate equal to or better than 26/30 is con-
sidered good enough and acceptable. It means that if
in 26 runs out of the 30 runs, we have evolved a per-
fect solution according to the training data set, we do
not have to increase the number of individuals (max-
imum generations or population size) to get a better
success rate than this. Not Needed (NN) is mentioned
in Table 3 and Table 4 to indicate that the acceptable
success rate is achieved and there is no need to run
more experiments.
5.2 Evolution of the Circuits Using G1
Type Grammars
As described in section 5.1, the first part of the experi-
ments ran for this work evolves the current state of the
system, the input variables and their values, the out-
put of the system, and the following states, using the
structure of G1 Type Grammars. Population sizes of
100 and a maximum of 30 generations were used for
the three circuits’ starting points. Each experiment is
run 30 times, and the success rates are presented ac-
cordingly, where the success rate reflects the number
of runs in which the system produced a perfect solu-
tion.
For JK-FF, it can be seen in Table 3 that a high
success rate of 29/30 is achieved. Since this is a high
success and the resulting graph (all graphs discussed
in this paper refer to the mean of maximum fitness
values across generations) showed no progress in the
evolution of the individuals due to the tiny error bars,
no more experiments were run in this case.
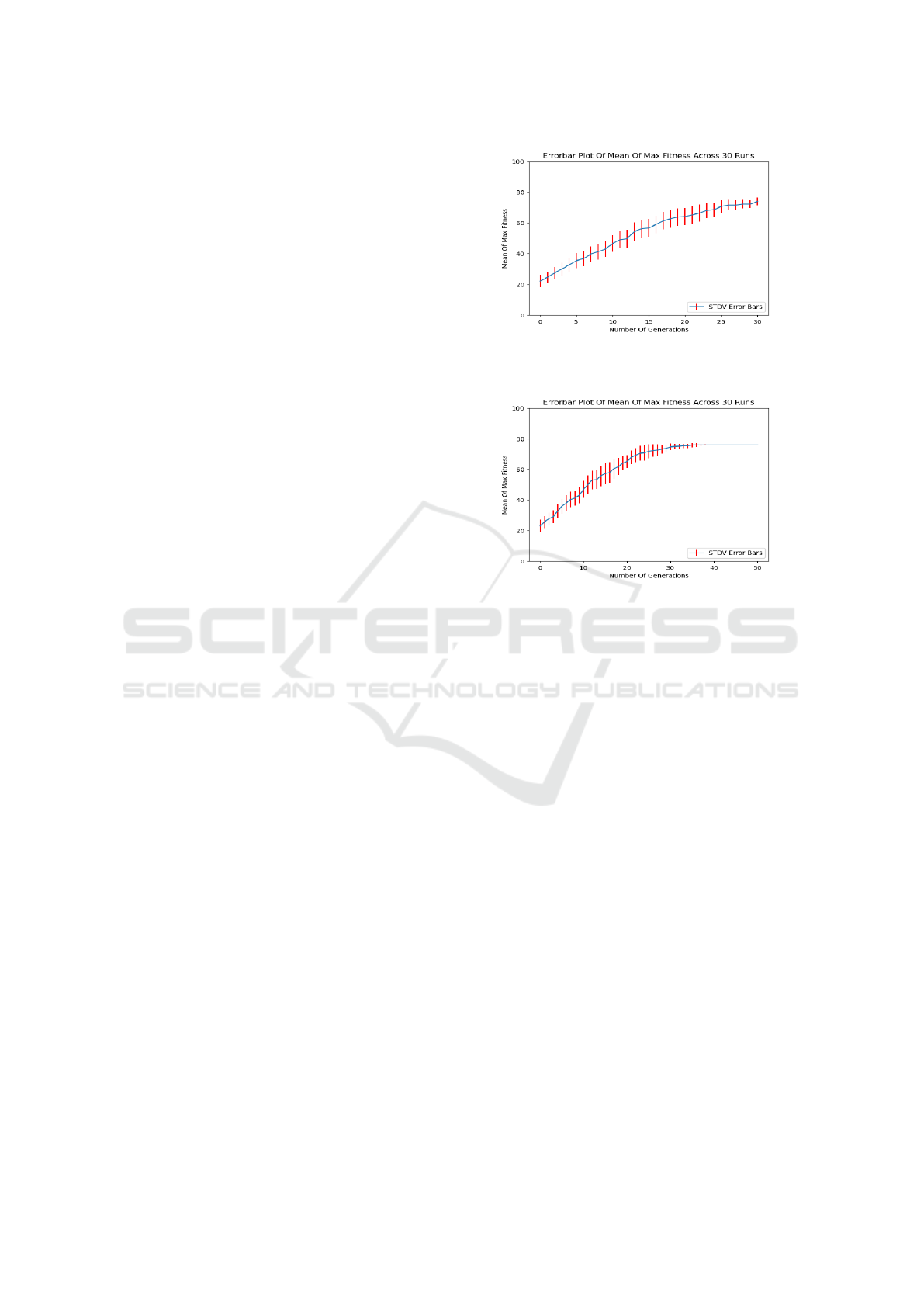
For 3-bit UDC, with a population size of 100 and
30 generations, a success rate of 20/30 was achieved.
The resulting graph (Figure 7) showed no ongoing
progress through the significantly lengthened error
bars. The second experiment was run with 50 gen-
erations, and a success rate of 26/30 was achieved to
improve the score. Since the resulting graph (shown
in Figure 8) showed no progress, and the success rate
was good enough, no experiments were run further.
For the 8FE, with the population size of 100 and
30 generations, only two solutions were found out of
30 runs, so the number of generations was increased
to 50 and 100, respectively. Still, a maximum suc-
cess rate of 17/30 was achieved. The population was
increased to 500 to improve the success rate, which
increased to 30/30.
Figure 7: Mean of the best fitness values across generations
recorded in the evolution of UDC using G1 Type Grammar
with max. of 30 generations.
Figure 8: Mean of the best fitness values across generations
recorded in the evolution of UDC using G1 Type Grammar
with max. of 50 generations.
Since a success rate equal to or higher than 26/30
is considered good enough in this work, the computa-
tional cost in terms of time taken for the evolution to
hit this success rate for the relevant circuits is shown
in Table 5.
For all the experiments, all evolved solutions per-
formed flawlessly on the test data set, which is one of
the perks of using the method proposed to design the
training data set.
5.3 Evolution of the Circuits Using G2
Type Grammars
As noted in Section 5.1, the experiments ran using
G2 Type Grammars employed a starting population
size of 1,000. With 60 generations, the success rate
08/30 was achieved for the JK-FF, so the number of
generations was increased until we got no progress in
the graph at the maximum generations of 300. After
that, the population size was increased to 2000, and
with the maximum generation of 150, a success rate
of 27/30 was achieved (shown in Table 4), which was
good enough, so no experiments were run further. An
example code of a fully evolved sequential block of
JK-FF using G2 Type Grammar is shown in Figure 9.
Note that since the FSM used for this circuit is a 2-
Grammatical Evolution of Synthesizable Finite State Machine-Based Behavioural Level Hardware Description Language Codes
229

Table 3: Results of evolved circuits using G1 Type Grammars, shown according to the number of generations and population
size. (STrD: Success rate on training data set; STeD: Success rate on test data set of evolved solutions; NN: Not Needed).
Pop. Size = 100 Pop. Size = 500
Max. Gens. = 30 Max. Gens. = 50 Max. Gens. = 100
Circuit
STrD
STeD
STrD
STeD
STrD
STeD
STrD
STeD
JK-Flip Flop 29/30 29/29 NN NN NN NN NN NN
Up-Down Counter 20/30 20/20 26/30 26/26 NN NN NN NN
8-Floor Elevator 02/30 02/02 09/30 09/09 17/30 17/17 30/30 30/30
Table 4: Results of evolved circuits using G2 Type Grammars, shown according to the number of generations and population
size.
Circuit
Pop. Size = 1,000 Pop. Size = 2,000
Max. Gens. = 60 Max. Gens. = 150 Max. Gens. = 300 Max. Gens. = 150
STrD STeD STrD STeD STrD STeD STrD STeD
JK-Flip Flop 08/30 08/08 16/30 16/16 21/30 21/21 27/30 27/27
Up-Down Counter 27/30 27/27 NN NN NN NN NN NN
8-Floor Elevator 15/30 15/15 29/30 29/29 NN NN NN NN
Table 5: Time taken by the evolution of the circuits to hit a
good enough success rate on the training dataset.
Circuit STrD
No. of
Individuals
Time
(secs)
G1
JK 29/30 15,000 6.15
UDC 26/30 25,000 19.62
8FE 30/30 50,000 659.67
G2
JK 27/30 300,000 4187.75
UDC 27/30 60,000 528.91
8FE 29/30 150,000 5075.67
state machine and according to the code definitions of
states ‘S0 = 0’ and ‘S1 = 1’, you can see that ‘S0’ and
‘S1’ can be seen at the RHS of some assignments as
well which are reflecting their 1-bit values of ‘0’ and
‘1’ respectively.
For 3-bit UDC, the first experiment with a popula-
tion size of 1,000 and 60 generations achieved a suc-
cess rate of 27/30, which is a high and good success
rate, so no further experiments were run.
In the case of the 8FE, the first experiment with
a population size of 1,000 and 60 generations gave a
success rate of 15/30. The number of generations was
then increased to 150, giving a success rate of 29/30,
which is an acceptable success rate, so no further ex-
periments were run. The time taken for the evolution
to get an acceptable success rate for the relevant cir-
cuit is shown in Table 5.
Comparison of our evolutionary work presented in
this work with either state-of-the-art presented works
or works which are similar to some extent is shown
in Table 6. This comparison is shown in terms of the
evolutionary approach used in the work, the form or
parts of the evolved design, the design type, and the
number of individuals used per run during the evo-
lution. Since there is no work shown in the literature
where JK-FF evolved from the perspective of an FSM,
we are unable to compare it with any other work. 3-bit
always @(posedge clk) begin
if(!rst) begin
if (state == 0) begin
q <= k;
q <= S0;
if (j == S1) begin
state <= 1;
end
else begin
q <= S0;
end
end
else if (state == k) begin
q <= 1;
state <= S0;
end
else begin
q <= S1;
end
end
else begin
q <= 0;
state <= S0;
end
end
Figure 9: Fully evolved code of JK-FF using G2 Type
Grammar.
UDC is compared to state-of-the-art works presented
in the literature, and it can be seen that this is the first
work which has evolved the complete FSM of 3-bit
UDC on a behavioural level using the minimum indi-
viduals comparatively. A complete FSM for 8FE or
any floor elevator has not evolved before. However,
the evolution of 8FE is compared to a 7-state Discrete
Finite Automata (DFA) of a floor elevator and is also
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
230

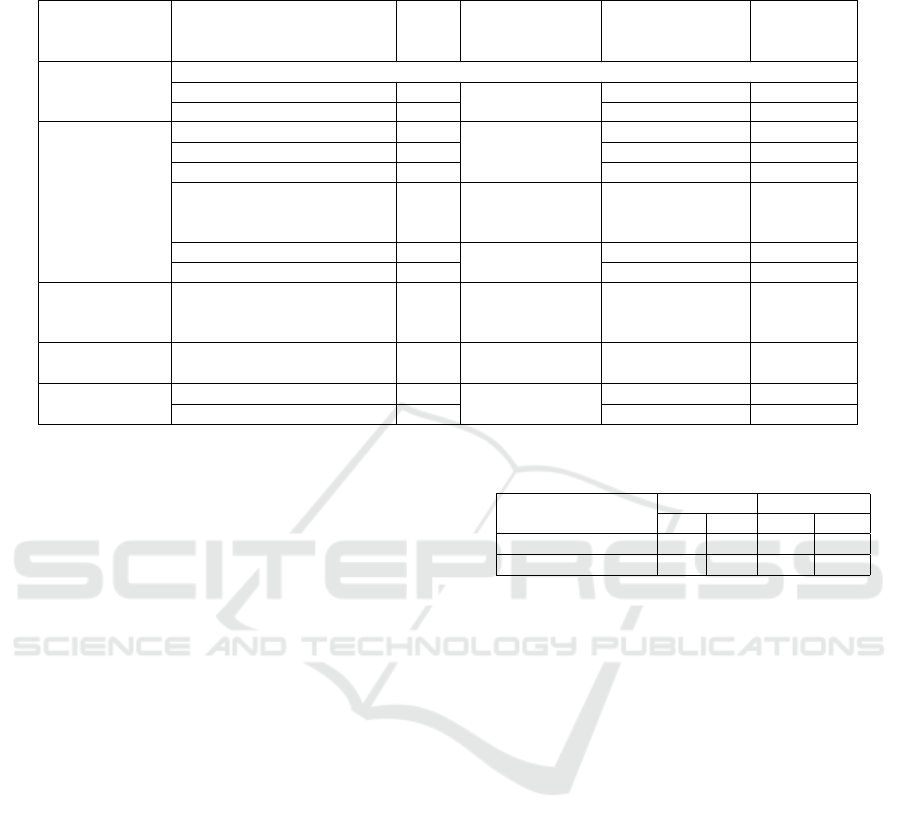
Table 6: Comparison with the state-of-the-art or somewhat similar works. (PCE: Partial code evolved; FCE: Full code
evolved).
Circuit Work
Evol.
appr.
used
Evolved
form/parts
of design
Design type
Number of
indiv. used
per run
No comparison given in literature
This work (PCE) GE Behavioral-level 3,000JK-FF
This work (FCE) GE
Complete FSM
Behavioral-level 300,000
Manovit et al., 1998 GA Gate-level 5,500,000
Chongstitvatana et al., 1999 GA Gate-level 5,000,000
Aporntewan et al., 2001 GA
State transition
functions
Gate-level 6,400,000
Soliman et al., 2004 GA
Combinational
and sequential
cells
Gate-level 150,000
This work (PCE) GE Behavioral-level 5,000
3-bit UDC
This work (FCE) GE
Complete FSM
Behavioral-level 60,000
DFA of floor
elevator
(not a circuit)
Lucas et al., 2003 ES
Transition
matrix
- 1,000,000
Elevator door
control circuit
Tsarev et al., 2011 GA Complete FSM - 2,000
This work (PCE) GE Behavioral-level 50,000
8FE
This work (FCE) GE
Complete FSM
Behavioral-level 150,000
compared to a 6-state elevator door control unit. It
is highlighted that this work is the first to evolve any
floor elevator using GE on a behavioural level.
6 SYNTHESIS COMPARISON OF
GOLD AND EVOLVED
CIRCUITS
This section evaluates the performance of synthesised
circuits to demonstrate how well they compare with
Gold circuits on actual silicon. Circuits meeting an
acceptable success rate in G1 and G2 Type Grammars
are selected for synthesis. Genus Synthesis Solution
by Cadence uses GPDK 45, 90, and 180 nm Comple-
mentary Metal-Oxide Semiconductor (CMOS) tech-
nologies for synthesis. The circuits operate at a clock
frequency of 100 MHz, with the reset signal config-
ured to the ideal network in the constraints file. Syn-
thesis is conducted at the Fast Corner (FC) and Slow
Corner (SC) for all technologies. FC represents opti-
mal operating conditions with factors like supply volt-
age and temperature at their most favourable, while
SC simulates worst-case conditions with lower sup-
ply voltage or higher temperature. Table 7 provides
details on temperature and supply voltage.
Since the complete synthesis reports contain ex-
tensive detail, a summary is provided in Table 8. This
summary presents the percentage by which the per-
formance of the evolved solutions’ synthesis reports
is better or worse than that of the Gold circuits. Per-
centages highlighted in bold and green indicate that
Table 7: Nominal temperature and supply voltage for rele-
vant technologies.
Parameters
90 nm 180 nm
FC SC FC SC
Temperature (°C) 0 125 0 125
Voltage (V) 1.1 0.9 1.98 1.62
the synthesis solutions of the evolved circuits out-
performed the Gold circuits in terms of circuit area
(cell count) and Power-Delay Product (PDP). Red in-
dicates that the performance of the evolved circuits
is worse than the Gold circuits, while blue signifies
equivalent performance.
The summary table reveals that the evolved cir-
cuits of JK-FF generally performed on par with the
Gold circuits based on the best values taken from
the group of solution circuits in terms of both area
and PDP. While the synthesis reports for UDC show
that the evolved UDC circuits did not perform as
well as the evolved JK-FF circuits, they still matched
or surpassed the Gold UDC circuits over 70% of
the time overall. However, the synthesis reports for
8FE indicate significantly improved performance of
the evolved 8FE solutions compared to the other two
evolved circuits, with evolved values surpassing the
Gold circuits more than 95% of the time. Given that
8FE is a complex, real-world circuit, its superior syn-
thesis performance underscores the credibility of us-
ing such a system for automatically synthesizable dig-
ital sequential design using HDL.
Grammatical Evolution of Synthesizable Finite State Machine-Based Behavioural Level Hardware Description Language Codes
231

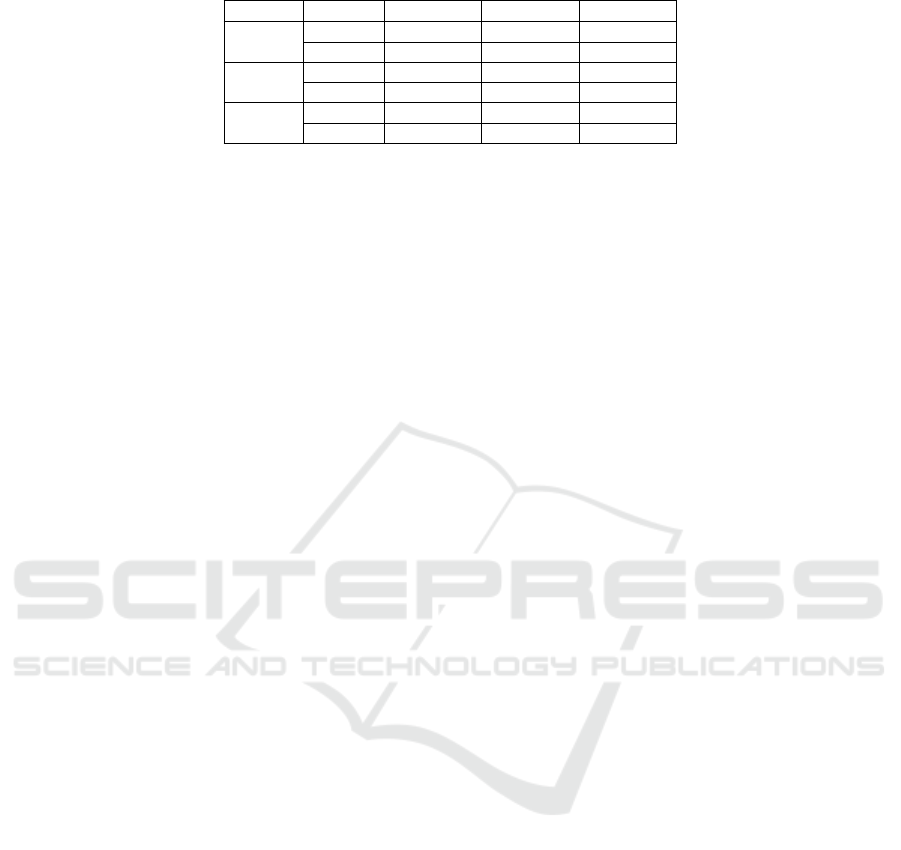
Table 8: Summary of the synthesis reports showing the performance of synthesized solutions in percentages.
Circuit Param. 45 nm 90 nm 180 nm
Area (50+50)% 100% 100%
JK-FF
PDP 100% 100% (50+50)%
Area 100% (50+50)% (50+50)%
UDC
PDP (75+25)% (50+50)% (50+50)%
Area 100% (75+25)% 100%
8FE
PDP 100% 100% 100%
7 CONCLUSION AND FUTURE
WORK
The automatic partial and complete HDL code gener-
ation of three digital sequential circuits, JK-FF, 3-bit
UDC, and 8FE, from the perspective of FSM, is pre-
sented here using GE as the ML engine on two differ-
ent kinds of grammars for each circuit labelled as G1
Type Grammars and G2 Type Grammars. In addition,
evolved solutions of all three circuits are synthesised
to show that all the evolved circuits are perfectly syn-
thesizable. This work uses a specialised method to
generate training data sets, which gives a one hun-
dred percent performance of evolved solutions on the
unseen test data set. To the best of the author’s knowl-
edge, this is the first work that has evolved some of the
highly used and crucial sequential circuits/modules
from the perspective of an FSM, such as JK-FF, an
essential memory element for digital circuits, as they
could not find any work in literature which has done
this. Also, this is the first work to evolve the full
and partial synthesizable codes of all these three cir-
cuits on a behavioural level from the perspective of an
FSM using an end-to-end automated system involving
just one evolutionary stage. Future work will focus
on evolving synthesizable full and partial HDL codes
of more complex sequential circuits through the pro-
posed system and the technique of training data set
generation.
ACKNOWLEDGMENTS
This work was supported by the Science Foundation
Ireland (SFI) grant 16/IA/4605.
REFERENCES
Ali, M., Kshirsagar, M., Naredo, E., and Ryan, C. (2021).
Towards automatic grammatical evolution for real-
world symbolic regression. In Proceedings of the 13th
International Joint Conference on Computational In-
telligence - Volume 1: ECTA,, pages 68–78. INSTICC.
Aporntewan, C. and Chongstitvatana, P. (2001). An on-line
evolvable hardware for learning finite-state machine.
In Proceedings of International Conference on Intelli-
gent Technologies.
Bao, J. et al. (2012). Fault diagnostic method of elevator
control system based on finite state machine. Journal
of Computer Applications, 32(06):1692.
Cadence (1998). Cadence design systems.
https://www.cadence.com/.
Chongstitvatana, P. and Aporntewan, C. (1999). Improv-
ing correctness of finite-state machine synthesis from
multiple partial input/output sequences. In Proceed-
ings of the First NASA/DoD Workshop on Evolvable
Hardware, pages 262–266.
Ciletti, M. D. (2010). Advanced Digital Design with the
Verilog HDL. Prentice Hall Press, USA, 2nd edition.
Eagle (1988). Eagle by autodesk. https://www.autodesk.
com/products/eagle/overview. [Online; accessed 09-
Jan-20242].
Hemmi, H., Mizoguchi, J., and Shimohara, K. (1996).
Development and evolution of hardware behaviors.
In Sanchez, E. and Tomassini, M., editors, Towards
Evolvable Hardware (TEH), pages 250–265, Berlin,
Heidelberg. Springer Berlin Heidelberg.
Kalganova, T. (2000). Bidirectional incremental evolu-
tion in extrinsic evolvable hardware. In Proceedings.
The Second NASA/DoD Workshop on Evolvable Hard-
ware, pages 65–74.
Kicad (1992). Kicad electronic design automation. https:
//www.kicad.org/. [Online; accessed 09-Jan-20242].
Klimovich, A. S. and Solov’ev, V. V. (2010). Transfor-
mation of a mealy finite-state machine into a moore
finite-state machine by splitting internal states. Jour-
nal of Computer and Systems Sciences International,
49(6):900–908.
Koza, J. R. (1992). Genetic Programming: On the Pro-
gramming of Computers by Means of Natural Selec-
tion. MIT Press, Cambridge, MA, USA.
Liang, H., Luo, W., and Wang, X. (2009). A three-step
decomposition method for the evolutionary design of
sequential logic circuits. Genetic Programming and
Evolvable Machines, 10(3):231–262.
Lucas, S. and Reynolds, T. (2003). Learning dfa: evolution
versus evidence driven state merging. In The 2003
Congress on Evolutionary Computation, 2003. CEC
’03., volume 1, pages 351–358 Vol.1.
Majeed, B., Carvalho, S., Dias, D. M., Youssef, A., Mur-
phy, A., and Ryan, C. (2023). Performance upgrade of
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
232

sequence detector evolution using grammatical evo-
lution and lexicase parent selection method. In Col-
let, P., Gardashova, L., El Zant, S., and Abdulkari-
mova, U., editors, Complex Computational Ecosys-
tems, pages 90–103, Cham. Springer Nature Switzer-
land.
Majeed., B., Ryan., C., McEllin., J., Youssef., A., Dias.,
D., Murphy., A., and Carvalho., S. (2023). Evolving
behavioural level sequence detectors in systemverilog
using grammatical evolution. In Proceedings of the
15th International Conference on Agents and Artifi-
cial Intelligence - Volume 3: ICAART, pages 475–483.
Manovit, C., Aporntewan, C., and Chongstitvatana, P.
(1998). Synthesis of synchronous sequential logic cir-
cuits from partial input/output sequences. In Sipper,
M., Mange, D., and P
´
erez-Uribe, A., editors, Evolv-
able Systems: From Biology to Hardware, pages 98–
105, Berlin, Heidelberg. Springer Berlin Heidelberg.
Markon, S., Kise, H., Kita, H., and Bartz-Beielstein, T.
(2006). Optimal control of multicar elevator systems
by genetic algorithms. Control of Traffic Systems in
Buildings, pages 221–233.
Miller, J. F. (2011). Cartesian Genetic Programming, pages
17–34. Springer Berlin Heidelberg, Berlin, Heidel-
berg.
Mirjalili, S. (2019). Genetic Algorithm, pages 43–55.
Springer International Publishing, Cham.
Mizoguchi, J., Hemmi, H., and Shimohara, K. (1994).
Production genetic algorithms for automated hard-
ware design through an evolutionary process. In Pro-
ceedings of the First IEEE Conference on Evolution-
ary Computation. IEEE World Congress on Compu-
tational Intelligence, pages 661–664 vol.2, Orlando,
FL, USA. IEEE.
Morris, M. and Ciletti, M. D. (2007). Digital design. Pear-
son Prentice Hall, New Jersey, USA.
Murphy, A., Murphy, G., Amaral, J., Mota Dias, D.,
Naredo, E., and Ryan, C. (2021). Towards incorpo-
rating human knowledge in fuzzy pattern tree evolu-
tion. In European Conference on Genetic Program-
ming (Part of EvoStar), pages 66–81. Springer.
Navabi, Z. (2007). VHDL: Modular Design and Synthesis
of Cores and Systems. McGraw-Hill, New York.
Pham, T. H., Prodan, I., Genon-Catalot, D., and Lef
`
evre,
L. (2015). Efficient energy management for an ele-
vator system under a constrained optimization frame-
work. In 2015 19th International Conference on Sys-
tem Theory, Control and Computing (ICSTCC), pages
613–618.
Rudolph, G. (2012). Evolutionary Strategies, pages 673–
698. Springer Berlin Heidelberg.
Ryan, C., Collins, J. J., and Neill, M. O. (1998). Gram-
matical evolution: Evolving programs for an arbitrary
language. In European Conference on Genetic Pro-
gramming, pages 83–96, Berlin, Heidelberg. Springer.
Shanthi, A., Singaram, L., and Parthasarathi, R. (2005).
Evolution of asynchronous sequential circuits. In
2005 NASA/DoD Conference on Evolvable Hardware
(EH’05), pages 93–96, Washington, DC, USA. IEEE.
Solido (2005). Solido design solutions. https://eda.sw.
siemens.com/en-US/ic/solido/. [Online; accessed 09-
Jan-20242].
Soliman, A. and Abbas, H. (2004). Synchronous sequen-
tial circuits design using evolutionary algorithms. In
Canadian Conference on Electrical and Computer
Engineering 2004 (IEEE Cat. No.04CH37513), vol-
ume 4, pages 2013–2016 Vol.4.
Spear, C. (2008). SystemVerilog for Verification, Second
Edition: A Guide to Learning the Testbench Language
Features. Springer, New York, 2nd edition.
Stomeo, E., Kalganova, T., and Lambert, C. (2006). Gener-
alized disjunction decomposition for evolvable hard-
ware. IEEE Trans Syst Man Cybern B Cybern,
36(5):1024–1043.
Tao, Y., Cao, J., Zhang, Y., Lin, J., and Li, M. (2012). Using
module-level evolvable hardware approach in design
of sequential logic circuits. In 2012 IEEE Congress
on Evolutionary Computation (CEC), pages 1–8, New
York. IEEE.
Tsarev, F. and Egorov, K. (2011). Finite state machine in-
duction using genetic algorithm based on testing and
model checking. In Proceedings of the 13th annual
conference companion on Genetic and evolutionary
computation, GECCO ’11, page 759–762, New York,
NY, USA. Association for Computing Machinery.
Xiong, F. and Rafla, N. I. (2009). On-chip intrinsic evolu-
tion methodology for sequential logic circuit design.
In 2009 52nd IEEE International Midwest Symposium
on Circuits and Systems, pages 200–203, New York.
IEEE.
Youssef, A., Majeed, B., and Ryan, C. (2021). Optimizing
combinational logic circuits using grammatical evo-
lution. In 2021 3rd Novel Intelligent and Leading
Emerging Sciences Conference (NILES), pages 87–92,
New York. IEEE, IEEE.
Zhang, S., Yin, Q., and Wang, J. (2022). Elevator dynamic
monitoring and early warning system based on ma-
chine learning algorithm. IET Networks, n/a(n/a).
Zhiwu, Z., Jian’an, L., Xinfeng, C., and Liming, Z. (2011).
Design of sequential logic circuits based on evolv-
able hardware. In IEEE 2011 10th International
Conference on Electronic Measurement Instruments
(ICEMI), volume 3, pages 240–243.
Grammatical Evolution of Synthesizable Finite State Machine-Based Behavioural Level Hardware Description Language Codes
233