Exploiting Data Spatial Dependencies for Employee Turnover Prediction
Sandra Maria Pereira
1 a
, J
´
essica da Assunc¸
˜
ao Almeida de Lima
2
, Alessandro Garcia Vieira
2 b
and Wladmir Cardoso Brand
˜
ao
1,2 c
1
Institute of Exact Sciences and Informatics, Pontifical Catholic University of Minas Gerais,
Dom Jose Gaspar Street, 500, Belo Horizonte, Brazil
2
S
´
olides S.A., Tom
´
e de Souza Street, 845, Belo Horizonte, Brazil
Keywords:
Predictive Analytics, Spatial Models, Spatial Dependence, Machine Learning, Turnover Prediction.
Abstract:
Machine learning techniques have been increasingly employed to address problems within the field of human
resources. A significant issue in this domain is predicting employee turnover, related to the probability of an
employee leaving the company. Employee turnover is directly related to the availability of knowledge and
resources that affect the continuity of the company’s goods and services supply. Managing employee turnover
involves multiple areas of expertise, rendering it a complex problem. This article proposes a methodology
to determine whether prediction problems exhibits spatial dependence, thereby demanding the use of spatial
models over non-spatial models for optimal resolution. Experimental results show that significant differences
arise when analyzing correlations that consider the geographical positioning of the data. Particularly, predic-
tion models that use geographic features to predict employee turnover outperform prediction models that do
not use them, with gains ranging from 9.6% to 19.6% in the standard deviation of MAPE, from 5.5% to 10.4%
in MAE, and from 0.99% to 2.9% in RMSE.
1 INTRODUCTION
Complex phenomena often exhibit non trivial be-
havior patterns, testing our ability to predict them.
Highly unlikely events, such as sudden epidemic out-
breaks, demand a careful approach for risk man-
agement (Taleb, 2010). Employee turnover is one
such complex problem, characterized by employees
leaving an organization, resulting in significant gaps
in the qualified workforce and compromising the
company’s productivity and competitiveness (Lazzari
et al., 2022). It stands out due to its multidisciplinary
nature, by focusing on the analysis of behavior and
interpersonal relationships in the workplace, drawing
on knowledge from psychology, computer science,
mathematics, and other disciplines to understand and
anticipate organizational challenges.
Turnover is one of the most significant problem
companies face during their life cycle. Recent stud-
ies on employee turnover prediction using machine
learning often prove the solutions is usually specific
to a particular context, making generalization a chal-
a
https://orcid.org/0009-0006-3926-4603
b
https://orcid.org/0000-0002-9921-3588
c
https://orcid.org/0000-0002-1523-1616
lenging problem (Zhao et al., 2019).
Geosciences studies traditionally focus on phys-
ical phenomena or environmental studies (Dramsch,
2020). The growing relevance of spatial econo-
metrics highlights the importance of understanding
social phenomena with a strong geospatial empha-
sis (Anselin, 2021). This underscores the need to
consider not only the interactions between variables
but also the influence of spatial context in the analysis
and development of computational models.
This article proposes a methodology to assess the
existence of spatial dependencies in prediction prob-
lems, particularly in the employee turnover predic-
tion problem. Experiments were conducted using lin-
ear regression models, spatial and non-spatial data
from Brazilian open government data with the register
of employee’s admissions and terminations. Particu-
larly, one used data from two regions in the Minas
Gerais state in Brazil, between the years from 2018 to
2021, to create comparable results and demonstrate
the existence of such spatial dependencies.
Experimental results show significant gains in all
analyses performed on the georeferenced datasets.
Notably, prediction models that use geographic fea-
tures outperform prediction models that do not use
250
Pereira, S., de Lima, J., Vieira, A. and Brandão, W.
Exploiting Data Spatial Dependencies for Employee Turnover Prediction.
DOI: 10.5220/0012948600003825
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 20th International Conference on Web Information Systems and Technologies (WEBIST 2024), pages 250-257
ISBN: 978-989-758-718-4; ISSN: 2184-3252
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

them, with gains ranging from 9.6% to 19.6% in the
standard deviation of MAPE, from 5.5% to 10.4% in
MAE, and from 0.99% to 2.9% in RMSE.
The reminder of this article is organized as fol-
lows: in Section 2 one present the background, in
Section 3 one present the proposed methodology, in
Section 4 one present experimental setup, in Section 5
one present experimental results, and finally, in Sec-
tion 6 one present conclusion and future work.
2 BACKGROUND
2.1 Spatial Data
Spatial data refers to data that have a location compo-
nent, which mean that they are associated to a specific
spatial position (Pebesma and Bivand, 2023). This
data is used to describe the properties and relations
between objects and events. They might be present in
different forms, such as points, representing specific
coordinates, lines, representing routes or limits and
polygons, representing regions.
Geospatial data are a subset of spatial data that in-
cludes the coordinates of the position of an object or
phenomenon on the Earth’s surface. These data in-
clude not only location with latitude, longitude and
altitude, but also attributes that describe the properties
of objects or geographic events. While all geospatial
data are also spatial data, not all spatial data is also
a geospatial data, since geospatial data require an ex-
plicit reference to their geographical coordinates (Aj-
jali, 2023).
Geospatial data are critical in representing and an-
alyzing the physical world, offering precise details
on the location and properties of several phenomena.
These data include raster data, typically used for im-
ages and continuous data fields, and vector data, in-
cluding points, lines, and polygons. The accurate rep-
resentation of geospatial data relies on the selection of
multiple scales and projections, ensuring the fidelity
of spatial relationships (Oshan et al., 2022).
2.2 Spatial Analisys
Spatial analysis aims to directly measure properties
and relationships of a phenomena, taking into account
its spatial positioning. Understanding how data from
phenomena occurring in space are distributed is a sig-
nificant challenge to address crucial questions in sev-
eral fields of knowledge.
Spatial dependency refers to the principle that the
location of a geographical object or phenomenon in-
fluences, and is influenced by, other nearby objects or
phenomena. This concept is crucial to spatial analy-
sis, as it suggests that spatial patterns are not random
but are the result of proximity and interaction between
geographic elements.
The rationale for spatial dependence analysis is
that identical datasets can produce different results
when considering their spatial positioning, as illus-
trated in Figure 1. Even with the same number of ob-
servations, distinct spatial distributions can reveal pat-
terns and insights that traditional data analysis might
miss (Anselin and Bera, 1998).
(a) Non spatial. (b) Spatial.
Figure 1: Feature distributions types.
2.3 Spatial Autocorrelation
Spatial autocorrelation is a measure that assesses the
degree of similarity or dependence between values
of an attribute at different geographical locations. It
indicates how similar the characteristics of a phe-
nomenon at a given location are to the characteristics
at nearby locations. If nearby locations have simi-
lar characteristics, spatial autocorrelation is positive,
otherwise, autocorrelation is negative. This measure
is essential to understand spatial patterns, as it takes
into account the influence that geographical proximity
has on the variables under consideration (Wang et al.,
2016; Rey et al., 2021).
2.3.1 Measures of Spatial Autocorrelation
Weight Matrix. The weight matrix is a mathemat-
ical representation that specifies the degree of prox-
imity and influence that one location has over other
locations. Each element W
ij
in the matrix represents
the weight assigned to the relationship between loca-
tions i and j. Specifically:
• i and j are indices referring to different locations
in the dataset.
• W
ij
quantifies the strength or significance of the
spatial connection between location i and j.
Moran’s I. The Moran’s I is a statistical measure
used to quantify spatial autocorrelation in a geospatial
dataset. It assesses the degree of similarity between
values of a variable at geographically close locations
and helps identify patterns of spatial aggregation or
Exploiting Data Spatial Dependencies for Employee Turnover Prediction
251

dispersion. A positive Moran’s I value indicates that
nearby locations tend to have similar characteristics,
whereas a negative value suggests that nearby loca-
tions have different characteristics (Chen, 2013). For-
mally, Moran’s I is defined as:
I =
N
W
∑
i
∑
j
w
i j
(x
i
− ¯x)(x
j
− ¯x)
∑
i
(x
i
− ¯x)
2
(1)
where N is the number of spatial units indexed by
i and j, x represents the variable of interest, ¯x is the
mean of x, and w
i j
is the spatial weight between units
i and j. The sum of all spatial weights is denoted as
W . When the index value is close to +1, it indicates a
strong positive spatial autocorrelation, meaning sim-
ilar values cluster together in space. A value close
to -1 suggests a strong negative spatial autocorrela-
tion, where dissimilar values are spatially clustered.
A value around 0 indicates a random spatial pattern
with no discernible clustering (Chen, 2023).
2.4 Employee Turnover
Employee turnover is defined as the process by which
employees leave an organization and are replaced by
new ones. This phenomenon can be analyzed from
several dimensions, including the types of turnover
and the factors that influence it. Voluntary turnover
occurs when an employee decides to leave the com-
pany, which may be motivated by different reasons
such as seeking new job opportunities, dissatisfaction
with the current job, personal issues, or a desire for
a change of environment. Involuntary turnover oc-
curs when the company decides to terminate the em-
ployee, which can also be due to several reasons, such
as poor performance, organizational restructuring, or
cost-cutting measures (Thibault Landry et al., 2017).
In this article, in line with its purpose of analyz-
ing the impacts of spatial dependence on predicting
the likelihood an employee holds a position in a com-
pany, one considered both voluntary and involuntary
turnover.
2.5 Open Government Data
Open government data are typically defined as
datasets that is available to the public and can be ac-
cessed and used without significant restrictions, ex-
cept to protect privacy and security (Wirtz et al.,
2022). These databases are publicly available data
provided by governments to promote transparency
and citizen participation.
Open Government Data are typically made avail-
able to the public through digital platforms in several
formats (Nikiforova and McBride, 2021) and con-
sists of informational resources whose availability can
influence the digital economy and promote innova-
tion (Luo and Tang, 2024).
2.6 Evaluation Metrics
To evaluate the impact of geospatial features on solv-
ing real-world problems, different comparative met-
rics can be used. Below one present some of these
metrics:
2.6.1 Pearson Correlation
r =
n
∑
xy −
∑
x
∑
y
p
[n
∑
x
2
− (
∑
x)
2
][n
∑
y
2
− (
∑
y)
2
]
(2)
Where r is the Pearson correlation coefficient, n is the
number of data points (pairs of scores). x and y are
the individual data points for the two variables being
compared.
The denominator of the formula contains the product
of two square roots. Each square root represents the
standard deviations of the respective variables.
2.6.2 ANOVA f-Statistic
F =
MSB
MSW
(3)
Where F is F-statistic in ANOVA, MSB is Mean
Square Between (Between-Groups Mean Square),
MSW is Mean Square Within (Within-Groups Mean
Square).
MSB =
∑
k
i=1
n
i
(
¯
X
i
−
¯
X)
2
k − 1
(4)
Where n
i
is the number of observations in group i,
¯
X
i
is the mean of the observations in group i,
¯
X is the
overall mean of all observations across all groups, k
is the number of groups being compared.
MSW =
∑
k
i=1
∑
n
i
j=1
(X
i j
−
¯
X
i
)
2
N − k
(5)
Where n
i
is the number of observations in group i,
X
i j
is the value of the j-th observation in group i,
¯
X
i
is the mean of the observations in group i, N − k
represents the degrees of freedom associated with the
within-group variance, where N is the total number of
observations and k is the number of groups.
2.6.3 MAPE (Mean Absolute Percentage Error)
MAPE =
1
n
n
∑
i=1




A
i
− F
i
A
i




× 100% (6)
WEBIST 2024 - 20th International Conference on Web Information Systems and Technologies
252

Where MAPE stands for Mean Absolute Percentage
Error, n is the number of data points or observations,
A
i
represents the actual value for the i-th observation,
F
i
represents the forecasted value for the i-th observa-
tion,



A
i
−F
i
A
i



calculates the absolute percentage error
for the i-th observation.
2.6.4 MAE (Mean Absolute Error)
MAE =
1
n
n
∑
i=1
|A
i
− F
i
| (7)
Where MAE stands for Mean Absolute Error, n is the
number of data points or observations, A
i
represents
the actual value for the i-th observation, F
i
represents
the forecasted value for the i-th observation, |A
i
− F
i
|
calculates the absolute error for the i-th observation.
2.6.5 RMSE (Root Mean Squared Error)
RMSE =
s
1
n
n
∑
i=1
(A
i
− F
i
)
2
(8)
Where RMSE stands for Root Mean Squared Error, n
is the number of data points or observations, A
i
repre-
sents the actual value for the i-th observation, F
i
rep-
resents the forecasted value for the i-th observation,
(A
i
− F
i
)
2
calculates the squared error for the i-th ob-
servation.
The square root of the mean squared error is taken to
return the result to the original units of the data.
3 METHODOLOGY
Figure 2 outlines the proposed methodology to evalu-
ate the impacts of geographical positioning in predic-
tive machine learning models. This methodology pro-
vides a comprehensive framework for conducting data
analysis, modeling, and result evaluation, enabling a
deeper understanding of the problem.
3.1 Comparison of Methods
Spatial Dependence:
• Linear Regression does not consider any spatial
relationships or dependencies. It treats each vari-
able independently and performs a simple linear
regression using only the selected column.
• Geo Spatial Linear Regression incorporates spa-
tial dependency by calculating spatial weights us-
ing K-Nearest Neighbors (KNN) and applying a
spatial lag to the Employment Time variable. This
method considers the influence of neighboring ob-
servations in the prediction process.
Figure 2: Guidelines for using a spatial model.
Complexity:
• Linear Regression is simpler and focuses on a
single-variable linear regression without any spa-
tial considerations.
• Geo Spatial Linear Regression is more complex,
involving the creation of spatial weights, calcula-
tion of spatial lags, and the use of multiple vari-
ables in the regression model.
Use Cases:
• Linear Regression is more appropriate for stan-
dard regression tasks where the goal is to under-
stand the linear relationship between individual
variables and the target variable, without consid-
ering spatial factors.
• Geo Spatial Linear Regression is suited for sce-
narios where spatial relationships are important,
such as geospatial data analysis where the loca-
tion or proximity of data points might influence
the outcome.
3.2 Conceptual Database
The conceptual dataset was structured through data
cleaning and standardization, as each year’s records
had differences in dictionaries and formats such as
ASCII and UTF-8. The structuring process occurred
in two stages:
1. Selection of Relevant Columns: initially, all
columns with redundant or duplicate information
were removed. All columns containing categori-
cal data were transformed into binary data, and the
original columns were then removed. Columns
with variance lower than 5% were removed.
Exploiting Data Spatial Dependencies for Employee Turnover Prediction
253

2. Selection of Relevant Records: records related to
business categories in the Technology and Com-
munication sector were selected. Records with
null values were removed. Records outside 96.4%
of the normal distribution were removed.
Libraries such as Pandas are used for data manip-
ulation, NumPy for numerical calculations, and SciPy
for statistical and scientific operations. Subsequently,
the data is normalized and transformed using Scikit-
learn for data preprocessing and normalization. This
process results in a prepared dataset ready for explo-
ration using advanced spatial analysis and modeling
techniques.
Geographic data is associated with features, trans-
forming it into a geospatial database to enable the use
of spatial models. Python libraries for handling spa-
tial data were used to conduct the experiments, such
as GeoPandas, Shapely, and PySAL.
4 EXPERIMENTAL SETUP
To evaluate the proposed methodology one use in the
experiments a conceptual dataset derived from three
Brazilian open government data.
RAIS (Annual Social Information Report): legal
record documenting the hiring and dismissals carried
out by Brazilian companies. This source provides a
detailed view of labour relations in the country. This
dataset is administered by the Ministry of Labor and
Employment of the Brazilian government. encom-
passing over 60 critical variables such as gender, age,
disability status, company area, job code, salary, and
length of employment.
DTB (Division of Brazilian Territory): provides
geo-referenced data on Brazilian municipalities. This
includes their polygons, as well as the latitude and
longitude of their administrative centers. This dataset
is administered and distributed by the Brazilian In-
stitute of Geography and Statistics. Brazil is geo-
politically divided into 27 federate units or states,
which are further divided into meso-regions. The
DBT dataset contains these geopolitical divisions, in-
cluding municipality codes, boundary polygons, and
geographic coordinates of the municipal centers.
Social Data: also distributed by the Brazilian
Institute of Geography and Statistics, it contains the
Human Development Index, longevity index, average
income index, education index, and other socio-
demographic indices of the Brazilian population.
The performance of the proposed methodology
was evaluated using metrics such as standard error of
regression and regression coefficients (Feitosa et al.,
2021). Manhattan distance was used as a proximity
metric for neighbor selection in spatial models.
Linear regression models were trained to capture
spatial patterns in the data (Son et al., 2014). MAE,
MAPE and RMSE metrics were all used to assess
and compare the performance of different models.
These metrics provided insights into the variations of
the models in relation to the non-georeferenced and
georeferenced data.
5 EXPERIMENTAL RESULTS
The scope of the results and discussions presented is
limited to describing how the outcomes may vary de-
pending on the consideration of geographic reference
or not, using regression models.
The results of the experiments were obtained us-
ing three datasets. Two datasets are independent and
refer to the set of cities that comprise the Metropoli-
tan Region of Belo Horizonte (RMBH), a big city
in Brazil, and a set of cities that make up the South
and Southwest regions of the Brazilian state of Minas
Gerais (SSMG). The third dataset is formed by their
union, denoted as RMSS. Table 1 demonstrates the
composition of the datasets.
Table 1: Dataset characteristics.
RMSS
Lines 202,417
Municipalities 139
Lower left (-48.277, -22.858)
Upper right (-42.552, -15.799)
RMBH
Lines 188,672
Municipalities 49
Lower left (-48.823, -21.999)
Upper right (-42.409, -15.327)
SSMG
Lines 13,745
Municipalities 90
Lower left (-47.240, -22.922)
Upper right (-43.976, -20.218)
Comparison metrics were employed to conduct a
comparative analysis between two datasets, one with
geographical positioning and the other without, us-
ing linear regression models. Regarding the features,
those with the highest scores, non-null values, and
presence in both SSMG and RMBH datasets were se-
WEBIST 2024 - 20th International Conference on Web Information Systems and Technologies
254

lected.
5.1 Correlation Analysis
The correlation analysis aimed to identify the most
influential variables crucial to construct the datasets
used in this investigation. Despite encompassing
comprehensive employment data across Brazil with
a multitude of variables, the analysis surprisingly re-
vealed very low correlations among them. This un-
expected finding indicates the complexity of the rela-
tionships within the dataset and suggests that alterna-
tive approaches may be necessary to address the re-
search problem effectively. Figure 3 shows the vari-
ability of each feature.
Figure 3: Feature correlation.
From Figure 3 one observe that the location as-
signs distinct score values for each feature, highlight-
ing features ibge subsector 20, HDI longev 2010,
HDI educ 2010, and estab size 07, which exhibit
inverse correlations. Regarding the importance of fea-
tures, a variation was observed, indicating that differ-
ent locations have distinct scores for the variables, as
shown by Figure 4.
Figure 4: Feature score.
From Figure 4 one observe that the two datasets
have very distinct scores for each variable, and that
the RMSS dataset, although predominantly composed
of RMBH data, undergoes significant changes when
combined with the SSMG dataset, which has a more
homogeneous variation in the scores of the variables.
5.1.1 Spatial Autocorrelation Analysis
In spatial analysis, one are interested in evaluate
whether a feature has a correlation with its neigh-
borhood or if its distribution is random. The anal-
ysis consists on verifying the variability of the de-
pendent feature, employment time, across the three
datasets, and two other predictor features, race
04
and HDI educ2000, in the individual datasets RMBH
and SSMG, as presented in Table 2. These predictor
variables alternate between True and False in the two
datasets.
Table 2: Spatial Autocorrelation of Different Features
Across Datasets. A) Spatial Autocorrelation; B) Expected
I; C) Observed I; D) I p-value.
Dataset A B C D
Days on Leave
RMSS False -0.008 0.019 0.269
RMBH False -0.021 -0.010 0.396
SSMG False -0.011 0.078 0.094
race 04
RMSS True -0.008 0.122 0.009
RMBH False -0.016 0.081 0.129
SSMG True -0.013 0.112 0.038
HDI educ 2000
RMSS True -0.008 0.141 0.003
RMBH True -0.025 0.220 0.004
SSMG False -0.011 0.067 0.126
For the analysis, the Moran’s I index was used.
Expected Moran’s I refers to the expected value of the
Moran’s I index under the null hypothesis of no spa-
tial autocorrelation. This value is calculated assum-
ing there is no spatial pattern in the data and serves
as a comparison base for the observed value of the
Moran’s I index.
The observed Moran’s I is the actual calculated
value of the Moran’s I index derived from the ob-
served data. It quantifies the degree of spatial autocor-
relation, indicating how similar or dissimilar values
are spatially distributed across the study area. This
measure is obtained without assuming any initial hy-
pothesis about the spatial distribution, thus providing
an unbiased reflection of the spatial patterns inherent
in the data.
The I p-value is the statistical significance value
associated with the observed Moran’s I. It indicates
the probability of observing a Moran’s I value equal
to or more extreme than the observed one under the
null hypothesis, of no spatial autocorrelation. A low
p-value, usually less than 0.05, suggests statistically
significant evidence of spatial autocorrelation in the
data, implying that the observed spatial pattern is un-
likely to have occurred by random chance alone. This
Exploiting Data Spatial Dependencies for Employee Turnover Prediction
255

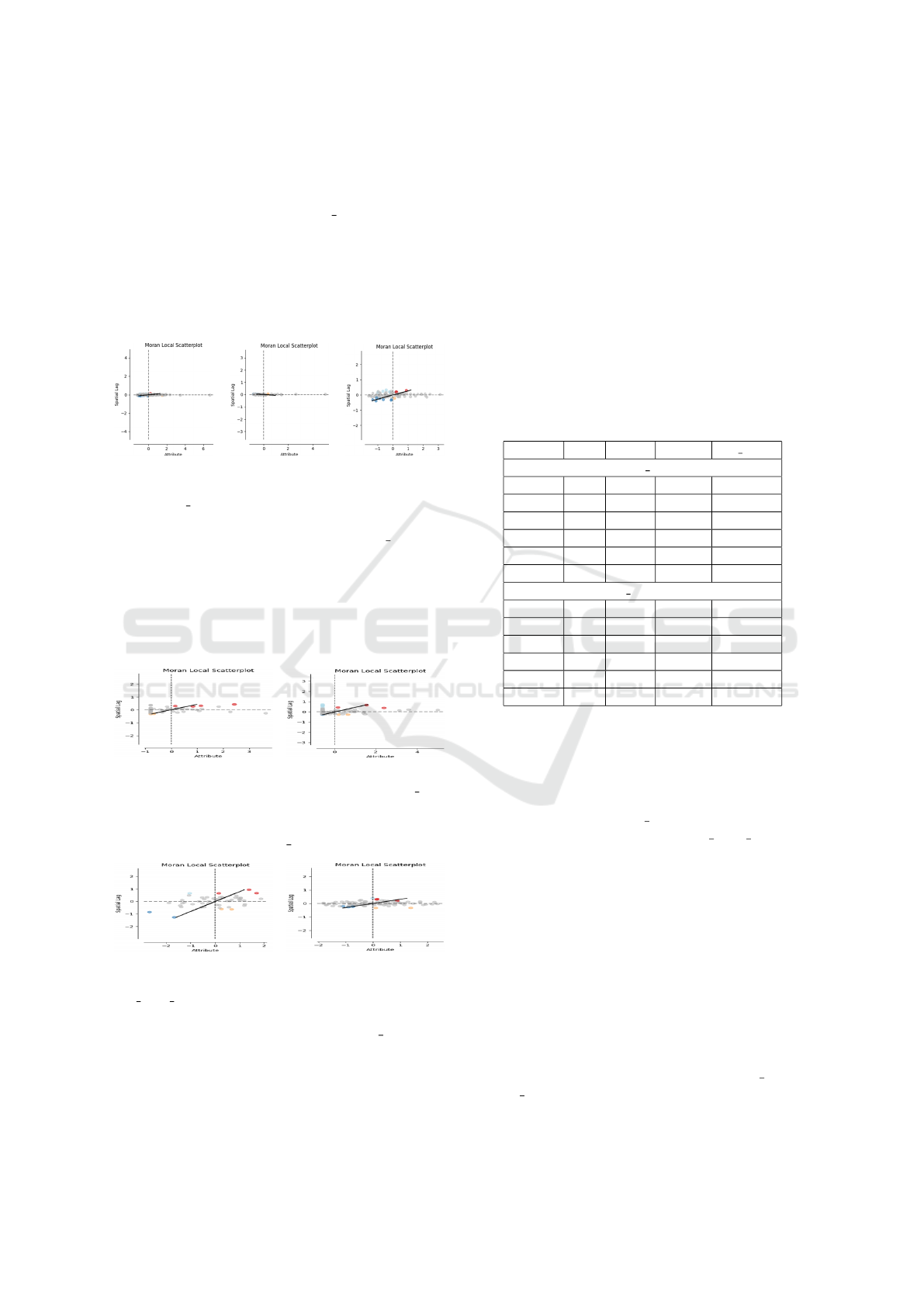
helps in confirming whether the spatial clustering or
dispersion observed in the data is meaningful.
Regarding the dependent variable, from Table 2
one observe that for Employment Time there is no
spatial dependence in any of the datasets. However,
from Figures 5a, 5b, and 5c one observe that there
are variations in many degrees. It is also notewor-
thy that the formation of clusters varies depending
on whether the datasets are analyzed independently
or collectively.
(a) RMSS. (b) RMBH. (c) SSMG.
Figure 5: Spatial autocorrelation distribution:
Employment Time.
Regarding the predictor variable race 04, it is
possible to observe from Table 2 that there is no spa-
tial autocorrelation for the RMBH dataset, whereas
there is such correlation for the SSMG dataset. From
Figures 6a and 6b one observe the existing variation,
with clusters forming in the region where the feature
exhibits spatial correlation.
(a) RMBH. (b) SSMG.
Figure 6: Spatial autocorrelation distribution: race 4.
From Figure 7 one observe the spacial autocorre-
lation of the variable idhed 2000.
(a) RMBH. (b) SSMG.
Figure 7: Spatial autocorrelation distribution:
HDI educ 2000.
Regarding the predictor variable idhed 2000, it is
possible to observe from Table 2 that there is no spa-
tial autocorrelation for the RMBH dataset, whereas
there is such correlation for the SSMG dataset. From
Figure 7a one observe the existing variation, and from
Figure 7b one observe clusters forming in the region
where the feature exhibits spatial correlation.
5.2 Metrics
This experiment consisted of comparing the MAE
(Mean Absolute Error) and RMSE (Root Mean
Squared Error) metrics, as well as conducting a de-
tailed study of MAPE (Mean Absolute Percentage Er-
ror). Linear regression and spatial regression analy-
ses were performed, involving univariate analyses, for
both non-georeferenced and georeferenced datasets
RMBH and SSMG.
Table 3: Performance of prediction models for different fea-
tures, datasets, and geographic configurations.
Dataset Geo MAE RMSE std mape
race 04
RMBH no 0.168 0.209 2441.50
RMBH yes 0.151 0.206 1961.66
Gain % 10.37 1.68 19.65
SSMG no 0.153 0.192 2224.06
SSMG yes 0.138 0.186 1798.95
Gain % 9.81 2.86 19.11
HDI educ2000
RMBH no 0.159 0.207 2095.19
RMBH yes 0.150 0.205 1894.22
Gain % 5.46 0.99 9.59
SSMG no 0.153 0.192 2224.06
SSMG yes 0.138 0.186 1788.42
Gain % 9.91 2.90 19.58
The univariate linear and spatial regression analy-
sis (Griffith, 2000) aimed to individually measure the
representativeness of each feature in relation to the
duration of time an individual remains employed at a
company. Two variables were chosen for the exper-
iments: the variable race 04, characterized by spa-
tial randomness, and the variable HDI educ 2000, ex-
hibiting spatial dependence.
6 CONCLUSION
This paper proposed a methodology to assess the exis-
tence of spatial dependencies in prediction problems,
particularly in the employee turnover prediction prob-
lem. The experiments were crucial in validating the
hypothesis that the inclusion of geographic attributes
can significantly enhance the accuracy of predictive
models used to estimate employee turnover. The pres-
ence of spatial autocorrelation in the race 04 and
idhed 2000 features in the independent datasets sug-
gests that spatial interactions can substantially impact
WEBIST 2024 - 20th International Conference on Web Information Systems and Technologies
256

the predictive accuracy of these variables.
Experimental results revealed differences in the
performance of predictive models when comparing
georeferenced and non-georeferenced data. Particu-
larly, prediction models that use geographic features
outperformed prediction models that do not use them,
with gains ranging from 9.6% to 19.6% in the stan-
dard deviation of MAPE, from 5.5% to 10.4% in
MAE, and from 0.99% to 2.9% in RMSE. These re-
sults highlight the importance of considering the spa-
tial context when building predictive models, as incor-
porating geographic variables can lead to significant
improvements in prediction accuracy.
For future research, one intent to investigate mul-
tivariate spatial analyses and explore more sophisti-
cated spatial models to optimize employee turnover
prediction. Advanced models such as Spatial Au-
toregressive Models (SAR) and Spatial Error Mod-
els (SEM) offer more refined perspectives on spatial
interactions that may impact employee tenure. Addi-
tionally, the use of Spatial Neural Networks and Hi-
erarchical Bayesian Models can provide deeper and
more precise insights by capturing complexities in
spatial dependencies and data heterogeneity.
ACKNOWLEDGEMENTS
The authors thank the Pontif
´
ıcia Universidade
Cat
´
olica de Minas Gerais – PUC-Minas and
Coordenac¸
˜
ao de Aperfeic¸oamento de Pessoal de
N
´
ıvel Superior — CAPES (CAPES – Grant PROAP
88887.842889/2023-00 – PUC/MG, Grant PDPG
88887.708960/2022-00 – PUC/MG - Inform
´
atica,
and Finance Code 001).
REFERENCES
Ajjali, W. (2023). Coordinate systems and projections.
In ArcGIS Pro e ArcGIS Online, Springer Text-
books in Earth Sciences, Geography and Environ-
ment. Springer, Cham.
Anselin, L. (2021). Spatial models in econometric research.
In Oxford Research Encyclopedia of Economics and
Finance.
Anselin, L. and Bera, A. (1998). Spatial dependence in lin-
ear regression models with an introduction to spatial
econometrics. In Ullah, A. and Giles, D. E., editors,
Handbook of Applied Economic Statistics, pages 237–
289. Marcel Dekker.
Chen, Y. (2013). New approaches for calculating
moran’s index of spatial autocorrelation. PloS one,
8(7):e68336.
Chen, Y. (2023). Spatial autocorrelation equation based on
moran’s index. Scientific Reports, 13(1):19296.
Dramsch, J. S. (2020). 70 years of machine learning in geo-
science in review. Advances in Geophysics, 61:1–55.
Feitosa, F., Barros, J., Marques, E., and Giannotti, M.
(2021). Measuring changes in residential segregation
in s
˜
ao paulo in the 2000s. In Urban Socio-Economic
Segregation and Income Inequality, pages 507–523.
Springer International Publishing.
Griffith, D. A. (2000). A linear regression solution to the
spatial autocorrelation problem. Journal of Geograph-
ical Systems, 2:141–156.
Lazzari, M., Alvarez, J. M., and Ruggieri, S. (2022). Pre-
dicting and explaining employee turnover intention.
International Journal of Data Science and Analytics,
14(3):279–292.
Luo, Y. and Tang, Z. (2024). The impact of open gov-
ernment data on the digital economy: Evidence from
china. SSRN.
Nikiforova, A. and McBride, K. (2021). Open government
data portal usability: A user-centred usability analysis
of 41 open government data portals. Telematics and
Informatics, 58:101539.
Oshan, T., Wolf, L., Sachdeva, M., et al. (2022). A scoping
review on the multiplicity of scale in spatial analysis.
Journal of Geographical Systems, 24:293–324.
Pebesma, E. and Bivand, R. (2023). Spatial data science:
With applications in R. Chapman and Hall/CRC.
Rey, S. J., Anselin, L., and Li, W. (2021). Handbook of
Spatial Analysis in the Social Sciences. Edward Elgar
Publishing.
Son, W., Hwang, S. W., and Ahn, H. K. (2014). Mssq:
Manhattan spatial skyline queries. Information Sys-
tems, 40:67–83.
Taleb, N. N. (2010). The Black Swan: The Impact of the
Highly Improbable. Random House, 2nd edition.
Thibault Landry, A., Schweyer, A., and Whillans, A.
(2017). Winning the war for talent: Modern motiva-
tional methods for attracting and retaining employees.
Compensation & Benefits Review, 49(4):230–246.
Wang, J.-F., Zhang, T.-L., and Fu, B.-J. (2016). A measure
of spatial stratified heterogeneity. Ecological Indica-
tors, 67:250–256.
Wirtz, B. W., Weyerer, J. C., Becker, M., and M
¨
uller, W. M.
(2022). Open government data: A systematic litera-
ture review of empirical research. Electronic Markets,
32(4):2381–2404.
Zhao, Y., Hryniewicki, M. K., Cheng, F., Fu, B., and Zhu,
X. (2019). Employee turnover prediction with ma-
chine learning: A reliable approach. In Sani, A.
M. M., Shaout, K., and Abbass, H. A., editors, Intel-
ligent Systems and Applications: Proceedings of the
2018 Intelligent Systems Conference (IntelliSys) Vol-
ume 2, pages 737–758. Springer International Publish-
ing.
Exploiting Data Spatial Dependencies for Employee Turnover Prediction
257