Educational Evolutionary Neural Architecture Search for Time Series

Prediction

Martha Isabel Escalona-Llaguno

1 a

and Sergio M. Sarmiento-Rosales

2 b

Universidad Aut

onoma de Zacatecas, Academic Unit of Electrical Engineering,

Circuito Cerro del Gato s/n, Col. Progreso, Zacatecas, Zac., 98060, Mexico

Tecnologico de Monterrey, School of Engineering and Sciences, Ave. Lago de Guadalupe Km 3.5,

Atizap

an de Zaragoza, Edo. M

exico, 52926, Mexico

{m.c.miell.2607, sarmiento.rosales.sm}@gmail.com

Keywords:

Evolutionary Neural Architecture Search (NAS), Time Series.

Abstract:

This paper presents a sophisticated tool designed to teach Evolutionary Neural Architecture Search (ENAS)

in time series analysis. The goal is to create a ﬂexible and modular algorithm that helps to understand evo-

lutionary algorithms in the context of neural architecture optimization. The tool allows parameter tuning and

search space exploration. Its initial setup can include a population size of 20 individuals, spanning 5 genera-

tions, with an elitism rate of 20% and crossover and mutation probabilities set to 90% and 10%, respectively.

However, these hyperparameters are completely modular, so that the effect on the algorithm can be studied.

The parameter ranges from 1 to 20 for neurons and delays. The neural networks are extensively trained us-

ing the MATLAB narnet function and the PJM hourly energy consumption dataset, which is split into 70%

for training, 15% for validation, and 15% for testing. The goal is to maximize the correlation coefﬁcient r

obtained from the test dataset. This approach offers an interactive platform for experimentation and learning

about the evolutionary process of neural architectures, thus improving the understanding of evolutionary al-

gorithms applied to Neural Architecture Search (NAS). Our experiments show efﬁciency due to the limited

search space and the absence of specialized hardware requirements such as GPU, making it accessible and

practical for educational and research environments. Using only an AMD Ryzen 7 7800X3D CPU, all ar-

chitectures within the search space were trained in less than 3 hours, demonstrating the agility of ENAS in

various conﬁgurations and its effectiveness in facilitating practical understanding of the evolutionary process

in NAS. All datasets, tutorials and essential codes to apply this work are publicly accessible at the following

link: https://github.com/SergioSarmientoRosales/ENAS-Time-Series.

1 INTRODUCTION

Evolutionary Neural Architecture Search (ENAS) is a

cutting-edge approach to optimizing neural networks

that has garnered signiﬁcant attention and success,

particularly in ﬁelds like image classiﬁcation and

restoration. Now, its application in the intricate do-

main of time series analysis presents new opportuni-

ties and challenges (Elsken et al., 2019). Time series

data is characterized by its sequential nature, evolv-

ing and requiring models that can accurately capture

and adapt to subtle patterns and trends (Fadlalla and

Lin, 2001). ENAS, drawing inspiration from natu-

ral evolutionary processes, navigates through a vast

landscape of potential neural network architectures. It

https://orcid.org/0000-0002-5818-5234

https://orcid.org/0000-0001-9219-7223

identiﬁes and reﬁnes conﬁgurations that demonstrate

superior performance in handling the unique com-

plexities of time series data, such as trends, season-

ality, and irregularities, ensuring more accurate pre-

dictions and better model adaptability. (Pham et al.,

2018).

The application of ENAS in time series analysis

opens up avenues for tackling challenges such as fore-

casting, anomaly detection, and pattern recognition

within temporal data streams (Rosenberger, 2022).

However, despite the promising outcomes, the intri-

cacies inherent in evolutionary algorithms can pose

barriers to understanding and practical implemen-

tation, particularly in educational settings (Miikku-

lainen et al., 2024). Bridging this gap requires a di-

dactic approach that simpliﬁes the core concepts of

ENAS while retaining its efﬁcacy in optimizing neu-

ral architectures for time series tasks.

234

Escalona-Llaguno, M. and Sarmiento-Rosales, S.

Educational Evolutionary Neural Architecture Search for Time Series Prediction.

DOI: 10.5220/0012948900003837

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 234-241

ISBN: 978-989-758-721-4; ISSN: 2184-3236

Despite the promising outcomes of ENAS, its

complexity, rooted in evolutionary algorithms, can

present challenges in terms of understanding and

practical implementation, especially in educational

contexts (Miikkulainen et al., 2024)). This complex-

ity often stems from the intricate optimization pro-

cesses and the myriad of parameters and conﬁgura-

tions involved in training neural architectures using

evolutionary methods.

By delving into the fundamental principles of

ENAS and its application in the context of time series,

this endeavor aims to elucidate the intricacies of evo-

lutionary neural architecture search in a comprehensi-

ble manner (Li and Talwalkar, 2020). Through prac-

tical demonstrations and interactive learning experi-

ences, learners can grasp the nuances of ENAS and its

implications for enhancing the capabilities of neural

networks in handling time-dependent data structures.

To address these challenges and bridge the gap be-

tween theoretical concepts and practical applications,

a didactic approach is essential. This approach in-

volves breaking down the core concepts of ENAS into

understandable components while preserving its ef-

fectiveness in optimizing neural architectures for time

series tasks. By simplifying the learning curve and

providing interactive learning experiences, students

and practitioners can grasp the nuances of ENAS

more effectively and apply this knowledge to real-

world scenarios.

In this study, our aim is to delve deeper into the

fundamental principles of ENAS and explore its spe-

ciﬁc application in the context of time series anal-

ysis. We aim to elucidate the intricacies of evolu-

tionary neural architecture search in a comprehensi-

ble manner, making it accessible to a wider audience.

Through practical demonstrations, interactive tools,

and real-world examples, we seek to enhance under-

standing, facilitate learning, and encourage further re-

search in the ﬁeld of time series forecasting using evo-

lutionary techniques.

2 BACKGROUND

Time series forecasting is a critical task in various

ﬁelds, such as ﬁnance (Fadlalla and Lin, 2001; El-

liott and Timmermann, 2016), weather forecasting

(Abhishek et al., 2012; Gneiting and Raftery, 2005),

and stock market analysis (Shah et al., 2019; Chong

et al., 2017). In ﬁnance, accurate forecasting can in-

ﬂuence investment strategies, risk management, and

economic planning (Fadlalla and Lin, 2001). For in-

stance, predicting future stock prices or economic in-

dicators can provide signiﬁcant advantages to traders

and policy makers. In weather forecasting, predict-

ing climatic conditions like rainfall, temperature, and

extreme weather events helps in disaster prepared-

ness and agricultural planning. Similarly, in the stock

market, understanding future price movements based

on historical data is crucial for developing trading

strategies and mitigating ﬁnancial risks (Chong et al.,

2017). The ability to accurately predict future trends

and patterns based on historical data is essential for

making informed decisions.

Traditional methods for time series forecasting of-

ten rely on statistical techniques, mathematical mod-

els, physical models, or simplistic machine learning

models. These methods include approaches like Au-

toregressive Integrated Moving Average (ARIMA),

Exponential Smoothing, and various regression mod-

els (Box et al., 2015; Hamilton, 2020). Although

these methods have been widely used and have proven

effective in many scenarios, they often struggle with

the increasing complexity of modern data. These tra-

ditional methods typically assume linear relationships

and may not adequately capture the non-linear and

complex dependencies present in real-world time se-

ries data (Hyndman and Athanasopoulos, 2018). As

a result, there is a growing need for more advanced

techniques that can handle the complexities of time

series data, providing more accurate and reliable pre-

dictions (Lim et al., 2021).

ENAS has emerged as a promising approach to

optimizing neural networks for time series forecasting

(Liu et al., 2021). Unlike manual design or traditional

hyperparameter tuning methods, ENAS leverages the

principles of natural evolution to automatically dis-

cover and optimize architectures of neural networks.

This approach reduces the burden of manual interven-

tion and improves the performance of neural networks

in capturing complex temporal dependencies and pat-

terns present in time series data (Liu et al., 2021;

Pham et al., 2018). By automating the design process,

ENAS can explore a vast search space of potential

architectures, identifying the most effective conﬁgu-

rations without extensive human input (Elsken et al.,

2019).

ENAS offers a signiﬁcant advantage in the domain

of time series forecasting due to its ability to adapt

and evolve neural architectures speciﬁcally tailored

to handle the intricate dynamics of time-dependent

data (Liang and Sun, 2024). Traditional forecast-

ing methods may overlook optimal conﬁgurations due

to their limited exploration of the search space. In

contrast, ENAS explores a diverse range of architec-

tures and hyperparameters, uncovering conﬁgurations

that may offer superior performance (Liang and Sun,

2024). This adaptability and optimization potentially

Educational Evolutionary Neural Architecture Search for Time Series Prediction

235

make ENAS a valuable tool for researchers and practi-

tioners aiming to enhance the accuracy and reliability

of time series forecasting models (Zoph et al., 2018;

Real et al., 2019).

However, the main challenge of ENAS lies in its

practical application. ENAS commonly focuses on

deep neural networks in vast search spaces, leading to

computationally expensive evaluation processes (Ren

et al., 2021). This often makes its use in real sce-

narios prohibitive. Efﬁcient evaluation methods exist,

but there is still a need to theoretically understand how

these methods work, which often requires specialized

techniques and knowledge that are usually available

only to expert researchers (Xie et al., 2023; Liu et al.,

2021). This combination of factors and the associated

high computational cost signiﬁcantly limit the access

and widespread adoption of ENAS in the scientiﬁc

and professional community.

While ENAS presents a promising avenue for op-

timizing neural networks in time series forecasting,

its practical implementation faces notable challenges.

The inherent complexity of deep neural networks in

vast search spaces requires computationally intensive

evaluation processes, often making their application

in real-world scenarios impractical due to prohibitive

computational costs and time requirements (Liu et al.,

2021). Despite the availability of efﬁcient evaluation

methods, there remains a crucial need for comprehen-

sive theoretical understanding and specialized exper-

tise, creating barriers to widespread adoption among

researchers and practitioners. Addressing these chal-

lenges will be critical to unlocking the full potential of

ENAS and harnessing its beneﬁts to improve the accu-

racy and reliability of time series forecasting models

in various domains.

3 METHODOLOGY

Our methodology for developing the advanced ENAS

teaching tool applied to time series involves several

key steps aimed at creating an agile and modular algo-

rithm that improves the understanding of evolutionary

algorithms in neural architecture optimization.

We deﬁne clear objectives and requirements for

our ENAS teaching tool. These objectives include

enhancing the accessibility and effectiveness of time

series forecasting through ENAS, improving user ex-

perience, and ensuring scalability and ﬂexibility.

Based on these objectives, we design and imple-

ment a modular and agile algorithm that can adapt

to different user needs and scenarios. This involves

developing intuitive interfaces, integrating interactive

features, and incorporating educational elements to

facilitate learning and understanding.

Throughout the development process, we continu-

ously evaluate and iterate on our tool, gathering feed-

back from users. This iterative approach allows us to

reﬁne and enhance the tool’s functionality, usability,

and educational value.

Additionally, we leverage the strengths of ENAS,

such as its ability to navigate complex search spaces

and identify optimal neural architectures. By harness-

ing these capabilities, we aim to advance the state-of-

the-art in time series forecasting, making it accessible

and effective for a broader range of applications.

Overall, our methodology emphasizes a system-

atic and iterative approach, combining thorough anal-

ysis, user-centered design principles, and the utiliza-

tion of ENAS strengths to develop an advanced teach-

ing tool for time series forecasting.

3.1 Initial Conﬁguration Settings

The algorithm can start its execution in different ini-

tializations, from choosing the population type with

a random seed, a crucial step to ensure reproducibil-

ity of the results in subsequent runs. This random

seed serves as a starting point to generate random se-

quences and numbers, maintaining consistency and

reproducibility in different runs of the algorithm. The

default conﬁguration serves as a starting parameter,

however it is recommended to play with each of the

parameters in order to understand the contribution of

each hyperparameter. The ”default” values are se-

lected based on established standards and best prac-

tices observed in the literature, ensuring a robust and

effective optimization process (Liu et al., 2021).

One of the key features of our algorithm is its ﬂex-

ibility and adaptability. Each of these parameters can

be easily modiﬁed without any programming knowl-

edge. This ﬂexibility allows researchers and practi-

tioners to ﬁne-tune the algorithm to speciﬁc require-

ments and goals, making it a versatile tool for explo-

ration and experimentation.

To address concerns about computational com-

plexity and execution time, we strategically designed

a small search space for the algorithm. Speciﬁcally,

the search space ranges between 1 and 20 for both the

number of neurons and the delays in the neural archi-

tectures. This design choice limits the total number

of possible architectures to only 400, signiﬁcantly re-

ducing the computational load (L

opez et al., 2019).

By restricting the search space, we can perform

a comprehensive exploration of architectural conﬁg-

urations while keeping the computational cost man-

ageable. This approach allows us to perform multiple

experiments in a reasonable period, avoiding the need

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

236

for specialized hardware such as GPU. As a result,

researchers and educators can efﬁciently run experi-

ments, analyze results, and gain insights without sig-

niﬁcant hardware dependencies.

3.2 Evolutionary Algorithm

The generation of the population signiﬁes the com-

mencement of the evolutionary process within our

algorithm. Each individual in the population is as-

signed a genotype, which contains crucial informa-

tion regarding the architecture of the neural network,

speciﬁcally the number of neurons in the hidden layer

and the delays in the time series data. This genotype

serves as a blueprint for constructing the artiﬁcial neu-

ral network (ANN).

To ensure smooth transitions and effective explo-

ration of the search space, the generated genotype

is encoded using Gray code. This technique, com-

monly used in evolutionary algorithms, minimizes

abrupt changes between adjacent genotypes. By re-

ducing these sudden changes, gray code facilitates

a more systematic exploration of the search space,

which enhances the algorithm’s ability to ﬁnd opti-

mal solutions (Fogel and Computation, 1995; Eiben

and Smith, 2015).

Each individual, along with its decoded version

using the Gray code, is stored in a data structure for

subsequent manipulation and evaluation during the

evolutionary process. As the algorithm progresses

through generations, it undergoes selection mecha-

nisms to identify the best individuals based on prede-

ﬁned evaluation metrics. This selection process, of-

ten implemented through techniques like tournament

selection or roulette wheel selection, aims to retain

and promote individuals with favorable characteris-

tics (Ahn and Ramakrishna, 2003).

To prevent premature convergence and maintain

diversity within the population, the evolutionary pro-

cess introduces random individuals in each genera-

tion. Additionally, crossover and mutation operations

are employed to generate diverse and adaptive off-

spring over multiple generations. Crossover involves

selecting two parent individuals through tournament

selection and combining their genetic information to

produce new offspring. This process blends features

from both parents, creating a diverse range of poten-

tial solutions. Mutation, on the other hand, introduces

small random changes to the genetic material of indi-

viduals, which helps explore new areas of the solution

space and promotes innovation. These techniques col-

lectively support the evolution of solutions by ensur-

ing ongoing variation and adaptation (De Jong, 2017).

These evolutionary mechanisms collectively con-

tribute to the search for optimal solutions for the

given problem. By maintaining diversity, promoting

favorable traits, and introducing variability through

crossover and mutation, the algorithm continuously

explores and reﬁnes solutions, ultimately aiming

to converge toward the most effective and efﬁcient

ANNs for time series analysis.

3.3 Datasets

We use the Pennsylvania-New Jersey-Maryland

(PJM) Hourly Energy Consumption Dataset from

PJM Interconnection LLC, a regional transmission or-

ganization (RTO) in the United States that is part of

the Eastern Interconnection grid (Robikscube, 2024;

panambY, 2024). PJM operates an electric transmis-

sion system that covers Delaware, Illinois, Indiana,

Kentucky, Maryland, Michigan, New Jersey, North

Carolina, Ohio, Pennsylvania, Tennessee, Virginia,

West Virginia and the District of Columbia. The

choice of this dataset for our research is due to its

notable advantages for experimentation and research.

The free availability of this data makes it a versatile

and convenient option for carrying out comparative

studies and analyses in different regions, thus giving

researchers the freedom to conduct experiments and

validate their discoveries using diverse data sets. This

approach contributes to the robustness and generaliza-

tion of the results, especially in the analysis of energy

demand and electrical efﬁciency. However, our ap-

proach is not limited to this dataset but can be substi-

tuted by any other time series data set. We highly rec-

ommend using data sets that exhibit seasonality prop-

erties, as this can lead to more accurate results (Hyn-

dman and Athanasopoulos, 2018; Shumway et al.,

2000). On the other hand, it should be noted that sea-

sonality is not a strict requirement, since our main ob-

jective is to be didactic and not necessarily obtain the

best results in terms of predictive performance.

3.4 Neural Network Training

During the training process within our evolutionary

algorithm, each individual in the population under-

goes a decoding step to extract information regarding

the number of neurons and delays speciﬁed by their

genotype. This decoding process is crucial for conﬁg-

uring the neural network architecture accurately. Fol-

lowing this, adjustments are made to ensure that nei-

ther the number of neurons nor the delays fall below

1. This precaution is necessary due to the possibility

of mutations occurring during the evolutionary pro-

cess, and it helps avoid any parameter from becoming

0, which could lead to invalid conﬁgurations.

Educational Evolutionary Neural Architecture Search for Time Series Prediction

237

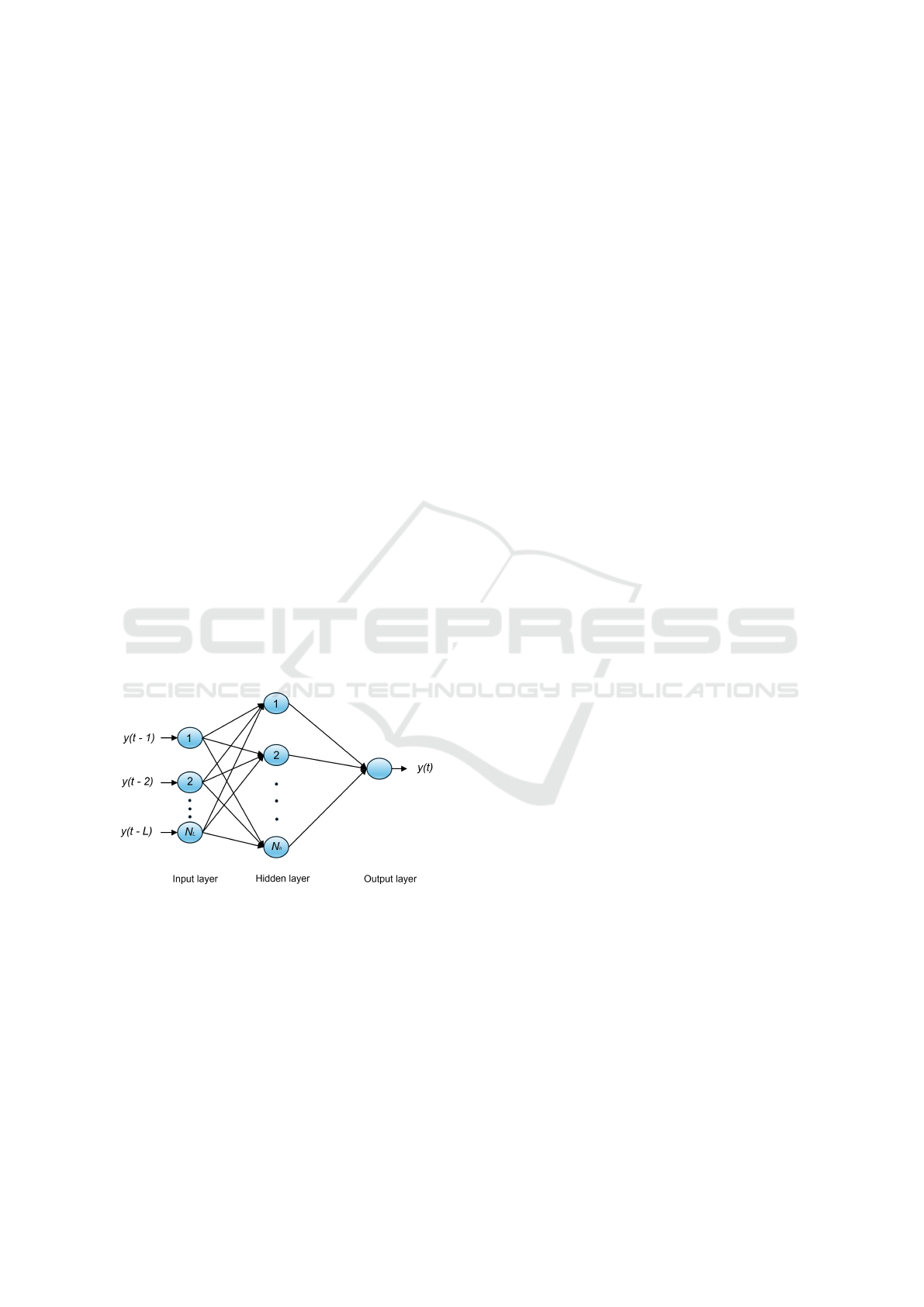
Subsequently, a neural network model is created

using MATLAB’s narnet version 5 (See Figure 1), a

powerful tool provided by MathWorks (MathWorks,

2024). This function takes the decoded parameters as

inputs and constructs a neural network model tailored

to the speciﬁed architecture. The time series data set

is then prepared for training, validation, and testing

stages, ensuring that the data is appropriately parti-

tioned to facilitate robust model evaluation.

The neural network is trained using the

Levenberg-Marquardt algorithm, a widely used

optimization technique for training ANNs. Through-

out the training process, the algorithm monitors the

progress of the neural network, adjusting weights and

biases to minimize errors and improve performance.

Once training is complete, the trained neural net-

work model undergoes a thorough evaluation using an

independent test dataset. Evaluation metrics such as

the correlation coefﬁcient ”r” are computed and we

use the objective to maximize the evolutionary algo-

rithm. These results are stored for further analysis and

comparison, providing a comprehensive and system-

atic approach to training and evaluating neural net-

work models within the framework of evolutionary

search for neural architectures applied to time series

analysis.

This process ensures that the trained models are

rigorously evaluated and optimized, leading to the

discovery of effective neural network architectures for

time series forecasting and analysis.

Figure 1: ANN Model Architecture.

4 RESULTS

This work introduces an advanced tool designed to

teach ENAS applied to time series data. The tool aims

to provide a ﬂexible and modular algorithm that aids

in understanding evolutionary algorithms for optimiz-

ing neural architectures. Its modular design allows

users to easily adjust parameters and the search space,

enabling the exploration of various conﬁgurations and

optimization strategies.

The optimization problem tackled here involves

both the number of neurons in the hidden layer and

the number of delays, showcasing the complexity and

versatility of the neural architectures that can be ex-

plored with this tool.

The tool offers an interactive and educational

platform for experimenting with and learning about

neural architecture evolution, enhancing comprehen-

sion of evolutionary algorithms in Neural Architec-

ture Search (NAS). Its efﬁciency is underscored by a

constrained search space and no need for specialized

hardware, such as GPUs, making ENAS both acces-

sible and practical for educational and research pur-

poses.

Our code serves as a robust resource for under-

standing evolutionary algorithms in ENAS. The mod-

ular nature of the tool allows for a virtually inﬁnite

number of experiments by adjusting parameters such

as population size, number of generations, population

type, crossover, mutation, elitism probability, and di-

versity addition.

We extended our research to multiple datasets to

gain a comprehensive view. The results were highly

competitive, demonstrating our approach’s effective-

ness in automatic neural network searches.

Throughout the study, the evolutionary algorithm

proved capable of identifying optimal solutions even

when surpassing the initial limits, such as exceeding

the proposed limit of 20 neurons or delays. Notably,

the correlation coefﬁcient r was around 0.99 for the

test data set across all results. This emphasizes the ef-

fectiveness of our educational tool, which is designed

to be intuitive and accessible, making it valuable for

both students and researchers, including those with-

out advanced programming expertise.

In Table 1, we present the detailed results of the

best individuals obtained for each data set. It is im-

portant to note that we chose to use the default hyper-

parameters during the search process. This decision

was made with the purpose of establishing a standard

comparison point and evaluating the effectiveness of

our algorithm in different scenarios in a consistent and

equitable manner. These results offer a broader and

more detailed view of how our approach performs

on the task of automatic neural network search on a

variety of data sets, supporting our tool’s ability to

adapt and generate competitive solutions in various

contexts.

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

238

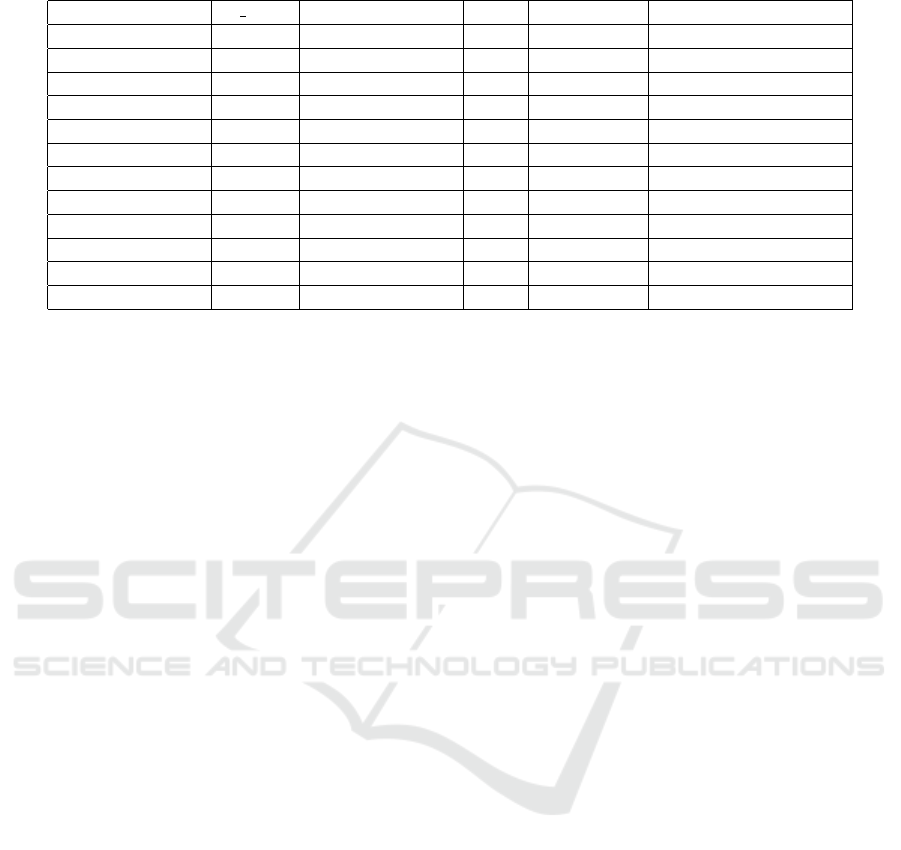
Table 1: Best Individuals in Different Datasets.

Dataset r Test Hidden Neurons Lags Generation Time (Approx hours)

PJM Load hourly 0.99423 17 21 3 0.5

PJME hourly 0.99661 21 27 5 3

PJMW hourly 0.99388 17 27 3 2

NI hourly 0.99624 17 28 3 3

FE hourly 0.99506 17 27 2 1

EKPC hourly 0.98426 17 27 3 2

DUQ hourly 0.99413 18 26 3 1.5

DOM hourly 0.99286 18 28 5 1

DEOK hourly 0.99038 18 19 5 1

DAYTON hourly 0.99417 30 27 5 3

COMED hourly 0.99440 17 27 3 1

AEP hourly 0.9948 17 27 4 1.5

5 CONCLUSIONS

In conclusion, this work introduces an advanced tool

tailored speciﬁcally for teaching ENAS in the context

of time series analysis. The primary goal of this tool

is to develop a ﬂexible and modular algorithm that

enhances comprehension of evolutionary algorithms

in optimizing neural architectures. The modularity of

the algorithm allows for dynamic adjustments in pa-

rameters and search space, empowering users to ex-

plore various conﬁgurations and optimization strate-

gies.

A notable aspect of our approach is the consider-

ation of the optimization problem, which depends on

both the number of neurons in the hidden layer and

the number of delays. This reﬂects the complexity

and versatility of neural architectures that can be ex-

plored and optimized using our tool.

The interactive and educational platform pro-

vided by this approach facilitates experimentation and

learning about the evolution of neural architectures,

thereby enhancing understanding of evolutionary al-

gorithms applied to NAS. Moreover, the efﬁciency

demonstrated in our experiments is attributed to the

restricted search space and absence of specialized

hardware requirements like GPUs, making ENAS ac-

cessible and practical in educational and research set-

tings.

Our code serves as a robust tool for comprehend-

ing evolutionary algorithms in ENAS, allowing for a

wide range of experiments due to its modular nature.

Examples presented in this paper showcase results ob-

tained from experiments using different population

types, demonstrating the versatility and effectiveness

of our approach.

In the experiment with a random population, we

observe convergence in architectures sharing simi-

lar characteristics, highlighting the evolutionary pro-

cess’s effectiveness. The experiment with a uniform

population also yields promising results, especially in

exploring the search space comprehensively in the ini-

tial generation.

Overall, this work contributes signiﬁcantly to the

ﬁeld of ENAS by providing a comprehensive tool for

understanding and optimizing neural architectures in

time series analysis. The future of this research lies in

further reﬁning and expanding the capabilities of our

approach, potentially leading to signiﬁcant advance-

ments in neural architecture optimization and appli-

cation.

6 BROADER IMPACT AND

FUTURE WORK

Our work is focused on democratizing the learning

and application of ENAS for students, profession-

als, or enthusiasts who are not familiar with evolu-

tionary algorithms. With this goal in mind, we have

developed easy-to-use and highly customizable code.

This code allows users to conﬁgure the system speciﬁ-

cally and efﬁciently, without requiring extensive prior

knowledge in the ﬁeld of Neural Architecture Search

and evolutionary algorithms.

The importance of this contribution lies in the

elimination of entry barriers for those who wish to

explore and apply NAS in their research or projects.

By simplifying the process and making the technol-

ogy more accessible, we hope to encourage greater

adoption and understanding of NAS in the scientiﬁc

community. Furthermore, encouraging experimenta-

tion and active learning in this ﬁeld can lead to signif-

icant discoveries and advances in the development of

more efﬁcient and effective neural architectures.

Educational Evolutionary Neural Architecture Search for Time Series Prediction

239

An important aspect to highlight is that it is not

necessary to use specialized technologies such as

GPUs or TPUs to carry out the experiments. Al-

though these technologies can signiﬁcantly speed up

the neural network training process, our approach has

been designed to be efﬁcient and accessible, allowing

experiments to be performed effectively using only a

CPU. This is possible because the search space we

have deﬁned contains only 400 possible architectures.

This restriction on the search space not only reduces

the computational complexity but also makes the opti-

mization process manageable even with limited hard-

ware resources. Furthermore, this feature of our

method allows for greater reproducibility and scala-

bility, since experiments can be performed in more

common and affordable hardware environments. This

facilitates the adoption of our approach in various aca-

demic and research institutions, where computational

resources may be limited.

On the other hand, our work has several limita-

tions. Firstly, our code has been developed in MAT-

LAB which, although it is specialized research soft-

ware, is not accessible to the general public. For this

reason, in future work it is proposed to translate the

code to Python using libraries such as PyTorch or Ten-

sorFlow. This will allow the code to be used in open

source environments, thus expanding its accessibility

and potential to a broader community of students, re-

searchers and professionals.

Also, it’s important to know that our current ap-

proach is speciﬁcally designed to work with time se-

ries. However, to achieve a completely modular ap-

proach adaptable to a wide range of applications, we

propose the development of a modular NAS. This new

approach would allow users to select the speciﬁc task

they want to tackle, such as image restoration, image

classiﬁcation, or natural language processing.

By adopting a modular approach, users could ex-

change data sets and search spaces in a ﬂexible and

customizable manner. This would not only increase

the versatility of our approach but also make it appli-

cable to a variety of domains and speciﬁc needs.

Finally, new efﬁcient evaluation methods can be

successfully applied in our approach. For exam-

ple, implementing a Population Memory ((Xie et al.,

2023; Liu et al., 2021)) could prevent retraining of

the same models. In the current state of our code, the

evolutionary algorithm, upon converging, can con-

tinue training the same architectures until the speci-

ﬁed number of generations is completed. This is due

to the limited range of the search space and in some

cases can even result in overﬂows, where variable val-

ues exceed the deﬁned range of 1 to 20.

ACKNOWLEDGEMENTS

The authors would like to acknowledge the ﬁnancial

support provided by the National Council of Human-

ities, Sciences and Technologies (CONAHCyT).

REFERENCES

Abhishek, K., Singh, M. P., Ghosh, S., and Anand, A.

(2012). Weather forecasting model using artiﬁcial

neural network. Procedia Technology, 4:311–318.

Ahn, C. W. and Ramakrishna, R. S. (2003). Elitism-based

compact genetic algorithms. IEEE Transactions on

Evolutionary Computation, 7(4):367–385.

Box, G. E., Jenkins, G. M., Reinsel, G. C., and Ljung, G. M.

(2015). Time series analysis: forecasting and control.

John Wiley & Sons.

Chong, E., Han, C., and Park, F. C. (2017). Deep learn-

ing networks for stock market analysis and prediction:

Methodology, data representations, and case studies.

Expert Systems with Applications, 83:187–205.

De Jong, K. (2017). Evolutionary computation: a uniﬁed

approach. In Proceedings of the Genetic and Evolu-

tionary Computation Conference Companion, pages

373–388.

Eiben, A. E. and Smith, J. E. (2015). Introduction to evolu-

tionary computing. Springer.

Elliott, G. and Timmermann, A. (2016). Forecasting in eco-

nomics and ﬁnance. Annual Review of Economics,

8:81–110.

Elsken, T., Metzen, J. H., and Hutter, F. (2019). Neural

architecture search: A survey. Journal of Machine

Learning Research, 20(55):1–21.

Fadlalla, A. and Lin, C.-H. (2001). An analysis of the ap-

plications of neural networks in ﬁnance. Interfaces,

31(4):112–122.

Fogel, D. B. and Computation, E. (1995). Toward a new

philosophy of machine intelligence. IEEE Evolution-

ary Computation, 1080.

Gneiting, T. and Raftery, A. E. (2005). Weather forecast-

ing with ensemble methods. Science, 310(5746):248–

249.

Hamilton, J. D. (2020). Time series analysis. Princeton

university press.

Hyndman, R. J. and Athanasopoulos, G. (2018). Forecast-

ing: principles and practice. OTexts.

Li, L. and Talwalkar, A. (2020). Random search and re-

producibility for neural architecture search. In Un-

certainty in artiﬁcial intelligence, pages 367–377.

PMLR.

Liang, Z. and Sun, Y. (2024). Evolutionary neural architec-

ture search for multivariate time series forecasting. In

Asian Conference on Machine Learning, pages 771–

786. PMLR.

Lim, B., Arık, S.

O., Loeff, N., and Pﬁster, T. (2021).

Temporal fusion transformers for interpretable multi-

horizon time series forecasting. International Journal

of Forecasting, 37(4):1748–1764.

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

240

Liu, Y., Sun, Y., Xue, B., Zhang, M., Yen, G. G., and Tan,

K. C. (2021). A survey on evolutionary neural archi-

tecture search. IEEE transactions on neural networks

and learning systems, 34(2):550–570.

opez, G., Sarmiento-Rosales, S. M., Gueymard, C. A.,

Marzo, A., Alonso-Montesinos, J., Polo, J., Mart

ın-

Chivelet, N., Ferrada, P., Barbero, J., Batlles, F. J.,

et al. (2019). Effect of cloudiness on solar radia-

tion forecasting. Solar Energy Resource Management

for Electricity Generation from Local Level to Global

Scale; Nova Science Publishers: New York, NY, USA,

pages 1–11.

MathWorks (2024). Design Time Series NARX Feed-

back Neural Networks. https://la.mathworks.com/

help/deeplearning/ref/narnet.html. Accessed: 2024-

05-31.

Miikkulainen, R., Liang, J., Meyerson, E., Rawal, A., Fink,

D., Francon, O., Raju, B., Shahrzad, H., Navruzyan,

A., Duffy, N., et al. (2024). Evolving deep neural net-

works. In Artiﬁcial intelligence in the age of neural

networks and brain computing, pages 269–287. Else-

vier.

panambY (2024). Hourly energy consumption. https://

github.com/panambY/Hourly Energy Consumption.

GitHub repository. Accessed: 2024-05-31.

Pham, H., Guan, M., Zoph, B., Le, Q., and Dean, J.

(2018). Efﬁcient neural architecture search via param-

eters sharing. In International conference on machine

learning, pages 4095–4104. PMLR.

Real, E., Aggarwal, A., Huang, Y., and Le, Q. V. (2019).

Regularized evolution for image classiﬁer architecture

search. In Proceedings of the aaai conference on arti-

ﬁcial intelligence, volume 33, pages 4780–4789.

Ren, P., Xiao, Y., Chang, X., Huang, P.-Y., Li, Z., Chen,

X., and Wang, X. (2021). A comprehensive survey of

neural architecture search: Challenges and solutions.

ACM Computing Surveys (CSUR), 54(4):1–34.

Robikscube (2024). Hourly energy consumption.

https://www.kaggle.com/datasets/robikscube/

hourly-energy-consumption/data. Accessed: 2024-

05-31.

Rosenberger, D. (2022). Automated machine learning for

time series forecasting.

Shah, D., Isah, H., and Zulkernine, F. (2019). Stock market

analysis: A review and taxonomy of prediction tech-

niques. International Journal of Financial Studies,

7(2):26.

Shumway, R. H., Stoffer, D. S., and Stoffer, D. S. (2000).

Time series analysis and its applications, volume 3.

Springer.

Xie, X., Song, X., Lv, Z., Yen, G. G., Ding, W., and

Sun, Y. (2023). Efﬁcient evaluation methods for neu-

ral architecture search: A survey. arXiv preprint

arXiv:2301.05919.

Zoph, B., Vasudevan, V., Shlens, J., and Le, Q. V. (2018).

Learning transferable architectures for scalable image

recognition. In Proceedings of the IEEE conference on

computer vision and pattern recognition, pages 8697–

8710.

Educational Evolutionary Neural Architecture Search for Time Series Prediction

241