Improving the Performance of Deep Q Network in Decision Making

Environment: Applying Multi-Head Attention into DQN

Ziyi Lu

School of Electronic and Electrical Engineering, Shanghai University of Engineering Science, Shanghai, China

Keywords: Deep Q-Network(DQN), Multi-Head Attention, Deep Learning, Reinforcement Learning, Mahjong.

Abstract: Deep q-network (DQN) is a deep reinforcement learning algorithm. It has been used to solve value function-

based reinforcement learning problems, and with deep neural networks, it can solve complex decision-making

tasks. Multi-Head Attention is a mechanism that can capture various aspects of the input data in parallel,

improving the model's capacity to recognize complex patterns in the data. Mahjong, being a traditional multi-

player imperfect information card game, fits well in training and testing a decision-making model. This study

introduces an application of combination of DQN and Multi-Head Attention mechanism, seeking to enhance

the performance of DQN models by leveraging the benefits of multi-head attention. Through RL Card

platform, which provides a variant of mahjong model that can be used for training, the paper applies the Multi-

Head Attention with its original DQN agent for mahjong. The trained model shows a higher winning rate in

the battle against the baseline model, demonstrating the promotion the combination brings to the mahjong

agent model.

1 INTRODUCTION

In the domain of games, especially in the area towards

decision-making, deep learning(LeCun et al., 2015)

has been pivotal in achieving milestones that were

previously thought to be decades away. In the perfect

information game, AlphaGo utilized deep learning and

tree search to outperform human masters for the first

time, which subsequently caused a research boom in

deep learning in computer gaming. In incomplete

information games, AI using deep learning has been

used in Texas Hold'em(Bowling, et al., 2015),

Doudizhu(Zha et al., 2021) and even DOTA(Berner et

al., 2019).

A notable application of deep learning in gaming is

Deep Q-Network (DQN)(Mnih et al., 2013). It has

been applied to seven Atari games and proved

outstanding performance on six of the games.

Multi-Head Attention(Vaswani et al., 2017) is a

pivotal feature in modern neural network architectures

that allows for concurrent processing of information

across multiple subspaces and positions. This

capability leads to a richer understanding of the input

data, enhancing the model's performance on complex

tasks involving significant contextual interpretation.

https://orcid.org/0009-0004-9946-1516

Originating in China in the late 1800s, Mahjong, a

popular game involving tiles, has since captivated

hundreds of millions of enthusiasts worldwide. It's a

multi-player game that unfolds over several rounds,

characterized by its element of incomplete

information. Players must employ strategy, skill, and

calculation, though luck also plays a role in the game's

outcome.

In the environment of mahjong, the agent

continuously assesses the present condition of the

game to maximize some form of cumulative reward.

This is akin to decision-making processes in real-

world applications, making games an excellent

platform for developing and testing AI algorithms.

Many methods based on the DQN algorithm have

been attempted to be used in mahjong games. In 2021,

DQN has been applied to mahjong with search

algorithm(Sun, 2021). In the case, DRL makes game

trees work better in complex states. However, due to

the influence of the sparse mahjong rewards, the

model meets a lot of draw situations in the game. In

the same year, an improved DQN model towards

mahjong is proposed. It promotes the model with

Double DQN and improved valuation function for

search algorithms(Lei et al., 2021).

522

Lu, Z.

Improving the Performance of Deep Q Network in Decision Making Environment: Applying Multi-Head Attention into DQN.

DOI: 10.5220/0012958200004508

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Engineering Management, Information Technology and Intelligence (EMITI 2024), pages 522-526

ISBN: 978-989-758-713-9

In this paper, the author tries to promote the

performance of the DQN agent for mahjong by

integrating the multi-head attention mechanism into it.

The RL Card platform(Zha et al., 2021) will be used

to test the model.

2 BASIC KNOWLEDGE OF THE

ALGORITHMS

2.1 Double DQN

With advancements in reinforcement learning,

researchers developed the DQN, which enhances the

traditional Q-learning algorithm by integrating deep

learning. DQN computes the Q-value for each action

to inform decision-making, similar to its predecessor.

And it has been proved to be able to master the

difficult control strategies of the Atari 2600 computer

game.

However, like traditional Q-learning, DQN still

suffers from the problem of overestimating Q-values,

which can lead to sub-optimal policy decisions. To

mitigate this issue, the Double DQN was introduced,

building upon DQN by employing a dual network

architecture to reduce Q-value overestimation by

decoupling the selection from the evaluation of the

action.

The DQN algorithm has two neural networks, the

original network and the target network, and although

they have the same structure, the weight updates are

not synchronized. The loss function of the DQN

algorithm's weight updates is defined using the mean

squared error with the following expression:

(1)

(2)

where a is the execution action,

t+1

is the reward

score,

is the current game state information,

t+1

is the next game state information,

is the network

weight,

is the discount factor, and Q(S, a)

represents the valuation of executing action a in state

S. The use of the max operation in the DQN algorithm

for both selecting and evaluating actions introduces an

overestimation bias. This occurs because the

algorithm might frequently choose actions with

exaggerated value estimations, which can adversely

affect the learning of optimal strategies. This issue

highlights a fundamental challenge in reinforcement

learning that needs to be addressed to enhance the

accuracy and reliability of value-based learning

algorithms like DQN. For this reason, the Double

DQN(Van et al., 2016) algorithm decouples the

selection and measurement of actions and rewrites

equation (2) in the following form:

𝑌



Double DQN

𝑅





𝛾𝑄𝑆



,argmax 𝑄𝑆



, 𝑎; 𝜃



, 𝜃



′

 (3)

2.2 Attention

2.2.1 Scaled Dot-Product Attention

Multi-head attention is a feature that plays a crucial

role in the Transformer model, enhancing its

capability to handle diverse data representations

simultaneously. Introduced in 2017, it utilizes parallel

processing heads to capture various data aspects,

significantly enriching the input's representation. This

mechanism underpins the Transformer's advanced

performance across many complex tasks, particularly

in natural language processing.

Figure 1: Scaled Dot-Product

Attention

In actuality, the output matrix is computed from the

attention function, which is simultaneously calculated

on a set of queries organized into a matrix Q.

Attention𝑄, 𝐾, 𝑉  softmax











𝑉 (4)

The dimension of queries and keys is represented by

and

refers to values of dimension in the

equation. The weights on the values are obtained using

a softmax function.

() [( ( ,; ))]

LEYQSa

θθ

=−

DQN

max ( , ; )

tt tt

YR QSa

Improving the Performance of Deep Q Network in Decision Making Environment: Applying Multi-Head Attention into DQN

523

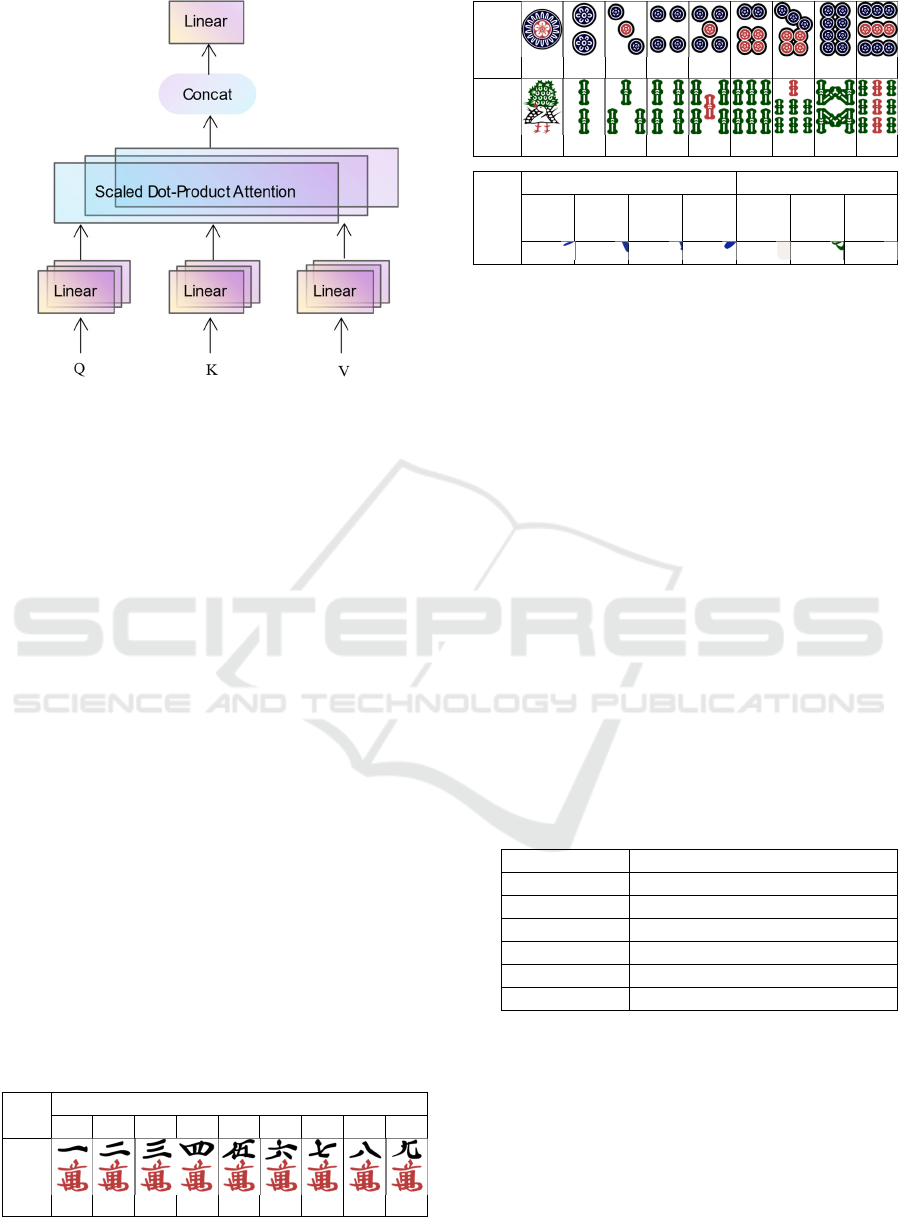
Figure 2: Multi-Head Attention.

This enhanced method utilizes multiple linear

projections to repeatedly alter the dimensions of keys,

queries, and values, boosting the model's capacity to

simultaneously process information across various

subspaces. The subsequent execution of attention

functions on these transformed sets and the

aggregation of their outputs enable a more nuanced

and effective synthesis of information, leading to

superior performance in tasks requiring complex

relational understanding and data integration. The

method is depicted schematically in Figure 2.

3 FEATURES AND MODEL

STRUCTURES

3.1 Features of RL Mahjong

According to the mahjong environment provided in

the RL Card platform, there are 136 tiles, divided into

34 different types, with four tiles of each type. The 34

tile types include three suits—Manzu, Pinzu, and Souzu,

each ranging from 1 to 9, along with 7 different Honor

tiles. A game, comprising multiple rounds, ends upon

meeting the winning condition(Ron).

Table 1: Mahjong Tiles.

umbers

nzu

Pinz

Sou

nors

Winds Dra

ons

Ton Nan Shaa Pei Haku Hats

Chun

3.2 Actions of the Agent

The actions of the agent are as follows:

● Chow: an agent has the option to take a tile that has

just been discarded by opponent on the left to create a

meld. After performing a Chow, the agent must

discard another tile.

● Pong/Kong: an agent has the option to take a tile that

has just been discarded by another player to create a

triplet/quad. This move might result in the skipping of

another player's turn. After performing a Pong, the

agent must discard another tile. After performing a

Kong, the agent will draw another tile and discard one.

● Discard: Discard is the main action the agent would

do in a mahjong game. The discard problem in

Mahjong can be modeled in this ways: as a 34-class

classification problem, where each class corresponds

to one of the 34 unique tile types in the game.

● Ron: In RL mahjong, Ron or not is judged by

whether a player has got 4 sets of tiles or more.

3.3 Encoding of Actions

Table 2: Encoding of Actions.

Indices Correspondin

Tiles

0~8 Souzu, i.e., 1~9s

9~17 Manzu, i.e., 1~9

18~26 Pinzu, i.e., 1~9p

27~29 Hatsu, Chun, Haku

30~33 Ton, Nan, Shaa, Pei

34~36 Pon

, Chow, Kon

Encoding the tiles of a player into four distinct

channels makes it easier to transfer mahjong data,

which helps to process the deep learning algorithms.

EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence

524

4 EXPERIMENTS

4.1 Framework

Figure 3: Training procedure of Multi-Head Attention

combined DQN mahjong model.

Figure 3 shows the training process of combining

MultiHeadAttention and Double DQN network model,

the specific steps are as follows:

●Extract Visible Information: Gather every visible

game information, including the agent's hand, the

discards of all players, the count of remaining cards in

the deck, and the count of game rounds.

●Making Decision: Based on the a priori knowledge

of Mahjong, encode the visible information into

feature data. Make decisions by analyzing the

available data currently.

● Estimate: Evaluate the Action’s Q Value.

● Get result: By training the Double DQN neural

network with the gradient descent algorithm based on

the execution actions, reward scores, current game

state information and next game state information, get

the mahjong learning model.

● Circulate: Loop through this process until the total

number of training steps is reached.

4.2 Setting of the Algorithm

Table 3. Experimental parameter.

Paramete

Value

Batch size 512

Replay memory size 20000

reed

star

1.0

reed

0.1

Learning rate 0.00005

Discount factor

0.9

The settings of the parameters of DQN are the same

for both models. The relevant parameter settings are

shown in Table 3.

4.3 Results

Figure 4: Loss comparison.

The paper pre-trained the original DQN model and the

DQN with Multi-Head Attention agent.

Loss is computed as follows:

●Sample Data: Sample the data such as states,

actions, rewards, next states from the experience

replay buffer.

●Compute Best next Actions using Q-Network:

The Q-network predicts Q-values for next states.

●Loss Computation and Gradient Descent: The Q-

network is updated by training on the present state

batch, the decision made, and the target Q-values

computed. The calculation of loss in reinforcement

learning models employing Q-learning is essential for

refining the predictions of Q-values. This loss,

typically determined by mean squared error, serves to

adjust the predictive model towards greater accuracy

in estimating the expected rewards from actions taken,

thus directly influencing the learning progress and

performance of the agent. This step updates the Q-

network parameters through backpropagation.

Figure 4 shows the loss at each step for both

models.It shows that comparing to the DQN model,

DQN with Multi-Head Attention’s loss curve is lower

in the later stage.

Figure 5: Win rate of vs 3 DQN Agents.

Improving the Performance of Deep Q Network in Decision Making Environment: Applying Multi-Head Attention into DQN

525

The paper tested four agents in total: one DQN agent

enhanced with multi-head attention and three standard

DQN agents. Let them play 1,000 games per episode,

with win rates calculated over a total of 100 episodes.

Figure 5 outlines that the win rate of the Multi-Head

Attention-enhanced DQN agent is significantly higher

compared to the baseline DQN agents. This

enhancement demonstrates a substantial improvement

in model performance.

5 CONCLUSION

In this article, a mahjong based on Deep Q Network is

chosen as the baseline. By combining DQN with

multi-head attention mechanism, the paper promote

the model’s performance. The outcomes of the

experiments show that the algorithm improves the win

rate on RL mahjong by 12 percentage points compared

to the original implemented DQN algorithm. The

superior performance shows that multi-head attention

mechanism can significantly improve the decision

making ability of DQN models in adversarial

environments.

It is acknowledged that various of problems in

reality have a lot of traits in common. For example,

imperfect information, intricate rules for operation and

complex distribution of incentives. Therefore, the

paper gives a new way of optimising decision making

models in real life problems.

REFERENCES

LeCun, Y., Bengio, Y., & Hinton, G. (2015). Deep

learning. nature, 521(7553), 436-444.

Bowling, M., Burch, N., Johanson, M., & Tammelin, O.

(2015). Heads-up limit hold’em poker is

solved. Science, 347(6218), 145-149.

Zha, D., Xie, J., Ma, W., Zhang, S., Lian, X., Hu, X., & Liu,

J. (2021, July). Douzero: Mastering doudizhu with self-

play deep reinforcement learning. In international Conf.

on machine learning (pp. 12333-12344). PMLR.

Berner, C., Brockman, G., Chan, B., Cheung, V., Dębiak,

P., Dennison, C., ... & Zhang, S. (2019). Dota 2 with

large scale deep Reinforcement Learning. arXiv

preprint arXiv:1912.06680.

Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,

Antonoglou, I., Wierstra, D., & Riedmiller, M. (2013).

Playing atari with deep reinforcement learning. arXiv

preprint arXiv:1312.5602.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., ... & Polosukhin, I. (2017). Attention

is all you need. Advances in neural information

processing systems, 30.

Sun, Yiling. Based on Expectimax Search, research on

algorithm for games with incomplete information. [D].

Beijing: Beijing Jiaotong University, 2021.

Lei, Jiewei, Jiayang Wang, Hang Ren, Tianwei Yan, & Wei

Huang. (2021). An incomplete information game

algorithm based on Expectimax search with Double

DQN. Computer Engineering, 47(3), 304-310.

Zha, D., Lai, K. H., Cao, Y., Huang, S., Wei, R., Guo, J., &

Hu, X. (2019). Rlcard: A toolkit for reinforcement

learning in card games. arXiv preprint arXiv:

1910.04376.

Van Hasselt, H., Guez, A., & Silver, D. (2016, March).

Deep reinforcement learning with double q-learning.

In Proceedings of the AAAI conference on artificial

intelligence (Vol. 30, No. 1).

EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence

526