Inheriting Thompson Sampling for Movie Recommendation

Junyan Shi

College of Information, ShanghaiTech University, Pinghu, Zhejiang, China

Keywords: Movie Recommendation System, Thompson Sampling, Inheriting Thompson Sampling.

Abstract: This paper is committed to solving the problem of selecting movie genres for movie recommendation through

historical rating analysis. For the recommendation problem, it is well known that using the Thompson

Sampling(TS) algorithm is a very good method. However, the traditional Thompson Sampling deals with a

Bernoulli invariant problem but the movie-recommended problem is a non-Bernoulli and continuously

changing problem. So, this study improves the Thompson Sampling algorithm with the concept of inheritance

to fit the movie recommendation problem. The research replaces the Beta distribution of the Thompson

Sampling algorithm with a normal distribution and introduces an inheritance proportion to inherit the

experience. The Inheritance Thompson Sampling helps cinema owners decide in real-time which genre of

movie to play to improve the mean rating of the movies in the cinema. The research findings indicate that,

compared to the Thompson Sampling algorithm, the Inheritance Thompson Sampling can reduce the total

regret by 50% to 30%.

1 INTRODUCTION

In today’s era of information explosion, movie

recommendation systems have become a crucial

aspect of cinema business operations. As demands of

audiences for movie quality and content continue to

rise, cinemas must constantly seek new methods to

meet the diverse needs of their patrons. Utilizing past

years' ratings and viewing data across different genres

to predict and determine which movies to introduce

in a given year has emerged as an intelligent

recommendation mechanism. The essence of this

recommendation system lies in analyzing historical

viewing data to explore audience interests and

preferences, thereby providing more personalized and

precise recommendations.

The ratings of different types of movies that have

been attempted in the past few years and now are

important criteria for cinemas to make judgments. By

analyzing and mining this data, cinemas can identify

the currently most popular and trending movie

genres, allowing them to introduce similar types of

movies strategically to enhance the appeal and

competitiveness of their theaters. This data-driven

recommendation system not only helps cinemas

https://orcid.org/ 0009-0000-4323-7903

better understand audience demands but also reduces

market risks and improves return on investment.

The TS (Thompson Sampling) algorithm, as a

classical multi-armed bandit algorithm, exhibits high

applicability and efficiency. The TS algorithm

balances between exploiting the potential best

strategies and exploring new strategies continually,

thereby achieving optimized decisions in uncertain

environments. However, the TS algorithm does not

perform well in situations where the number of

samples is extremely limited. The number of movies

that can be played in cinemas within a year is very

limited. To address this issue, this paper uses a variant

of the TS algorithm called Inheriting Thompson

Sampling. In the movie recommendation system, the

Inheriting Thompson Sampling algorithm can

dynamically adjust the recommendation weights of

various movie genres, enabling real-time perception

and adjustment of audience interests, to enhance the

accuracy and efficiency of the recommendation

system.

This research focuses on exploring the movie

recommendation system based on rating data across

different genres and analyzing the application and

effectiveness of the Inheriting Thompson Sampling

algorithm in this recommendation system. Finally,

Shi, J.

Inheriting Thompson Sampling for Movie Recommendation.

DOI: 10.5220/0012958800004508

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Engineering Management, Information Technology and Intelligence (EMITI 2024), pages 559-563

ISBN: 978-989-758-713-9

559

this paper successfully reduces the regret between the

reward obtained and the optimal reward significantly

when the samples of sampling are very limited.

2 PROBLEM FORMULATION

Multi-armed bandits (MAB) are a systematic way of

modeling sequential decision problems. It aims to

balance the exploration of uncertain options and the

exploitation of known variable options. This

interesting name of the problem comes from a story:

a gambler enters a casino and sits in front of a slot

machine with multiple arms. When he chooses an arm

to pull, the machine generates a random reward that

follows a certain distribution. Because the

distribution of each machine is unknown in advance

by the gambler, he can only use experience to

speculate the real distribution. But next, a serious

problem appears, he will face the dilemma: spending

rounds to pull the arms that already have good returns

in the past might get a good reword. But spending

rounds to pull the arms that have not been fully

explored might find a better arm and get a higher

reward. How to balance between exploration and

exploitation is the key to the MAB problem.

More formally, Multi-Armed Bandit (MAB) solves

the exploration-exploitation dilemma in sequential

decision problems. Let K = {1, . . . , K} be the set of

possible arms/actions to choose from and T = {1, 2, .

. . , n} be the time instants. So, it means at every time-

step t ∈ T the agent has to select one of the K arms.

Then each time an action i is taken, a random reward

ri(Di) is obtained from the unknown distribution Di.

The goal of the problem is to maximize total reward

in n rounds.

The movie recommendation system can be seen as

an MAB problem. Each "arm" in the MAB problem

corresponds to a movie option available for

recommendation, with different arms representing

different genres of movies. When a user interacts with

the recommendation system by selecting a movie, it's

akin to pulling an arm in the MAB problem. The

reward obtained from the chosen movie reflects the

user's feedback, which is the rating of this kind of

movie. However, the movie recommendation system

has a big different from the traditional MAB

problems. First, the probability distributions of

different genres of movies vary every year. It is both

related to previous years and has changed.

3 ALGORITHM

The Thompson Sampling (TS) algorithm was first

proposed in 1933 to address the dual arm slot machine

problem of how to allocate experimental energy in

clinical trials. And now it has been applied in

financial investment, advertising placement, and

other fields.

Algorithm 1: Thompson Sampling.

Initialize the α= (α

,…, α

) and β=

(β

,…, β

)；

for Time index t ← 1 to n do

Sample θ

∼Beta (α

, β

) for each arm

i=1,...,K.

= argmax(θ

)

apply action a

and observe reward r

if r

== 1 then

= α

+ 1

else

= β

+ 1

end if

end for

In algorithm 1, first Initialize α and β vectors.

These vectors represent the number of successes and

failures, respectively, for each arm in the bandit

problem. Then for each round t from 1 to n, where n

is the total number of rounds, for each arm i from 1 to

k where k is the total number of arms, sample a

probability

from a Beta distribution with

parameters

and β

. The Beta distribution is

parameterized by α and β, where α represents the

number of successes and β represents the number of

failures. Then choose the action that maximizes the

sampled probabilities θ

. Apply action a

and observe

the resulting reward r

. In the TS problem, this would

be a binary reward, 1 for success, and 0 for failure.

Finally, update the parameters α and β based on the

observed reward rt. If the reward is 1 which means

success, increment the corresponding α value;

otherwise, increment the corresponding β value. In

summary, the traditional Thompson Sampling is used

for a Bernoulli MAB problem. It gives a Beta prior

distribution for the probability of each action

succeeding.

The traditional Thompson Sampling does not fit

the movie recommendation system very well. Since

each type of movie has different levels of popularity

each year, Thompson Sampling should to resampled

whenever the data set has a rapid change. When the

number of samples that can be extracted is very

limited each time, it undoubtedly causes significant

waste. The movie rating is not a Bernoulli result but

EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence

560

a number in a special interval representative of the

favorite level of the movie.

To deal with the problem above, this paper

proposes a variant of the Thompson Sampling

algorithm for the movie recommendation system. It

will not completely abandon previous experience but

rather partly inherit it. Specifically, for the problem

of data set change and lack of sampling, use the

previous result as the prior distribution and a certain

proportion as an empirical existence. For the non-

Bernoulli reward, use the normal distribution instead

of the Beta distribution.

Algorithm 2: Inheriting Thompson Sampling.

Input: inheritance proportion x

for year index y ← 0 to Y do

for time index t ← 1 to T/Y do

if y = 0 and t < K then

= t

else

Sample θ

∼Normal (µ

*(1-x)+x*h

sqrt(B

/(4*T

(t)))) for each

arm i=1,...,K.

= argmax(θ

)

End if

apply action a

and observe reward

total_reward

= total_reward

+ r

(t+1) = T

(t) + 1

=(total_reward

+x*h

(t+1)+x)

End for

Reset T

and total_reward

for each arm

i=1,...,K.

For i ← 1 to k do

= µ

*(1-x) + h

End for

Algorithm 2 gives the overall process of the ITS

algorithm. First, input an x representing the

proportion of inheritance. At the beginning, sampling

every arm once is the prior distribution. Then for each

year y, sample θ

from the normal distribution with µ

as the mean and sqrt(B2/(4*T

(t))) as the variance

where B is the difference between the maximum

possible reward value and the minimum possible

reward value. µ

is the mean reward of the i-th arm

and T

(t) is the number of samples received from arm

i until round t. Then choose the arm i with the largest

sampling θ

for pulling and get a random reward r

the round t. Then update the mean reward of arm i

with the received reward rt. After the time t finishes

the loop, update the history mean h by the previous

mean µ. For each loop, record the total reward to

calculate the result of cumulative regret.

4 NUMERICAL EXPERIMENT

To evaluate the performance of the ITS algorithm,

this paper uses a real-world dataset, the MovieLens

1M dataset. Movie recommendation systems collect

user viewing data, enabling in-depth data analysis and

market research. This data helps cinema owners

understand user interests and behaviors, guiding the

arrangement of films. Moreover, this data can also

provide cinema owners with insights for business

partnerships and content acquisitions, helping them

collaborate more effectively with content providers to

deliver high-quality content to audiences. When

audiences can easily find the content they love, their

satisfaction and experience significantly improve.

This reflects not only in their viewing process but also

impacts their overall impression of the cinema.

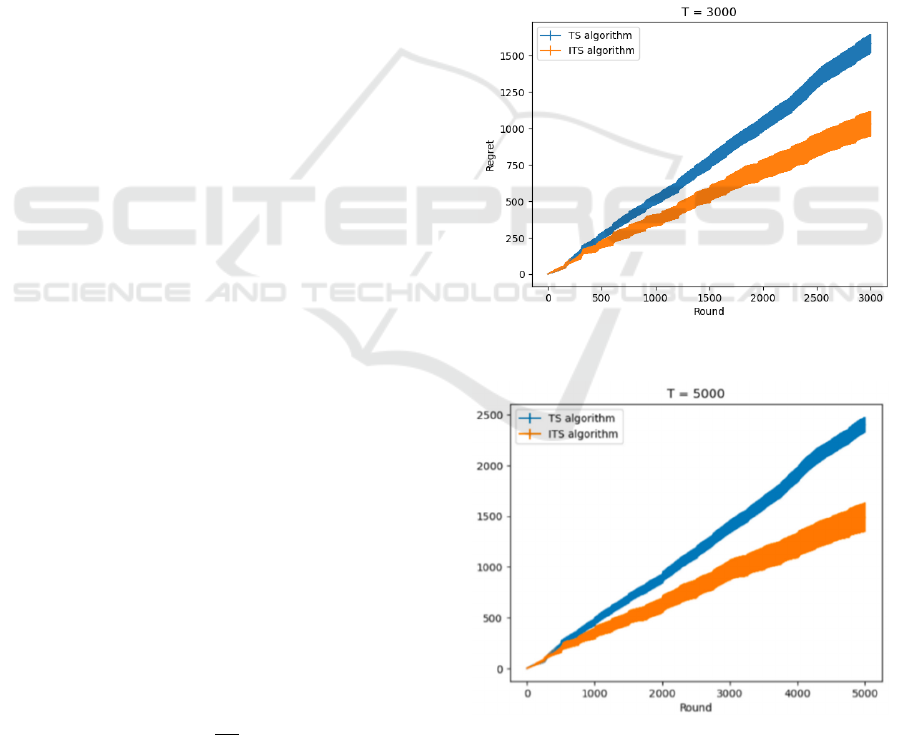
Figure 1: when T=3000.

Figure 2: when T=5000.

Inheriting Thompson Sampling for Movie Recommendation

561

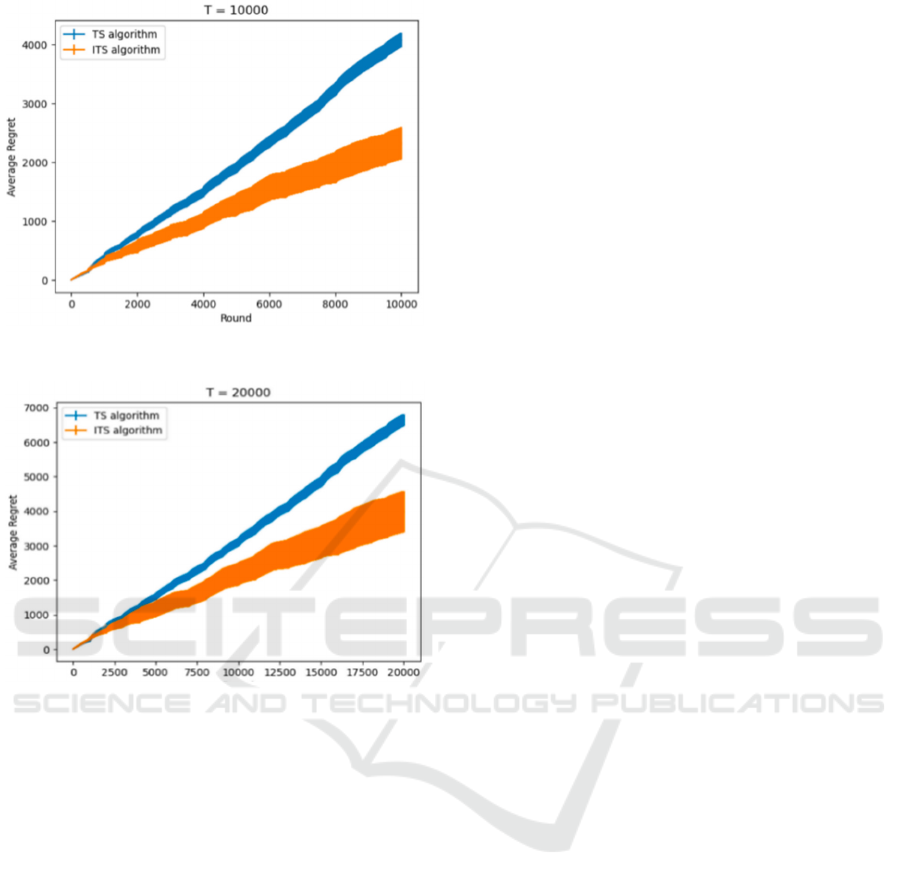
Figure 3: when T=10000.

Figure 4: when T=20000.

High user satisfaction typically leads to higher user

retention rates which brings long-term benefits to the

cinema.

MovieLens 1M dataset is used for movie

recommendation services, which includes 1 million

ratings on 4000 movies with 18 genres. This dataset

contains 6000 users, spanning from 1980 to 2000.

This dataset is widely used for training and validating

recommendation system algorithms and can simulate

real situations to the greatest extent possible. The

MovieLens 1M dataset includes three files,

movies.dat, users.dat, and ratings.dat. The rating.dat

includes all ratings from users, each rating record

includes the user number who gave the rating, the

movie number corresponding to the rating, and the

time when the rating was given. The users.dat

includes the gender, age, occupation, and

corresponding user ID of each user. The movies.dat

includes the name and number of each movie, along

with one or more corresponding movie categories. To

reduce complexity and simplify the algorithm, this

paper overlooks the differences between different

users such as age and gender.

For this dataset, the algorithm first extracts the

ratings for the different movieIDs from rating.dat.

Then mapping these movie IDs to the corresponding

movies and divide these ratings into different genres

from movie.dat. Then these ratings are divided once

again into different parts based on the year. Next, the

algorithm models each genre of movie in the dataset

using independent bandit arms. Further, the

inheritance proportion x is set to 30%. Considering

that a cinema has a very limited number of movies

that can be screened in a year and the gap is very large,

the total round of the sampling is set to 5000, 10000,

and 20000. To compare the algorithm, the total regret

is the average reward of the optimal solution

multiplied by the total number of rounds minus the

actual reward observed.

The performance of the TS and ITS algorithms in

different sampling times is shown in Figure 1,2,3,4.

In each figure, it runs 100 experiments with the

same setting and plots the average regret together

with an error bar. In each figure, The horizontal axis

represents the number of samplings, and the vertical

axis represents the total regret from round 0 to t. The

blue bar is obtained by the TS algorithm and the

yellow bar is obtained by the ITS algorithm. The

lower the regret for the same round, the better the

algorithm's effectiveness. The width of the bar

represents the variance of the algorithm.

It can be clearly observed that the Inheriting

Thompson Sampling has a 30% to 50% improvement

in the total regret. Because every time the dataset

changes, the TS algorithm discards all historical data,

requiring it to resample all bandits to estimate the

current distribution. However the ITS algorithm

obtained a rough distribution using previous data.

This greatly reduces the cost of the exploration phase,

allowing for early identification of better bandits.

However, the yellow bars are thicker than the blue

bars, and as T increases, the blue bars do not become

significantly thicker, while the degree to which the

yellow bars become thicker is more pronounced. This

indicates that the Inheriting

Thompson Sampling

algorithm has a larger variance than the

Thompson

Sampling and increases over time,

5 CONCLUSIONS

This research has successfully adapted the Inheriting

Thompson Sampling(ITS) algorithm to the movie

recommendation system. Compared to the traditional

Thompson Sampling(TS) algorithm, the ITS

EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence

562

algorithm inherits experience in a certain proportion,

which greatly increases the accuracy and positive

feedback of recommendations. In the real world, the

owner of the cinema cannot obtain real-time

information on all ratings of a movie. The owner can

only judge whether to continue playing that type of

movie based on the ratings of the audience in his

cinema. So ITS algorithm can help him make more

accurate decisions. The ITS algorithm can also be

applied in financial investment and other fields with

changing models.

However, the Inheriting Thompson Sampling is

not exactly accurate since the algorithm does not take

into account the differences between different films

of the same genre because of the complexity. The

need to adjust the inheritance proportion x according

to actual conditions also limits the universality of the

code. Therefore, the adaptive inheritance proportion

is worth further research.

REFERENCES

Sivakumar, P et al. (2021). Movie Success and Rating

Prediction Using Data Mining Algorithms.

Kwon, S., and Cha, M. (2013). Modeling temporal

dynamics of movie tastes for recommendation.

Proceedings of the sixth ACM international conference

on Web search and data mining, 363-372.

Russo, D. J. et al (2018). A Tutorial on Thompson

Sampling. Foundations and Trends® in Machine

Learning, 11(1), 1–96.

Berry, D.A. and Fristedt, B (1985). Bandit Problems:

Sequential Allocation of Experiments (Monographs on

Statistics and Applied Probability);Chapman Hall,

Volume 5, p. 7.

Varaiya, P. , et al. (1985). Extensions of the multiarmed

bandit problem: the discounted case. IEEE

Transactions on Automatic Control, 30(5), 426-439.

William R. Thompson (1933). On the likelihood that one

unknown probability exceeds another in view of the

evidence of two samples. Biometrika, 25(3-4):285-294

Korda, N. , et al . (2013). Thompson sampling for 1-

dimensional exponential family bandits. Advances in

neural information processing systems, 1448-1456.

Kaufmann, E. , Korda, N. , & Rémi Munos. (2012).

Thompson sampling: an asymptotically optimal finite

time analysis. Springer Berlin Heidelberg.

Ferreira KJ, et al (2018). Online network revenue

management using thompson sampling. Operations

research, 66(6): 1586-1602

Agrawal, S. and Goyal, N.(2013). Further optimal regret

bounds for thompson sampling. In Artificial

Intelligence and Statistics. 99–107.

MovieLens 1M Dataset.

https://grouplens.org/datasets/movielens/1m/

Inheriting Thompson Sampling for Movie Recommendation

563