Forecasting Demand of Shared Bikes Based on ARIMA Model

Yiming Wang

International Business School Suzhou at XJTLU, Xi’an Jiaotong-Liverpool University, Suzhou, 215000, China

Keywords: Shared Bike, Demand Prediction, ARIMA.

Abstract: This research uses the ARIMA model to analyse and predict the hourly demand of shared bikes in Seoul, for

the model is a better time series model and is suitable for studying the relationship between hours and bicycle

demand. Firstly, the researcher processes the data and selects the data sets needed for the study from the

original data. Secondly, the researcher conducts ADF testing on the data to detect whether differentiation is

needed. Furthermore, through the ACF and PACF images, the p value and q value are determined. Finally,

this paper plots against the fitted model and predicts five periods backward. The prediction results are

consistent with the trend of the curve based on ARIMA model. The experiment yields hourly changes, which

can help enterprises adjust bicycles’ number deployed in a timely manner. However, this research only studies

the relationship between time and demand for shared bicycles, and do not consider the short-term impact of

other factors, like weather and special events on demand. Subsequent researchers can conduct further research

based on this paper.

1 INTRODUCTION

Currently, many factors affect the demand of shared

bikes. Based on this problem, different scholars have

established different models to predict it. Li et al. (Li

et al., 2024) proposed a Multi-scale Spatiotemporal

Graph Convolutional Network (MSTGCN) model.

They noticed that travel demand has different spatial

dependencies at different scales, which can

effectively mine the multi-scale spatiotemporal

characteristics of shared bicycle demand and offer

direction for the future. Accurately forecast public

transportation travel demand. To accurately grasp the

number around the subway station, Yang and Jin

(Yang and Jin, 2023) proposed a prediction method

based on ridge regression. The demand for bicycles at

the three test sites exhibited a pattern of being higher

on vacations than on working days, according to the

forecast findings. Using data mining approaches,

Sathishkumar et al. (Sathishkumar et al., 2020)

predicted and discovered that the temperature and

hour were thought to be the most significant variables

in the hourly rental bicycle count.

Yang et al. (Yang et al., 2020) improved short-

term demand forecasting for shared bicycle systems

using traffic graph structure data. This method may

https://orcid.org/0009-0003-8657-8283

be readily applied to various applications such as

predicting the dynamics of public transportation

systems, and it can be expanded to many current

models that use geographical data. Some restrictions

and potential areas for more research are also

covered. Wei et al. (Wei et al. 2023) considered how

the built environment interacts with demand for

shared bicycles. They employed the Gradient

Boosting Decision Tree (GBDT) model and the

Shapley Additive Explanation (SHAP) method to

forecast demand for shared bicycle travel, analyse the

factors that influence it, and make recommendations

for future developments in the shared bicycle space.

To strengthen the prediction analysis of bicycle

demand, Ramkumar and Saideep (Ramkumar and

Saideep, 2023) proposed a quantum computing

algorithm and used quantum Bayesian network to

anticipate. Compared with the classic algorithm, it

provides calculation acceleration and can speed up

the calculation of the request of shared bikes.

Based on the clustering and prediction analysis of

Dynamic Time Warping (DTW), Le and Leung (Le

and Leung, 2023) performed a spatiotemporal

analysis of shared bicycle demand. Following this,

they employed Bike-share Service (BSS) to carry out

an extensive investigation of the spatiotemporal

Wang, Y.

Forecasting Demand of Shared Bikes Based on ARIMA Model.

DOI: 10.5220/0012961400004508

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Engineering Management, Information Technology and Intelligence (EMITI 2024), pages 659-664

ISBN: 978-989-758-713-9

659

pattern and its influence on land use in urban areas.

Cycle station clusters with varying attributes and use

trends were found by using time series clustering.

Moreover, it is shown that different machine learning

models can accurately predict site kinds based on

surrounding characteristics. Using the demand of

previous identical cases as additional characteristics,

César Peláez-Rodríguez et al. (César Peláez-

Rodríguez et al., 2024) solved the demand prediction

problem by predicting the urging of shared bikes

using machine learning and deep learning multi-

variable time series approaches. In order to answer

questions like how to evaluate many models and

choose the best model for prediction in various

locations, as well as if there is a best prediction model

that is applicable everywhere, Zhang et al. (Zhang et

al., 2023) employed the Latent Dirichlet Allocation

(LDA) model and a computation approach: Area2vec,

a novel approach to urban spatial area similarity,

creates a multi-model visual comparison analysis

system. For forecasting how many people would

check out and how many will come in at each bike

station, a new deep model of a graph convolutional

network (GCN) was proposed by Zi et al. (Zi et al.,

2021). On four actual data sets of bicycle sharing, the

suggested model reliably produced results. Beats the

latest cutting-edge techniques.

Various researchers have achieved varying

degrees of breakthroughs using different models or

methods. However, all the above studies have the

problem of small amount of data and single data type.

In view of this, the following research will use the

AutoRegressive Integrated Moving Average

(ARIMA) model to predict the demand for shared

bicycles, introducing more data and more diverse data

types, to obtain a more accurate demand curve for

shared bicycles.

2 METHODOLOGY

2.1 Data Source and Description

The information is derived from the Kaggle platform

and shows how many bicycles were leased in Seoul

each hour between December 2017 and November

2018. The original data includes temperature,

humidity, wind speed, visibility and other variables.

To facilitate the conduct of this study, only two

variables, rental volume and time, are retained.

2.2 Indicator Selection and Description

The researcher first screened the selected categories

from the original data, as shown in Table 1. In this

study, the researcher used the hourly bicycle demand

as an indicator to explore changes in the hourly

bicycle demand. The variations in the number of

people using shared bicycles at different times

correspond to variations in the population in the same

area, which can be used to timely change the number

of shared bicycles and increase the deployment

efficiency of bicycles.

Table 1: Attribute information for raw data.

Fiel

Instruction Value Range

BA Bicycle Amount [0, 3556]

I Interval 1 hour

2.3 Method Introduction

The AutoRegressive Integrated Moving Average

(ARIMA) model will be used in this study's forecasts.

A statistical model used for forecasting and time

series analysis is the ARIMA model. The term

ARIMA refers to the combination of an

AutoRegressive (AR), a Differential (I), and a

Moving Average (MA) component. The ARIMA

model consists of three primary parts:

Autoregressive (AR) component: This refers to

the linear combination of previous observations

included in the model. This means that there is a

relationship between observations at the current

moment and observations at past moments. The AR

part is denoted by p, which represents the number of

past moments considered in the model. The formula

is:

𝑋



= 𝑐 + 𝜑



𝑋



+ 𝜑



𝑋



+ ⋯ + 𝜑



𝑋



+ 𝜖



(1)

Differential (I) component: This refers to the

difference operation taken to make the time series

stationary. A stationary time series is one in which the

variance and mean do not change over the course of

the series. The I part is represented by d, which

represents the number of times of differentiation. The

formula is:



𝑋





= 𝑋



−𝑋



(2)

Moving Average (MA) Component: This refers to

the linear combination of previous period errors in the

model. The MA part is represented by q, which

represents the number of past errors considered in the

model. The formula is:

𝑋



= 𝜇 + 𝜖



+ 𝜃



𝜖



+ 𝜃



𝜖



+ ⋯ + 𝜃



𝜖



(3)

EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence

660

ARIMA(p, d, q) is a representation of the ARIMA

model, where p, d, and q stand for the orders of

moving average, difference, and autoregression,

respectively. The equation is:

𝑋



= 𝑐 + 𝜑



𝑋



+ 𝜑



𝑋



+ ⋯ + 𝜑



𝑋



−

𝜃



𝜀



−𝜃



𝜀



−⋯−𝜃



𝜀



(4)

The value of the time series at time t is represented

by 𝑋



, and the constant term (intercept)

𝑐 . The

AutoRegressive coefficients, 𝜑



, 𝜑



, ⋯ , 𝜑



, indicate

the weights based on previous data. The previous time

series observations are denoted by 𝑋



, 𝑋



, ⋯ ,

𝑋



. The white noise error term, 𝜀



, denotes the

portion of the model that is random and not explained.

The Moving Average coefficients 𝜃



, 𝜃



, ⋯ , 𝜃



indicate the weights based on previous mistakes. The

previous mistakes are 𝜀



, 𝜀



, ⋯ , 𝜀



3 RESULTS AND DISCUSSION

3.1 ADF Test

When determining whether a time series is stationary,

the Augmented Dickey-Fuller (ADF) test has as its

null hypothesis that it is not. To begin with, the

sequence is stationary if the p value is less than 0.1

(0.05 is an acceptable criteria as well). This suggests

that at the 0.1 level, the null hypothesis is rejected.

Second, before executing the test, a first-order or

second-order difference can be made if the sequence

is not stationary. Test up until the sequence reaches a

stop. Thirdly, utilize the second-order difference as

the ultimate difference order if it is still not stationary.

According to Table 2, the volume of hourly

shared bicycle rentals has a t statistic of -6.947, a p

value of 0.000, and critical values for the 1%, 5%, and

10% of the rental cycle that are -3.431, -2.862, and -

2.567. When the p value is less than 0.000, it is clear

that the null hypothesis is rejected with greater than

99% confidence, suggesting that the series is now

stationary.

Table 2: ADF test.

Differencing

Order

t p

Critical Value

1% 5% 10%

0 -6.94 0.000 -3.43 -2.86 -2.56

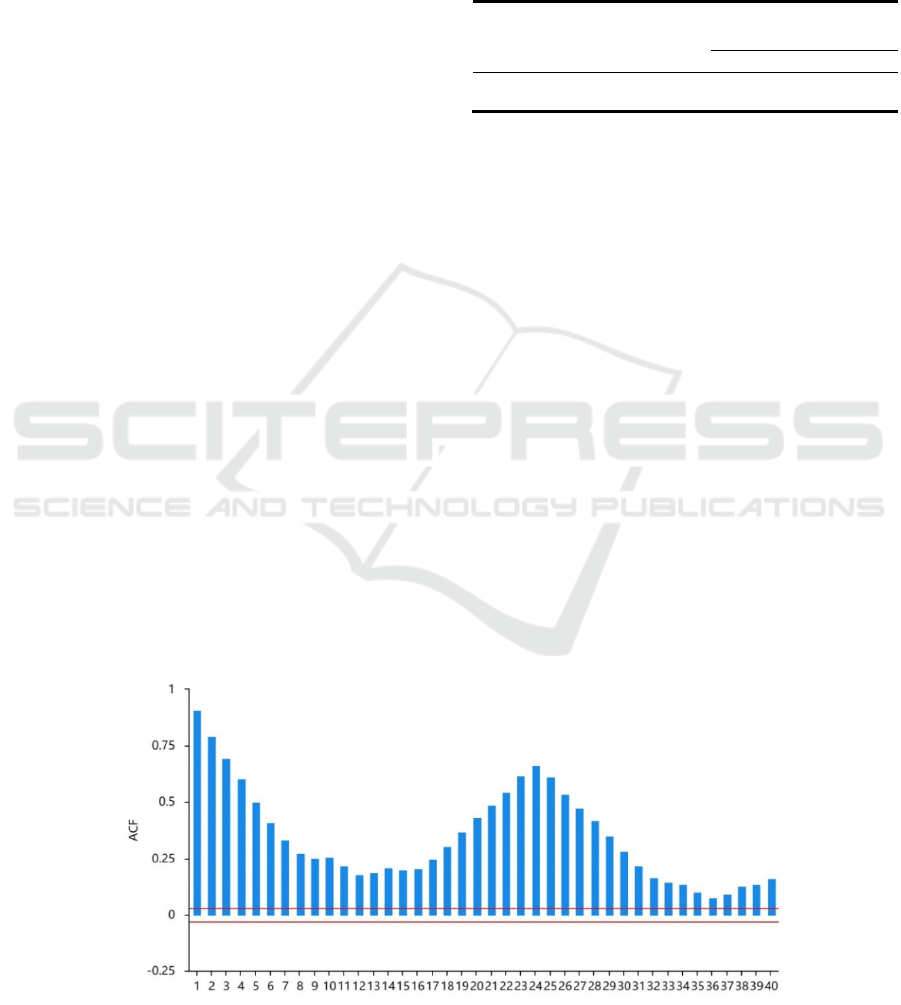
3.2 ACF and PACF Test

Analyzing the ACF and PACF graphs is necessary to

determine the autoregressive order (p) and the

moving average order (q).

Firstly, if the PACF graph is uncensored and the

ACF graph is censored at order q (ACF is 0 after a

certain lag order), the model may be simplified to

MA(q). Secondly, if the ACF chart is uncensored and

the PACF graph is at p censored at the order (PACF

is 0 after a specified lag order), the model may be

simplified to AR (p). Thirdly, you must select the

proper ARIMA order if both of the two charts are

greatly uncensored. The most important order in the

PACF can be designated as the p value, and for ACF,

it’s q value. Fourthly, the data will be white noise and

unusable if the two graphs are both suppressed.

ARMA modelling methodology. Drawing on the

numerical data and the ACF and PACF graphs,

SPSSAU determines and suggests that the moving

average order should be 1 and the autoregressive

order should be 1.

Figure 1: ACF plot.

Forecasting Demand of Shared Bikes Based on ARIMA Model

661

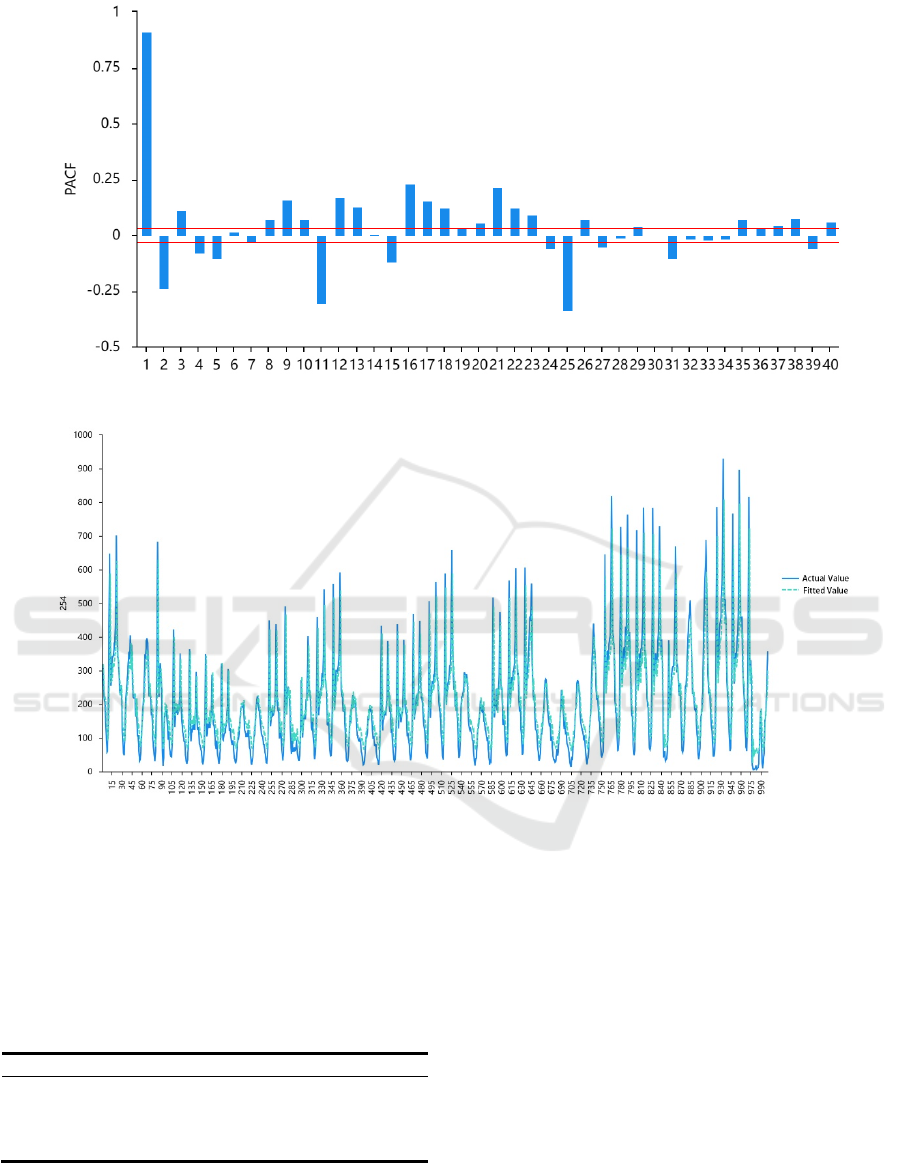
Figure 2: PACF plot.

Figure 3: Numerical model actual value and fitted value.

3.3 Model Evaluation

In order to further increase the rigor of the

experiment, the researcher compares models by

taking different p values and q values to select the

optimal model, as shown in Table 3.

Table 3: Model Evaluation.

Model RMSE AIC BIC

ARIMA(1,0,1) 90.9250 25776.341 25799.077

ARIMA

(

2,0,1

)

90.7170 25768.389 25796.808

ARIMA(1,0,2) 90.5979 25762.705 25791.125

ARIMA

(

2,0,2

)

90.580 25763.822 25797.925

From Table 3, it can be seen that ARIMA(1,0,2)

has the smallest comprehensive value of RMSE, AIC,

and BIC, so p=1, q=2 is selected.

3.4 ARMA Prediction

3.4.1 Model Building Results

As shown in Table 4 (SE is the abbreviation of

Standard Error), all of the components are clearly to

be seen.

First, even when the p value is higher than 0.05,

the table presents the model construction results and

often doesn't need much attention.

Second, while comparing various analytical

models, the information criteria AIC and BIC values

are employed. It is preferable if the two numbers are

lower. The changes in these two values may be

compared if multiple analysis is carried out in order

to fully understand the optimization process of model

creation.

EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence

662

Table 4: ARMA(1,2) model parameter table.

3.4.2 Model Formula

According to ARMA(1,2) Model Parameter Table,

the available model formula is: 𝑦



𝑡



= 51.131 +

0.771 × 𝑦



+ 0.181 × 𝜀



− 0.135 × 𝜀



3.4.3 Type Q Statistic Information

According to Table 5, which also includes the p-value

and statistical magnitude: First, in order to use the

ARMA model, the model residual must be white

noise, meaning it cannot include any autocorrelation.

The Q statistic test may be used for the white noise

test (null hypothesis: the residual is white noise). To

verify whether the residual's first six-order

autocorrelation coefficients fulfill white noise, for

instance, Q6 is utilized in the second scenario. When

there is a larger than 0.1 matching p value, the white

noise test is passed, proving that the data is not white

noise. Q6 may frequently be answered immediately.

Just finish the analysis. Thirdly, if the white noise

assumption is not supported (p<0.05), the model does

not fit well; otherwise, it is frequently regarded as

normally applicable.

Table 5: Model Q statistics table.

Ite

Statistics

value

Q1 0.042 0.837

Q2 0.502 0.778

Q3 0.748 0.862

Q4 9.117 0.058

Q5 12.105 0.033*

Q6 12.140 0.059

3.4.4 Model Fitting and Prediction

Judging from the fitting and prediction of the

numerical model results in figure 3, the numerical

model has a high degree of fitting and is close to the

distribution state of the true value. Therefore, this

model can meet the prediction requirements and can

be used to predict the number of shared bicycle

rentals in Seoul every hour in the future.

The results show that Q6's p-value is greater than

0.05, which means that at the significance level of

0.05, the null hypothesis cannot be ruled out. White

noise makes up the model's residual, and it essentially

satisfies the conditions.

According to the forecast value in the next five

days in Table 6, the number of shared bicycle rentals

in Seoul will gradually decrease from 327.841 units

to 256.539 units in the next five periods.

Table 6: Prediction in five periods.

Predictio

T=1 T=2 T=3 T=4 T=5

Value 327.841 295.981 279.305 266.449 256.539

4 CONCLUSION

This study conducted a univariate prediction of the

hourly shared bicycle demand in Seoul based on the

ARIMA model and obtained relatively accurate

results. This shows that future bicycle demand can be

predicted through time series models. And the more

data samples, the stronger the prediction accuracy.

Based on this, time expansion can be carried out, such

as extending the study of hourly bicycle demand to

studying daily, monthly, and yearly bicycle demand.

In addition, comparative analysis in different

locations can also be conducted, such as studying the

difference in demand between Suzhou and Singapore

at the same time to conduct comparative analysis and

draw conclusions.

On the one hand, this can help companies adjust

the amount of bicycles deployed in a timely manner

to reduce maintenance costs. On the other hand, it can

avoid the situation where too many shared bicycles

affect the appearance of the city and improve the

cleanliness of the city. However, this study only

considered the impact of time on shared bicycles, and

did not consider the short-term impact of other

weather factors such as temperature, precipitation,

wind speed, or special events such as concerts and

marathons on the demand for bicycles. Follow-up

researchers’ further research can be carried out based

on this.

Item Sign Coefficient SE Z P 95%CI

Constant c 51.131 6.878 7.434 0.000 37.651 ~ 64.612

AR α1 0.771 0.027 28.158 0.000 0.717 ~ 0.825

MA β1 0.181 0.032 5.670 0.000 0.119 ~ 0.244

Β2 -0.135 0.048 -2.785 0.005 -0.230 ~ -0.040

Forecasting Demand of Shared Bikes Based on ARIMA Model

663

REFERENCES

Alexis, C, Alison, H., Andy, T., Yang, Y.X., 2020.

Improving short-term demand forecast in bike-sharing

systems by utilizing graph structure information about

flows. In Computers, Environment and Urban System,

83.

An, S., Wei, J., Zhang, Y.T., 2023. Shared bicycle demand

forecast considering the interactive influence of the

built environment. In Science, Technology and

Engineering, 23(26): 11424-11430.

Carmen, K., Leung, E., 2023. Demand for bike sharing is

analyzed spatially and temporally using predictive

analytics and DTW-based clustering. In Transportation

Research Part E: Logistics and Transportation Review,

180.

Chen, H., Chen, L., Xiong, W., Zi, W.J., 2021. TAGCN:

Utilizing a temporal attention graph convolution

network, station-level demand prediction is achieved

for bike-sharing systems. In Information Sciences, 561,

274-285.

Cho, Y.Y., Park, J., Sathishkumar, V.E., 2020. Predicting

the demand for bike sharing in a large metropolis by

using data mining techniques. In Computer

Communications, 153, 353-366.

Ding, X.M., et al., 2024. Public transportation travel

demand prediction based on multi-scale spatio-

temporal graph convolutional network - taking taxis

and shared bicycles as examples. In Computer

Applications, 1-10.

Dušan, F., et al., 2024. Demand forecasting for bike sharing

and cable cars utilizing multivariate time series

techniques based on machine learning and deep

learning. In Expert Systems with Applications, 238.

Harikrishnakumar, R., Nannapaneni, S., 2023. Forecasting

Bike Sharing Demand Using Quantum Bayesian

Network. In Expert Systems with Applications, 221,

119749.

Jin, Q., Yang, X.Y., 2023. Demand prediction for shared

bicycles in subway station areas based on machine

learning. In Journal of Shijiazhuang Railway University

(Natural Science Edition).

Liu, T., Ma, C.X., 2024. Forecasting demand for shared

bicycles using a combination of deep learning

algorithms. In Physica A: Statistical Mechanics and its

Applications, 635, 129492.

Rao, N., et al., 2023. Multi-model visual comparative

analysis for shared bicycle demand forecasting. In High

Technology Communications, 33(12): 1323-1332.

EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence

664