
Research and Parameter Setting Recommendations for the UCB
Algorithm Based on Advertisement Deployment on the Amazon
Website
Yuankun Zhou
a
SWJTU-Leeds Joint School, Southwest Jiaotong University, Xian Road, Pidu, Chengdu, China
Keywords: Multi-Armed Bandits, Upper Confidence Bound (UCB) Algorithms, Exploration and Exploitation Trade-Off,
Machine Learning Applications.
Abstract: The multi-armed bandit problem, a cornerstone of decision-making theory, primarily addresses the critical
balance between exploration and exploitation to optimize choices. This problem is intrinsically linked with
numerous real-world applications, spanning diverse sectors from business to healthcare. It has inspired a
variety of algorithms, among which the Upper Confidence Bound (UCB) algorithm stands out. The UCB
algorithm, noted for its approach of setting an upper confidence interval for each option as a decision criterion,
has captured the attention of many scholars. This paper contextualizes its discussion within the framework of
advertisement deployment for products on Amazon, employing various algorithms to simulate ad campaigns
and analyze their effectiveness. It summarizes the unique characteristics and appropriate contexts for each
algorithm and explores enhancements through structural and parameter adjustments. Based on extensive
experimental data, the study offers recommendations for algorithm parameter settings in various scenarios,
aimed at maximizing the practical application and effectiveness of these algorithms in real-world settings.
This research not only enhances understanding of algorithmic adaptations but also provides valuable insights
for their application across different operational environments.
1 INTRODUCTION
The multi-bandit algorithm is a classical algorithm.
The concept of bandit problem was first proposed by
William R. Thompson in 1933 (Lattimore and
Szepesv ́ari, 2020), and its original purpose is to find
the better solution between two problems. At the
beginning, the number of arms considered in the
bandit problem was only two, that is, each decision
was a simple choice between two arms. The whole
problem was mostly theoretical reasoning within the
scope of mathematics, and no computer algorithm
had been introduced to deal with it h it(THOMPSON,
1933).
The bandit problem has attracted the attention of
many scholars. As the problem continues to develop,
computer algorithms have been introduced into the
problem. Computers have used relevant algorithms to
greatly improve people's ability to deal with the
bandit problem. There are also more and more
a
https://orcid.org/0009-0001-3850-3426
variables brought by environmental factors. With the
introduction of deep learning, the mulit-bandit
algorithm has become more complex and powerful.
As the multi-armed bandit problem evolved, the
sophistication of the algorithms used to address it also
increased significantly. The core objective remained:
to optimize the selection of arms to maximize
rewards. However, the inclusion of multiple arms
introduced greater complexity, requiring algorithms
to efficiently learn and adapt based on the outcomes
of previous selections.
This issue has given rise to numerous algorithms,
along with their variations and extensions, such as the
epsilon-decreasing strategy or contextual bandits,
where additional information about each arm's
context is used to make decisions, represent the
continuous advancement in the field of bandit
algorithms. These methods have proved vital in
numerous applications, from online advertising and
web page optimization to clinical trial design and
financial portfolio selection, showcasing the
Zhou, Y.
Research and Parameter Setting Recommendations for the UCB Algorithm Based on Advertisement Deployment on the Amazon Website.
DOI: 10.5220/0012968400004508
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Engineering Management, Information Technology and Intelligence (EMITI 2024), pages 685-691
ISBN: 978-989-758-713-9
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
685

versatility and power of multi-bandit algorithms in
dealing with complex, uncertain environments.
The applications of multi-armed bandit
algorithms are extensive and impactful across various
domains. In advertising, these algorithms optimize ad
placements by continuously adjusting to user
responses, thereby maximizing click-through rates
and overall campaign effectiveness. This dynamic
approach reduces wastage of ad spend and improves
the relevance of ads shown to users.
Today, advertising permeates every aspect of
people's lives, and for any product, the best way to
gain visibility is through advertising. Advertising
significantly boosts production and consumption by
ensuring that the right products reach the right people.
It generates billions in revenue; according to Statista,
global advertising expenditure is projected to reach
$1.089 trillion in 2024(https://www.statista.com,
2024). This represents a vast market, and enhancing
the quality and precision of advertising campaigns
can yield substantial benefits. Employing superior
algorithms for advertising promotions is undoubtedly
a strategy that can lead to significant economic
advantages.
In the field of applications, numerous scholars
have engaged in practical implementations in this
direction. X. Zhang and colleagues have employed
multi-armed bandit algorithms in a broader context of
generalized item recommendations, striving to make
optimal decisions(). Meanwhile, W. Chen and
associates have utilized the combinatorial Multi-
Armed Bandit (CMAB) framework specifically for
targeted advertising recommendations, addressing
real-world challenges. This paper specially targets the
advertisement deployment on the Amazon shopping
website, utilizing Amazon product data to enable
algorithms to simulate advertising campaigns. By
analyzing the performance of each algorithm based
on data-driven simulations, the study identifies
distinctive features and optimizes parameter settings
for each method. It also provides empirical
recommendations for parameter adjustments tailored
to different scenarios, aiming to maximize
algorithmic performance. This approach not only
enhances the efficiency of advertisement placements
but also contributes to a deeper understanding of how
adaptive algorithms can be fine-tuned for specific
marketing challenges.
2 ALGORITHM MODEL
The Upper Confidence Bound (UCB) algorithm
embodies the optimism principle in uncertain
situations. It assumes that the best possible outcome
is likely and exploits current knowledge to minimize
long-term regret. By optimistically estimating
potential rewards from actions, the UCB algorithm
balances exploring new options and exploiting known
ones, effectively guiding decision-making processes
toward the most rewarding outcomes. This strategy is
crucial for problems like online ad placement and
clinical trials, where decisions must adapt to evolving
data.
In the UCB algorithm, after each decision-making
iteration, the algorithm assigns an Upper Confidence
Bound (UCB) to each arm based on the results
obtained. In the subsequent round, the arm with the
highest UCB is selected, which is anticipated to yield
the greatest return. This cycle is continuously
repeated to ensure that each decision represents the
theoretically optimal choice. While specific
procedures and the calculation method of the UCB
may vary among different UCB algorithms, the
underlying philosophy remains consistent.
For each round 𝑡=1,2,3,…,𝑛, the algorithm
must select an arm 𝐴
from the set
1,2,3,...,𝑖
Upon
making a decision, a random reward 𝑋
is received.
The reward probabilities for each arm are
independent. The cumulative reward for an arm is
defined as 𝐸𝑖 = ∑
𝑋
.The average expected return
for each arm is given by µ𝑖=
∑
, where𝑇
is the
number of times arm 𝑖 has been selected up to round
𝑡. The regret is defined as smaxi(µi) · T −∑T t =
1X , which quantifies the difference between the
cumulative reward of always choosing the optimal
arm and the cumulative reward actually accrued.
2.1 Algorithms Used in the Study
Lattimore presents a classical UCB algorithm and its
derived improved algorithm Asymptotic Optimality
UCB in his paper. For the classical UCB algorithm,
the UCB of each arm can be derived from P:
𝑃μ≥μ+
(
/
)
≤δ for all δ∈
(
0,1
)
(1)
Here, the reward probability of Lattimore's
default arm is consistent with 1-subgaussian random
variables.
The Asymptotic Optimality UCB. Distinct from
the classical UCB, its principal feature is the
elimination of the need to specify the horizon n,
which is the total number of algorithmic explorations.
This is greatly beneficial in practical applications
where the optimal number of explorations is often
unknown. The Asymptotic Optimality UCB
EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence
686

effectively addresses this issue by adjusting the UCB
of each arm based on the number of explorations
already conducted, thus making the algorithm
independent of the total number of rounds. The UCB
for each arm is calculated using the following
formular:
𝐴
=maxμ
(
𝑡−1
)
+
(
)
(
)
(2)
Where 𝑓(𝑡) = 1 + 𝑡 \𝑙𝑜𝑔^2(𝑡) (3)
Jamieson et al. present an alternative Upper
Confidence Bound (UCB) algorithm in their paper,
which adheres to the logic of the classical UCB
framework but incorporates additional parameters.
This augmentation allows for a more flexible
adjustment of the algorithm, enabling it to adapt to a
wider and more complex array of environments
(Jamieson et al., 2014). The computation of the UCB
is as follows
𝑃= μ
+
(
1+β
)
1+
√
ε
(
)
(
)
(
)
(
)
(4)
Where , , and are employed to adjust the algorithm
to suit various environments. The term represents the
standard deviation of the Gaussian distribution, with
the variance being specified as , where and denote
the distribution's range limits.
Garivier and Cappé introduced a novel
computation method for the Upper Confidence
Bound in their paper, incorporating the concept of
Bernoulli Kullback-Leibler (KL) divergence:
𝐷
KL
(
𝑃∥𝑄
)
= 𝑝log
+
(
1 −𝑝
)
log
(5)
KL divergence is typically employed to quantify
the difference between two probability distributions,
p and q. Garivier and Cappé utilized this measure to
supplant the standard calculation in UCB algorithms.
They determine the greatest divergence P that
satisfies the inequality when each arm's value is
below a certain threshold, thus designating P as the
UCB for each arm(Garivier and Capp´e, 2011).
For each arm, the UCB is given by:
𝑃
= 𝑀𝑎𝑥𝑇
(
𝑡
)
∗𝐷
KL
μ
, 𝑇
(
𝑡
)
≤log
(
𝑡
)
+ 𝑐log
(
log
(
𝑡
))
(6)
It should be noted that, in contrast to other UCB
algorithms, the KL-UCB algorithm stipulates that the
reward for each arm must lie within the range [0,1].
This necessitates the transformation of rewards
greater than 1 into winning probabilities prior to
computation.
In the aforementioned algorithm, it is evident that
the computation of the UCB for each arm is relatively
complex, signifying that the algorithm demands
greater computational resources and time. This aspect
becomes apparent during the implementation phase,
where the KL-UCB algorithm requires more time to
process an equivalent number of calculations.
3 AMAZON SHOPPING
RECOMMENDATIONS
3.1 Experimental Background
The experiment constructs a scenario that simulates
the advertisement deployment for products on the
Amazon shopping website. In practical applications,
decisions regarding what to promote and to whom are
crucial, and the data sources are diverse,
encompassing aspects such as product sales, user
reviews, view counts, and prices. From the user's
perspective, demographic factors like gender and age
are considered. Moreover, complex composite data,
such as the purchasing rates of different genders for
various products or the acceptance of differing price
ranges by various age groups, are also integral. These
considerations are critical for designers of advertising
push algorithms.
This paper simplifies the environment by focusing
solely on the impact of product reviews on
advertisement efficacy, treating successful product
sales as a successful advertisement push. It explores
the performance of different algorithms and considers
how adjustments in parameters and structures can
optimize these algorithms. Importantly, while the
simulated environment is singular and defined, real-
world applications are complex and multifaceted.
Based on the experimental results, this study provides
recommendations for algorithmic parameter settings
in other environments to enhance performance under
unknown conditions, thereby ensuring the practical
applicability of the algorithms.
3.2 Experimental Setting
The study employed a dataset from the Amazon
shopping platform that encompasses an array of
products, user ratings on a scale from 0.5 to 5, and
sales figures. The intent was to discern the product
ratings that correlate with the highest purchase
likelihood and to tailor product recommendations
accordingly. The task assigned to the algorithm was
to emulate advertising campaigns based on varying
Research and Parameter Setting Recommendations for the UCB Algorithm Based on Advertisement Deployment on the Amazon Website
687
ratings. The success of an advertisement push was
quantified by actual product purchases recorded in the
database, which, in turn, provided a reward signal to
the algorithm. The overarching aim of the algorithm
was to optimize its selection strategy to favor
products with the highest purchase rates at specific
rating levels, thus mitigating the accumulation of
regret—a measure of the opportunity loss when not
choosing the optimal action.
This simulation reflects the quintessential
dilemmas in real-world advertising optimization
faced by digital platforms: which products to promote
and how to effectively allocate promotional efforts.
Through this research, the authors sought not only to
benchmark the performance of diverse algorithms but
also to enhance their algorithms to maximize the
return on advertising investment. This enhancement
is critical, as it could lead to improved customer
engagement, targeted marketing efficiency, and,
ultimately, increased sales revenue.
3.3 Simulated Result
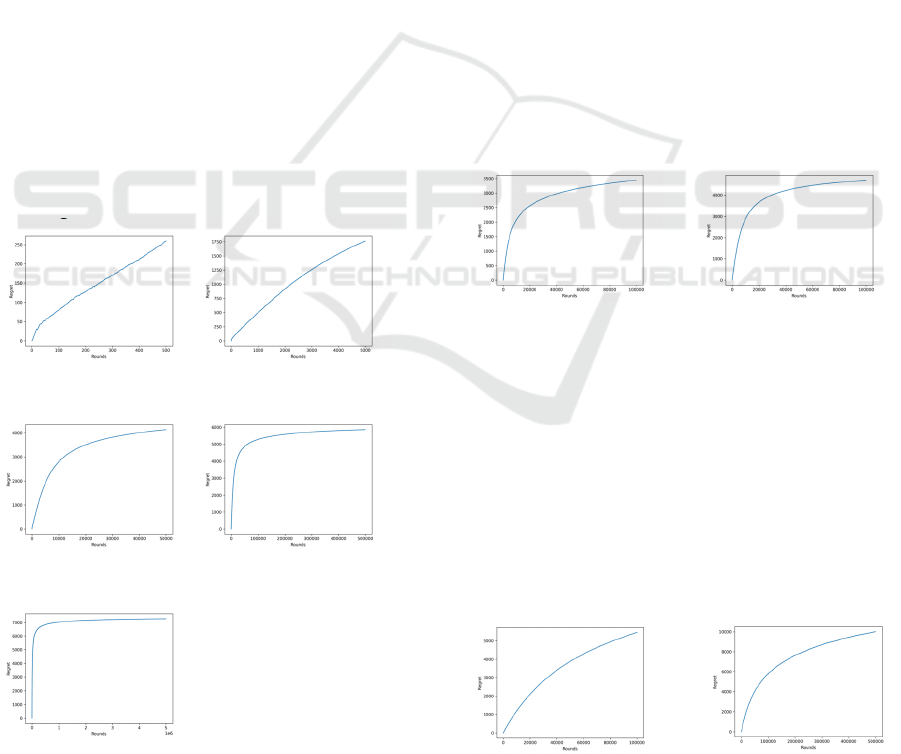
For the classical UCB algorithm, simulations were
conducted with the horizon n set at 500, 5,000,
50,000, 500,000, and 5,000,000, respectively. The
outcomes of these simulations are depicted in Figures
1 through 5.
Figure 1: n=500. Figure 2: n=5,000.
Figure 3 n=50,000. Figure 4: n=500,000.
Figure 5: n=5,000,000.
From Figures 1 to 5, it is evident that as the number
of explorations increases, the accumulation of
algorithmic regret also increases, though not in a
strictly linear manner. From Figure 1 with n=500 to
Figure 5 with n=5,000,000, the number of
explorations has increased by a factor of 10,000, yet
the accumulation of regret has only increased by
approximately 50 times. This observation suggests
that while regret does escalate with more
explorations, its rate of increase diminishes as the
number of explorations grows, indicating a sub-linear
relationship between exploration quantity and regret
accumulation. With the increase in the number of
explorations, the variation in the Regret of the UCB
algorithm exhibits a logarithmic form, which is
consistent with its theoretical Regret behavior.
For the Asymptotic Optimality UCB algorithm,
the number of explorations, n, is set to 100,000 and
contrasted its results with the classical UCB
algorithm addressed in the previous query. It is
important to clarify that this specification of n as
100,000 does not represent a parameter passed to the
Asymptotic Optimality UCB algorithm but merely
sets a stopping point for the exploratory process
within the program. If desired, the Asymptotic
Optimality UCB algorithm is fully capable of
continuing its exploration beyond this limit.
Figure 6: Asymptotic Figure 7: Classical UCB.
Optimality UCB.
The results reveal that the Asymptotic Optimality
UCB algorithm accumulates less Regret and does not
require pre-specification of the number of
explorations. This characteristic bears significant
implications for practical applications.
For the Lil'UCB algorithm, the number of
experimental runs was set to 100,000 and 500,000,
respectively. Following the recommendations of
Jamieson et al., is set to 0.01, was set to 1,and
within the open interval (0, 1).
Figure 8: n=100,000. Figure 9: n=500,000.
EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence
688
The experimental outcomes indicate that the
performance of the algorithm was suboptimal. This
subpar performance is attributed not to inherent
deficiencies in the algorithm itself but to a parameter
configuration ill-suited to the experimental context.
Subsequent sections will discuss enhancements to the
algorithm, including modifications to the coefficient
settings and recommendations for other operational
environments.
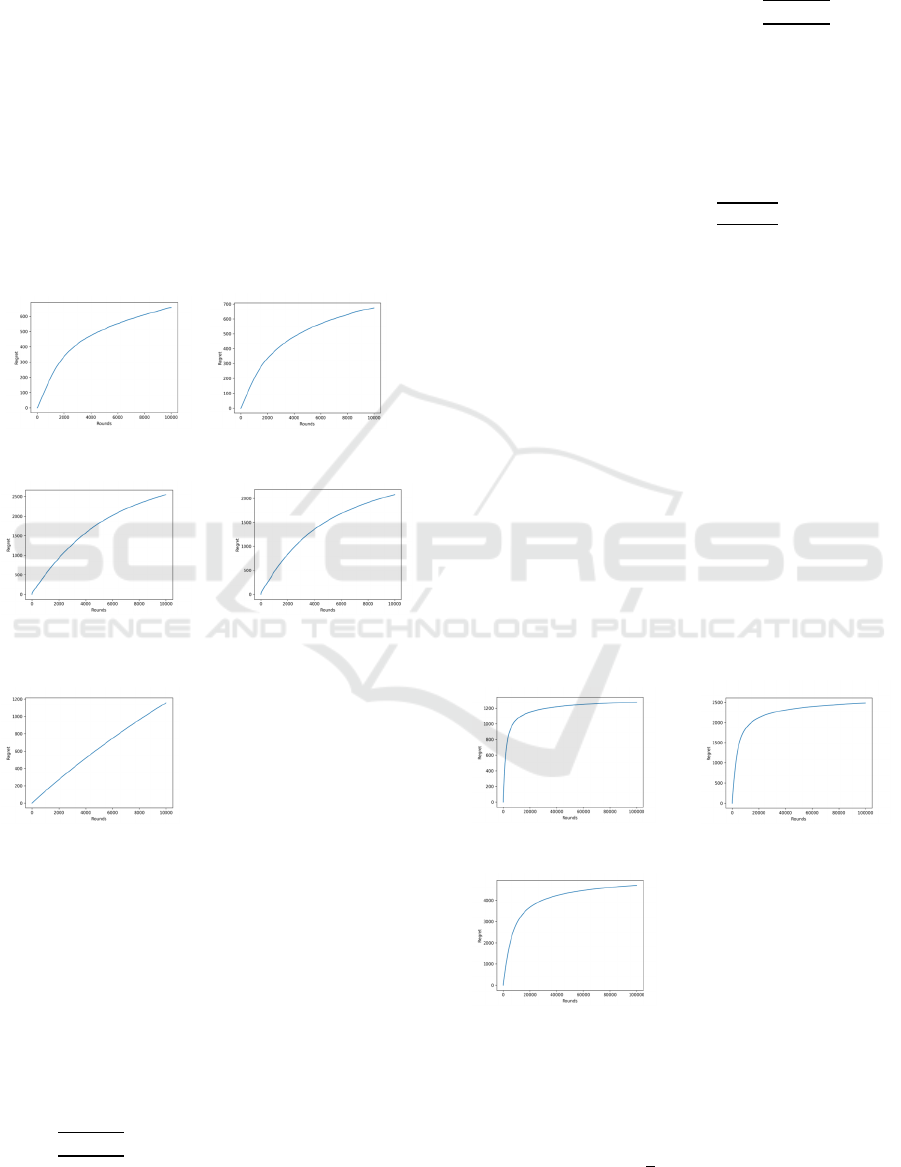
In the case of KL-UCB, two distinct methods
were employed for calculating the UCB of each arm:
linear root-finding and bisection root-finding. The
number of explorations, n, was set at 10,000, and the
results were compared with three other algorithms,
yielding the following outcomes:
Figure 10: KL-UCB:Linear. Figure 11: KL-UCB:bisection.
Figure 12: Classical UCB. Figure 13: Asymptotic
Optimality UCB.
Figure: 14: Lil'UCB.
The results indicate that KL-UCB outperforms the
others, attributable to its parameter configuration and
algorithmic framework being more conducive to
environments with fewer exploration instances,
specifically at lower values of n. This will be
elaborated upon in the subsequent sections.
3.4 Improvement
In the preceding experiments, the UCB algorithm's
computation of the UCB for each arm was denoted as
μ
+
(
/
)
, under the condition that δ must be
significantly smaller than 1/𝑛, concretely set as δ=
1/𝑛
during experimentation. It is manifest from the
formula that the exploration extent of different arms
by the algorithm is determined by
(
/
)
, which
constitutes the crux of the entire algorithm.
Consequently, one can modulate the overall
exploratory behaviour of the algorithm to adapt to
varying environments by introducing a coefficient
within the radical .The revised computation for UCB
is as follows:
𝑃
= 𝜇
+
(
/
)
(7)
Subsequent empirical observations revealed a
direct proportionality between the exploration of
suboptimal choices by the algorithm and the
coefficient 𝑐; Larger 𝑐 values resulted in more
extensive exploration of suboptimal options. This
strategy enables the algorithm to more effectively
mitigate the selection of erroneous options due to
low-probability events. However, this may also
precipitate a wasteful expenditure of resources, as the
algorithm could allocate an excessive number of
explorations to suboptimal options, culminating in an
augmented accumulation of loss or, in algorithmic
vernacular, a heightened aggregation of Regret.
Therefore, striking an optimal balance in exploration
levels is paramount to enhancing algorithmic
efficacy. The algorithm's performance for c =1, 2, and
4, set against the backdrop of the antecedent Amazon
product dataset, is delineated below.
Figure 15: c = 1. Figure 16: c = 2.
Figure 17: c = 4.
The outcomes indicate that a larger coefficient c
correlates with an increased accrual of regret from
1200 (Fig.15) to more than 4000 (Fig.17). Drawing
upon additional experimental data, it is advised to set
the coefficient c to
(
max
(
μ
)
−min
(
μ
))
. Here,
Research and Parameter Setting Recommendations for the UCB Algorithm Based on Advertisement Deployment on the Amazon Website
689

max
(
μ
)
symbolizes the winning probability of the
optimal choice, and min
(
μ
)
that of the least
favorable choice. The rationale is that the degree of
exploration by the algorithm should be contingent on
the interval between the best and worst options; the
narrower the interval, the more indistinguishable the
options, and thus, the more challenging it is to discern
the optimal choice, necessitating a more extensive
exploration. Notably, both max
(
𝜇
)
and min
(
𝜇
)
are
based on pre-experimental empirical estimations,
rendering the algorithm's performance highly
dependent on these preliminary assessments. The
recommendations presented here serve as a heuristic,
and parameter tuning may require further specificity
to adapt to alternative scenarios.
The empirical data from previous Lil'UCB
experiments reveal that, for different values of n, the
algorithm's accumulation of regret follows a trend
resembling a linear increase. This suggests that the
algorithm's control mechanism, represented by
𝑃= μ
+
(
1+β
)
1+
√
ε
(
)
(
)
(
)
(
)
(8)
It does not effectively facilitate an increased
frequency in selecting the optimal option over time.
This issue is primarily due to the parameter settings.
In terms of the algorithm's objectives, as the selection
count for an option increases, its average winning rate
should become more certain and its UCB should
decrease accordingly. Therefore, an enhancement can
be introduced into the
(
)
(
)
(
)
(
)
component by incorporating a variable c, which
impacts 𝑇_𝑖 to 'amplify' the effect of 𝑇_𝑖 , leading to
a decrease in the overall UCB value as the selection
count for an option increases. The revised formula for
UCB is now denoted as:
𝑃= μ
+
(
1+β
)
1+
√
ε
(
)
(
)
(
)
∗
(
)
(9)
Furthermore, the selection of 𝑐 must also consider
the total number of explorations 𝑛 . Based on
extensive experimentation, it is advised to set to a
relatively universal value of 𝑐, aiming for enhanced
performance. The experimental results are as follows,
for n =100,000 and n = 500,000:
Figure 18: n=100,000. Figure 19: n=500,000.
As can be observed, the algorithm, after the
enhancements, has reduced the regret to one-tenth of
its initial magnitude, significantly boosting
performance and decreasing inefficiencies. The
relatively universal parameter 10
/𝑛 has already
shown commendable performance; however, the
parameters can still be specifically tailored to better
suit the environment of Amazon product
advertisement campaigns. By evolving the simple
addition of the parameter 𝑐 to 𝑐𝑇
and specifically
set value, significant improvements in algorithmic
performance are achieved. This modification allows
the algorithm to identify the optimal option more
rapidly, thus minimizing wastage. Below is the
description of the revised algorithm:
𝑃= μ
+
(
1+β
)
1+
√
ε
(
)
(
)
(
)
∗
(
)
(10)
Where c = 10
/𝑛 . The performance of the
algorithm after the specificity-enhanced
improvements is as follows:
Figure 20: n=100,000. Figure 21: n=500,000.
It is evident that the performance of the algorithm
has significantly improved, achieving the optimal
choice with a minimal number of explorations. The
data corroborate this, showing that the accumulation
of regret is exceptionally low. It is important to note
that this performance is due to parameters specifically
tailored to a particular environment, and such
performance may not be replicable in different
settings. Particularly in scenarios where there is
minimal variance among options, this parameter
setting does not sufficiently explore suboptimal
choices, which could lead to erroneous decisions by
the algorithm. For other scenarios, a more general
parameter setting of is deemed safer.
EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence
690

The form should be completed and signed by one
author on behalf of all the other authors.
4 CONCLUSIONS
The experimental results illustrate that different
algorithms excel in specific environments. The
Asymptotic Optimality UCB, with its advantage of
not requiring a preset number of explorations, is
particularly suitable for exploring unknown
environments in practical applications. The Lil'UCB,
with its array of adjustable parameters, allows for
tailored settings to enhance adaptability across
diverse environments. The KL-UCB, despite its
computational complexity, demonstrates superior
performance with a limited number of explorations
and exhibits robustness against environmental
variations, suggesting that it can perform well across
a range of scenarios without the need for specific
adjustments.
In addition to the UCB variants discussed in detail
above, numerous other derivatives have been
proposed, such as the UCB-g (greediness) algorithm
by Z. Wang et al(Wang et al., 2018)., the k-Nearest
Neighbour UCB algorithm by H. Reeve et al(Reeve
et al., 2018)., and the Restless-UCB by S. Wang
et al(Wang et al., 2020). Each algorithm brings
unique advantages, but a pivotal issue in practical
applications is how to select the appropriate algorithm
and set parameters effectively, often proving more
crucial than the study of the algorithm itself.
The experimental outcomes discussed underscore
that the efficacy of an application is not solely
dependent on the algorithm itself, but significantly on
the selection and calibration of the algorithm. This
paper provides recommendations for choosing
algorithms and setting parameters tailored to specific
scenarios, offering guidance for practical
implementations
REFERENCES
Chen, W., Wang, Y., and Yuan, Y. (2013). Combinatorial
multi-armed bandit: General framework and applica-
tions. In International conference on machine learning,
pages 151–159. PMLR.
Garivier, A. and Capp´e, O. (2011). The kl-ucb algorithm
for bounded stochastic bandits and beyond. In
Proceedings of the 24th annual conference on learning
theory, pages 359–376. JMLR Workshop and
Conference Proceedings.
Jamieson, K., Malloy, M., Nowak, R., and Bubeck, S.
(2014). lil’ucb: An optimal exploration algorithm for
multi-armed bandits. In Conference on Learning
Theory, pages 423–439. PMLR.
Lattimore, T. and Szepesv´ari, C. (2020). Bandit
algorithms.Cambridge University Press.
Reeve, H., Mellor, J., and Brown, G. (2018). The k-nearest
neighbour ucb algorithm for multi-armed bandits with
covariates. In Algorithmic Learning Theory, pages
725–752. PMLR.
Thompson, W. R. (1933). On The Likelhood That One
Unknown Probability Exceeds Another In view of the
Evidence of Two Samples. Biometrika, 25(3-4):285–
294.
Wang, S., Huang, L., and Lui, J. (2020). Restless-ucb,
anefficient and low-complexity algorithm for online
restless bandits. Advances in Neural Information
Processing Systems, 33:11878–11889.
Wang, Z., Zhou, R., and Shen, C. (2018). Regional multi-
armed bandits. In International Conference on Artificial
Intelligence and Statistics, pages 510–518.PMLR.
Zhang, X., Xie, H., Li, H., and CS Lui, J. (2020). Con-
versational contextual bandit: Algorithm and
application. In Proceedings of the web conf. 2020,
pages 662–672.
Statista. 2024. Advertising – Worldwide. [Online].
[Accessed 17 April 2024]. Available from: https://
www.statista.com/outlook/amo/advertising/worldwide
#ad-spending
Research and Parameter Setting Recommendations for the UCB Algorithm Based on Advertisement Deployment on the Amazon Website
691
