Advancing House Price Forecasting: Linear Regression and Deep

Learning Models Analysis

Fengyuan Tian

Victoria College, University of Toronto, Toronto, Canada

Keywords: Linear Regression, Feedforward Neural Network, Deep Learning Techniques.

Abstract: The prediction of housing prices has received widespread attention from researchers due to its importance.

This study offers a comprehensive analysis of house price forecasting, employing both traditional linear

regression models and advanced deep learning techniques to enhance prediction accuracy. Through

meticulous comparison and experimentation, deep learning methods, particularly feedforward neural

networks, emerged as significantly superior in capturing complex nonlinear relationships and high-

dimensional data patterns compared to linear regression models. In order to improve prediction performance,

the research integrates data preparation, feature selection, and model evaluation as it methodically investigates

different aspects of the dynamics of the housing market. Results highlight the potential of deep learning

techniques to offer substantial improvements over conventional models, particularly in recognizing spatial

and temporal trends in house pricing data. Future research aims to integrate external factors like economic

indicators and urban development parameters to refine and expand predictive capabilities. It is anticipated

that this strategic approach will improve the model's accuracy and usefulness in real-world real estate market

analysis, enabling better informed decision-making processes.

1 INTRODUCTION

House pricing is a complex area that depends on

many different elements (Cho, 1996), including size,

location, amenities, and state of the economy. It is

essential for buyers, sellers, real estate agents, and

policymakers to comprehend and forecast house

prices to make well-informed decisions. (Cynthia,

2019) Not only that, but house prices are a way for

many people to manage their money. (UB, 2023)

Fluctuations in house prices not only reflect socio-

economic conditions and people's income and

consumption levels, but also play a very important

role in the capital markets. Therefore, the ability to

predict house prices has become a major concern and

a necessity for people. (Madhuri, 2019) While

traditional statistical techniques like linear regression

have been commonly utilized to analyze house, prices

based on different attributes, the emergence of deep

learning has provided new opportunities to improve

prediction accuracy and address the complexities of

real estate data. (John, 2007) This study seeks to

investigate and contrast the efficacy of linear

https://orcid.org/0009-0008-5816-9737

regression models and deep learning methodologies

in forecasting house prices, underscoring the

importance of advanced modeling strategies in

today's real estate industry.

In the world of real estate price prediction,

extensive research has been conducted using both

conventional statistical methods and modern machine

learning techniques. (Zietz, 2008) Initially, studies

primarily focused on linear regression models to

identify the key factors that influence house prices.

One of the most fundamental forecasting techniques

is based on the assumption that a target value, such as

the price of a house, and one or more independent

variables, such as the size, location, age, etc., have a

linear connection. However, over the past few years,

there has been a shift towards using deep learning

models to discover intricate patterns in the data and

to perform more difficult training. (Geerts, 2023)

Studies have demonstrated that these methods can

significantly enhance prediction accuracy compared

to traditional models. The features of the data, the

intricacy of the issue, and the prediction's accuracy

requirements all influence the model selection.

794

Tian, F.

Advancing House Price Forecasting: Linear Regression and Deep Learning Models Analysis.

DOI: 10.5220/0012973500004508

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Engineering Management, Information Technology and Intelligence (EMITI 2024), pages 794-798

ISBN: 978-989-758-713-9

(Geerts, 2023) Typically, the best model is identified

through cross-validation, tuning hyperparameters,

and comparing performance evaluation metrics of

different models. Moreover, researchers have also

explored hybrid models that combine linear

regression with machine learning techniques, striking

a balance between interpretability and prediction

performance.(Cloyne, 2019) These advancements

highlight the ever-evolving nature of research in

house price prediction and the continuous endeavor to

refine predictive models (Durganjali, 2019).

In the field of house price forecasting, this study's

main goal is to carefully compare deep learning

techniques with linear regression models. Initially,

the study employs linear regression as a baseline to

gauge prediction accuracy using conventional

features. Subsequently, it delves into the realm of

deep learning models to scrutinize their efficacy in

capturing intricate non-linear relationships and high-

dimensional data structures. The study then

meticulously assesses and contrasts the predictive

capabilities of these models to discern the most

efficient approach for house price prediction.

Furthermore, it scrutinizes the significance of diverse

features in predicting house prices and investigates

how variations in model configurations influence

performance outcomes. The results of the experiment

highlight how deep learning methods can surpass

conventional models in performance, particularly in

capturing spatial and temporal trends. This research

not only enriches the scholarly discourse on real

estate price prediction but also furnishes valuable

insights for real estate market stakeholders,

emphasizing the imperative of leveraging advanced

computational methodologies for informed decision-

making.

2 METHODOLOGY

2.1 Dataset Description and

Preprocessing

The dataset employed in this study comprises

residential housing sales data, covering an extensive

array of attributes, including the quantity of

bedrooms, baths, and square footage of the living

area, lot size, floors, waterfront status, view quality,

condition, above ground living area square footage,

basement area square footage, year built, and

renovation year. Originating from a publicly

accessible source as Kaggle, this dataset mirrors real-

world housing market dynamics, providing a robust

foundation for predictive modeling of house prices.

Data preprocessing involved handling missing

values, normalizing numerical features to a uniform

scale, and encoding categorical variables to facilitate

the use in machine learning models. This step ensures

that the data fed into the model is clean and

standardized, thereby improving the reliability of

predictions.

2.2 Proposed Approach

The core objective of this research is to predict

housing prices using a blend of linear regression and

deep learning methodologies, thereby leveraging the

strengths of both traditional statistical models and

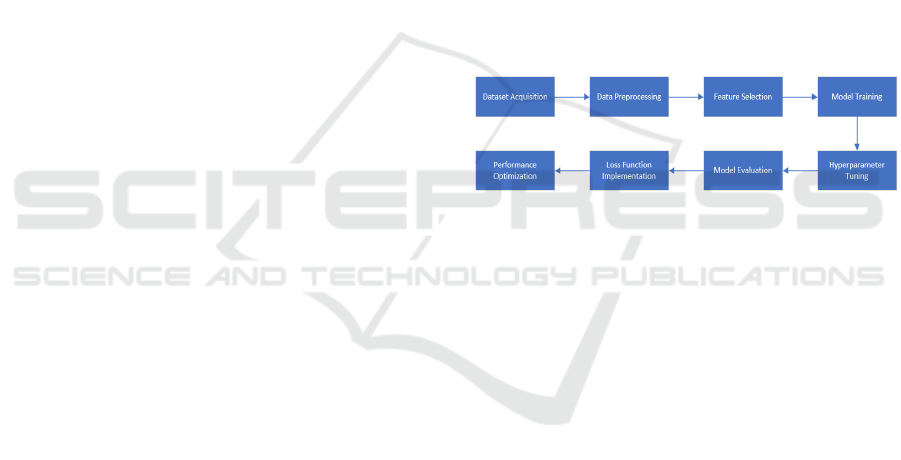
advanced neural networks. The proposed approach

involves a systematic process, starting from data

preprocessing, feature selection, model training, and

finally, evaluation of model performance. The

pipeline of this model is illustrated in Figure 1,

showcasing the seamless integration of these steps to

predict housing prices accurately.

Figure 1: The pipeline of the model (Photo/Picture credit:

Original).

2.2.1 Linear Regression Model

Linear regression is the main statistical method

utilized in the predictive modeling of this study.

When this approach is used, the relationship between

the dependent and independent variables is described

by fitting a linear equation to the observed data.

Linear regression is a practical technique for

examining the factors influencing property prices

because it is simple to comprehend and implement. In

order to establish a baseline model and capitalize on

its capacity to clarify the relative importance of

different factors in predicting property prices, this

study uses linear regression. The steps involved in

implementing the model are choosing pertinent

features, fitting the model to the training set, and

using the model to forecast unknown data.

Linear regression models describe the relationship

between independent parameters (like the area,

location, and age of the property) and a dependent

variable (like housing pricing) by fitting a linear

equation to observed data. The basic formula can be

represented as:

01122 nn

YXX X

ββ β β

=+ + ++ + (1)

Advancing House Price Forecasting: Linear Regression and Deep Learning Models Analysis

795

Here, 𝑌 is represented as the dependent variable

(house prices).

𝑋



, 𝑋



…,𝑋



are represented as the

independent variables (factors affecting house prices).

The intercept of the equation, denoted as

𝛽



represents the expected value of Y in the scenario

where all independent variables (

𝑋



) are zero.

𝛽



, 𝛽



,…,𝛽



are the coefficients for each

independent variable. These coefficients determine

the weight or importance of each variable in

predicting the dependent variable. ε is the error term,

explaining why the values that are observed are

different from predicted values. The internal

workflow of a linear regression model mainly

includes the following steps: Feature Selection:

Selecting features from the data that are highly

correlated with house price predictions. Model

Training: Estimating the model's coefficients (β) by

minimizing the error (usually by the method of least

squares) using the training dataset. Model Evaluation:

Assessing the predictive ability of the model using a

test dataset, primarily through statistical measures

such as R² and Mean Squared Error (MSE).

Predicting Unknown Data: Making predictions using

the trained model and new independent variable data.

The linear regression model has the benefit of

being simple to comprehend and utilize, making it an

effective tool for figuring out how specific variables

impact housing prices. In practical applications,

however, the linear regression method's premise of a

linear connection between independent and

dependent variables could be constraining. Therefore,

when working with complicated data structures,

investigating, and implementing deep learning

models becomes essential to enhancing prediction

accuracy.

2.2.2 Deep Learning Model

This study goes beyond conventional techniques by

employing a deep learning strategy to capture

complicated nonlinear correlations in the data. It

specifically uses a feedforward neural network, which

is characterized by the layers in its neural network and

is capable of learning intricate patterns using

optimization and backpropagation techniques. The

deep learning model's architecture consists of

multiple hidden layers, each with a certain number of

neurons and activation functions to boost the model's

ability to predict outcomes. The preprocessed dataset

is used in this study's training of the deep learning

model, and its hyperparameters are carefully tuned to

optimize performance. The inclusion of this model

shows the commitment to employing cutting edge

technology to anticipate real estate values while

considering the intricate dynamics of the housing

industry. Regarding the Deep Learning Model, this

research adopts a feedforward neural network

(FFNN) to explore the complexities within the

housing market data. An FFNN is defined by layers

of neurons ordered forward, with no cycles or loops

between layers; instead, the output of one layer

becomes the input of the following layer. This deep

learning model has an output layer, several hidden

layers, and an input layer as part of its design.

The input layer receives the initial data (in this

case, features of the housing market like square

footage, location, etc.), while the hidden layers are

responsible for extracting patterns and relationships

from this data through a combination of weights,

biases, and activation functions. The model is able to

learn complicated patterns because each hidden layer

neuron computes the weighted total of its inputs, adds

a bias, and then uses an activation function to

introduce non-linearity. The output layer produces the

final prediction, such as the price of a house. The

FFNN is trained using backpropagation and gradient

descent algorithms. Through the use of a chain rule,

backpropagation determines the gradient of the loss

function—in this case, mean squared error—with

respect to each weight and bias in the network,

working backward through the network from the

output layer. Gradient descent then uses these

gradients to update the weights and biases,

minimizing the loss function over time and improving

the model's predictive accuracy.

This research's use of this model shows how

committed the authors are to utilizing cutting-edge

technology to estimate real estate prices while

accounting for the intricate dynamics of the market.

In order to maximize the performance of the model,

hyperparameters such as the number of hidden layers,

the number of neurons per layer, and the learning rate

must be carefully tuned.

2.2.3 Loss Function

Within deep learning, the loss function plays a pivotal

role in guiding the training process. For this study, the

Mean Squared Error (MSE) loss function is used as a

standard choice for regression problems. The average

squared difference between the estimated and real

values is measured by the MSE loss function, which

offers a quantitative foundation for model

optimization. The formula for MSE is expressed as：

(2)

EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence

796

Where

𝑌



represents the true value and

𝑌





denotes the

predicted value. The choice of MSE as the loss

function is motivated by its effectiveness in

emphasizing larger errors, thereby ensuring that the

model is accurately fine-tuned to predict housing

prices with high precision.

2.3 Implementation Details

The implementation of the proposed methodology

was carried out on M1 MacOS system, ensuring

efficient handling of the extensive computations

required by deep learning models. The study also uses

Python 3.6.8 to do deep learning works. Data

augmentation techniques were not applied due to the

nature of the dataset; however, feature engineering

played a crucial role in enhancing model

performance. Key hyperparameters, including the

learning rate, number of epochs, and batch size, were

carefully selected through a series of experiments to

balance model accuracy and training efficiency. The

use of regularization techniques, such as dropout in

the deep learning model, was also explored to prevent

overfitting and improve generalization to unseen data.

3 RESULTS AND DISCUSSION

This chapter delineates the analysis and discussion on

the outcomes derived from the application of linear

regression and deep learning models for house price

prediction, as illustrated in Figures 2, Figure 3 and

Figure 4 comprehension the performance of the two

models in terms of accuracy and loss, respectively,

requires a comprehension of the figures.

3.1 Accuracy Analysis

Figure 2 depicts the training and validation accuracy

over epochs for the deep learning model. There is a

clear upward trajectory in training accuracy,

suggesting the model's increasing proficiency in

predicting house prices with each epoch. The

validation accuracy, represented by a dashed line,

also shows an incremental rise but at a slower rate

compared to the training accuracy. This discrepancy

suggests that although the model is learning well,

overfitting to the training set may be starting.

However, the constancy of accuracy gain highlights

the model's ability to reasonably generalize from

training data to unknown data.

Figure 2: Training and Validation Accuracy over Epochs

(Photo/Picture credit: Original).

3.2 Model Complexity and Overfitting

The visualization of model loss in Figure 3 illustrates

a sharp decrease in training loss, which stabilizes as

epochs increase. Conversely, the validation loss

declines and plateaus much earlier, suggesting that

the model is capable of quickly learning patterns

within the data. The minimal gap between the training

and validation loss indicates that the model is

complex enough to learn the underlying trends

without overfitting significantly. The early plateauing

of the validation loss suggests that additional training

epochs beyond this point would not necessarily result

in better generalization, which is an essential insight

for preventing unnecessary computational expenses

and potential overfitting.

Figure 3: Model Loss

(Photo/Picture credit: Original).

3.3 Interpretation of Results

In Figure 4, it can be observed that the relationship

between house characteristics and their predicted

prices. The sinusoidal pattern, indicative of the data's

cyclical nature, suggests that there are repeating

trends in house pricing data, which could be

associated with seasonal factors or market cycles.

This highlights the importance of temporal features in

Advancing House Price Forecasting: Linear Regression and Deep Learning Models Analysis

797

predicting house prices and indicates the model's

ability to capture and learn from these cyclical

patterns.

Figure 4: Sinusoidal Trends in Predicted House Prices

(Photo/Picture credit: Original).

As a result, the experimental results articulated in

this chapter demonstrate the significance of each

experiment conducted in this study. The analysis of

accuracy and loss across different models reveals

crucial insights into model performance and

complexity. The experiments validate the relevance

of deep learning in predicting house prices, with

implications on both the ability to learn from the data

and the practical consideration of model training

efficiency. The synthesis of these findings

substantiates the profound utility of advanced

computational techniques in the real estate market

analysis.

4 CONCLUSIONS

This study presents a comprehensive analysis of

house price forecasting, employing both traditional

linear regression models and advanced deep learning

techniques to enhance prediction accuracy. Through

a thorough comparison between traditional statistical

methods and cutting-edge deep learning models, the

study aimed to pinpoint the most effective approach

for real estate price prediction. In order to improve

prediction performance, a methodical approach that

included feature selection, data preparation, and

model evaluation is developed to examine the

complex dynamics of the housing market. At the heart

of the methodology lay the implementation of a

feedforward neural network, meticulously optimized

through hyperparameter tuning and benchmarked

against a linear regression baseline, showcasing its

superior capacity to capture complex nonlinear

relationships and high-dimensional data patterns.

Extensive experiments were conducted to assess

the proposed method, revealing that the deep learning

approach significantly outperformed traditional linear

regression models in accuracy and its ability to model

intricate data interactions. The experimental

outcomes underscored the potential of deep learning

techniques to offer substantial enhancements over

conventional prediction models, particularly in

discerning spatial and temporal trends in house

pricing data. In future endeavors, the integration of

external factors such as economic indicators and

urban development parameters will be pursued as the

next stage of research. This research trajectory will

delve into analyzing the influence of broader socio-

economic elements on house prices, aiming to refine

and broaden the predictive capabilities of models.

This strategic direction is anticipated to further

augment the model's utility and precision in real-

world estate market analysis.

REFERENCES

Cho, M., (1996). House Price Dynamics: A Survey of

Theoretical and Empirical Issues. Journal of Housing

Research, vol. 7(2), pp: 145–72.

Cynthia, M., Gong., Colin, L., Helen X.H., Bao., (2019).

Smarter information, smarter consumers. Insights into

the housing market, Journal of Business Research, vol.

97, pp: 51-64.

UB, D., and Saxena, S., (2023). Real Estate Property Price

Estimator Using Machine Learning. International Conf.

on Computational Intelligence and Sustainable

Engineering Solutions (CISES), pp: 895-900.

Madhuri, C. R., Anuradha, G., and Pujitha, M.V., (2019).

House Price Prediction Using Regression Techniques:

A Comparative Study. International Conference on

Smart Structures and Systems (ICSSS), pp: 1-5.

John, Y., Campbell, João., Cocco, F., (2007). How do house

prices affect consumption. Evidence from micro data,

Journal of Monetary Economics, vol. 54, pp: 591-621.

Zietz, J., Zietz, E.N. & Sirmans, G.S. (2008). Determinants

of House Prices: A Quantile Regression Approach. J

Real Estate Finance Econ, vol. 37, pp: 317–333.

Geerts, M., Vanden, Broucke, S., Weerdt, J., (2023). A

Survey of Methods and Input Data Types for House

Price Prediction.

Black., Angela., et al. (2006). House Prices, Fundamentals

and Bubbles. Journal of Business Finance &

Accounting, vol. 33(9), pp. 1535–1555.

Cloyne., James., Kilian, H., Ethan, Ilzetzki., and Henrik, K.,

(2019). The Effect of House Prices on Household

Borrowing: A New Approach. American Economic

Review, vol. 109 (6), pp: 2104-36.

Durganjali, P., and Pujitha, M.V., (2019). House Resale

Price Prediction Using Classification Algorithms.

International Conference on Smart Structures and

Systems (ICSSS), Chennai, pp: 1-4.

EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence

798