Research on Valve Network Model for Complex Industrial Pipeline

Networks

Xiao Luo*, Shuang Zhou, Yufang Zheng, Xiaoyan Han, Yichao Cao and Wenjie Ding*

School of Mechanical Engineering, Ningxia University, Yinchuan City, Ningxia Hui Autonomous Region 750021

Keywords: Pipeline Network, Valve Network Model, Model Establishment, Dynamic Characteristics.

Abstract: In the study of valve failure behavior, traditional methods often treat valves as isolated individuals or fixed

resistance components, leading to misjudgments about valve performance and the accuracy of pipeline

network models, and further affecting the efficiency of fault detection and handling. Therefore, this research

analyzes the current status of industrial pipeline networks and summarizes the existing problems in current

studies. It proposes a new approach to judge the failure behavior of valve networks in complex industrial

pipeline networks, considering the relationship between valve opening and resistance, and establishes a

model correlating valve failures with pipeline flow rates. Additionally, a computer-based valve network

information model is established, taking into account the mutual influence relationship between valve

clusters in the pipeline network and modeling the entire pipeline network. This model provides convenience

for the input and computation of large-scale pipeline network operational data sets into computers.

1 INTRODUCTION

Valves are an essential component of complex

industrial pipe networks, forming the structure of the

network along with straight pipes, elbows, and

pipeline accessories. Since valves are movable

components with variable flow and resistance, they

have a relatively high failure frequency and thus

become the main object of study for pipeline

network operation and maintenance.

In existing research, one approach is to study the

characteristics and fault manifestations of valves as

independent entities, examining the changes in

various parameters under single-valve failure

conditions. Another approach treats valves as fixed

resistance elements and studies pipeline network

failures based on network models. However, in real-

world industrial pipe networks, valve parameters

dynamically change, and valves are used jointly to

form a valve network with interconnected

information. Existing pipeline network models

cannot be directly used for discriminating valve

failure behaviors. Therefore, in-depth research on

the valve network model of complex industrial pipe

networks is crucial for effectively managing

intelligent valves and improving industrial

production safety.

Particularly noteworthy is the fact that complex

industrial pipe network systems typically consist of

hundreds or even thousands of valves and pipelines,

resulting in a massive operational dataset. With the

continuous innovation of industrial technology,

valves are gradually moving towards intelligence

and the Internet of Things (IoT). High-end valves,

which possess self-information collection, storage,

transmission, and self-diagnostic capabilities, have

become a trend in valve development. Currently,

pipeline network valves are gradually developing

towards the IoT, with massive numbers of valves

being managed through cloud-edge collaboration

techniques. Effectively categorizing and processing

this vast amount of operational data has become the

key to enhancing the efficiency of pipeline valve

management.

2 ANALYSIS OF CURRENT

RESEARCH STATUS

2.1 Characterization of Valve Faults

In studies that treat valves as independent entities,

Luo, X., Zhou, S., Zheng, Y., Han, X., Cao, Y. and Ding, W.

Research on Valve Network Model for Complex Industrial Pipeline Networks.

DOI: 10.5220/0012978300004536

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Data Mining, E-Learning, and Information Systems (DMEIS 2024), pages 119-129

ISBN: 978-989-758-715-3

119

scholars often analyze current signals and vibration

signals to delve into the fault characteristics of

valves. Fabio and his team (Fabio et al, 2023), for

instance, utilized current signals, acoustic emission

signals, and vibration signals to represent valve

faults during hydraulic valve fault diagnosis. In their

specific experiments, they achieved nearly 99%

accuracy in fault characterization using current and

vibration signals. Liu and his colleagues (Liu et al,

2024) conducted vibration analysis and fault

diagnosis research on water hydraulic relief valves,

employing changes in external vibration response to

diagnose internal faults. They collected and

processed displacement signals and voltage signals

from valve vibrations for fault diagnosis. Yang and

his team (Yang et al, 2021) analyzed vibration faults

in control valves and proposed optimization

solutions. Zeng and his team (Zeng et al, 2021), in

their study of electric valve fault characteristics,

analyzed and processed acquired current signals,

vibration signals, and acoustic emission signals.

They proposed a method for electric valve signal

processing and feature extraction, extracting fault

features such as effective current value, peak impact

current, stroke time, effective value of acoustic

emission signals, acceleration level, impact

frequency, and acceleration frequency domain

signals to represent the fault state of the valve. Xiao

and his colleagues (Xiao et al, 2020) utilized

vibration signals, pressure signals, and key phase

signals for fault diagnosis of reciprocating

compressor air valves using a deep convolutional

neural network. Their experiments demonstrated that

vibration signals and pressure signals had the highest

diagnostic accuracy when used in a two-dimensional

CNN. From these studies, it is evident that valve

vibration is closely related to faults. Therefore, in the

study of valve networks in industrial pipe networks,

vibration signals can be selected to represent valve

faults.

It is noteworthy that scholars such as Venkata

(Venkata, 2018) have placed valves within pipe

networks and studied the dynamic correlation

between flow pattern changes and valve vibrations

caused by individual control valves through the

training of neural network models. Based on this,

they conducted fault diagnosis on the valves.

However, in practical applications, valves always

operate as a part of the pipe network system and

cannot function independently from the network.

Therefore, following the approach of Venkata and

other scholars, we will delve deeper into the

correlation between valve vibrations and pipe

network flow rates, aiming to establish a model that

links valve vibrations with changes in pipe network

flow. This approach will provide a more

comprehensive understanding of valve behavior

within complex pipe networks and facilitate more

accurate fault diagnosis and management.

2.2 Aspects of Establishing Pipeline

Network Models

In the field of pipeline network modeling, scholars

primarily adopt various modeling techniques such as

neural network training, algorithm-based model

training, graph theory, and Kirchhoff's laws. To

simplify the expression of the pipeline network

model, valves are generally treated as fixed

resistance elements. However, in actual pipeline

network operations, valves are dynamic components

with variable flow rates and variable resistances,

resulting in a higher frequency of failures. Therefore,

when establishing pipeline network models, it is

crucial to incorporate additional valve

characterization parameters to investigate the failure

behavior of valves within the network. By doing so,

the models can more accurately reflect the dynamic

characteristics of the pipeline network, including the

impact of valve failures, and provide valuable

insights for fault diagnosis, flow optimization, and

energy management.

When utilizing neural network model training

and algorithmic model training to establish pipeline

network models, it is often the case that feature data

is directly trained and acquired, making it difficult to

directly incorporate valve characterization

parameters into the model. Scholars such as Wang

(Wang, 2010) have established a hybrid correlation

matrix that includes valve information based on a

planar pipeline network. Through matrix scanning

methods, a valve network model is established to

enable the search for closed valves and valve

shutdown areas during fault isolation. Other scholars,

such as Kim (Kim et al, 2022 and Kaliatka et al,

2012), have developed neural network models for

water supply pipeline networks. By training the

models using pressure data sets from both normal

operating conditions (without leaks) and different

leakage rates in laboratory pipeline networks,

reliable fault diagnosis models have been obtained.

Zhou (Zhou et al, 2008 and Lin, 2017) and other

scholars have employed algorithmic training to

obtain pipeline network models, and the correctness

DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems

120

of these models has been verified through

experiments.

When establishing a pipe network model based

on graph theory and Kirchhoff's laws, it is possible

to incorporate additional representation parameters

for valves into the expressed physical model.

Shuang (Shuang, 2017) explored the modeling

method for urban water supply pipe networks based

on graph theory, effectively describing the

topological structure of the pipe network using

adjacency matrices and incidence matrices. He

established a topological structure representation for

the water supply pipe network and developed a

hydraulic calculation model for the pipe network by

combining the laws of mass conservation and energy

conservation with the Hazen-Williams formula.

Scholars such as Lei (Lei, 2011) and Pecci (Pecci et

al, 2020 and Wang et al, 2005) also adopted a

hydraulic calculation model for pipe network

leakage conditions based on graph theory and

Kirchhoff's laws. In the case of pipeline leakage, a

node is added to the leaky pipeline, dividing it into

two segments, and then the model is used to

calculate the changes in pressure at each node and

flow rates in the pipe segments. Scholars like

Manservigi (Manservigi et al, 2022) utilized

physics-based equations to calculate all measurable

variables in district heating networks (DHN),

including flow rate, temperature, and pressure. They

established a pipe network model to detect and

identify the most common faults affecting DHN

pipelines, namely water leakage, heat loss, and

pressure loss. Zhou (Zhou et al, 2017) and other

scholars proposed an "object-oriented" approach to

calculate the hydraulic conditions of irregular

networks. Li (Li et al, 2004) and colleagues

simplified the hydraulic mathematical model based

on the symmetrical characteristics of the supply and

return pipe networks in branched systems,

considering pressure verification for flow-limiting

users and analysis of pipe network fault conditions

when establishing the calculation model.

Therefore, we can draw insights from scholars'

approaches in using graph theory and Kirchhoff's

laws to establish pipe network models. By

incorporating representation parameters for valves

into the pipe network, we can delve deeper into the

study of valves and valve network failures within the

pipe network. This will provide theoretical support

for the optimization and fault diagnosis of the pipe

network system.

3 APPROACH TO

ESTABLISHING A PHYSICAL

MODEL LINKING VIBRATION

PARAMETERS OF VALVE

STEMS WITH FLOW

FLUCTUATIONS IN A PIPE

NETWORK SYSTEM

After reviewing relevant literature, it has been found

that scholars have established neural network

models linking vibration information of individual

valves with flow pattern changes in pipe networks.

However, these models do not fully capture the

essence of the coupling between valve mechanical

failures and fluid motion. Therefore, there is a need

to establish a physical model that connects valve

vibration information with flow variations in the

pipe network system. Such a model would reveal the

fundamental coupling between valve mechanical

failures and fluid motion, providing scholars with a

clearer and deeper understanding of the interactions

involved.

The Bernoulli equation for ideal fluids is as

follows (1):

𝑝+

𝜌𝑣



+ 𝜌𝑔ℎ= 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡

(1)

Namely (2):

𝑝



𝜌𝑣





+ 𝜌𝑔ℎ



= 𝑝



𝜌𝑣





+ 𝜌𝑔ℎ



(2)

The resistance to the flow of actual fluids in pipe

networks can be categorized into two types: friction

resistance (also known as frictional loss or along-

the-way resistance) and local resistance. These

resistances result in two types of energy losses:

along-the-way loss ℎ



and local loss ℎ



respectively (Ma et al, 2011).

Local pressure loss (3):

𝑃



= 𝜉

𝜌𝑣



(3)

Frictional pressure loss or along-the-way

pressure loss (4):

𝑃



= 𝜆

𝑙

𝑑

𝜌𝑣



(4)

In the formula (3)(4): 𝜆: Frictional Resistance

Coefficient; 𝑙: Length of Pipe Section (𝑚); 𝑑: Pipe

Diameter ( 𝑚); 𝜌: Fluid Density ( 𝑘𝑔/𝑚



); 𝑣:

Average Cross-sectional Velocity (𝑚/𝑠); 𝜉: Local

Research on Valve Network Model for Complex Industrial Pipeline Networks

121

Resistance Coefficient. Therefore, the Bernoulli

equation for actual fluids is as follows (5):

𝑝



𝜌𝑣





+ 𝜌𝑔ℎ



= 𝑝



𝜌𝑣





+ 𝜌𝑔ℎ



+ 𝑃



+ 𝑃



(5)

𝑝



𝜌𝑣





+ 𝜌𝑔ℎ



= 𝑝



𝜌𝑣





+ 𝜌𝑔ℎ



+ 𝜉

𝜌𝑣



+ 𝜆

𝑙

𝑑

𝜌𝑣



(6)

𝑝





𝜌𝑣







+ 𝜌𝑔ℎ



= 𝑝





𝜌𝑣







+ 𝜌𝑔ℎ



+ 𝜉+ ∆𝜉

𝜌𝑣′



+ 𝜆

𝑙

𝑑

𝜌𝑣′



(7)

By subtracting equation (7) from equation (6),

we can obtain (8):

∆𝑣=

𝑓





∆𝜉



(8)

Wherein, according to the continuity equation,

we have (9)(10)(11):

𝑄=

𝐴



𝑣



𝐴



𝑣



𝐴

𝑣 (9)

𝑣



𝐴

𝑣

𝐴



(10)

𝑣



𝐴

𝑣

𝐴



(11)

It is known that there is a relationship between

the acceleration of the valve body, 𝑎



, and the

vibration displacement of the valve stem, 𝑋, as

follows (12)(13):

𝑎



𝑑



𝑋

𝑑

𝑡



= 𝜔



𝐴

𝑠𝑖𝑛𝜔+ 𝜑+ 𝜋

(12)

𝑋=

𝑓





𝑎





(13)

Therefore, the objective is to explore the

relationship between the local resistance coefficient

of the valve and the vibration displacement of the

valve stem. To address this issue, we need to

conduct further analysis and calculations (14):

∆𝜉=

𝑓





𝑋



(14)

By doing so, we can establish a physical model

that characterizes the relationship between the

vibration parameters of a single valve stem and the

flow velocity fluctuations in the pipeline system (15).

∆𝑣= 𝐹



𝑋



(15)

By doing so, we can derive a physical model that

describes the relationship between the vibration

parameters of a single valve stem and the flow rate

fluctuations in the pipeline system (16).

∆𝑄= 𝐹



𝑋



(16)

The overall modeling approach is as shown in

Figure 1:

Figure 1: Establishment of a physical model for the relationship between valve stem vibration parameters and pipeline

network system flow parameters.

DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems

122

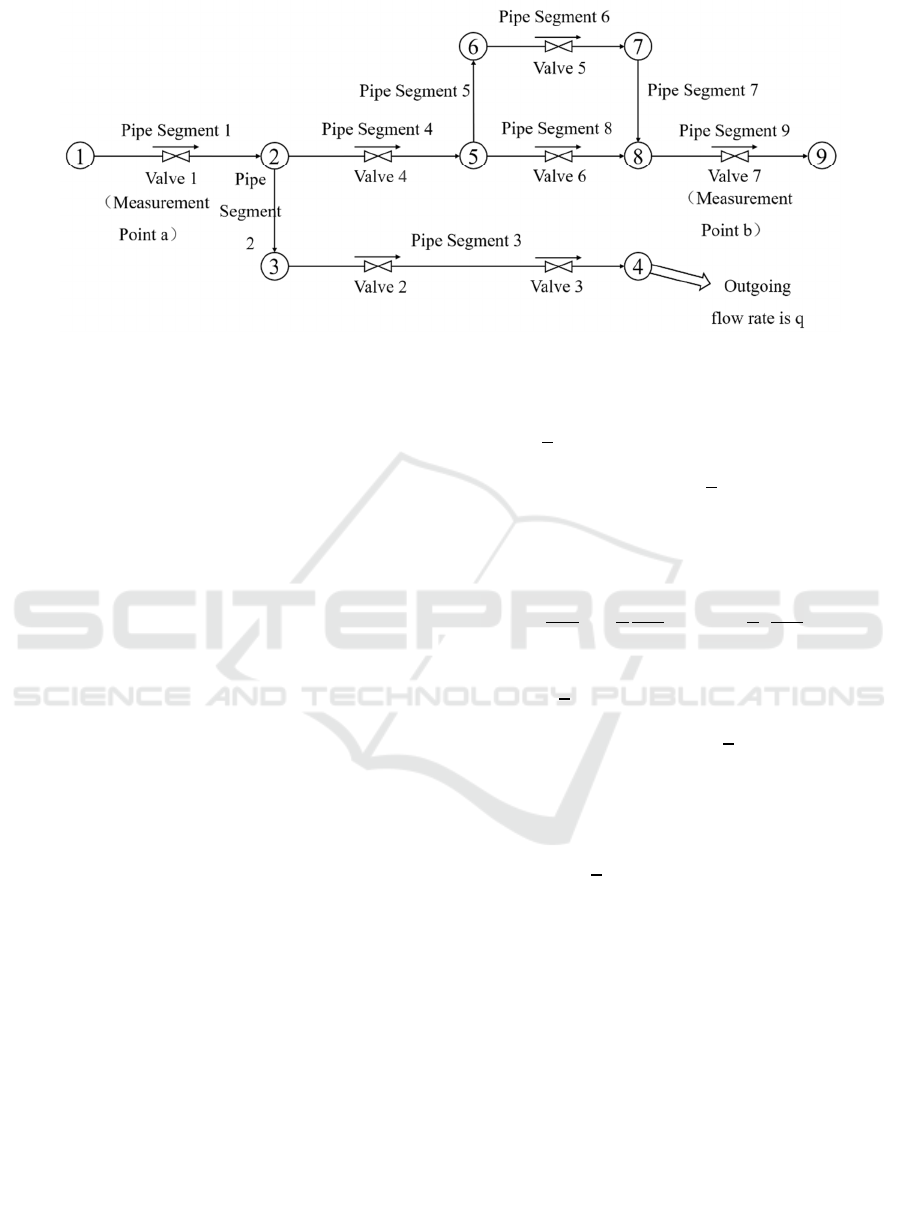
Figure 2: Schematic diagram of sub-network 1.

4 ESTABLISHMENT OF A

COMPUTER-BASED VALVE

NETWORK INFORMATION

MODEL

A computer-based valve network information model

is established to categorize and process a vast

amount of pipeline network operational data,

facilitating the input and computation of large

datasets on computers. This model also takes into

account the mutual influence relationships among

valve clusters in the pipeline network, enabling the

modeling of the entire pipeline network and

facilitating the analysis of the valve network within

the pipeline network. Complex industrial pipeline

networks can be divided into several sub-networks,

and the characteristics of the complex industrial

pipeline network can be derived by studying the

characteristics of the sub-networks. As shown in

Figure 2, it is a schematic diagram of a sub-network.

The computer-based valve network information

model is established based on the fundamental fluid

mechanics equation-Bernoulli's equation. Taking

Sub-network 1 as an example to establish a data

processing model for the pipeline network, a method

for establishing a dataset processing model for the

valve network in complex industrial pipeline

networks can be derived, thereby establishing the

corresponding valve network information model.

4.1 Bernoulli's Equation

The Bernoulli equation for actual fluids is (17):

𝑝



𝜌𝑣





+ 𝜌𝑔ℎ



= 𝑝



𝜌𝑣





+ 𝜌𝑔ℎ



+ 𝑃



+ 𝑃



(17)

Let (18)(19):

∆𝑃= 𝑃



+ 𝑃



(18)

∆𝑃= 𝜉

𝜌𝑣



+ 𝜆

𝑙

𝑑

𝜌𝑣



= 𝜉+ 𝜆

𝑙

𝑑



𝜌𝑣



(19)

Then we have (20):

𝑝



𝜌𝑣





+ 𝜌𝑔ℎ



= 𝑝



𝜌𝑣





+ 𝜌𝑔ℎ



+ ∆𝑃

(20)

We can derive the pressure drop equation as follows

(21):

𝑝



= 𝑝



𝜌𝑣





−𝑣





+ 𝜌𝑔ℎ



−ℎ



−∆𝑃

(21)

4.2 Impedance Calculation (Ma et al,

2011)

For any pipe network system, it consists of

numerous pipe segments connected in series and

parallel. According to fluid mechanics, in a series of

pipe segments, the total impedance 𝑆



of the series is

equal to the sum of the impedances 𝑆



of each

individual pipe segment. That is (22):

𝑆



= 𝑆









(22)

In the formula (22), m represents the number of

Research on Valve Network Model for Complex Industrial Pipeline Networks

123

pipe segments connected in series.

When the gravitational effects are equal in each

loop, the relationship between the total impedance

𝑆



of the parallel pipe segments and the impedance

𝑆



of each individual parallel pipe segment is as

follows (23):



𝑆



= 



𝑆









(23)

In the formula (23), n represents the number of

pipe segments connected in parallel.

Sometimes the resistance characteristics of

parallel pipelines are analyzed by using the general

derivative (24).

𝑎



= 𝑎









(24)

In the formula (24), n represents the number of

pipe segments connected in parallel. 𝑎



represents

the total conductance of the parallel pipeline (25). 𝑎



represents the conductance of each individual

pipe segment (26).

𝑎





𝑆



(25)

𝑎





𝑆



(26)

Using the aforementioned calculation methods

for impedance in parallel and series pipe segments,

the total impedance value of the entire pipe network

can be gradually determined. To solve this problem,

necessary calculations will be performed using

Python 𝑆



code.

4.3 The Dataset Processing Model for

Pipeline Networks

When calculating the impedance of a pipeline

network system, it is common to divide the network

into series and parallel sections, calculate their

impedances separately, and then determine the

overall impedance of the network. This same

approach is applicable when establishing the dataset

processing model for pipeline networks.

The establishment approach for the dataset

processing model of pipeline networks involves the

following steps:

Pressure Drop Equation (21):

𝑝



= 𝑝



𝜌(𝑣





−𝑣





) + 𝜌𝑔(ℎ



−ℎ



) −∆𝑃

(21)

Impedance Relationship:

Series Connection (22):

𝑆



= 𝑆









(22)

Parallel Connection (23):



𝑆



= 



𝑆









(23)

Pressure Drop in a Single Pipe Segment (27):

∆𝑃



= (𝜉



+𝜆



𝑙



𝑑



)

𝜌𝑣





(27)

Pressure Drop in the Pipeline Network (28):

∆𝑃= (𝜉



+ 𝜆



𝑙



𝑑



)

𝜌𝑣







∆𝑃





∆𝑃



(28)

Divide the valve network of a complex industrial

pipeline into several sub-networks, and select points

a and b in each sub-network as measurement points:

(1) Measure the flow velocity 𝑣



, pressure 𝑝



and height ℎ



at point a in the pipeline network.

(2) Calculate the flow rate 𝑣



and height ℎ



point b in the pipeline network based on the

structural information of the network (as the

calculation of flow rate can be simply and directly

derived from the pipeline structure, unaffected by

factors such as gravity and valves, whereas pressure

is influenced by gravity, valves, and other

components).

(3) Based on the series and parallel relationships

of the pipe segments, a table is established to import

the data of each pipe segment in the pipeline

network.

(4) Each column of the table can be expressed in

matrix form, and the pressure drop in each pipe

segment of the pipeline network can be obtained

through matrix operations.

(5) The pressure at point b in the pipeline

network is calculated as 𝑝



using the pressure

equation derived from the Bernoulli equation for real

fluids.

(6) The pressure at point b in the calculated

pipeline network, denoted as 𝑝



, is subtracted from

the actually measured pressure at point b in the

pipeline network. Based on the calculation results, it

is determined whether there is a fault in the pipeline

network.

(7) If there is a fault in the pipeline network, the

flow fluctuations ∆𝑣



, ∆𝑣



,…,∆𝑣



in each pipe

segment are calculated. A relationship between the

DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems

124

pipeline flow fluctuations and valve vibrations is

established as ∆𝑄= 𝐹

(

𝑋

)

. Based on the magnitude

of the flow fluctuations, the specific location of the

failed valve in the pipeline network is determined.

(8) By repeating steps (1) to (7) with another

sub-network, it can be determined whether there is

valve failure in the complex industrial pipeline

network.

Taking subnetwork 1 as an example, the

following dataset processing model for the pipeline

network is established. For subnetwork 1, analyzing

its structure reveals that the main trunk of the

pipeline network consists of pipe segments 1-4-8-9.

Among them, pipe segments 2 and 3 are connected

in series and are also serially connected at branch

point 2 of the main trunk. Pipe segments 5, 6, and 7

are connected in series and are in parallel with pipe

segment 8 in the main trunk. The expression

methods for various parameters of pipe segment i in

the pipeline network are as follows: Pipe length is 𝑙



;

Pipe diameter is 𝑑



; Friction resistance coefficient is

𝜆



; The flow velocity of each pipe segment is 𝑣



; The

flow rate of the pipe segment is represented by 𝑄



which is calculated based on 𝑣



and 𝑑



(29).

𝑄



= 𝑣



𝜋(

𝑑



)



(29)

The local resistance coefficient of valve i in the

pipe segment is 𝜉



For each pipe segment in subnetwork 1, Tables 1

and 2 can be established as follows.

Calculate the impedance ∆𝑃



of the parallel

section in Subnetwork 1:

Resistance relationship: Parallel connection (23):



𝑆



= 



𝑆









(23)

Generally, (24) is used to represent it.

𝑎



= 𝑎









(24)

Where (25)(26):

𝑎





𝑆



(25)

𝑎





𝑆



(26)

The resistance of each pipe segment (30):

𝑆



= 𝜉



+𝜆



𝑙



𝑑



(30)

The pressure drop of each pipe segment (31):

∆𝑃



= (𝜉



+ 𝜆



𝑙



𝑑



)

𝜌𝑣





(31)

Then it follows that (32)(33)(34)(35):

Table 1: Parameters of parallel pipe segments in subnetwork 1.

Matrix

Code

A (Diagonal

matrix

)

J (Diagonal

matrix

)

B (Diagonal

matrix

)

C (Diagonal

matrix

)

D (Diagonal

matrix

)

Number

Local resistance

coefficient 𝜉



Change in local

resistance

coefficient ∆𝜉



Friction

resistance

coefficient 𝜆



Pipe length 𝑙



Pipe diameter

𝑑



Calculation

𝑏









𝜉



∆𝜉



𝜆



𝑙



𝑑



𝑏



2 0

∆𝜉



𝜆



𝑙



𝑑



𝑏



𝜉



∆𝜉



𝜆



𝑙



𝑑



𝑏



4 0

∆𝜉



𝜆



𝑙



𝑑



𝑏



Table 2: Parameters of serial pipe segments in subnetwork 1.

Matrix

Code

(Diagonal

matrix

)

(Diagonal

matrix

)

(Diagonal

matrix

)

(Diagonal

matrix

)

(Diagonal

matrix

)

(Diagonal

matrix

)

Number

Pipe

segment

low rate 𝑄



Calculate

ipe segmen

low velocit

𝑣



Local

resistance

coefficient 𝜉



Change in

local

resistance

oefficient ∆𝜉



Friction

resistance

coefficient 𝜆



ipe length 𝑙



Pipe

diameter 𝑑



Calculation

𝑏









𝑄



𝑣



𝜉



∆𝜉



𝜆



𝑙



𝑑



𝑏



𝑄



𝑣



∆𝜉



𝜆



𝑙



𝑑



𝑏



𝑄



𝑣



𝜉



+ 𝜉



∆𝜉



𝜆



𝑙



𝑑



𝑏



𝑄



𝑣



𝜉



∆𝜉



𝜆



𝑙



𝑑



𝑏



𝑄



𝑣



𝜉



∆𝜉



𝜆



𝑙



𝑑



𝑏



Research on Valve Network Model for Complex Industrial Pipeline Networks

125

𝑆





𝐴





𝐽





𝐵



𝐶



𝐷



⎣

⎢

⎡

𝑆



𝑆



𝑆



𝑆



⎦

⎥

⎤

(32)

𝑆



= 𝑆



+ 𝑆



+ 𝑆



(33)

𝑎



= 𝑎



+ 𝑎



(34)

∆𝑃



𝜌𝑣





𝑆



(35)

Calculate the impedance ∆𝑃



of the serial section

in Subnetwork 1:

Resistance relationship: Serial connection:

Series Connection (22):

𝑆



= 𝑆









(22)

The resistance of each pipe segment (30):

𝑆



= 𝜉



+𝜆



𝑙



𝑑



(30)

The pressure drop of each pipe segment (31):

∆𝑃



= (𝜉



+ 𝜆



𝑙



𝑑



)

𝜌𝑣





(31)

Then it follows that (36)(37):

∆𝑃







𝐸







𝐹





𝐾





𝐺



𝐻



𝐼





𝜌



⎣

⎢

⎡

𝑃



𝑃



𝑃



𝑃



𝑃



⎦

⎥

⎤

(36)

∆𝑃



= 𝑃



+ 𝑃



+ 𝑃



+ 𝑃



+ 𝑃



(37)

Then, for Subnetwork 1, it follows that (38)(39):

∆𝑃= ∆𝑃



+ ∆𝑃



(38)

𝑝



= 𝑝



𝜌

(

𝑣





−𝑣





)

+ 𝜌𝑔

(

ℎ



−ℎ



)

−

𝜌𝑣2

ξ+ (

𝜆

𝑑

l)=

= 𝑝



𝜌

(

𝑣





−𝑣





)

+ 𝜌𝑔

(

ℎ



−ℎ



)

−(∆𝑃



+ ∆𝑃



)

(39)

For the valve network in a complex industrial

pipeline network, only by importing the flow rate,

pressure, and other relevant parameters of each

valve into the corresponding table using the

aforementioned approach, and obtaining the

corresponding matrix, can the desired pressure drop

be calculated. By comparing this calculated result

with the actual measured pressure in the pipeline

network, it is possible to determine whether there is

a leak in the network. This table (matrix) can store

vast datasets of industrial pipeline networks, and the

computation of these datasets can be carried out

through computers, avoiding the uncertainty and

immense workload associated with manual

calculations. It provides convenience for computer

input and computation of large datasets, enhancing

the efficiency of pipeline valve management.

5 CONCLUSION

In the research on the valve network model of

complex industrial pipeline networks, focus has been

placed on the identification and establishment of

industrial pipeline network models, the storage and

computation of vast pipeline datasets, and the fault

diagnosis of valves in the pipeline network. A new

approach to judge the failure behavior of valve

networks in complex industrial pipeline networks is

proposed, considering the relationship between

valve opening and resistance, and establishing a

model correlating valve failures with pipeline flow

rates. By analyzing the operational data of the

pipeline network, it is possible to determine whether

the valves are failing, enabling efficient and

intelligent management of valves in the pipeline

network. A computer-based valve network

information model is established, with the measured

vast pipeline dataset input into the computer through

tables. The elements in the tables can be expressed

as matrices, and through matrix operations, the

required data can be quickly and accurately obtained,

providing convenience for the input and

computation of vast datasets on computers. At the

same time, considering the mutual influence

relationship among valve clusters in the pipeline

network, the entire pipeline network is modeled,

facilitating the analysis of the valve network within

the pipeline network. This in-depth research on the

valve network model of complex industrial pipeline

networks focuses on issues such as model

establishment, storage, and computation, providing a

theoretical foundation for managing massive valves

through cloud-edge collaboration and effectively

categorizing and processing vast operational data.

This enhances the management efficiency of

pipeline valves.

DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems

126

ACKNOWLEDGMENT

Fund Name: Research and Development of Remote

Monitoring and Diagnostic System for High-End

Control Valves (Instrumentation and Control

Instruments) and Its Application Research

Fund Number: 2022BEE02002.

REFERENCES

Fabio, C., Federica, M., Antonio, B., et al, J, 2023.

Electrical and mechanical data fusion for hydraulic

valve leakage diagnosis. Measurement Science and

Technology,vol.34,no.4.DOI:10.1088/1361-6501/ACB3

Liu, X., Nie, S., Zhang, Z., et al, J 2014. Research on

vibration analysis and fault diagnosis of water

hydraulic relief valve. Chinese Hydraulics &

Pneumatics, no.05, pp.126-130. https://kns.cnki.n

et/kcms2/article/abstract?v=DFdco8SIy0JTfM29N93F

M3SNrIUvhnu1jqVWGNt4gEVWa5Q4WUenzd1zpF

mHlzWBvGQDde9MQQGW_YFWtVoZS9vp2GkaW

lVILlUb8Rbxy6LNQ0JFSaE5zSU1gImC1u5g&unipla

tform=NZKPT&language=CHS

Yang, S., Liu, S., Wu, N., et al, J, 2021. Analysis and

treatment of vibration fault of pressure control valve in

degassing condenser of nuclear power plant. Chinese

Hydraulics & Pneumatics, vol.41, no.11, pp.92-95.

https://kns.cnki.net/kcms2/article/abstract?v=DFdco8S

Iy0KZ48T1f9TvUsC5QrhqevkLpOViBLq5IRAWY71

ophHNDyYTx9VvwaID5aVjCr5CMbThL5WLJ_aD7

awWB2GpOHjnAmppK4gqYyjPEtGA_upusafQ_Ckg

rg_dGfFwbQ6hXzU=&uniplatform=NZKPT&langua

ge=CHS

Zeng, J., Liu, C., Zhang, S., et al, J, 2021. Research on

Fault Characteristic Analysis and Detection Methods

of Electric Valves. Electronic Measurement

Technology, vol.44, no.13, pp.171-176. https://kns.

cnki.net/kcms2/article/abstract?v=DFdco8SIy0Lh29ku

1xq8uQ92kv95PiDVHdKvlaOM1bJ6-MRrkgDZWiu9

3KRmzaEM3Spq0Qj9fLLQwShaLKitss0B6SzTjJeugt

JtG6r2de83C9jeLMh26OhDiT5AMQY2PY5OTnPQL

jM=&uniplatform=NZKPT&language=CHS

Xiao, S., Nie, A., Zhang, Z., et al, 2020. Fault Diagnosis

of a Reciprocating Compressor Air Valve Based on

Deep Learning. APPLIED SCIENCES-BASEL, vol.

10, no. 18, DOI: 10.3390/APP10186596

Venkata, S., Rao, S., J, 2019. Fault Detection of a Flow

Control Valve Using Vibration Analysis and Support

Vector Machine. Electronics, vol.8, no.10. DOI:10.

3390/electronics8101062

Venkata, S., Rao, S., J, 2018. Estimation of Flow Rate

Through Analysis of Pipe Vibration. Acta Mechanica

et Automatica, vol.12, no.4, pp.294-300. DOI:

10.2478/ama-2018-0045

Wang, P., D, 2010. Research on Reliability of Heating

System Based on Graph Theory. Harbin Institute of

Technology. https://kns.cnki.net/kcms2/article/abstract

?v=DFdco8SIy0LUfHaTm7GX37_FIsHlE2NRAsLpH

UJYogU9RlfKqr720nY1uOEYuonPMmb56rK9m23bz

8SenWNbYSFthFVJDaqzT6c3XD6ChvIYVuDeVdvY

eOnDb7A3ErpE&uniplatform=NZKPT&language=CHS

Kim, H., Choi, D., Yoo, D., et al, J, 2022. Development of

the Methodology for Pipe Burst Detection in Multi-

Regional Water Supply Networks Using Sensor

Network Maps and Deep Neural Networks.

Sustainability, vol.14, no.22. DOI:10.3390/

SU142215104

Kaliatka, A., Valinčius, M., J, 2012. Modeling of pipe

break accident in a district heating system using

RELAP5 computer code. Energy, vol.44, no.1,

pp.813-819. DOI：10.1016/j.energy.2012.05.011

Zhou, Z., Zou, P., Tan, H., et al, J, 2008. Identification of

Resistance Characteristics of Heating Network Based

on Hybrid Genetic-Ant Algorithm. Journal of Harbin

Institute of Technology, vol.40, no.11, pp.1761-1765.

https://kns.cnki.net/kcms2/article/abstract?v=DFdco8S

Iy0LGBigKfHIWrK5mRSlDd4Q07CuwPRhAYquwi

RgtFeMoJ34uMS2tDCfJl7Dvv9Tkl3bO488O2QzIY4

K0PBzLKcg007hPISl4QFWCw8HwdNdGtegJnZxOb

gQ9&uniplatform=NZKPT&language=CHS

Lin, C., J, 2017. A Hybrid Heuristic Optimization

Approach for Leak Detection in Pipe Networks Using

Ordinal Optimization Approach and the Symbiotic

Organism Search. Water, vol.9, no.10. DIO:10.

3390/w9100812

Shuang, Q., 2017. Modeling and Analysis of Cascading

Failures in Complex Networks and Reliability of

Urban Water Supply Networks, Beijing Jiaotong

University Press. Beijing, 1st edition. http://

book.ucdrs.superlib.net/views/specific/2929/bookDeta

il.jsp?dxNumber=000016592491&d=FAC99F4506D9

4390F01D097C42242933&fenlei=182016020403

Lei, C., Zou, P., J, 2011. Fault Diagnosis of Heating

Pipeline Network Leakage Based on Two-Level BP

Neural Network. Journal of Harbin Institute of

Technology, vol.43, no.02, pp.75-79. https://kns.

cnki.net/kcms2/article/abstract?v=DFdco8SIy0IjVcBB

GD2z-9X4a3kwhB6OYg1Xdd5_LXgqYdqE5G1cwsx

1wvASHdYLz6tvI_UgDeR2iBc88ix5kaFTzkhUK-c4

Ra96wYjQYJkST7ZTZR-vceFUIyz83bLo&uniplatfor

m=NZKPT&language=CHS

Pecci, F., Parpas, P., Stoianov, I., J. 2020. Sequential

Convex Optimization for Detecting and Locating

Blockages in Water Distribution Networks. Journal of

Water Resources Planning and Management, vol.146,

no.8. DOI: 10.1061/ASCE.WR.1943-5452.0001233

Wang, X., Zou, P., Zhou, Z., J, 2005. Topological

Structure and Hydraulic Process Simulation of

Complex Spatial Heating Network. Journal of System

Research on Valve Network Model for Complex Industrial Pipeline Networks

127

Simulation, no.03, pp.563-566+570. https://kns.cn

ki.net/kcms2/article/abstract?v=DFdco8SIy0INTsEe-k

e0ccsd3eBT3hRCjFKIbVSpsLUQZkFbnA6NpEp05U

dBe58HZEMhMWbaowCFCR880PCIYDvwGxU-78

X-Nql5OxgOOzHOB3wb_pT5_HD2guW5gzE3&uni

platform=NZKPT&language=CHS

Manservigi, L., Bahlawan, H., Losi, E., et al, J, 2022. A

diagnostic approach for fault detection and

identification in district heating networks. Energy,

vol.251. DOI:10.1016/J.ENERGY.2022.123988

Zhou, H., Wang, H., Zhu, T., J, 2017. A Hydraulic

Calculation Method for Three-Dimensional Heating

Pipeline Network. Chinese Journal of Computational

Physics, vol.34, no.03, pp.355-364. https://kns.cnki.

net/kcms2/article/abstract?v=DFdco8SIy0JuXOmOK

Mlh9unyejbrpjeZO1W2dDuK5rpawaNCyuJUkZd3JP

39DTe8aCfLZeKHsz_Mjz1DvonY9L_pOYUD2qcnf

RXQYEyJXh2l74E5rByGu391lJ29RN_nymp8K0y5K

gE=&uniplatform=NZKPT&language=CHS

Li, X., Wang, X., Zhou, Z., et al, J, 2004. Simulation

Analysis of Hydraulic Conditions in Tree-shaped

Heating Pipeline Network. Gas & Heat, vol.10,

pp.554-557. https://kns.cnki.net/kcms2/article/abstract

?v=DFdco8SIy0ISjbvXsBw-y-mIftvdycZPt1upvM2r

iBpTkyyICPRGYQdOK-61fbS_Asc8is9WF1Ypz8-ub

8C_vucgPAHarqRDGtF3NKHukSb9ly9WaDVF0xz8

FBMHqJRW&uniplatform=NZKPT&language=CHS

Ma, Q., Guo, J., 2011. Fluid Mechanics and Transmission

and Distribution Pipe Network, Metallurgical Industry

Press. Beijing, 1st edition. http://book.ucdrs.

superlib.net/views/specific/2929/bookDetail.jsp?dxNu

mber=000008167352&d=5002F793BA863A6BF2911

63C63530EA0&fenlei=18201201

APPENDIX

The derivation process of formula (32) is as follows:

𝑆





𝐴





𝐽





𝐵



𝐶



𝐷



= 

𝜉



𝜉



+

⎣

⎢

⎡

∆𝜉



∆𝜉



∆𝜉



∆𝜉



⎦

⎥

⎤

⎣

⎢

⎡

𝜆



𝜆



𝜆



𝜆



⎦

⎥

⎤

⎣

⎢

⎡

𝑙



𝑙



𝑙



𝑙



⎦

⎥

⎤

⎣

⎢

⎡

𝑏



𝑏



𝑏



𝑏



⎦

⎥

⎤

⎣

⎢

⎡

∆𝜉



∆𝜉



∆𝜉



∆𝜉



⎦

⎥

⎤

⎣

⎢

⎡

𝜉



+ 𝜆



𝑙



𝑏



𝜆



𝑙



𝑏



𝜉



+ 𝜆



𝑙



𝑏



𝜆



𝑙



𝑏



⎦

⎥

⎤

⎣

⎢

⎡

∆𝜉



∆𝜉



∆𝜉



∆𝜉



⎦

⎥

⎤

⎣

⎢

⎡

𝑅



𝑅



𝑅



𝑅



⎦

⎥

⎤

⎣

⎢

⎡

𝑆



𝑆



𝑆



𝑆



⎦

⎥

⎤

The derivation process of formula (36) is as follows:

∆𝑃







𝐸







𝐹





𝐾





𝐺



𝐻



𝐼





𝜌



DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems

128

⎣

⎢

⎡

𝑣



𝑣



𝑣



𝑣



𝑣



⎦

⎥

⎤



⎩

⎪

⎨

⎪

⎧

⎣

⎢

⎡

𝜉



𝜉



+ 𝜉



𝜉



𝜉



⎦

⎥

⎤

⎣

⎢

⎡

∆𝜉



∆𝜉



∆𝜉



∆𝜉



∆𝜉



⎦

⎥

⎤

⎣

⎢

⎡

𝜆



𝜆



𝜆



𝜆



𝜆



⎦

⎥

⎤

⎣

⎢

⎡

𝑙



𝑙



𝑙



𝑙



𝑙



⎦

⎥

⎤

⎣

⎢

⎡

𝑏



𝑏



𝑏



𝑏



𝑏



⎦

⎥

⎤

⎭

⎪

⎬

⎪

⎫



𝜌



⎣

⎢

⎡

𝑣



𝑣



𝑣



𝑣



𝑣



⎦

⎥

⎤



⎩

⎪

⎨

⎪

⎧

⎣

⎢

⎡

∆𝜉



∆𝜉



∆𝜉



∆𝜉



∆𝜉



⎦

⎥

⎤

⎣

⎢

⎡

𝜉



+ 𝜆



𝑙



𝑏



𝜆



𝑙



𝑙



𝜉



+ 𝜉



+ 𝜆



𝑙



𝑙



𝜉



+ 𝜆



𝑙



𝑙



𝜉



+ 𝜆



𝑙



𝑙



⎦

⎥

⎤

⎭

⎪

⎬

⎪

⎫



𝜌



⎩

⎪

⎨

⎪

⎧

⎣

⎢

⎡

∆𝜉



∆𝜉



∆𝜉



∆𝜉



∆𝜉



⎦

⎥

⎤

⎣

⎢

⎡

𝑅



𝑅



𝑅



𝑅



𝑅



⎦

⎥

⎤

⎭

⎪

⎬

⎪

⎫

⎣

⎢

⎡

𝑣



𝑣



𝑣



𝑣



𝑣



⎦

⎥

⎤





𝜌



⎣

⎢

⎡

𝑆



𝑆



𝑆



𝑆



𝑆



⎦

⎥

⎤

⎣

⎢

⎡

𝑣



𝑣



𝑣



𝑣



𝑣



⎦

⎥

⎤





𝜌

=

⎣

⎢

⎡

𝑃



𝑃



𝑃



𝑃



𝑃



⎦

⎥

⎤

Research on Valve Network Model for Complex Industrial Pipeline Networks

129