Genetic Programming for 5×5 Matrix Multiplication
Rik Timmer
1 a
, Jesse Kommandeur
2 b
, Jonathan Koutstaal
2 c
, Eric S. Fraga
3 d
and
Daan van den Berg
1,2 e
1
Department of Computer Science, VU Amsterdam, The Netherlands
2
Master Information Studies, UvA Amsterdam, The Netherlands
3
Department of Chemical Engineering, University College London (UCL), U.K.
Keywords:
Genetic Programming, Matrix Multiplication, Complexity, Strassen’s Algorithm.
Abstract:
Using genetic programming, we fail in evolving an algorithm that correctly multiplies two 5×5 matrices. We
do make progress on the issue however, identifying an experimental setting that could potentially lead to such
algorithm which until now, has not been successfully done. We discuss earlier work, experimental results and
possible ways forward.
1 MATRIX MULTIPLICATION
“Still open” is what Lance Fortnow answered when
he was asked for the status of the P
?
= NP problem
in 2009; he could have easily repeated those words in
2021, when the problem turned 50 years old (Fortnow,
2009; Fortnow, 2021). As it stands, the most monu-
mental problem in computer science, which roughly
asks whether problems that can be solved in expo-
nential time can also be solved in polynomial time,
still remains unsolved. There has been significant
progress on many aspects, ranging from algorithmics
(Applegate et al., 2009) to phase transitions (Sleegers
and van den Berg, 2022) and numerical diversity
(Van Den Berg and Adriaans, 2021; Sazhinov et al.,
2023; Zhang and Korf, 1996), but strictly speaking,
exponential-time problems such as the traveling tour-
nament problem (Verduin et al., 2023a; Verduin et al.,
2023b) or the traveling thief problem (Chagas and
Wagner, 2020; Chagas et al., 2021; Chagas and Wag-
ner, 2022) are still classified as ‘unfeasibly hard’,
while polynomial-time problems such as sorting a list
of numbers, minimum spanning tree and graph con-
nectivity are classified as ‘easy’.
But this is all theory, and practice tells us different
stories. First of all: size matters. For some ‘unfea-
a
https://orcid.org/0009-0030-0000-0482
b
https://orcid.org/0009-0000-2282-6960
c
https://orcid.org/0009-0008-5556-7537
d
https://orcid.org/0000-0002-5732-6082
e
https://orcid.org/0000-0001-5060-3342
sible problems’ in NP, such as the traveling tourna-
ment problem, the number of cities never realistically
exceeds 50, limiting the influence of its exponential
complexity solving algorithm. Conversely, for finding
the minimum spanning tree, which is ‘only’ in P, in-
stances of millions of nodes still require so much time
that special techniques have to be deployed on top of
the solving algorithm, which is of only logarithmic
complexity (Mohapatra and Ray, 2022). For sorting a
list of integers, again in P, the instance size (length of
the list) can easily exceed 10
12
records, making even
a polynomial time algorithm slow (O’malley, 2008).
Second, there is time criticality. It is easy to appre-
ciate the gravity of speed when an algorithm makes
decisions for steering a self-driving car, launching a
rocket or controlling a nuclear power plant, but also
in less mission-critical applications like gaming and
administration, speed is essential. A game in which
the AI needs 2 seconds to respond is unplayable, and
waiting a few minutes for an application’s sort opera-
tion to complete is simply unacceptable to most peo-
ple – such software would not be used.
Third, there is frequency. Some operations, like
stock market order execution, processing sensory data
in weather stations, or 3D graphics rendering involve
a high number of function calls, sometimes millions
per second. Although the algorithms in the individ-
ual function calls can be quite small and of very low
computational complexity, the sheer volume and re-
lentless continuity (varying from hours for stock mar-
kets to full continuum for weather stations) can still
push computational systems to the edge of their per-
Timmer, R., Kommandeur, J., Koutstaal, J., Fraga, E. and van den Berg, D.
Genetic Programming for 5×5 Matrix Multiplication.
DOI: 10.5220/0012990600003837
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 269-278
ISBN: 978-989-758-721-4; ISSN: 2184-3236
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
269

formance.
To matrix multiplication, all of the above apply.
The problem is in P ever since Jacques Philippe Marie
Binet described it in 1812 – long before Alan Turing
conceptualized the first computer. Binet’s algorithm,
colloquially dubbed the ‘standard’ algorithm, requires
O(n
3
) operations
1
for multiplying two n × n matrices
(Fig. 1). But even though it is ‘only’ in P, matrix mul-
tiplication occurs so often that shaving its complexity
is still well worth the effort. In computer graphics
rendering, matrix multiplication can be used to repre-
sent color values, and can be processed on dedicated
hardware (Larsen and McAllister, 2001). In (con-
volutional) neural networks, one of the most prolific
fields from artificial intelligence, weights and outputs
in matrices are multiplied to process data (Soltaniyeh
et al., 2022; Chen et al., 2020). Probability val-
ues in Markov Models used in reinforcement learning
and natural language processing make use of matrix
multiplication (Yegnanarayanan, 2013), and even the
chaotic numerical models for weather prediction rely
on matrix multiplication (Wilson et al., 2018). So of-
ten this routine is called, that optimizing the efficiency
of this operation, which ‘only in P’ can be consid-
ered the basis for the subsequent improvements in ef-
ficiency of higher-level models that use the operation.
An early optimization therefore has not gone to
waste. In 1969, a German mathematician named
Volker Strassen showed that 2×2 matrices can be
multiplied by seven multiplications instead of eight
(Strassen et al., 1969), thereby dropping the complex-
ity from O(n
2
log(8)
) = O(n
3
) to O(n
2
log(7)
) ≈ O(n
2.81
)
(see Figure 1 for a complete example on 3×3). As
an unintuitive and not very straightforward result, the
next general improvement was not realized by a bril-
liant human being, but by an AI (Fawzi et al., 2022a;
Fawzi et al., 2022b). Google’s AlphaTensor found a
76-multiplication algorithm on a 4×5 times matrices.
The same algorithm for two 5×5 matrices would drop
the complexity of the problem to ≈ O(n
2.69
).
The structure of all these algorithms for ma-
trix multiplication is strongly similar. A list of h-
equations consist of two multi-term factors, and a
list c-equations, one for each output cell, each which
sums a number of h-equations (Fig. 1). In our view,
this structural homogeneity invites an approach with
genetic programming (GP). But we are not the first
to try genetic programming for matrix multiplication,
so we will introduce some basic concepts and diffi-
culties of genetic programming, and review earlier
efforts on matrix multiplication. After that, in Sec-
tion 4, the algorithmic details of our GP-algorithm
1
One could even make an argument θ(n
3
) operations,
especially if the matrices do not contain zeroes.
‘Evolver’ will be explained. It evolutionary manip-
ulates a randomly initialized matrix multiplication al-
gorithm (‘MMalgorithm’) to function correctly. There
are several algorithmic switches and multiple runs, all
giving rise to different results, which will be discussed
in Section 6, along with some reflections and forward-
looking statements.
2 GENETIC PROGRAMMING
Genetic programming (Koza, 1992) is the application
of genetic algorithms for the manipulation of math-
ematical expressions or code, usually represented as
trees consisting of variables, constants, and opera-
tions, collectively known as the terminal set. The
challenge for model identification is not only gener-
ating suitable expressions, but determining values of
any constants in these expressions. The key difficulty
here is that suitable bounds on the parameters in the
proposed model structure are not known. Many op-
timization methods, e.g. genetic algorithms, assume
that the search space variables are bounded so that the
identification of new solutions in the search space is
well defined.
Koza introduces genetic programming first by de-
scribing genetic algorithms and the problem of repre-
sentation (Koza, 1992). In his book, constant terms
in the resulting program were identified through op-
erations such as - x x to yield 0 and % x x to yield
1, and subsequent additions or substractions of these
terms. Although in principle such an approach can
generate any constant value, the length of programs
required could be intractable and hence likely to be in-
efficient for the identification of general floating point
valued constant terms. Such terms will appear in re-
gression problems, in particular, where we wish to
identify not only the structure of a fitting equation but
also the coefficients in such equations.
Eggermont & Van Hemert (Eggermont and van
Hemert, 2001) considered the terminal set to include
specific integer values, defined by terminal set =
x ∪
{
w|w ∈ Z ∧−b ≤ w ≤ b
}
for some value of b, the
bounds on the interval of integer values. Niewenhuis
et al. introduce constants using a random number gen-
erator and then bound that particular constant, r say,
to [−10
l
, +10
l
] where l =
⌈
log
10
|
r
|⌉
(Niewenhuis and
van den Berg, 2022; Niewenhuis et al., 2024; Niewen-
huis and van den Berg, 2023). Koza applies genetic
programming to a curve fitting (symbolic regression)
problem with constant terminal symbols to introduce
constant valued parameters into the equation space,
using the symbol ‘←’ for the terminal (Koza, 1994).
In the given example, The value of the constant termi-
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
270

Figure 1: Two algorithms for 3imes3 matrix multiplication; the default algorithm (middle block) requires 27 h-equations,
whereas only 23 h-equations are needed for the algorithm by German mathematician Volker Strassen (lower block, adaption
for 3imes3 made by Julian Laderman (Laderman, 1976)).
nal is generated randomly from [-1,1] whenever such
a symbol is encountered for the first time, either in
the initial population or as the result of a mutation
operation. Koza & Rice denote this terminal symbol
by R and call it an ephemeral random floating point
constant atom (Koza and Rice, 1991). Koza et al. fur-
ther generalise the handling of such terms by intro-
ducing perturbable numerical values, denoted by ℜ,
and which can be subsequently modified by pertur-
bation using a Gaussian probability distribution with
standard deviation 1.0, a method used for controller
design, including both topology and tuning (Yu et al.,
2000; Koza et al., 2000).
Oltean & Diosan also solve regression problems
but do not indicate how they introduce constants into
their programs (Oltean and Diosan, 2009). They do
refer to the book by Koza, although that book also
does not specify how to handle constants such as
floating point numbers.
Chow et al. consider having all control variables,
i.e. the design or search variables, mapped from
x ∈ (−∞, +∞) to y ∈ (−µ, +µ) (Chow et al., 2001).
The mapping they use is y = tan
−1
(x) where µ =
π
2
.
This approach is appealing as it avoids any a priori
need to specify bounds. The disadvantage is that there
may be a difficulty in making small changes in the
values away from the origin. For the purpose of model
identification, the benefits of this mapping outweigh
the potential disadvantages.
In our study, the problem of setting correct bounds
mainly appear in the algorithmic settings, as de-
scribed in Section 4. Indeed, the variability in the
results give rise to the question of the parameters’ cor-
rectly setting. For our experiments, the issue appears
to be equally important as it was for earlier studies.
Genetic Programming for 5×5 Matrix Multiplication
271

3 EXISTING GA-APPROACHES
The earliest endeavour of genetic programming to
matrix multiplication we found was a 2001-paper by
Kolen & Bruce, who deploy a full genetic algorithm,
including crossover, to find an algorithm to correctly
multiply two 2×2 matrices (Kolen and Bruce, 2001).
The paper contains several hints into the hardness of
the problem (“Initial experiments [] yielded dismal re-
sults”), and their approach is tinkered with a lot of ap-
parently incidental variables, but nonetheless they re-
port finding a Strassen-equivalent algorithm in as few
as 91 generations. From apparently 610 new individ-
uals per generation, this might suggest that their ap-
proach might be able to find these solutions in 55,510
objective function evaluations. Not bad.
A study from 2009 by Oh & Moon deploys a
genetic algorithm for finding an MM-algorithm on
2×2 matrices (Oh and Moon, 2009). Equipped with
a crossover followed by a two step “local optimiza-
tion”, these authors report 608 Strassen-equivalent so-
lutions in 9 distinct groups. Apparently, they only use
5 different fitness values which raises the question of
plateaus in the fitness landscapes. Their experiments
might run on a maximum of (only) 15,000 evalua-
tions. Particularly inspiring is their attempt to classify
the grouped solutions in a Sammon mapping diagram
(Oh and Moon, 2009).
In 2010, Deng et al. (Deng et al., 2010) reported
similar solutions to Oh and Moon on 2×2 matrices,
but with a faster search algorithm. The results are
grouped again, but additionally, they suggest a so-
lution for 3×3 matrices. The most interesting point
of the paper is the following observation: for 2×2, a
proof exists that shows 7 elementary multiplications
is the absolute minimum one needs for algorithm,
giving Strassen’s its O(n
2
log(7)
) ≈ O(n
2.81
) complex-
ity. For matrices of 3×3 however, they do not sup-
ply such proof, but mention the fastest known algo-
rithm requires 23 multiplications, giving a complex-
ity of O(n
3
log(23)
) ≈ O(n
2.85
). Worse than Strassen’s
complexity; one would need to oust two more mul-
tiplications to obtain a better algorithm, but the key
takeaway is that it is different from both the standard
algorithm and Strassen’s. This suggests that for dif-
ferent n, different (magnitudes of) improvement are
possible and most of all: that the space of possible
algorithms for matrix multiplication is still worth ex-
ploring.
A 2012 paper by Andr
´
as Jo
´
o , Anik
´
o Ek
´
art, and
Juan P. Neirotti evolves 3×3 matrices and in fact finds
multiple solutions with 23 multiplications, the best
‘pure 3×3 solution’ corresponding to a complexity of
O(n
3
log(23)
) ≈ O(n
2.85
) (also see the previous para-
graph) (Joo et al., 2012). Their approach, a genetic
algorithm deploying 3 different crossover types and 3
different mutation types, also nearly found a solution
with 22 multiplications at a fitness of 0.9978 where 1
is maximum. The authors do remind us however, that
for 3×3 matrices, the lower bound is at 19 multipli-
cations. This suggests that an algorithm could exist at
complexity O(n
3
log(19)
) ≈ O(n
2.68
), much more effi-
cient than Strassen’s complexity of O(n
2.81
). Whether
such an algorithm does exist however, still remains to
be seen.
In 2015, a rather comprehensive thesis on the sub-
ject was written by Zachary A. MacDonald for a BSc
and honours degree at the Saint Mary’s University in
Canada (MacDonald, 2016). Possibly not peer re-
viewed, but certainly graded, it is the only publication
in this list that actually honours us with source code.
MacDonald provides a way of searching for matrix
multiplication algorithms, and reports (near) exhaus-
tive results on 2×2 in under 90 minutes, due to exten-
sive parallelization. He also suggests a way forward
for 3×3 matrices, but has apparently missed Jo
´
o et
al.’s work. A more extensive investigation into these
two studies is surely recommendable.
In 2020, Bidgoli et al. reported further extensions
on earlier results by Kolen & Bruce, Oh&Moon, Deng
et al. and Jo
´
o et al (Bidgoli et al., 2020). Reporting
160,000 solutions or 701 distinct solutions on 2×2, all
with the same complexity as Strassen, the most so far.
These results really demand an open repository; one
can’t help wondering how all these solutions would
look in a Sammon mapping such as done by Oh &
Moon. The search algorithm of choice is a ‘Micro
GA’, a genetic algorithm with a very small population
size. This is particularly interesting considering the
huge combinatorial space of algorithms, as it might
save significantly save on objective function evalua-
tions.
But the biggest surprise in matrix multiplica-
tion history was no doubt delivered by AlphaTensor
(Fawzi et al., 2022a; Fawzi et al., 2022b). Drawing
from superior performance in games such as go and
chess (Silver et al., 2018), the agent learns a gam-
ified version of matrix multiplication by reinforce-
ment learning. It performs so well, that it learns to
multiply 5×5 matrices with only 76 multiplications,
apparently achieving complexity of O(n
5
log(76)
) ≈
O(n
2.69
), dodging Strassen’s complexity of O(n
2.81
)
by quite a bit.
So with all this in mind, could genetic program-
ming find algorithms to calculate 5×5 matrix multi-
plication? Can it outperform Strassen’s? Or even Al-
phaTensor’s? Judging by our results, the answer is
no. But from the myriad choices to be made when de-
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
272

veloping a GP-routine, we do identify one particular
setting that seems to lead in a promising direction.
4 EXPERIMENT
4.1 Evaluating the Algorithm
In our experiment, one single problem instance con-
sists of 3 matrices M
a
, M
b
and M
prod
, for which
M
a
× M
b
= M
prod
. All matrices are sized 5 by 5 inte-
gers, and M
a
, M
b
hold values uniformly chosen from
[-10, 10]. In other words: one problem instance is
a triplet of three 5×5 matrices, of which the third
(M
prod
) is the product of the multiplication of the
two others (M
a
and M
b
). The evolving MMalgorithm
takes the two matrices M
a
and M
b
as input, and mul-
tiplies them according to its rules to produce a third
matrix M
out
. The quality of the output is then assessed
by comparing M
out
to the correct output M
prod
. This
is done in two ways simultaneously:
1. By assessing the number of incorrect cells in the
output matrix M
out
with respect to the correct out-
put M
prod
. The recorded values per generation
are averages over the outputs of all Matrix triplets
used in the run.
2. By taking the average cell difference between
M
out
and M
prod
. The recorded values per gener-
ation are (again) averages over the outputs of all
Matrix triplets used in the run,
While both values were recorded, only the second
value, the average cell difference between M
out
and
M
prod
, was taken as the objective value. The imme-
diate motivation is that the number of incorrect cells
ranges between 0 and 25 for a single instance, which
amounts to only 26 different objective values. That’s
quite low for one problem instance, especially con-
sidering the theoretically infinite algorithm space of
MMalgorithm. We suspect our hill climbing approach
might not function well under such circumstances, but
nevertheless, the unused feature of incorrect cells un-
expectedly turned out to play a key role in making
genetic programming useful for matrix multiplication
in our setting.
4.2 Initializing the Algorithm
The main loop of the experiment, Evolver, a (1+1)
evolutionary algorithm, attempts to iteratively im-
prove MMalgorithm’s source code to solve matrix
multiplications. MMalgorithm starts with 125 h-
equations and 25 c-equations, which are all randomly
constructed. An h-equation always consists of two
multiplied factors: a left hand factor consisting of
summed and subtracted cell values a
i, j
from matrix
M
a
and a right hand factor consisting of summed and
subtracted cell values b
i, j
from matrix M
b
. Two ex-
amples:
h
31
= (a
1,4
)(b
1,5
− b
4,2
− b
1,1
+ b
1,5
) (1)
h
106
= (a
4,3
+ a
4,4
− a
3,1
)(b
1,5
− b
4,2
) (2)
The 125 initial h-equations are initialized with ex-
actly 5 terms, randomly divided between the two fac-
tors. The left hand factor of each h-equations con-
sists of randomly chosen cells from M
a
, with pluses
and minuses randomly assigned; the right hand fac-
tor consists of randomly chosen cells from M
b
, again
with pluses and minuses randomly assigned. The al-
gorithm does not prevent a matrix cell to appear more
than once in a factor.
Besides the 125 initial h-equations, the initialized
code also contains 25 c-equations, which are initial-
ized as a sum of exactly 5 randomly chosen h-values.
One example:
c
5,5
= (h
8
− h
92
+ h
114
− h
16
− h
85
) (3)
Again, the pluses and minuses are randomly assigned,
and there is a chance of 7.78% that an h-term ap-
pears more than once in a c-equations. The acute
reader might have noticed that the number of 25 c-
equations stems directly from the size of the product
matrix M
prod
from the problem instances. In general,
MMalgorithm has exactly one c-equation for each cell
in its output matrix M
out
.
4.3 Evolving the Algorithm
After initializing MMalgorithm with 125 h-equations
and 25 c-equations, Evolver starts to iteratively ap-
ply mutations to the MMalgorithm’s equations, in an
effort to improve its performance on multiplying ma-
trices. Each generation, it sequqntially applies n
mut
mutations, and n
mut
is fixed to 1 ≤ n
mut
≤ 5 for the
entirety of a run, which is always 1,000,000 genera-
tions long. Whenever Evolver applies a mutation to
MMalgorithm’s source code, it first selects one of 8
types with uniform probability:
1. The mutation add a-variable introduces of a ran-
domly selected cell variable a
i, j
from matrix M
a
into a the left-hand factor of a randomly selected
h-equation. Even though the maximum number
of a-variables is 4 during initialization, there is no
upper bound during the evolutionary run. The new
a-variable gets a plus or minus sign at random.
Genetic Programming for 5×5 Matrix Multiplication
273

2. The mutation remove a-variable randomly se-
lects an h-equation with 2 or more a-variables
in its left hand factor. From these a-variables, it
deletes one at random. If the selected h-equation
has only one a-variable, the mutation is aban-
doned and Evolver moves to the next generation.
3. Add b-variable entails the introduction of a ran-
domly selected cell variable b
i, j
from matrix M
b
into a the right-hand factor of a randomly selected
h-equation. Even though the maximum number
of b-variables is 4 during initialization, there is no
upper bound during the evolutionary run. The new
b-variable gets a plus or minus sign at random.
4. The mutation remove b-variable randomly se-
lects an h-equation with 2 or more b-variables in
its right hand factor. From these b-variables, it
deletes one at random. If the selected h-equation
has only one b-variable, the mutation is aban-
doned and Evolver moves to the next generation.
5. The mutation add h-equation introduces a com-
pletely new h-equation into the MMalgorithm
with two factors, one consisting of between 1 and
4 randomly selected terms from matrix M
a
, the
second between 1 and 4 randomly selected terms
from matrix M
b
so that the total is exactly 5, ex-
actly like in the random initialization procedure.
This mutation type is the only one sensitive to the
Cap - NoCap algorithmic setting, which is ex-
plained in the end of this subsection.
6. Remove h-equation randomly selects an existing
h-equation from MMalgorithm and removes it. It
also removes it from any c-equations it might ap-
pear in.
7. The mutation add h to c randomly selects an ex-
isting h-equation, and inserts it into a randomly
selected c-term. The new h-term gets a plus or
minus sign at random.
8. The mutation remove h from c randomly selects
one of the 25 c-equations, and removes one of its
h-terms at random.
As every mutation is randomly chosen from the 8
types mentioned above, a mutation type may occur
more than once per generation iff n
mut
≥ 2. When
n
mut
= 5, there is even a 79% chance of selecting
a mutation type twice. But this applies to mutation
types only; when mutation parameters are also taken
into account, the chances of duplicates occurring are
very small.
There are two boolean switches to the algorithm,
both of which are set beforehand and remain un-
changed throughout the run. The first, Cap - NoCap
toggles an upper limit of 250 h-equations, when set
to Cap. If the limit is reached, and mutation 5 (“add
h-equation”) is selected in a generation, Evolver ig-
nores it and moves to the next generation, reiter-
ating its mutation routine. If there are fewer than
250 h-equations, an h-mutation is added without au-
tomatically inserting it to a c-equation. When set
to NoCap, and mutation 5 (“add h-equation”) is se-
lected, a new randomized h-equation is added which
is immediately added to a c-equation, regardless of
whether MMalgorithm has more or fewer than 250 h-
equations.
Second, the switch EQ - NOEQ determines
whether Evolver accepts only mutations that result
in better mutated MMAlgorithms, or whether it also
accepts equally good mutated MMAlgorithms. When
set to EQ mode, mutated MMAlgorithms that have the
same average cell difference are also accepted, when
set to NOEQ, only better mutated MMAlgorithms are
accepted.
Even though all runs completed 1 million genera-
tions on a 128-core AMD Rome 7H12 CPU 2.4 GHz,
time budgets varied greatly between runs. The short-
est run, evaluating 5 matrix triplets, with settings Cap
- noCap and EQ - NoEQ took a little over 65 minutes
to complete. The longest run, evaluating 25 matrix
triplets, with settings NoCap - EQ and n
mut
= 5 re-
quired a time budget just shy of 120 hours, or 5 days.
All code and results, as well as some additional fig-
ures, can be found in an online open repository (Tim-
mer, 2024).
5 RESULTS
When looking at the results for average cell differ-
ence, the end results monotonously get worse when
the number of matrix triplets increase, and this is
true for all settings of Cap - NoCap, and all num-
bers of mutations per generation 1 ≤ n
mut
≤ 5 (See
Fig.2), signalling that the current approach might be
facilitating specific algorithms. We don’t want that
of course, we want general algorithms, that can cor-
rectly multiply any two algorithms, and not just the
ones from our instance set. But interestingly enough,
the increase of the average cell difference after 10
6
generations does seem to slow down when evaluat-
ing more matrix triplets, though whether it converges
remains open for now. We surely hope so, because
that would mean the results have some degree of reg-
ularity, but the numbers are too small to call a defini-
tive conclusion now, or even meaningfully fit a func-
tion. On intuition, NoCap - EQ looks most conver-
gent, with a curve somewhat like α−
β
n
with α, β ≥ 1,
while results for the setting Cap - EQ more look like
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
274

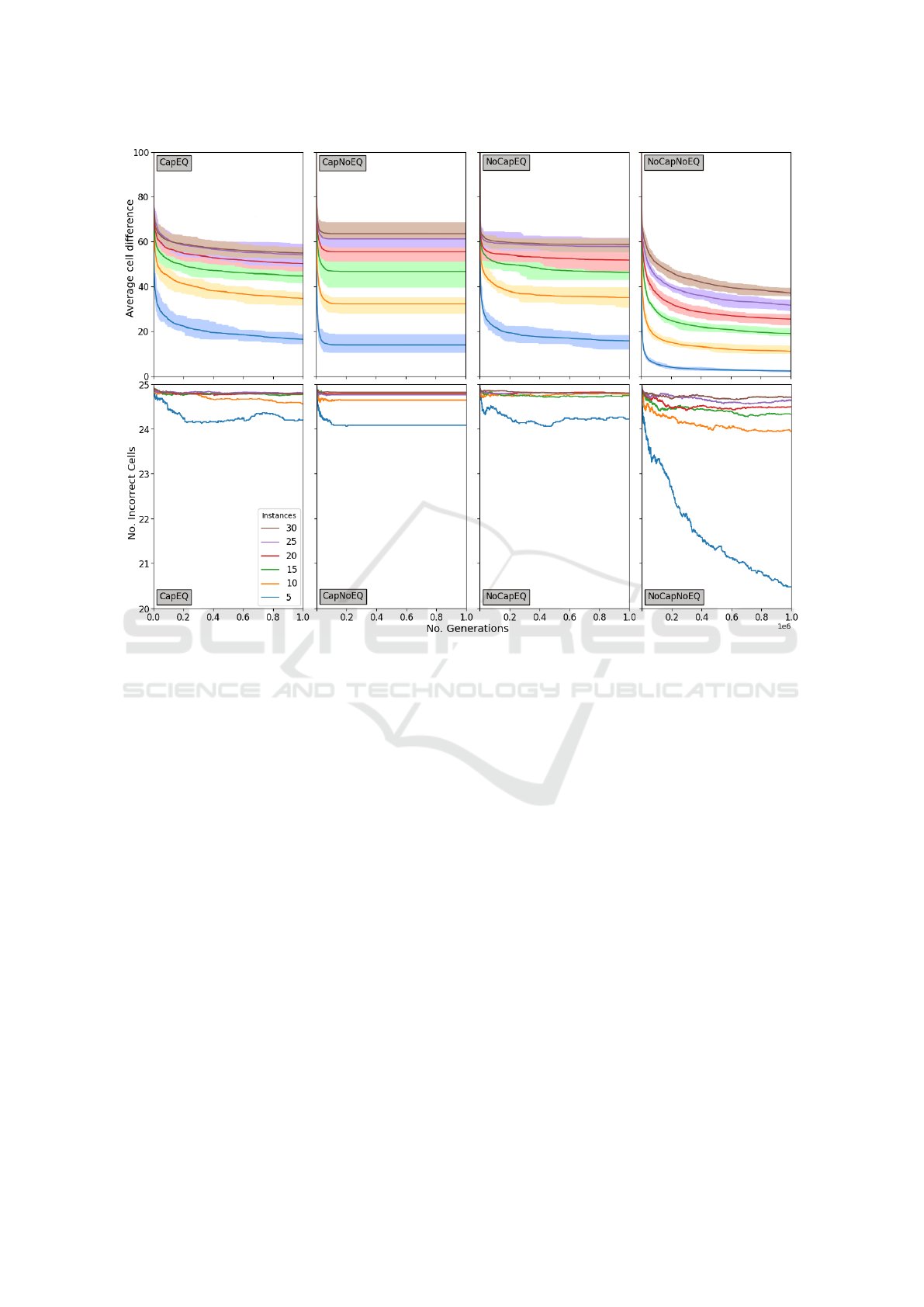
Figure 2: Results for runs with 1 mutation per generation. Top row: The average cell difference increases with the number of
matrix triplet instances (distance between the converged lines), but the increase tends to slow down. Although the NoCap -
NoEQ setting shows the fastest increase, its absolute values are lowest. Bottom row: The average number of incorrect cells is
hardly insightful, except in the NoCap - NoEQ setting with 5 problem instances, where its improvement hasn’t stopped even
after 1M evaluations.
O(n · log(n)), and Cap - NoEQ could remind one of
O(n
f racαβ)
), which are non-convergent. The setting
NoCap - NoEQ looks least convergent, with some of
its lower n
mut
settings even appearing close to linear.
This setting does however give the best absolute re-
sults, with a cell difference between 2.37 and 37.17
in its 1-mutation setting. For nearly all other settings,
the cell difference ranges from over 10 to over 55.
When it comes to number of incorrect cells, it
seems that our intuition for not using it as an objective
value was right. Recalling that the number of cells is
25, and then observing that in only 5 out of 120 set-
tings that number even dropped below 24, confirm it
was not the right objective for this experiment. These
five settings are all NoCap - NoEQ, with 23.54, 23.62
and 23.72 incorrect cells for 1,2, and 3 mutations on 5
matrix triplets and 23.94 for 1 mutation on 10 matrix
triplets. But by far the best value of 20.48 incorrect
cells (still very high) was for 1 mutation on 5 matrix
triplets. The most interesting observation here how-
ever, is that this value, unlike the average cells differ-
ence, has not converged (Fig.2, bottom-right subfig-
ure). It is therefore possible that this setting of NoCap
- NoEQ with n
mut
= 1 on 5 matrix triplets has substan-
tial potential of improving further.
In terms of evolved program length, results var-
ied wildly for different settings. In Cap - EQ, final
programs nearly always contained 250 h-equations,
almost none of which were survivors from initial-
ization. For Cap - NoEQ between 70 and 140
h-equations, with generally more h-equations with
higher values of n
mut
. For NoCap - EQ, the number of
h-equations fluctuated between 14 and 55, the higher
numbers all present in runs with 5 matrix triplets. Fi-
nally for NoCap - NoEQ, the results were almost pre-
cisely inverse: fluctuating numbers of h-equations,
ranging from 233 to 237, but inversely related to n
mut
.
In settings Cap - EQ and NoCap - EQ, every c-
equation in an evolved program had slightly over 2
h-equations on average. For Cap - NoEQ this was
slightly over 4, and for NoCap - NoEQ, as many as
6.5 on average, but nearly 15 for n
mut
= 1 and 5 ma-
Genetic Programming for 5×5 Matrix Multiplication
275

trix triplets, the best setting in our experiment. Is that
a coincidence? Why would the best performing set-
ting also have the largest c-equationS?
6 CONCLUSION & DISCUSSION
In the current algorithmic setup, there’s only one set-
ting that raises hope of ever finding a correctly func-
tioning 5×5 matrix multiplication algorithm. It’s
NoCap - NoEQ, with 1 mutation per iteration, and it
needs to run for over a million generations. The rea-
son for this is the spectacular drop in the number of
incorrect cells in the output, a measure we just collat-
erally measured, and never expected to be the leading
pointer for future directions. For 1M generations in
this setting, it hasn’t converged, and therefore the eas-
iest way forward would be just to increase the compu-
tational budget for this setting only. But there’s more.
We made a lot of arbitrary choices when initializ-
ing an MMalgorithms. The number 125 h-equations
might feel natural, as it is exactly the number of
the standard algorithm (5
3
). But initializing the h-
equations with a total of 5 variables is nearly a random
choice. The algorithm discovered by AlphaTensor
has h-equations with both fewer and many more vari-
ables, in wild distributions such as 10 a-variables with
1 b-variable. So what’s right? Nobody knows. Fur-
thermore, h-equations are currently initialized with 5
variables, not 5 different variables, but even if they
were different, mutations might produce duplicate
variables into a single term. Whether that reduces the
algorithms performance is unknown, but to us, it does
feel unnatural to some extent. Maybe it should be
prohibited.
The EQ-setting is in many ways problematic. Al-
though to some degree it is desirable to navigate
plateaus in the evolutionary landscape, these can be
huge for applications in genetic programming. Ev-
ery h-equation that is not immediately added to a
c-equation can lead to an excessive amount of non-
functional code in the algorithm (a phenomenon
known as ‘bloating’). Once bloated, the Evolver be-
comes largely paralyzed, as mutations inside those
useless h-equations also have no effect, but are still
accepted because of the same EQ-setting. On the other
hand, we want Evolver to accept neutral mutations,
as we don’t know how many local optima there are in
the algorithm landscape, or how they are distributed.
It seems therefore, that there is a lot of room for fine-
tuning the interplay between Cap - NoCap, EQ-NoEQ,
the various mutation types, and the values for n
mut
. In
the current experiment however, just one setting con-
vincingly not gets stuck in a local optimum, and that
is (again) NoCap - NoEQ with 1 mutation on 5 matrix
triplets.
The observation that larger numbers of matrix
triplets always lead to worse performance is worri-
some. We want an evolved matrix multiplication al-
gorithm to be general, meaning it multiplies all ma-
trices correctly, and the fact that more matrices lead
to higher (average) errors does not speak to its favour.
The trends do, however. When the number of ma-
trix triplets doubles from 5 to 10, no less than 16 out
of 20 algorithmic settings have a higher than dou-
ble increase in average cell difference. But when
the number of matrix triplets increases sixfold to 30,
the worst algorithmic setting (Cap - NoEQ with 1
mutation) has increased by a factor 3.87, while the
best algorithmic setting (NoCap - NoEQ with 1 mu-
tation) has increased by a factor of only 2.26. In
other words: when the number of instances increases
linearly, errors for all algorithmic settings increase
sublinearly. This could be taken as a sign that the
evolved MMalgorithms do show a trend towards gen-
erality but for now, numbers are too small to make a
decisive call. Besides, convergence ratios might be
much worse when higher values in the cells of ma-
trix triplets are used. All of this remains to be seen in
future work.
The results on program length are of very little
significance to matrix multiplication itself; after all,
none of the experiments resulted in a correctly work-
ing program. They do tell us something about the
operation of Evolver though, and the lesson to be
learned is that it is not necessarily the Cap setting that
caps the program; the NoEQ setting also contributes
hugely, possibly from massively refusing the addi-
tion of useless code. One particular puzzling take-
away from these observations on program length is
that the best setting from the experiment also had the
largest number of h-terms in its c-equations: a stag-
gering number of 15 – on average. Such a pattern
is neither typical for the standard algorithm, nor for
Strassen’s, nor for AlphaTensor’s.
Finally, for the reproducibility of these results, it
would have been better to have also saved the matrix
triplets, besides all the resulting MMalgorithms after
evolution. The matrix triplets were made on the fly,
used on the fly, but not saved, which is an omission
we are to blame for. However, as they were uniformly
randomly generated, we expect no significant devia-
tion in the results after a rerun.
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
276

REFERENCES
Applegate, D. L., Bixby, R. E., Chv
´
atal, V., Cook, W.,
Espinoza, D. G., Goycoolea, M., and Helsgaun, K.
(2009). Certification of an optimal tsp tour through
85,900 cities. Operations Research Letters, 37(1):11–
15.
Bidgoli, A. A., Trumble, S., and Rahnamayan, S. (2020).
Discovering numerous strassen’s equivalent equations
using a simple micro multimodal ga: Evolution in ac-
tion. In 2020 IEEE Congress on Evolutionary Com-
putation (CEC), pages 1–8. IEEE.
Chagas, J. B., Blank, J., Wagner, M., Souza, M. J., and
Deb, K. (2021). A non-dominated sorting based
customized random-key genetic algorithm for the bi-
objective traveling thief problem. Journal of Heuris-
tics, 27(3):267–301.
Chagas, J. B. and Wagner, M. (2020). Ants can orienteer
a thief in their robbery. Operations Research Letters,
48(6):708–714.
Chagas, J. B. and Wagner, M. (2022). Efficiently solving
the thief orienteering problem with a max–min ant
colony optimization approach. Optimization Letters,
16(8):2313–2331.
Chen, Y., Xie, Y., Song, L., Chen, F., and Tang, T. (2020).
A survey of accelerator architectures for deep neural
networks. Engineering, 6(3):264–274.
Chow, C. K., Tsui, H. T., and Lee, T. (2001). Optimiza-
tion on unbounded solution space using dynamic ge-
netic algorithms. In IJCNN’01. International Joint
Conference on Neural Networks. Proceedings (Cat.
No.01CH37222), volume 4, pages 2349–2354 vol.4.
Deng, S.-J., Zhou, Y.-R., Min, H.-Q., and Zhu, J.-H. (2010).
Random search algorithm for 2× 2 matrices multi-
plication problem. In Third International Workshop
on Advanced Computational Intelligence, pages 409–
413. IEEE.
Eggermont, J. and van Hemert, J. (2001). Adaptive genetic
programming applied to new and existing simple re-
gression problems. In Miller, J., Tomassini, M., Lanzi,
P., Ryan, C., Tettamanzi, A., and Langdon, W., edi-
tors, GENETIC PROGRAMMING, PROCEEDINGS,
volume 2038 of Lecture Notes in Computer Science,
pages 23–35, HEIDELBERGER PLATZ 3, D-14197
BERLIN, GERMANY. EvoNet, Network Excellence
Evolut Comp; EvoGP; EvoNet Working Grp Genet
Programming, SPRINGER-VERLAG BERLIN. 4th
European Conference on Genetic Programming (Eu-
roGP 2001), COMO, ITALY, APR 18-20, 2001.
Fawzi, A., Balog, M., Huang, A., Hubert, T., Romera-
Paredes, B., Barekatain, M., Novikov, A., R Ruiz,
F. J., Schrittwieser, J., Swirszcz, G., et al. (2022a).
Discovering faster matrix multiplication algorithms
with reinforcement learning. Nature, 610(7930):47–
53.
Fawzi, A., Balog, M., Romera-Paredes, B., Hassabis, D.,
and Kohli, P. (2022b). Discovering novel algorithms
with alphatensor.
Fortnow, L. (2009). The status of the p versus np problem.
Communications of the ACM, 52(9):78–86.
Fortnow, L. (2021). Fifty years of p vs. np and the possi-
bility of the impossible. Communications of the ACM,
65(1):76–85.
Joo, A., Ekart, A., and Neirotti, J. P. (2012). Genetic al-
gorithms for discovery of matrix multiplication meth-
ods. IEEE transactions on evolutionary computation,
16(5):749–751.
Kolen, J. F. and Bruce, P. (2001). Evolutionary search for
matrix multiplication algorithms. In FLAIRS confer-
ence, pages 161–165. Citeseer.
Koza, J. and Rice, J. (1991). Genetic generation of both
the weights and architecture for a neural network. In
IJCNN-91-SEATTLE : International Joint Conference
on Neural Networks, Vols 1 and 2, pages B397–B404,
New York. Int Neural Network Soc, I E E E. Inter-
national Joint Conf on Neural Networks ( IJCNN-91-
SEATTLE ), Seattle, WA, Jul 08-12, 1991.
Koza, J., Yu, J., Keane, M., and Mydlowec, W. (2000). Evo-
lution of a controller with a free variable using genetic
programming. In Poli, R., Banzhaf, W., Langdon, W.,
Miller, J., Nordin, P., and Forgarty, T., editors, Genetic
Programming, Proceedings, volume 1802 of Lecture
Notes in Computer Science, pages 91–105, Heidel-
berger Platz 3, D-14197 Berlin, Germany. Napier
Univ; Marconi Communicat Ltd; Evonet; EvoGP,
Springer-Verlag Berlin. European Conference on Ge-
netic Programming (EuroGP 2000), EDINBURGH,
SCOTLAND, APR 15-16, 2000.
Koza, J. R. (1992). Genetic Programming: On the Pro-
gramming of Computers by Means of Natural Selec-
tion. MIT Press, Cambridge, MA, USA.
Koza, J. R. (1994). Genetic programming as a means for
programming computers by natural-selection. Statis-
tics and Computing, 4(2):87–112.
Laderman, J. D. (1976). A noncommutative algorithm for
multiplying 3*3 matrices using 23 multiplications.
Larsen, E. S. and McAllister, D. (2001). Fast matrix mul-
tiplies using graphics hardware. In Proceedings of
the 2001 ACM/IEEE Conference on Supercomputing,
pages 55–55.
MacDonald, Z. A. (2016). Investigation of efficient meth-
ods for the determination of strassen-type algorithms
for fast matrix multiplication.
Mohapatra, C. and Ray, B. B. (2022). A survey on large
datasets minimum spanning trees. In International
Symposium on Artificial Intelligence, pages 26–35.
Springer.
Niewenhuis, D., Salhi, A., and van den Berg, D. (2024).
Making hard (er) benchmark functions: Genetic pro-
gramming.
Niewenhuis, D. and van den Berg, D. (2022). Making
hard(er) bechmark test functions. In IJCCI, pages 29–
38.
Niewenhuis, D. and van den Berg, D. (2023). Classical
benchmark functions, but harder (in press). Springer.
Oh, S. and Moon, B.-R. (2009). Automatic reproduction of
a genius algorithm: Strassen’s algorithm revisited by
genetic search. IEEE Transactions on Evolutionary
Computation, 14(2):246–251.
Genetic Programming for 5×5 Matrix Multiplication
277

Oltean, M. and Diosan, L. (2009). An autonomous gp-based
system for regression and classification problems. AP-
PLIED SOFT COMPUTING, 9(1):49–60.
O’malley, O. (2008). Terabyte sort on apache hadoop.
Yahoo, available online at: http://sortbenchmark.
org/Yahoo-Hadoop. pdf,(May), pages 1–3.
Sazhinov, N., Horn, R., Adriaans, P., and van den Berg, D.
(2023). The partition problem, and how the distribu-
tion of input bits affects the solving process (submit-
ted).
Silver, D., Hubert, T., Schrittwieser, J., Antonoglou, I., Lai,
M., Guez, A., Lanctot, M., Sifre, L., Kumaran, D.,
Graepel, T., et al. (2018). A general reinforcement
learning algorithm that masters chess, shogi, and go
through self-play. Science, 362(6419):1140–1144.
Sleegers, J. and van den Berg, D. (2022). The hardest hamil-
tonian cycle problem instances: The plateau of yes
and the cliff of no. SN Computer Science, 3(5):1–16.
Soltaniyeh, M., Martin, R. P., and Nagarakatte, S. (2022).
An accelerator for sparse convolutional neural net-
works leveraging systolic general matrix-matrix mul-
tiplication. ACM Transactions on Architecture and
Code Optimization (TACO), 19(3):1–26.
Strassen, V. et al. (1969). Gaussian elimination is not opti-
mal. Numerische mathematik, 13(4):354–356.
Timmer, R. (2024). Repository containing source material:
https://github.com/hendrikctimmer/gen prog mm.
Van Den Berg, D. and Adriaans, P. (2021). Subset sum and
the distribution of information. In IJCCI, pages 134–
140.
Verduin, K., Thomson, S. L., and van den Berg, D.
(2023a). Too constrained for genetic algorithms. too
hard for evolutionary computing. the traveling tourna-
ment problem.
Verduin, K., Weise, T., and van den Berg, D. (2023b). Why
is the traveling tournament problem not solved with
genetic algorithms?
Wilson, T., Tan, P.-N., and Luo, L. (2018). A low rank
weighted graph convolutional approach to weather
prediction. In 2018 IEEE International Conference
on Data Mining (ICDM), pages 627–636. IEEE.
Yegnanarayanan, V. (2013). An application of matrix mul-
tiplication. Resonance, 18(4):368–377.
Yu, J., Keane, M., and Koza, J. (2000). Automatic design
of both topology and tuning of a common parameter-
ized controller for two families of plants using genetic
programming. In Proceedings of the 2000 IEEE Inter-
national Symposium on Computer-aided Control Sys-
tem Design, pages 234–242, 345 E 47th St, New York,
NY 10017 USA. IEEE Control Syst Soc; Amer Soc
Mech Engineers; European Union Control Assoc; Soc
Instrument & Control Engineers, IEEE. Joint 2000
Conference on Control Applications and Computer-
Aided Control Systems Design Symposium, Anchor-
age, AK, Sep 25-27, 2000.
Zhang, W. and Korf, R. E. (1996). A study of complex-
ity transitions on the asymmetric traveling salesman
problem. Artificial Intelligence, 81(1-2):223–239.
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
278