An Explainable Classiﬁer Using Diffusion Dynamics for Misinformation

Detection on Twitter

Arghya Kundu and Uyen Trang Nguyen

Electrical and Computer Engineering, York University, Toronto, Canada

Keywords:

Misinformation, XAI, Social Network, Twitter.

Abstract:

Misinformation, often spread via social media, can cause panic and social unrest, making its detection crucial.

Automated detection models have emerged, using methods like text mining, usage of social media user prop-

erties, and propagation pattern analysis. However, most of these models do not effectively use the diffusion

pattern of the information and are essentially black boxes, and thus are often uninterpretable. This paper pro-

poses an ensemble based classiﬁer with high accuracy for misinformation detection using the diffusion pattern

of a post in Twitter. Additionally, the particular design of the classiﬁer enables intrinsic explainability. Further-

more, in addition to using different temporal and spatial properties of diffusion cascades this paper introduces

features motivated from the science behind the spread of an infectious disease in epidemiology, specially from

recent studies conducted for the analysis of the COVID-19 pandemic. Finally, this paper presents the results

of the comparison of the classiﬁer with baseline models and quantitative evaluation of the explainability.

1 INTRODUCTION

Misinformation refers to inaccurate or misleading

news that is propagated through various digital or ana-

log communication channels. Misinformation is cor-

rosive as it has a propensity to cause panic in the pop-

ulation and social unrest. Studies point out that people

refrain from spreading misinformation if they know it

to be false (Zubiaga et al., 2016). However, identify-

ing false news is non-trivial and this motivates the ef-

fort of misinformation detection. Journalists and fact-

checking websites such as PolitiFact.com can be used

to track and detect misinformation. However, their

underlying methodology is manual, thus being prone

to poor coverage and low speed. Therefore, it is nec-

essary to develop automated approaches to facilitate

real-time misinformation tracking and debunking.

Most of the previous work related to automated

misinformation detection focuses on news content,

user metadata, source credibility and propagation cas-

cades. These methods mostly do not consider or tend

to oversimplify the structural information associated

with misinformation propagation. However, the prop-

agation patterns have been shown to provide useful

insights for identifying misinformation.

A landmark study conducted on Twitter found that

the diffusion cascades of misinformation is different

from that of true information (Vosoughi et al., 2018).

Speciﬁcally, misinformation propagates signiﬁcantly

farther, faster, deeper, and broader. Moreover, in a

separate recent study (Juul and Ugander, 2021) on the

same dataset used in (Vosoughi et al., 2018), the au-

thors found that these differences in diffusion patterns

on Twitter can be attributed to the “infectiousness”

of the posts (tweets). They concluded that misin-

formation is more “infectious” than true information.

While the mentioned studies provide empirical evi-

dence that misinformation can be differentiated based

on the propagation cascades and “infectiousness”, it

remains unclear how it can be properly used to create

veriﬁable automated detection mechanisms.

Additionally, modern AI systems solve complex

problems but often produce unexplainable results. For

misinformation detection, user trust in the model im-

pacts their view of an article’s credibility. Explain-

able AI (XAI) models produce interpretable results

(Mishima and Yamana, 2022). Previous XAI research

on misinformation detection has mainly focused on

content and social context, often overlooking propa-

gation cascades.

This motivated us to investigate this approach fur-

ther, focusing solely on diffusion patterns to identify

misinformation and provide explanations based on the

model’s intrinsic properties. In this study, we pro-

pose an ensemble misinformation detection model us-

ing spatio-temporal and epidemiological features of

348

Kundu, A. and Nguyen, U.

An Explainable Classiﬁer Using Diffusion Dynamics for Misinformation Detection on Twitter.

DOI: 10.5220/0012990700003838

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2024) - Volume 1: KDIR, pages 348-357

ISBN: 978-989-758-716-0; ISSN: 2184-3228

diffusion cascades with intrinsic explanation genera-

tions for users. Then, we compare the accuracy of our

proposed model against ﬁve state-of-the-art misinfor-

mation detection models. Finally, we validate the ex-

plainability of our model using quantitative metrics.

The contributions of this paper are as follows:

• Firstly, this study only uses propagation patterns

of social media posts to develop a misinformation

detection model as opposed to most prior work

which uses additional characteristics like content-

based, source based and style-based methods.

• Secondly, we propose an ensemble system for

misinformation detection by applying three clas-

siﬁers, namely, K-nearest neighbour, decision tree

and multilayer perceptron (MLP). Furthermore,

the ensemble system is designed in a speciﬁc way

to always provide intrinsic explainability.

• Thirdly, this paper uses temporal and spatial prop-

erties of diffusion cascades, along with features

inspired by epidemiology, particularly insights

from recent COVID-19 studies.

The paper is structured as follows. Section 2 de-

tails the related work. Section 3 discusses the datasets

used in the study. Section 4 explains the tweet prop-

agation structures. Section 5 discusses the method-

ology to build the misinformation detection system.

Section 6 focuses on the model’s explainability. Sec-

tion 7 discusses the experimental results. Section 8

details the explainability evaluation. Finally, Section

9 concludes the paper.

2 RELATED WORK

2.1 Automatic Misinformation

Detection

Automatic misinformation detection on social media

platforms is grounded on the use of traditional classi-

ﬁers that detect fake news deriving from the pioneer-

ing study of information credibility on Twitter (Car-

los Castillo and Poblete, 2011). In following works

(Xiaomo Liu and Shah, 2015) (Ma et al., 2015), dif-

ferent sets of unique features were used to classify

whether a news is credible. Most of these prior works

attempted to classify the veracity of spreading news

using information beyond the text content, such as

post popularity, user credibility features, and more.

However, these studies did not take into account the

propagation structure of a post. In this paper, we

focuses on using the diffusion cascade of the posts

(tweets).

Nevertheless, some studies have investigated cap-

turing the temporal traits of a post. One study intro-

duced a time-series-ﬁtting model (Kwon et al., 2013),

focusing on the temporal properties of a single fea-

ture – tweet volume. Another study (Ma et al., 2015)

expanded upon this model by using dynamic time se-

ries to capture the variation of a set of social context

features. In addition, another study (Friggeri et al.,

2014) characterized the structure of misinformation

cascades on Facebook by analyzing comments.

However, these studies does not effectively take

into account the relevance of the spread of misinfor-

mation to that of an infectious disease. In this study

we took motivation from the ﬁeld of epidemiology

and account for the spatio-temporal features originat-

ing from the study of the spread of infectious diseases,

speciﬁcally from the recent studies conducted for the

analysis of the COVID-19 pandemic.

2.2 Explainability of Models

Approaches to explainable machine learning are

generally classiﬁed into two categories: intrinsic

explainability and post-hoc explainability. Intrin-

sic interpretability is achieved by constructing self-

explanatory models which incorporate interpretabil-

ity directly to their structures. In contrast, the post-

hoc XAI requires creating a second model to provide

explanations for an existing model which is consid-

ered as a black-box. Studies have shown that intrinsic

XAIs provide better explanations than post-hoc XAIs

(Du et al., 2018), however they have a trade-off with

accuracy. Moreover, existing XAI models for misin-

formation detection often overlook propagation statis-

tics. This motivated us to design an XAI model that

generates explanations solely from diffusion charac-

teristics of the tweet. The proposed model offers both

intrinsic explainability and high accuracy.

Nevertheless, evaluating XAI models remains cru-

cial, yet due to the nascent nature of this ﬁeld, con-

sensus on explanation evaluation is lacking. A recent

survey (Mishima and Yamana, 2022) highlighted that

many XAI models lack standardized evaluation meth-

ods; they often rely on informal assessments or even

skip evaluation altogether. In this study, we use three

quantitative metrics to evaluate the explainability of

our model.

3 DATASET

For evaluation of our model we use the popular pub-

licly available datasets (Ma et al., 2017), Twitter15

and Twitter16, which have been widely adopted as

An Explainable Classiﬁer Using Diffusion Dynamics for Misinformation Detection on Twitter

349

standard data in the ﬁeld of misinformation detection.

Some important characteristics of the dataset are men-

tioned in Table 1.

Table 1: Basic Statistics of the datasets.

Statistic Twitter15 Twitter16

# Users 306,402 168,659

# Tweets 331,612 204,820

Max. # retweets 2,990 999

Min. # retweets 97 100

Avg. # retweets 493 479

4 PROPAGATION STRUCTURE

REPRESENTATIONS

Propagation networks of information on social media

are represented in various ways. For this study we

employ the following two representations,

• Hop based structure

• Time based structure

4.1 Hop Based Structure

In this type of structure, the diffusion of a post is rep-

resented as a directed acyclic graph, with the root of

the tree being the source tweet and the corresponding

children being the retweets.

The advantage of using this representation lies in

its ability to readily leverage the spatial properties of

post diffusion. Additionally, this method of represen-

tation effectively captures the user-follower relation-

ship of tweets propagation in Twitter.

4.1.1 Analysis of the Representation

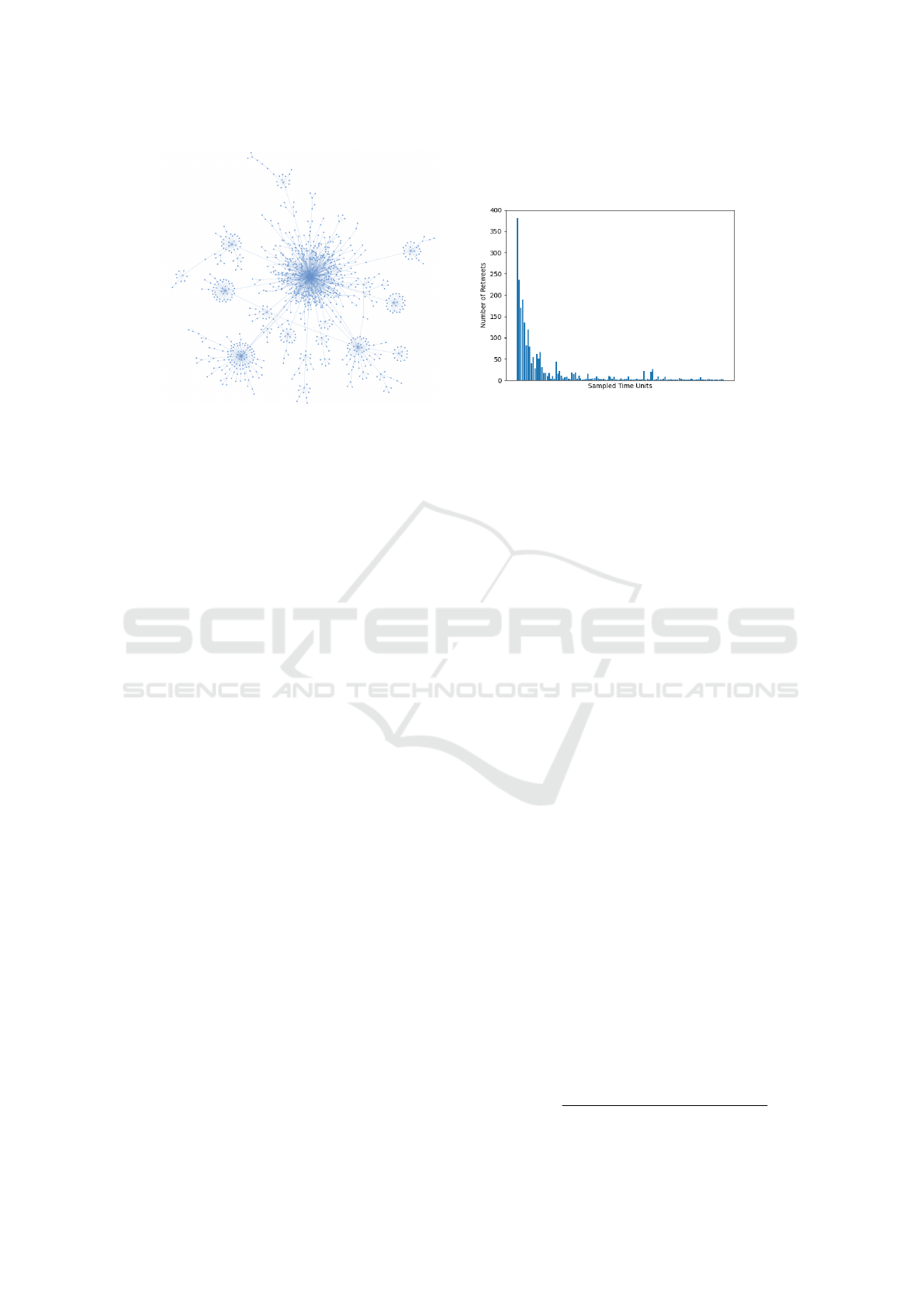
Figure 1a depicts a random news dissemination sam-

ple in hop based cascade representation. The source

tweet is located at the centre of the biggest cluster and

all other nodes represents the successive retweets.

The following observations were made,

• Maximum number of retweets are made directly

from the source tweet.

• Most of the graphs have at least one dense cluster

which does not include the source tweet i.e the

tree has at least one very popular retweet.

4.2 Time Based Structure

In this cascade representation, we calculate the time

delay between a retweet and its source tweet. Using

this delay, the retweet is positioned on the relevant

stack using a sampling time. The sampling time (d)

is chosen to be 60 minutes for this study. The ad-

vantage of using this representation is the ease of us-

ing the temporal properties of the diffusion of a post.

This representation effectively captures the life-cycle,

popularity of a post and the amount of interactions

accounted by the tweet over time.

4.2.1 Analysis of the Representation

Figure 1b depicts a random news dissemination sam-

ple in time based propagation representation.

Following are some observations:

• During the ﬁrst couple of hours the tweet had the

farthest spread. That is, the news penetrated with

more traction in the social media.

• Most of the plots follow an approximation of

power law distribution.

Table 2: Feature Categorization.

Number Feature Type

1 Number of Nodes Spatial Feature

2 Total Diffusion Time Temporal Feature

3 Total Peaks Temporal Feature

4 Mean of timestamps delays Temporal Feature

5 Basic Reproduction Number Epidemiological Feature

6 Basic Transmission Rate Epidemiological Feature

7 Super Spreaders Epidemiological Feature

8 Growth Acceleration Epidemiological Feature

9 Average Growth Speed Epidemiological Feature

10 SD of Timestamps Delays Temporal Feature

11 RMSSD of Timestamps Delays Temporal Feature

12 Height Spatial Feature

5 METHODOLOGY

This section details the methodology of our explain-

able ensemble classiﬁer.

5.1 Feature Selection

The following features are used as referred in Table 2

along with their corresponding feature type.

5.1.1 Number of Nodes

This represents the number of unique users involved

in the diffusion of information. Thus, for a news dis-

semination pattern N

= {R

, reT

, ..,reT

}

number of nodes = card(N

) (1)

where R

is the source tweet, reT

is a retweet and

card{S} is the cardinality of the set S.

5.1.2 Total Diffusion Time

This represents the total time taken for the informa-

tion to propagate in the network, i.e. the life time of

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

350

(a) Hop Based Cascade sample (b) Time Based Cascade sample

Figure 1: Sample Propagation Structure Representations.

the news in Twitter.

Total Diffusion Time = t(reT

) −t(R

) (2)

where t(x) is the timestamp of the tweet object x and

reT

is the last retweet

5.1.3 Total Peaks

This feature constitutes the number of nodes having

timestamp value greater than the graph mean times-

tamp. Thus,

TP = card{v ∈ V | G(v, E)[time] > mean(G(V, E)[time])}

(3)

where V are the nodes in the diffusion cascade

G(V,E).

5.1.4 Basic Reproduction Number

In epidemiology, the basic reproduction number is the

expected number of cases directly generated by one

case in a population where all individuals are suscep-

tible to the disease (NG et al., 2006) More precisely, it

is the number of secondary infections produced by an

infected individual. This number is important in de-

termining how quickly a disease will spread through a

population. For this study we deﬁne the basic repro-

duction number (R0) as the number of retweets di-

rectly from the source tweet (R

R0 = card{e ∈ E | e ∈ G(V, e) ∧ G(R

, e)} (4)

where R

is the source tweet and card{S} is the car-

dinality.

5.1.5 Basic Transmission Rate

The Susceptible-Exposed-Infectious (SIR) model is

used to render a simple model for the spread of a in-

fectious disease. The basic transmission rate (denoted

β) is deﬁned as the number of effective contacts made

by an infected person per unit time in a given popu-

lation. In this study, we interpret basic transmission

rate as the number of retweets made during the ﬁrst

day (T d) of the source tweet.

β = card{v ∈ V | G(v,E)[time] ⩽ G(R

, E)[time] + T d}

(5)

where R

is the source tweet and G(V,E) is diffusion

cascade.

5.1.6 Super Spreaders

In an investigation conducted (Brainard et al., 2023)

to analyze the transmission of coronavirus infec-

tions, researchers observed a signiﬁcant impact on

the spread of the virus were attributable to individ-

uals identiﬁed as ‘super spreaders’. Super spreaders

are individuals with greater than average propensity to

infect. Within this study, we delineate super spread-

ers (SS) as the number nodes exhibiting an edge count

exceeding the average edge count.

SS = card{v ∈ V | G(v, E) > mean(E)} (6)

where G(V,E) is the diffusion cascade and E are the

edges.

5.1.7 Growth Acceleration

In epidemiology, Growth Acceleration is deﬁned as

the (cases \ day

). Recently, in a study it has been

shown that Growth Speed and Growth acceleration

are very effective for the analysis of the COVID-19

pandemic (Utsunomiya et al., 2020). In this study, we

consider the edges i.e the retweets as the cases and

deﬁne Growth Acceleration (GA) as follows,

GA =

∑

i=1

(G(v, E)[time] − G(R

, E)[time])

(7)

An Explainable Classiﬁer Using Diffusion Dynamics for Misinformation Detection on Twitter

351

where G(V,E) is diffusion cascade and V are the

nodes.

5.1.8 Average Growth Speed

Additionally, as mentioned previously Growth speed

was also shown to be very effective in the analy-

sis of the COVID-19 pandemic (Utsunomiya et al.,

2020). In this study, we deﬁne Average Growth Speed

(avgGS) as follows,

avgGS =

heightG(V, E)

(avg. timestamps delays)

(8)

where (avg. timestamps delays) is the average of all

the timestamp delays and height of G(V, E) is the

length of the longest path from the root to the farthest

node in the diffusion tree.

5.1.9 Standard Deviation of Timestamps Delays

Using this feature we try to take into account the mea-

sure of the spread of values from the mean.

σ =

V − 1

∑

i=1

−

(9)

where t are the individual timestamp delays of each

retweet from the source tweet.

5.1.10 RMSSD of Timestamps Delays

We also consider the root mean square of successive

differences between retweet timestamps (RMSSD).

In medical science, RMSSD is considered the pri-

mary time domain measure used to estimate the va-

gally mediated changes (Minarini, 2020). RMSSD

reﬂects the peak-to-peak variance in a time series

data. As mentioned in subsection 4.2.1, during the

initial stages of propagation, claims exhibit the widest

spread, with minimal successive differences between

retweets. Consequently, we integrated RMSSD as a

feature in our model to capture early-hour changes in

news dissemination ﬂow.

RMSSD =

mean{diff{t1, t2, ..,tN}

} (10)

where t are the individual timestamp delays of each

retweet from the source tweet.

5.1.11 Height

Represents the length of the path from source tweet to

its farthest retweet node.

Height =

reT

∑

1 (11)

where R

is the source tweet and reT

is the farthest

retweet.

5.2 Data Preparation

Firstly, The datasets contained four annotations

namely true rumours, non-rumours, false rumours

and unveriﬁed rumours. As our study focuses on bi-

nary classiﬁcation, we re-annotated to two class labels

namely, true and fake news and disregarded the unver-

iﬁed rumours. Secondly, we normalized the features

by scaling and translating. We used the Min Max Nor-

malization method. Finally, For a fair comparison,we

randomly split the datasets into 80% for training and

20% for testing.

5.3 Classiﬁcation Model

For this study we used a voting classiﬁer. A vot-

ing classiﬁer is a ensemble machine learning classi-

ﬁer that trains various base models and predicts on

the basis of aggregating the ﬁndings of each base es-

timator. Voting classiﬁers has been shown to reduce

the aggregate errors of a variety of the base models

and increase ﬁnal accuracy. The aggregating criteria

used in this study is hard voting which is the com-

bined decision of the class label that has been pre-

dicted most frequently by the classiﬁcation models.

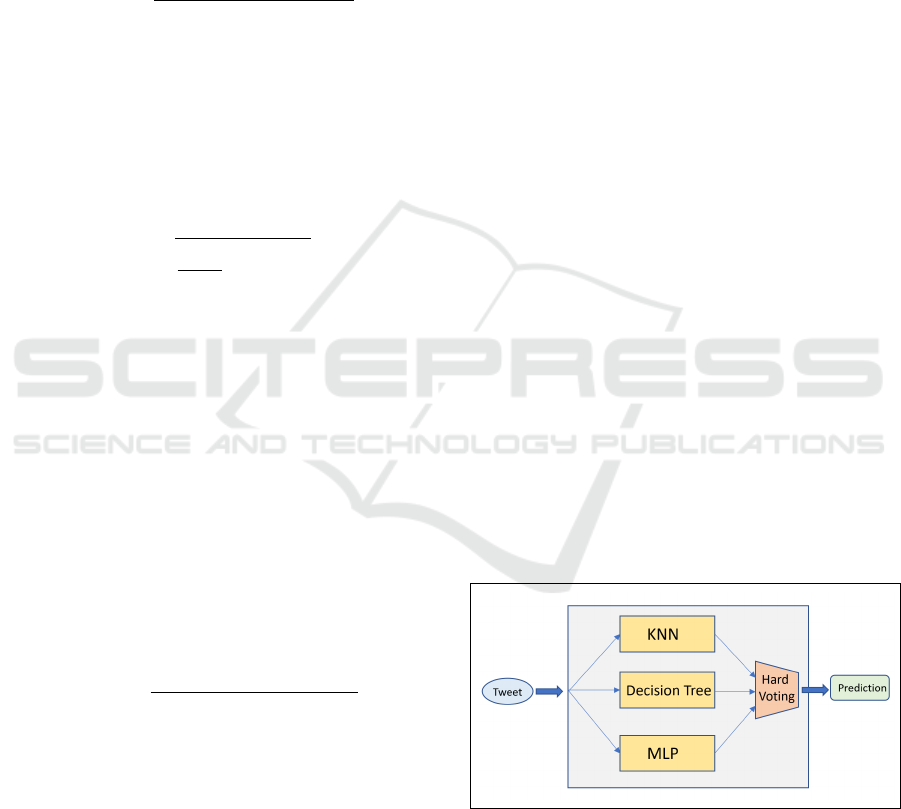
The base models used are as follows, refer Figure 2 :

• KNN Classiﬁer

• Decision Tree Classiﬁer

• Multi-layer Perceptron classiﬁer

Thus, the predicted class label ˆy of our proposed clas-

siﬁer is as follows,

ˆy = mode{C

(x),C

(x)} (12)

where C

(x) is the predicted class label of classiﬁer i.

Figure 2: Voting Classiﬁer Flowchart.

6 EXPLANABILITY OF MODEL

Research shows that intrinsic explainable AI (XAI)

provide better explanations than post-hoc XAIs (Du

et al., 2018), though sometimes with reduced accu-

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

352

racy. Our method balances intrinsic model explana-

tions via KNN and decision tree (DT) classiﬁers while

maintaining high accuracy.

The following two methods were used to accomplish

this,

• Firstly, the unique design of the ensemble classi-

ﬁer asserts that at least one intrinsic explainable

classiﬁer is part of the ﬁnal aggregated vote. That

is, in the best case scenario both the intrinsic ex-

plainable classiﬁers (KNN or DT) have the same

predicted label. Whereas, in the average/worst

case scenario along with MLP classiﬁer either

KNN or DT classiﬁer has the same predicted label

which can be used to provide intrinsic explainabil-

ity.

• Secondly, we added MLP to balance the accuracy-

explainability trade-off in intrinsic XAIs. Al-

though, MLP is not an intrinsic explainable algo-

rithm on its own, the combination the three clas-

siﬁers provides intrinsic explainability along with

high accuracy.

6.1 KNN Classiﬁer

In system interpretability, KNN relies on similarity

and distance, making it inherently interpretable as the

nearest neighbors provide explanations.

For providing human readable explanations for a

given prediction, we employed the following steps:

1. Collect nearest K neighbours of considered point

(P).

2. Filter out same-class neighbors of P, which are

inherently higher in number.

3. Project (P

new

) using arithmetic mean of ﬁltered

points.

4. Get the four highest correlated features between

new

and P using Manhattan distance.

5. Display the number of nearby same class label

neighbours and the highest correlated features.

6.2 Decision Tree Classiﬁer

A decision tree provides a hierarchy of very speciﬁc

questions and predicts outcomes based on decision

rules (if-then-else rules). The answer to one question

guides the prediction process down various branches

of the tree. At the bottom of the tree is the prediction.

Hence, for interpretations, we review decisions by

traversing top-to-bottom tree paths and noting ques-

tion responses for explanations. To this direction we

used the following steps,

1. Fetch the decision rules from the classiﬁer.

2. Use the rules to showcase the answers the speciﬁc

rule addresses.

3. Every rule corresponds to one feature, delivering

a local explanation for that feature’s value.

4. For a given point (P), traversing the decision tree

from top to bottom reveals explanations for the

predicted class label. Inherently the number of the

explanations is the depth of the decision tree.

7 EVALUATION OF

CLASSIFICATION MODEL

In this section we discuss the results of the individual

and ensemble classiﬁers. We used Twitter16 dataset

for selecting the parameters and Twitter15 for testing.

7.1 Individual Classiﬁers

7.1.1 KNN Classiﬁer

The number of neighbors used in this model is ten.

Table 3 shows the results from the k-nearest neigh-

bors classiﬁer with varying hyper-parameters. From

the table, we can see that the model using Manhat-

tan as the distance metric performs the best, achieving

the highest accuracy and precision, along with a good

overall recall. This is rational as studies have shown

that Manhattan distance (L1 norm) ususally performs

better than common distance measures in the case of

high dimensional data.

Table 3: Results of the KNN classiﬁer on Twitter16.

Distance metric Accuracy Precision Recall

Cosine 0.8123 0.8436 0.8787

Manhattan 0.8129 0.8591 0.8865

Correlation 0.8045 0.7899 0.8934

Euclidean 0.8104 0.8087 0.8799

BrayCurtis 0.7903 0.7832 0.8811

7.1.2 Decision Tree Classiﬁer

The maximum depth of the tree is chosen to be three,

in order to reduce computational complexity. Table

4 depicts the results with varying hyper-parameters.

It can be observed that the results are better with the

entropy splitting criterion. However, the accuracy is

almost the same for both the splitting methods. This

is reasonable as the internal working of both the split-

ting methods are very similar. Nevertheless, for the

ensemble model we choose the entropy criterion.

An Explainable Classiﬁer Using Diffusion Dynamics for Misinformation Detection on Twitter

353

Table 4: Results of the Decision Tree classiﬁer on Twit-

ter16.

Splitting criterion Accuracy Precision Recall

Gini 0.8117 0.8548 0.8676

Entropy 0.8123 0.8679 0.8815

7.1.3 Multi-Layer Perceptron Classiﬁer

The MLP classiﬁer has been conﬁgured with two

hidden layers containing (5,2) units respectively.

Limited-memory BFGS (lbfgs) algorithm has been

used for weight optimization as it converges faster and

performs better for small datasets. Table 5 depicts the

results. It can be observed from the results that the

accuracy and recall is highest with the Sigmoid acti-

vation function. As the number of hidden layers is

very low in this model the vanishing gradient prob-

lem does not play a signiﬁcant role and hence the ac-

curacy using sigmoid function is higher compared to

other activation functions.

Table 5: Results of the MLP classiﬁer on Twitter16.

Activation function Accuracy Precision Recall

Tanh 0.7945 0.7712 0.9117

Sigmoid 0.8231 0.8574 0.8905

ReLU 0.8117 0.8419 0.8620

7.2 Ensemble Classiﬁer

The results for the individual classiﬁers are shown in

Table 6 with the optimum parameter conﬁgurations.

Firstly, It can be observed that MLP classiﬁer has the

highest accuracy of 82.31%, however the precision is

low with 0.8574.

Table 6: Results of the individual classiﬁers on Twitter16.

Type Accuracy Precision Recall

KNN classiﬁer 0.8129 0.8591 0.8865

MLP classiﬁer 0.8231 0.8574 0.8905

Decision tree classiﬁer 0.8123 0.8679 0.8815

Secondly, the KNN classiﬁer also has a high ac-

curacy of 81.29% with the low recall and precision.

Finally, the precision is highest in the case of the de-

cision tree classiﬁer with 0.8679, with an accuracy al-

most similar to that of the KNN classiﬁer. Thus, it can

be reasoned that a combination of these three clas-

siﬁers might produce better results. This motivated

us to implement an ensemble voting classiﬁer for this

study.

Table 7 depicts the results for the Voting Classiﬁer.

Table 7: Results of the Voting Classiﬁer on Twitter16.

Type Accuracy Precision Recall

Voting Classiﬁer 0.8522 0.8843 0.8917

It can be inferred from Table 7 that the accuracy

has increased to 85.22 % with the use of the voting

classiﬁer. Ensemble methods like the voting classiﬁer

are ideal for reducing the variance in models, thereby

increasing the accuracy of predictions. The variance

is eliminated when multiple classiﬁers are combined

to form a single prediction. Additionally, it can be

observed that the precision and recall of the voting

classiﬁer are also high with 0.8843 and 0.8917 re-

spectively. From our experiments, it can be reasoned

that the voting ensemble outperforms all the individ-

ual models.

7.3 Baseline Model Comparison

We compared our proposed model with the following

ﬁve state-of-the-art misinformation detection models,

1. CSI (Ruchansky et al., 2017): A misinformation

detection model that captures temporal patterns

using an LSTM to analyze user activity and cal-

culates user scores.

2. tCNN (Yang et al., 2023): a modiﬁed convolution

neural network that learns the local variations of

user proﬁle sequence, combining with the source

tweet features.

3. CRNN (Liu and Wu, 2018): a state-of-the-art

joint CNN and RNN model that learns local and

global variations of retweet user proﬁles, together

with the resource tweet.

4. dEFEND (Shu et al., 2019): a state-of-the-art co-

attention-based misinformation detection model

that learns the correlation between the source ar-

ticle’s sentences and user proﬁles.

5. GCAN (Lu and Li, 2020): a state-of-the-art

graph-aware co-Attention network based misin-

formation classiﬁer that uses user proﬁles meta-

data, news content and propagation pattern.

Table 8 compares our approach to the industry

standards. It can be inferred that our proposed model

outperforms most of the state-of-the-art approaches

on both datasets in terms of accuracy while attaining

highest precision and recall. In particular, our model

achieves an accuracy of 84.47% and 85.22% on the

datasets respectively. Although GCAN achieved the

highest accuracy, the precision and recall are low due

to the class imbalance in the datasets, where GCAN

favors the majority class, leading to higher accu-

racy but poorer minority class detection. Whereas,

our model received at par accuracy with GCAN with

higher precision and recall. Furthermore, GCAN in

addition to propagation pattern uses the user proﬁle

metadata and tweet content, which might not always

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

354

be available in real-world scenarios. Whereas, our

model solely uses the diffusion pattern to create a

classiﬁer.

Table 8: Experimental results on Twitter15 (T15) and Twit-

ter16 (T16) datasets.

Method Recall Precision Accuracy

T15 T16 T15 T16 T15 T16

tCNN 0.5206 0.6262 0.5199 0.6248 0.5881 0.7374

CRNN 0.5305 0.6433 0.5296 0.6419 0.5919 0.7576

CSI 0.6867 0.6309 0.6991 0.6321 0.6987 0.6612

dEFEND 0.6611 0.6384 0.6584 0.6365 0.7383 0.7016

GCAN 0.8295 0.7632 0.8257 0.7594 0.8767 0.9084

Our model 0.8512 0.8917 0.8568 0.8843 0.8447 0.8522

7.4 Ablation Study

To study the contribution of each feature type towards

the ensemble classiﬁer, we carry out ablation experi-

ments. The results are shown in Table 9. The ablation

experiments include the following three variants:

• w/o Spatial: Removing the spatial features of the

ensemble classiﬁer.

• w/o Temporal: Removing the temporal compo-

nents of the ensemble classiﬁer.

• w/o Epidemiological: Removing the epidemio-

logical features of the ensemble classiﬁer.

Table 9: Results of the Ablation experiments using Twit-

ter16.

Type Accuracy Precision Recall

w/o Spatial 0.8213 0.8229 0.8078

w/o Temporal 0.8256 0.8594 0.8810

w/o Epidemiological 0.7714 0.7803 0.8276

Voting classiﬁer 0.8522 0.8843 0.8917

From Table 9, we can observe that all ablation

variants drop some accuracy compared with the pri-

mary model. Speciﬁcally, when removing the spa-

tial features, the accuracy drops by 3.1%, the preci-

sion and recall also dropped. The replacement of the

temporal features caused the accuracy to decrease by

2.7% with lower precision and recall. However, the

accuracy drop was most signiﬁcant when the epidemi-

ological features were removed, accounting to 8.1%

along with lowest precision and recall. This corrob-

orates that epidemiological features inspired from the

study on COVID-19, play an essential role for mis-

information detection using propagation cascades. In

conclusion, overall the primary model, with the three

component types involved, provides a better choice

compared to the ablation variants.

8 EVALUATION OF

EXPLAINABILITY OF THE

MODEL

Evaluation of an XAI model essential, as it provides

a way to understand its practical implication.

8.1 Sample Explanation

Figure 3 displays the explanations generated by our

model on a random data point (P), where KNN clas-

siﬁer and DT classiﬁer had the same predicted class

label. We can observe that, three explanations were

generated for the DT classiﬁer, which is logical as the

depth of the tree was three. Furthermore for point P,

the KNN classiﬁer interpretations were made from the

seven nearby fake tweets out of the ten neighbours.

An interesting observation can also be made that ex-

planations for both the classiﬁers almost correspond

for the same statistical properties of the propagation

cascade.

Figure 3: Explanation generated for a random sample (P).

8.1.1 Metrics Used

We evaluated the model’s interpretability using the

three metrics mentioned below. These are exten-

sions of three metrics used in (ElShawi et al., 2021)

for evaluating interpretability frameworks like LIME,

SHAP, LORE and more.

• Stability: Similar instances should have similar

explanations.

• Separability: Different instances should yield dif-

ferent explanations.

• Identity: Identical instances must produce identi-

cal explanations.

An Explainable Classiﬁer Using Diffusion Dynamics for Misinformation Detection on Twitter

355

For measuring the metrics we randomly select 100

data points and create the testing dataset using their

class labels and generated explanations. The stability

metric is measured by applying K-means clustering

with two clusters to group explanations in the testing

dataset. For simplicity, we use the three explanations

generated by the decision tree (DT), converting each

explanation string into a unique numerical value to

form an integer array. The assigned cluster labels are

then compared with the predicted class labels to eval-

uate whether instances of the same class have simi-

lar explanations. To measure the separability metric,

two subsets S1 and S2 of the testing dataset are se-

lected corresponding to different class labels. Then,

for each instance in S1, its explanation is compared

with all other explanations of instances in S2. If the

explanation have no duplicates, it satisﬁes the sepa-

rability metric. Finally, the identity of the explana-

tions offered by the various deterministic techniques

may be easily measured theoretically. The explana-

tions generated by the decision tree is rule based thus

conforming to complete identity conservation. Addi-

tionally, due to the nature of KNN alrogithm identical

instances will have identical explanations.

8.1.2 Results

The experimental ﬁndings can be seen in Table 10.

The ﬁgures in this table show the percentage of in-

stances that meet the speciﬁed metrics. From the table

we can infer that identity metric is 100%, as identical

instances will have a similar explanations. The stabil-

ity is very high, thus conforming that instances with

same class labels have comparable interpretations. Fi-

nally, the separability is also very high, thus acknowl-

edging that dissimilar instances have dissimilar expla-

nations.

9 CONCLUSION

This paper demonstrates the effectiveness of an

ensemble-based classiﬁer using a tweet’s diffusion

pattern for accurate misinformation detection. We im-

prove the classiﬁcation by using features inspired by

epidemiology and recent COVID-19 research, while

providing understandable predictions. The intrinsic

explanations help users to understand the predicted

class label without compromising accuracy.

Future work will focus on the following areas:

• Incorporating statistical and qualitative measures

to evaluate the results and generated explanations.

• Expanding the model’s applicability to other so-

cial networks such as Instagram and Facebook.

• Investigate and document how hyperparameters,

such as the value of k in k-NN, sampling rate, af-

fect model performance.

• Conduct deeper analysis on the consistency and

comparability of explanations generated by differ-

ent models (e.g., k-NN vs. DT).

Table 10: Metrics for the evaluation of explanations.

Metric Score

Stability 89%

Separability 97%

Identity 100%

REFERENCES

Brainard, J., Jones, N. R., Harrison, F. C., Hammer, C. C.,

and Lake, I. R. (2023). Super-spreaders of novel coro-

naviruses that cause sars, mers and covid-19: a sys-

tematic review. Annals of Epidemiology, 82:66–76.e6.

Carlos Castillo, M. M. and Poblete, B. (2011). Information

credibility on twitter. page 675–684.

Du, M., Liu, N., and Hu, X. (2018). Techniques for inter-

pretable machine learning.

ElShawi, R., Sherif, Y., Al-Mallah, M., and Sakr, S. (2021).

Interpretability in healthcare: A comparative study

of local machine learning interpretability techniques.

Computational Intelligence, 37(4):1633–1650.

Friggeri, A., Adamic, L., Eckles, D., and Cheng, J. (2014).

Rumor cascades. Proceedings of the 8th International

Conference on Weblogs and Social Media, ICWSM

2014, pages 101–110.

Juul, J. L. and Ugander, J. (2021). Comparing informa-

tion diffusion mechanisms by matching on cascade

size. Proceedings of the National Academy of Sci-

ences, 118(46).

Kwon, S., Cha, M., Jung, K., Chen, W., and Wang, Y.

(2013). Prominent features of rumor propagation in

online social media. In 2013 IEEE 13th International

Conference on Data Mining, pages 1103–1108.

Liu, Y. and Wu, Y.-F. (2018). Early detection of fake news

on social media through propagation path classiﬁca-

tion with recurrent and convolutional networks. Pro-

ceedings of the AAAI Conference on Artiﬁcial Intelli-

gence, 32(1).

Lu, Y.-J. and Li, C.-T. (2020). GCAN: Graph-aware co-

attention networks for explainable fake news detec-

tion on social media. In Proceedings of the 58th An-

nual Meeting of the Association for Computational

Linguistics.

Ma, J., Gao, W., Wei, Z., Lu, Y., and Wong, K.-F. (2015).

Detect rumors using time series of social context in-

formation on microblogging websites.

Ma, J., Gao, W., and Wong, K.-F. (2017). Detect rumors in

microblog posts using propagation structure via kernel

learning. In Proceedings of the 55th Annual Meeting

of the Association for Computational Linguistics (Vol-

ume 1: Long Papers).

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

356

Minarini, G. (2020). Root mean square of the successive

differences as marker of the parasympathetic system

and difference in the outcome after ans stimulation. In

Aslanidis, T., editor, Autonomic Nervous System Mon-

itoring, chapter 2. IntechOpen, Rijeka.

Mishima, K. and Yamana, H. (2022). A survey on ex-

plainable fake news detection. IEICE Trans. Inf. Syst.,

E105.D(7):1249–1257.

NG, B., K, G., B, B., and Caley P, Philp D, M. J. (2006).

Using mathematical models to assess responses to

an outbreak of an emerged viral respiratory disease.

National Centre for Epidemiology and Population

Health.

Ruchansky, N., Seo, S., and Liu, Y. (2017). Csi: A hybrid

deep model for fake news detection. pages 797–806.

Shu, K., Cui, L., Wang, S., Lee, D., and Liu, H. (2019). De-

fend: Explainable fake news detection. In Proceed-

ings of the 25th ACM SIGKDD International Confer-

ence on Knowledge Discovery & Data Mining, KDD

’19, page 395–405, New York, NY, USA. Association

for Computing Machinery.

Utsunomiya, Y. T., Utsunomiya, A. T. H., Torrecilha, R.

B. P., de C

assia Paula, S., Milanesi, M., and Garcia,

J. F. (2020). Growth rate and acceleration analysis

of the covid-19 pandemic reveals the effect of public

health measures in real time. medRxiv.

Vosoughi, S., Roy, D., and Aral, S. (2018). The spread of

true and false news online. Science, 359:1146–1151.

Xiaomo Liu, Armineh Nourbakhsh, Q. L. R. F. and Shah, S.

(2015). Real-time rumor debunking on twitter. page

1867–1870.

Yang, Y., Zheng, L., Zhang, J., Cui, Q., Li, Z., and Yu,

P. S. (2023). Ti-cnn: Convolutional neural networks

for fake news detection.

Zubiaga, A., Liakata, M., Procter, R., Wong Sak Hoi, G.,

and Tolmie, P. (2016). Analysing how people orient

to and spread rumours in social media by looking at

conversational threads. PLOS ONE, 11(3):1–29.

An Explainable Classiﬁer Using Diffusion Dynamics for Misinformation Detection on Twitter

357