Predictive Models for United States House Prices

Hongyi Yang

Financial Technology College, Shenzhen University, 3688 Nanhai Road, Shenzhen, China

Keywords: United States House Prices, Random Forest, XGBoost, AdaBoost.

Abstract: House prices are a crucial indicator affecting citizens' lives, directly impacting individuals' and families'

financial situations, as well as the stability and development of entire communities. Therefore, it is imperative

to conduct in-depth research on the societal impact of house price prediction models, exploring their effects

on housing markets, economic development, social welfare, and potential challenges and issues. This study

addresses the issue of accurate house price prediction by conducting extensive analyses on four ensemble

learning models: Random Forest, XGBoost, AdaBoost, and Stacking. The selected metrics for assessing

model performance in this experiment include RMSE, R-squared, Explained Variance Score, and MAPE. The

results demonstrate that the Random Forest model excels across multiple evaluation metrics, outperforming

other models with the lowest RMSE and MAPE values. XGBoost shows strong competitiveness, providing

accurate predictions and effectively capturing nonlinear relationships in the data, albeit slightly inferior to

Random Forest. AdaBoost and Stacking exhibit moderate performance, possibly limited by their ability to

handle complex relationships and noisy data.

1 INTRODUCTION

The property market has always been a dynamic and

promising field. With the acceleration of urbanization

and continuous economic development, an increasing

number of people are choosing to purchase properties

as a long-term investment and lifestyle choice. This

situation is not only prevalent in major cities but also

in some small towns, villages, and countryside areas.

The growing demand not only drives the steady

increase in property prices but also makes real estate

an attractive option for investors. In such an

environment, accurate prediction of property prices is

crucial for real estate developers, investors, and

ordinary home buyers. However, property prices are

often influenced by various factors, including

economic factors, physical factors, and individual

subjective factors. Therefore, there is a greater need

for a robust model to predict real estate prices.

In the domain of house price prediction, a

multitude of scholars explore diverse modeling

methodologies to investigate various scenarios. These

models include support vector machines, random

forests, decision tree models, and others.

This paper aims to construct a superior predictive

model for US house prices by comparing various

techniques. We'll use a Kaggle dataset covering fifty

US cities, with sales price as the target variable and

factors like state, city, living area, and rooms as

predictors.

For modeling, we primarily selected ensemble

learning models for comparison. Ensemble learning

models make decisions and predictions by combining

the predictions of multiple base models. They

typically achieve better performance than traditional

models and have been widely applied in practice.

Therefore, this study selects four different ensemble

learning models for comparative analysis: Random

Forest (RF), Adaptive Boosting (AdaBoost), Extreme

Gradient Boosting (XGBoost), and Stacking model.

In Section 2, this paper will review related studies.

Section 3 will provide a detailed introduction to the

selected models and their basic principles. The

specific experimental procedures and analysis of

experimental results will be outlined in Section 4. In

Section 5, we will offer the general conclusions of the

paper, followed by a compilation of all references.

2 RELATED WORK

In the field of housing price prediction, researchers

have adopted various methods to analyze and solve

different needs and problems. In the early days,

scholars mainly used hedonic pricing models to

conduct research on housing price prediction. Until

Yang, H.

Predictive Models for United States House Prices.

DOI: 10.5220/0012990800004601

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Innovations in Applied Mathematics, Physics and Astronomy (IAMPA 2024), pages 38-45

ISBN: 978-989-758-722-1

now, this is still a common research method. Some

scholars have used the hedonic pricing model to

analyze the impact of the urban railway network on

Bangkok housing prices, because this model can

better maintain simplicity and avoid overfitting

(Tekouabou et al., 2024). However, this model also

has shortcomings in capturing nonlinear

relationships. Therefore, researchers began to use

machine learning models (Zhan et al., 2023). This has

brought a wealth of research content to the field of

housing price prediction. For example, some

researchers used convolutional neural networks

(CNN) to analyze a data set of 3,000 houses in the

United States by considering visual cues. The mean

absolute error (MAE) obtained excellent results

(Yousif et al., 2023). Some scholars have also found

that listing prices have a significant impact on

housing prices, that is, the anchoring effect.

Therefore, they introduced anchoring effects and

listing price-related indicators into the model to

optimize the model (Song and Ma, 2024). They used

a variety of machine learning models such as

generalized linear models (LASSO and Ridge) and

decision trees for training. Experiments have shown

that by introducing anchoring effect indicators, it

helps to significantly improve the model evaluation

index R2. In addition, some scholars have compared

the predictive capabilities of various Bayesian

models, such as horizontal Bayesian vector

autoregression (bvar - 1) and differential Bayesian

vector autoregression (BVAR-d) (Haan and

Boelhouwer, 2024). In this way, they study the impact

of credit-constrained and unconstrained households'

borrowing capacity on house prices.

In order to solve the shortcomings of traditional

machine learning models in housing price prediction,

such as low model prediction accuracy and

insufficient generalization ability, ensemble learning

models have begun to receive more attention. Some

scholars have used the whale algorithm based on the

ensemble learning model to optimize the support

vector regression model and predict housing prices in

Beijing, Shanghai, Tianjin and Chongqing, and have

obtained results with higher prediction accuracy than

traditional models (Wang et al., 2021). In addition,

some scholars have a similar purpose to this article,

aiming to select the best housing price prediction

model for the Spanish real estate market. They used a

variety of ensemble learning methods for comparison,

including bagging, boosting and random forest. In the

end, bagging was chosen because the results in

MAPE and COD were slightly better. There are also

Korean researchers who have taken a different

approach and considered the prices of buildings and

land respectively to predict the real estate market

(José-Luis et al., 2020). They also used two integrated

learning models, random forest and XGBoost, and

proved that XGBoost has better results in this data set

(Kim et al., 2021). Finally, some scholars have also

studied the impact of noise on housing prices, an

environmental factor that is very rare in normal data

sets (Kamtziridis & Tsoumakas, 2023). They used the

XGBoost ensemble learning model to predict housing

prices in Thessaloniki, proving that the impact of

noise on prices in different areas of the same city is

significantly different.

Although there have been considerable research

results in the field of housing price prediction, since

housing price fluctuations are affected by various

complex factors, they are prone to problems such as

strong subjectivity, low accuracy, and inability to

fully reflect real demand. Therefore, there is still a

need for research when facing different data sets and

influencing factors

3 METHODOLOGIES

In this study, we first preprocessed the features

contained in the dataset and conducted basic data

analysis on the preprocessed data. Subsequently, we

constructed various models and trained them using

the dataset. These models include RF, XGBoost,

AdaBoost, and Stacking model. We obtained

corresponding results by training these models and

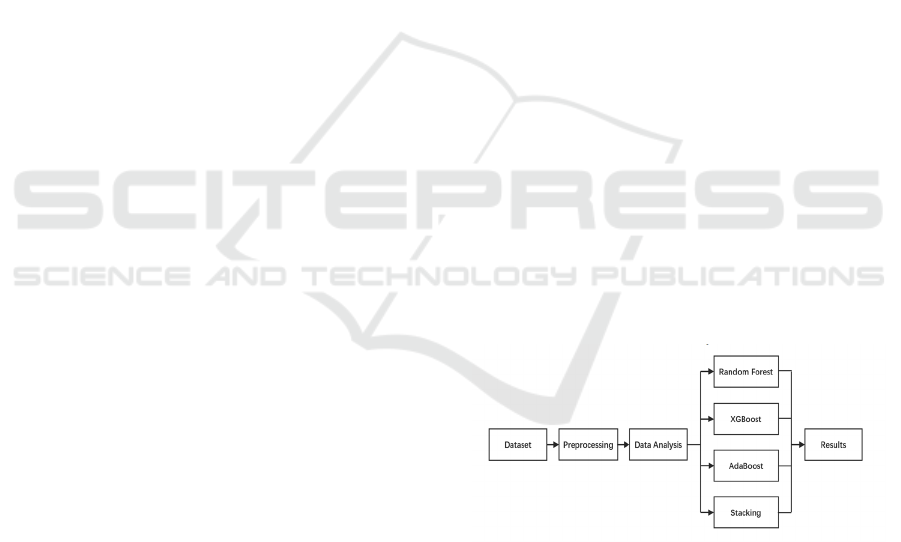
further analyzed the results. Figure 1 illustrates the

overall workflow of this study.

Figure 1: Research Workflow (Picture credit: Original).

3.1 Data Preprocessing and Data

Analysis

Before constructing various models, we need to

preprocess the selected dataset. As the dataset

provided is highly complete without any missing or

outlier values, there is no need for imputation or

handling missing data values. However, several

features in the dataset are qualitative values, so we

need to convert qualitative data into numerical data.

Predictive Models for United States House Prices

We chose to convert them into numerical data using

label encoding.

Next, we conducted basic data analysis on the

dataset, where we observed the distribution of data

and the correlation between variables. Detailed

results are provided in the following sections.

During the data analysis stage, we observed that

some features exhibited high similarity in the dataset.

This high similarity might lead to multicollinearity

issues during model training, thereby reducing the

model's generalization ability. Therefore, in the

feature selection process, we chose not to include

these features in the model training. The scale of the

dataset significantly affects the performance of

models when using certain machine learning

algorithms. To address this, Min-Max scaling was

introduced in this study to transform the dataset,

scaling each feature into a designated range

separately, i.e., transforming them between 0 and 1.

3.2 Model Construction

Four different models were chosen for the

comparison of house price prediction. Random Forest

is renowned for its ensemble learning approach. The

Random Forest algorithm performs well with high-

dimensional datasets and exhibits robustness when

handling large-scale data (Li, 2023). XGBoost, a

gradient boosting algorithm, stands out for its ability

to handle various data types and complex

relationships, making it suitable for tasks requiring

high prediction accuracy. Its success is also credited

to its excellent resilience against overfitting (Demir

and Sahin, 2023). AdaBoost is another boosting

algorithm. It emphasizes iteratively improving model

performance by focusing on difficult-to-predict

instances, thereby enhancing prediction accuracy.

During training, the AdaBoost algorithm achieves

higher accuracy by continually reducing the error rate

of the next machine (Ender, 2022). Stacking is a

meta-ensemble learning technique that utilizes meta-

learners for final prediction, combining the strengths

of multiple base models to provide enhanced

performance and adaptability across various datasets.

To reduce model complexity and avoid excessive

stacking, only a dual-tiered framework was chosen:

fundamental learners and meta-learners. Moreover,

the second layer of stacking typically requires

relatively simple classifiers; hence, linear regression

was chosen as the second-layer classifier in this study

(Liu et al., 2022). By leveraging the unique

characteristics of these four models, our aim is to

comprehensively evaluate their performance in the

task of prediction.

3.2.1 RF

The RF predictor comprises M stochastic regression

trees. For the 𝑗



tree within a group of trees, the

forecasted outcome at each individual x is represented

as 𝑚



𝑥;∅



,𝜕



. Here, ∅



……,∅



represent

unrelated random variables, while 𝜕



stands for the

training variable (Sharma, harsora & Qgunleve,

2024). Therefore, the estimation of the 𝑗



tree can be

expressed as:

𝑚



(𝑥;∅



,∂



)

=

𝑋𝑖∈𝐴



(𝑥;∅



,∂



)





𝑁



(𝑥;∅



,∂



)

∈



(∅



)

(

)

Here, 𝜕



∗

∅



 represents the set of selected data

points prior to tree construction. 𝐴



𝑥;∅



,𝜕









refers to the cell containing x. The final formula can

be expressed as



𝑚

,

(

𝑥;∅



….∅



,∂



)

𝑀

𝑚



𝑥;∅



,∂









(

)

3.2.2 XGBoost

The algorithm is an ensemble learning method based

on gradient boosting. Its fundamental approach

involves combining weak classifiers, CART trees,

into a strong classifier using an additive model.

𝑦



()

=𝑓







(

𝑥



)

(

)

Here, 𝑦



()

represents the predicted value, and

(𝑥



)



denotes the weak classifier.

𝑜𝑏𝑗 =−



𝐺





𝐻



+𝜆





+ 𝛾T (4)

In the equation, 𝜆 is a fixed coefficient; 𝛾 is the

complexity coefficient; T is the number of nodes; G



represents the cumulative sum of the first-order

partial derivatives of the samples; H



denotes the

aggregate of the second-order partial derivatives of

the samples.

3.2.3 AdaBoost

Let's assume an initial training dataset 𝐷=

{(𝑥



,𝑦



),…,(𝑥



,𝑦



)}. We initialize the weights of n

samples, initially assuming a uniform distribution of

training sample weight distribution 𝐷



(𝑖). 𝐷



(𝑖)

IAMPA 2024 - International Conference on Innovations in Applied Mathematics, Physics and Astronomy

represents the weight of training set samples in the k-

th iteration; The quantity n represents the sample size,

while K denotes the maximum number of iterations.

We train a weak predictor ℎ



(𝑥) under the weighted

samples and compute its average error:

𝜀



𝑛

𝜀







(5)

Update the sample weights 𝐷



(

𝑖

)

and the weak

learner weights 𝑊



, where 𝛽











and 𝑍



are the

normalization factors for 𝐷



(𝑥



)





=1.

𝐷



(

𝑖

)

𝐷



(

𝑖

)

𝛽







𝑍



(6)

𝑊



ln (1/𝛽



) (7)

Then proceed to the next iteration until the

iteration reaches K, and finally obtain the strong

predictor.

𝐻

(

𝑥

)

=𝑊



ℎ



(

𝑥

)





(

)

3.2.4 Stacking Model

The Stacking model employs multiple diverse

algorithmic models for modeling. Initially, m

different learners are chosen to individually predict

the data. Subsequently, based on the outcomes

obtained from each learner, they are input into a

second-layer learner, ultimately resulting in the

prediction outcome (Figure 2).

Figure 2: The flowchart of the Stacking model (Picture

credit: Original)

4 EXPERIMENTAL PROCEDURE

AND RESULTS

4.1 Dataset Overview

This article selects the American housing price

dataset from Kaggle, which includes data on 39,982

residential properties in fifty cities across the United

States. Each entry in the dataset consists of 14

attributes (Table 1).

Table 1: Feature Description Table.

Attribute Description

Zip Code

A numeric code used for postal purposes, identifying specific geographic areas within the

United States.

Price The market value of the property, indicating its monetary worth.

Beds Number of sleeping spaces.

Baths Number of bathing places.

Living Space The habitable area within the property used for living.

Address The precise location details of the property.

City The name of the city where the property is situated.

State The U.S. state where the property is located.

Zip Code Density The population density within the zip code area.

Zip Code Population The number of people living in the area

County The name of the county where the property is situated.

Median Household Income The median income level of households within the area.

Latitude Coordinate parameters, used to determine the specific address of housing data.

Longitude Coordinate parameters, used to determine the specific address of housing data.

Predictive Models for United States House Prices

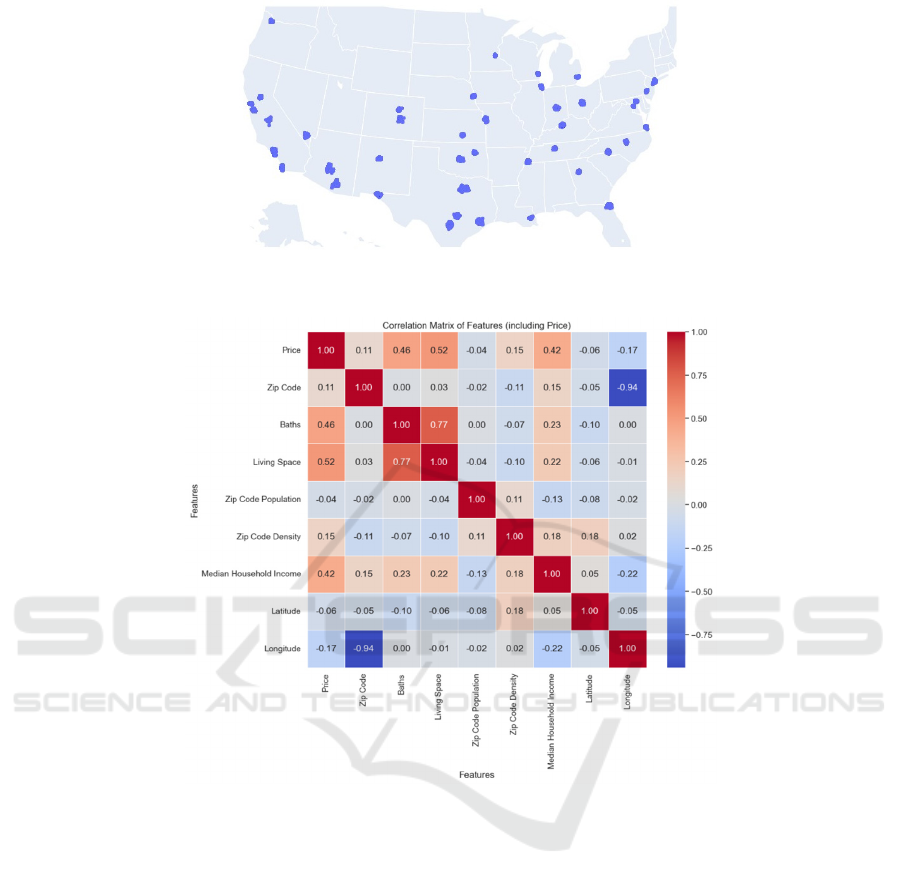
Figure 3: Address Scatter Plot Diagram (Picture credit: Original).

Figure 4: Correlation Matrix (Picture credit: Original).

As shown in Figure 3, the geographical

distribution of all houses in the dataset is depicted. It

can be observed that the houses in the dataset are

distributed across most states of the United States.

This distribution is obtained based on the latitude and

longitude of each house in the dataset.

For some redundant information in the dataset, we

selectively choose which to include in the model. For

example, among the features such as city, state,

county, and latitude and longitude, we only selected

the latitude and longitude of each house as its

geographical location feature. Following this, we

explored the correlation between the selected features

(Figure 4). It can be observed that some features have

a correlation coefficient greater than 0.7. Therefore,

we consider them to have significant

multicollinearity. To address this, we choose to retain

the feature that has a greater impact or importance on

the target variable and remove the other feature.

Additionally, considering their low correlation with

the 'Price' feature, we removed two features—

'Latitude' and 'Zip Code Population'—with

correlation coefficients less than 0.1.

4.2 Experimental Setup

In this experiment, all models were implemented in

Python using packages such as pandas, sklearn, and

seaborn. Below are the specific parameter settings for

each model used in the experiment.

In the RF, the number of trees in the decision tree

is adjusted to 100, while the other parameters remain

at their default settings.

Through random search technique, the optimal

parameter settings for the XGBoost model were

identified. The best parameter combination is as

follows: a learning rate of 0.14, a maximum depth of

4 for each tree, a subsample ratio of 0.93, a column

IAMPA 2024 - International Conference on Innovations in Applied Mathematics, Physics and Astronomy

subsample ratio of 0.62, a regularization alpha of 0.01

for each tree, a regularization lambda of 0.48, a

minimum split gain of 0.08 for each tree, and a total

of 139 trees.

The optimal hyperparameters for the Adaboost

model were determined through experimentation,

yielding the following configuration: a learning rate

of 0.01, utilizing the 'exponential' loss function, and

comprising 196 estimators.

The Stacking model operates with default

parameter settings.

4.3 Metric Selection

The selected metrics for evaluating model

performance in this experiment are RMSE, R-

squared, Explained Variance Score, and MAPE.

 Root Mean Squared Error (RMSE)

RMSE, frequently employed, assesses model

prediction errors comprehensively. It determines the

variance between predicted values from the model

and the actual values, squares this difference,

computes the average, and subsequently derives the

square root. A reduced RMSE signifies diminished

disparity between predicted values from the model

and the observed values, reflecting enhanced

precision in predictions.

RMSE=

√

MSE



𝑀

(𝑥



−𝑥



)







(9)

Where 𝑥



represents the actual value, 𝑥



represents the predicted value, and 𝑀 denotes the

number of predictions.

 Coefficient of Determination (R-squared)

Typically, the closer R-squared is to 1, the better the

model fits the observed data, and the higher the

proportion of variance that can be explained.

𝑅



(𝑦,𝑦

)=1−

(𝑦



−𝑦



)







(𝑦



−𝑦



)







(10)

In this equation, y

is obtained by taking the mean of

 Explained Variance Score

This metric measures the extent to which the model

explains the fluctuations in the dataset. A value of 1

indicates a perfect fit, while smaller values indicate

poorer performance.

Explained Variance Score(x

,𝑥

)

=1−

𝑉𝑎𝑟 {𝑥− 𝑥

}

𝑉𝑎𝑟 {𝑥}

(11)

Where 𝐱 represents the true value, 𝐱

represents the

predicted value.

 Mean Absolute Percentage Error (MAPE)

It quantifies the prediction errors of a model in

percentage terms.

MAPE =

𝑁

|

𝐴



−𝐹



𝐴







(12)

𝐴



represents the actual value, 𝐹



represents the

predicted value, and 𝑁 denotes the number of

forecasts.

4.4 Experiment Results Evaluation

Below are the displays of various evaluation metrics

for the four models used in the experiment (Table 2).

After comparing the performance metrics of

various models, it is evident that RF exhibits the

lowest RMSE performance, while Stacking's RMSE

performance slightly trails behind RF but remains

relatively low. This suggests that compared to the

other two models, both RF and Stacking have

relatively small average errors in predicting house

prices. The poorer RMSE performance of XGBoost

could be attributed to inadequate parameter settings

or issues such as noise in the dataset. AdaBoost's

RMSE, although better than XGBoost, still lags

behind RF and Stacking, which may be due to

improper selection of weak classifiers or data

imbalance issues.

Table 2: Experimental Results.

Model RMSE R-square

MAPE Explained Variance Score

Random Forest 388072 0.764986 47.266467 0.764983

XGboost 1605102 0.749524 53.692264 0.749565

Adaboost 1030023 0.655605 283.17976 0.295654

Stacking 439131 0.699079 51.009625 0.699079

Predictive Models for United States House Prices

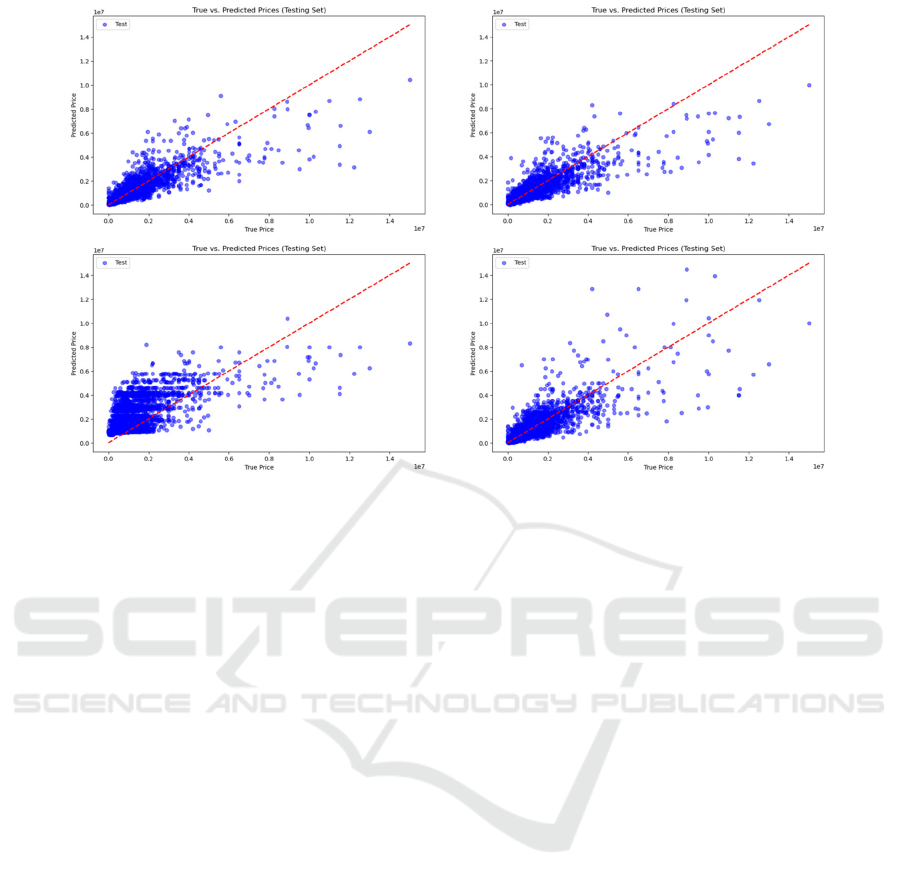
Figure 5: Scatter Plot (Picture credit: Original).

Similarly, in terms of R-squared and explained

variance score, RF achieves values closest to 1,

indicating the best fit among the models. The results

of XGBoost and Stacking are relatively close, while

AdaBoost exhibits a significantly larger difference in

R-squared and explained variance score, possibly

indicating issues with underfitting, overfitting, or data

imbalance.

RF also demonstrates the lowest MAPE score,

indicating the smallest average of absolute percentage

errors between predictions and actual values

compared to other models. XGBoost's slightly higher

MAPE may be attributed to its lower robustness

against outliers. AdaBoost exhibits a higher MAPE

compared to RF and XGBoost, indicating larger

percentage errors in its predictions. Stacking falls

between Random Forest and AdaBoost in terms of

MAPE, suggesting moderate prediction accuracy.

The results indicate that Random Forest

demonstrates superior predictive performance

compared to the other ensemble learning models

investigated, with Stacking showing competitive

performance but still trailing behind RF. XGBoost

and AdaBoost demonstrate relatively poorer

performance, potentially due to specific weaknesses

in their modeling approaches or issues with the

dataset.

In addition, we visualized the test set results of

each model, which facilitated a more intuitive

analysis. Figure 5 presents the visualization results of

the four ensemble learning models, with each point

representing a data point in the test set. In the scatter

plot, we opted for the x-axis to present the true data

values, while selecting the y-axis to represent the

forecasted information. The red line in the graph

indicates the scenario where the predicted values

equal the true values, representing the optimal

prediction. When a point lies on the red line, it

signifies accurate prediction.

Observing the visualization results of the four

models, we observed that the Random Forest and

XGBoost models tend to make relatively

conservative predictions, with predicted values

mostly lower than the true values, especially evident

as housing prices increase. In contrast, the Adaboost

model, although exhibiting similar characteristics to

Random Forest and XGBoost when housing prices

are high, often produces predicted values higher than

the true values when housing prices are low. The

Stacking model shows a more uniform distribution,

but tends to have higher errors, particularly when

housing prices are high.

5 CONCLUSION

To address the issue of accurate house price

prediction, this study conducted extensive analyses

on four ensemble learning models: Random Forest,

XGBoost, AdaBoost, and Stacking. Among them, the

Random Forest model consistently demonstrated

superior performance across multiple evaluation

IAMPA 2024 - International Conference on Innovations in Applied Mathematics, Physics and Astronomy

metrics, outperforming other models. It exhibited the

lowest RMSE and MAPE values. XGBoost showed

competitive performance, providing accurate

predictions and effectively capturing nonlinear

relationships in the data, albeit slightly inferior to

Random Forest. The performance of AdaBoost and

Stacking was moderate, possibly due to limitations in

handling complex relationships and noisy data.

Additionally, attention should be paid to the societal

impact of house price prediction. House prices are a

vital indicator affecting citizens' lives, directly

impacting individuals' and families' financial

situations, as well as the stability and development of

entire communities. Therefore, in-depth research on

the societal impact of house price prediction models

is warranted, exploring their effects on housing

markets, economic development, social welfare, and

potential challenges and issues.

REFERENCES

Tekouabou, S.C.K., Gherghina, Ş.C., Kameni, E.D. et

al. AI-Based on Machine Learning Methods for Urban

Real Estate Prediction: A Systematic Survey. Arch

Computat Methods Eng 31, 1079–1095 (2024).

Choujun Zhan, Yonglin Liu, Zeqiong Wu, Mingbo Zhao,

Tommy W.S. Chow, A hybrid machine learning

framework for forecasting house price, Expert Systems

with Applications, Volume 233,2023,120981, ISSN

0957-4174.

Yousif, A., Baraheem, S., Vaddi, S.S. et al. Real estate

pricing prediction via textual and visual

features. Machine Vision and Applications 34, 126

(2023).

Song, Y., Ma, X. Exploration of intelligent housing price

forecasting based on the anchoring effect. Neural

Comput & Applic 36, 2201–2214 (2024).

van der Drift, R., de Haan, J. & Boelhouwer, P. Forecasting

House Prices through Credit Conditions: A Bayesian

Approach. Comput Econ (2024).

Xiang Wang, Shen Gao, Shiyu Zhou, Yibin Guo, Yonghui

Duan, Daqing Wu, "Prediction of House Price Index

Based on Bagging Integrated WOA-SVR

Model", Mathematical Problems in Engineering, vol.

2021, Article ID 3744320, 15 pages, 2021.

José-Luis Alfaro-Navarro, Emilio L. Cano, Esteban Alfaro-

Cortés, Noelia García, Matías Gámez, Beatriz Larraz,

"A Fully Automated Adjustment of Ensemble Methods

in Machine Learning for Modeling Complex Real

Estate Systems", Complexity, vol. 2020, Article ID

5287263, 12 pages, 2020.

Kim, J.; Won, J.; Kim, H.; Heo, J. Machine-Learning-Based

Prediction of Land Prices in Seoul, South

Korea. Sustainability 2021, 13, 13088.

Kamtziridis, G., Vrakas, D. & Tsoumakas, G. Does noise

affect housing prices? A case study in the urban area of

Thessaloniki. EPJ Data Sci. 12, 50 (2023).

S. Li, "Application of Random Forest Algorithm in New

Media Network Operation Data Push," 2023 IEEE 15th

International Conference on Computational

Intelligence and Communication Networks (CICN),

Bangkok, Thailand, 2023, pp. 87-92.

Demir, S., Sahin, E.K. An investigation of feature selection

methods for soil liquefaction prediction based on tree-

based ensemble algorithms using AdaBoost, gradient

boosting, and XGBoost. Neural Comput &

Applic 2023,35, 3173–3190.

Ender Sevinç, An empowered AdaBoost algorithm

implementation: A COVID-19 dataset study,

Computers & Industrial Engineering, Volume

165,2022,107912,ISSN 0360-8352.

Liu, J.; Dong, X.; Zhao, H.; Tian, Y. Predictive Classifier

for Cardiovascular Disease Based on Stacking Model

Fusion. Processes 2022, 10, 749.

Sharma, H.; Harsora, H.; Ogunleye, B. An Optimal House

Price Prediction Algorithm:

XGBoost. Analytics 2024, 3, 30-45.

Predictive Models for United States House Prices