Research on Housing Prices Forecasts Based on A Multiple Linear

Regression Model

Yiwen Wang

School of Mathematics and Science, Shanghai Normal University, Shanghai, 201418, China

Keywords: Multiple Linear Regression, Predictive Modelling, Impact Factors, Housing Price.

Abstract: House prices have always been a hotly debated topic. However, the factors affecting them and the extent of

their influence have changed over time, so this paper aims to find a simple method of predicting house prices

that best fits the recent past. This paper collects a sample of 545 independent samples just updated this quarter.

By preprocessing the data and analyzing the multiple linear regression, accurate multiple linear regression

equations are obtained for prediction. Meanwhile, the diagnostic illustrates that the samples are independent,

there is no multicollinearity between the variables, and the residuals follow a normal distribution. 12

independent variables (Area, Bedroom, Bathroom, Story, Parking, Furnishing status, Guestroom, Basement,

Hot water, Air-conditioner, Main road, Preferred area) correspond to a significant positive effect on the

variable (Housing prices), with Area, Bathroom’s number, and Air-conditioner’s number being the top

three influencing factors. Overall, simple house price predictions can be made using the model developed in

this paper.

1 INTRODUCTION

In today's society, housing prices have become one of

the focuses of widespread concern. With the

acceleration of urbanization and population growth,

the development of the real estate market has

increasingly attracted widespread attention. Home

buyers, renters, investors, and policymakers have

taken great interest in the changes in house prices (Li,

2023 & Liao and Anwer, 2022). Especially in some

hotspot cities, the dramatic fluctuations of house

prices not only directly affect the living standards,

psychological health, and investment decisions of

residents, but also have a far-reaching impact on the

city's social stability and economic development

(Chun, 2020 & Kenyon et al., 2024). Against this

background, the significance of forecasting home

prices becomes more and more prominent.

Accurately predicting the future trend of housing

prices not only helps home buyers develop a

reasonable home purchase plan but also helps

investors grasp market opportunities and avoid

investment risks. Whereas house prices are

influenced by several factors, such as the impact of

global factors, advanced economies have a high

degree of synchronization in house prices, and

structural shocks are one of the main factors driving

volatility in house prices (Hirata et al., 2012).

In this paper, the issue of how to effectively

predict future housing prices changes will be

addressed. Initially, a thorough review of pertinent

literature will be conducted to organize existing

research findings and methodologies systematically.

Ding and Jiang combined the improved lion swarm

algorithm with the Backpropagation (BP) neural

network model for the housing prices prediction

problem. A model called Spiral search Lion Swarm

Optimization-BP was proposed by enhancing the lion

group algorithm's local search ability and global

search ability. The model showed better results in

second-hand housing prices prediction and improved

the convergence speed and training accuracy of the

BP neural network (Ding and Jiang, 2021). Luo et al.

discussed the use of multiple linear regression models

in housing prices forecasting. The authors used the

Python language to process house prices data for

selected regions in the U.S. Exploratory data analysis,

dummy variable setting, and variance inflation factor

correction were used to improve the accuracy and

robustness of the model. The conclusion highlights

the importance of optimizing the model to improve

forecasting accuracy (Luo et al., 2020). Moreover,

Zhan et al. integrated Hybrid Bayesian Optimization

Wang, Y.

Research on Housing Prices Forecasts Based on A Multiple Linear Regression Model.

DOI: 10.5220/0012991000004601

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Innovations in Applied Mathematics, Physics and Astronomy (IAMPA 2024), pages 53-59

ISBN: 978-989-758-722-1

(HBO) with ensemble techniques like Stacking

(HBOS), Bagging (HBOB), and Transformers

(HBOT) to predict house prices. They leverage

Bayesian Optimization for hyperparameter tuning,

enhancing prediction accuracy and stability. Using a

dataset of 1.89 million Hong Kong real estate

transactions from 1996 to 2021, they thoroughly

tested their approach (Zhan et al., 2023). By

illustrating housing prices predictions for 14,382

observations in 15 urban areas of Oslo, the

researchers' simulations validate LitBoost as a

tailored tree-boosting model for situations involving

data from different known populations with a limited

number of observations in each group. By limiting the

complexity of the gradient boosting tree, LitBoost can

express the final model as a local generalized additive

model (GAM), thus improving interpretability while

maintaining predictive power (Hjort et al., 2024).

They created a statistical model for forecasting

individual housing prices and for constructing a house

prices index from information on sales prices that

includes time, random (ZIP) effects, and

autoregression. The model is more effective than

S&P/Case-Shiller (Nagaraja, Brown and Zhao,

2011).

In summary, this study analyzes a dataset of 546

samples, each with 13 variables. The prediction

method is applied to these variables, and the resulting

predictions are analyzed and discussed. The findings

are summarized, and recommendations and prospects

are presented.

Through the research in this paper, the objective

is to provide valuable references for home buyers,

investors, policymakers, and participants in the real

estate market, to foster the stability and sustainable

development of the real estate market. Ultimately, by

providing a comprehensive understanding of the

drivers of housing prices, this research endeavors to

lay the foundation for a more resilient, equitable, and

sustainable real estate market that serves the needs of

both current and future generations.

2 METHODOLOGY

2.1 Data Sources and Description

This paper's dataset was obtained from the Kaggle

website. After examining the dataset with License:

CC0 public domain, its availability is 100%, and

because this dataset is updated every quarter, it is

timely, so this study is not prone to obsolescence.

This dataset contains 545 groups of data. Due to the

completeness of the data, they were all used as

samples for this study. The original CSV dataset was

preserved.

2.2 Variable Selection

Each sample was not excluded because there were no

missing data or variables inappropriate for analysis.

The final selected data contained 12 independent

variables (Area, Bedroom, Bathroom, Story, Parking,

Furnishing status, Guestroom, Basement, Hot water,

Air-conditioner, Main road, Preferred area, Housing

prices) and one dependent variable (Housing prices).

The specific descriptions are shown in Table 1:

Table 1: List of variables.

Variable

Logogram

Meaning

Area

𝑥



Total area of housing

Area_normalized

𝑥



Total normalized area of housing

Bedroom

𝑥



Total number of bedrooms

Bathroom

𝑥



Total number of bathrooms

Story

𝑥



Total number of stories

Parking

𝑥



Total number of Parking spaces

Furnishing status

𝑥



Unfurnished or Semi-furnished or Furnished

Guestroom

𝑥



Availability of guest rooms

Basement

𝑥



Availability of basement

Hot water

𝑥



Availability of heated water function

Air-conditioner

𝑥



Availability of air-conditioner

Main road

𝑥



Proximity to main roads

Preferred area

𝑥



Whether it is a preferred area

Housing prices

The transaction prices of the house

IAMPA 2024 - International Conference on Innovations in Applied Mathematics, Physics and Astronomy

2.3 Method Introduction

Data preprocessing is carried out first. Classify the

data, normalize the larger data “Area” in the

numerical independent variable to eliminate the

influence of the scale, and at the same time accelerate

the convergence speed of the model and increase the

stability of the model; assign values to the subtypes

of variables respectively. Then, the model is

established, and the data are imported to obtain the

indicators such as the goodness-of-fit 𝑅



, the

influence coefficient B, and so on, as well as the

regression equation. In the next step, diagnosis is

performed. Assessment is made from three

conditional assumptions of regression analysis:

sample independence, absence of multicollinearity

between independent variables, and normality of

residuals.

3 RESULTS AND DISCUSSION

3.1 Pre-Processing

According to the theory of multiple regression

analysis, the independent variables affecting house

prices are categorized into numerical and subtypes.

The categorized statistics of independent variables

are shown in Table 2, and the range of values for

subtyped variables is shown in Table 3.

Table 2: Categorized statistics of independent variables.

Classifications Variables

Subtyped independent

variables

Main road, Guestroom,

Basement, Hot water, Air-

conditioner, Preferred area,

Furnishing status

Numeric independent

variables

Area, Bedroom, Bathroom,

Story, Parking

Table 3: Range of values for subtyped independent

variables.

Variables Range

Main roa

0,1

Guestroom 0,1

Basement 0,1

Hot wate

0,1

-conditione

0,1

Preferred area 0,1

Furnishing status 1,2,3

3.1.1 Preprocessing of Numeric Variables

Since the value of “Area” 𝑥



in the numerical

independent variable is greater than the quadratic of

10, the normalization method is adopted to handle it

as 𝑥



. The normalization formula is as follows:

𝑥=





(1)

The ‘min’ in the formula represents the value's

minimum value in the numeric dependent variable,

while the ‘max’ represents the maximum value. The

other numeric variables are not treated because of

their small values.

3.1.2 Preprocessing of Subtyped

Variables

Since the data content of the independent variables













are all ‘yes’ or ‘no’, which

conforms to a 0-1 distribution, then take the values 0

or 1. The range of values for furnishing status is 1 for

unfurnished, 2 for semi-furnished, and 3 for

furnished, where 1, 2, and 3 are not numerical values,

but are simply factors used to represent the three

types.

3.2 Modeling of Multiple Linear

Regression

By importing the processed data into SPSS,

goodness-of-fit 𝑅



=0.680 can be obtained in the

model summary (Table 4), which means that the

twelve variables selected in this paper can explain

68% of the dependent variable. This shows that this

prediction analysis is significant.

It can also be noted that the value of the statistic F

obtained from the analysis of variance is 94.238. A

high F-statistic in regression signals that at least one

independent variable significantly impacts the

dependent variable, suggesting a non-random

relationship. It also indicates that the model

effectively explains much of the data's variability,

implying strong predictive power of the independent

variables. Moreover, the p-value is very close to zero,

indicating that the regression model is significant.

Table 4: Model summary.

R R

usted R

Statistic F

0.825 0.680 0.673 94.238 0.000 1.852

Research on Housing Prices Forecasts Based on A Multiple Linear Regression Model

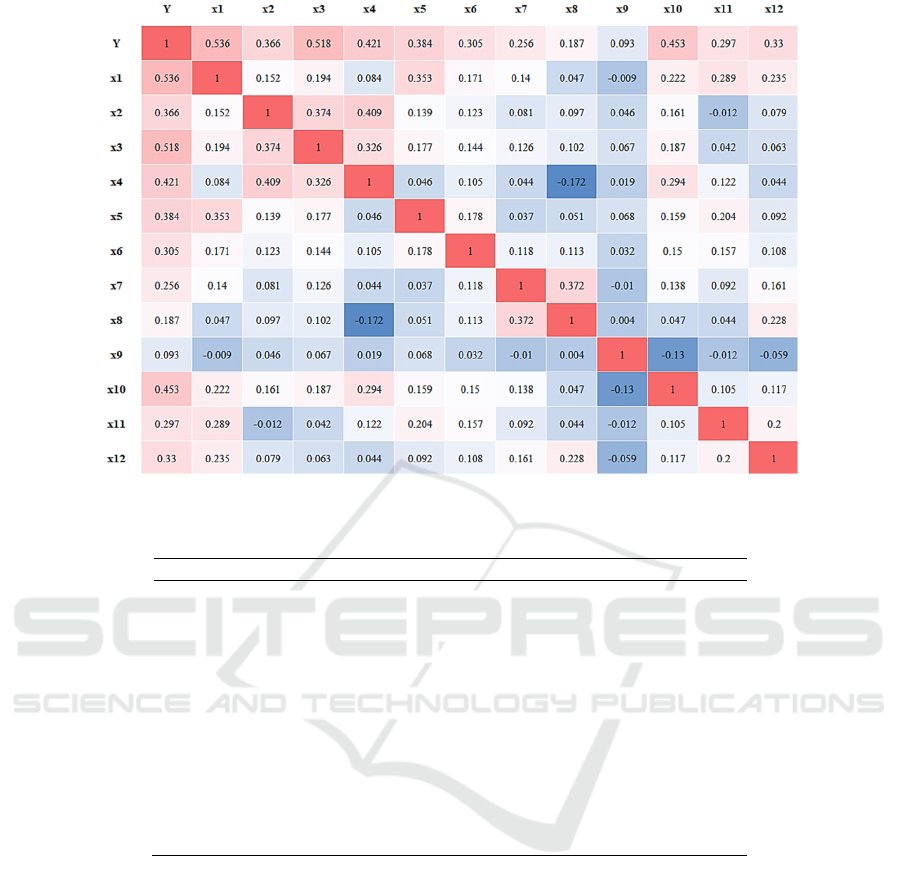
Figure 1: Pearson correlation.

Table 5: Regression coefficients table.

Beta t si

nificance tolerances VIF

(

Constant

)

-0.558 0.577

𝒙

𝟏

Area_normalize

0.283 10.024 0 0.755 1.325

𝒙

𝟐

Bedroom 0.047 1.644 0.101 0.731 1.368

𝒙

𝟑

Bathroom 0.266 9.551 0 0.777 1.287

𝒙

𝟒

Story 0.209 7.006 0 0.677 1.478

𝒙

𝟓

Parking 0.129 4.774 0 0.825 1.212

𝒙

𝟔

Furnishing status 0.087 3.381 0.001 0.913 1.096

𝒙

𝟕

Guestroom 0.061 2.259 0.024 0.825 1.213

𝒙

𝟖

Basement 0.091 3.243 0.001 0.757 1.321

𝒙

𝟗

Hot wate

0.098 3.909 0 0.962 1.039

𝒙

𝟏𝟎

-conditione

0.212 7.879 0 0.828 1.207

𝒙

𝟏𝟏

Main roa

0.079 2.97 0.003 0.853 1.173

𝒙

𝟏𝟐

Preferred area 0.147 5.585 0 0.871 1.149

According to the given Pearson correlation

coefficient matrix, the correlation between the

variables can be analyzed initially. The color of

Figure 1 shows that the red part is almost distributed

in the first column and the first row, except for the

diagonal, which indicates that the 12 independent

variables have a high degree of influence on Housing

prices. Area_normalized, Bathroom, Air-conditioner

and Story, all four variables have high correlation

(0.536, 0.518, 0.453, 0.421) with Housing prices. The

correlation between other variables and prices is

weaker but still positive, such as Furnishing status,

Main road, and Preferred area.

Moreover, in Table 5, except for the first column,

the first row, and the diagonal, the other parts of the

table are bluer, which indicates that except for the

dependent variable Housing prices, the correlation

between the other independent variables is weak.

Most of the correlation coefficients are below 0.2, and

some of them are even close to zero or less than zero.

The correlations between the variables are low except

for Area_normalized which is moderately positively

correlated with Parking (0.353), and Bedroom and

Bathroom which have some degree of positive

correlation (0.374). And the weak correlation of

independent variables is beneficial for modelling.

Going further, through Table 5, by looking at the

“Significance” column, it can be seen that the

significance values of 𝑥



to 𝑥



are less than 0.05, so

all the independent variables have a significant effect

on dependent variable Y. Secondly, by looking at the

column of influence coefficient B, it can be found that

IAMPA 2024 - International Conference on Innovations in Applied Mathematics, Physics and Astronomy

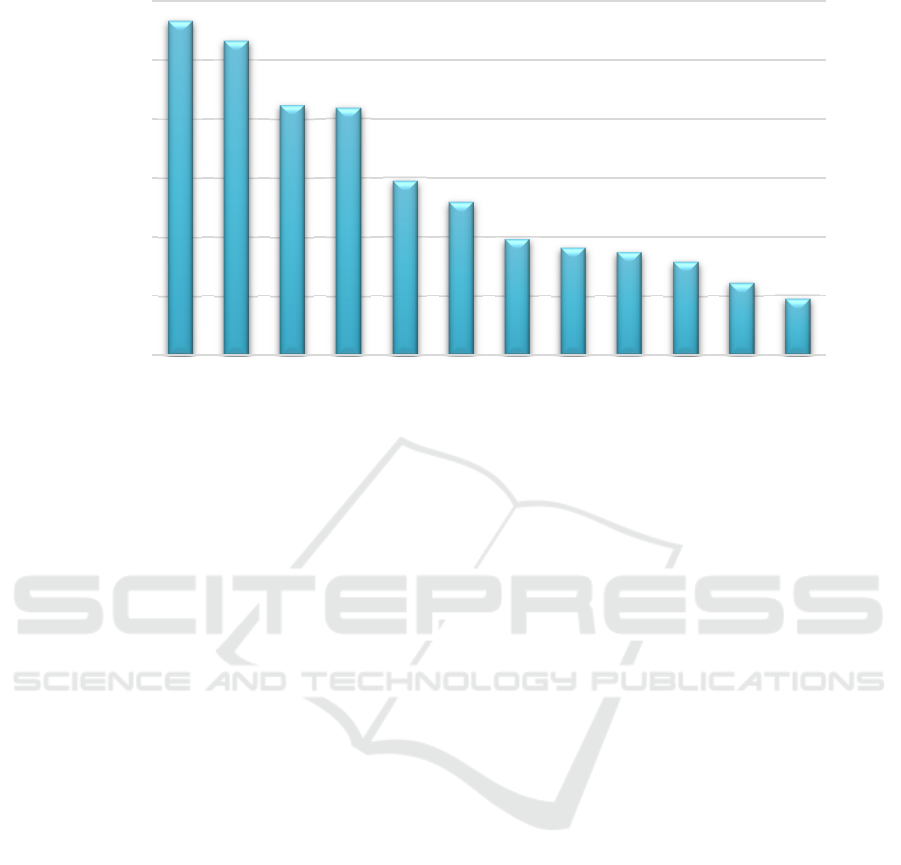
Figure 2: Standardized coefficient of influence of the independent variable on the dependent variable

the standardized coefficient Beta of all independent

variables is greater than 0, so all of these independent

variables have a positive influence on the dependent

variable Y. And the degree of influence from high to

low is:

𝑥



,𝑥



,𝑥



,𝑥



,𝑥



,𝑥



,𝑥



,𝑥



,𝑥



,𝑥



,𝑥



,𝑥



As shown in Figure 2:

The standardized coefficient Beta value from

Table 4 gives the following multiple linear regression

equation for the study in this paper:

𝐸



𝑌



=0.283𝑥



0.047𝑥



 ⋯  0.147𝑥



(2)

3.3 Model Diagnosis

By testing the conditional assumptions of the

regression analysis: that the samples are independent

of each other, that there is no multicollinearity

between the variables, and that the residuals follow a

normal distribution, it is possible to diagnose that the

multivariate linear regression model used in this

paper is reasonably usable.

3.3.1 Sample Independence

The value of the Durbin-Watson statistic can be

obtained from Table 4 Model Summary as 1.852, as

this value is close to 2, the samples are independent

and there is no autocorrelation between the residuals.

3.3.2 No Multicollinearity Between Variables

It can be noticed from the Table 5 coefficients table

that the Variance Inflation Factors (VIF) of all the

variables are within the range of 0 to 5, so it can be

shown that there is no extremely strong correlation

between the independent variables involved in this

study, i.e., it is proved that these 12 independent

variables are not similar and there is no need to delete

any of them.

3.3.3 Normality of Residuals

As can be seen from Figure 3, the residuals (the part

that does not match the model) follow almost a

normal distribution (the black curve in the figure).

Although some of them are beyond the highest point

of the normal distribution, it is known from the

previous section that the variables selected in this

paper explain 68% of the dependent variable, i.e., it is

still necessary to describe the remaining 32% by

looking for other variables that are not in this paper,

so it is reasonable to exceed them by a small amount.

0,05

0,1

0,15

0,2

0,25

0,3

x1 x3 x10 x4 x12 x5 x9 x8 x6 x11 x7 x2

Beta

Independent variables

Research on Housing Prices Forecasts Based on A Multiple Linear Regression Model

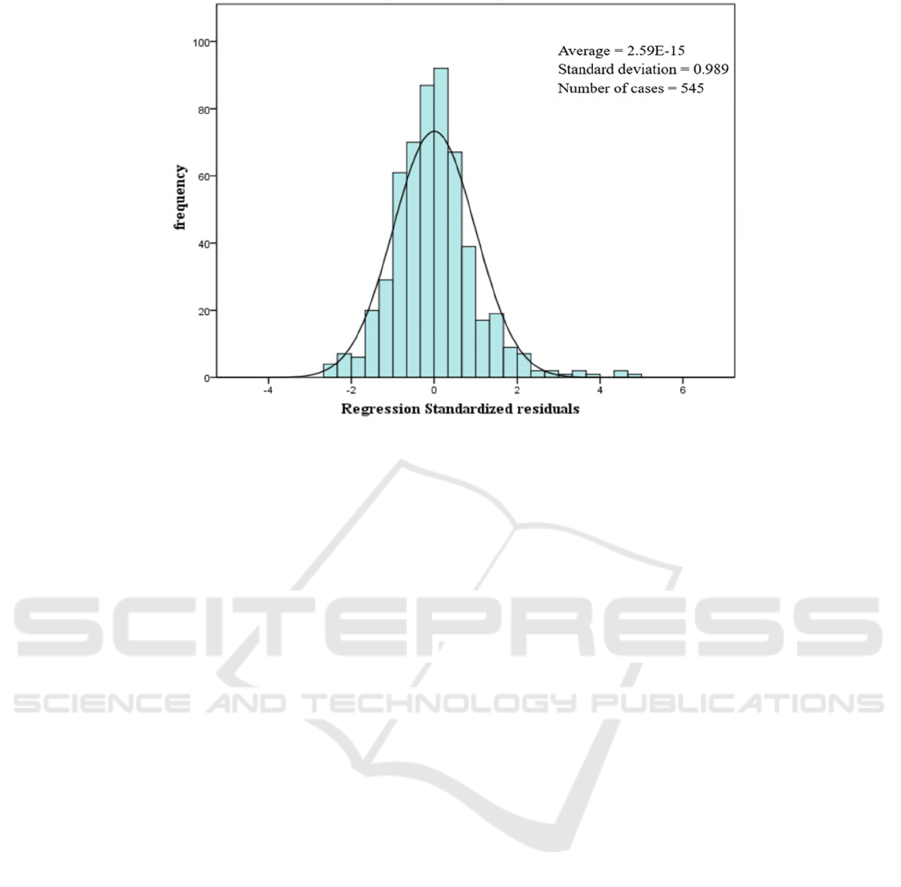
Figure 3: Residual distribution.

4 CONCLUSION

This paper obtained 545 samples updated quarterly

from the complete dataset with 12 independent

variables and 1 dependent variable. The multiple

linear regression model used in this paper was

diagnosed (conditional assumptions for regression

analysis) and proved to be stable, accurate, and

reliable.

The data was pre-processed by taking the

normalization of the numerical variables with large

values and also assigning labels to the sub-typed

variables. Pearson correlation coefficient matrix was

analyzed with the aid of SPSS, indicating that the

independent variables selected for this paper are

weakly correlated with each other and are highly

correlated with the dependent variable Y. Then the

data was put into a multiple linear regression model.

The model fits well with an R-squared value of 0.680,

indicating that the model explains 68% of the

variation in house prices. Moreover, it was found that

all the independent variables positively affect

respondent variable Y, which is significant. Their

degree of influence in descending order are Area,

Bathroom, Air-conditioner, Story, Preferred area,

Parking, Hot water, Basement, Furnishing status,

Main road, Guestroom, Bedroom

( 𝑥

,𝑥

). The

diagnostic test of the model reveals that the samples

are independent, there is no multicollinearity between

the variables, and the residuals follow a normal

distribution, so the model is informative. The final

result is a multiple linear standardized regression

equation that can be used to accurately predict house

prices by simply entering the desired values of each

independent variable.

This study will help people to estimate house

prices based on their individual needs. It can also help

better understand various factors' impact on housing

prices and inform analysis and decision-making in the

real estate market. In the future, the model can be

further improved by considering more factors such as

the Age of the house, Layout structure, School

district, Market supply and demand, Accessibility,

Scenery, Quality of construction, Economic factors,

etc. to improve the accuracy and applicability of the

forecast.

However, there are some limitations to the study.

The independent variable selected in this paper can

only explain 68% of Housing prices, so it is not

comprehensive enough, and it is necessary to go

further to find several variables that can explain the

remaining 32% so that it can better assist in

forecasting. In addition, the data used in this paper

may come from the same geographical area, so the

linear regression equation may not be appropriate for

all geographical areas. It is better to increase the

samples from different places to participate in the

prediction modelling.

REFERENCES

Li Y 2023 Kunming's property market rebounds as many

sales break 100 million yuan, developers take

IAMPA 2024 - International Conference on Innovations in Applied Mathematics, Physics and Astronomy

advantage of the situation to raise house prices to raise

concern. China Real Estate News. 10.

Liao Y Q and Anwer S 2022 An empirical study of public

concern and Shenzhen house prices based on TVP-

VAR model. SAR Economics. 01 97-100.

Chun H 2020 Do housing prices changes affect mental

health in South Korea? J. Ethiopian Journal of Health

Development. 34 48-59.

Kenyon G E, Arribas-Bel D, Robinson C, Gkountouna O,

Arbues P and Rey-Blanco D 2024 Intra-urban house

prices in madrid following the financial crisis: an

exploration of spatial inequality. Urban Sustain. 4 26.

Hirata H, Kose M A, Otrok C and Terrones M E 2012

Global House Prices Fluctuations: Synchronization and

Determinants. NBER International Seminar on

Macroeconomics. 9(1) 119-166.

Ding F and Jiang M Y 2021 House prices prediction based

on improved lion group algorithm and BP neural

network model. Journal of Shandong University

(Engineering Edition). 4 8-16.

Luo B W, Hong Z Y and Wang J Y 2020 Application of

multiple linear regression statistical modeling in house

prices prediction. Computer Age. 6 51-54.

Zhan C J, Liu Y L, Wu Z Q, Zhao M B and Chow Tommy

W S 2023 A hybrid machine learning framework for

forecasting house prices. Expert Systems with

Applications. 233 120981.

Hjort A, Scheel I, Sommervoll D E, Johan Pensar 2024

Locally interpretable tree boosting: An application to

house prices prediction. Decision Support Systems. 178

114106.

Nagaraja C H, Brown L D and Zhao L H 2011 An

autoregressive approach to house prices modelling. The

Annals of Applied Statistics. 5(1) 124-149.

Wang N, Lu Y F and Ge L F 2024 Research and simulation

of duration prediction model based on multiple linear

regression method. J. Project Management

Technology. 4 84-88.

Research on Housing Prices Forecasts Based on A Multiple Linear Regression Model