NODE and Contraction Methods for Dynamics Learning from

Human Expert Demonstrations

Tufail Ahmed

, Sangmoon Lee

and Ju H. Park

Department of Electronics and Electrical Engineering, Kyungpook National University, Daegu, Republic of Korea

Department of Electrical Engineering, Yeungnam University, Kyongsan, Republic of Korea

Keywords: Neural Ordinary Differential Equations (NODE), Learning from Demonstrations (LfD), Dynamic Systems,

Imitation Learning, Initial Value Problem, Contraction Theory.

Abstract: In this paper, we propose model-free or learning-from-demonstration methodologies for accurately estimating

the complex and nonlinear behaviors of dynamic systems such as mobile robots, robotic arm manipulators,

and unmanned aerial vehicles (UAVs). Under learning from demonstration (LfD), this study investigates two

different approaches: The first proposed methodology is the contraction theory, in which the assigned task

demonstration is practically performed by the human expert, who tries to learn and imitate it. On the other

hand, the same task learns and imitates by utilizing the neural ordinary differential equations (NODEs) for

dynamic systems. Using the concepts of both approaches, we tried to make it possible for the system to pick

up on and imitate the shown behavior or demonstration accurately. In dynamics learning, the proposed

contraction method utilizes the conceptual framework of the contraction theory, which ensures the motions

of dynamic systems that eventually converge to nominal or desired behavior. At the same time, NODE uses

the neural network with different configurations of hidden layers, learning rate, nonlinear activation function,

and ODE solver. A spiral trajectory is considered a human expert demonstration that is estimated by both

methodologies (i) NODE and (ii) contraction theory. For validation purposes, we compared the results of both

approaches.

1 INTRODUCTION

Learning by demonstration, or LfD for short, is a

useful strategy for rapidly enhancing robotic

efficiency. It enables robots to gain capabilities by

observing what they want to do. Focusing on allowing

the robotic device to program by itself, the human

operator demonstrates an action to the robot by

demonstrating how the operation ought to be

performed. Learning action patterns through as few

demos as possible is vital, and the quantity of storage

required is reduced when taught skills are concisely

represented (Khansari-Zadeh, et. al., 2011; Calinon,

S., et. al., 2007). It is possible to represent actions

from one point to another to ensure all come to an end

at a designated spot in state space (Schaal, S., 1999).

Simplifying more complex tasks can yield

fundamental components of robot automation

surveillance: sequences of one point to motions or

https://orcid.org/0000-0001-8252-952X

https://orcid.org/0000-0002-0218-2333

modeling between point actions (Kulic, D., et. al.,

2008). When an operator directs an autonomous

device throughout an activity, it automatically sees

the process from its point of view. LfD: While

dynamical actions specify how to emulate, one point

to another action includes steps made by human

experts to solve the problem (Dautenhahn, K., and

Nehaniv, C. L., 2002). Robotic trajectories are shown

via kinesthetic training to circumvent the matching

issue, whereby human observers passively guide the

robot along its ideal motion (B., Akgun, and

Subramanian, K., 2011). One of the earliest instances

of digital summoning taught via examples is

dynamical motion primitive concepts (DMP). DMP is

used to combine a linear dynamical system and a

nonlinear force factor, which is obtained in one demo

(Ijspeert, A., et. al., 2013). Poor replication could

occur from implementing restrictive stabilization

criteria. If one concentrates too heavily on precise

Ahmed, T., Lee, S. and Park, J.

NODE and Contraction Methods for Dynamics Learning from Human Expert Demonstrations.

DOI: 10.5220/0012992900003822

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 2, pages 205-211

ISBN: 978-989-758-717-7; ISSN: 2184-2809

205

reproduction, one may become less resilient to

disruptions, which could eventually cause deviation.

There are instances where precision suffers because

reliability is given precedence over efficiency. It

might not be the most effective solution if the intricate

dynamics underneath is fascinating. Finding the right

balance between studying the intricacies of kinetics

and maintaining stabilization in a system that changes

is difficult. Enabling robots and autonomous devices

to perform tasks efficiently within dynamic settings

and learning from demonstrated actions (LfD) is a

critical capability. Highly complex, non-linear

trajectories like spirals are a common challenge for

conventional LfD techniques. To enhance the

prediction and reproduction of these trajectories, this

work explores the application of contraction theory

and neural networks with ordinary differential

equations (neural ODEs). We examine such

approaches' theoretical underpinnings, real-world

applications, and comparative effectiveness.

The paper's remaining structure is as follows. In

the next section, the problem formulation of both

proposed methods (node and contraction theory) is

presented. In Section 3, we present the neural ODE

and contraction theory learning framework for

learning the dynamics of the dynamic systems. In

Section 4, we performed the simulation and

demonstrated the effectiveness of both the proposed

methodologies. Finally, we concluded the paper with

a summary and future research direction.

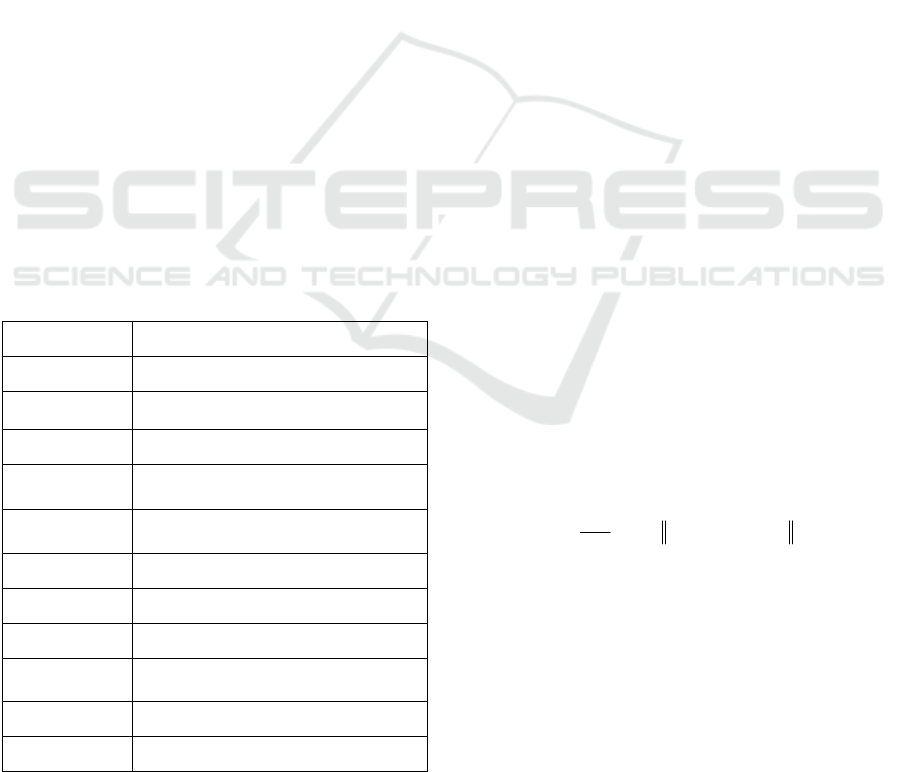
Table 1: Notations Used in This Paper.

Symbols Meanings

()

∗

Nominal trajectory

•

Rate of change of the state

()

Learn or estimated nonlinear function

()

Estimated current state

()

Estimated future state

initial time

final time

(()

Learn nonlinear function in NODE

(,)

true

Learn nonlinear function in

contraction

virtual displacement in trajectories

max

maximum eigen value of Jacobian

2 PROBLEM FORMULATION

We formulate the robotic system's state-to-state

motions as an autonomous dynamic system with a

nominal unknown trajectory

()

∗

made up of N

demonstration data points. A system's state can be

regarded as each demonstration data point. When a

trajectory moves with noise or disturbance, the

autonomous dynamic system is

()xf x

•

(1)

Where

is the learnable nonlinear function, and the

additive term represents the noise in the system. The

system without noise can be represented by the

below-mentioned equation.

()

•

(2)

We considered the single spiral trajectory as the

demonstration of the expert and try to estimate it

accurately using the neural ode and contraction

method. In this work, we use supervised learning

method for the given demonstration data, N. The

objective is to learn the nonlinear spiral function

accurately with the minimum loss value and try to

estimate the desired trajectory. The prediction of the

nonlinear function can be achieved by using the

below mentioned NODE equation.

100

() () ( (),,),(),,),

ii i

txtNODEfxttxttt

(3)

The objective is to minimize the difference

between the desired trajectory and the learned

nonlinear trajectory to find the optimal parameter

values which reduce the loss, we considered the

following loss minimization for the NODE.

min ( ) ( ( ))

ii i

xt gxt

−



(4)

Above mentioned equation expresses the loss

function. The parameters

, and values continuously

update until the loss values reach the least minimum,

or in other words the difference between the predicted

and observed state becomes negligible.

2.1 Forward Propagation

( ) ( ( ( ), , ), ( ), , ),

t ODESolve f x t t x t t t

(5)

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

206

2.2 Back-Propagation

() ((),,) ()

((),, )

(,,,),

() ()

((),, )

xt f xt t xt

LfxttL

ODESolve t t

xt x xt

fxt t









∂∂∂



∂∂∂



∂



∂







∂



∂



(6)

The implementation of the NODE architecture can be

considered with a basic neural network that is fully

connected and possesses one hidden layer.

21 12

()

(.(.() ) ),

dx t

WWxtb b

σσ

=++

(7)

where,

()xt

, is the particular system state,

and

are the matrix of weights,

and

are the bias

vectors, and

, is the nonlinear activation function.

The numerical technique Runge-Kutta is used to

solve the ODE to determine the system's state at any

given moment. we can reconfigure the NODE

network architecture by modifying the hidden layers

and learning rate of the neural network

11234

(( ), )

(( ) , )

()() ( 2 2 )

tth

sfxtt

sfxt st

sfxt hsth

xt xt s s s s

=++

=++++

(8)

In the contraction theory for the learned models. The

problem of system identification can be represented as

(,)

(,) (,) ( (,) (,)),

true

true L true L

xf xt

x f xt f xt f xt f xt

•

==+ −

(9)

The true function is unknown, approximated by

the contracting learning model.

3 MAIN RESULTS

Dynamic systems are mathematical methods that

depict or learn the evolution of a system's dynamics

across time and are capable of understanding complex

systems behaviours. The equation of an autonomous

dynamic system is:

()

( ( ), ),

dx t

fxt t

(10)

where,  ∈ 



are the system state,

,tT∈

time interval T, and : 



→



a vector field of

nonlinear function which defines the dynamics of the

system and which needs to be learned. If we look

around mobile robots, robotic arm manipulator,

UAVs, and many other industrial systems possess the

dynamic behaviours which are nonlinear, complex

and hard to learn. To tackle the nonlinear and

complex behaviours of such systems we considered

spiral trajectory for our work as the nonlinear and

complex dynamic system which can be express in

mathematical form mention below.

cos( )

sin( )

x r

y r

(11)

We learned the considered nonlinear spiral

trajectory with the proposed method of Neural

ordinary differential equations (NODE) which is

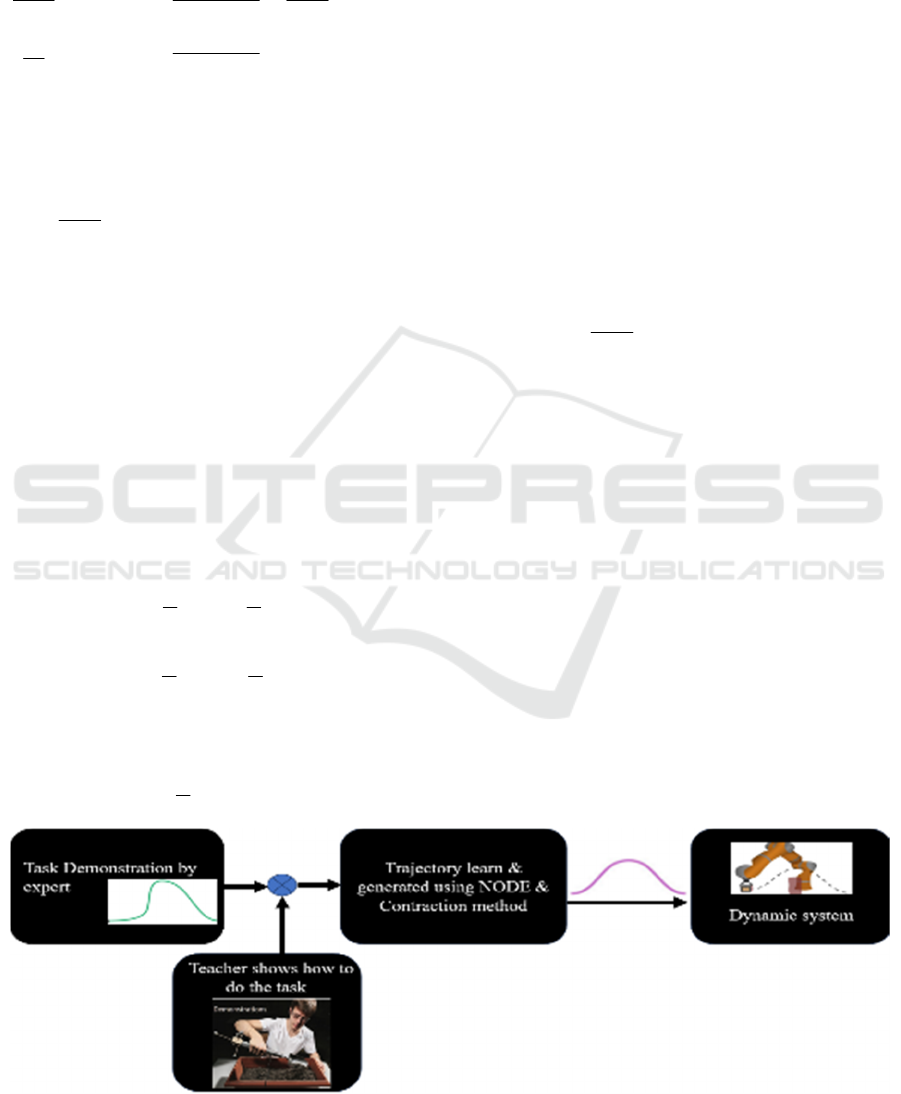
Figure 1: Overall view of proposed system.

NODE and Contraction Methods for Dynamics Learning from Human Expert Demonstrations

207

efficient in depicting time series data and dynamical

systems. To estimate “

”, the NODEs employ

neural networks described in equation.

((), )

xfxt t

•

(12)

The above-mentioned equation represents the

mathematical form of the neural ode. The initial state

of learnable nonlinear dynamic system “

”, is given

by the

()

. The nonlinear spiral function states

estimations acquired by the help of the neural

network, which optimized the learned parameters

for all given states. The optimized parameter reduced

the loss values between the encoded hidden states and

the predicted

() (()

Lxgxt

=−



(13)

In forward propagation it solves the ode and in

backward propagation it will compute the gradient

which updates the weights of neural network to

obtained the optimal values of learnable parameters.

The neural ode architecture implementation can be

represent as

2112

()

(. (.() ) ),

dx t

relu W relu W x t b b

=++

(14)

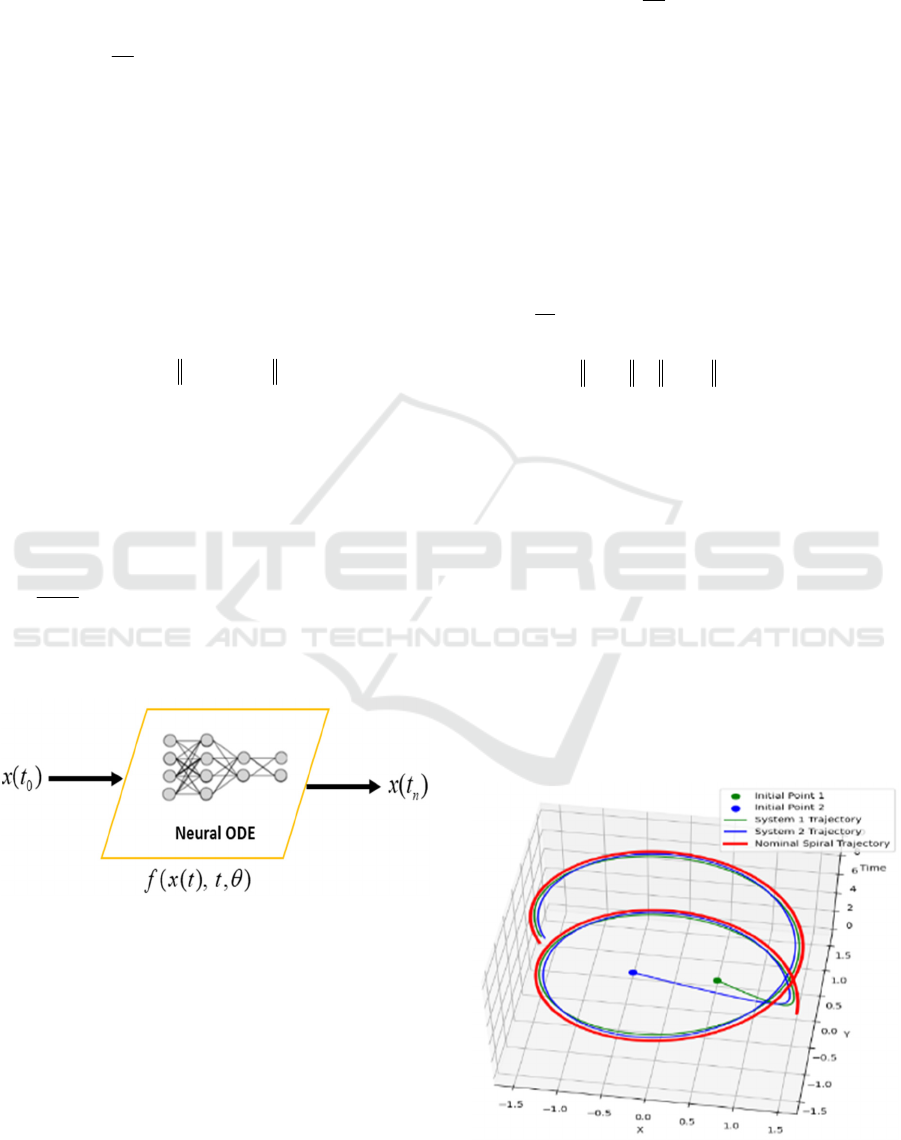
The visualization of the proposed NODE

framework is given below

Figure 2: NODE framework.

The other proposed method based on contraction

theory use to find the differential dynamics of the

spiral nonlinear and complex systems by considering

the contraction metric with uniform positive definite

matrix. It provides the incremental exponential

stability for the different trajectories started from the

different points. The mathematical expression is

express as

(,)xfxt

•

(15)

can be rewrite in the differential form

(,)

xxtx

δδ

•

∂

(16)

Where,

is the virtual displacement between

two neighbouring trajectories as the virtual

displacement decreases between two trajectories and

desired trajectory if they become one single trajectory

we can say that the system accurately estimated the

demonstrated trajectory and system exponentially

converge to the stability. If there exist a uniformly

positive definite metric M(x), and satisfy the

following conditions, we can say system is

contractive.

max

()

xM x xM x

δδ λδδ

≤−

(17)

() (0)

txe

δδ

−

≤

(18)

4 SIMULATION RESULTS

In this section, we discussed the performed

simulation and results obtained by using the both

methodologies of NODE and contraction.

4.1 Contraction Method

The results in Figure 3 show the difference between

the true or nominal trajectory and learned trajectories

which started from two different initial points and

tried to converge to the desired trajectory but due to

less stronger contraction term, the learned could not

reach the ideal trajectory accurately.

Figure 3: Less contraction system.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

208

In Figure 4 we can see the learned trajectory

approximate the true trajectory quite accurately and

the difference between the true and learned

trajectories are negligible and show the strong

contractive behaviour with the strong contractive

term considered during the learning.

Figure 4: Strong contraction system.

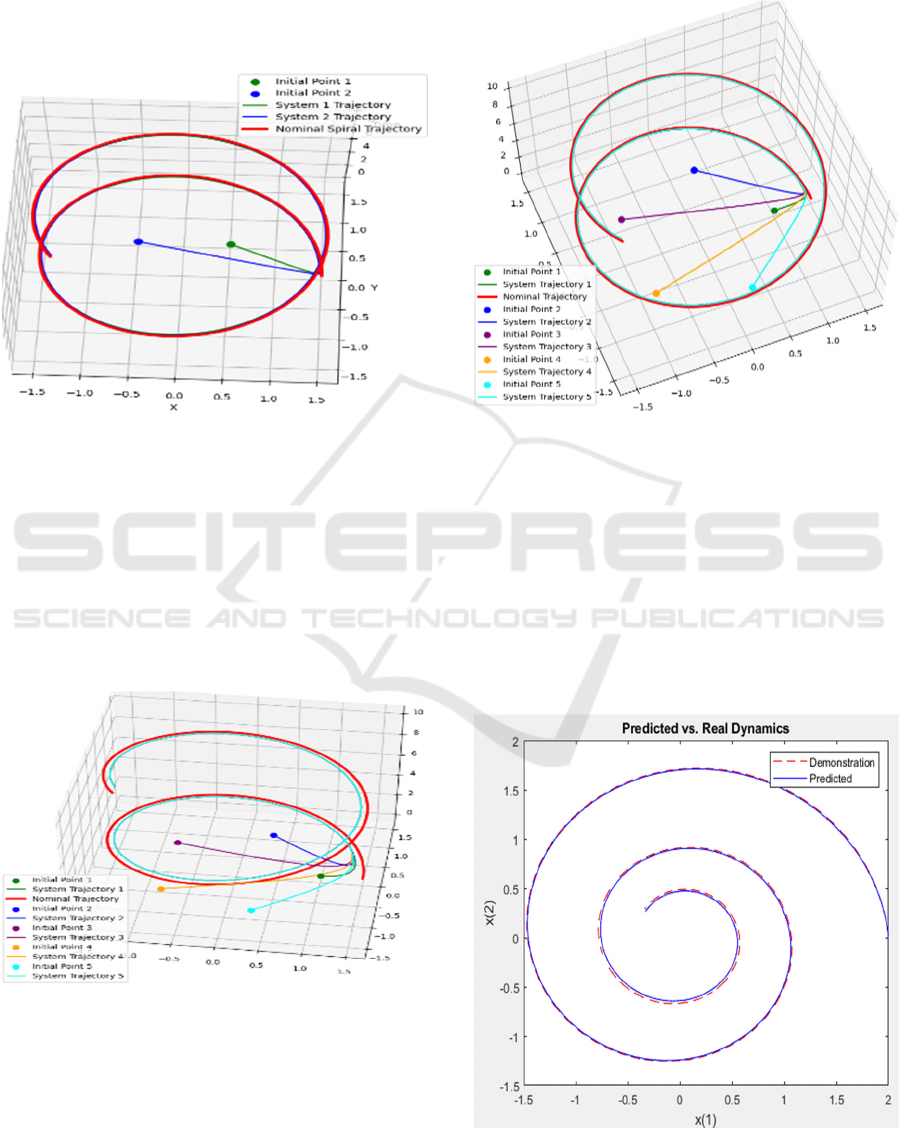
In Figure 5 we considered the five different

Trajectories which started from the different initial

points, in the first case we considered the minimal

contractive term and analysed whether the learned

trajectories reached the target trajectory accurately

but unfortunately, could not make it and showed the

huge difference between the learned and true

trajectories this is because the less strong contraction

term used during the learning.

Figure 5: Less contraction system.

In the above Figure 6 five different trajectories

started from the five different initial points, the results

show that all five trajectories converge into one single

trajectory as time goes on which proves the system is

highly contractive and stable. The difference between

the true and learned trajectories minimize this

happened due to strong contraction term considered

during the learning.

Figure 6: Strong contraction system.

4.2 Neural Ode’s

In the Figure 7 the Spiral trajectory is given as the

demonstration of the neural ordinary differential

network. The red dot line is the spiral demonstration

and a blue solid line in the estimation of the observed

values. we can see from the results the NODE based

architecture provide the accurate estimation but when

the initial value changes its performance, degrade due

to initial value problem.

Figure 7: NODE based dynamics learning.

NODE and Contraction Methods for Dynamics Learning from Human Expert Demonstrations

209

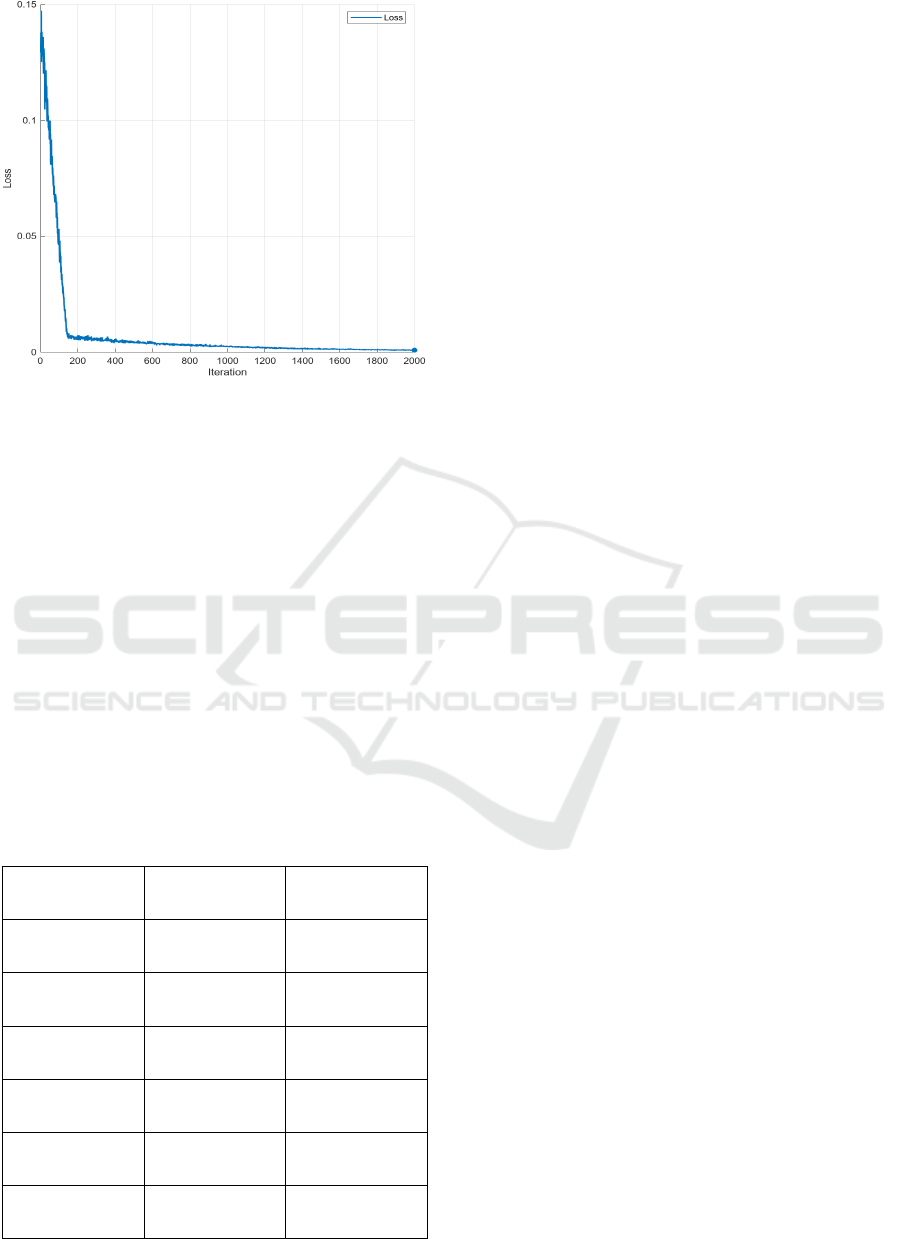
Figure 8: Learning Loss.

Figure 8 shows the learning of the NODE

framework over the iteration of 2000.

5 DISCUSSIONS

In this work, a comparative analysis conducted of two

different methods for the task of desired trajectories

estimation of dynamic systems given by the

demonstrations. Simulation performed on the spiral

trajectory of dynamic systems and evaluated based on

the performance metrics mentioned below in table 2.

The NODE method shows better accuracy for

trajectory estimation, in an unperturbed environment

but faces stability issues in a perturbed environment.

Table 2: Performance metric of NODE and contraction

methods.

Metric Neural ODE

Contraction

method

Accuracy More accurate Accurate

Robustness Moderate High

Convergence

Rate

Fast Faster

Computational

Efficiency

Efficient but

expensive

Efficient

Stability

Sensitive to

perturbation

Robust against

perturbation

Real Time

Application

Good after

training

Excellent

On the other hand, contraction method is less

accurate within an acceptable margin of accuracy but

robust and stable in trajectory estimation both in

perturbed and unperturbed conditions. Furthermore,

the contraction method can provide fast exponential

convergence as compared to NODE even in the

external disturbance. Contraction method is more

efficient both in computational efficiency and real-

time application implementations. These findings

show that both methods supersede each other in

different performance metrics. The selection of these

methods highly based on the type of applications.

6 CONCLUSIONS

The presented work tried to cover the dynamic

learning of dynamic systems by incorporating the

learning from the demonstration method. We

considered the spiral trajectory as the expert

demonstration data for any particular actions of the

dynamic system and used two different

methodologies NODE and Contraction theory to

learned these demonstration actions, NODE based

learning provides better accuracy and flexibility but

on the other hand, it is sensitive to the initial value

and demand long training time, require high

computational cost and lack of robustness under the

perturbed conditions for higher dimensional systems.

While the contraction theory provides the higher

stability, robust to the perturbation, produce good

response on the initial value problem,

computationally efficient. These two methods show

the trade-off between robustness and flexibility,

selection of these methodologies based on the

demand of the applications. In the future, the

proposed work will extent for the practical

implementation on robotic arm manipulator or mobile

robot dynamic systems with the insertion of obstacles

and perturbation. In this work correction term or

control term was not considered for the unseen data

and spurious attractor problems in future we

considered solving such problems with the

implementation of an appropriate control method,

stability is also not considered we plan to incorporate

the stability and safety constraints in the future work.

Furthermore, we planned to expand the proposed

work by considering the higher-dimension problem.

ACKNOWLEDGEMENTS

This work was supported in part by the National

Research Foundation of Korea (NRF) through

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

210

the Korea government, Ministry of Science and

ICT under the grant, RS-2024-00350118,

2019R1A5A8080290 and supported by Institute of

Information and Communication Technology

Planning & Evaluation (IITP) grant funded by the

Korea government (MSIT) (IITP-2024-RS-2022-

00156389).

REFERENCES

Khansari-Zadeh, S. M., and Billard, A. (2011). Learning

stable nonlinear dynamical systems with gaussian

mixture models. In IEEE Transactions on Robotics,

27(5):943–957.

Calinon, S., Guenter, F., and Billard, A. (2007). On

learning, representing and generalizing a task in a

humanoid robot. Transactions on Systems, Man, and

Cybernetics, 37(2):286–298.

Schaal, S. (1999). Is imitation learning the route to

humanoid robots? Trends in Cognitive Sciences, 3(6):

233 242.

Kulic, D., Takano, W., and Nakamura, Y. (2008).

Incremental learning, clustering and hierarchy

formation of whole-body motion patterns using

adaptive hidden Markov chains. The Int. Journal of

Robotics Research, 27(7): 761–784.

Dautenhahn, K., and Nehaniv, C. L. (2002). The agent-

based perspective on imitation. Cambridge, MA, USA:

MIT Press, pp. 1–40.

B., Akgun, and Subramanian, K. (2011). Robot learning

from demonstration: Kinaesthetic teaching vs.

teleoperation.

Ijspeert, A., Nakanishi, J., Pastor, P., Hoffmann, H., and

Schaal, S. (2013). Dynamical Movement Primitives:

learning attractor models for motor behaviours, Neural

Computation, 25(2):328–373.

NODE and Contraction Methods for Dynamics Learning from Human Expert Demonstrations

211