Research on Traffic Violation Factors in Vehicle Insurance Pricing
Based on Generalized Linear Model
Zhanhong Mu
Department of Mathematics, Imperial College London, London, SW7 2AZ, U.K.
Keywords: Traffic Violation Factor, Auto Insurance Pricing, Heterogeneity, Generalized Linear Model.
Abstract: Automobile insurance plays a pivotal role within the property insurance market. A meticulous examination
of diverse factors influencing the pricing of automobile insurance holds profound significance for insurance
companies in mitigating operational risks, drivers in actively cultivating better driving habits, and fostering a
secure and orderly traffic milieu. Presently, despite the inclusion of traffic violation factors in China's auto
insurance pricing, the coefficient often defaults to 1 in practice, thus lacking widespread implementation. To
effectively leverage the incentivizing and constraining effects of traffic violation factors on auto insurance
premiums, this study utilizes data encompassing traffic violations and auto insurance claims of vehicles within
a Chinese province from 2021 to 2023 as research samples. It delineates vehicle type, traffic violation
frequency, and traffic violation type as explanatory variables. Mindful of multicollinearity and vehicle type
heterogeneity, a generalized linear model is employed to scrutinize the correlation between traffic violations
and the intensity and frequency of auto insurance claims. The findings underscore that vehicle traffic
violations positively influence both claim intensity and frequency, with distinct vehicle types exhibiting
varying sensitivities to different types of traffic infractions.
1 INTRODUCTION
Auto insurance has an important position in the
property insurance market, not only because it
accounts for a high proportion of market size, but also
related to the operating efficiency of insurance
companies. Because it is closely related to people's
lives, especially the third party liability insurance
plays a special role in stabilizing social relations and
maintaining social order. Based on this background,
more and more insurance companies pay attention to
the pricing research of auto insurance products,
especially the premium determination has always
been a research hotspot of non-life insurance actuarial
pricing (Denuit M et al., & Klein N et al.). Whether
its calculation is accurate, reasonable and fair is of
great significance to all levels of society. A large
number of research results show that insurance
companies in developed countries such as for the
United States and Britain, in the process of
determining the vehicle insurance rate, the risk
factors are divided into three categories: from the
vehicle, from people, from the environment; and it
will give more consideration to the impact of the
driver's "from the person". China is currently based
on the model pricing, comprehensive consideration of
independent pricing coefficient, no compensation
preferential coefficient, traffic law coefficient of 3
floating factors, and finally complete the auto
insurance pricing. Although the traffic violation
coefficient has been introduced as an important
human factor, it is restricted by subjective and
objective factors in practice, and the coefficient is
default to 1 and not really used. The current pricing
factors in China are still dominated by vehicle type,
purchase price, vehicle age, use nature, number of
historical accidents, number of traffic violations and
other vehicle factors, which fails to fully match the
pricing of auto insurance with the underwriting risk.
Although existing literature studies have paid
attention to the impact of driving behavior on auto
insurance pricing, for example, Peng et al. (2016)
scored drivers' driving behavior and calculated
premiums based on it, and analyzed the dynamic
premium mechanism based on drivers' driving
behavior to realize the differentiation of insurance
premiums for auto insurance holders. Wang (2016)
found that it is a more scientific and reasonable way
to analyze auto insurance rates by taking driving
68
Mu, Z.
Research on Traffic Violation Factors in Vehicle Insurance Pricing Based on Generalized Linear Model.
DOI: 10.5220/0012993100004601
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Innovations in Applied Mathematics, Physics and Astronomy (IAMPA 2024), pages 68-77
ISBN: 978-989-758-722-1
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

behavior as a determining factor. Gao (2018)
analyzed the data of the Internet of vehicles and
established a Poisson generalized additive model to
predict the claim frequency. He believed that the
second principal component based on the estimation
of the velocity acceleration kernel density had a very
significant nonlinear influence on the claim
frequency and defined the principal component as a
driving behavior factor. However, there is no analysis
of the correlation between driving behaviors
involving traffic violations and vehicle claims, nor
does it consider the difference in sensitivity of
different models to traffic violations in real life.
Generalize Linear Model (GLM) is the mainstream
model used in current research on auto insurance
pricing. After summarizing the shortcomings of
traditional pricing, Zhang (2013) made a brief
introduction to GLM and pointed out the necessity of
applying GLM to auto insurance pricing. Moreover,
through detailed analysis of the data of auto insurance
claims of a European insurance company, it is proved
that GLM is indeed superior to traditional pricing
methods in auto insurance premium determination.
Wu (2018) demonstrated that GLM has a better effect
in the calculation of risk factors.
So, in order to give a solution to the above
problem, this paper analyzes and demonstrates the
necessity of introducing traffic violation factors into
auto insurance pricing through the generalized linear
model, aiming to promote the full consideration of the
use of traffic violation factors in auto insurance
pricing, reduce the accident rate and reduce the
operating risk of insurance companies through
scientific pricing, and guide vehicle drivers to
actively comply with traffic rules and develop good
driving habits.
2 RESEARCH DESIGN
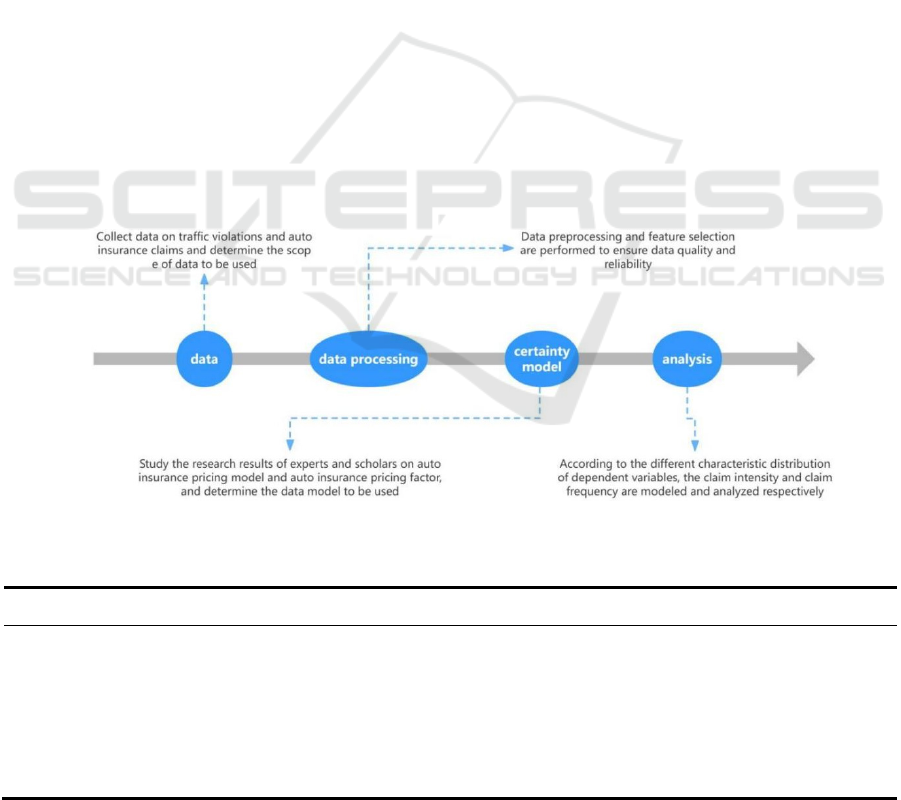
This study is carried out according to the following
design steps, as shown in Figure 1.
2.1 Data Description (Source and
Description)
This paper uses the real traffic violations and auto
insurance claims data of a certain province in China
from 2021 to 2023, and the relevant data is divided into
a total of 60,000 valid data in 8 fields, including vehicle
type, number of traffic violations, type of traffic
violations, year of claims occurrence, location,
whether claims occur, number of claims, and amount
of claims. A selection of the data is presented in Table
1.
Figure 1: Research flow chart (Picture credit: Original).
Table 1: Partial claim data.
Vehicle
type
Number of
violations
Types of traffic
violations
Year of the
claim
Location
Whether a claim has
occurred
Claim frequency
Total
claims
1 3 A、B1 2021 A City 1 3 2300
1 1 B1 2022 B City 1 2 1200
2 0
/
2022 C City 00 0
3 0
/
2023 D City 00 0
4 2 B1、G 2023 D City 1 3 12000
4 1 G 2021 E City 1 1 2000
5 0
/
2021 F City 00 0
5 1 G 2021 E City 1 1 2000
6 0
/
2021 G City 00 0
Research on Traffic Violation Factors in Vehicle Insurance Pricing Based on Generalized Linear Model
69

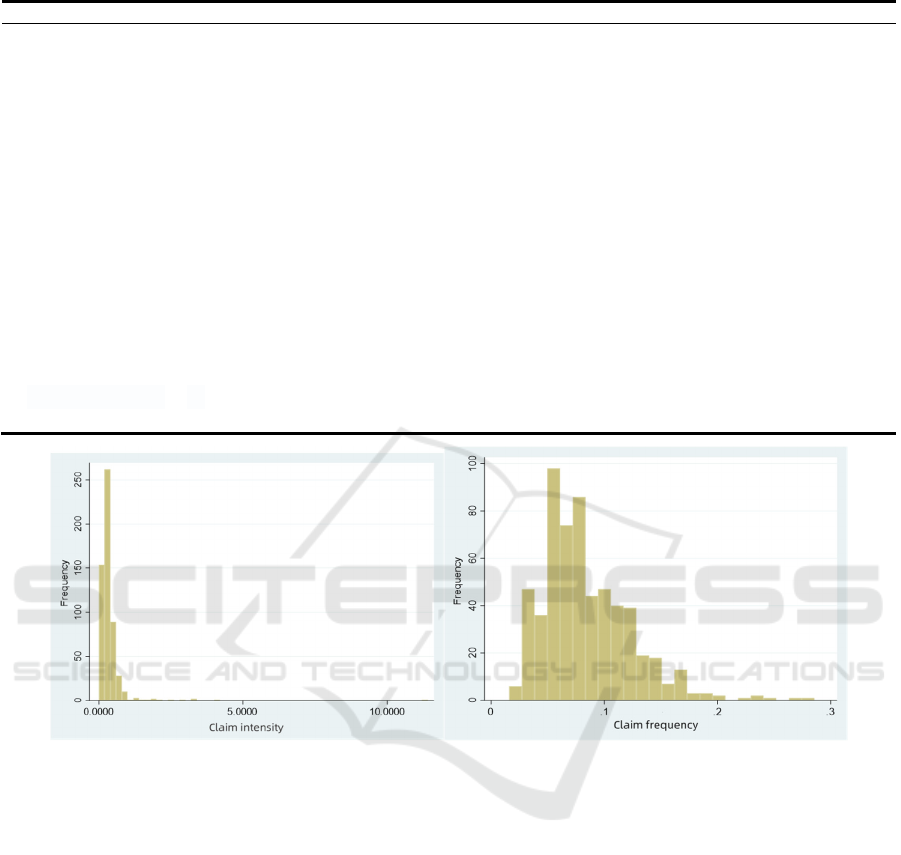
Table 2: Variable names and descriptions.
variable name Assi
g
nment and descri
p
tion
vehicle type Family car =1, business bus =2, non-business bus =3, business truck =4,
non-
b
usiness truck =5, special vehicle =6
Vio_num Number of violations (times)
Vio_type
Types of traffic violations： A (violation of traffic lights, etc.); B1 (exceeding 10% speed but
not reaching 50%), B2 (exceeding 50% speed, etc.); C (load exceeding the approved load
mass, etc.); D (not in accordance with the provisions of the installation of motor vehicle
plates, etc.); E (without a driving license, being revoked, driving a motor vehicle during the
suspension, etc.); F1 (driving a motor vehicle after drinking, etc.), F2 (driving a motor vehicle
after drunkenness, drug driving, etc.); G (fleeing after a traffic accident, etc.); H (failure to
use seat belts as required, make or receive phone calls while driving, fail to participate in
regular safety technical inspection, carry more than the approved number of passengers,
violate traffic markings or signs, park vehicles in violation of regulations, drive in the opposite
direction and other ille
g
al t
yp
es
)
Yea
r
Year of the claim
Location Where the traffic violation occurre
d
Whether a claim has occurred
（Y1）
Claim occurrence =1; No claims =0
Claim frequency（Y2）
The number of claims
Claim intensity（Y3）
Total claims/number of claims
Figure 2: Frequency distribution of claim intensity and Frequency distribution of claim frequency (Picture credit: Original).
According to Table 1, the type of vehicle, the
number of traffic violations, and the type of traffic
violations are determined as independent variables,
and the type of vehicle and the type of traffic
violations are subdivided. The type of vehicle is
divided into six categories: family car, business bus,
non-business bus, business truck, non-business truck,
and special vehicle, which are represented by
numbers 1-6 respectively. Traffic violations are
divided into 10 categories of violating traffic lights,
speeding, carrying more than the approved load mass,
not installing motor vehicle plates according to
regulations, not obtaining A driving license, driving a
motor vehicle during the suspension or suspension of
driving license, driving after drinking alcohol,
escaping after traffic accidents, and other violations,
respectively, expressed by letters A-H. Among them,
class B and class F are subdivided into B1, B2 and F1
and F2. The associated variable names, assignments,
and descriptions are shown in Table 2.
2.2 Data Processing
2.2.1 Analyze the Characteristics of
Dependent Variables
In auto insurance pricing, actuaries predict potential
losses based on available historical claims data, and
thus calculate the insurance premium ( 𝜋

). The
premium may be the product of the frequency of the
claim and the intensity of the claim by the following
formula:
𝜋

𝐸𝑓

𝐸𝑠

 (1)
Where Ef

 is the mean of the prediction of claim
frequency and Es

 is the mean of the prediction of
IAMPA 2024 - International Conference on Innovations in Applied Mathematics, Physics and Astronomy
70

claim intensity. Claim frequency refers to the number
of claims under the unit exposure policy; Claim
intensity refers to the average amount of a single
claim under the conditions under which the claim is
made. Therefore, the data characteristics of two
dependent variables, claim intensity and claim
frequency, need to be analyzed before modeling.
According to Figure 2, both claim intensity data
and claim frequency data present a skewed
distribution pattern, with the data in the middle
declining rapidly and the data on the right declining
slowly. The gaps in the data on the right indicate that
the probability of high claims intensity cases and high
claims intensity cases is very low respectively, which
accords with the characteristics of loss data under
normal circumstances. Therefore, the claim intensity
data can be applied to the gamma distribution, and the
claim frequency data can be applied to the Poisson
distribution.
2.2.2 Test Multicollinearity
Table 3: Multicollinearity test.
Variable VIF 1/VIF
Vio_num 2.16 0.462902
A 2.87 0.348153
B1 2.87 0.348153
B2 1.88 0.531626
C 1.88 0.531626
D 1.88 0.531626
E 1.88 0.531626
F1 1.88 0.531626
F2 1.88 0.531626
G 1.88 0.531626
H 12.65 0.079052
Testing multicollinearity refers to check whether
there is a high correlation between independent
variables in statistical modeling. When there is a high
correlation between independent variables, it will
lead to instability and inaccuracy of the model, so it
is necessary to conduct a multicollinearity test to
confirm whether this is the case. Variance inflation
factor (VIF) is a statistic used to measure the severity
of multicollinearity between multiple linear
independent variables. Generally speaking, when
VIF<10, indicating that there is no multicollinearity.
The number of traffic violations and the type of traffic
violations were selected for multicollinearity test, and
the classification variable of the type of violations
was converted into a dummy variable in the model.
Since the VIF value of H variable was 12.65, it could
be considered that it had a high degree of
multicollinearity, so the variable was deleted before
modeling. After H variable was deleted, the VIF
value between the variables was much less than 10. It
can be considered that there is no multicollinearity
between variables, and the specific test results are
shown in Table 3. The following empirical analysis
only conducted modeling analysis on nine types of
traffic violations: A, B1, B2, C, D, E, F1, F2 and G.
2.3 Model Determination
The generalized linear model is an extension of the
ordinary linear regression model. Its characteristic is
that the natural measure of the data is not forcibly
changed, and the data is allowed to have a nonlinear
and unsteady variance structure. Different association
functions can be used for modelling, so as to deal with
the relatively complex relationship between
dependent variables and independent variables
(Wang 2023). Therefore, the generalized linear model
is more suitable to explore the impact of traffic
violation factors on the frequency and intensity of
claims, so as to determine the traffic violation factors
with high impact.
The model is usually composed of random
components, system components, and connection
functions. Random components refer to the
probability distribution of the dependent variable Y,
system components are linear combinations of
independent variables, and the relationship between
random components and system components is
constructed by connection function (Wang & Wang,
2013). Therefore, the dependent variable of a
generalized linear model is a function transformation
form of the linear combination of independent
variables. Its basic form is as follows:

+===
−−
)()(][
11
iijiii
XggYE ξβημ
(2)
iii
uVYVar
ω
ϕ
/)()( =
(3)
Where g represents the connection function and
Var (x) is the variance function. The research of auto
insurance pricing usually adopts gamma distribution
for continuous data, Poisson distribution and negative
binomial distribution for discrete data.
3 EMPIRICAL ANALYSIS
In this paper, Stata17 software tool is applied to
ordinary laptop computer for data empirical analysis,
and the relationship between nine types of traffic
violations except H and the intensity and frequency
of claims is analyzed by generalized linear model, and
the influence of traffic violations frequency and
Research on Traffic Violation Factors in Vehicle Insurance Pricing Based on Generalized Linear Model
71

illegal types on the intensity of claims under different
vehicle types is further analyzed (Meng, Li & Gao,
2017). This paper studies the sensitivity of different
vehicle types to different types of traffic violations
and analyzes the reasons, and then draws the
conclusion that the analysis of traffic violations is
necessary to determine the pricing of auto insurance.
3.1 Analyze the Relationship Between
the Intensity of Claims and the
Number and Types of Traffic
Violations
3.1.1 Single Factor Analysis
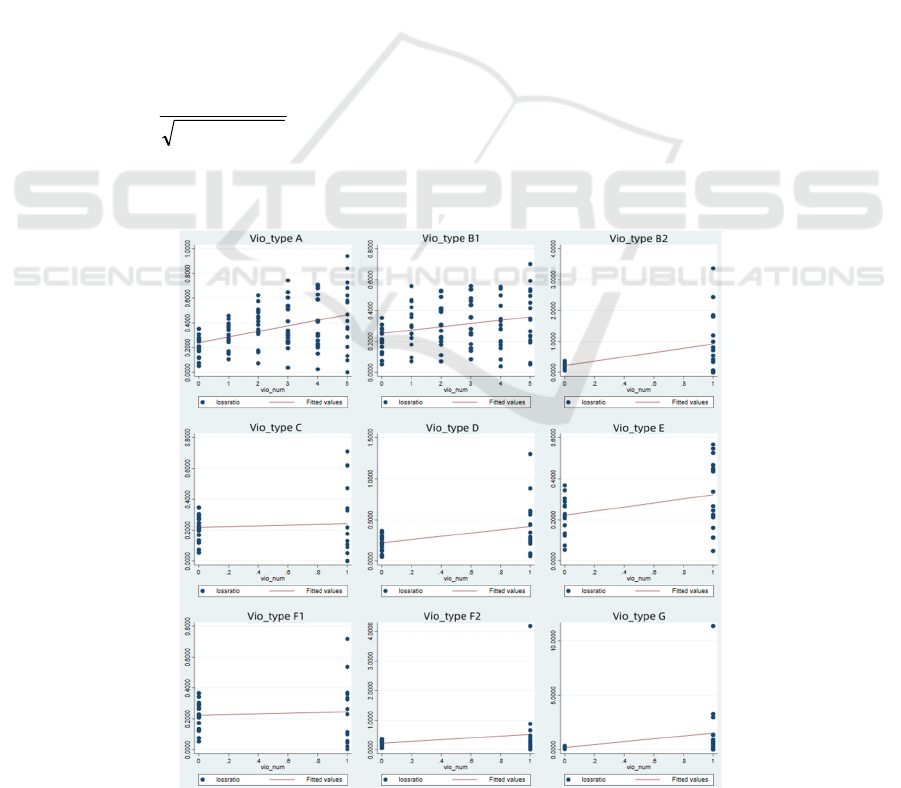
To help build the model, this paper first analyzes the
single-factor relationship between nine types of
traffic violations and the intensity of claims through
graphical analysis. The correlation coefficient is a
quantity used to study the degree of linear correlation
between variables, generally denoted by the letter r.
The formula is as follows:
(4)
Where, Cov(X,Y) refers to the covariance of X
and Y, Var[X] represents the variance of X, and
Var[Y] is the variance of Y.
Through the analysis of Figure 3 and Table 4, it
can be concluded that except for H traffic violations,
other traffic violations have a certain positive
correlation with the intensity of claims.
3.1.2 Claim Strength Analysis
According to the distribution characteristics of claim
intensity, combined with existing relevant studies, a
generalized linear model is adopted to analyze the
factors affecting claim intensity. The connection
function is logarithmic function, assuming that claim
intensity follows gamma distribution, the model
expression is as follows:
)()(][
2211
11
iiiiii
XXggYE ξββημ ++===
−−
(5)
Where, Y

represents the claim intensity, X

is the
variable that affects the claim intensity, including the
number of traffic violations and the type of traffic
violations.
Based on Stata17 software, maximum likelihood
estimation and probability distribution and
parameters of observed values were applied to
determine the degree of influence of each variable on
the dependent variable.
Figure 3: Scatter plot of single factor analysis between claim intensity and traffic violation type (Picture credit: Original).
()
()
[] []
YVarXVar
YXCov
YXr
,
, =
IAMPA 2024 - International Conference on Innovations in Applied Mathematics, Physics and Astronomy
72

Table 4: Parameter estimation results of the claim intensity model.
A B1 B2 C D E F1 F2 G
Lossratio\Vio_type 0.3936 0.2411 0.4533 0.0664 0.3943 0.3532 0.0762 0.2141 0.3266
Table 5: Parameter estimation results of the claim intensity model.
parameter Vio_type Estimate z p-value
Vio_num 0.037 3.98 0.000***
Vio_type A 0.5598273 3.23 0.001***
Vio_type B1 0.4342636 2.49 0.013 **
Vio_type B2 1.125105 4.95 0.000 ***
Vio_type C 0.2272258 0.99 0.320
Vio_type D 0.5231742 2.30 0.022**
Vio_type E 0.3800192 1.67 0.096*
Vio_type F1 0.2635232 1.15 0.249
Vio_type F2 0.7862879 3.46 0.001***
Vio_type G 1.476298 6.51 0.000***
Cons -1.714876 -10.34 0.000***
Note:***, ** and * respectively represent significant at the 1%, 5% and 10% levels, the same below.
As can be seen from Table 5, there is a significant
positive correlation between the number of traffic
violations and the intensity of claims. Among the
classification variables of traffic violation types, A,
B2, F2 and G are significant.
3.1.3 Heterogeneity Analysis of Vehicle
Types
Considering the different factors affecting the
occurrence of traffic violations and insurance claims of
different car types in real life, it is necessary to conduct
empirical research on the data of six groups of car
types, analyze the impact of the number and types of
traffic violations under different car types on the
intensity of claims, and study the sensitivity and causes
of different car types to different traffic violations.
Based on the data in Table 6, it can be observed
that there is a strong positive association between the
number of traffic violations for family cars, business
buses, and non-business buses and the frequency of
insurance claims. Conversely, there is no significant
correlation between the number of violations for
business trucks, non-business trucks, and special
vehicles and the intensity of claims. This could be
attributed to the fact that business trucks, non-
business trucks, and special vehicles are influenced
by their specific job roles and carry inherent risks. As
a result, even in the absence of traffic violations, these
vehicle types may still experience high levels of
insurance claims.
The data presented in Table 6 indicates that traffic
violations A, B1, B2, and G have a substantial impact
on the frequency of auto insurance claims for family
cars. This observation is consistent with the
prevalence of these violations in everyday life, such
as speeding, running red lights, drunk driving, and
hit-and-runs.In contrast, buses—whether business or
non-business — are less sensitive to various traffic
violations due to their primary function of passenger
transportation. Given the high driving risk and
involvement of multiple parties in case of accidents
associated with bus operations (e.g., public
transportation and tourism), there are stringent
requirements for driver quality. Consequently, this
results in lower rates of traffic violations and
subsequent insurance claims. For trucks and special
vehicles, specific types of traffic violations
significantly impact claim intensity. Notably, illegal
type B2 and F2 infractions are particularly impactful
for business trucks; illegal type G infractions have a
significant effect on non-business trucks; while
illegal type B2 infractions notably influence claim
intensity for special vehicles.
Research on Traffic Violation Factors in Vehicle Insurance Pricing Based on Generalized Linear Model
73

3.2 Examine How the Frequency of
Claims, the Quantity of Violations,
and the Categories of Traffic
Violations Are Interconnected
3.2.1 Single Factor Analysis
To facilitate model construction, this study initiates
with a graphical analysis of the relationship between
the nine categories of traffic violations and claim
frequency prior to modeling. As depicted in Figure 4
and detailed in Table 7, it is evident that all nine types
of traffic violations demonstrate a positive correlation
with claim frequency.
3.2.2 Analysis of Claim Frequency
Based on the distribution characteristics of claim
frequency and in conjunction with existing relevant
studies, a generalized linear model is employed to
analyze the factors affecting claim frequency. The
connection function takes the form of a logarithmic
function, assuming that the claim intensity follows a
gamma distribution. The model expression is as
follows:
)()(][
2211
11
iiiiii
XXggYE ξββημ ++===
−−
In this context, Y

represents the frequency of
claims, while X

denotes the variable affecting the
intensity of claims, including both the number and
type of traffic violations.
In Stata17, you can use the maximum likelihood
estimation method to estimate the probability
distribution and parameters of your data as well as
observed values. Additionally, you can determine the
extent to which each variable influences the
dependent variable through this approach.
Table 8 demonstrates a notable positive
correlation between the frequency of claims and the
quantity of traffic violations. Notably, when
examining specific types of traffic violations,
categories A, B2, D, and G exhibit heightened
significance among the categorical variables.
Table 6: Heterogeneity analysis of vehicle types.
Variable
Family car
coefficient value
Business bus
coefficient value
Non-business bus
coefficient value
Business truck
coefficient value
Non-business truck
coefficient value
Special vehicle
coefficient value
vio_num
0.047 *** 0.045*** 0.034 *** 0.027* 0.022 0.029
(4.08) ( 3.06 ) (3.23) (1.83) (1.13) (1.77)
vio_type
A
0.634*** 0.462 0.589*** 0.455 0.369 0.752
（2.96 ） （ 1.56 ） （3.09 ） （1.55 ） （ 1.09 ） （2.08 ）
B1
0.5562005*** 0.381 0.4233** 0.4040943 0.282 0.404
(2.59 ) (1.28 ) ( 2.20 ) ( 1.38 ) (0.83 ) ( 1.11 )
B2
0.8697436*** 0.933 0.504 1.521*** 1.101** 1.744 ***
( 3.08 ) ( 2.41 ) ( 2.01 ) (3.99 ) （2.51 ) ( 3.69 )
C
0.6119962 ** -0462 -0.29 0.351 0.2303469 0.414
(2.16 ) (-1.17 ) (-1.15 ) ( 0.94 ) ( 0.52 ) ( 0.87)
D
0.7756737*** 0.359 0.567** 0.311 0.3577837 0.384
( 2.75 ) ( 0.92 ) ( 2.26 ) ( 0.81 ) ( 0.81 ) (0.81 )
E
0.437 0.361 0.3435804 0.423 0.2179347 0.377
( 1.54 ) ( 0.93 ) ( 1.37 )
（ 1.10 )
( 0.49 ) (0.79 )
F1
0.271 -0.185 0.204 0.599 0.2159492 0.199
(0.96 ) ( -0.47 ) (0.81 ) ( 1.57 ) (0.49 ) ( 0.42 )
F2
0.482* 0.282 0.2111087 2.065*** 0.1681821 0.218
(1.70 ) ( 0.72 ) (0.84 ) (5.43 ) ( 0.38 ) (0.46 )
G
1.49 *** 0.437 0.859*** 0.701* 2.244422 *** 0.889*
(5.29 ) ( 1.12 ) ( 3.44 ) (1.83 )
（5.13 )
( 1.88 )
Intercept
-1.564 *** -1.874 *** -1.425 *** -1.975 *** -1.337639*** -2.201 ***
(-7.64 ) （-6.70 ) (-7.72 ) (-7.15 ) (-4.03 ) (-6.42 )
Note: Figures in () are standard error, the same below.
IAMPA 2024 - International Conference on Innovations in Applied Mathematics, Physics and Astronomy
74

Table 7: Parameter estimation results of the claim intensity model.
A B1 B2 C D E F1 F2 G
claimintensity\Vio_num 0.614 0.634 0.503 0.012 0.680 0.536 0.185 0.402 0.583
Figure 4:Scatter plot of single factor analysis between claim frequency and traffic violation type (Picture credit: Original).
Table 8: Parameter estimation results of the claim frequency model.
Paramete
r
Vio_type Estimate z
p
-value
Vio_num 0.172 15.62 0.000***
Vio
_
t
yp
e A 0.408 8.51 0.000***
Vio_type B1 0.07 -1.60 0.11
Vio
_
t
yp
e B2 0.23 3.24 0.001***
Vio
_
t
yp
e C 0.116 1.42 0.154
Vio_type D 0.107 1.68 0.068*
Vio
_
t
yp
e E 0.005 0.07 0.944
Vio_type F1 -0.119 -1.51 0.13
Vio
_
t
yp
e F2 0.046 0.62 0.537
Vio_type G 0.166 2.33 0.02**
Cons -2.731 -61.13 0.000***
Research on Traffic Violation Factors in Vehicle Insurance Pricing Based on Generalized Linear Model
75

Table 9: Results of heterogeneity analysis of vehicle types.
Variable
Family car
coefficient value
Business bus
coefficient
value
Non-business
bus coefficient
value
Business truck
coefficient
value
Non-business
truck coefficient
value
Special vehicle
coefficient
value
vio_num
0.204*** 0.151*** 0.170*** 0.131*** 0.194*** 0.203***
(12.23) (8.04) (9.54) (6.08) (9.96) (5.24)
vio_type
A
0.319*** 0.360*** 0.274*** 0.531*** 0.333*** 0.689***
(4.47) (4.42) (3.61) (5.41) (3.97) (4.05)
B1
-0.022 -0.066 -0.072 -0.005 -0.018 -0.235
(-0.34) (-0.87) (-1.00) (-0.06) (-0.24) (-1.58)
B2
0.265** 0.140 0.189 0.109 0.475*** 0.324
(2.44) (1.07) (1.63) (0.79) (4.04) (1.34)
C
-0.080 -0.092 -0.388*** 0.015 -0.065 0.013
(-0.65) (-0.51) (-2.71) (0.11) (-0.46) (0.05)
D
0.112 0.163 0.082 0.107 0.100 0.075
(0.98) (1.36) (0.68) (0.77) (0.75) (0.31)
E
0.012 -0.009 -0.025 0.069 -0.102 0.046
(0.11) (-0.07) (-0.20) (0.49) (-0.72) (0.18)
F1
-0.119 -0.232* -0.071 -0.075 -0.161 -0.079
(-0.95) (-1.68) (-0.56) (-0.51) (-1.11) (-0.31)
F2
-0.008 -0.158 -0.020 0.011 -0.131 0.442**
(-0.07) (-1.17) (-0.16) (0.08) (-0.91) (2.04)
G
0.197* 0.085 0.247** 0.045 0.163 0.253
(
1.77
)
(
0.69
)
(
2.17
)
(
0.32
)
(
1.26
)
(
1.10
)
Cons
-2.931*** -2.571*** -2.528*** -2.583*** -3.160*** -2.758***
(
-42.29
)
(
-33.92
)
(
-34.63
)
(
-30.05
)
(
-39.32
)
(
-18.27
)
3.2.3 Analysis of Heterogeneity in Vehicle
Types
In order to comprehensively understand the factors
influencing traffic violations and insurance claims
across various car types, empirical research was
conducted. This involved analyzing the frequency of
traffic violations for six distinct car categories, as well
as assessing the impact of these violations on claim
frequency. Additionally, the study aimed to
investigate the sensitivity and underlying causes of
different car types in relation to various traffic
violations. The analysis outcomes are presented in
Table 9.
As indicated in Table 9, the number of traffic
violations across all vehicle types demonstrates a
significant correlation with claim frequency at the 1%
test level. This suggests that a higher incidence of
traffic violations may reflect diminished adherence to
traffic regulations and more aggressive driving
tendencies among motorists. Consequently, this
heightened risk behavior is associated with an
increased likelihood of traffic accidents and
subsequent insurance claims. These findings are
consistent with empirical observations within the
field.
According to the heterogeneity test, it was found
that traffic violation types A, B2 and G for family cars
significantly affect claim frequency. Claim frequency
for business buses is significantly influenced by
traffic violation categories A and F1, while non-
business buses are impacted by categories A and B2.
Business trucks experience an impact on claim
frequency from categories A, B2, and F2; whereas
non-business trucks are affected by categories A, B2,
and G. Special vehicles demonstrate a notable effect
on claim frequency with categories A and F2.
4 CONCLUSION
In light of the shortcomings in current practices, such
as the inadequate integration of traffic violation
factors into auto insurance pricing, insufficient
analysis of relevant data in existing research, and the
oversight of variations in vehicle sensitivity to
different violation types, this study employs empirical
analysis to construct a generalized linear model. This
model, based on single-factor analysis of claim
intensity and frequency, explores the relationship
between these parameters and the number and nature
of traffic violations. Our findings indicate a positive
correlation between the frequency and severity of
insurance claims and the incidence of traffic
violations. Specifically, violations of types A, B1, B2,
D, and G exhibit a significant impact on claim
IAMPA 2024 - International Conference on Innovations in Applied Mathematics, Physics and Astronomy
76

severity, while types A, B2, D, and G are associated
with higher claim frequencies.
To address these insights, it is recommended that
insurance rate determinations consider the varying
sensitivity of vehicle types to different violations.
Implementing differentiated pricing based on these
factors would more accurately reflect the risk profile
associated with each vehicle-violation combination,
enhancing the fairness and effectiveness of the
insurance pricing model. While our study enhances
the alignment between traffic violation data and
insurance claims through the introduction of
connection functions and nonlinear transformations
in the generalized linear model, limitations persist.
These include the reliance on specific independent
variables and the inability to quantify analysis results
due to model assumptions. Building on these insights,
we explore alternative methodologies to refine our
analysis. By utilizing indicators such as auto
insurance rates, claim frequency, and severity as
labels, and incorporating parameters such as vehicle
type, violation count, violation category, claim
occurrence year, location, and claim frequency, we
identify traffic violation types with the greatest
impact on claim intensity and frequency.
We employ advanced machine learning
algorithms such as xgboost and lightGBM to train and
validate models, while employing Bayesian methods
for parameter adjustment to enhance the accuracy of
auto insurance premium predictions. Through these
efforts, we aim to further optimize the relationship
between traffic violations and insurance claims,
ultimately improving the robustness of insurance
pricing models.
REFERENCES
Denuit M, Maréchal X, Pitrebois S. Actuarial Modelling of
Claim Counts: Risk Classification ， Credibility and
Bonus-malus System. West Sussex: John
Wiley&Sons,2007．
Klein N, Denuit M, Lang S. Non-life Rate-making and Risk
Management with Bayesian Generalized Additive
Models for Location Scale and Shape. Insurance:
Mathematics and Economics,2014,55.
Peng J., Liu N., Zhao H. et al. Research on intelligent UBI
System. Computer Technology and Development,
2016(1):26.
Wang T.i, Hu Y., Xiao Y. Research on Innovation of
China's Auto Insurance Rate Determination Method --
Empirical Analysis of Auto Insurance rate
Determination based on Driving behavior. Price Theory
and Practice,2016(11):4.
Gao G., Meng S. Auto insurance rate factor analysis based
on big data of Internet of Vehicles. Insurance
Research,2018(1):11.
Zhang L., Lu D. Application of Generalized linear Model
in Non-life insurance premium Analysis. Mathematical
Statistics and Management.2013.05.011.
Wu Y., Luo Yeye. Empirical Study of Generalized linear
Model in actuarial Pricing of Auto Insurance. Internal
Combustion Engines and Accessories.2018.15.096.
Wang Z. Research on Auto Insurance rate Determination
based on double layered Generalized linear Model.
Chongqing Technology and Business
University,2023:53-55.
Wang X., Wang Y. Study on classification rate
determination of automobile insurance based on
Generalized linear Model, Insurance Research, 2013
(09):2-3.
Meng S., Li T., Gao G. Auto insurance claim probability
and cumulative loss prediction based on Machine
learning algorithm. Insurance Research,2017(10).
Research on Traffic Violation Factors in Vehicle Insurance Pricing Based on Generalized Linear Model
77