Automatic Placement of Digital Signals in Railway Digitalization: A
Constraint Approach
Sven L
¨
offler and Petra Hofstedt
Chair of Programming Languages and Compiler Construction,
Brandenburg University of Technology Cottbus - Senftenberg,
Konrad-Wachsmann-Allee 5, 03046 Cottbus, Germany
Keywords:
Constraint Satisfaction, Planning and Scheduling, Digitalization, Logistics, Decision Support Systems,
Operation Scheduling Problem.
Abstract:
The aim of digitalization is to streamline operations and conserve resources; however, the process itself often
requires significant intellectual and resource investment. This paper addresses a digitalization challenge within
the German railway system, focusing on the placement of digital signals at appropriate distances from existing
switches along station track sections, replacing analog signals. This study serves as a feasibility analysis
demonstrating how constraint programming can resolve the problem. We first formulate a constraint problem
that defines the issue, then demonstrate methods to accelerate the solution process of the model, making it
suitable for larger problems. This approach is validated through a series of tests using generated scenarios to
illustrate its applicability to real-world challenges.
1 INTRODUCTION
The German railway network currently spans approx-
imately 39,200 kilometers, of which around 33,400
kilometers are operated by Deutsche Bahn. The com-
pany has set a goal to digitize its infrastructure. While
the outcome of digitalization aims to simplify opera-
tions and save resources, the actual process of digiti-
zation is itself often complex and resource-intensive.
One of Deutsche Bahn’s objectives is to replace ex-
isting analog signals with digital ones, necessitating
the installation of new signals and sensors. There are
specific guidelines controling the placement of these
components that must be adhered to. Currently, this
planning process is conducted manually, evaluated,
and, upon successful review, either implemented or
re-planned.
To streamline and accelerate this process, this pa-
per proposes a feasibility study demonstrating how
such challenges can be addressed using constraint
programming. The remainder of the paper is struc-
tured as follows: Section 2 begins by examining
the DB planning problem in detail and provides an
overview of constraint programming. Section 3 dis-
cusses related work and highlights the differences
from this study. Section 4 introduces our constraint-
based model for solving the DB planning problem.
However, for many practical problems, merely gen-
erating a valid constraint model is insufficient; ad-
justments must also be made to enhance the solution
speed of the problem. Therefore, the latter part of
Section 4 explores various optimizations for our con-
straint model. Section 5 encompasses our test series
and evaluation of the approach. Finally, the conclud-
ing Section 6 summarizes the key points of the paper
and outlines future directions.
2 PRELIMINARIES
Below, we briefly introduce the Deutsche Bahn Plan-
ning Problem and explain the fundamentals of con-
straint programming.
2.1 The DB Planning Problem
In the context of the ”Deutsche Bahn” (DB), the fol-
lowing problem arose during the digitalization pro-
cess. We assume the following general setting, see
Figure 1. In general, for a given section of track that
includes a station, manual signals are to be replaced
with digital ones, whereby optimizing the train flow.
Trains (of different lengths) run on tracks. A
(main) track can be split into two (side) tracks by a
Löffler, S. and Hofstedt, P.
Automatic Placement of Digital Signals in Railway Digitalization: A Constraint Approach.
DOI: 10.5220/0012994800003822
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 101-112
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
101

switch, and two (side) tracks can also be joined by
a switch. Depending on the switch setting, a train
can thus move from the main track to one of the side
tracks or switch from a side track to the main track.
Switches and their positions are announced by sig-
nals. These signals usually announce the switch 70
meters in advance. The distance of 70 meters can be
reduced to a value of 50 meters in justified cases.
Figure 1 shows a diverging switch on the left and a
converging split on the right. The signals are marked
by s
i
. In the context of our considerations, only the
signals s
1a
, s
1b
and s
2a
, s
2b
are relevant (thus black).
There are also stations at which trains can stop or
drive through without stopping. A station usually has
several tracks. Trains can stop at platforms (marked
as boxes in Figure 1) on the tracks and pick up or drop
passengers. This means that there are often many
switches before and after stations to guide the trains
to the appropriate tracks. However, the signals of the
switches must not be located in the platform area. As
described above, switches can then be located at a dis-
tance of 70 meters (possibly less, but at least 50 me-
ters) after the signals.
A given railway network with corresponding
switches therefore has an influence on the maximum
length of platforms (in Figure 1: l
min
, l
max
) in the area
of the stations, depending on the placement of the sig-
nals, and therefore also on the maximum length of the
trains that are allowed to stop there.
The figure also shows durations (d in abstract time
units) for the passage or stop of trains in certain track
areas or at platforms.
The problem is that the trains passing through
the section have different lengths and require varying
amounts of time to traverse the individual segments.
Placing all digital signals at a distance of 70 meters
can result in some trains being unable to stop at cer-
tain platforms because the stopping area is too small
for the train’s length. Conversely, not all signals can
be uniformly set to a 50-meter distance to create the
largest possible stopping areas. It must be individu-
ally justified for each digital signal that a placement at
50 meters instead of 70 meters is necessary to achieve
maximum productivity.
This creates an optimization problem where the
digital signals must be positioned to maximize the
throughput rate of trains within the given time inter-
val while minimizing the deviation from the 70-meter
distance between all switches and their digital signals.
Determining the optimal throughput rate presents an
exponentially growing problem, which is rarely ver-
ifiable by hand. Currently, planning is done manu-
ally and subsequently reviewed by safety personnel,
resulting in numerous iterations in the planning and
control process until a satisfactory solution is found.
The quality of this solution in terms of the trains’
throughput rate is often not optimal.
Our approach initially focuses on a feasibility
study, hence we make some simplifications. We as-
sume that each train occupies each track component
for a specific duration d. This duration can vary de-
pending on the action performed during the traversal
of the track section. For example, whether a train
passes through a platform or stops and starts again.
Another initial simplification is that all trains come
from the same direction and continue in the same di-
rection. For our optimization problem, we consider
the following track components with their associated
parameters.
Tracks: Each track is occupied by a train for a spe-
cific duration d
Track
.
Switch (Diverging): A diverging switch splits a track
A into two other tracks B and C. Depending on the
switch setting, the train moves from track A to track
B or C. The occupancy duration d
switch
of the switch
depends on the setting (connection to track B or C)
d
split
∈ {d
B
,d
C
}.
Switch (Converging): Analogous to the diverging
switch, a converging switch merges two tracks A and
B into one track C. Depending on the switch set-
ting, the duration a train occupies it varies d
merge
∈
{d
A
,d
B
}.
Platform: Each platform has a minimum l
min
and
maximum length l
max
depending on whether the digi-
tal signal is 50 or 70 meters (or in between) from the
next switch. Trains can only use platforms that meet
the minimum length requirement. Trains have two op-
tions: either they stop at a platform, which takes a sig-
nificant amount of time, or they simply pass through
the platform. d
platform
∈ {d
driveT hrough
,d
stay
}
Train: A train has a specific length length and in-
formation stay about whether it needs to stop (stay =
true) at the platform or not (stay = f alse). If the train
needs to stop, it must stop at a platform that is long
enough and requires a corresponding amount of time.
If the train does not need to stop at the platform, it
will just pass through the platforms.
Thus, we face an optimization problem where
digital signals must be positioned to maximize the
throughput rate of trains within a given time inter-
val, while minimizing the deviation from the 70-meter
distance between all switches and a digital signal.
In our example DB Planning Problem in Fig-
ure 1, there are three incoming trains with differ-
ent lengths (l
Train1
= 100m, l
Train2
= 140m, l
Train3
=
160m) which must be navigated through a track net-
work with two switches and two platforms. Train 1
and Train 3 must stop at a sufficiently long platform,
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
102

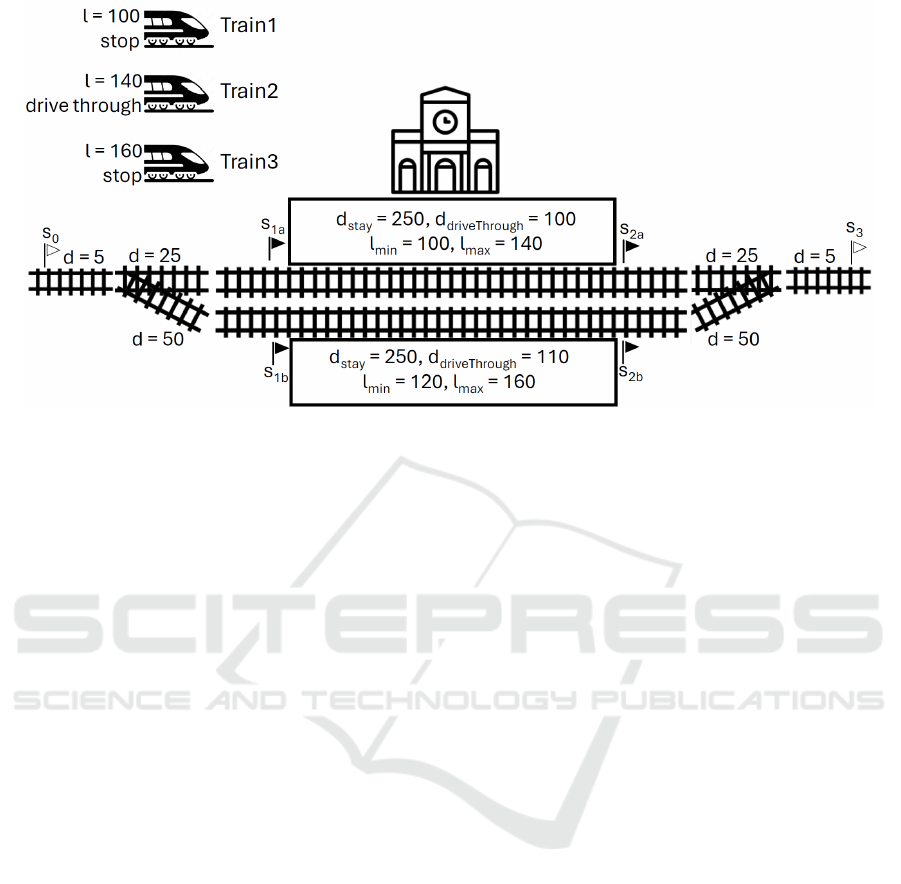
Figure 1: A simple example DB PLanning Problem.
whereas Train 2 only needs to pass through the track
sections without stopping. The goal is for Train 1 to
pass over the first track before Train 2, and Train 2
before Train 3. A train can only enter a track seg-
ment if no other train occupies it at the same time.
For the initial track segment (far left in the figure),
each train requires d
Track
= 5 time units (TU) to tra-
verse it. Depending on the switch position, trains then
require either d
B
= 25TU to reach the upper platform
or d
C
= 50TU to reach the lower platform. Depend-
ing on whether a train stops at the upper platform, it
will occupy this track segment for d
stay
= 250TU or
d
driveT hrough
= 100TU. For the lower platform, the
times are d
stay
= 250TU and d
driveT hrough
= 110TU,
respectively. After the platform, the trains proceed
through the second switch and the final track segment.
The planning objective is to assign track segments
and times to the trains such that:
No two trains occupy the same track segment si-
multaneously. Each train stops at a valid platform if
required. Trains leave the track segments as quickly
as possible. Platform lengths are minimized, as min-
imal platform lengths correspond to a 70-meter dis-
tance of digital signals from the switches.
To adapt to real-world conditions beyond the fea-
sibility study, it would be necessary to allow trains to
pass through the station in both directions. Addition-
ally, it might be required to specify individual occu-
pancy times for each pair of train and track section.
These enhancements will ensure the optimization
model accurately reflects the complexity of real-world
train scheduling and track usage.
2.2 Constraint Programming
Constraint programming (CP) is a methodology used
for the declarative modeling and solving of complex
problems, especially those classified as NP-complete
and NP-hard. CP is applied in various problem do-
mains, including rostering, graph coloring, optimiza-
tion, and satisfiability (SAT) problems (Marriott and
Stuckey, 1998). In this section, we introduce the
fundamental concepts of constraint programming that
underpin our approach.
The general process of constraint programming
consists of two distinct phases:
1. The declarative formulation and representation of
a problem as a constraint model. This involves
defining constraints, variables, and their interre-
lationships, thereby establishing the logical struc-
ture of the problem or solution.
2. The resolution of the constraint model using a
dedicated constraint solver. The solver functions
independently, like a self-contained black box, ad-
dressing the complexities of the problem.
In essence, the CP user’s role is to craft the
application-specific problem model using constraints
and to set up and initiate the solver. The solver then
autonomously applies advanced techniques to explore
potential solutions and find an optimal or satisfac-
tory outcome. This separation of responsibilities sim-
plifies the problem-solving process, allowing domain
experts to focus on the abstract representation of their
real-world challenges.
A constraint satisfaction problem (CSP) is for-
mally defined as a 3-tuple P = (X, D,C), comprising
Automatic Placement of Digital Signals in Railway Digitalization: A Constraint Approach
103

the following components: X = {x
1
,x
2
,...,x
n
} rep-
resents a set of variables. D = {D
1
,D
2
,...,D
n
} is a
collection of finite domains, where D
i
denotes the do-
main of variable x
i
. C = {c
1
,c
2
,...,c
m
} constitutes a
set of constraints, with each constraint c
j
defined over
a subset of variables from X (Apt, 2003).
A constraint, denoted by a tuple (X
′
,R), consists
of a relation R and an ordered set of variables X
′
,
which is a subset of X , over which the relation R is
defined (Dechter, 2003). For instance, examples of
constraints include ({x, y}, x < y), ({x,y,z},x+y = z),
or ({A,B},A → B). Given that the variables involved
in a constraint are explicitly identifiable within their
corresponding relation, we solely specify the relation
in the subsequent sections of this paper.
A solution of a CSP involves the instantiation of
all variables x
i
with values d
i
from their respective
domains D
i
, such that all constraints are satisfied.
Additionally, a constraint optimization problem
(COP) extends the scope of a CSP. In a COP, an opti-
mization variable x
opt
is explicitly identified, and the
objective is to minimize or maximize this variable to
reach an optimal solution.
A specific constraint we use, in addition to many
simple and intuitive constraints, is the count con-
straint. For an ordered set of variables {x
1
,...,x
n
} =
X, this constraint specifies that a particular value v ∈
N must appear exactly occ ∈ X times among the vari-
ables.
count(X,occ,v) ⇔
∑
x∈X
(
0 x ̸= v
1 x = v
!
= occ (1)
An example of a valid assignment for the
count constraint count({x
1
,x
2
,x
3
},occ,2) with
D
1
,D
2
,D
3
∈ {1,2,3,4,5} and D
occ
∈ {1,3} is
x
1
= 2,x
2
= 1,x
3
= 3, and occ = 1, because the value
2 occurs once in the variable assignement. Another
solution is, e.g. x
1
= 2, x
2
= 2, and x
3
= 2, where the
value 2 occurs 3 times, i.e. occ = 3.
3 RELATED WORK
Related work primarily focuses on the Operation
Scheduling Problem (OSP), whose greatest challenge
lies in efficiently allocating limited resources to a
large number of train operations, especially during
peak demand periods (Zhong et al., 2024).
Both the quality and the speed of planning the
station operation schedules are crucial. While train
operations can be represented through resource allo-
cation, the OSP can be described as optimizing the
use of resources for a large number of train opera-
tions without conflicts at the station. Conflicts be-
tween two operations arise from the simultaneous use
of the same resource, and railway operations must be
entirely conflict-free. Generally, the resources refer to
railway infrastructure such as tracks, platforms, sig-
nals, and switches.
There are many publications focused on the OSP
in railway stations (Caimi et al., 2012; Rodriguez,
2007). These works primarily address the creation of
train routes through multi-track station areas but do
not consider the possibility that platform length can
vary due to digitalization and the associated recon-
struction.
Carey and Carville (Carey and Carville, 2000;
Carey and Carville, 2003) proposed and tested models
and algorithms for train scheduling at a single, heavily
trafficked, complex station. Their later work (Carey
and Crawford, 2007) extended scheduling from a sin-
gle station to a railway corridor. Freling et al. (Frel-
ing et al., 2005) assigned train units to marshalling
tracks through a column generation algorithm but did
not discuss potential routing conflicts between sched-
uled train paths within different station areas. These
methods have the advantage of being based on prac-
tical rules, making planning decisions understandable
and acceptable to the schedulers, thus beneficial for
their improvement.
Based on the creation of optimization models,
many methods have been proposed to solve the plat-
form problem or the reception-departure line assign-
ment problem, mainly including mathematical pro-
gramming software (Billionnet, 2003; Zhang et al.,
2019), branch-and-bound methods (Caprara et al.,
2011), and heuristic algorithms (Liu and Kozan,
2009), such as the ant algorithm-based method (Yue
et al., 2006), local search algorithm (Qi et al.,
2016), global neighborhood search algorithm (Mu
and Dessouky, 2011), and customized simulated an-
nealing algorithm (Kang et al., 2019).
In the past decade, heuristic algorithms have been
continuously improved and published (e.g., water
drop algorithms (Siddique and Adeli, 2014), particle
swarm optimization with selective search (Hossain
et al., 2019), and discrete spider monkey optimization
(Akhand et al., 2020)). However, heuristic algorithms
often require a large number of experiments to find
the best parameter settings for each case due to their
sensitivity to parameters, and the quality of their so-
lutions is easily affected by random factors, making
direct evaluation difficult.
In summary, none of these approaches consider
the flexible size of a platform by adjusting signals,
thereby affecting its usability for trains of varying
lengths.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
104

4 A CONSTRAINT-BASED DB
APPROACH
In this section, we present our basic implementation
of the DB Planning Problem as a Constraint Opti-
mization Problem (COP). Fundamentally, we con-
sider the entire problem as a matrix of pairs of start
time and track segment of each train. This allows
to represent the concrete train sequence over a cer-
tain cutout of a railway net. The dimensions of
the matrix are the number of trains #Trains and
maximum number of track segments or components
maxComponents that each train must traverse to pass
through the entire track section. Subsequently, in
the tuple matrix M
i, j
= (component, startTime),i ∈
{1, 2, ..., #Trains}, j ∈ {1, 2, ..., maxComponents +
1}, we specify for each component when it is en-
tered by a respective train. The last component
maxComponent + 1 is needed to determine the time
when a train leaves the entire track section. If fewer
than the maximum number of components are needed
for a train, the tuples are filled with ”Completed”
components. See the following example which rep-
resents a solution for the problem given in Figure 1.
The maximum number of components that a train
must traverse in the example is 5 (which is also the
minimum number). Therefore, for three trains, we
generate a 3 × 6 matrix. A solution might look as
shown in Table 1.
In this solution, it is important to note that the first
and third trains must stop at a platform, while the sec-
ond train is allowed to pass through. This can be iden-
tified by the times at which a train enters a platform
and then moves on to the next component (stopping
requires at least 250 time units). At this point, nothing
has been said about the actual optimization value. The
goal is to minimize the sum of the platform lengths. In
this example, Platform 1 (upper platform) requires a
length of 100 meters and Platform 2 (lower platform)
requires 160 meters. All trains pass through and leave
the section after 495 TU. Both values (260 meters to-
tal length and 495 TU) are optimal for this example.
In the following sections, we will first present an
intuitive approach to modeling the DB Planning Prob-
lem. Additionally, we demonstrate improvements to
the model that increase its solution speed, making it
applicable to real-world problems.
4.1 An Intuitive COP for the DB
Planning Problem
Figure 2 illustrates our intuitive COP for the DB Plan-
ning Problem.
Variables and Domains (lines 1-12) This imple-
mentation reflects the previous considerations to store
the solution as a matrix. Specifically, there are
(#Trains × (maxComponents + 1)) component and
time variables X
C
i, j
(line 1) and X
T
i, j
(line 2), respec-
tively. These together represent the problem matrix
(as explained above, see e.g. Table 1) and indicate
which track components are traversed by train i in
what order, and the time when each component is
entered. These component variables can take val-
ues from 0 to number of existing components (line
7), where the values 1 to #Components are assigned
to real components, and the value 0 corresponds to
”Completed,” meaning no component. ”Completed”
can only occur when the train has completely left the
entire track section. The time variables X
T
i, j
take on
values between 0 and a precomputed maximum time
maxTime. The value for maxTime represents an upper
estimate of the total required time.
Since it is unclear whether and when a train will
reach a platform, an additional variable X
S
i, j
has been
introduced for each encounter of a train with a com-
ponent (line 3). Such a stop variable takes the value 0
if the corresponding component variable X
C
i, j
indicates
that it is not a platform. Otherwise, it takes the value
1 if a train stops at the platform, or the value 2 if all
trains passes through the platform without stopping
(line 9).
For each platform, an additional variable x
L
i
is in-
troduced (line 4), which indicates the length of the
platform i. The value range of this variable is between
the minimum length (l
min
i
) and the maximum length
(l
max
i
) of the platform, determined by the positioning
of the signals relative to the switch (line 10).
Finally, we need a variable x
Total
T
(line 5) that rep-
resents the total time required for all trains to traverse
the segment, and a variable x
Total
L
that represents the
total length of the platforms. We utilize our generated
COP twice to minimize both values. According to the
railway operator, the flow of trains has priority, so in
the first run, the COP is minimized with respect to the
total time x
Total
T
(line 26). In a second run, this to-
tal time is then fixed for x
Total
T
, and the problem is
optimized with respect to the length of the platforms
x
Total
L
(line 26). Thus, we first calculate a solution
where trains can pass through the segment as quickly
as possible, and then we seek a solution where the
trains can pass through the segment equally quickly,
but the platforms are as short as necessary.
Constraints (lines 13-26). The following section
explains the key constraints of the COP. Simplifica-
tions have been made in the representation in Figure
2 for better understanding.
Automatic Placement of Digital Signals in Railway Digitalization: A Constraint Approach
105

Table 1: A possible solution to the DB Planning Problem (Comp
i
denotes the corresponding component) from Figure 1.
Comp
1
Time
1
Comp
2
Time
2
Comp
3
Time
3
Comp
4
Time
4
Comp
5
Time
5
Comp
6
Time
6
Train 1 StartTrack 0 Switch1 5 Platform1 30 Switch2 280 EndTrack 305 Completed 310
Train 2 StartTrack 5 Switch1 30 Platform2 80 Switch2 190 EndTrack 240 Completed 245
Train 3 StartTrack 30 Switch1 80 Platform2 190 Switch2 440 EndTrack 490 Completed 495
P = (X,D,C, f ) with:
1 X = X
C
= {x
C
i, j
| ∀i ∈ {1,...,#Trains}, j ∈ {1,...,maxComponents + 1}} ∪ (Component variables)
2 X
T
= {x
T
i, j
| ∀i ∈ {1,...,#Trains}, j ∈ {1,...,maxComponents + 1}} ∪ (Time variables)
3 X
S
= {x
S
i, j
| ∀i ∈ {1,...,#Trains}, j ∈ {1,...,maxComponents + 1}} ∪ (Stop variables)
4 X
L
= {x
L
i
| ∀i ∈ {1,...,#Platforms}} ∪ (Length variables)
5 {x
Total
T
} ∪ (Total time variable)
6 {x
Total
L
} (Total length variable)
7 D = D
C
= {D
C
i, j
| D
C
i, j
= {0,1,...,#Components}} ∪
8 D
T
= {D
T
i, j
| D
T
i, j
= {0,1,...,maxTime}} ∪
9 D
S
= {D
T
i, j
| D
S
i, j
= {0,1,2}} ∪
10 D
L
= {D
L
i
| D
L
i
= {l
min
i
,l
min
i
+ 1,..., l
max
i
}} ∪
11 D
Total
T
= {0,1,...,maxTime} ∪
12 D
Total
L
= {0,1,...,maxLength}
13 C = C
Start
= {x
C
i,0
= StartTrack | ∀i ∈ {1, 2, ..., #Trains}} ∪ (Start constraints)
14 = C
End
= {count(EndTrack,{x
C
i,0
,x
C
i,1
,...,x
C
i,maxComponent
},1} | ∀i ∈ {1,2,...,#Trains}} ∪
(End constraints)
15 = C
Platform
= {x
C
i, j
̸= Platform ⇔ x
S
i, j
= 0 | ∀x
C
i, j
∈ X
C
} ∪ (Platform constraints)
16 C
Train
= {x
T
i,1
< x
T
i+1,1
| ∀ j ∈ {1, 2, ..., #Trains}} ∪ (Train sequencing constraints)
17 C
Time
= {(x
C
i, j
= Completed) ⇒ (x
T
i, j
= x
T
i, j+1
) | ∀x
C
i, j
∈ X
C
} ∪ (Time constraints)
18 {(x
T
i, j
+time(x
C
i, j
) ≤ x
T
i, j+1
) | ∀x
C
i, j
∈ X
C
} ∪
19 {(x
Total
T
= max(x
T
i,maxComponent
| ∀i ∈ {1,2,...,#Trains})} ∪
20 C
Component
= {(x
C
i, j
= EndTrack) ⇒ (x
C
i, j+1
= Completed) | ∀x
C
i, j
∈ X
C
} ∪ (Component order constraints)
21 {(x
C
i, j
= Component) ⇒ (x
C
i, j+1
= successor(Component)) | ∀x
C
i, j
∈ X
C
} ∪
22 C
Different
= {(x
C
i
1
, j
1
= x
C
i
2
, j
2
) ⇒ ((x
C
i
1
, j
1
= Completed) ∨ (x
T
i
1
, j
1
≥ x
T
i
2
, j
2
+1
) ∨ (x
T
i
2
, j
2
≥ x
T
i
1
, j
1
+1
))
| ∀x
C
i
1
, j
1
,x
C
i
2
, j
2
∈ X
C
,x
C
i
1
, j
1
̸= x
C
i
2
, j
2
} ∪ (Different component constraints)
23 C
Stop
= {(stay(Train
i
) ⇔ count(1, {x
S
i,0
,x
S
i,1
,...,x
S
i,maxComponent
},1} | ∀i ∈ {1,2,...,#Trains}} ∪
(Stop constraints)
24 C
Length
= {(x
C
i, j
= Platform) ⇒ (x
L
S
i
≥ l
i
) | ∀x
C
i, j
∈ X
C
} ∪ (Length constraints)
25 {(x
Total
L
= sum(x
L
i
| ∀i ∈ {1,2,...,#Platforms})} (Total length constraint)
26 minimize(x
Total
T
) or minimize(x
Total
L
)
Figure 2: A COP for the DB Planning Problem.
The start constraints C
Start
(line 13) specify that
each train must initially be at the StartTrack. Since
this COP is only a feasibility study, we have not in-
cluded multiple different StartTracks. This would
certainly be feasible in reality, where trains could
come from different origines.
The end constraints C
End
(line 14) serve a simi-
lar function, ensuring that each train ends up at the
EndTrack. The difference in this constraint is that
it is unclear at which point the EndTrack will appear
in the sequence of components. This depends on the
number of track segments in each parallel sequence of
platforms and other components. Since only ”Com-
pleted” can follow the EndTrack, it is sufficient to
require that the end component appears once in each
train’s component sequence. This is ensured by the
specified count constraint.
The platform constraints C
Platform
(line 15) ensure
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
106

that the stop variables take the value 0 precisely when
the component is not a platform. Conversely, these
variables must either take the value 1 (stop) or 2 (pass-
through).
The train constraints C
Train
(line 16) ensure that
the first train enters the StartTrack before the second
train, the second before the third, and so on.
The time constraints C
Time
encompass three dif-
ferent types of constraints. The first type (line 17)
ensures that if a component variable takes the value
”Completed,” the entry time for the following com-
ponent (which must also be ”Completed”) must be the
same. This propagates the final time within the tuple
matrix to the back, allowing the final arrival times to
be read from the last column.
The second type of constraint (line 18) ensures
that the following component (c
j+1
) can be entered
no earlier than when the previous component (c
j
) is
entered (x
T
i, j
) and is no longer blocked by passing
through or stopping (time(x
C
i, j
)). The function time
here is a simplified representation, as switch and plat-
form components may have different occupancy times
depending on whether the train is directed in one di-
rection or another or stops at a platform versus pass-
ing through. In the actual implementation, this con-
straint is represented by several other constraints that
are semantically equivalent to the one of Figure 2.
The third type of time constraint (line 19) ensures
that the variable x
Total
T
takes the maximum time of
all the last components. Since we specify one more
component in our set of variables than needed to tra-
verse the segment, the last component must always
be a ”Completed” component. This component has
an associated time value exactly equal to x
T
i, j
, the time
at which train i leaves the last real component.
The component constraints C
Component
specify that
only ”Completed” can follow the EndTrack (line 20),
and that each normal component can only be followed
by a component that logically succeeds it (line 21).
The successor function here is an abstraction. For a
switch, the successor depends on the switch’s setting.
Technically, this was implemented through various
constraints that are semantically equivalent to the one
described here. This constraint also ensures that only
other ”Completed” components can follow a ”Com-
pleted” component.
The different occupancy constraints C
Different
(line
22) state that each component can be occupied by
only one train at a time. If two trains i
1
and i
2
have
the same component, they must occupy it at differ-
ent times, unless the component is the ”Completed”
component, which can be occupied by all trains si-
multaneously.
The stop constraints C
Stop
(line 23) specify that if
a train Train
i
is to stop within the entire component
segment, it must do so at exactly one platform. This
is true if and only if one of the stop variables x
S
i, j
as-
signed to the train takes the value 1.
Finally, we have the length constraints C
Length
(line 24), which require that a train i can only stop
at or pass through a platform S
i
if the length of the
platform x
L
S
i
is greater than or equal to the length l
i
of
the train.
Additionally, there is a length constraint (line 25)
that sums the lengths of all platforms x
L
i
and assigns
the result to the variable x
Total
L
.
Finally, the objective function needs to be speci-
fied. In the case of the first COP, this involves min-
imizing the total time variable x
Total
T
. In the case
of the second COP, it involves minimizing the total
length of all platforms x
Total
L
(line 26).
4.2 Optimization of the COP for
Real-World Applications
Although the model presented in Figure 2 is correct, it
has some hidden weaknesses that prevent it from find-
ing solutions for real problems efficiently or proving
their feasibility quickly. These weaknesses in solving
arise from the manner in which a solver processes the
constraints.
Weak Propagation. Let us consider line 21. For
Switch1 (diverging) in the example from Figure 1, the
constraint (x
C
i, j
= Switch1) ⇒ ((x
C
i, j+1
= Platform1) ∨
(x
C
i, j+1
= Platform2)) holds. While this is correct,
there are hidden issues related to propagation in con-
junction with the time constraints x
T
i, j
+ time(x
C
i, j
) ≤
x
T
i, j+1
(line 18). Individually, both constraints are fine.
However, their combination leads to weaker propaga-
tion than expected.
In our example, according to the component con-
straint from line 21, if Switch1 is part of the com-
ponent sequence, the next component must be either
Platform1 or Platform2. Consequently, the next com-
ponent must occupy at least 100 TU (the minimum
occupancy time for either track). The problem is that
this cannot be immediately inferred by the COP. This
is because the variable x
C
i, j
is not yet uniquely deter-
mined and can still take on two possible values: either
Platform1 or Platform2. Therefore, the time function
cannot perform calculations, as it requires a definitive
variable assignment.
This problem can be circumvented by combin-
ing the two constraints from lines 18 and 21 into a
new constraint. Possible solutions include developing
a new, accurate constraint with appropriate propaga-
Automatic Placement of Digital Signals in Railway Digitalization: A Constraint Approach
107

tors or using model transformation methods such as
tabularization (Akg
¨
un et al., 2018) or regularization
(L
¨
offler et al., 2021; L
¨
offler, 2022).
In this work, we used both regularization and
transformation into element constraints to increase
the propagation strength.
The Direction of the Constraints. Normally, con-
straints are undirected. This means that from the con-
straint R = U/I, we can also derive U = R · I and
I = U/R. This is also true in our model; however,
the use of implications results in a forward propaga-
tion from the beginning to the end. The component
constraints (lines 20 and 21), as well as the time con-
straints (lines 17 to 19), always imply a subsequent
component or time for the current and the next seg-
ment. However, it is not possible to infer information
backward (from the next component to the previous
one).
In a solver search strategy that assigns variables
from front to back, this may not seem problematic at
first glance. However, first, we cannot assume such
a search strategy, and second, this overlooks the fact
that the last element is known (”Completed”) and that
only ”Completed” elements or the LastTrack can pre-
cede it. This means that, at least for the components,
we also need backward propagation.
For the temporal constraints, the need for back-
ward propagation is somewhat harder to see. How-
ever, since this is a COP, once we have found an
initial solution for our target value X
Total
T
, we will
only be searching for better solutions. Therefore, af-
ter finding an initial solution, we have a restriction
on the total time, which simultaneously constrains
the times for each train to leave the last segment
(x
T
i,maxComponents+1
). This means that, due to the nature
of how COP problems are solved, backward propaga-
tion is inherently necessary to propagate these con-
strained departure times to their preceding compo-
nents.
The problem of missing backward propagation in
the solution method of the solvers can be addressed
in both cases either by adding additional constraints
that consider the backward direction or by increasing
the level of consistency, e.g., by transforming the con-
straints (as mentioned in the previous paragraph using
regularization and tabularization).
To solve the problem for the components, we have
replaced all C
Component
constraints (lines 20 and 21)
affecting the same train with a regular constraint that
utilizes a deterministic finite automaton (DFA) rep-
resenting the entire track network. This automaton
ensures that components are automatically connected
in both directions. Specifically, if a component x
C
i, j
is known, it can be inferred that x
C
i, j+1
is the sub-
sequent component and x
C
i, j−1
is the preceding com-
ponent. For Platforms, Switches (converging), and
Tracks, the next component is always uniquely deter-
mined. In the case of Switches (diverging), there are
two possible successors. Conversely, for Platforms,
Switches (diverging), and Tracks, the predecessor is
always unique, whereas for Switches (converging),
there are two possible predecessors.
For the time constraints C
Time
, we have created an
additional constraint that, for each variable x
C
i, j
, deter-
mines and propagates the minimum required times of
all possible components (i.e., the remaining elements
in the domain of x
C
i, j
). Together, these constraints en-
sure that time can also be propagated backward (i.e.,
from later components to earlier components). This
leads to significant time savings, as it allows for the
rapid elimination of many time values that cannot be
part of a solution.
Parallelization of COPs. Parallelizing constraint
problems is a promising approach to accelerate the
solving of COPs. The most commonly used ap-
proaches are parallel search (R
´
egin et al., 2013) and
portfolio-based methods (R
´
egin and Malapert, 2018).
Both approaches can achieve superlinear speedup
in the solution time. Parallelizing COPs is gener-
ally challenging due to the high interaction of indi-
vidual components within a COP. However, the port-
folio approach offers a straightforward way for de-
velopers to parallelize the problem. In this approach,
a COP is solved independently in different versions,
and only the best optimization value found so far is
shared among them. This approach minimizes com-
munication overhead while allowing for quicker ex-
clusion of search space regions that yield worse opti-
mization values than those already known from other
versions.
Different versions of a model can involve using
various search strategies, different constraints, or dif-
ferent modeling approaches. It is even possible to
use different solvers in this way. The portfolio ap-
proach has proven to be very effective and easy to ap-
ply, making it widely used in real-world applications.
More information on the portfolio approach can be
found in (R
´
egin and Malapert, 2018). In our work,
we employed a portfolio approach with four different
search strategies.
The Search. As previously mentioned, the solution
speed of a COP heavily depends on the search strategy
used in the solver. For the DB Planning Problem, as-
signing component variables and time variables from
”front” to ”back” seems logical. However, classical
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
108

search strategies in solvers do not necessarily operate
this way. Some strategies, like wdeg and dom/wdeg,
follow conflict-driven approaches (Boussemart et al.,
2004). These approaches are based on complex cal-
culations to estimate future good decisions based on
decisions made so far or the underlying constraint net-
work. The resulting behavior typically does not re-
semble an ordered assignment of variables according
to their index order during creation.
For general problems, this approach is usually
very effective. However, as shown in other works
(L
¨
offler et al., 2024) , using problem-specific knowl-
edge in solver searches is a crucial factor for solution
speed. Therefore, it is advisable to design a targeted
problem-specific search strategy to explore the search
space as quickly as possible.
Currently, we have not yet developed a specific
search strategy to expedite problem-solving. How-
ever, we consider this a highly promising area for fu-
ture research.
Improving the Objective Function. It is possible
to further refine the objective function. For example,
when searching for a minimal end time x
Total
T
, we
encounter the problem that if a train A has to wait for
another train B to clear a track segment, train A can
wait directly at the previous component, at another
earlier component, or split the waiting time across
multiple components. This results in many equivalent
solutions that may all need to be explored. There-
fore, in our objective function, we assigned a high
weight w
high
to the final time and included the inter-
mediate times of individual components with a very
small weight w
small
.
minimize(w
high
∗ x
Total
T
+ w
small
∗ x
T
1,1
+ w
small
∗ x
T
1,2
+
... +w
small
∗ x
T
#Trains,maxComponents+1
)
(2)
The high weight w
high
must be chosen such that a
change in the total time x
Total
T
has a greater influence
than the weighted sum of the changes in the interme-
diate times x
T
i, j
.
This results in a prioritization of minimizing the
total time x
Total
T
over minimizing the individual in-
termediate times x
T
i, j
. This approach can also be
used to similarly include the minimization of platform
lengths x
Total
L
. By simply adding the weighted sum of
the total required length of the platforms, multiplied
by a similarly small weight, to the objective function:
x
Total
L
∗ w
small
. The search considers then also a min-
imal platform length (as well as a maximum distance
between switches and signals) with subordinate prior-
ity.
Due to the time limit of the search and the subordi-
nate priority of minimal length under minimal time, it
cannot be guaranteed that the shortest platform length
for the highest train throughput rate will always be
found. Therefore, it still makes sense to solve the sec-
ond constraint optimization problem (COP) with the
input of the maximum time and the minimization of
only the platform length x
Total
L
.
5 EXPERIMENTS AND RESULTS
All experiments were conducted on an LG Gram lap-
top with an 11th generation Intel(R) Core(TM) i7-
1165G7 quad-core processor running at 2.80GHz and
16GB of DDR3 RAM running at 2803MHz. The op-
erating system is Microsoft Windows 10 Enterprise.
The programming language used was Java with
JDK version 17.0.7 and the constraint solver Choco-
Solver version 4.10.7 (Prud’homme et al., 2017).
We generated 10 random station scenarios for
each combination of different numbers of trains (5,
10, 15, 20) and platforms (5, 10, 15, 20), resulting
in a total of 10 * 4 * 4 = 160 different test sce-
narios. For all problem instances, a time limit of 5
minutes was set for both determining a solution that
maximizes the throughput of trains through the track
section (minimize the total time x
Total
T
) and avoid-
ing distances under 70 meters between switches and
signals (minimize the total platform length x
Total
L
).
This previously introduced two-stage approach (first
minimizing x
Total
T
yieldings x
T
opt
, second minimizing
x
Total
L
with fixed x
T
opt
) ensures that initially, train flow
is maximized, followed by determining adjustments
to position signals closer than 70 meters to switches.
Table 2 presents the results of the 160 different
test runs. The first two columns indicate the num-
ber of trains and the number of Platforms in the track
segment. The column ∅DisArea shows the average
minimal and maximal summed platform length for
the 10 instances with the same number of trains and
platforms. The column ∅Dis represents the required
length for the fastest processing of the trains as calcu-
lated by our method. The time required for the trains
in Time Units (TU) is provided in the column ∅Time.
The last four columns provide insights into the so-
lution process. They indicate the average solution
time for computing the fastest processing of the trains
∅SolT(T) and for computing the shortest platforms
∅SolT(S). Additionally, the number of instances that
were completely and globally optimally solved is pro-
vided #comp(T) resp. #comp(L). The last row of
the Table 2 provides the average results across all in-
stances instances and the sums of the numbers of op-
Automatic Placement of Digital Signals in Railway Digitalization: A Constraint Approach
109

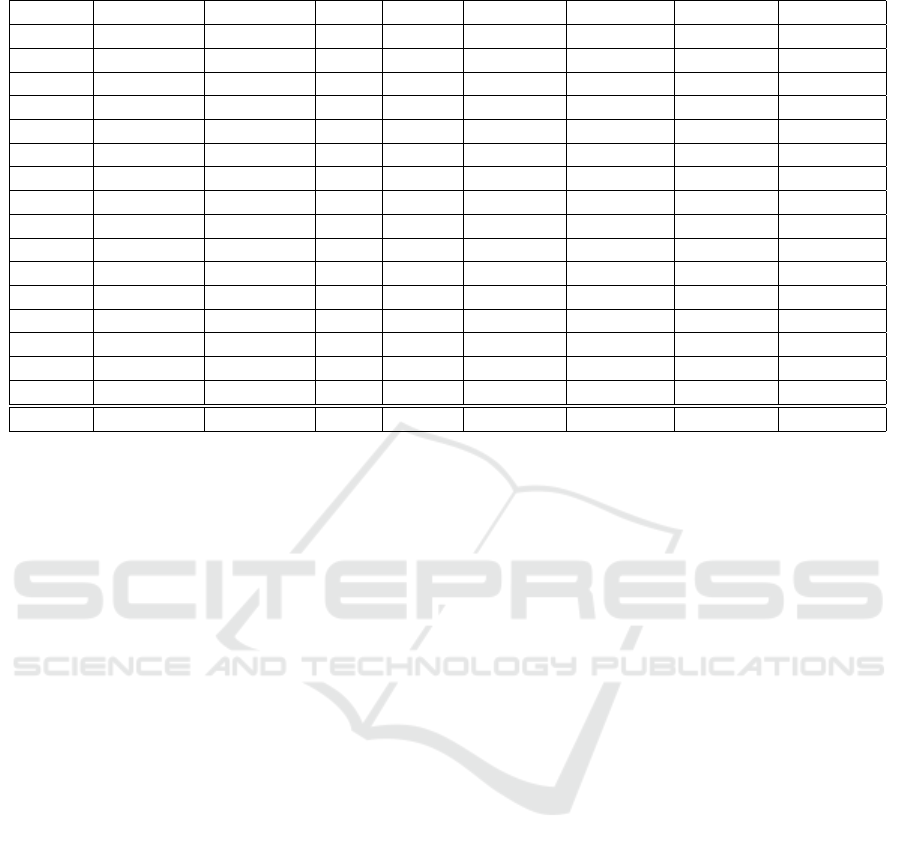
Table 2: Results of 160 different DB Planning Problems.
#Trains #Platforms ∅DisArea ∅Dis ∅Time ∅SolT(T) #Comp(T) ∅SolT(L) #Comp(L)
5 5 602-802 646 2039 248s 3 119s 7
5 10 1208-1608 1240 2124 265 s 2 166s 6
5 15 1786-2386 1856 3019 300 s 1 230s 3
5 20 2424-3224 2486 4067 300 s 0 199s 4
10 5 602-802 672 3922 300 s 0 150s 5
10 10 1208-1608 1302 3526 300 s 0 270s 1
10 15 1786-2386 1876 4438 300 s 0 271s 1
10 20 2424-3224 2516 5299 300 s 0 241s 2
15 5 602-802 676 4981 300 s 0 180s 4
15 10 1222-1622 1300 4389 300 s 0 271s 1
15 15 1786-2386 1898 5442 300 s 0 271s 1
15 20 2424-3224 2514 6278 300 s 0 243s 2
20 5 602-802 680 6052 300 s 0 181s 4
20 10 1222-1622 1314 5176 300 s 0 272s 1
20 15 1786-2386 1898 6379 300 s 0 273s 1
20 20 2424-3224 2522 7241 300 s 0 245s 2
12.5 12.5 1506-2006 1587 4648 298s 6 224s 45
timally solved instances (#Comp(T) and #Comp(L)),
resp.
First and foremost, it should be noted that the fact
that we were able to solve all 160 cases (though not
all globally optimal) represents a success for our fea-
sibility study. While these test cases were randomly
generated track segments, we believe that this solu-
tion method can be applied to comparably sized real-
world track segments. Ultimately, it needs to be eval-
uated with the railway employees who currently per-
form this process manually, to determine whether the
time units required for all trains to pass through are
better or worse than the manually determined ones.
In total, the fastest train passage was found in 6
cases (#Comp(T)). With further optimization of the
model, better search strategies, and more computa-
tion time (currently limited to 5 minutes), it is may
possible to achieve even better results.
The second computation step (calculating the min-
imal platform lengths to maximize the distance to
the signals) utilizes the results of the first calcula-
tion to set an upper bound on the maximum time and
then minimizes the platform lengths. This calculation
more frequently results in a global solution (in 45 out
of 160 cases). This means that in 45 cases, it was
proven that no better solution exists regarding the dis-
tance of the signals to the switches, where the trains
can pass just as quickly. In the other 115 cases, this
could not be definitively confirmed before reaching
the timeout, but no better solution was found either.
The result that the second computation is here un-
necessary (the second COP does not find a better so-
lution for x
Total
L
than the first COP in any case) is
due to the fact that we already incorporated platform
length into the objective function during the first com-
putation. Thus, the second computation served as a
verification of the first. It can be observed that the
calculated required platform lengths tend to be at the
lower end of the range (1587 in the range from 1506 to
2006), indicating a high quality of results. The lower
bound is unattainable because it simply represents the
sum of all minimal platform lengths, while the up-
per bound is the sum of all maximal platform lengths.
The lower bound cannot be reached because, by def-
inition, at least one platform must have a maximum
length for a train with a length of 180 meters.
A trend can be observed where an increase in the
number of trains more significantly reduces the num-
ber of problems that can be fully solved compared to
an increase in the number of platforms. From this, we
can infer that larger track segments can likely still be
managed as long as the number of trains does not in-
crease excessively. If the number of trains increases
significantly, it may be possible to divide them into
separate problems, first finding a solution for the first
20 trains, then for the next 20, and so on. This ap-
proach cannot guarantee a globally optimal solution;
however, we believe that the solution quality will still
be superior to that achieved through manual planning.
6 CONCLUSION AND FUTURE
WORK
We presented the Deutsche Bahn planning problem
for the digitization and placement of digital signals.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
110

To address this, we developed a custom constraint
model, discussed and performed improvements (par-
allelization, model transformations, search strategies,
and objective functions) to make the model applica-
ble to real-world problems. It was demonstrated that
the approach works for generated (hypothetical) prob-
lems with up to 20 trains and 20 platforms.
Future work includes expanding the scenario to
incorporate additional components and various direc-
tions, as well as the consideration of real station sce-
narios. Furthermore, additional model optimizations
will be undertaken to enhance solution speed and,
consequently, solution quality within limited time
frames. Finally, it is essential to have the computed
solutions evaluated by railway experts.
REFERENCES
Akg
¨
un,
¨
O., Gent, I. P., Jefferson, C., Miguel, I., Nightin-
gale, P., and Salamon, A. Z. (2018). Automatic dis-
covery and exploitation of promising subproblems for
tabulation. In Principles and Practice of Constraint
Programming - 24th International Conference, CP
2018, Lille, France, August 27-31, 2018, Proceedings,
pages 3–12.
Akhand, M. A. H., Ayon, S. I., Shahriyar, S. A., Siddique,
N. H., and Adeli, H. (2020). Discrete spider monkey
optimization for travelling salesman problem. Appl.
Soft Comput., 86.
Apt, K. (2003). Constraint satisfaction problems: exam-
ples. Cambridge University Press. Principles of Con-
straint Programming: chapter 2.
Billionnet, A. (2003). Using integer programming to
solve the train-platforming problem. Transp. Sci.,
37(2):213–222.
Boussemart, F., Hemery, F., Lecoutre, C., and Sais, L.
(2004). Boosting systematic search by weighting con-
straints. In Proceedings of the 16th Eureopean Con-
ference on Artificial Intelligence, ECAI’2004, includ-
ing Prestigious Applicants of Intelligent Systems, PAIS
2004, Valencia, Spain, August 22-27, pages 146–150.
Caimi, G., Fuchsberger, M., Laumanns, M., and L
¨
uthi,
M. (2012). A model predictive control approach for
discrete-time rescheduling in complex central railway
station areas. Comput. Oper. Res., 39(11):2578–2593.
Caprara, A., Galli, L., and Toth, P. (2011). Solution of the
train platforming problem. Transp. Sci., 45(2):246–
257.
Carey, M. and Carville, S. (2000). Testing schedule perfor-
mance and reliability for train stations. J. Oper. Res.
Soc., 51(6):666–682.
Carey, M. and Carville, S. (2003). Scheduling and platform-
ing trains at busy complex stations. Transportation
Research Part A: Policy and Practice, 37(3):195–224.
Carey, M. and Crawford, I. (2007). Scheduling trains on a
network of busy complex stations. Transportation Re-
search Part B: Methodological, 41(2):159–178. Ad-
vanced Modelling of Train Operations in Stations and
Networks.
Dechter, R. (2003). Constraint networks. pages 25–49.
Elsevier Morgan Kaufmann. Constraint processing:
chapter 2.
Freling, R., Lentink, R. M., Kroon, L. G., and Huisman, D.
(2005). Shunting of passenger train units in a railway
station. Transp. Sci., 39(2):261–272.
Hossain, S. I., Akhand, M. A. H., Shuvo, M. I. R., Siddique,
N. H., and Adeli, H. (2019). Optimization of univer-
sity course scheduling problem using particle swarm
optimization with selective search. Expert Syst. Appl.,
127:9–24.
Kang, L., Lu, Z., and Meng, Q. (2019). Stochastic sched-
ule–based optimization model for track allocations in
large railway stations. Transportation Engineering,
Part A: Systems, 145(3).
Liu, S. Q. and Kozan, E. (2009). Scheduling trains as a
blocking parallel-machine job shop scheduling prob-
lem. Comput. Oper. Res., 36(10):2840–2852.
L
¨
offler, S. (2022). Optimierung und Regularisierung von
Constraint Satisfaction-Problemen (CSPs). PhD the-
sis, Brandenburg University of Technology, Cottbus,
Germany.
L
¨
offler, S., Becker, I., and Hofstedt, P. (2024). Enhancing
constraint optimization problems with greedy search
and clustering: A focus on the traveling salesman
problem. In Rocha, A. P., Steels, L., and van den
Herik, H. J., editors, Proceedings of the 16th Inter-
national Conference on Agents and Artificial Intelli-
gence, ICAART 2024, Volume 3, Rome, Italy, Febru-
ary 24-26, 2024, pages 1170–1178. SCITEPRESS.
L
¨
offler, S., Becker, I., Kroll, F., and Hofstedt, P. (2021).
A survey of constraint transformation methods. In
51. Jahrestagung der Gesellschaft f
¨
ur Informatik, IN-
FORMATIK 2021 - Computer Science & Sustain-
ability, Berlin, Germany, 27. September - 1. Okto-
ber, 2021, volume P-314 of LNI, pages 1107–1120.
Gesellschaft f
¨
ur Informatik, Bonn.
Marriott, K. and Stuckey, P. J. (1998). Programming with
Constraints - An Introduction. MIT Press, Cambridge.
Mu, S. and Dessouky, M. (2011). Scheduling freight trains
traveling on complex networks. Transportation Re-
search Part B: Methodological, 45(7):1103–1123.
Prud’homme, C., Fages, J.-G., and Lorca, X. (2017). Choco
documentation.
Qi, J., Yang, L., Gao, Y., Li, S., and Gao, Z. (2016). In-
tegrated multi-track station layout design and train
scheduling models on railway corridors. Transporta-
tion Research Part C: Emerging Technologies, 69:91–
119.
R
´
egin, J. and Malapert, A. (2018). Parallel constraint pro-
gramming. In Hamadi, Y. and Sais, L., editors, Hand-
book of Parallel Constraint Reasoning, pages 337–
379. Springer.
R
´
egin, J., Rezgui, M., and Malapert, A. (2013). Embarrass-
ingly parallel search. In Principles and Practice of
Constraint Programming - 19th International Confer-
ence, CP 2013, Uppsala, Sweden, September 16-20,
2013. Proceedings, pages 596–610.
Automatic Placement of Digital Signals in Railway Digitalization: A Constraint Approach
111

Rodriguez, J. (2007). A constraint programming model for
real-time train scheduling at junctions. Transporta-
tion Research Part B: Methodological, 41(2):231–
245. Advanced Modelling of Train Operations in Sta-
tions and Networks.
Siddique, N. H. and Adeli, H. (2014). Water drop algo-
rithms. Int. J. Artif. Intell. Tools, 23(6).
Yue, Y., Zhou, L., Sun, Q., and Yue, Q. (2006). An ant
algorithm for the reception-departure line assignment
problem. International Conference on Mechatronics
and Automation, pages 2284–2289.
Zhang, Q., Zhu, X., and Wang, L. (2019). Track alloca-
tion optimization in multi-direction high-speed rail-
way stations. Symmetry, 11(4):459.
Zhong, M., Yue, Y., Zhou, L., and Zhu, J. (2024). Paral-
lel optimization method of train scheduling and shunt-
ing at complex high-speed railway stations. Comput.
Aided Civ. Infrastructure Eng., 39(5):731–755.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
112