A Hybrid Constraint- and Search-Based Approach on the Stockyard

Planning Problem

Sonja Breuß, Sven L

ofﬂer and Petra Hofstedt

Chair of Programming Languages and Compiler Construction, Brandenburg University of Technology

Cottbus-Senftenberg, Konrad-Wachsmann-Allee 5, Cottbus, Germany

{s.breuss, sven.loefﬂer, hofstedt}@b-tu.de

Keywords:

Planning and Scheduling, Decision Support Systems, Stockyard Planning Problem, SPP, Constraint

Programming, CSP, COP.

Abstract:

The stockyard planning problem (SPP) is a critical task in the global economy, involving the efﬁcient trans-

portation and storage of bulk materials such as iron ore or coal. At material turnover points such as harbors,

the SPP optimizes when, where and which materials are unloaded from import vessels (imported), moved

between areas on the stockyard (transported), loaded onto export vessels (exported) and mixed with other ma-

terials (blended). This is important for reducing mooring times of ships and meeting timely demands. The

current approach to solving the SPP in real systems is manual, which is stressful and error-prone. This paper

proposes a hybrid approach using both constraint programming and greedy search algorithms to solve the SPP.

The proposed method splits the planning process into smaller problems, alleviating computational issues while

maintaining overall solution quality.

1 INTRODUCTION

In the global economy, during the process of produc-

ing and distributing goods, material has to be trans-

ported all over the world. Bulk materials such as

iron ore or coal, delivered by large overseas ships,

must be prepared for further transportation on smaller

ships for inland water at large ports by means of so-

called stockpiles, where the materials are stored and

blended together. The stockyard planning problem

(SPP) deals with the task of how to do so in a time

efﬁcient manner, as to reduce mooring times of ships

and to fulﬁll timely demands. In the present, the SPP

is solved by human workers who are subject to high

levels of stress due to the complexity of the task and

the pressure to not cause errors. Our aim is to develop

a tool to aid the workers in planning and to relieve

stress as well as reduce human error.

Our industrial partner ABB - Sales Minerals and

Mining, Engineering Sub-station and Power Genera-

tion, Service Metals branch ofﬁce Cottbus implements

and operates stockpile monitoring and management

systems all over the world. Supporting their customer

companies, such as ports, in the scheduling process,

is a part of their work. In this, they have recognized

signiﬁcant potential for optimization in the schedul-

ing process.

In (L

ofﬂer et al., 2023) we have presented an ap-

proach to solve the SPP using a constraint-based ap-

proach. While we have already obtained good results

with a constraint system that plans ahead for a few

hours, planning further ahead poses some additional

problems. The constraint system may grow up to a

point where results are not computed in an appropri-

ate time frame or the available computation power

is not sufﬁcient to compute a result at all. Splitting

the planning process into multiple smaller problems

solves the computation issues, but presents the issue

of ﬁnding a good overall solution using the greedy

partial solutions. In this paper, we present a hy-

brid approach using both constraint-programming and

greedy search.

The paper follows the structure: In Section 2,

we introduce the SPP in general as well as speci-

ﬁed for our setup. In Section 3, we discuss basics of

constraint programming as well as search algorithms.

Section 4 gives an overview on related work. In Sec-

tion 5, we discuss our greedy approach for solving the

SPP using constraint programming. In Section 6, we

discuss the results. Finally, our work is concluded and

possible future research options are pointed out.

Breuß, S., Löfﬂer, S. and Hofstedt, P.

A Hybrid Constraint- and Search-Based Approach on the Stockyard Planning Problem.

DOI: 10.5220/0012995000003822

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 113-125

ISBN: 978-989-758-717-7; ISSN: 2184-2809

113

2 THE STOCKYARD PLANNING

PROBLEM

In this section we introduce and explain the Stockyard

Planning Problem (SPP) with its workings and com-

ponents. We ﬁrst discuss the general structure of the

SPP and later get into speciﬁcs for our scenario.

2.1 General Characteristics of the SPP

A stockyard system typically includes import vehi-

cles I = {I

, I

, . . . }, each consisting of a sequence of

weight and material speciﬁcations. These sequences

indicate the order in which speciﬁc weights of ma-

terials must be unloaded from the import ship. The

stockyard itself is divided into different stockpiles

H = {H

, H

, . . . , H

}, which are further subdivided

into various areas H

= {h

i, j

} with a certain capac-

ity c

i, j

. In addition, there are export vehicles E =

, E

, . . . }, which, similar to the import vehicles,

contain a sequence list specifying the order of the ex-

port actions and how much of each material must be

loaded onto the respective ship. These components

are connected through a conveyor belt network, while

adding to and removing material from stockpiles or

vehicles is done by several transport vehicles T . A

transport vehicle can either add material to a stock-

pile (stacker), remove material from a stockpile (re-

claimer), or can do both (stacker-reclaimer) at differ-

ent times.

In any moment, each area of the stockyard sys-

tem (i.e. import ship, stockpile area, export ship) has

a certain amount of material on it or it is empty. A

snapshot of the system at any point in time contains

the mass and material type for each area. We call this

a stockyard state. A tabular view of a stockyard state

is depicted in Figure 1 in state q

and state q

i+1

Possible actions include unloading import vehi-

cles to stockpile areas (import actions), transporting

material from a stockpile area to another as needed

(transport actions), blending together materials of dif-

ferent quality to obtain material of a desired qual-

ity (blending actions), and exporting needed material

from stockpile areas to the export vehicles (export ac-

tions). Each action has a route, speciﬁc source and

destination areas, as well as the mass and material

that is moved. The goal of the SPP is to compute a se-

quence of actions to load and unload vehicles as time-

efﬁcient and (optionally) resource-efﬁcient as possi-

ble, according to given loading and unloading plans.

The plans pre-deﬁne the order in which import and

export vehicles need to be unloaded and loaded. It is

possible to execute multiple actions in parallel, which

poses the additional problem of ensuring that parallel

actions do not share the same resources like transport

vehicles or conveyor belts, as these resources are ex-

clusive. Parallel actions using the same resources are

forbidden.

For each type of action, we can deﬁne speciﬁc

routes as sequences of vehicles and conveyor belts,

e.g. for import actions we have sequences: Import ve-

hicle (ship unloader) - path of conveyor belts - trans-

port vehicle (stacker). Let route

be the set of im-

port routes, route

the set of transport routes, route

the set of export routes, and route

the set of blend-

ing routes. We can think of a single blending route

as three combined sub-routes B1, B2 and B3, where

the destinations of B1 and B2 are equal to the source

of B3 but otherwise each have exclusive resources so

that: B1 and B2 start at distinct source vehicles, then

each have a path of conveyor belts that both end at a

speciﬁc belt b

. Sub-route B3 starts at belt b

and then

has a path of conveyor belts ending at a destination

vehicle.

A step move is a combination of import, transport,

blending, and export actions for each type that do not

hinder each other, i.e. that are not using the same re-

sources and vehicles with no vehicles blocking each

other. A general schema for a step move is shown

in Figure 1. Transport vehicles can block each other

by working on the same stockpile area or by having

its counter-weight hang into an area where another

vehicle works or has its counter-weight. Two vehi-

cles could work next to adjacent conveyor belts and

may be unable to pass each other, which has to be ac-

counted for.

Each conveyor belt and each vehicle can be used

for at most one action at a time, so usage has to be

exclusive. We call the resulting stockyard state of a

step move a step solution.

To solve the SPP, we need to ﬁnd a sequence of

step moves beginning from the initial conﬁguration

that results in the desired ﬁnal conﬁguration of the

stockyard. An example is given in Section 2.3.

2.2 Introducing Our Scenario

The speciﬁc stockyard system that we implemented is

shown in Figure 2. In our system, we deal with three

types of material, Q1, Q2 and Q3, the latter can be

blended i.e. mixed together from Q1 and Q2. While

there can be multiple import ships as well as multiple

export ships, only one of each are depicted, as only

one ship can be unloaded resp. loaded at the same

time. Each import ship and export ship can have mul-

tiple hatches (areas), which need to be unloaded resp.

loaded in order. In the image, the import ship has

hatches loaded with materials Q1 and Q2, then more

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

114

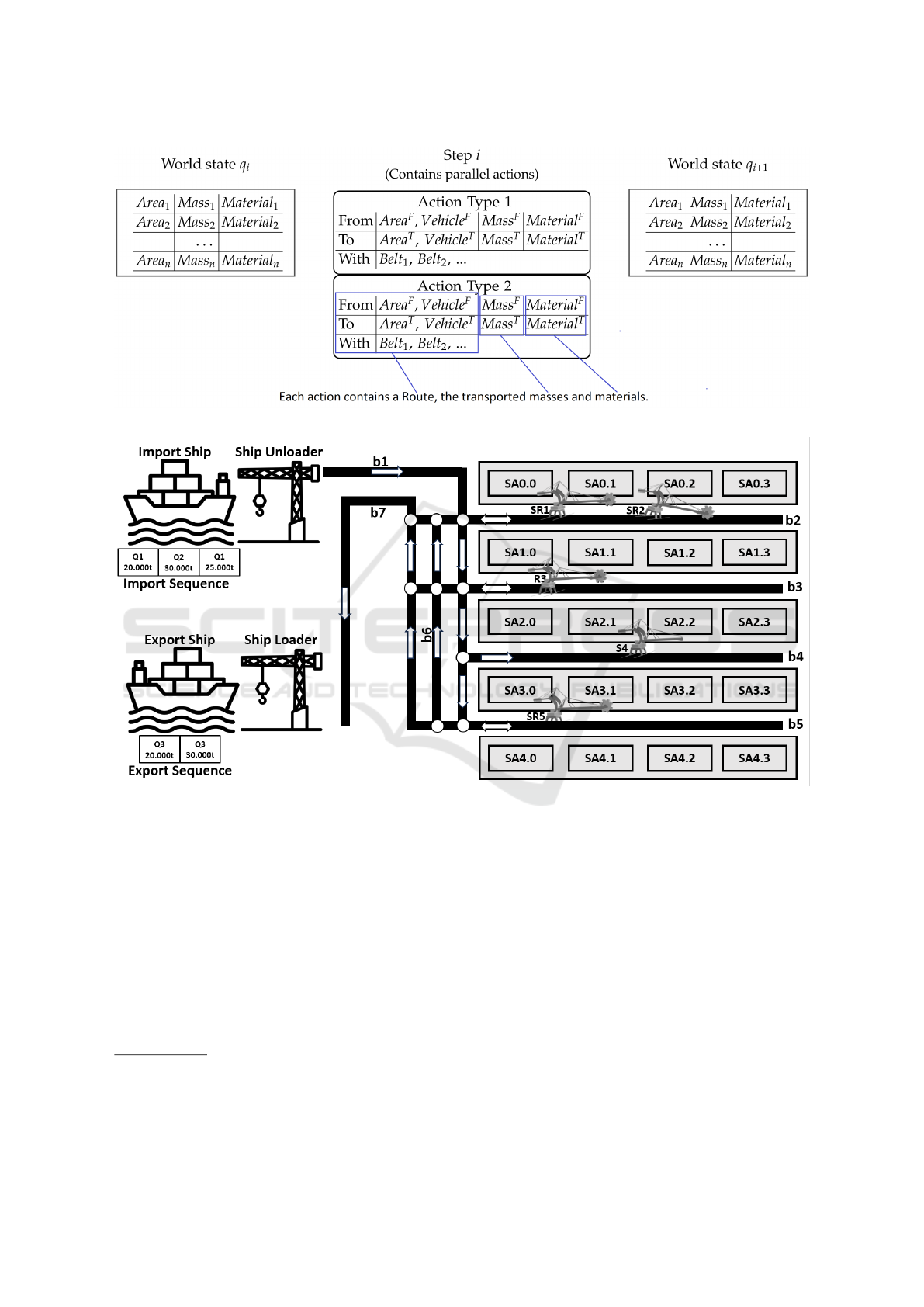
Figure 1: General structure of a step move.

Figure 2: Our SPP Scenario.

Q1. The export ship needs to be loaded with material

Q3, which needs to be blended from materials Q1 and

Q2.

The stockyard consists of ﬁve stockpiles SA0 to

SA4, each possessing four areas. Each stockpile area

can hold a certain amount of material.

In Figure 2,

all stockpiles and stockpile areas have the same size.

In reality, this is usually not the case.

The stockpiles are connected through a conveyor

belt network. Belts b1, b6 and b7 have only one di-

rection, whereas belts b2 to b5 can move in both di-

rections. The white circles are connection points be-

In the implementations this is depicted as a tuple (mass

in tons, material)

To protect the data of our partner ABB, the materials

and stockpile sizes used in this paper differ from reality.

tween the belts to let material switch belts.

There are machines sitting on conveyor belts b2 to

b5 which are able to move material from the belts to

the stockpile areas or vice versa. The different ma-

chines have different capabilities, machines SR1, SR2

and SR5 are able to add and remove from stockpile ar-

eas (stacker/reclaimer), R3 is able to remove material

(reclaimer) and S4 is able to add material (stacker).

In Figure 2 the two machines SR1 and SR2 appear

to be working on the same conveyor belt b2 which is

practically impossible, as each machine needs its own

belt. In reality, belt b2 are two side-by-side conveyor

belts b2a and b2b that are treated as one belt. The

two machines are unable to pass each other, result-

ing in SR1 being able to work on areas 0, 1, and 2 of

stockpiles SA0 and SA1, with SR2 being able to work

A Hybrid Constraint- and Search-Based Approach on the Stockyard Planning Problem

115

on areas 1,2, and 3. The machines are able to work in

parallel, as long as their positions don’t hinder each

other, i.e. as long as SR2 is on the right of SR1.

In our scenario, at most one action of each ac-

tion type can be executed at once. Given this, for

each step move, there are (|route

| + 1) · (|route

| +

1) · (|route

| + 1) · (|route

| + 1) many possible route

combinations where route

, route

are the sets of import, export, transport and blending

routes respectively. The added route for each factor

being no action of that type happening. This number

is a gross maximum for the number of parallel routes,

as there may be routes that are impossible to be used

in parallel. At the same time, this number vastly un-

derestimates the number of possible action combina-

tions. For each route, there is a large number of pos-

sible actions stemming from multiple stockpile areas

being sources or destinations for a route, as well as a

substantial number of possible masses being used.

In our system, almost each stockyard vehicle can

work on 8 stockpile areas. Almost every area can be

serviced by 2 vehicles. For simpliﬁcation purposes,

we assume that these numbers hold for every area and

vehicle. An import action has 21 possible destination

areas with 20 on the stockyard and 1 on the export.

With 2 possibilities to access every area, there are 42

different ways for import actions alone. Export ac-

tions have a number of possibilities analog to import

actions, just in reverse. Transport actions have 20 pos-

sible source areas, 19 destination areas, each serviced

by 2 vehicles, resulting in 20 · 19 · 2 · 2 possibilities.

Blending actions with 2 source and 1 destination areas

are more complicated with 20 ·19·18 ·2 ·2 ·2 options,

of which many are impossible due to vehicle restric-

tions. Any step move consisting of 0 or 1 of each

action types has a great number of possibilities since

every number has to be multiplied, even under exclu-

sion of concurrent parallel actions. On top of that,

different masses can be moved, which again increases

the number of possible actions. Thus the problem size

for a single step move is massive at a magnitude of

options. We will be looking at some conditions

in our system that cause actions and parallel actions

to be impossible.

The layout of the conveyor belt network makes

some actions and combinations impossible. For in-

stance, it is impossible to remove anything from

stockpiles SA2 and SA3 via belt b4, as it only has

a stacker which can add material to stockpile areas.

Usage of conveyor belts has to be exclusive for each

action. When ensuring this, action combinations may

get impossible, such as an export from SA2.0 via belts

b3-b1-b5-b7, while a transport happens from SA4.1

to SA0.3 via belts b5-b6-b2. The belt b5 is used for

both of these actions and thus, their combination is

impossible. Machines need to be spaced apart prop-

erly. This means that any two machines are not able

to work on the same stockpile area, e.g. SR1 and R3

cannot both work on SA1.1. Further, for belt b2,

the machines SR1 and SR2 cannot work in the same

spot. SR1 always has to be on the left of SR2, as

the machines cannot pass each other. In order to not

fall over, each machine possesses a counter-weight.

These counter-weights when working on a stockpile

reach onto the opposite stockpile, e.g. if R3 is work-

ing on SA1.1, then its counter-weight is hanging into

area SA2.1. If there is a counter-weight in an area,

there cannot be any machine working on that stock-

pile or having its counter-weight in the same area. For

the given example, this means that S4 cannot work on

SA2.1 nor on SA3.1.

2.3 Example Action on Our Stockyard

Let us look at some possible example action combi-

nations, i.e. step moves, for our scenario from Figure

2, which are depicted in Figure 3. For understand-

ing purposes, we simplify the problem and only look

at the ﬁrst spots in the import and export sequences.

The ﬁgure shows three states of the stockyard, the ini-

tial state q

on the left, a step state q

in the middle,

and the ﬁnal state q

on the right. Some of the empty

stockyard areas are omitted in this ﬁgure. In between

the stockyard states, step moves with three (resp. two)

actions are depicted, each with source and destina-

tion vehicles and mass and material that are moved,

as well as the belts used. Import actions have a yel-

low background, blending actions have a green back-

ground, and export actions have a red background.

In the initial state, there is 20,000t of material Q1

on the import ship. On the stockyard, the following

stockpile areas have material: SA0.0 has 10,000t of

Q3 that was blended from Q1 and Q2 in previous

steps, SA2.2 has 8,000t of material Q2, SA3.3 has

12,000t of Q1. The export ship and all other stock-

pile areas are empty.

The goal is to have 20,000t of Q3 on the export

ship at the end of the solution process.

In the ﬁrst step (see Figure 3), the following ac-

tions are executed in parallel: Importing 8,000t of Q1

to SA3.0 via belts b1 and b4 and machine S4. Blend-

ing 8,000t of Q1 from SA3.3 and 4,000t Q2 from

SA2.2 to make 12,000t of Q3 and put it on SA0.3,

with SR5 putting Q1 on belt b5 which is then trans-

ported on belt b6, Q2 is put on b3 by R3 and also

transported to belt b6. Belt b6 functions as a blend-

ing belt here. The blended material is then put on belt

b2a and moved to SA0.3 by SR2. Exporting 8,000t of

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

116

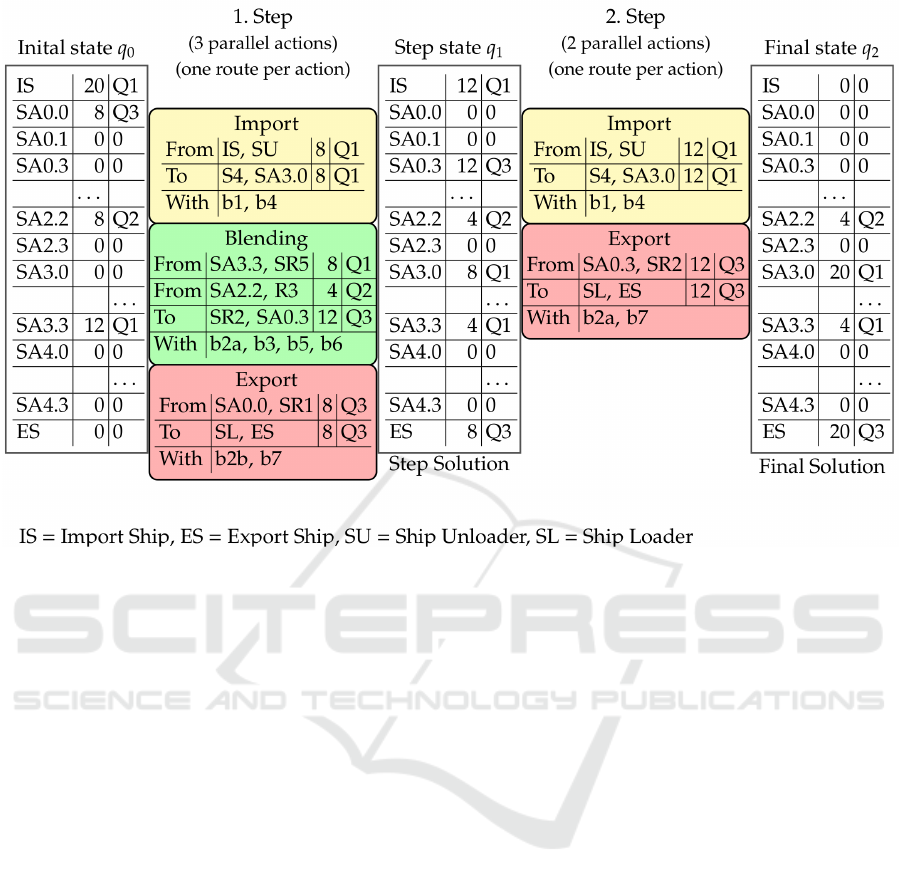
Figure 3: An example action on our SPP scenario.

Q3 from SA0.0 by using belt b2b that is connected to

SR1, and then transported over b7 to the export ship.

After these actions, the stockyard looks as fol-

lows: On the import ship, there is 12,000t of material

Q1. On the stockyard, we have 2,000t of Q3 on SA0.0,

12,000t of Q3 on SA0.3, 4,000t of Q2 on SA2.2, 8,000t

of material Q1 on SA3.0, 4,000t of Q1 on SA3.3, and

all other stockpile areas being empty. The export ship

has 8,000t of Q3, and thus only 12,000t more of ma-

terial Q3 are needed.

In the second step, the remaining 12,000t of mate-

rial Q1 are imported from the import ship, emptying

this slot in the import sequence. From SA0.3, 12,000t

of material Q3 are exported, which fulﬁlls the export

goal and the solution process ends.

3 PRELIMINARIES

In this section, the basics of constraint programming

are introduced, and trees and tree search algorithm

principles are discussed.

3.1 Basics of Constraint Programming

Constraint Programming (CP) is a powerful concept

to solve problems with incomplete information that

are often NP-complete or even NP-hard. The CP

user formulates requirements for variables and rela-

tions in a declarative manner, which then get solved

by a constraint solver in a sort of ”black box”. In

this paper, we look at Finite Domain Constraints (FD-

Constraints).

A constraint satisfaction problem (CSP) is de-

ﬁned as a 3-tuple P = (X, D, C) (Marriott and Stuckey,

1998).

For a set of variables X = {x

, x

, ·· · , x

} we de-

ﬁne domains D = {D

, D

, ·· · , D

} where D

is the

domain of x

. Note that the domains are ﬁnite sets.

Let C = {c

, c

, ·· · , c

} be a set of constraints,

each over a subset X

′

of variables of X.

A constraint c is a tuple (X

′

, R), with R being a

relation over X

′

Solving a CSP yields a solution where all vari-

ables x

are instantiated with a value d

of domain

such that all constraints are satisﬁed (Marriott

and Stuckey, 1998). Examples of constraints are

({A, B}, A ⇐⇒ B) or ({x, y, z}, x − y ≥ z). For the

rest of the paper, we will refer to constraints only by

their relations.

CSPs can be used for optimization, by extending

a CSP with an optimization function f which assigns

a numerical value x

opt

to each found solution of the

CSP. This value is maximized or minimized. This is

called a constraint optimization problem (COP), de-

ﬁned as a 4-tuple P = (X , D, C, f ) (Dechter, 2003).

A Hybrid Constraint- and Search-Based Approach on the Stockyard Planning Problem

117

The following COP 1 is an example for a COP,

which describes the problem of ﬁnding a rectan-

gle with sides a and b with only integer val-

ues {1, 2, 3, 4, 5} (e.g. in cm) for a and b, such

that the area A is maximum while at the same

time the perimeter P must not be greater than 15.

COP 1 = (X, D, C, f ) with X = {a, b, A, P}, D =

= D

= {1, 2, 3, 4, 5}, D

= {1, 2, ..., 25}, D

{1, 2, ..., 15}}, the Constraints C = {(a ∗ b = A), (2 ∗

a + 2 ∗ b ≤ P)} and the optimization function f = A.

It aims to maximize the area. An optimal solution of

this COP is a = 4, b = 3, A = 12, and P = 14.

When solving FD-CSPs, the solver has two gen-

eral types of actions. Creating elemental consistency

between the constraints, and doing a backtracking

depth based search (Apt, 2003; Dechter, 2003; Mar-

riott and Stuckey, 1998). During the search part, in-

dividual variables are instantiated to a value in their

domain (backtracking depth search) and the rest of

the domains restricted according to the affected con-

straints (creating consistency). This process is con-

tinued until either a solution is found or the CSP can’t

be solved with an instantiated variable. In the latter

case, backtracking is performed, which means that

the last variable assignment for a variable x

is un-

done, the corresponding value d

is removed from the

domain D

, and the search continues with a different

assignment d

∈ D

for the variable x

. More informa-

tion about constraints and constraint solving methods

can be found in (Marriott and Stuckey, 1998; Dechter,

2003; Apt, 2003).

3.2 Search Algorithms on Trees

Search problems can be depicted as directional

graphs. A set of vertices v ∈ V and a set of edges e ∈

E, where each edge is a tuple of vertices e = (v1, v2)

make up the tuple T = (V, E) that is a graph (Diestel,

2017). For the representation of the behaviour of a

search algorithm, we use trees (i.e. undirected, acyclic

graphs). The nodes of these graphs or trees represent

states or conﬁguration, the edges stand for state tran-

sitions or search steps. Such trees are called search

trees or decision trees. Let v0 ∈ V be the root of a

tree, i.e. the initial conﬁguration of a system. Further

let depth(v) denote the distance of a node v to v0,

where every edge corresponds to an additional dis-

tance of 1 with the overall distance being the num-

ber of edges on the shortest path from v to v0, where

depth(v0) = 0.

For our application of the stockyard planning

problem, a node will represent the state of the system,

an edge from node v

to v

i+1

stands for a step move

from state v

to successor state v

i+i

(or step solution,

resp.). All nodes with distance k are system states

after k step moves. A node v ̸= v0 without succes-

sor nodes is called a leaf. Leaves are either solutions

to the search problem or dead ends. Dead ends arise

from there being no more possible solution step (or

the depth having reached a previously set maximum).

A characteristic that many search algorithms share

is greediness. In any greedy algorithm, for each state,

the next step is chosen according to what is seen as

best at that speciﬁc point. There is no look-ahead

to compute the best solution for what might come

or look-back to change past partial solutions. Some

widely known greedy algorithms are Dijkstra’s short-

est path algorithm for positively weighed graphs (Di-

jkstra, 1959) or Kruskal (Kruskal, 1956) and Prim’s

algorithms (Prim, 1957) for minimal spanning trees.

Greedy algorithms are not able to ﬁnd a globally op-

timal solution for every problem, but they ﬁnd locally

optimal solutions in a reasonable amount of time,

which often approximate the global solution well.

This makes them especially well-suited for runtime-

sensitive optimization problems (Cormen et al., 2009,

Chapter 16).

If the aim is to traverse an entire graph or tree

systematically, some of the most well-known algo-

rithms are Depth-First-Search (DFS) and Breadth-

First-Search (BFS) (Cormen et al., 2009). Both algo-

rithms aim to visit every node of a graph starting from

a starting node v

. The former algorithm explores a

graph in-depth, meaning that for each node, one un-

known adjacent node is chosen from which the search

is continued. If a node doesn’t have any unknown ad-

jacent nodes, the algorithm will backtrack to continue

the search. For BFS, all adjacent nodes of a node are

saved and visited in order of discovery. When using

BFS on trees starting with a root v

, nodes are visited

in order of increasing depth ﬁrst.

For graphs of unknown, possibly inﬁnite depths d,

DFS is not complete and not optimal. For big graphs,

BFS needs a massive amount of storage b

where b

is the breadth. Thus, for bigger problems, a greedy

approach is favorable.

4 RELATED WORK

In this section we discuss related approaches to solv-

ing the SPP, as well as the usage of Monte Carlo Tree

Search for our approach.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

118

4.1 Related Approaches to Solving the

SPP

The relevance of the SPP in the real world has resulted

in a variety of research, each focusing on different as-

pects of the problem. These aspects include but are

not limited to: Train and ship scheduling to and from

the stockyard, resource management on the stockyard,

management of machine movements, ensuring avail-

ability of blended materials on the stockyard, routing

constraints on the stockyard.

The paper (Abdekhodaee et al., 2004) presents an

approach focused on train scheduling from mines, us-

ing greedy heuristics for different parts of the prob-

lem. Junior, Rocha and Salles (Junior et al., 2020)

regard stockyards connected to coal mines. The focus

lays on distributing material efﬁciently on the stock-

yard as well as train scheduling. Blending of materi-

als and conveyor belt concurrency are not touched on.

In (Babu et al., 2015), the aim is to improve stockyard

efﬁciency and reduce delays, by optimizing ship and

train scheduling and stockyard planning, using greedy

heuristic-based algorithms. Special attention is given

to reducing idle times and delays of ships and trains,

not so much on distribution of goods on stockpiles.

Blending of materials, conveyor belt concurrency and

different types of machines are not regarded. Xie,

Neumann and Neumann (Xie et al., 2021) discuss the

Stockpile Blending Problem (SBP) which addresses

the challenge of producing material of speciﬁc qual-

ity from material of different qualities. The available

source material qualities are not certain, as in min-

ing, one cannot determine deﬁnitely in advance which

qualities of material are mined. The SBP deals with

possibilities and calculating different mixing ratios to

achieve a deﬁnitive goal. This is different from our

problem as our materials and mixing ratios are set in

advance. The SBP does not touch on machine move-

ments nor routing constraints.

None of the given research shares the combination

of aspects present in our stockyard system, thus in

ofﬂer et al., 2023) we designed a COP ﬁt to our re-

quirements for the ﬁrst time, but solved it using com-

plete constraint-based search.

4.2 Monte Carlo Tree Search

Monte Carlo Tree Search (MCTS) is an algorithm

that combines classic tree search with reinforcement

learning (Metropolis and Ulam, 1949; Winands et al.,

2008). It is often used for simulating games, espe-

cially for bigger search trees where minimax search

(Russell and Norvig, 2020, pp.149-150) can be un-

feasible.

For each search depth, a number of options are ex-

plored and given a success value. The success value

is determined by simulating the action from the op-

tion and afterwards a number of random steps, un-

til either a ﬁnal solution or dead end is reached or a

certain number of steps is exceeded. Each of these

resolutions possesses a value which then gets back-

propagated up to the root of the existing search tree,

adjusting the success value of all steps that were used.

This approach is done for each explored option on a

depth. The most promising option is then chosen as

the next step and the next depth is explored.

While this approach is promising to ﬁnd a good

solution, it is very time-consuming when applied to

our problem setup. The search tree that is often given

for MCTS does not exist in our case, so we have to

construct it ourselves. If a full search tree was con-

structed, there would be a massive number of options

(around 10

) for every solution step, as discussed in

Section 2.2. This is an unfeasible amount of possibil-

ities to compute in a reasonable time. The run-time to

ﬁnd a satisfying number of random solutions to calcu-

late a score for each option would grow to infeasible

lengths quickly, which defeats the purpose of ﬁnding

a solution in a short amount of time. Doing random

simulations once per possible step move would still

have a high run-time, as there is a big number of them

(see Section 2.2). As our system is highly depen-

dent on given import, stockpile, and export contents

as well as the desired outcome, MCTS cannot be done

preemptively for a number of conﬁgurations to reduce

the run-time during active usage.

5 A CONSTRAINT-BASED

GREEDY SEARCH APPROACH

FOR THE SPP

Computing a schedule to solve the SPP for a short

planning period is discussed in (L

ofﬂer et al., 2023)

using a pure Constraint Programming (CP) approach.

In contrast, now we try to compute longer schedules

(more steps) through optimizing one or a few steps

at a time (while besides following the same general

approach).

In Section 5.1 we discuss the necessary, general

changes to make the COP ﬁt our new greedy step-by-

step approach. The design of a score function used

for greedy choice is discussed in Section 5.2. In Sec-

tion 5.3 we introduce Random Restart DFS as our ap-

proach to ﬁnd a good solution to the SPP.

A Hybrid Constraint- and Search-Based Approach on the Stockyard Planning Problem

119

5.1 Remodeling the COP

When planning for longer time intervals using a pure

CP-approach, computation time grows to unfeasible

lengths or it becomes impossible to compute any re-

sult with the available hardware. To account for this

problem, we can divide the SPP into smaller prob-

lems and use a greedy approach, planning one step

or a small number of steps at a time. Each solution

step has the result of the previous step as the input,

and we solve until a ﬁnal conﬁguration (global solu-

tion) is reached or a pre-calculated number of solution

steps is exceeded. This lowers overall computation

time as each problem gets solved faster. For an even

lower computation time, we use a parallel portfolio

approach that does parallel runs on the same input but

with different search strategies and returns multiple

step solutions. This increases the solving speed as

the different models share their calculated score val-

ues with each other which results in a faster domain

reduction. For the next step, the best found step solu-

tion is chosen.

The constraint model has a multitude of variables

for different parts of the stockyard, and constraints

that ensure system consistency. For each import ship

there are variables representing material and mass

for each area on the ship, the same variables exist

for every stockpile and every export ship. For ev-

ery stockyard vehicle, the possible working positions

are stored in a variable. To be able to execute step

moves, there are multiple variables that store possible

sources, destinations, masses and materials for every

action type. Across these variables, constraints are

placed to forbid the parallel execution of actions that

hinder each other or are impossible with the given ma-

terials and masses, as well as to keep the system con-

sistent. E.g. in our scenario from Figure 2 if a mass x

is removed from stockpile area SA0.1 and placed on

stockpile area SA4.0, the resulting mass of SA0.1 has

to be the previous mass minus x, for SA4.0 it has to be

the old mass of SA4.0 plus x.

In (L

ofﬂer et al., 2023) we solved the SPP in one

step, i.e. the search for the entire action sequence from

the start conﬁguration to the ﬁnal conﬁguration was

computed at once and with the aim of a global op-

timal solution. When the problem is divided into a

sequence of smaller steps, the time intervals need to

be divided as well. As different actions may take dif-

ferent amounts of time and multiple actions begin or

ﬁnish at different times, dividing time intervals is not

straight-forward.

In the previous pure-CP approach, the optimiza-

tion variable for the COP was the time which was

minimized. When looking at the problem as a se-

quence of time steps, it is not as easy to minimize the

time, as that would require looking back to and alter-

ing previous step solutions or planning ahead multiple

steps, which would defeat the step-by-step approach

entirely and result in a much higher runtime. In Sec-

tion 5.2 we thus design a score function to rate system

states in relation to the goal system state. This score

function is maximized during the solution process of

the COP, its maximal value is reached when the goal

system state is reached. The closer a given system

state is to the goal system state, the higher the score.

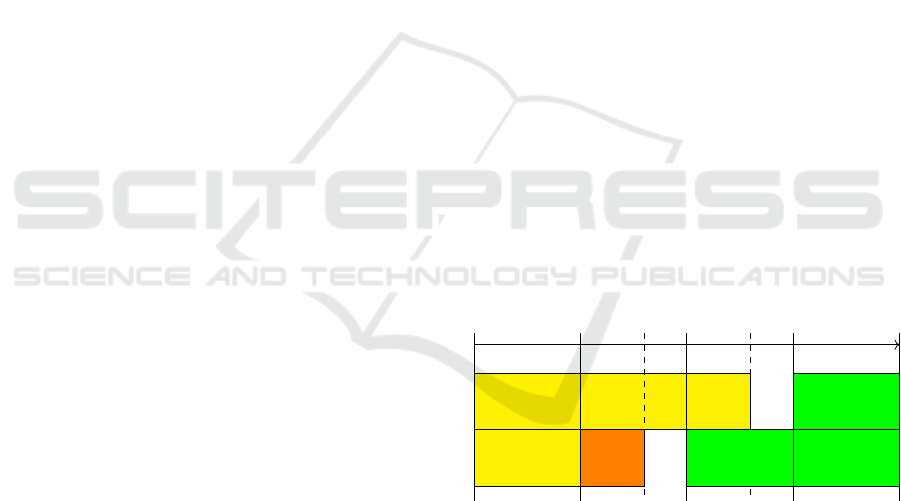
Taking into account this property, it is not use-

ful to assign dynamic time blocks as before. The

time blocks would be maxed out to result in the high-

est possible score, resulting in quasi-uniform time

blocks. We opted to omit this calculation and instead

set all time blocks to a static but freely selectable uni-

form length, as illustrated in Figure 4. These blocks

function as time frames for each solution step. This

means that all actions have to be complete when a

block is ﬁnished. Any actions with longer duration

than a block allows are implemented as repeated sin-

gular actions occurring over consecutive blocks of

time. Upper bounds for the maximum amount of

moved material during one time block are restricted

through speed limitations of vehicles and conveyor

belts. It is possible that an action does not take the

entire time block, e.g. if less material is moved than

the speed limitations allow. This results in small idle

blocks, as seen in Figure 4 with the orange transport

block.

Time intervals

Imp. → H1.1 Imp. → H1.1 Imp. → H1.1

Imp. → H2.1

H2.1 → H1.2

H1.1 → Exp.

H2.1 → Exp. H2.1 → Exp.

Figure 4: Time intervals caused by parallel streams of im-

port (yellow), transportation (orange) and export (green)

moves.

With the COP maximizing the score function, we

are overall aiming to achieve a minimal number of

time blocks needed to meet the goal system state.

Alternatively, time intervals could depend on the

duration of actions. For this, one could construct a

score function that is normalized on the property of

used time. Whenever an action begins or ends, a new

time interval begins and the next actions beginning

alongside the running ones are calculated. This ap-

proach results in a very ﬂuent planning process with-

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

120

out any idle times that can occur with the uniform

time blocks. However, calculating the duration for

an action turns out to be rather hard when deciding

on how long to execute it. E.g. if an import action for

2000t is done in 0.5 time units and the same action for

8000t is done in 2 time units, the normalized score

function would return the same score for both, then

one would need one or multiple additional measures

to decide on the duration of an action, e.g. system re-

activity after different possible duration lengths.

The usage of the static time blocks yields negligi-

ble inaccuracies and is faster compared to a normal-

ized score function with additional measures.

It is not guaranteed to ﬁnd an optimal solution

with this step-by-step approach, as each step solution

is computed greedily without knowledge of previous

or possible future steps. Additionally, as the con-

straint solver maximizes the given score function, it

stops when no better score can be found for the solu-

tion step. However, there may be multiple solutions

that have the same score, but are in reality not equally

good. The solver will use the ﬁrst solution with the

highest score and disregard the others, even though

they may result in a faster overall solution. Using the

greedy step-by-step approach allows us to ﬁnd a good

solution for similarly sized and bigger problems sig-

niﬁcantly faster than we were able to in (L

ofﬂer et al.,

2023).

5.2 Design of a Score Function for a

Greedy Step-by-Step Approach

For each step, we solve a COP. Inputs of the COP are

the start conﬁguration X

with contents of import and

export vehicles as well as stockpile areas, and the ﬁ-

nal conﬁguration X

of what contents are desired in

the concerning components of the stockyard system.

Any given ﬁnal conﬁguration can be partially unde-

ﬁned. Generally, import ships are to be emptied and

the export ships are to be ﬁlled, but the contents of

speciﬁc stockpile areas tend to be irrelevant and can

be marked as arbitrary by setting those values to -1 in

We are aiming to maximize the result of the score

function f (X ). It evaluates a stockyard state X, i.e.

the contents of the stockyard during a speciﬁc mo-

ment.

f (X) =w

imp

· m

imp

+ w

exp

· m

exp

+ w

exm

· m

exm

+ w

· m

+ w

mpre f

· m

mpre f

(1)

In the equation, all w values refer to weights given

to each score value, and m values are the masses.

• m

imp

denotes the mass of material imported in the

current step

• m

exp

is the total mass of material exported so far,

including the material exported in the current step

• m

exm

refers to the amount of material on the stock-

yard that is ready to be exported, i.e. the material

exists in the correct quality and type

• m

is the mass that is moved through a transport

action in the current step

• m

mpre f

denotes the amount of material that is in a

preferable spot according to given material pref-

erences

Material preferences map different materials to dif-

ferent stockpiles, to ensure that possible occurring

blending operations are easily executable. The ma-

terial preferences need to be determined for every in-

dividual stockyard system, and are thus not generally

applicable. Within a speciﬁc stockyard system, dif-

ferent stockyard areas can have different weights per

preference, as in practice, preferences depend largely

on the existing stock on each stockpile area. One can

disregard w

mpre f

and m

mpre f

for any system and use

the universal function for a simpliﬁed score value cal-

culation.

The weights given to the masses are typically or-

dered by importance of the action. It is most impor-

tant to fulﬁll the exports in order to minimize moor-

ing times for the export ships and make space on the

stockyard, and then to fulﬁll the imports to minimize

mooring times of import ships and to provide mate-

rial for the export. Producing the requested materials

for the export or having them on the stockyard is a

useful prerequisite for fulﬁlling the export and thus

less important than import and export themselves, but

nonetheless important. Complying to the material

preferences is not obligatory, but can result in a higher

number of possible actions in future step moves. The

last weight given to the transports is a small negative

value, as we do not want to do transports that are not

needed. However, this does not mean that a trans-

port cannot be meaningful. The results of a transport,

for example, can lead to materials being in the right

place according to material preferences, generating a

positive score that outweighs the minor negative costs

associated with the transport operation. Therefore,

transports are only carried out in the planning if they

lead to a positive impact. Shifting materials back and

forth between locations is categorically ruled out in

this process.

Let us now calculate an example score, using the

situation given in Figure 3. Masses are given in thou-

sand tons. In state q

there are 20,000t of material Q1

on the import ship, 8,000t of material Q3 on SA0.0,

8,000t of Q2 on SA2.2 and 12,000t of Q1 on SA3.3.

All other spots are empty. Let the weights be as fol-

A Hybrid Constraint- and Search-Based Approach on the Stockyard Planning Problem

121

lows: w

imp

= 1000, w

exp

= 2000, w

exm

= 500, w

−1, w

mpre f

= 100, and let there be material prefer-

ences for storing material Q3 on stockpile 0, Q1 on

stockpile 3 and 4, and Q2 on stockpiles 1 and 2. The

weight for exported material is the highest as our pri-

mary goal is to fulﬁll the exports. As it is important

to empty the import ships, the weight for material im-

ported in one step is the second highest overall. Ma-

terial that is ready for export has a high weight as

well, though not as high as material that is already

exported. We aim to have a big amount of material

ready for export as fast as possible, so this score aids

in that. Abiding by material placement preferences

enhances the reactivity of the system, i.e. the num-

ber of possible moves for future step moves, thus it

gets a small positive score. To reduce unnecessary

machine runtime, transport moves have a small neg-

ative weight so that they are not executed unless it

improves the overall score, e.g. by putting some ma-

terial in a favorable spot. The score for the initial

state q

is f (q

) = 26000. After the import, blending

and export moves are completed in the ﬁrst step, the

score for the following state q

is as follows: f (q

) =

1000·8 +2000 · 8+500 ·12 − 1·0 +100 · 28 = 32800.

After the second step resulting in state q

, the score

amounts to f (q

) = 54800.

Our score function is simple and functional and

therefore fast to run and easy to understand. How-

ever, we currently do not account for choosing spe-

ciﬁc areas for import or transport moves, i.e. certain

stock conﬁgurations can result in moves being hin-

dered. E.g. if material Q1 lies on a stockpile area h

i, j

and material Q2 lies on a neighbored stockpile area.

They cannot be blended together into Q3 as there is

no way to reclaim both materials at the same time

if they are reclaimed by the same machine or if one

machine has its counter-weight in the area where the

other reclaiming machine needs to work, as discussed

in Section 2.

Thus there is opportunity to optimize the score

function in the future, possibly by incorporating

methods of machine learning to learn a score func-

tion that is customized for each stockpile system and

recurring tasks.

5.3 Introducing Random Restart DFS

With the use of greedy search to compute solutions, it

is not ensured that the ﬁrst solution found has a min-

imum amount of steps. The result of our score func-

tion introduced in Section 5.2 is maximized for every

solution step in a solving run. With an optimally cho-

sen score function, this results in a minimal number

of steps. As this cannot be guaranteed with our score

function, we opt to compute multiple solutions and

choose the one with the lowest number of steps.

Computing all solutions however is not feasible,

even if we limit the number s of subsequently pro-

cessed steps and the amount m of step moves for each

step. Computing the score of every move for a se-

quence of s steps would result in an order of m

solv-

ing runs. Realistically, m would be around 50 and s

around 15 for a simpler problem, which would result

in around 3e + 25 runs, which is not feasible. If the

number of possible step moves was reduced signif-

icantly, an MCTS approach as discussed in Section

4.2 would be possible.

Initially, a ﬁrst solution is obtained by means of a

simple greedy search, which corresponds to a single

branch in the search tree. Selecting a few additional

solving runs for generating additional solutions, i.e.

branches, and then choosing the fastest one is a better

approach. There are multiple ways to select starting

points for additional solutions. We call the process

of re-starting the solving process at a known search

node to generate additional solutions ”branching out”

and the process Random Restart Depth First Search

(RRDFS). This search procedure branches out from

randomly chosen search nodes in order to guarantee a

wide distribution of additional solutions. We are ﬁrst

explaining by way of an example, before discussing

the algorithm more generally.

m n

Figure 5: Simple search tree with 6 global solutions, 3 step

sequences are highlighted.

Figure 5 shows a simple search tree with 6 solu-

tions (i, k, l, m, o, p), of which we will discuss 3. Let

the red thick path (a − b − e − i) be our initial solu-

tion found by the greedy approach. This means that

according to our evaluation function, the interim so-

lutions b, e, and i each have the highest score value at

its branch, denoted as x

opt

, and therefore, according

to our calculation, they have made the most signiﬁ-

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

122

cant progress per step move, making them the most

promising. All other paths from root to the leaves

are distinct search paths, with each edge symboliz-

ing one step move resulting in the next node, i.e. the

next step solution. When an additional step solution is

computed for a depth k, all previously computed step

solutions for depth k are excluded from being found

again.

In Figure 5, let the green dotted path (a−c −g−l)

be the second search path found after the initial search

path. It is distinct from the ﬁrst solution from the

ﬁrst step, ﬁnding step solution c instead of the pre-

viously chosen solution b. Before searching for so-

lution c, a constraint is added to prevent ﬁnding so-

lution b again. As the objective value x

opt

for b was

the highest one found, solution c has an equally good

or slightly worse objective value for x

opt

compared to

b. For the second step, constraints are added to pre-

vent ﬁnding any previously found solutions for depth

2, which in this case is only solution d. This pattern

is continued for the rest of the search. Let the blue

dashed path (a−b− f − j−o) be the third search path

that is explored. Starting with node b after having

copied the path (a − b) from the ﬁrst solution, it ﬁnds

a new step solution f , under the additional constraints

of not ﬁnding neither solution e nor solution g. This

solution takes more steps than the red thick solution

and the greed dotted solution. In reality, when look-

ing for better solutions than the already found ones,

the search would stop at solution j where no ﬁnal so-

lution is reached yet. Solution o is a ﬁnal solution

which would be reached after an additional step. For

data generation, the search would look further than

depth 3.

Consider Algorithm 1 which implements the ran-

dom selection of the start node for the next run. Input

is a search tree T which has all previously found step

solutions, each connected to the previous step solu-

tion. The root node has the starting conﬁguration of

the system and depth 0. The goal of the algorithm is

to ﬁnd a next node v to re-start a DFS with in order to

ﬁnd another solution.

In line 1, we obtain the set leaves which has all

nodes that are found at the end of a search run and are

either a global solution. Following, in line 2 the mini-

mum depth of all the end nodes is determined, which

will act as the maximum bound in the next line. The

depth for the next start is chosen randomly in line 3

from all possible starting depths, which range from

0 (root) to 1 step before the earliest possible solution

(minD - 1), as to not look for solutions that take longer

than what has already been found. In line 4, we obtain

a list of all possible starting nodes of the found depth.

From the list, we choose a random index in line 5. Fi-

nally, in line 6, we obtain the step solution v using the

previously chosen index on dNodes, which we return

in line 7. The step solution v is the next starting point

for Random Restart DFS.

Data: existing partial search tree T

Result: next node v to restart with

1 leaves := set of leaves ;

2 minD := minimum depth of nodes in leaves ;

3 nextDepth := random(0, minD − 1);

4 dNodes := list of possible starting nodes with

depth nextDepth;

5 nextIndex := random(0, length(dNodes) − 1);

6 v := dNodes[nextIndex];

7 return v;

Algorithm 1: Random Restart Selection.

By doing this random approach multiple times, we

obtain a plethora of global solutions and dead ends

that can be further evaluated for the lowest number of

steps. In the future, evaluation metrics over resource

efﬁciency or other measures could be applied as well.

The random choice of the next search depth en-

sures a big variety of starting depths, with no prefer-

ence for earlier (i.e. lower depth) or later (i.e. higher

depth) starting points. From the chosen depth, one

starting solution within that depth is chosen randomly.

This 2-step random selection has no bias for depths

that were chosen previously for restarts.

Consider the alternative method of choosing a

starting solution from all eligible starting solutions.

Due to the exponentially increasing number of solu-

tions at higher depths in the search tree, this method

has a bias for starting solutions of higher depths.

Thus, the method in our Algorithm 1 is preferred.

6 EVALUATION

In Section 6.1 we introduce our test cases and evaluate

their results in Section 6.2.

6.1 Our Test Cases

We generated and examined two types of 50 random

test conﬁgurations each. Type 1 has an import se-

quence of length 5 to 10, alternating between materi-

als Q1 and Q2. At the beginning, the stockpiles were

either empty or completely ﬁlled (with a probability

of 50 %). The material type (Q1 or Q2) was ran-

domly chosen with a distribution matching the mix-

ing ratios to create material Q3. The demand from

the export ships is at around 20% to 50% of the com-

bined content of the import ships. In type 2, the setup

A Hybrid Constraint- and Search-Based Approach on the Stockyard Planning Problem

123

is the same, though the demand from the export ships

is slightly less or the same as the combined content of

the import ships, so that the planning horizon is sig-

niﬁcantly extended. In principle, all problems were

solvable.

All experiments were carried out on a Dell com-

puter featuring an 4th Gen Intel(R) Core(TM) i7-

4770 quad-core processor running at a clock speed of

3.40 GHz and 32 GB DDR3 RAM, operating at 3401

MHz. The operating system used was MicrosoftWin-

dows 10 Enterprise. The Java programming language

with JDK version 17.0.5 and the constraint solver

Choco-Solver version 4.10.7 (Prud’homme et al.,

2017) was utilised.

6.2 Results

Our results showcase considerable improvements in

multiple areas when compared to our previous ap-

proach in (L

ofﬂer et al., 2023). We chose to evalu-

ate the following characteristics, as shown in Tables

1 and 2: The Planning Time denotes the number of

hours planned, i.e. the number of step solutions (here,

one step solution equates to one planned hour). The

Solving Time is the total program runtime in minutes

to ﬁnd an overall solution. The Solving Time per hour

denotes the average runtime in seconds to ﬁnd a step

solution, i.e. to plan for one hour. The #parallel

moves is the total number of moves executed in par-

allel throughout all step solutions, with the ∅parallel

moves being its average per step solution. All these

characteristics are evaluated for their minimum, max-

imum and average values.

Each test case could be solved in an acceptable

runtime which was not yet possible with the previous

approach in (L

ofﬂer et al., 2023). In regards to the

runtime, it is apparent that the runtime, Solving time,

does not increase linearly, but rather super-linearly as

visible in the increasing value of solving time per hour

for larger problems. The smaller the problem, i.e. the

less hours to plan for, the faster it is. This non-linear

increase has to do with the increase of the constraint

number and the domain sizes of the variables. The

runtime for shorter planning periods is very good, and

the one for longer periods is still acceptable. It may be

possible to improve the program runtime even more in

the future.

The most notable result is in the number of si-

multaneous parallel moves parallel moves. In a step

move, at most 3 actions can be executed in parallel

(import, export, blending or transport). Transport ac-

tions are only done when necessary, as they generally

don’t contribute to an optimal planned schedule (see

Section 2). In Table 1 we see that the average number

of parallel actions per step move is at 2.84 (in Table 2

at 2.81) and thus very close to the desired 3 actions.

The number of average parallel actions for the tested

minimum times is less close to the optimum (2.38 and

2.14 resp.). Executing three actions at once might not

always be possible, e.g. if there is no material Q3 pro-

duced yet, an export action cannot take place. This

means that our results are very close to or at an opti-

mal solution and our system works very efﬁciently.

Our program has valuable beneﬁts for assisting the

workers in the planning process. We recommend to

have the results monitored by these experts and to not

use them without human approval.

Presently our results are evaluated by our partner

ABB with help of expert knowledge and a digital twin

of a real plant. We aim to continue testing our step-

by-step approach for a variety of sizes of plants. We

expect the program to be able to perform in an accept-

able time for at least medium-sized plants and possi-

bly for big plants too.

7 CONCLUSION AND FUTURE

WORK

In this paper, we have remodeled our COP presented

in (L

ofﬂer et al., 2023) for solving the SPP using a

hybrid approach combining constraing programming

with a step-by-step greedy search. This allows us to

plan a schedule for bigger systems over longer periods

of time. We introduced random restart DFS to com-

pute further and possibly better solutions for the SPP

than what was found in a ﬁrst greedy run. Our ap-

proach guarantees a fair distribution of starting points

for re-runs and could be applied to a variety of prob-

lems aiming to expand search trees.

The score function we designed in 5.2 has po-

tential to be optimized in the future, possibly with

machine learning techniques, e.g. a reinforcement

learning algorithm trained on data generated with the

greedy approach and multiple runs presented in this

paper. This also presents opportunity to bring in ad-

ditional goals, e.g. minimizing machine usage.

Altering the random restart DFS to ﬁt a variety

of goals and requirements is another topic worthy ex-

ploring later on. On the topic of data generation, it

might be possible to save multiple step solutions per

solution step and generate from there, improving run-

time during data generation. Algorithms linking iden-

tical step solutions in the search tree can help generate

more data without additional solving runs.

Using our approach for the digital twin of a real

stockyard system has yielded satisfying results. Go-

ing forward, we are aiming to test our approach for

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

124

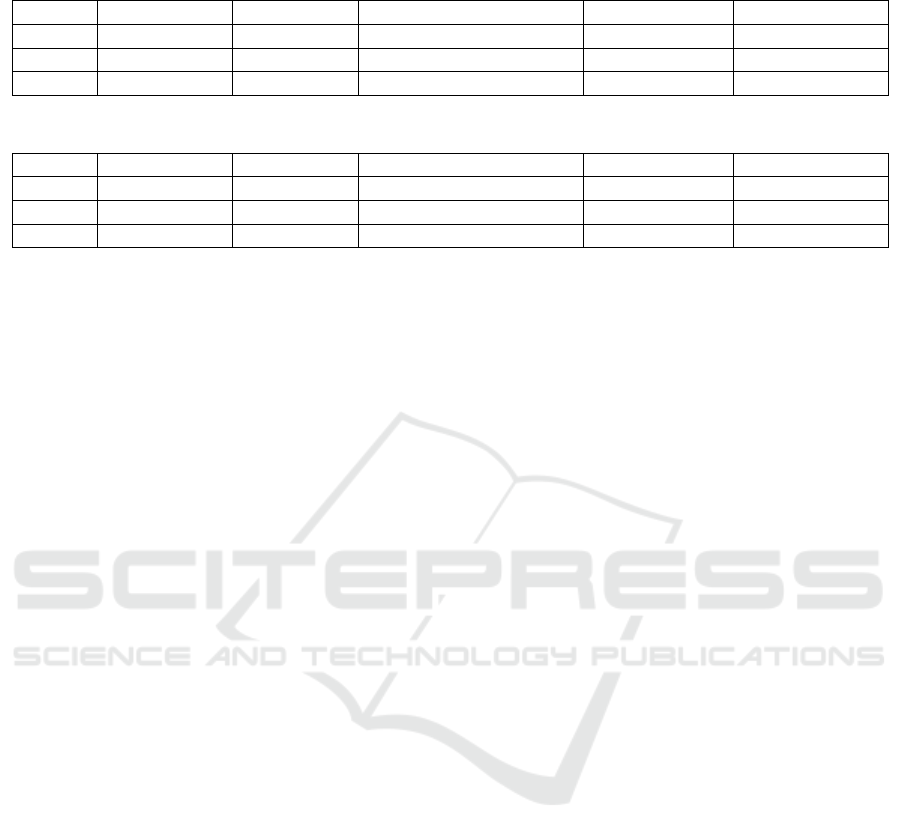
Table 1: Results of 50 different stockpile problems of type 1.

Planning time Solving time Solving time per hour (s) #parallel moves ∅parallel moves

min 8 h 2.28 min 15.22 23 2.38

max 28 h 31.32 min 70.13 69 2.96

average 14.82 h 8.94 min 33.58 43.06 2.84

Table 2: Results of 50 different stockpile problems of type 2.

Planning time Solving time Solving time per hour (s) #parallel moves ∅parallel moves

min 18 h 10.15 min 28.14 51 2.14

max 64 h 81.77 min 91.89 154 2.98

average 35.22 h 62.06 min 56.23 97.20 2.81

more and bigger real stockyard systems and have our

results be veriﬁed by experts.

REFERENCES

Abdekhodaee, A. H., Dunstall, S., Ernst, A. T., and Lam,

L. (2004). Integration of stockyard and rail network:

a scheduling case study. In 5th Asia-Paciﬁc indus-

trial engineering and management systems confer-

ence. Gold Coast, Australia, page 1–16.

Apt, K. (2003). Principles of Constraint Programming.

Cambridge University Press, New York, NY, USA.

Babu, S. A. I., Pratap, S., Lahoti, G., Fernandes, K. J.,

Tiwari, M. K., Mount, M., and Xiong, Y. (2015).

Minimizing delay of ships in bulk terminals by si-

multaneous ship scheduling, stockyard planning and

train scheduling. Maritime Economics & Logistics,

17:464–492.

Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein, C.

(2009). Introduction to Algorithms, 3rd Edition. MIT

Press.

Dechter, R. (2003). Constraint processing. Elsevier Morgan

Kaufmann.

Diestel, R. (2017). Graph Theory. Springer Publishing

Company, Incorporated, 5th edition.

Dijkstra, E. W. (1959). A note on two problems in connex-

ion with graphs. Numerische Mathematik, 1(1):269–

271.

Junior, M. W. J. S., de Oliveira Rocha, H. R., and Salles,

J. L. F. (2020). A multi-product mathematical model

for iron ore stockyard planning problem. Brazilian

Journal of Development, 6(7):45076–45089.

Kruskal, J. B. (1956). On the Shortest Spanning Subtree

of a Graph and the Traveling Salesman Problem. In

Proceedings of the American Mathematical Society,

volume 7, No.1, pages 48–50.

ofﬂer, S., Becker, I., and Hofstedt, P. (2023). A ﬁnite-

domain constraint-based approach on the stockyard

planning problem. In Strauss, C., Amagasa, T., Kotsis,

G., Tjoa, A. M., and Khalil, I., editors, Database and

Expert Systems Applications - 34th International Con-

ference, DEXA 2023, Part II, volume 14147 of Lecture

Notes in Computer Science, pages 126–133. Springer.

Marriott, K. and Stuckey, P. J. (1998). Programming with

Constraints - An Introduction. MIT Press, Cambridge.

Metropolis, N. and Ulam, S. (1949). The monte carlo

method. Journal of the American Statistical Associ-

ation, 44(247):335–341. PMID: 18139350.

Prim, R. C. (1957). Shortest connection networks and some

generalizations. The Bell System Technical Journal,

36(6):1389–1401.

Prud’homme, C., Fages, J.-G., and Lorca, X. (2017). Choco

documentation.

Russell, S. and Norvig, P. (2020). Artiﬁcial Intelligence: A

Modern Approach (4th Edition). Pearson.

Winands, M. H. M., Bj

ornsson, Y., and Saito, J.-T. (2008).

Monte-carlo tree search solver. In van den Herik, H. J.,

Xu, X., Ma, Z., and Winands, M. H. M., editors, Com-

puters and Games, pages 25–36, Berlin, Heidelberg.

Springer Berlin Heidelberg.

Xie, Y., Neumann, A., and Neumann, F. (2021). Heuris-

tic strategies for solving complex interacting stock-

pile blending problem with chance constraints. In

Chicano, F. and Krawiec, K., editors, GECCO ’21:

Genetic and Evolutionary Computation Conference,

Lille, France, July 10-14, 2021, pages 1079–1087.

ACM.

A Hybrid Constraint- and Search-Based Approach on the Stockyard Planning Problem

125