Comparative Analysis of Real-Time Time Series Representation Across
RNNs, Deep Learning Frameworks, and Early Stopping
Ming-Chang Lee
a
, Jia-Chun Lin
b
and Sokratis Katsikas
c
Department of Information Security and Communication Technology, Norwegian University of Science and Technology
(NTNU), Gjøvik, Norway
Keywords:
Comparative Analysis, Performance Evaluation, Real-Time Time Series Representation, Recurrent Neural
Networks, Deep Learning Frameworks, Early Stopping.
Abstract:
Real-Time time series representation is becoming increasingly crucial in data mining applications, enabling
timely clustering and classification of time series without requiring parameter configuration and tuning in
advance. Currently, the implementation of real-time time series representation relies on a fixed setting, con-
sisting of a single type of recurrent neural network (RNN) within a specific deep learning framework, along
with the adoption of early stopping. It remains unclear how leveraging different types of RNNs available in
various deep learning frameworks, combined with the use of early stopping, influences the quality of repre-
sentation and the efficiency of representation time. Arbitrarily selecting an RNN variant from a deep learning
framework and activating the early stopping function for implementing a real-time time series representation
approach may negatively impact the performance of the representation. Therefore, in this paper, we aim to
investigate the impact of these factors on real-time time series representation. We implemented a state-of-the-
art real-time time series representation approach using multiple well-established RNN variants supported by
three widely used deep learning frameworks, with and without the adoption of early stopping. We analyzed
the performance of each implementation using real-world open-source time series data. The findings from
our evaluation provide valuable guidance on selecting the most appropriate RNN variant, deciding whether to
adopt early stopping, and choosing a deep learning framework for real-time time series representation.
1 INTRODUCTION
In recent years, the increasing integration of the
Internet of Things (IoT) within the cyber-physical
world has led to a surge in the demand for time se-
ries analysis tasks such as clustering, classification,
anomaly detection, forecasting, and indexing (Lee
et al., 2020b; Lee et al., 2020a; Lee et al., 2021b;
Ratanamahatana et al., 2005; Bagnall et al., 2017; Is-
mail Fawaz et al., 2019).This surge is primarily driven
by the constant measurement and collection of large
volumes of time series data from interconnected de-
vices and sensors. However, analyzing raw time se-
ries data poses challenges due to its high computa-
tional cost and memory requirements (Ding et al.,
2008). To address this, high-level representation ap-
proaches have emerged as a solution. These ap-
proaches aim to extract features from time series data
a
https://orcid.org/0000-0003-2484-4366
b
https://orcid.org/0000-0003-3374-8536
c
https://orcid.org/0000-0003-2966-9683
or reduce its dimensionality while retaining its essen-
tial characteristics, thereby enabling effective and ef-
ficient time series analysis (Aghabozorgi et al., 2015).
Several time series representation approaches
have been introduced, including Symbolic Aggre-
gate Approximation (Lin et al., 2007), Piecewise
Aggregate Approximation (Keogh et al., 2001), and
the clipped representation approach (Bagnall et al.,
2006). However, these methods typically operate
solely on fixed-length time series rather than continu-
ously updating or streaming time series data. Before
generating a representation, these approaches require
preprocessing the time series using z-normalization,
which is a commonly employed technique in time se-
ries normalization (Dau et al., 2019).
However, z-normalization might cause two
distinct time series to become indistinguish-
able (H
¨
oppner, 2014), potentially misguiding the
representation approaches and negatively impacting
subsequent data mining tasks (Lee et al., 2024b).
Furthermore, many representation approaches require
Lee, M., Lin, J. and Katsikas, S.
Comparative Analysis of Real-Time Time Series Representation Across RNNs, Deep Learning Frameworks, and Early Stopping.
DOI: 10.5220/0012996700003838
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2024) - Volume 1: KDIR, pages 371-382
ISBN: 978-989-758-716-0; ISSN: 2184-3228
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
371

users to preconfigure and fine-tune parameters such
as time series length, sliding window size, or alphabet
size (Lin et al., 2007). Inadequate parameter values
may result in poor representations, compromising the
effectiveness of subsequent data mining operations.
Based on our investigation, only NP-Free, a real-
time time series representation method developed by
Lee et al. (Lee et al., 2023), meets the criteria for
real-time time series representation. Unlike other ap-
proaches, NP-Free operates on ongoing time series
without the need for z-normalization and does not
require parameter tuning. It uniquely converts raw
time series into root-mean-square error (RMSE) se-
ries in real time, ensuring that the resulting RMSE se-
ries represents the original raw series. However, this
approach has only been implemented using a single
type of recurrent neural network (RNN), specifically
Long Short-Term Memory (LSTM) within a specific
deep learning (DL) framework, namely Deeplearn-
ing4j (Deeplearning4j, 2023), along with the adoption
of the early stopping function (EarlyStopping, 2023).
In reality, several other DL frameworks have
been introduced and widely used, such as Tensor-
Flow (Abadi et al., 2016) and PyTorch (Paszke et al.,
2019). These frameworks aim to simplify the com-
plex data analysis process by providing comprehen-
sive libraries and tools for building, training, and de-
ploying machine learning models (Nguyen et al.,
2019). While numerous surveys and analyses have
compared different DL frameworks, they have pri-
marily focused on specific tasks (e.g., anomaly de-
tection and natural language processing) or different
types of computing environments.
To provide a comprehensive evaluation of how
these different factors impact real-time time series
representation, we implemented NP-Free using five
RNN variants, with and without the early stopping
function, across three DL frameworks. We conducted
a series of experiments using open-source time se-
ries data to evaluate all the implementations. The
results demonstrate that the choice of RNN variants,
DL frameworks, and the early stopping function sig-
nificantly influence both representation quality and
time efficiency. Therefore, it is crucial to carefully
consider the selection of these factors when design-
ing and implementing a real-time time series repre-
sentation approach. The experimental results show
that NP-Free implemented with DL4J, using LSTM
and the early stopping function, provides more sta-
ble RMSE series than NP-Free implemented with Py-
Torch or TensorFlow (TFK), regardless of whether the
early stopping function in PyTorch or TFK is acti-
vated.
The rest of this paper is structured as follows: Sec-
tion 2 introduces the background related to RNNs,
DL frameworks, and NP-Free. Section 3 provides an
overview of the related work. In Section 4, we present
and detail our evaluation setup and results. Finally, in
Section 5, we conclude the paper and outline direc-
tions for future work.
2 BACKGROUND
In this section, we introduce various RNNs, several
well-known DL Frameworks, early stopping, and the
main design of NP-Free.
2.1 RNN Variants
An RNN is a type of artificial neural network de-
signed to process sequential data or time series (Hop-
field, 1982). Unlike traditional feedforward neural
networks, RNNs have looping connections that allow
them to maintain a hidden state or memory of pre-
vious inputs. This recurrent structure makes RNNs
well-suited for tasks involving sequential or time se-
ries data. In an RNN, each time step in a time se-
ries is processed sequentially, with the network han-
dling each element one at a time and updating its in-
ternal state based on the current input and previous
state. This allows RNNs to capture dependencies and
patterns across different time steps. However, RNNs
face challenges in capturing long-term dependencies
and may suffer from the vanishing gradient problem,
which hinders their ability to learn from distant past
inputs.
LSTM (Hochreiter and Schmidhuber, 1997) is an
RNN variant designed to capture long-term depen-
dencies and model temporal sequences. The struc-
tural framework of an LSTM resembles that of con-
ventional RNN, with a key distinction being the pres-
ence of memory blocks as nonlinear units within
each hidden layer. Each memory block operates au-
tonomously, housing its own memory cells, and is
equipped with three essential gates: the input gate,
the output gate, and the forget gate. The input gate
determines whether incoming data should be stored in
the memory cell. The output gate decides whether the
current content of the memory should be output. The
forget gate determines whether the existing content
within the memory cell should be retained or erased.
The use of these gates allows LSTM to address the
vanishing gradient problem (Hochreiter, 1998) by en-
abling gradients to flow unchanged.
Gated Recurrent Unit (GRU), introduced by Cho
et al. (Cho et al., 2014), is another RNN variant de-
signed to adaptively capture dependencies at various
KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval
372

time scales. The core concept of GRU is to utilize
gating mechanisms to selectively update the hidden
state of the network at each time step. These mecha-
nisms manage the flow of information into and out of
the network. GRU consists of two key components: a
reset gate and an update gate. The reset gate controls
how much of the past information to forget, while the
update gate determines how much of the new infor-
mation to add.
Bidirectional Long Short-Term Memory (BiL-
STM) (Graves and Schmidhuber, 2005) is an exten-
sion of the standard LSTM network that improves its
ability to capture context from both past and future
data in a sequence. It consists of two LSTM layers:
one processes the input sequence in the forward di-
rection (left to right), and the other processes it in the
backward direction (right to left). By combining the
outputs from both directions, BiLSTM can better un-
derstand the full context of the data, making it partic-
ularly useful for tasks like speech recognition, natural
language processing, and time series prediction.
Bidirectional Gated Recurrent Unit (BiGRU) (Liu
et al., 2021) is an extension of the standard GRU net-
work designed to capture information from both past
and future contexts in sequential data. Similar to BiL-
STM, BiGRU consists of two GRU layers: one pro-
cesses the input sequence in the forward direction,
and the other processes it in the backward direction,
aiming to better capture the full context of the data.
2.2 DL Frameworks
In recent years, several DL frameworks have been de-
veloped by academia, industry, and open-source com-
munities. These frameworks share the goal of provid-
ing high-level abstractions and application program-
ming interfaces (APIs) for building, training, and de-
ploying deep learning models. Such abstractions sim-
plify the complex process of designing neural net-
works, allowing practitioners to focus on solving their
specific problems rather than dealing with low-level
implementation details (Ketkar and Santana, 2017).
TensorFlow (Abadi et al., 2016) is an open-source
DL framework developed by the Google Brain team
and is one of the most popular DL frameworks. Ten-
sorFlow uses dataflow graphs to encapsulate both the
computational logic of an algorithm and the corre-
sponding state on which the algorithm operates. This
means that users can define the entire computation
graph before executing it. TensorFlow supports a
wide range of neural network architectures and can
utilize hardware acceleration using graphics process-
ing units (GPUs) to speed up model training and in-
ference for both small-scale and large-scale applica-
tions. However, TensorFlow’s complexity arises from
its low-level API, which can be challenging to use. To
improve its user-friendliness and accessibility, Ten-
sorFlow is often paired with Keras (Keras, 2023), a
popular Python library known for its high-level, mod-
ular, and user-friendly API.
PyTorch (Paszke et al., 2019) is an open-source
deep learning framework that offers a flexible and
user-friendly environment for developing and train-
ing machine learning models, particularly neural net-
works. It is widely used in various AI and deep learn-
ing applications, such as computer vision and natu-
ral language processing. PyTorch stands out with its
high-performance C++ runtime, allowing developers
to deploy models in production environments without
relying on Python for inference (Ketkar and Santana,
2017). PyTorch is known for its dynamic computa-
tional graph, enabling flexible model architecture de-
sign and easier debugging. It also places a strong em-
phasis on tensor computation and benefits from robust
GPU acceleration capabilities. Additionally, PyTorch
supports the ONNX format, facilitating easy model
interchangeability.
Deeplearning4j, introduced by Skymind in
2014 (Deeplearning4j, 2023; Wang et al., 2019), is
an open-source distributed deep learning framework
designed exclusively for the Java programming
language and the Java Virtual Machine (JVM) envi-
ronment. It aims to bring deep neural networks and
machine learning capabilities to the JVM ecosystem.
Deeplearning4j is known for its scalability and
compatibility with popular programming languages,
allowing Java and Scala developers to build and train
deep learning models. Key features include support
for various neural network architectures, distributed
computing capabilities, compatibility with Hadoop
and Spark for big data processing, and integration
with other deep learning libraries like Keras. How-
ever, compared to PyTorch, Deeplearning4j has a
steeper learning curve due to its lower-level APIs
and the need for a solid understanding of Java and
deep learning concepts. Additionally, development,
updates, and new features for Deeplearning4j may
not be as rapid as those for other DL frameworks.
2.3 Early Stopping
Early stopping (EarlyStopping, 2023) is a technique
used during the training of machine learning models,
particularly neural networks, to prevent overfitting.
Overfitting occurs when a model learns the training
data too well, including its noise and outliers, result-
ing in poor generalization to new, unseen data. The
basic idea of early stopping is to monitor the model’s
Comparative Analysis of Real-Time Time Series Representation Across RNNs, Deep Learning Frameworks, and Early Stopping
373

performance on a validation dataset during training.
Training is stopped when the performance on the vali-
dation set begins to degrade, indicating that the model
has started to overfit the training data.
The detailed workflow of early stopping involves
splitting the dataset into training, validation, and test
sets. During training, the model’s performance on the
validation set is continuously monitored. If the per-
formance does not improve for a specified number of
epochs, known as the patience parameter, training is
stopped. The model parameters from the epoch with
the best validation performance are then used. This
approach helps ensure the model generalizes well to
new, unseen data by stopping the training process be-
fore overfitting occurs.
2.4 NP-Free
NP-Free, introduced by Lee et al. (Lee et al., 2023),
is a real-time time series representation approach that
eliminates the need for z-normalization and parame-
ter tuning. It directly transforms raw time series into
root-mean-square error (RMSE) series in real time,
serving as an alternative to z-normalization in cluster-
ing applications.
NP-Free utilizes Long Short-Term Memory
(LSTM) and the Look-Back and Predict-Forward
strategy from RePAD (Lee et al., 2020b) to gener-
ate time series representations. Specifically, NP-Free
predicts the next data point based on three histori-
cal data points and calculates the RMSE between the
observed and predicted values, converting the target
time series into an RMSE series. Figure 1 illustrates
the pseudo code of NP-Free, where t denotes the cur-
rent time point, starting from 0. Let c
t
be the real
data point collected at time point t, and
b
c
t
be the data
point predicted by NP-Free at t. NP-Free uses three
data points to predict the next one. The first LSTM
model is trained at t = 2 with c
0
, c
1
, and c
2
as input,
and it predicts
b
c
3
. This process repeats as t advances,
continuously training new LSTM models and making
predictions based on the three most recent data points.
At t = 5, NP-Free computes the prediction er-
ror using the well-known Root-Mean-Square Error
(RMSE) metric, as shown in Equation 1.
RMSE
t
=
s
∑
t
z=t−2
(c
z
−
b
c
z
)
2
3
, t ≥ 5 (1)
After deriving RMSE
5
, NP-Free predicts
b
c
6
(see
lines 9 and 10 of Figure 1). At t = 6, NP-Free re-
peats the procedure to calculate RMSE
6
and predict
b
c
7
. When t = 7, NP-Free calculates RMSE
7
and
thd
RMSE
using Equation 2.
Figure 1: The pseudo code of NP-Free (Lee et al., 2023).
thd
RMSE
= µ
RMSE
+ 3 · σ (2)
In Equation 2, µ
RMSE
and σ represent the average
RMSE and standard deviation at time point t, calcu-
lated using Equations 3 and 4, respectively.
µ
RMSE
=
(
1
t−4
·
∑
t
z=5
RMSE
z
, 7 ≤ t < w + 4
1
w
·
∑
t
z=t−w+1
RMSE
z
, t ≥ w + 4
(3)
σ =



q
∑
t
z=5
(RMSE
z
−µ
RMSE
)
2
t−4
, 7 ≤ t < w + 4
q
∑
t
z=t−w+1
(RMSE
z
−µ
RMSE
)
2
w
, t ≥ w + 4
(4)
Here, w limits the number of historical RMSE values
considered to prevent exhausting system resources.
Whenever the time point t advances to 7 or be-
yond (i.e., line 11 or line 23 of Figure 1 evaluates
to true), NP-Free recalculates RMSE
t
and thd
RMSE
.
If RMSE
t
is not greater than the threshold (as indi-
cated in lines 15 and 28), NP-Free immediately out-
puts RMSE
t
. Otherwise, NP-Free attempts to adapt to
potential pattern changes by retraining a new LSTM
model to re-predict
b
c
t
and recalculate both RMSE
t
and
thd
RMSE
either at the current time point (lines 17 to
20) or the next (lines 24 to 27). If the recalculated
RMSE
t
is no larger than thd
RMSE
, NP-Free immedi-
ately outputs RMSE
t
. Otherwise, it outputs RMSE
t
and performs LSTM model retraining at the next time
point. This iterative process dynamically converts a
time series into an RMSE series on the fly.
As previously mentioned, NP-Free distinguishes
itself from conventional representation methods by
KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval
374

eliminating preprocessing steps like z-normalization.
This feature allows NP-Free to serve as an alternative
normalization approach in clustering applications.
3 RELATED WORK
Several studies have compared DL frameworks. For
example, Kovalev et al. (Kovalev et al., 2016) eval-
uated the training time, prediction time, and classifi-
cation accuracy of a fully connected neural network
using five different DL frameworks: Theano with
Keras, Torch, Caffe, TensorFlow, and Deeplearning4j.
Zhang et al. (Zhang et al., 2022) introduced a bench-
mark that included six DL frameworks, various mo-
bile devices, and fifteen DL models for image classi-
fication, object detection, semantic segmentation, and
text classification. Their analysis revealed that no sin-
gle DL framework is superior across all tested scenar-
ios and highlighted that the influence of DL frame-
works may surpass both DL algorithm design and
hardware capacity considerations. Despite the valu-
able insights provided by these studies, their findings
do not address our specific question regarding the in-
fluence of different RNNs, DL frameworks, and the
early stopping function on real-time time series rep-
resentation.
Nguyen et al. (Nguyen et al., 2019) surveyed
various DL frameworks, analyzing their strengths
and weaknesses, but did not perform experimental
comparisons. Wang et al. (Wang et al., 2019) as-
sessed several DL frameworks on interface proper-
ties, deployment capabilities, performance, and de-
sign, providing recommendations for different sce-
narios. However, neither study addresses the specific
question of this paper: the impact of RNN variants,
DL frameworks, and the early stopping function on
real-time time series representation.
A work more closely related to our paper is the
study conducted by Lee and Lin (Lee and Lin, 2023).
In their research, they evaluated the impact of three
DL frameworks—TensorFlow with Keras, PyTorch,
and Deeplearning4j—on two real-time lightweight
time series anomaly detection approaches, RePAD
(Lee et al., 2020b) and SALAD (Lee et al., 2021b).
Their results indicated that DL frameworks signifi-
cantly impact the detection accuracy of the two se-
lected approaches. However, it is important to note
that their evaluation did not consider the impact of
different RNN variants, as the two approaches were
exclusively implemented using one type of RNN,
specifically LSTM, and focused on real-time time
series anomaly detection. Consequently, there is a
knowledge gap regarding the influence of RNN vari-
ants, DL frameworks, and the early stopping function
on real-time time series representation.
4 EVALUATION
In this section, we detail how we conducted a com-
parative analysis of real-time time series representa-
tion. Recall that NP-Free was originally implemented
using LSTM in Deeplearning4j. To understand the
impact of various RNNs, DL frameworks, and early
stopping on the performance of NP-Free, we imple-
mented NP-Free using five different types of RNNs:
RNN, LSTM, GRU, Bi-LSTM, and Bi-GRU, across
three different DL frameworks: TensorFlow-Keras,
PyTorch, and Deeplearning4j, both with and without
early stopping.
In our evaluation, we used TensorFlow-Keras ver-
sion 2.9.1, PyTorch version 1.13.1, and Deeplearn-
ing4j version 0.7-SNAPSHOT. It is important to
note that Deeplearning4j officially supports only the
LSTM architecture; it does not support RNN, Bi-
LSTM, GRU, or Bi-GRU. Consequently, we imple-
mented NP-Free using the LSTM architecture within
the Deeplearning4j framework, referring to this spe-
cific implementation as DL4J-LSTM, which denotes
the use of LSTM in Deeplearning4j for NP-Free.
A similar issue arises with PyTorch. PyTorch of-
ficially supports RNN, LSTM, and GRU but does not
support the other two RNN variants. Due to this limi-
tation, we could only implement NP-Free with the ar-
chitectures supported by PyTorch: RNN, LSTM, and
GRU. These implementations are referred to as PT-
RNN, PT-LSTM, and PT-GRU, respectively.
Additionally, to assess the impact of early stop-
ping on real-time time series representation across
different RNNs and DL frameworks, we considered
two scenarios. In Scenario 1, early stopping was not
adopted by each implementation. In this case, each
implementation was configured with the epoch pa-
rameter set to 50 to ensure fairness and consistency.
Table 1 lists all implementations studied in Scenario
1. The term “N/A” indicates that the corresponding
implementation is not available due to lack of support
from the corresponding DL framework.
Table 1: The nine implementations studied in Scenario 1.
PyTorch TensorFlow-Keras Deeplearning4j
RNN PT-RNN TFK-RNN N/A
LSTM PT-LSTM TFK-LSTM DL4J-LSTM
GRU PT-GRU TFK-GRU N/A
BiLSTM N/A TFK-BiLSTM N/A
BiGRU N/A TFK-BiGRU N/A
Comparative Analysis of Real-Time Time Series Representation Across RNNs, Deep Learning Frameworks, and Early Stopping
375

Conversely, in Scenario 2, early stopping was
adopted. It is important to note that early stopping
(EarlyStopping, 2023) was not officially supported
by PyTorch at the time of evaluation. Therefore, in
Scenario 2, we excluded all implementations related
to PyTorch, resulting in only six implementations as
shown in Table 2 being evaluated and compared.
Table 2: The six implementations studied in Scenario 2.
TensorFlow-Keras Deeplearning4j
RNN TFK-RNN N/A
LSTM TFK-LSTM DL4J-LSTM
GRU TFK-GRU N/A
BiLSTM TFK-BiLSTM N/A
BiGRU TFK-BiGRU N/A
4.1 Configuration and Environment
To guarantee a fair evaluation, all implementations
were configured with identical hyperparameters and
parameters, as detailed in Table 3. These settings
were originally suggested and employed in prior stud-
ies by (Lee et al., 2021a; Lee et al., 2023; Lee et al.,
2024b). We adopted these settings for all our experi-
ments. Each implementation consists of a single hid-
den layer with 10 hidden units and uses three his-
torical data points (Look-Back parameter) to predict
the next data point (Predict-Forward parameter). The
models were trained for 50 epochs with a learning
rate of 0.005, using the tanh activation function and
a fixed random seed of 140 to ensure reproducibility.
Additionally, the patience parameter of 5, the default
setting in Deeplearning4j, was used when the early
stopping function was activated.
Table 3: Configuration used for all implementations.
Hyperparameters/parameters Value
The Look-Back parameter 3
The Predict-Forward parameter 1
The number of hidden layers 1
The number of hidden units 10
The number of epochs 50
Learning rate 0.005
Activation function tanh
Random seed 140
Patience parameter 5
The evaluation of each implementation was con-
ducted separately on a MacBook running macOS
14.5, equipped with a 2.6 GHz 6-Core Intel Core i7
processor and 16GB DDR4 SDRAM. It is important
to note that the decision to use a standard laptop, with-
out GPUs or high-performance computing resources,
was intentional. This approach aims to assess how the
combination of RNN variants, DL frameworks, and
early stopping impacts the performance of real-time
time series representation in a typical computing en-
vironment.
4.2 Real-World Time Series Data
To evaluate the nine implementations, we used a real-
world open-source time series dataset collected by
the Human Dynamics and Controls Laboratory at
the University of Illinois at Urbana-Champaign (Hel-
wig and Hsiao-Wecksler, 2022), available from the
UC Irvine Machine Learning Repository (Helwig and
Hsiao-Wecksler, 2022). This dataset is related to mul-
tivariate gait time series for biomechanical analysis
of human locomotion. It consists of bilateral (left,
right) joint angle (ankle, knee, hip) time series data
collected from 10 subjects under three walking con-
ditions: unbraced (normal walking on a treadmill),
knee-braced (walking on a treadmill with a knee brace
on the right knee), and ankle-braced (walking on a
treadmill with an ankle brace on the right ankle).
For each condition, each subject’s data comprises
10 consecutive gait cycles (replications), where each
gait cycle starts and ends at heel-strike. Six joint an-
gles are included, which cover all combinations of leg
(left and right) and joint (ankle, knee, hip). Thus, this
dataset forms a six-dimensional array of joint angle
data: 10 subjects × 3 conditions × 10 replications ×
2 legs × 3 joints × 101 time points. The total number
of time series in this dataset is 1800, with each time
series consisting of 101 data points.
4.3 Evaluation Methodology
To evaluate the representation ability of each imple-
mentation and its impact on a time series classifica-
tion task, we analyzed the dataset to identify which
subject had the most stable time series under a spe-
cific combination of walking condition, leg, and joint
in their 10 replications. By ‘stable’, we mean that
the 10 time series in the 10 replications are similar
to each other. Once such a subject and combination
were identified, each implementation in Scenarios 1
and 2 was applied to generate a representation (i.e.,
an RMSE series) for each of the subject’s time series
under that specific combination. The representation
quality and time efficiency were then evaluated. Fi-
nally, their impact on time series classification were
assessed.
To achieve the above evaluation, we first calcu-
lated the average Euclidean distance (ED) for all sub-
jects under a specific combination of walking con-
dition, leg, and joint after applying the min-max
KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval
376

normalization (Codecademy, 2024) on each time se-
ries. As shown in Table 4, the combination of Un-
braced Left Knee resulted in the smallest average ED
with the smallest standard deviation (SD). In other
words, all subjects exhibit stable time series under the
Unbraced Left Knee combination. This is illustrated
in Figure 2, where each subject has 10 similar time
series collected from their left knee when unbraced.
Table 4: Average Euclidean distance of all subjects’ time
series under different combinations.
Combination Average ED SD
Unbraced Left Ankle 6.65 ·10
−3
2.45 ·10
−3
Unbraced Left Knee 2.96 ·10
−3
1.07 ·10
−3
Unbraced Left Hip 3.04 ·10
−3
1.14 ·10
−3
Unbraced Right Ankle 6.14 ·10
−3
2.13 ·10
−3
Unbraced Right Knee 3.29 ·10
−3
1.24 ·10
−3
Unbraced Right Hip 3.24 ·10
−3
1.26 ·10
−3
KneeBrace Left Ankle 8.76 ·10
−3
3.33 ·10
−3
KneeBrace Left Knee 4.19 ·10
−3
1.60 ·10
−3
KneeBrace Left Hip 4.00 · 10
−3
1.51 ·10
−3
KneeBrace Right Ankle 11.07 · 10
−3
3.24 ·10
−3
KneeBrace Right Knee 8.83 ·10
−3
2.72 ·10
−3
KneeBrace Right Hip 4.24 · 10
−3
1.45 ·10
−3
AnkleBrace Left Ankle 7.81 ·10
−3
2.75 ·10
−3
AnkleBrace Left Knee 4.07 ·10
−3
1.43 ·10
−3
AnkleBrace Left Hip 4.22 · 10
−3
1.52 ·10
−3
AnkleBrace Right Ankle 11.06 ·10
−3
3.52 ·10
−3
AnkleBrace Right Knee 4.86 · 10
−3
1.57 ·10
−3
AnkleBrace Right Hip 4.04 ·10
−3
1.51 ·10
−3
Following the previous experiment, we continued
to identify which subject has the most stable time se-
ries under the Unbraced Left Knee combination. To
do it, we separately calculated the average ED for
each subject under the Unbraced Left Knee combi-
nation and present the results in Table 5. It is ap-
parent that subject S9 has the lowest average ED with
the smallest SD. This can be confirmed from the sub-
figure for subject S9 in Figure 2, where all 10 time
series are almost overlapping.
Table 5: Average Euclidean distance of each subjects’ time
series under the Unbraced Left Knee combination.
Subject Average ED SD
S1 2.91 ·10
−3
0.80 ·10
−3
S2 2.51 ·10
−3
1.01 ·10
−3
S3 2.72 ·10
−3
1.19 ·10
−3
S4 3.25 ·10
−3
1.02 ·10
−3
S5 2.19 ·10
−3
0.86 ·10
−3
S6 3.54 ·10
−3
1.45 ·10
−3
S7 2.81 ·10
−3
0.91 ·10
−3
S8 4.07 ·10
−3
1.63 ·10
−3
S9 2.15 ·10
−3
0.62 ·10
−3
S10 3.40 ·10
−3
1.21 ·10
−3
Based on the above results, we used subject S9’s
10 time series under the Unbraced Left Knee combi-
nation to evaluate each implementation in Scenarios
1 and 2. Because these 10 time series are the most
similar to each other, they provide a suitable basis for
achieving a fair and realistic comparison and evalua-
tion among different implementations.
4.4 Scenario 1
In Scenario 1, all nine implementations of NP-
Free did not adopt early stopping. We used each
implementation to generate an RMSE series for
each of subject S9’s time series under the Un-
braced Left Knee combination and then calculate the
average ED for the 10 generated RMSE series. Addi-
tionally, we measured the time each implementation
took to generate an RMSE series, referred to as trans-
formation time in this paper.
Table 6 shows the results of each implementa-
tion. We can see that DL4J-LSTM outperforms all
the other implementations because it resulted in the
smallest average ED among them. In other words,
the RMSE series generated by DL4J-LSTM are more
similar to each other compared to the RMSE series
generated by any other implementation. This phe-
nomenon can be observed in Figure 3. Apparently,
the 10 RMSE series generated by DL4J-LSTM had a
high degree of overlap compared to the RMSE series
generated by other implementations.
However, in terms of transformation time, DL4J-
LSTM performs well, but not the best. Instead, all
three implementations related to PyTorch are the most
time-efficient, particularly PT-LSTM, which had an
average transformation time of 1.52 seconds. Never-
theless, all PyTorch-related implementations resulted
in a much higher ED than DL4J-LSTM, implying that
PyTorch cannot guarantee to generate a stable RMSE
series to represent the original time series.
Table 6: Performance of each implementation in Scenario 1.
ED of RMSE series (10
−3
)
Transformation time
(sec)
Average SD Average SD
DL4J-LSTM 3.19 0.90 8.20 0.44
TFK-RNN 25.81 7.29 24.77 4.26
TFK-LSTM 16.96 5.14 79.20 2.99
TFK-GRU 21.58 6.79 77.69 2.02
TFK-BiLSTM 17.59 5.07 144.81 3.00
TFK-BiGRU 22.63 5.55 141.09 5.77
PT-RNN 22.03 9.48 2.09 0.16
PT-LSTM 15.25 4.93 1.52 0.10
PT-GRU 18.10 6.54 2.08 0.29
Comparative Analysis of Real-Time Time Series Representation Across RNNs, Deep Learning Frameworks, and Early Stopping
377

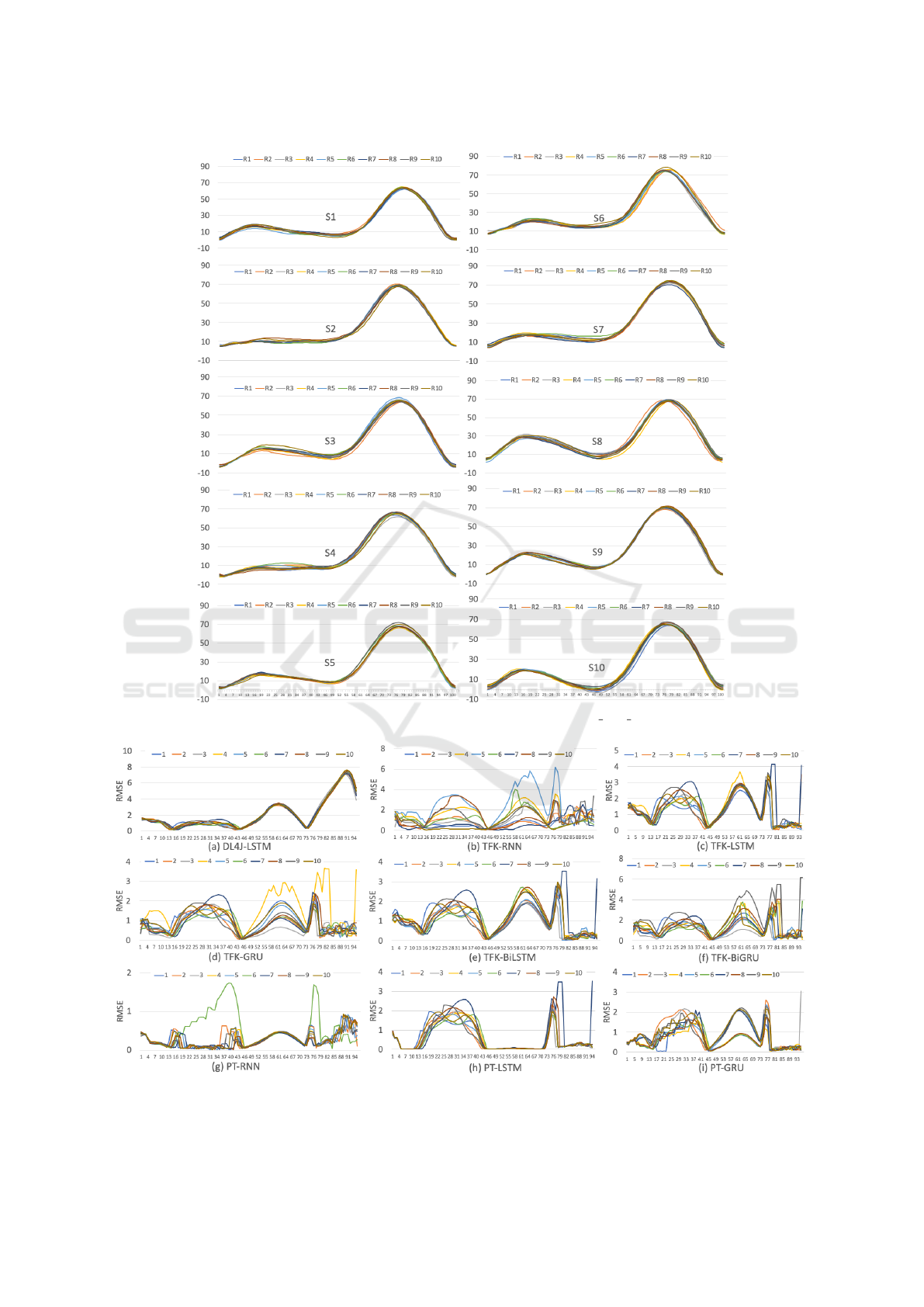
Figure 2: The original gait time series of each subject under the Unbraced Left Knee combination.
Figure 3: Visualization of RMSE series generated by each implementation in Scenario 1.
KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval
378

Among the three DL frameworks studied in this
paper, TensorFlow-Keras resulted in the worst per-
formance in terms of both representation ability and
transformation time, regardless of the RNNs used.
Similar poor results were also observed by Lee et
al. in their study in (Lee and Lin, 2023; Lee et al.,
2024a).
To further evaluate the impact of each implemen-
tation to time series classification, we used each im-
plementation to transform each raw time series of
each subject under the Unbraced Left Knee combina-
tion into an RMSE series. We then evaluated how ac-
curately the well-known k-means algorithm from the
tslearn package (Tavenard et al., 2020), a Python li-
brary specifically designed for time series analysis,
could classify RMSE series into their corresponding
subjects.
Table 7 lists the classification accuracy rate
achieved by each implementation in Scenario 1.
DL4J-LSTM resulted in the highest accuracy rate of
84%, indicating that 84 out of 100 time series were
correctly classified by the k-means algorithm into
their corresponding subjects, with only 16 incorrectly
classified. This good performance is attributed to
DL4J-LSTM’s superior ability to generate stable and
similar RMSE series representations for any specific
subject.
Table 7: The classification accuracy rate achieved by each
implementation in Scenario 1.
Implementation Classification accuracy rate
DL4J-LSTM 84% (= 84/100)
TFK-RNN 0% (= 0/100)
TFK-LSTM 55% (= 55/100)
TFK-GRU 42% (= 42/100)
TFK-BiLSTM 55% (= 55/100)
TFK-BiGRU 41% (= 41/100)
PT-RNN 43% (= 43/100)
PT-LSTM 54% (= 54/100)
PT-GRU 54% (= 54/100)
On the contrary, TFK-RNN performed the worst
among all the implementations because none of the
RMSE series generated by TFK-RNN could be cor-
rectly classified by the k-means algorithm, leading
to the classification accuracy rate of 0. This can be
explained by the fact that it led to the highest aver-
age ED, as shown in Table 6. Although TensorFlow-
Keras in combination with the other RNNs resulted
in a higher classification accuracy rate, the results are
still not satisfactory. Similarly, all PyTorch-related
implementations resulted in unsatisfactory classifica-
tion accuracy, ranging between 43% and 54%. This
is because these implementations were unable to gen-
erate stable and similar RMSE series for any specific
subject.
In summary, DL4J-LSTM proved to be a suitable
implementation choice for NP-Free when early stop-
ping was not adopted, whereas the other implementa-
tions were not suitable for NP-Free.
Note that while the RMSE series generated by
DL4J-LSTM are more similar to each other, they do
not indicate better prediction accuracy compared to
the time series predictions of the TFK and PT im-
plementations. As shown in Figure 3, most RMSE
values fall between 0 and 3.5 for the PT implemen-
tations, between 0 and 6.1 for TFK implementations,
and between 0 and 7.8 for DL4J-LSTM. Since lower
RMSE values correspond to higher prediction accu-
racy, this scenario shows that although the prediction
accuracy of TFK and PT implementations surpasses
that of DL4J-LSTM, they do not produce RMSE se-
ries as consistent as those generated by DL4J-LSTM.
4.5 Scenario 2
In Scenario 2, we evaluated all implementations of
NP-Free with early stopping enabled. Recall that
early stopping was not officially supported by Py-
Torch at the time of evaluation, so the three imple-
mentations related to PyTorch were excluded. Similar
to Scenario 1, we used each of the six implementa-
tions to generate an RMSE series for each of subject
S9’s time series under the Unbraced Left Knee com-
bination and then calculate the average ED for the 10
generated RMSE series. Furthermore, we measured
the transformation time each implementation took to
generate an RMSE series.
Table 8 lists the performance of each implemen-
tation. It is clear to see that DL4J-LSTM performs
the best among all the compared implementations,
as it resulted in the smallest average ED. This indi-
cates that the ten RMSE series transformed by DL4J-
LSTM for subject S9 under the Unbraced Left Knee
combination are closer to each other compared to the
RMSE series transformed by any other implementa-
tion for the same subject under the same combina-
tion. This can be observed in Figure 4. In other
words, DL4J-LSTM provides the best representation
ability to preserve the characteristics of the original
time series, even with the adoption of early stopping.
Furthermore, DL4J-LSTM offers the best time effi-
ciency with a transformation time of only 5.97 sec-
onds, making it 3.73, 13.02, 14.70, 22.65, and 22.15
times faster than TFK-RNN, TFK-LSTM, TKF-GRU,
TFK-BiLSTM, and TFK-BiGRU, respectively.
We continued to evaluate how each implementa-
tion impacts time series classification by employing
the k-means algorithm to classify all the RMSE series
Comparative Analysis of Real-Time Time Series Representation Across RNNs, Deep Learning Frameworks, and Early Stopping
379

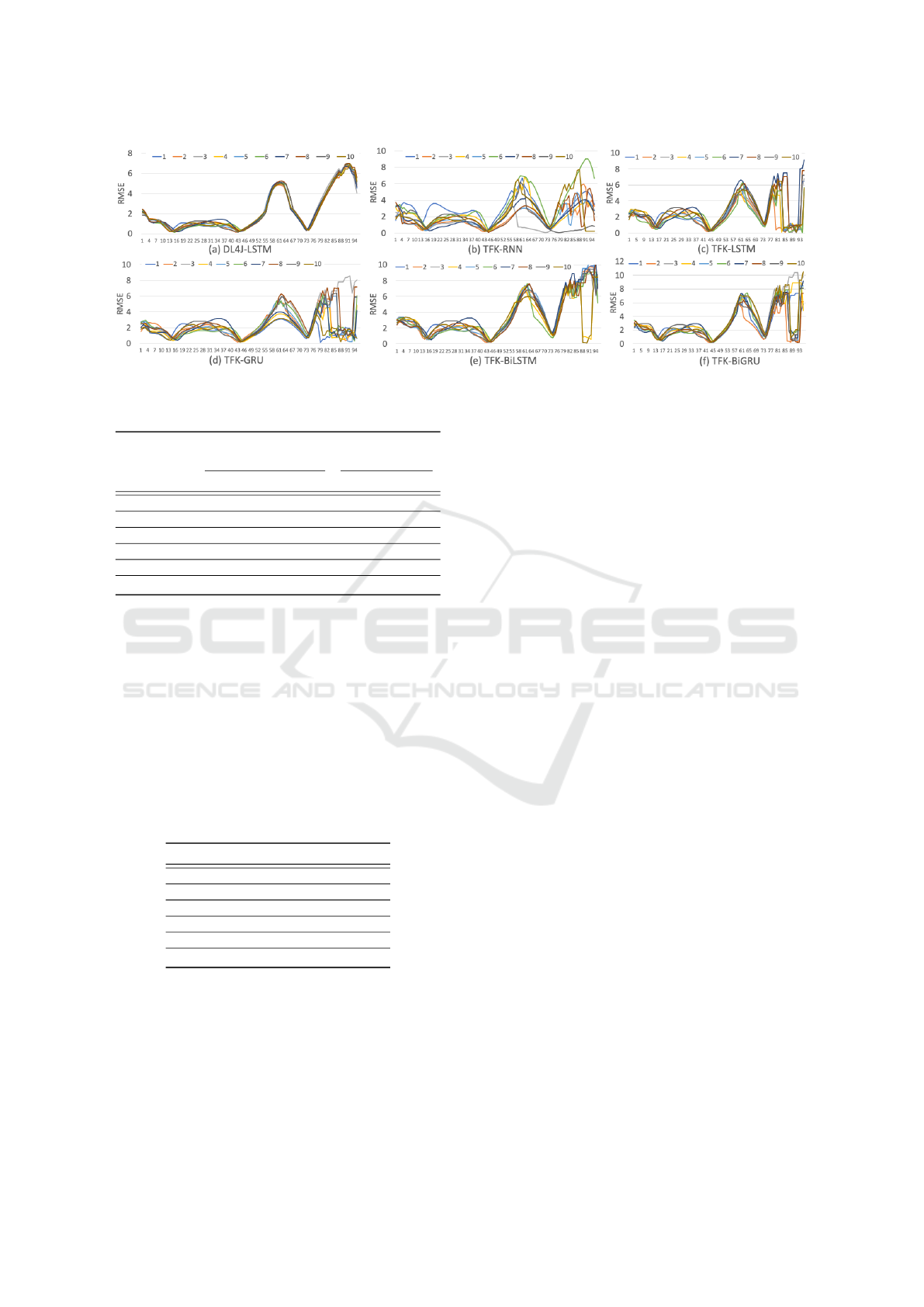
Figure 4: Visualization of RMSE series generated by each implementation in Scenario 2.
Table 8: Performance of each implementation in Scenario 2.
ED of RMSE series (10
−3
)
Transformation time
(sec)
Average SD Average SD
DL4J-LSTM 3.89 0.85 5.97 0.38
TFK-RNN 20.06 5.52 22.29 2.36
TFK-LSTM 16.01 3.64 77.72 2.46
TFK-GRU 22.65 9.55 87.74 5.12
TFK-BiLSTM 12.63 6.59 135.25 2.94
TFK-BiGRU 16.52 6.26 132.22 4.31
transformed by each implementation, similar to what
we did in Scenario 1. Table 9 lists the classification
accuracy rate achieved by each implementation. Ev-
idently, DL4J-LSTM with early stopping led to the
best classification performance. However, when any
TFK-related implementation was tested, they misled
k-means, resulting in a classification accuracy rate
lower than 60%. Based on the above results, it is con-
firmed that DL4J-LSTM with early stopping is rec-
ommended for implementing NP-Free.
Table 9: The classification accuracy rate achieved by each
implementation in Scenario 2.
Implementation Classification accuracy rate
DL4J-LSTM 94% (= 94/100)
TFK-RNN 0% (= 0/100)
TFK-LSTM 48% (= 48/100)
TFK-GRU 48% (= 48/100)
TFK-BiLSTM 55% (= 55/100)
TFK-BiGRU 59% (= 59/100)
If we cross-compare the results from Scenario 1
and Scenario 2 (please compare Table 6 with Table
8, and compare Table 7 with Table 9), we can see
that adopting early stopping for DL4J-LSTM is the
most recommended implementation strategy. This ap-
proach significantly reduces the average transforma-
tion time for each time series from 8.20 seconds to
5.97 seconds. Although it slightly increases the aver-
age ED from 3.19 ·10
−3
to 3.89·10
−3
, it does not neg-
atively affect k-means’ classification. Instead, it led to
a higher accuracy rate, increasing from 84% to 94%.
To understand the reason behind this, we analyzed the
results and found that DL4J-LSTM with early stop-
ping was able to generate more distinct and stable
RMSE series for each subject’s original time series,
resulting in a higher classification accuracy rate.
Therefore, DL4J-LSTM with early stopping
emerges as the most recommended choice due to its
superior ability to preserve the characteristics of the
original time series, its time-efficient processing, and
its ability to lead k-means algorithm to achieve high
classification accuracy.
5 CONCLUSIONS AND FUTURE
WORK
In this paper, we investigated how three well-known
DL frameworks (TensorFlow-Keras, PyTorch, and
Deeplearning4j), five different types of RNNs (RNN,
LSTM, GRU, Bi-LSTM, Bi-GRU), and the early
stopping function impact real-time time series repre-
sentation. We conducted a series of experiments using
a state-of-the-art real-time time series representation
method named NP-Free and real-world, open-source
multivariate gait time series data. These experiments
evaluated different implementation choices in terms
of their representation ability, time efficiency, and im-
pact on time series classification.
The results indicate that RNN variants, DL frame-
works, and early stopping significantly impact not
only representation quality and time efficiency but
also subsequent time series classification. Accord-
ing to the results, TensorFlow-Keras is not recom-
mended, regardless of which RNN is used, because it
leads to unstable RMSE series generation and higher
time consumption when transforming a time series
KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval
380

into an RMSE series. On the other hand, PyTorch
is the most efficient DL framework among the three,
enabling NP-Free to provide instant processing and
RMSE generation. However, similar to TensorFlow-
Keras, it generates unstable RMSE series that cannot
preserve the characteristics of the original time series.
Deeplearning4j is considered the most suitable DL
framework among the three studied. Although it only
supports LSTM rather than other RNNs, this com-
bination preserves the characteristics of the original
time series in a time-efficient manner, leading to satis-
factory classification accuracy, especially when early
stopping is enabled. Therefore, DL4J-LSTM with
early stopping is the most recommended choice due
to its superior ability to preserve the characteristics of
the original time series, time-efficient processing, and
enabling k-means algorithm to achieve high classifi-
cation accuracy. Our study offers valuable guidelines
for future research on real-time time series represen-
tation using deep learning.
In our future work, we plan to enhance the time ef-
ficiency of NP-Free by adopting strategies such as re-
ducing the number of hidden units and the number of
epochs. Additionally, we intend to release the source
code for all the implementations studied in this paper,
with the aim of advancing research in this area.
ACKNOWLEDEGMENTS
The authors would like to thank the anonymous edi-
tors and reviewers for their reviews and valuable sug-
gestions for this article. This work received funding
from the Research Council of Norway through the SFI
Norwegian Centre for Cybersecurity in Critical Sec-
tors (NORCICS), project no. 310105.
REFERENCES
Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, A., Dean,
J., Devin, M., Ghemawat, S., Irving, G., Isard, M.,
et al. (2016). Tensorflow: a system for large-scale
machine learning. In Osdi, volume 16, pages 265–
283. Savannah, GA, USA.
Aghabozorgi, S., Shirkhorshidi, A. S., and Wah, T. Y.
(2015). Time-series clustering–a decade review. In-
formation systems, 53:16–38.
Bagnall, A., Lines, J., Bostrom, A., Large, J., and Keogh, E.
(2017). The great time series classification bake off: a
review and experimental evaluation of recent algorith-
mic advances. Data mining and knowledge discovery,
31:606–660.
Bagnall, A., Ratanamahatana, C. A., Keogh, E., Lonardi, S.,
and Janacek, G. (2006). A bit level representation for
time series data mining with shape based similarity.
Data mining and knowledge discovery, 13(1):11–40.
Cho, K., Van Merri
¨
enboer, B., Bahdanau, D., and Bengio,
Y. (2014). On the properties of neural machine trans-
lation: Encoder-decoder approaches. arXiv preprint
arXiv:1409.1259.
Codecademy (2024). Normalization. https://www.
codecademy.com/article/normalization. [Online; ac-
cessed 25-September-2024].
Dau, H. A., Bagnall, A., Kamgar, K., Yeh, C.-C. M., Zhu,
Y., Gharghabi, S., Ratanamahatana, C. A., and Keogh,
E. (2019). The ucr time series archive. IEEE/CAA
Journal of Automatica Sinica, 6(6):1293–1305.
Deeplearning4j (2023). Introduction to core Deeplearning4j
concepts. https://deeplearning4j.konduit.ai/. [Online;
accessed 24-September-2024].
Ding, H., Trajcevski, G., Scheuermann, P., Wang, X., and
Keogh, E. (2008). Querying and mining of time series
data: experimental comparison of representations and
distance measures. Proceedings of the VLDB Endow-
ment, 1(2):1542–1552.
EarlyStopping (2023). What is early stopping? https:
//deeplearning4j.konduit.ai/. [Online; accessed 24-
September-2024].
Graves, A. and Schmidhuber, J. (2005). Framewise
phoneme classification with bidirectional lstm and
other neural network architectures. Neural networks,
18(5-6):602–610.
Helwig, N. and Hsiao-Wecksler, E. (2022). Multivariate
Gait Data. UCI Machine Learning Repository. DOI:
https://doi.org/10.24432/C5861T.
Hochreiter, S. (1998). The vanishing gradient problem dur-
ing learning recurrent neural nets and problem solu-
tions. International Journal of Uncertainty, Fuzziness
and Knowledge-Based Systems, 6(02):107–116.
Hochreiter, S. and Schmidhuber, J. (1997). Long short-term
memory. Neural computation, 9(8):1735–1780.
Hopfield, J. J. (1982). Neural networks and physical sys-
tems with emergent collective computational abili-
ties. Proceedings of the national academy of sciences,
79(8):2554–2558.
H
¨
oppner, F. (2014). Less is more: similarity of time series
under linear transformations. In Proceedings of the
2014 SIAM International Conference on Data Mining,
pages 560–568. SIAM.
Ismail Fawaz, H., Forestier, G., Weber, J., Idoumghar, L.,
and Muller, P.-A. (2019). Deep learning for time series
classification: a review. Data mining and knowledge
discovery, 33(4):917–963.
Keogh, E., Chakrabarti, K., Pazzani, M., and Mehrotra, S.
(2001). Dimensionality reduction for fast similarity
search in large time series databases. Knowledge and
information Systems, 3:263–286.
Keras (2023). Keras - a deep learning API written in
python. https://keras.io/about/. [Online; accessed 25-
September-2024].
Ketkar, N. and Santana, E. (2017). Deep learning with
Python, volume 1. Springer.
Kovalev, V., Kalinovsky, A., and Kovalev, S. (2016). Deep
learning with theano, torch, caffe, tensorflow, and
Comparative Analysis of Real-Time Time Series Representation Across RNNs, Deep Learning Frameworks, and Early Stopping
381

deeplearning4j: Which one is the best in speed and
accuracy?
Lee, M.-C. and Lin, J.-C. (2023). Impact of deep learn-
ing libraries on online adaptive lightweight time series
anomaly detection. In Proceedings of the 18th Inter-
national Conference on Software Technologies - IC-
SOFT, pages 106–116. INSTICC, SciTePress. https:
//arxiv.org/pdf/2305.00595.
Lee, M.-C., Lin, J.-C., and Gan, E. G. (2020a). ReRe: A
lightweight real-time ready-to-go anomaly detection
approach for time series. In 2020 IEEE 44th Annual
Computers, Software, and Applications Conference
(COMPSAC), pages 322–327. IEEE. arXiv preprint
arXiv:2004.02319.
Lee, M.-C., Lin, J.-C., and Gran, E. G. (2020b). RePAD:
real-time proactive anomaly detection for time series.
In Advanced Information Networking and Applica-
tions: Proceedings of the 34th International Confer-
ence on Advanced Information Networking and Ap-
plications (AINA-2020), pages 1291–1302. Springer.
arXiv preprint arXiv:2001.08922.
Lee, M.-C., Lin, J.-C., and Gran, E. G. (2021a). How far
should we look back to achieve effective real-time
time-series anomaly detection? In Advanced Infor-
mation Networking and Applications: Proceedings of
the 35th International Conference on Advanced In-
formation Networking and Applications (AINA-2021),
Volume 1, pages 136–148. Springer. arXiv preprint
arXiv:2102.06560.
Lee, M.-C., Lin, J.-C., and Gran, E. G. (2021b). SALAD:
Self-adaptive lightweight anomaly detection for real-
time recurrent time series. In 2021 IEEE 45th An-
nual Computers, Software, and Applications Confer-
ence (COMPSAC), pages 344–349. IEEE.
Lee, M.-C., Lin, J.-C., and Katsikas, S. (2024a). Impact
of recurrent neural networks and deep learning frame-
works on real-time lightweight time series anomaly
detection. The 26th International Conference on In-
formation and Communications Security, 26-28 Au-
gust, 2024, Mytilene, Lesvos, Greece (ICICS2024),
arXiv preprint arXiv:2407.18439.
Lee, M.-C., Lin, J.-C., and Stolz, V. (2023). NP-Free: A
Real-Time Normalization-free and Parameter-tuning-
free Representation Approach for Open-ended Time
Series. In 2023 IEEE 47th Annual Computers,
Software, and Applications Conference (COMPSAC),
pages 334–339. IEEE. https://arxiv.org/pdf/2304.
06168.
Lee, M.-C., Lin, J.-C., and Stolz, V. (2024b). Evalua-
tion of K-Means Time Series Clustering Based on
Z-Normalization and NP-Free. In Proceedings of
the 13th International Conference on Pattern Recog-
nition Applications and Methods - ICPRAM, pages
469–477. INSTICC, SciTePress. https://arxiv.org/pdf/
2401.15773.
Lin, J., Keogh, E., Wei, L., and Lonardi, S. (2007). Ex-
periencing sax: a novel symbolic representation of
time series. Data Mining and knowledge discovery,
15:107–144.
Liu, X., Wang, Y., Wang, X., Xu, H., Li, C., and Xin, X.
(2021). Bi-directional gated recurrent unit neural net-
work based nonlinear equalizer for coherent optical
communication system. Optics Express, 29(4):5923–
5933.
Nguyen, G., Dlugolinsky, S., Bob
´
ak, M., Tran, V.,
L
´
opez Garc
´
ıa,
´
A., Heredia, I., Mal
´
ık, P., and Hluch
`
y,
L. (2019). Machine learning and deep learning frame-
works and libraries for large-scale data mining: a sur-
vey. Artificial Intelligence Review, 52:77–124.
Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,
Chanan, G., Killeen, T., Lin, Z., Gimelshein, N.,
Antiga, L., et al. (2019). Pytorch: An imperative style,
high-performance deep learning library. Advances in
neural information processing systems, 32.
Ratanamahatana, C., Keogh, E., Bagnall, A. J., and Lonardi,
S. (2005). A novel bit level time series representation
with implication of similarity search and clustering. In
Advances in Knowledge Discovery and Data Mining:
9th Pacific-Asia Conference, PAKDD 2005, Hanoi,
Vietnam, May 18-20, 2005. Proceedings 9, pages 771–
777. Springer.
Tavenard, R., Faouzi, J., Vandewiele, G., Divo, F., Androz,
G., Holtz, C., Payne, M., Yurchak, R., Rußwurm, M.,
Kolar, K., and Woods, E. (2020). Tslearn, a machine
learning toolkit for time series data. Journal of Ma-
chine Learning Research, 21(118):1–6.
Wang, Z., Liu, K., Li, J., Zhu, Y., and Zhang, Y. (2019).
Various frameworks and libraries of machine learning
and deep learning: a survey. Archives of computa-
tional methods in engineering, pages 1–24.
Zhang, Q., Li, X., Che, X., Ma, X., Zhou, A., Xu, M.,
Wang, S., Ma, Y., and Liu, X. (2022). A comprehen-
sive benchmark of deep learning libraries on mobile
devices. In Proceedings of the ACM Web Conference
2022, pages 3298–3307.
KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval
382