Quantum Neural Network Design via Quantum Deep Reinforcement

Learning

Anca-Ioana Muscalagiu

Babes

-Bolyai University, Cluj-Napoca, Romania

Keywords:

Quantum Deep Reinforcement Learning, Neural Architecture Search, Quantum Neural Network,

Parameterized Quantum Circuit, Quantum Machine Learning, Variational Quantum Algorithm.

Abstract:

Quantum neural networks (QNNs) are a signiﬁcant advancement at the intersection of quantum computing

and artiﬁcial intelligence, potentially offering superior performance over classical models. However, designing

optimal QNN architectures is challenging due to the necessity for deep quantum mechanics knowledge and the

complexity of manual design. To address these challenges, this paper introduces a novel approach to automated

QNN design using quantum deep reinforcement learning. Our method extends beyond simple quantum circuits

by applying quantum reinforcement learning to design parameterized quantum circuits, integrating them into

trainable QNNs. As one of the ﬁrst methods to autonomously generate optimal QNN architectures using

quantum reinforcement learning, we aim to evaluate these architectures on various machine learning datasets

to determine their accuracy and effectiveness, moving towards more efﬁcient quantum computing solutions.

1 INTRODUCTION

Neural Architecture Search (NAS) is a key paradigm

in deep learning, playing a signiﬁcant role within

the ﬁeld of Automated Machine Learning (AutoML)

(Elsken et al., 2019). The objective of AutoML is to

apply effective machine-learning techniques to a vari-

ety of problems automatically, reducing reliance on

manual engineering and leveraging domain-speciﬁc

expertise. NAS achieves this by automating the de-

sign of optimal neural network architectures for var-

ious tasks. This approach not only enables the dis-

covery of new architectures for unexplored problems

but also has the potential to optimize existing bench-

marks across different domains. By using search al-

gorithms, NAS explores a vast space of potential ar-

chitectures, aiming to minimize an objective function

that measures performance, such as various loss func-

tions. The search iteratively reﬁnes itself, improving

upon the most promising architectures to discover su-

perior solutions.

Extending this concept to quantum computing,

Quantum Neural Network Architecture Search (QN-

NAS) automates the design of Quantum Neural Net-

works (QNNs). QNNs integrate classical neural lay-

ers with parametrized quantum circuits (PQCs), har-

nessing quantum mechanics for enhanced data pro-

https://orcid.org/0009-0000-3139-4311

cessing capabilities. In QNNAS, the ﬁrst and the

last layers are ﬁxed classical layers tailored to the in-

vestigated problem. The input layer transforms the

classical data and loads it into a quantum register,

while the output layer extracts the expectation values

from the qubit register back to their classical encod-

ing. The focus of QNNAS is on optimizing the hidden

layers, which are generated through the architecture

search algorithm. This involves exploring conﬁgura-

tions such as the number of qubits per layer, types of

quantum operations, and inter-layer connectivity. By

ﬁxing the input and output layers, the algorithm can

concentrate on ﬁne-tuning the hidden layers for max-

imum efﬁciency and effectiveness.

Automating the design of these networks is crucial

due to the complexities involved in designing PQCs,

which require extensive quantum mechanics knowl-

edge. Automation simpliﬁes this process, making

QNNs more accessible and practical for various appli-

cations. The development of optimal QNNs through

QNNAS holds promise for signiﬁcant advancements

in quantum machine learning, potentially revolution-

izing the ﬁeld by solving problems previously deemed

too complex.

In the following sections, this paper explores

Quantum Neural Network Architecture Search (QN-

NAS), focusing on automating the design of Quantum

Neural Networks (QNNs). Firstly, the paper outlines

560

Muscalagiu, A.

Quantum Neural Network Design via Quantum Deep Reinforcement Learning.

DOI: 10.5220/0012997500003837

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 560-567

ISBN: 978-989-758-721-4; ISSN: 2184-3236

our original contributions and reviews the state of the

art, comparing classical computing approaches with

the developments brought by quantum algorithms ap-

plied in QNNAS across three primary research direc-

tions. Afterwards, we provide a section about theoret-

ical foundations, which covers the basic concepts be-

hind our methodology: reinforcement learning, quan-

tum computing, and quantum reinforcement learn-

ing (QRL), highlighting differences from classical RL

and potential quantum speedups. The investigated ap-

proach discusses our modelling of the quantum rein-

forcement task and the training process of the agent.

Furthermore, we present some initial experiments, in-

cluding the experiemental settings and results, which

validate the feasibility of the approach. Finally, the

paper concludes with insights and future development

directions for our proposed technique.

1.1 Original Contributions

This paper introduces a novel approach to Quantum

Neural Architecture Search (QNNAS), a ﬁeld that has

been scarcely explored and predominantly addressed

through classical methodologies. Our research distin-

guishes itself in several ways:

• Novel Approach. To the best of our knowledge,

this work is one of the ﬁrst to apply QRL speciﬁ-

cally to optimize Parameterized Quantum Circuits

(PQCs). Prior studies have focused on construct-

ing general quantum circuits, using quantum state

ﬁdelity as the primary metric. While general cir-

cuits can be part of a learning process and are of-

ten less costly to implement, they lack the ﬂexi-

bility that PQCs offer. General circuits are typi-

cally ﬁxed in structure and do not allow for easy

modiﬁcation of parameters to adapt to new data or

learning objectives, making them less suitable for

tasks like machine learning. Therefore, in con-

trast to previous work, we design PQCs through

QRL and integrate them into Quantum Neural

Networks (QNNs), using the accuracy of these

QNNs as a metric. The performance is measured

after training the generated architectures on spe-

ciﬁc datasets in the context of the machine learn-

ing problem they were designed for. This repre-

sents a signiﬁcant departure from existing litera-

ture of QRL applied in QNNAS.

• Theoretical and Practical Contributions. We not

only provide a comprehensive theoretical model

of the QRL algorithm tailored for this applica-

tion but also present a practical implementation.

Our proof of concept, which includes a publicly

available QRL implementation for QNN circuit

construction, successfully generates an architec-

ture for classifying the Iris dataset (Fisher, 1988).

This demonstrates the practical viability of our ap-

proach.

Our research combines theoretical innovation with

practical application, laying a foundation for future

investigations and implementations of QRL in opti-

mizing QNN architectures.

2 CURRENT STATE OF THE ART

The current literature on Quantum Neural Archi-

tecture Search (QNNAS) is signiﬁcantly inﬂuenced

by advancements in Classical Neural Architecture

Search (NAS). While NAS has a substantial and well-

established corpus of research with over 1000 papers

published, QNNAS is still in its early stages, with

most studies emerging in the last two years. This

slower growth is due to the relatively recent devel-

opment of Quantum Neural Networks (QNNs). The

approaches in QNNAS generally adapt classical NAS

techniques to the speciﬁc structure and constraints of

QNNs, utilizing both discrete and continuous repre-

sentation methods.

Classical approaches to QNNAS often utilize re-

inforcement learning (RL) or evolutionary algorithms

(EAs) for discrete architecture optimization. Exam-

ples include the benchmark RL method (Kuo et al.,

2021), which trains an agent to place gates in quan-

tum circuits to minimize circuit length while main-

taining ﬁdelity, and EQAS-PQC (Ding and Spector,

2022), an evolutionary algorithm that evolves QNN

architectures through genetic operations, evaluating

ﬁtness based on QNN ﬁdelity. Continuous represen-

tation approaches, such as differentiable architecture

search (DARTS), model circuits as directed acyclic

graphs (DAGs) and use a weighted sum of primitive

operations for differentiable search, achieving high ﬁ-

delities in QNN architectures for tasks like 2-qubit

Bell states and 4-qubit circuits (Zhang et al., 2022).

While classical approaches have made signiﬁcant

contributions to QNNAS, quantum approaches offer

the potential for remarkable improvements in perfor-

mance and efﬁciency. Among these quantum ap-

proaches, QDARTS (Wu et al., 2023), EQNAS (Li

et al., 2023) and QRL (Chen, 2023) have emerged

as the most recent research directions with promis-

ing outcomes in comparison to their classical coun-

terparts.

EQNAS combines the classical EAs applied in

QNNAS with quantum computing. It represents

quantum neural architectures as a chromosome en-

coded in a quantum register and employs quantum

operations to evolve the population of candidate ar-

Quantum Neural Network Design via Quantum Deep Reinforcement Learning

561

chitectures. As far as we know, this is the only study

in the current literature that applies the quantum cir-

cuits to machine learning tasks, achieving notable re-

sults. Speciﬁcally, their algorithm improves the accu-

racy of QNNs by up to 5% and signiﬁcantly reduces

the number of parameters compared to the original

QNN. Our study similarly utilizes these evaluation

metrics. In contrast to their method, which solely op-

timizes known architectures, our approach extends to

both optimizing existing architectures and generating

entirely new ones for previously unexplored problems

in quantum machine learning.

Another research direction is QDARTS, a quan-

tum version of the classical DARTS algorithm, repre-

sents QNNs as directed acyclic graphs (DAGs) and

uses quantum operations to optimize the computa-

tions. One of the tasks on which the authors applied

QNNAS was image classiﬁcation. In this experiment,

the optimized QuantumDARTS model was compared

to benchmark QCNN and CNN models from the liter-

ature, on the MNIST dataset. QuantumDARTS con-

sistently outperformed both, demonstrating superior

accuracy and cost-efﬁciency with fewer parameters,

its performance reminaing robust under circuit noise

conditions.

The last of the novel methods applied in QN-

NAS that has shown potential is quantum reinforce-

ment learning (QRL) (Chen, 2023). This approach

is based on the modeling of the Classical Reinforce-

ment Learning Framework for QNNAS (Kuo et al.,

2021), aiming to further optimize it through the in-

troduction of quantum operations. In this approach,

the agent’s role is to design a quantum circuit that

achieves the desired outcome. The environment rep-

resents the quantum circuit itself, and the agent in-

teracts with it by selecting quantum gates and plac-

ing them at speciﬁc locations within the circuit. Our

method aims to continue to pave the path for this par-

ticular research direction, which is very scarcely and

least explored among all three. We focus on studying

the automated optimization and design of actual pa-

rameterized quantum circuits (PQCs) trained on ma-

chine learning tasks, not only of general circuits. Un-

like previous research, which primarily used ﬁdelity

as a metric, we use accuracy as our metric to evalu-

ate their performance on the learning task. Further-

more, we integrate much more complex circuits and

adopt a different modeling of the reinforcement learn-

ing problem. While previous approaches generated

circuits with two or at most three qubits, our method

aims to signiﬁcantly enhance the efﬁciency and effec-

tiveness of QRL in optimizing quantum neural net-

work architectures by using larger and more complex

circuits.

3 THEORETICAL BASIS

In this chapter, we present the theoretical foundations

necessary for deﬁning our methodology and modeling

of the problem, covering essential concepts in both

reinforcement learning and quantum computing.

3.1 Deep Reinforcement Learning

Reinforcement Learning (RL) is a machine learning

paradigm where an agent interacts with an environ-

ment E to maximize cumulative rewards. The agent

perceives the state s ∈ S of the environment and takes

actions a ∈ A , leading to state transitions and receiv-

ing rewards r. The agent’s behavior is deﬁned by a

policy π : S → A, aiming to ﬁnd an optimal policy π

∗

that maximizes the expected return:

∗

= argmax

∞

∑

t=0

t+1

| π

, (1)

where γ ∈ [0, 1] is the discount factor. Q-Learning

is an off-policy RL algorithm that learns the optimal

action-value function Q

∗

(s, a), representing the ex-

pected utility of taking action a in state s, which is

initially set to arbitrary values, such as zero or small

random values, to indicate that the utility of these ac-

tions is unknown. The Q-value update rule is:

Q(s

, a

) ← Q(s

, a

) +α



t+1

+ γmax

′

Q(s

t+1

, a

′

)

− Q(s

, a

)],

(2)

where α is the learning rate. Deep Q-Learning uses a

neural network, the Deep Q-Network (DQN), to ap-

proximate the Q-value function. The network param-

eters θ are optimized to minimize the loss:

L(θ) = E

(s,a,r,s

′

)∼D

h

r + γmax

′

Q(s

′

, a

′

;θ)

− Q(s, a; θ)



(3)

where D is the experience replay buffer storing tuples

(s, a, r, s

′

3.2 Quantum Computing

In this section, the fundamental concepts of quantum

computing essential for understanding Quantum Neu-

ral Networks (QNNs) are introduced. Qubits, analo-

gous to classical bits, are the basic units of quantum

information. Unlike classical bits, a qubit can exist in

a superposition state, expressed in bra-ket notation as:

|s⟩ = α|0⟩ +β|1⟩, with α, β ∈ C, and |α|

+ |β|

= 1

(4)

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

562

Here, |0⟩ and |1⟩ are the basis states. During

measurement, a qubit collapses to one of these states

with probabilities |α|

and |β|

, respectively. Quan-

tum gates, represented by unitary operators U , modify

qubit states. This concept extends to multi-qubit sys-

tems, typically initialized in the computational basis

state |0⟩

⊗n

3.3 Parameterized Quantum Circuits.

Quantum Neural Networks

Parameterized Quantum Circuits (PQCs) are quantum

circuits with gates that depend on a set of trainable pa-

rameters, similar to the weights in an Artiﬁcial Neural

Network. These circuits are used in variational algo-

rithms where the parameters are optimized to min-

imize a cost function. Quantum Neural Networks

(QNNs) use PQCs to model and learn from data, con-

sisting of an input layer, a series of parameterized

quantum gates (similar to hidden layers in classical

neural networks), and an output measurement. Dur-

ing training, the parameters of the quantum gates are

adjusted to minimize a loss function, akin to weight

updates in classical neural networks. An example of

a PQC is displayed in Figure 1:

Figure 1: Example of a PQC architecture.

A Quantum Neural Network is composed of sev-

eral essential components, which include:

• Encoding Layer. Prepares input data of any data

type for quantum processing by encoding or trans-

forming it into a suitable numeric representation

through classical operations. This layer is crucial

for data preprocessing, enhancing expressibility,

and preserving information.

• Parameterized Quantum Circuit. Consists of vari-

able quantum gates with trainable parameters. It

includes the encoding circuit, which encodes clas-

sical data into a quantum register using R

ro-

tations based on input features, and the parame-

terized circuit, comprising repeated R

(θ), R

(θ)

or R

(θ) rotations and an entangling scheme with

CX , CY or CZ gates. The parameters θ represent

the trainable weights which get updated during

training.

• Post Processing Layer. Receives the probability

vector from the quantum circuit, containing the

probabilities of measuring states |i

..i

⟩, and com-

putes expectation values for possible outputs.

The learning process in a Quantum Neural Net-

work (QNN) involves adjusting the parameters θ of

the quantum gates to minimize a loss function L(θ).

The parameter update rule can be expressed as:

t+1

= θ

− η∇

L(θ

) (5)

where θ

represents the parameters at iteration t, η is

the learning rate, and ∇

L(θ

) is the gradient of the

loss function with respect to the parameters.

3.4 Quantum Reinforcement Learning

Quantum Reinforcement Learning (QRL) lever-

ages quantum computing to enhance Reinforcement

Learning (RL) algorithms by exploiting superposi-

tion, entanglement, and quantum parallelism. In

QRL, the classical neural network in the Deep Q-

Network (DQN) algorithm is replaced with a Quan-

tum Neural Network to approximate Q-values (Du

et al., 2020).

The QRL framework retains essential components

of classical Q-learning: a target network, epsilon-

greedy policy, and experience replay. In this pa-

per, we employ the Double Q-Learning Algorithm

(Van Hasselt et al., 2016), which addresses overesti-

mation bias by using two sets of Q-values: the policy

network for action selection and the target network

for value estimation. The Q-network PQC, U

(s), is

parameterized by θ, with the target network U

(s)

being an episodic snapshot of U

(s). This method re-

duces bias, leading to more accurate action value esti-

mations and improved performance in reinforcement

learning tasks.

4 INVESTIGATED APPROACH

In this section, we outline the methodology adopted in

our study, encompassing the detailed modeling of the

reinforcement learning task and the subsequent train-

ing process of the quantum agent.

Quantum Neural Network Design via Quantum Deep Reinforcement Learning

563

4.1 Modelling of the Reinforcement

Learning Task

In this paper, we propose the following modelling

for the reinforcement task: A state in the environ-

ment is deﬁned as a parameterized quantum circuit

(PQC), reﬂecting the current conﬁguration of quan-

tum gates. Subsequently, an action involves the place-

ment of a quantum gate within the circuit architecture.

The agent selects actions that determine the type of

the gate to be added to the PQC. Afterwards, the re-

ward is measured through the accuracy of the gener-

ated QNN when assessed on a speciﬁc dataset, which

acts as the primary performance metric for the opti-

mization process.

Our method allows the agent to incrementally

build a PQC, adding one layer at a time. The agent

can position the following types of quantum gates on

these layers:

• Parameterizable Gates. These gates are essen-

tial in parameterized quantum circuits, function-

ing similarly to weights in artiﬁcial neural net-

works. The speciﬁc gates used include parame-

terizable rotation gates such as R

(θ), R

(θ), and

(θ). Each gate performs a rotation around a

speciﬁc axis on the Bloch sphere with angle θ.

• Entanglement Gates. A few of the gates in this

category are CX, CY, and CZ, which are respon-

sible for creating quantum entanglement between

qubits.

• Standard Gates. Additional standard gates like

RX, RY, and RZ may be used to perform basic

quantum operations.

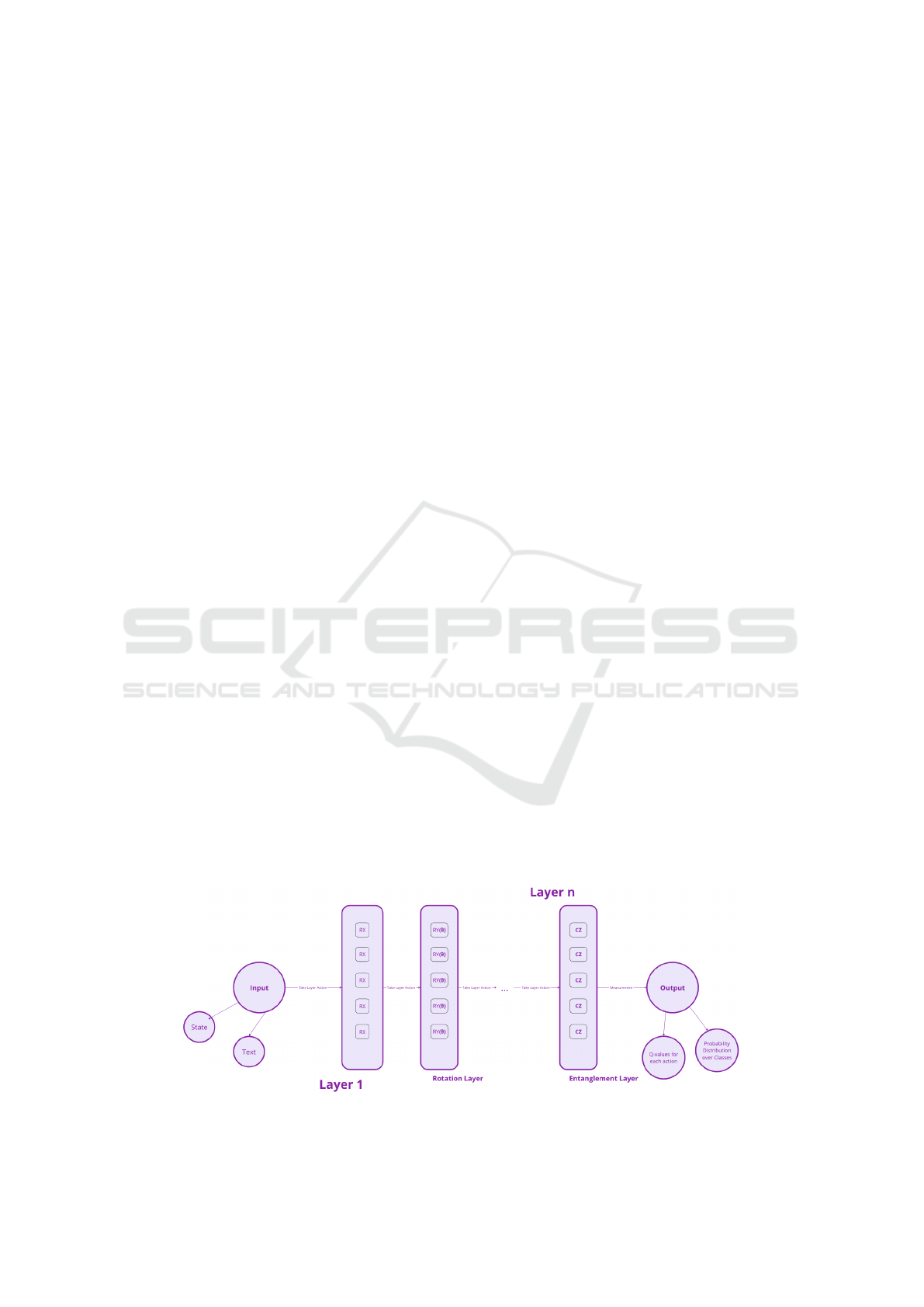
Figure 2 illustrates an example of a state in the en-

vironment, depicting the architecture of a parameter-

ized quantum circuit (PQC) after the agent has placed

the gates on the layers.

The central part of the ﬁgure represents the archi-

tecture of the PQC, which is integrated with the input

and output layers to form the actual QNN. The input

layer can handle various types of data, such as text for

supervised learning tasks or states for reinforcement

learning problems. Depending on the speciﬁc ma-

chine learning task, the output layer can generate dif-

ferent metrics, including probabilities for each class

in classiﬁcation problems, Q-values for reinforcement

learning, or other relevant outputs.

At each step of the process, the current state,

which represents the architecture of a parameterized

quantum circuit (PQC), is incorporated into the quan-

tum neural network (QNN) to generate a new child

network. This child network is then trained on a cus-

tom dataset tailored to the speciﬁc task. For super-

vised learning problems, the performance of the child

network is evaluated by assessing its accuracy on the

dataset. This accuracy metric serves as the reward, in-

dicating how well the generated architecture handles

the given problem.

On the other hand, in reinforcement learning

tasks, the child network acts as an estimator for the

agent within the environment. The agent’s actions

are based on the current PQC architecture and in-

volve estimating the values of these actions using the

generated PQC. The training involves playing the ac-

tions within the environment, which provides feed-

back in the form of rewards. Here, the performance

consists of the best reward obtained by the agent in

the subproblem, guiding the agent’s learning process.

This iterative cycle of generating, training, and eval-

uating the child network continues until the end of

the episode, with the goal of reﬁning the PQC archi-

tecture to optimize performance for the given task,

whether it is a supervised learning or reinforcement

learning problem.

At the end of an episode, which consists of a series

of steps, the environment is reset with an empty archi-

tecture, prompting the agent to place gates anew from

the beginning. An episode concludes after a ﬁxed

number of steps, ideally set to less than 10. This limi-

Figure 2: Overview of the Generated Circuit from the Environment State.

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

564

tation is intentional, aiming to create simple architec-

tures that are less prone to overﬁtting. The primary

goal of Quantum Neural Architecture Search (QN-

NAS) is not only to achieve high accuracy but also

to minimize the number of layers and parameters re-

quiring training. Despite the ﬁxed number of steps per

episode, the agent has the ﬂexibility to skip placing a

gate on a layer, which leads to generating architec-

tures with a variable length.

4.2 Agent Training Process

In order to reach an optimal policy that generates high

performance QNNs, the agent must undergo training

for multiple episodes within the environment. An

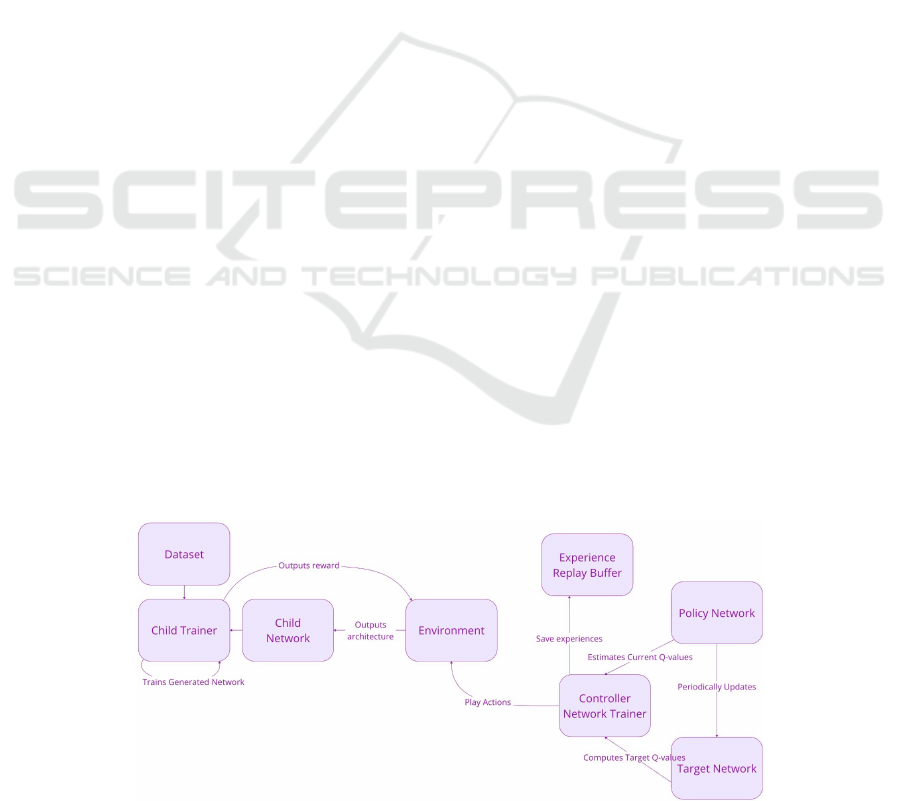
overview of the entire training process is displayed

in Figure 3. During each episode, the agent oper-

ates within an environment where it performs actions,

speciﬁcally choosing and placing quantum gates in

the PQC. Each of these actions, along with the re-

sulting rewards, are systematically stored in the Ex-

perience Replay Buffer. This buffer plays a crucial

role by maintaining a diverse set of experiences that

are utilized as input during training, thereby prevent-

ing the agent from overﬁtting to recent experiences

and enhancing its ability to generalize across differ-

ent states.

The actual quantum agent is represented through

the Controller Network Trainer, which utilizes the ex-

periences stored in the Experience Replay Buffer to

compute optimal action values. It achieves this by

estimating the current Q-values, which quantify the

expected cumulative reward of executing speciﬁc ac-

tions in given states. These Q-values are critical as

they guide the agent in understanding the long-term

beneﬁts of its actions. The Policy Network, which is

the core decision-making component of the agent, se-

lects actions based on its current Q-value estimates.

This network’s parameters are updated by minimiz-

ing the loss function derived from the computed Q-

values, thereby improving its policy and enabling the

agent to make more informed decisions about which

quantum gates to place in the PQC.

To ensure the stability and consistency of the

training process, the Target Network provides stable

Q-value targets. This network is periodically updated

to match the Policy Network’s parameters. This peri-

odic update is essential for mitigating oscillations and

preventing divergence that can occur during training.

The Target Network offers a stable reference for the

Policy Network, facilitating steady learning progres-

sion. The interaction between the Policy Network and

the Target Network ensures that the agent’s learning

process remains robust and reliable over time.

Overall, this training process equips the quantum

agent with the capability to effectively learn and reﬁne

the architecture of PQCs. By optimizing the place-

ment of quantum gates, the agent aims to enhance the

performance of quantum neural networks (QNNs),

achieving a balance between high accuracy and mini-

mal complexity. The ultimate objective is not only to

improve the accuracy of QNNs but also to minimize

the number of layers and parameters, thereby reduc-

ing the risk of overﬁtting and enhancing the general-

izability of the quantum models.

5 INITIAL EXPERIMENTS

To evaluate the effectiveness of our proposed Quan-

tum Neural Architecture Search (QNNAS) approach,

we conducted some initial experiments to create a

proof of concept for the proposed method. The ex-

periment focused on generating architectures to clas-

sify irises using the well-known Iris dataset. These

experiments aimed to assess the capability of our re-

inforcement learning-based framework in generating

efﬁcient parameterized quantum circuits (PQCs) tai-

lored for speciﬁc machine learning tasks.

Figure 3: Overview of the Training Process in our Quantum Reinforcement Learning Approach.

Quantum Neural Network Design via Quantum Deep Reinforcement Learning

565

5.1 Experimental Setup

The initial experiments were conducted under speciﬁc

reinforcement learning hyperparameters and an opti-

mized architecture for the controller network. The

maximum length of the architecture, which represents

the state, was set to 4, based on the difﬁculty of the

problem. Given that the Iris classiﬁcation task should

not require overly complex architectures, limiting the

length to 4 layers ensures that the generated parame-

terized quantum circuits (PQCs) remain manageable

in both size and complexity. While playing the en-

vironment, the agent had a set of possible gates to

choose from, including rotation gates R

(θ), R

(θ),

(θ), and entanglement gates CX, CY, CZ. These

gates provide the necessary operations to create and

manipulate quantum states effectively.

The reinforcement learning framework was con-

ﬁgured with a discount rate of 0.99, which ensures

that the agent values future rewards almost as much

as immediate rewards, promoting long-term strategy

over short-term gains. The learning rate was set to 1

× 10

−4

, allowing the agent to update its policy grad-

ually and avoid drastic changes that could destabilize

the learning process.

The architecture of the controller network was

carefully designed to facilitate effective decision-

making. It included an initial linear layer that mapped

the input features (4 dimensions) to a higher dimen-

sional space (16 dimensions), followed by a ReLU

activation function to introduce non-linearity. The

next layer was a quantum layer incorporating R

(θ),

(θ) and R

(θ) rotations operating on a 16-qubit

duced the observation values, from which the Q-

values for each of the seven possible actions were ex-

tracted. This design ensures that the controller net-

work can effectively process input data and determine

the optimal quantum gates to place within the PQC.

5.2 Experimental Results

As previously mentioned, the initial experiments fo-

cused on the classiﬁcation problem of Iris ﬂowers,

categorized into three different classes. The dataset

for this experiment was the Iris dataset, comprising

150 samples. The input features, which included the

length and width of the sepals and petals measured in

centimeters, determined the number of qubits in the

generated parameterized quantum circuit.

The agent was tasked with generating a PQC ar-

chitecture from scratch to achieve a high classiﬁcation

accuracy. The resulting architecture, as shown in Fig-

ure 4, consisted of a combination of rotation and con-

trolled gates. Speciﬁcally, it included layers of R

(θ)

and R

(θ) gates applied to individual qubits, followed

by entanglement created through CY gates.

Figure 4: Generated Architecture.

5.2.1 Results Analysis

The generated PQC was trained using the custom

dataset, and its performance was evaluated based on

the classiﬁcation accuracy. The best accuracy attained

by the generated architecture was 70%. This result

serves as a proof of concept, demonstrating the feasi-

bility of our reinforcement learning-based approach

to effectively design quantum circuits for machine

learning tasks. However, it is important to note that

further analysis and optimization of the best architec-

tures for the controller network are necessary to en-

hance performance.

The experimental setup and results indicate that

the agent was able to learn and generate PQC archi-

tectures that are capable of performing the given task

with a reasonable degree of accuracy. The architec-

ture generated was relatively simple, with a limited

number of layers and parameters, aligning with our

objective of minimizing complexity to avoid overﬁt-

ting.

These initial experiments demonstrate the feasi-

bility of our approach and set the stage for further

optimization of the QNNAS framework. While they

highlight the potential of QRL in generating effective

PQC architectures, it is important to note that compar-

isons were not possible for the Iris classiﬁcation task,

as prior work focused mainly on generating Quantum

Convolutional Neural Networks (QCNNs). These ini-

tial experiments serve as a proof of concept, and in

future work, we aim to generate QCNNs using the

proposed method in order to compare with quantum

evolutionary approaches.

6 FURTHER ADVANCEMENTS

As previously mentioned, this paper introduced a

novel approach to Quantum Neural Architecture

Search using Quantum Reinforcement Learning. In

future work, we will conduct extensive experiments

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

566

across various machine learning tasks and architec-

tures to better understand and optimize our approach.

The set of problems for which we aim to au-

tomatically design QNN architectures encompasses

both reinforcement learning and supervised learn-

ing tasks. In the context of reinforcement learn-

ing, we plan to focus on well-known environments

such as the CartPole environment and Frozen Lake.

These environments will allow us to test the capabil-

ities of our QNNAS framework in generating effec-

tive QNNs that can learn optimal policies and adapt

to their conditions. For supervised learning tasks,

our experiments will focus on classiﬁcation problems

using established datasets, speciﬁcally the Iris and

MNIST datasets. We will continue our work with

the Iris dataset, aiming to improve the performance

of our generated architectures. On the other hand, the

MNIST dataset will help us evaluate the robustness

and generalization capability of our approach in gen-

erating QCNNs and compare our results with other

quantum approaches.

By conducting these experiments across both rein-

forcement learning and supervised learning domains,

we intend to compare the performance of our gen-

erated QNNs against benchmark architectures in the

state of the art of Quantum Machine Learning.

7 CONCLUSION

In this paper, we have presented a novel approach to

Quantum Neural Architecture Search (QNNAS) us-

ing Quantum Reinforcement Learning (QRL). Our

proposed method automates the design of Quantum

Neural Networks (QNNs) by generating parameter-

ized quantum circuits (PQCs) tailored to speciﬁc ma-

chine learning tasks. This proof of concept has

demonstrated the feasibility and potential of our ap-

proach through initial experiments, particularly in the

context of classifying the Iris dataset. The experimen-

tal results underscore the capability of our reinforce-

ment learning-based framework to generate efﬁcient

PQCs, paving the way for future work that will in-

volve a broader range of machine learning tasks and a

variety of controller network architectures.

8 CODE AVAILABILITY

The implementation of our approach is pub-

licly available at https://github.com/915-Muscalagiu-

AncaIoana/QNNAS-Implementation.

ACKNOWLEDGEMENTS

The work presented became real with the help of our

supportive professors. Therefore we would like to ex-

press our gratitude to Associate Professor Maria Iu-

liana Bocicor.

REFERENCES

Chen, S. Y.-C. (2023). Quantum reinforcement learning for

quantum architecture search. In Proceedings of the

2023 International Workshop on Quantum Classical

Cooperative, pages 17–20.

Ding, L. and Spector, L. (2022). Evolutionary quantum ar-

chitecture search for parametrized quantum circuits.

In Proceedings of the Genetic and Evolutionary Com-

putation Conference Companion, pages 2190–2195.

Du, Y., Hsieh, M.-H., Liu, T., and Tao, D. (2020). Expres-

sive power of parametrized quantum circuits. Physical

Review Research, 2(3):033125.

Elsken, T., Metzen, J. H., and Hutter, F. (2019). Neural

architecture search: A survey. The Journal of Machine

Learning Research, 20(1):1997–2017.

Fisher, R. A. (1988). Iris. UCI Machine Learning Reposi-

tory. DOI: https://doi.org/10.24432/C56C76.

Kuo, E.-J., Fang, Y.-L. L., and Chen, S. Y.-C. (2021). Quan-

tum architecture search via deep reinforcement learn-

ing. arXiv preprint arXiv:2104.07715.

Li, Y., Liu, R., Hao, X., Shang, R., Zhao, P., and Jiao, L.

(2023). Eqnas: Evolutionary quantum neural architec-

ture search for image classiﬁcation. Neural Networks,

168:471–483.

Van Hasselt, H., Guez, A., and Silver, D. (2016). Deep re-

inforcement learning with double q-learning. In Pro-

ceedings of the AAAI conference on artiﬁcial intelli-

gence, volume 30.

Wu, W., Yan, G., Lu, X., Pan, K., and Yan, J. (2023).

QuantumDARTS: Differentiable quantum architec-

ture search for variational quantum algorithms. In

Krause, A., Brunskill, E., Cho, K., Engelhardt, B.,

Sabato, S., and Scarlett, J., editors, Proceedings of the

40th International Conference on Machine Learning,

volume 202 of Proceedings of Machine Learning Re-

search, pages 37745–37764. PMLR.

Zhang, S.-X., Hsieh, C.-Y., Zhang, S., and Yao, H. (2022).

Differentiable quantum architecture search. Quantum

Science and Technology, 7(4):045023.

Quantum Neural Network Design via Quantum Deep Reinforcement Learning

567