Analysis of Truncated Singular Value Decomposition for Koopman

Operator-Based Lane Change Model

Chinnawut Nantabut

The Sirindhorn International Thai-German Graduate School of Engineering, King Mongkut’s University of Technology

North Bangkok, 1518 Pracharat 1 Road, Wongsawang, Bangsue, Bangkok, Thailand

Keywords:

Automated Driving, System Identiﬁcation, Lane Change Model, Koopman Operator, Truncated Singular

Value Decomposition.

Abstract:

Understanding and modeling complex dynamic systems is crucial for enhancing vehicle performance and

safety, especially in the context of autonomous driving. Recently, popular methods such as Koopman operators

and their approximators, known as Extended Dynamic Mode Decomposition (EDMD), have emerged for

their effectiveness in transforming strongly nonlinear system behavior into linear representations. This allows

them to be integrated with conventional linear controllers. To achieve this, Singular Value Decomposition

(SVD), speciﬁcally truncated SVD, is employed to approximate Koopman operators from extensive datasets

efﬁciently. This study evaluates different basis functions used in EDMD and ranks for truncated SVD for

representing lane change behavior models, aiming to balance computational efﬁciency with information loss.

The ﬁndings, however, suggest that the technique of truncated SVD does not necessarily achieve substantial

reductions in computational training time and results in signiﬁcant information loss.

1 INTRODUCTION

In automotive engineering, model or system identi-

ﬁcation is crucial for understanding the behavior of

trafﬁc participants under various driving conditions.

This understanding is essential for improving vehi-

cle performance and safety, particularly when trans-

ferring insights from scene analysis in these scenar-

ios to autonomous vehicles, enhancing their decision-

making accuracy.

Given the complexity of modeling such behav-

iors, the underlying dynamic systems are inherently

nonlinear. To address these challenges, various mod-

eling techniques are employed, particularly black-

box models, which do not require explicit logical or

physical representations of the relationship between

inputs and outputs. Examples of these data-driven

approaches include neural networks, series models,

and autoregressive models (Mauroy and Goncalves,

2020).

One of the prominent data-driven approaches is

the Koopman operator. Although initially developed

long ago (Koopman, 1931), it has gained renewed at-

tention in modern applications for capturing the be-

havior of dynamical systems. Its appeal lies in its

https://orcid.org/0000-0002-5767-6023

connection to classical methods, the ability to in-

tegrate measurement-based formulations suitable for

machine learning, and the potential for simpliﬁcation

in real-world applications (Brunton et al., 2021). An-

other advantage is that it provides a global representa-

tion of the system, unlike instantaneous linearization

or dynamic linearization, which offer only a local ap-

proximation of the model around a speciﬁc operating

point.

Since Koopman operators are theoretically

inﬁnite-dimensional, the Extended Dynamic Mode

Decomposition (EDMD) method is employed to

approximate them using a set of smaller, more

manageable basis functions.

Koopman operators have been widely applied to

model identiﬁcation, particularly within the automo-

tive industry (Manzoor et al., 2023). Notable exam-

ples include (Cibulka et al., 2019), where a single-

track model derived from a twin-track model was

used to generate trajectory data by varying tire forces

and kinematic variables. Their ﬁndings showed that

increased model complexity does not necessarily im-

prove accuracy. Similarly, (Yu et al., 2022a) assessed

model ﬁdelity in lane-change scenarios using vari-

ous systems, while (Yu et al., 2022b) demonstrated

the ability of Koopman operators to reduce compu-

676

Nantabut, C.

Analysis of Truncated Singular Value Decomposition for Koopman Operator-Based Lane Change Model.

DOI: 10.5220/0012997800003822

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 676-683

ISBN: 978-989-758-717-7; ISSN: 2184-2809

tational complexities in vehicle tracking across dif-

ferent road types. Moreover, (Kim et al., 2022) ap-

plied Koopman operators to model lane-keeping sys-

tems by deﬁning states based on lateral dynamics and

tire models, utilizing a Linear Quadratic Regulator

(LQR) for control. Their follow-up work (Kim et al.,

2023) compared multiple basis functions for model

identiﬁcation, introducing systematic selection meth-

ods and signal normalization techniques. Meanwhile,

(Joglekar et al., 2023) investigated function approxi-

mators for Koopman operators in path-tracking appli-

cations.

The operators, particularly when paired with

model predictive control (MPC), have gained traction

for transforming nonlinear models into linear forms,

enhancing controller performance as shown by (Abra-

ham et al., 2017). (Gupta et al., 2022) addressed eco-

driving for electric vehicles using the Koopman oper-

ator with simulator data for high-performance MPC.

Similarly, (Buzhardt and Tallapragada, 2022) gener-

ated trajectories using a half-car and a terramechanics

model in deformable off-road scenarios, applying the

Koopman operator to lift states like vertical displace-

ment and using MPC for regulation.

Recent studies highlight the increasing use of neu-

ral networks as function approximators for the Koop-

man operator. For example, (Han et al., 2020) demon-

strated the integration of Koopman operators with

MPC, contrasting it with reinforcement learning ap-

proaches (RL). Similarly, (Xiao et al., 2023) enhanced

long-term predictability by combining deep neural

networks with Koopman operators, utilizing real driv-

ing data. In another study, (Guo et al., 2023) focused

on lane-changing scenarios with shared control sys-

tems, forming the Koopman operator through neural

networks and comparing the resulting paths to real

driver trajectories. Additionally, (Chen et al., 2024a)

employed neural networks to reformulate states into

input constraints for MPC, while (Bongiovanni et al.,

2024) applied the Koopman operator to model the

behavior of electrical throttle valves. Innovatively,

(Chen et al., 2024b) used neural network-based au-

toencoders for approximating ldriving behavior and

implemented adaptive MPC to handle parameter vari-

ations, showcasing the growing synergy between neu-

ral networks and Koopman operators in automotive

applications.

As mentioned earlier, Koopman operators enable

a linear representation of dynamic systems, which can

be framed in a linear state-space formulation using a

system matrix. To identify this matrix from the avail-

able data, it is necessary to invert a matrix constructed

from these data values. Given that this matrix is typ-

ically large and asymmetric, Singular Value Decom-

position (SVD) is utilized to enhance numerical sta-

bility. Additionally, due to the substantial size of the

data, the approximation technique known as truncated

SVD is employed to reduce the dimensions of the ma-

trices involved in the SVD process while preserving

as much essential information as possible from the

original inverted matrix. These methodologies not

only expedite the training process required to derive

the system matrix but also come with the trade-off of

potential information loss.

Procedures like truncated SVD have not been

thoroughly explored in the literature, with similar in-

vestigations primarily found in (Wilson, 2023), which

aimed to tackle the overﬁtting problem. However, this

study did not address the systematic approximation

rank of the matrix, and its application was outside

the realm of automotive contexts, concentrating in-

stead on simple dynamic models. This gap highlights

the need for further research into the utilization of

truncated SVD speciﬁcally within automotive appli-

cations, where the complexities of dynamic systems

demand more robust identiﬁcation techniques.

In this paper, the use of truncated SVD for ap-

proximating the system matrix derived from the ba-

sis functions utilized in EDMD is investigated, as

discussed in Section 2. The focus is centered on a

use case involving lane-changing behavior. Initially,

data is generated using simple geometric models, fol-

lowed by the introduction and selection of basis func-

tions that serve as approximators. The process of cal-

culating system dynamics through SVD is detailed,

highlighting the signiﬁcance of the truncated version

and the procedure for selecting the appropriate matrix

rank. All implementations are conducted in Python,

as outlined in Section 3. Finally, the resulting approx-

imations are analyzed and discussed in comparison to

the original matrix, considering aspects such as infor-

mation loss and time complexity.

It is important to note that topics like MPC as a

controller are not within the scope of this work and

are therefore excluded. Unlike the majority of the lit-

erature reviewed, the primary focus is on system or

model identiﬁcation through the application of Koop-

man operators, alongside the associated techniques of

EDMD and truncated SVD.

2 METHOD

The analysis presented in this paper is summarized in

Figure 1. First, a simpliﬁed vehicle model for lane

change behavior is explained in Section 2.1, leading

to the generation of trajectories denoted as T . Next,

the primary focus of this paper - system identiﬁcation

Analysis of Truncated Singular Value Decomposition for Koopman Operator-Based Lane Change Model

677

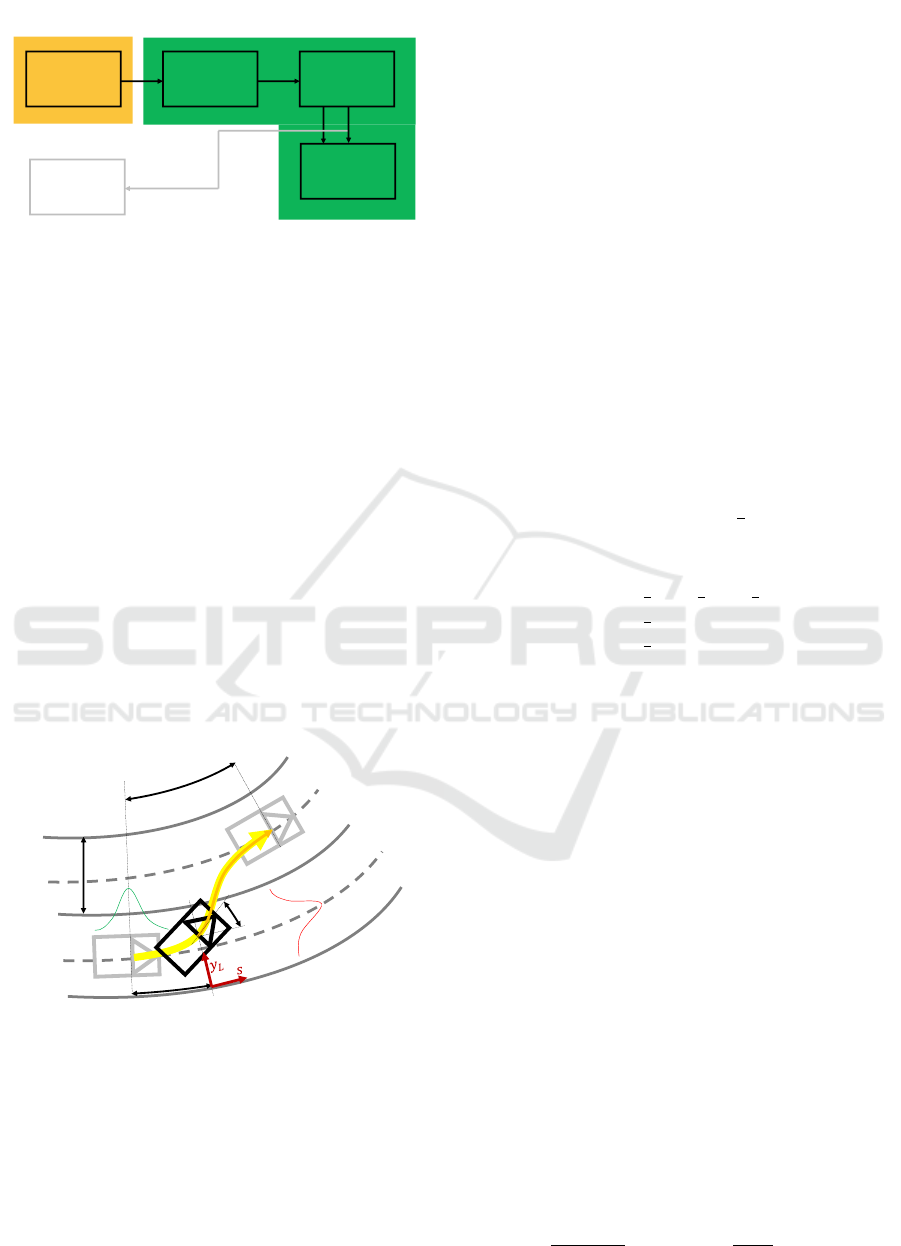
2.1: Lane

Change

Model

2.2.1:

Koopman

Operator

2.2.2:

Truncated

SVD

System Identification

𝒯

𝑨

෩

𝑨

2.2.3:

Reconstruction

Error

Controller

𝒦(𝒯)

Figure 1: Analysis steps for the truncated SVD-based

Koopman operator in a lane change model.

- is executed as detailed in Section 2.2, which consists

of three steps.

The Koopman operator K and the EDMD, along

with their basis functions Φ, are introduced in Section

2.2.1. The transformed trajectories K (T ) or their ap-

proximators Φ(T ) are then used to determine the sys-

tem matrix A

A, which describes the linear system.

Subsequently, an appropriate truncated SVD, se-

lected based on speciﬁc criteria, is discussed in Sec-

tion 2.2.2, resulting in the approximated system ma-

trix

A. While the model for these trajectories is typ-

ically employed for controller design, this aspect is

not addressed in the current paper. Finally, the orig-

inal matrix A

A and the approximated one

A are com-

pared to form the reconstruction errors, as discussed

in Section 2.2.3.

2.1 Lane Change Model

𝓣

𝑤

𝐿

𝑥

𝐿

𝑑

𝐿

𝒩

𝜓

𝒩

Figure 2: The calculation of lane change trajectories T is

based on (Schreier, 2017).

Since, in this paper, real data were not collected to ap-

proximate the model described by the Koopman oper-

ator, a mathematically simpliﬁed model proposed by

(Schreier, 2017) is used instead, as depicted in Figure

Additionally, the longitudinal and lateral move-

ment of the vehicle can be modeled independently.

The vehicle transitions from the right to the left lane

of width w

in the Frenet-Serret frame, also known as

the lane frame, discribed by the coordinates s and y

The s axis runs along the right edge of the right lane,

whereas the y

axis is perpendicular to it and directed

to the left.

Furthermore, the vehicle is located at the posi-

tion (x

) and is oriented to the lane at an angle

ψ. The longitudinal length of the complete trajectory,

depicted in yellow, is deﬁned by d

. Starting from the

current pose, including the vehicle’s position and ori-

entation, a trajectory T in orange is generated until

the vehicle reaches the middle line of the left lane.

To model the longitudinal movement, a constant

acceleration model is utilized. In this model, the

longitudinal state at time step k is deﬁned as X

s,k

]

, where s

denotes the longitudinal dis-

placement along the road, v

s,k

represents the longitu-

dinal velocity, and a

s,k

indicates the longitudinal ac-

celeration at time step k. The next state X

s,k+1

can be

sampled from the normal distribution N

, as shown in

green in Figure 2:





k+1

s,k+1





∼ N





1 T

0 1 T

0 0 1









s,k









T 1





(1)

where the ﬁrst argument of the expression denotes the

mean vector, and the second one is represented by the

covariance matrix that depends on the sample time T

and the standard deviation in the longitudinal acceler-

ation σ

To model the lateral movement, which is approxi-

mated by sinusoidal geometry, the initial lateral posi-

tion y

L,0

is generated from the normal distribution N

as shown in red in Figure 2:

L,0

∼ N (0.5w

,σ

(2)

where σ

denotes the standard deviation in the lateral

displacement.

The start angle ψ

can be sampled from a uniform

distribution U, with the exclusion of zero:

∼ U]0,ψ

0,max

(3)

where ψ

0,max

is the maximal possible initial yaw an-

gle.

As derived in (Schreier, 2017), where y

L,0

must

also be larger than 0.5w

, the longitudinal length of

the complete trajectory d

can then be calculated by:

2tan(ψ

)

cos

sin

−1

L,0

−2

, (4)

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

678

as well as the current longitudinal displacement x

sin

−1

L,0

−2

. (5)

The initial position is then deﬁned by (x

L,0

where the longitudinal position at time step k = 0 is

set to s

= x

. The longitudinal position s

is updated

using the constant acceleration model. The new lat-

eral position y

L,k

is then computed by:

L,k

sin

+ x

) −

+ w

. (6)

Subsequently, the trajectories for the following

system identiﬁcation T can be deﬁned by a set of N

trajectories T

, denoted by:

max

[

k=0

{(s

L,k

)

(7)

where k

max

= max

{k∥(s

+ x

) ≤ d

2.2 System Identiﬁcation

Once the trajectories are generated in Section 2.1, the

next step is to understand how the system evolves

based on the presented data. Given the assumption

that the system is complex and nonlinear, Koopman

operators and EDMD are employed to elevate the sys-

tem into a higher-dimensional space where it can be

described linearly. This transformation enables the

application of typical linear modeling techniques such

as LQR or linear MPC.

Section 2.2.1 elaborates on the Koopman opera-

tor and its approximators, EDMD, highlighting their

roles in system transformation. Subsequently, to op-

timize computational efﬁciency, Section 2.2.2 dis-

cusses the reduction of linear system dynamics using

truncated SVD, focusing on methods to select an ap-

propriate threshold.

Finally, Section 2.2.3 covers the methods for re-

constructing truncated trajectories and compares them

with the original trajectories.

2.2.1 Koopman Operator

The concept of the Koopman operator K is to trans-

form or ”lift” the original nonlinearly dependent ad-

jacent states to another space where the relationship

between the new or lifted states becomes linear, as

illustrated in Figure 3. Here, the original states are

described by trajectories obtained from the previous

section, consisting of tuples representing longitudi-

nal displacement s and the lateral displacement y

𝑠

𝑦

𝐿

ǁ𝑠

෤𝑦

𝐿

𝒦

−1

k+1

Figure 3: The Koopman operator K ”lifts” states at differ-

ent time steps, from (s,y

) to ( ˜s, ˜y

). This transformation

converts the nonlinear dependency among adjacent states

into a linear one. Dealing with the lifted states becomes

more manageable compared to the original states.

Since these trajectories are generated from sinusoidal

curves, the transition from one state to another is in-

herently nonlinear. With the Koopman operator K ,

the states can be transformed into the lifted ones

K (s,y

) such that

K (s,y

)

k+1

= A

AK (s,y

)

(8)

where A

A is the system matrix describing the linear de-

pendency between the current (at time step k) lifted

states ( ˜s, ˜y

)

= K (s,y

)

, and the next lifted states

( ˜s, ˜y

)

k+1

= K (s,y

)

k+1

Since the Koopman operator is inﬁnite-

dimensional, it can only be approximated using

EDMD. (8) can then be transformed into:

Φ(s,y

)

k+1

≈A

AΦ(s,y

)

(9)

where Φ denotes the function approximator that aims

to describe the linearity as accurately as possible.

There are various options for selecting function

approximators. A common approach involves using

a set of basis functions to construct them. One widely

used type is the monomial basis:

(s,y

) =













, (10)

where N

denotes the highest order of polynomials.

Another common type is the thin plate spline ra-

dial basis, described by:

(s,y

) =







∥s −c

∥

log(∥s −c

∥

)

∥y

−c

∥

log(∥y

−c

∥

)







, (11)

Analysis of Truncated Singular Value Decomposition for Koopman Operator-Based Lane Change Model

679

where ∥·∥

denotes the l

-norm (which, in this con-

text, is simply the absolute value), and the constants

as well as c

are randomly chosen.

At the end, the transformed trajectory K (T

) is ob-

tained, which can be approximated as:

Φ(T

) =

max

[

k=0

{Φ(s

L,k

)

(12)

2.2.2 Truncated SVD

In the case of EDMD, once the states are lifted using

the operator Φ, the lifted states are then stored and

utilized for subsequent training processes. To deter-

mine the system matrix A

A that captures the linearity,

the inversion of K (s,y

)

in (8) or Φ(s, y

)

in (9) is

necessary. This involves employing SVD for numer-

ical stability, which can also be truncated to expedite

the training process. However, not only two tuples

of Φ(s,y

)

are utilized, but the entire trajectories are

used to determine the system matrix A

A. At ﬁrst, a so-

called snapshot matrix of trajectory T

, X

, can be de-

ﬁned as:



Φ(s

L,0

)

... Φ(s

max

−1

L,k

max

−1

)



(13)

and its right-shifted snapshot matrix X

′

is denoted by:

′



Φ(s

L,1

)

... Φ(s

max

L,k

max

)



(14)

Consequently, the total snapshot matrix of all tra-

jectories T , X

X , is computed by:

X =



... X



, (15)

and its total shifted snapshot matrix X

′

is denoted by:

′



′

... X

′



. (16)

The linear dynamics of the system can be approx-

imated, using the system matrix A

A, by:

′

≈A

X ,

(17)

analogous to (8) and (9).

Since the matrix X

X is not square, its pseudo-

inverse or Moore-Penrose inverse X

†

is computed in-

stead to calculate the system matrix A

A ≈X

′

†

′

†

′

†

(18)

where X

†

= X

(X X

X X

)

−1

as derived from the so-

called normal equation.

Alternatively, the snapshot real matrix X

X can be

reformulated using SVD, resulting in the form:

X =U

UΣ

ΣV

(19)

which results in the pseudo-inverse X

†

of the form:

†

= V Σ

−1

V Σ

−1

V Σ

−1

(20)

where the Σ

Σ-matrix is displayed as:

Σ =







0 0 ... 0 0 ... 0

0 σ

0 ... 0 0 ... 0

. ... σ

max

0 ... 0

0 0 0 . . . 0 0 . . . 0







, (21)

given that this matrix (and therefore X

X ) has a rank

of r

max

, the singular values are sorted in descending

order, namely σ

≥ σ

≥ ... ≥ σ

max

By choosing a speciﬁc rank r ≤ r

max

, an approxi-

mated

X in the truncated SVD is obtained by:

X =

(22)

where

U = U

:,1:r

Σ = Σ

1:r,1:r

, and

V = V

1:r,:

Now, the question of how to systematically choose

the rank r is posed. As suggested in (Brunton and

Kutz, 2019), the percentual accumulated ”energy” up

to rank r can be calculated as:

= 100% ·

∑

i=1

∑

max

i=1

(23)

Typically, the empirical values of E

= 90% or

= 99% are used to determine the appropriate rank,

resulting in a good representation

X of the original

snapshot matrix X

X . Alternatively, a hard threshold

(HT) based on the ratio β =

of the dimensions of the

(snapshot) matrix X

n×m

and the median of its singular

values σ

med

is recommended by (Gavish and Donoho,

2014). The hard threshold r

is calculated by:

= ω(β)σ

med

(24)

where ω(β) is based purely on the ratio β and can be

calculated accordingly. Since some values of the rela-

tionship between β and ω are provided, interpolation

techniques can be employed to roughly determine the

hard threshold rank r

used to approximate the snap-

shot matrix X

X .

The system matrix A

A can be approximated by an

approximated system matrix

A = X

′

−1

′

−1

′

−1

(25)

Analogous to (9), the approximated system dy-

namics can then be described as:

Φ(s,y

)

k+1

≈

AΦ(s,y

)

(26)

The next states (s,y

)

k+1

can then be retrieved by

inverting the operator Φ.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

680

2.2.3 Reconstruction Error

To evaluate model ﬁdelity, the Frobenius norm ∥B

B∥

of a matrix B

B can be used, where ∥B

B∥

∑

i j

and b

i j

denotes the elements of the matrix B

B. This

norm allows for a comparison of the system dynam-

ics between the full-ranked system matrix A

A and its

truncated version

The relative reconstruction error of the truncated

matrix

A is represented by:

∥A

A −

A∥

∥A

A∥

(27)

The time consumption of the truncated matrix

can also be measured relative to the full matrix A

(28)

All the steps outlined in Figure 1 are summarized

in Algorithm 1 for the easy implementation of the

analysis proposed in this paper. This includes the def-

inition of necessary variables, the collection of data,

the execution of truncated SVD, and the analysis of

the results using various metrics.

3 SIMULATION

All parameters utilized in the previous section, as

summarized in Algorithm 1, are deﬁned here. The

comparison between the original data and the Koop-

man operators using different types of basis func-

tions is illustrated. Additionally, qualitative trajecto-

ries based on truncated SVD with various rank selec-

tions are compared and analyzed. Finally, the time

consumption for these processes is also discussed.

3.1 Setup

Taken from the original paper for modeling lane

change behavior (Schreier, 2017), the lane width

is set to 3.5 m. With the vehicle width w

of 1.5 m, the standard deviation of lateral deviation

0.5(w

−w

) =

m, whereas the value of the

longitudinal direction σ

0.2

. The time constant

T is set to 0.1 s. The initial kinematic variables are

= 0 m, v

= 10

, and a

= 0

. The vehicle can

start with a maximal orientation of ψ

= 15

◦

To ensure both basis functions have the same di-

mension, N

is set to 2. Furthermore, the constants c

and c

are sampled from a uniform distribution rang-

ing between −

and +

Step I: Deﬁne all parameters:

1. Lane Change Model:

(a) Road geometry w

(b) Standard deviations: σ

, and σ

(d) Kinematic variables a

, v

, s

, and ψ

0,max

2. Basis function:

(a) Monomial N

(b) Thin plate spline radial c

and c

Step II: Collecting data: Trajectory puffer T

For each trajectory i, T

←

0 :

1. Sample the initial lateral displacement

L,k

= y

L,0

from (2) and the initial yaw angle

from (3)

2. Calculate the trajectory’s longitudinal length

from (4) and the current displacement

= x

from (5)

3. T

← {(s

L,k

)}

4. While s

≤ d

(a) Update the longitudinal displacement s

using (1) and the lateral displacement y

L,k

using (6)

(b) T

← T

∪{(s

L,k

)}

5. Update T ← T ∪T

Step III: Truncated SVD

1. Calculate snapshot matrices X

X and X

′

based

on (13), (14), (15) and (16)

2. Use SVD on the snapshot matric X

X using (19)

3. Calculate the rank r using (23) or (24)

4. Construct truncated snapshot matrix

X using

(22) and the system matrix

A using (25)

Step IV: Evaluation

1. Calculate the relative reconstruction error

using (18), (25) and (27) and the relative

time consumption

using (28)

Algorithm 1: Truncated SVD for Koopman Operator-Based

Lane Change Model.

3.2 Results

In Figure 4, a single trajectory illustrating a lane

change maneuver (from the red right middle lane to

the green left middle lane) is depicted in blue, based

on the approach by (Schreier, 2017) as detailed in

Section 2.1. The vehicle follows a simple sinusoidal

pattern, returning to the right lane after exceeding

the maximum longitudinal displacement d

, as pre-

viously discussed.

Analysis of Truncated Singular Value Decomposition for Koopman Operator-Based Lane Change Model

681

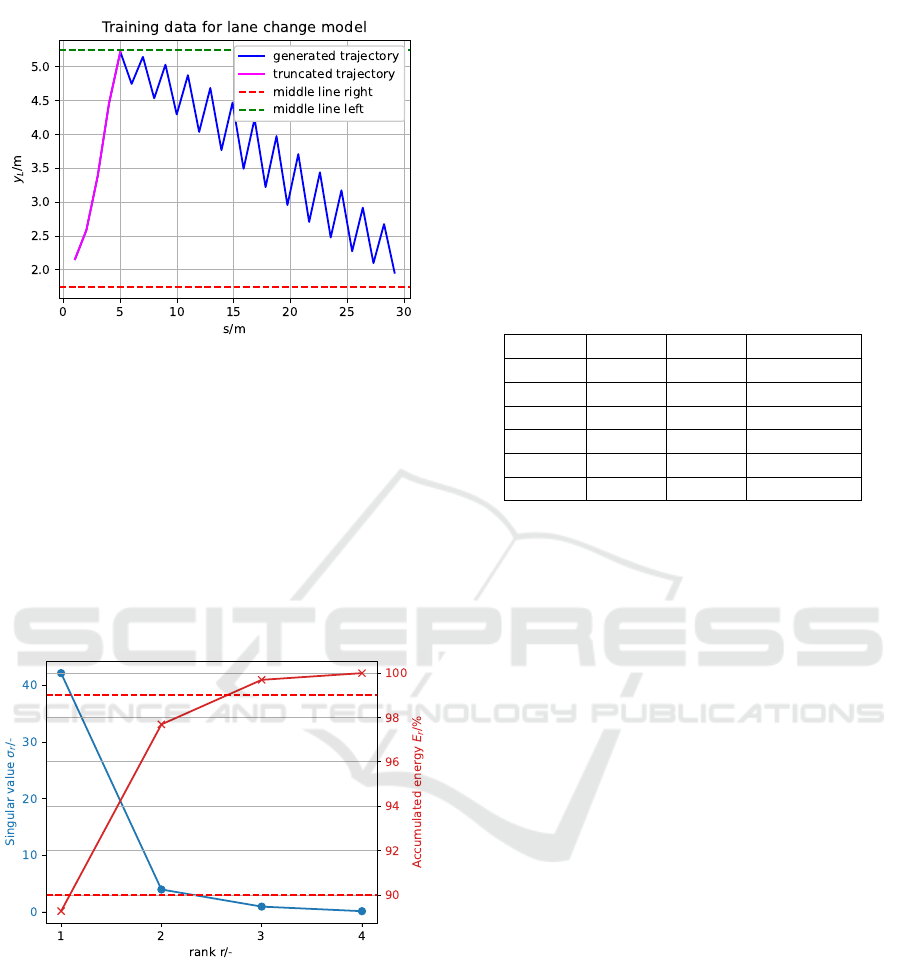
Figure 4: An exemplary original trajectory used for training

the system matrix A

A or

A illustrates a disadvantage of choos-

ing this model when the longitudinal displacement (s

)

reaches the maximum longitudinal sinusoidal length d

, as

explained in Equation 7.

Subsequently, strong oscillations occur, stemming

from the constant acceleration model used for longi-

tudinal movement, impacting the lateral movement as

well. Therefore, the generated data needs truncation

before further model training. However, this trunca-

tion results, as shown in magenta, in shorter trajec-

tories than anticipated, potentially leading to model

overﬁtting.

Figure 5: The sorted singular values σ

and their accumu-

lated energy E

are visualized against their ranks r, using

the example of monomial basis functions. Horizontal lines

representing the empirical values E

= 90% and E

= 99%

are also plotted to aid in identifying their corresponding sin-

gular value.

Now, the truncated trajectory is subjected to trun-

cated SVD by constructing the matrix X

X and sorting

its singular values σ

. The accumulated energy E

calculated for each singular value, and their values

are plotted in Figure 5 using monomial basic func-

tions. In this example, it is observed that approxi-

mately E

= 90 % is achieved directly at the ﬁrst sin-

gular value (E

≈89%), as it is relatively large (≥30)

compared to the others. According to the plot, the

third singular value corresponds to E

= 99%.

However, upon calculating the hard threshold rank

, it is found that it exceeds 4. Therefore, the full

rank is used in this case instead. Additionally, simi-

lar observations have been made for the radial basis

functions, resulting in identical rank selections.

Table 1: Comparison of the truncated SVD performance

= 90%, E

= 99% and HT : hard threshold) based on

different basis functions (m: monomial and r: thin plate

spline radial), including metrics such as the relative recon-

struction error and the time consumption.

Basis rank r RE

/% min{

}/%

m,90%

1 99.54 89.97

m,99%

3 95.76 96.47

m,HT

4 (full) 0 100

r,90%

1 98.14 95.16

r,99%

3 60.81 97.21

r,HT

4 (full) 0 100

The relative reconstruction error RE

and the min-

inmal relative time consumption min{

} of the sys-

tem matrix A

A are compared in Table 1. It is observed

for each type of basis function that the reconstruction

error decreases with higher rank selections.

Additionally, in the lane change model with the

previously collected data, the radial basis function

demonstrates superior model ﬁdelity. However, with

truncated SVD, the reconstruction errors are rela-

tively large (> 50%), prompting the use of the full-

ranked matrix A

A due to the hard threshold.

Furthermore, truncated SVD does not consistently

reduce time consumption, as evidenced by cases

where

exceeds 100 %. The minimal time consump-

tion is highlighted here, underscoring the potential for

reduced computation time with truncated SVD.

4 CONCLUSIONS

This study investigates the efﬁcacy of truncated SVD

in conjunction with Koopman operators and EDMD

for system identiﬁcation in the context of lane change

behavior. The results indicate that while these tech-

niques do not necessarily lead to a signiﬁcant reduc-

tion in the computational time required for training

the system matrix, they entail a compromise in model

ﬁdelity.

To validate these ﬁndings, future research will

explore the use of diverse datasets for training and

conduct a more comprehensive statistical analysis, as

well as analyze controllers not covered here.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

682

REFERENCES

Abraham, I., Torre, G. D. L., and Murphey, T. D.

(2017). Model-based control using koopman opera-

tors. CoRR, abs/1709.01568.

Bongiovanni, N., Mavkov, B., Martins, R., and Allibert,

G. (2024). Data-Driven Nonlinear System Identiﬁca-

tion of a Throttle Valve Using Koopman Representa-

tion. In American Control Conference (ACC 2024),

Toronto, Canada.

Brunton, S. L., Budi

c, M., Kaiser, E., and Kutz, J. N.

(2021). Modern koopman theory for dynamical sys-

tems.

Brunton, S. L. and Kutz, J. N. (2019). Data-Driven Science

and Engineering: Machine Learning, Dynamical Sys-

tems, and Control. Cambridge University Press, USA,

1st edition.

Buzhardt, J. and Tallapragada, P. (2022). A koopman op-

erator approach for the vertical stabilization of an off-

road vehicle. IFAC-PapersOnLine, 55(37):675–680.

2nd Modeling, Estimation and Control Conference

MECC 2022.

Chen, H., He, X., Cheng, S., and Lv, C. (2024a). Deep

koopman operator-informed safety command gover-

nor for autonomous vehicles. IEEE/ASME Transac-

tions on Mechatronics, pages 1–11.

Chen, Z., Chen, X., Liu, J., Cen, L., and Gui, W. (2024b).

Learning model predictive control of nonlinear sys-

tems with time-varying parameters using koopman

operator. Applied Mathematics and Computation,

470:128577.

Cibulka, V., Hanis, T., and Hromcik, M. (2019). Data-

driven identiﬁcation of vehicle dynamics using koop-

man operator. 2019 22nd International Conference on

Process Control (PC19), pages 167–172.

Gavish, M. and Donoho, D. L. (2014). The optimal hard

threshold for singular values is 4/

√

3. IEEE Transac-

tions on Information Theory, 60(8):5040–5053.

Guo, W., Zhao, S., Cao, H., Yi, B., and Song, X.

(2023). Koopman operator-based driver-vehicle dy-

namic model for shared control systems. Applied

Mathematical Modelling, 114:423–446.

Gupta, S., Shen, D., Karbowski, D., and Rousseau, A.

(2022). Koopman model predictive control for eco-

driving of automated vehicles. In 2022 American Con-

trol Conference (ACC), pages 2443–2448.

Han, Y., Hao, W., and Vaidya, U. (2020). Deep learning

of koopman representation for control. In 2020 59th

IEEE Conference on Decision and Control (CDC),

pages 1890–1895.

Joglekar, A., Samak, C., Samak, T., Kosaraju, K. C.,

Smereka, J., Brudnak, M., Gorsich, D., Krovi, V., and

Vaidya, U. (2023). Analytical construction of koop-

man edmd candidate functions for optimal control

of ackermann-steered vehicles. IFAC-PapersOnLine,

56(3):619–624. 3rd Modeling, Estimation and Con-

trol Conference MECC 2023.

Kim, J. S., Quan, Y. S., and Chung, C. C. (2022). Data-

driven modeling and control for lane keeping sys-

tem of automated driving vehicles: Koopman opera-

tor approach. In 2022 22nd International Conference

on Control, Automation and Systems (ICCAS), pages

1049–1055.

Kim, J. S., Quan, Y. S., and Chung, C. C. (2023). Koop-

man operator-based model identiﬁcation and control

for automated driving vehicle. International Jour-

nal of Control, Automation and Systems 21, page

2431–2443.

Koopman, B. O. (1931). Hamiltonian systems and transfor-

mation in hilbert space. Proceedings of the National

Academy of Sciences, 17(5):315–318.

Manzoor, W. A., Rawashdeh, S., and Mohammadi, A.

(2023). Vehicular applications of koopman operator

theory—a survey. IEEE Access, 11:25917–25931.

Mauroy, A. and Goncalves, J. (2020). Koopman-based

lifting techniques for nonlinear systems identiﬁca-

tion. IEEE Transactions on Automatic Control,

65(6):2550–2565.

Schreier, M. (2017). Bayesian environment representa-

tion, prediction, and criticality assessment for driver

assistance systems. at - Automatisierungstechnik,

65(2):151–152.

Wilson, D. (2023). Koopman operator inspired nonlinear

system identiﬁcation. SIAM Journal on Applied Dy-

namical Systems, 22(2):1445–1471.

Xiao, Y., Zhang, X., Xu, X., Liu, X., and Liu, J. (2023).

Deep neural networks with koopman operators for

modeling and control of autonomous vehicles. IEEE

Transactions on Intelligent Vehicles, 8(1):135–146.

Yu, S., Shen, C., and Ersal, T. (2022a). Autonomous driv-

ing using linear model predictive control with a koop-

man operator based bilinear vehicle model. IFAC-

PapersOnLine, 55(24):254–259. 10th IFAC Sympo-

sium on Advances in Automotive Control AAC 2022.

Yu, S., Sheng, E., Zhang, Y., Li, Y., Chen, H., and Hao, Y.

(2022b). Efﬁcient nonlinear model predictive control

of automated vehicles. Mathematics, 10(21).

Analysis of Truncated Singular Value Decomposition for Koopman Operator-Based Lane Change Model

683