A Comparison of Advanced Machine Learning Models for Food Import

Forecasting

Corrado Mio

and Siddhartha Shakya

EBTIC, Khalifa University of Science and Technology, Abu DHabi, U.A.E.

Keywords:

Food Import, Time Series, Forecasting, Neural Network.

Abstract:

Food security is responsible for food availability, access and price stability. Food import is used to ensure

availability when local production is inadequate and diversity when local production is not possible. Food

import prediction is one of the tools used to ensure food security. In this case study, we analyze Neural

Network Forecasting models applied to a food import dataset to understand whether these models, when

applied to small time series, perform better than statistical or regression models. And if it is better to use short

or long forecast horizons.

1 INTRODUCTION

In 1996 the World Food Summit (Shaw, 1996), de-

ﬁned food security as the condition in which all indi-

viduals have access to food in a simple and economi-

cal way. There are four important aspects to consider,

as deﬁned by the Food and Agriculture Organization

(FAO) (FAO, 2006):

• Availability. Food availability depends on local

production, import, distribution, and market.

• Stability. Stability in food security is about the

access and can depend on political or economical

conditions.

• Access. Access to food is physical (it is physically

available near where the consumer lives) and eco-

nomical (it is not expensive).

• Utilization. Food utilization is related to nutri-

tional ability, preparation, and healthcare.

Food imports are used to help insufﬁcient local

production, to ensure stable prices, and to increase the

diversity of food availability.

To ensure food security and to assist economic

planning, the main tool is forecasting, a mix of art (be-

cause to select the model to use is based on expert’s

experience) and science based on historical data, used

to predict future requirements. Unfortunately, there

is no best prediction model, due to the inﬁnite be-

haviors of history. In practice, different models are

https://orcid.org/0000-0002-1087-4866

https://orcid.org/0000-0002-9924-9222

tested to ﬁnd the one with the best performance for

each time series, using some measurement that evalu-

ates the quality of the prediction.

In our research, we analyze complex datasets that

contain several time series that cover production, ex-

port, and import of different products from different

countries. Regularities are rare, forcing the neces-

sity to use an approach in which multiple models are

tested to identify the best one for each time series. In

this work, only Neural Network models are analyzed,

with the aim of improving our forecasting system and

enhancing the prediction accuracy.

The rest of the paper is organized as follows. Sec-

tion 2 a literature review is presented where Machine

Learning algorithms are used for food import predic-

tions. Section 3 presents the main concepts used in

the article. Section 4 describes the dataset used in the

experiments. Section 5 describes the algorithms used,

with a short description of each of them. The results

of the experiments are described in Section 6. Sec-

tion 7 concludes this work.

2 RELATED WORKS

Forecasting can be obtained using one of several mod-

els available for analysis, from simple linear models

(Mahalakshmi et al., 2016) to ones based on neural

networks (Mahmoud and Mohammed, 2021). One of

the most used models is ARIMA (Auto-regressive In-

tegrated Moving Average), studied in (Sharma et al.,

568

Mio, C. and Shakya, S.

A Comparison of Advanced Machine Learning Models for Food Import Forecasting.

DOI: 10.5220/0012998100003837

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 568-575

ISBN: 978-989-758-721-4; ISSN: 2184-3236

2018; Fattah et al., 2018; Mahajan et al., 2020).

ARIMA is just a member of a rich set of models com-

prising SARIMAX (ARIMA for Seasonal series with

eXogenous variables) (Choiriyah et al., 2020). Be-

cause ARIMA is a linear model, it is not able to

detect non-linear behaviors. In this case, it is pos-

sible to use other models as Even Gray Forecast-

ing model (EGF) (Song et al., 2020) or Recursive

Dynamic model (Sheng and Song, 2019), but sev-

eral others are available. A rich class of non-linear

models is based on neural networks, such as models

based on Recurrent Neural Network (RNN) (Alka-

abi and Shakya, 2022; Khargharia et al., 2022) and

Convolutional Neural Network (CNN) (Rathod et al.,

2018). In recent years, an alternative to the RNN

has emerged: the Transformer, based on the Atten-

tion Mechanism (Vaswani et al., 2017). This model

is more efﬁcient and scales better than classical RNN,

and, given its properties, it has been used also in time

series models (Wen et al., 2022).

In the article (Mio et al., 2023) they compare 33

models, discovering that the SARIMAX and KNN-

based models are competitive against more complex

strategies. In theory, the main problem of complex

models is the high number of parameters to train,

which, together with the small size of time series,

does not allow one to obtain sufﬁciently robust mod-

els. However, this hypothesis needs to be veriﬁed.

In this work we investigate Neural Network mod-

els speciﬁc to time series (Table 3) as Transformer

(Liu et al., 2023), N-BEATS (Neural basis expan-

sion analysis for interpretable time series) (Oreshkin

et al., 2019), N-HiTS (Neural hierarchical interpola-

tion for time series) (Challu et al., 2023), DLinear

(Dense Linear Neural Network) (Zeng et al., 2023),

NLinear (Reversible normalization for accurate time-

series) (Kim et al., 2021) TCN (Temporal convolu-

tional Neural Network) (Hewage et al., 2020), TFT

(Temporal fusion transformers) (Lim et al., 2021),

TiDE (Time-series dense encoder) (Das et al., 2023),

TSMixer (Lightweight MLP-Mixer model for multi-

variate Time Series) (Ekambaram, 2023)

3 BACKGROUND

In a time series (TS) there exists a temporal order

between its values, that is, the value in the time

slot t

depends on what happened in previous ones

. . . , t

k−2

k−1

In a time series (TS) there exists a temporal order

between its values. For any integer i, the value i in

k−i

indicates the past time slot from the reference t

and is named lags.

A TS is univariate (for each time slot there is a sin-

gle value) or multivariate. It can contain exogenous

variables (input features) that can be used to improve

prediction. In turn, the exogenous variables can be

classiﬁed into two categories: 1) variables whose val-

ues are known only in the past (for example the daily

temperature), 2) variables whose values are known

also in the future (for example the day of week).

In this work, we are interested only in univariate

TS with exogenous variables of the ﬁrst category.

Let X be the input features, y the target, y

the cur-

rent target value to predict, and L ⊂ N

the set of past

lags (for example L = {1, 2}) from the current time

slot t = 0, F the forecasting model used for the pre-

dictions and H (for example H = {0}) the forecasting

horizon (FH), that is the list of future lags where the

target must be predicted.

The models can be classiﬁed according to how

they use the past to predict the current target and how

they use the predicted values to ﬁll the FH (Mio et al.,

2023; Alzaidi et al., 2022):

∀t, u : t ∈ L ⊂ N

, u ∈ L

⊂ N

1) y

= F(y

i−t

)

2) y

= F(y

i−t

, X

i−t

)

3) y

= F(y

i−t

, X

i−u

)

1. the prediction depends only on the past lags t

speciﬁed in L (L

2. as 1) where input features are used, at the same

past lags (L

= L)

3. as 2) where lags for the target (t) and input fea-

tures (u) are selected separately (L

̸= L)

Case 1) is used when the model is not able to use

input features (for example ARIMA or some mod-

els based on RNN). Case 2) is used often with neu-

ral network models because they require in input a

tensor where the data dimension containing the target

and, when available, the correspondent input features.

Case 3) is used with tabular models (for example, Lin-

ear Regression, KNN) because the columns of the ma-

trix can be selected in arbitrary way. In this work only

case 1) and case 2) models were used.

To predict the target for the complete FH H =

{0, 1, 2. . . } there are different strategies. The ﬁrst is

to use the current prediction y

to predict the next one

i+1

, then, to use y

i+1

to predict y

i+2

and so on, in the

recursive way (“recursive” column in Table 1). The

second approach is to use different instances of the

same algorithm F for each time slot (“models” col-

umn of Table 1) and the third is to predict the com-

plete horizon in a single step (“horizon” column of

A Comparison of Advanced Machine Learning Models for Food Import Forecasting

569

Table 1: Prediction of the forecasting horizon using multi-

ple steps or multiple models.

recursive models

i+0

= F(y

i−t

, X

i−t

) y

i+0

= F

i−t

, X

i−t

)

i+1

= F(y

i−t+1

, X

i−t+1

) y

i+1

= F

i−t

, X

i−t

)

·· · ·· ·

i+h

= F(y

i−t+h

, X

i−t+h

) y

i+h

= F

i−t

, X

i−t

)

t ∈ L ⊂ N

h ∈ H ⊂ N

Table 2: Prediction of the forecasting horizon in a single

step using a single model.

horizon

i+h

} = F(y

i−t

, X

i−t

)

t ∈ L ⊂ N

, h ∈ H ⊂ N

Table 2). This method can be used only when the

algorithm is capable of processing multivariate TS:

in this case, the multiple target values are the predic-

tions in FH. In theory this reduces error propagation,

but it doesn’t use recent information. An intermediate

approach (direct+recursive) is to predict a small win-

dow of consecutive time slots, than to move the win-

dow to cover the horizon. This approach is reasonable

when the forecasting window is not predeﬁned. Hav-

ing multiple instances of the same algorithm to pre-

dict different (not) overlapped windows seems not to

be very useful.

4 THE DATASET

4.1 General Structure

The dataset analyzed contains monthly imports for 51

different products from 54 countries over a period of

7 years (7 × 12 = 84 months). It includes 352 TS,

arranged in 29568 (= 352 ×84) rows and 12 columns.

The columns can be classiﬁed into 5 categories:

1. the column specifying which product is imported

from which country (string). It is used as time

series identiﬁer

2. the import date (datetime)

3. the quantity of imported product (ﬂoat), the TS

target

4. 5 columns containing ﬁnancial information (the

ﬁrst set of input features, ﬂoats)

5. 4 columns containing weather information (the

second set of input features, ﬂoats)

We used a seasonality of 12 months because this

is the most common among all TS.

Figure 1: Correlations between imported products and

weather/ﬁnancial features. From top to bottom: a) dataset

as single time series, b) based on product, c) based on coun-

try, d) based on product/country (3 rows) .

Analyzing the correlation between the target and

the ﬁnancial and weather features, using the Pearson

correlation index, we found that:

1. considering the dataset as a single TS, there is not

an evident correlation between the target and the

other features: in Figure 1 (a), all cells are dark

(very low correlation) except the ﬁrst one (the cor-

relation of the target with itself)

2. considering the TS based only on products, there

are light correlations with the weather features: in

Figure 1 (b), the weather rows contain more light

cells than the ﬁnancial rows

3. considering the TS based only on countries, there

are light correlations with the ﬁnancial features:

in Figure 1 (c), the ﬁnancial rows contain more

light cells than the weather rows

4. analyzing each TS separately, there are correla-

tions with both feature sets: in Figure 1 (d), the

light cells are distributed in all rows

The existence of (light) correlations between tar-

get and input features suggests that the prediction

could be improved if they are included in the train-

ing.

4.2 Time Series

A visual inspection of the TS “time vs target” plots

highlights some patterns:

1. evident seasonality (Figure 2 (a))

to visualize all 352 TS in the image, they are organized

in 3 rows each one with 117 columns

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

570

Figure 2: Some examples of time series patterns: a) with

seasonality, b) trend without seasonality, c) with spikes, d)

noisy, e) heteroscedastic.

2. trend but without an evident seasonality (Figure 2

(b))

3. occasional import spikes (Figure 2 (c))

4. noisy behavior (Figure 2 (d))

5. heteroscedastic behavior (Figure 2 (e))

The Augmented Dickey-Fuller test is used to ana-

lyze the TS stationarity: we found 211 TS (69.9%) al-

ready stationary, 100 (28.4%) stationary after the ﬁrst

differencing, 29 (8.2%) after the second one and 13

(3.7%) at the third one.

The Autocorrelation Function is used to under-

stand if the series behaves as a random walk, it con-

tains trend or seasonality. There are 157 TS (44.6%)

with a random walk-like behavior, 64 (18.2%) with

a trend, 60 (17.0%) with seasonality, 18 (5.1%) with

trend and seasonality. The remaining 53 TS (15.0%)

have unclassiﬁable behavior.

The Partial Autocorrelation Function is used to

identify the auto-regressive behavior, that is, if the TS

behavior depends on the past. There are 128 (36.4%)

TS without an evident dependency on the past, 221

(62.8%) with a dependency only with the previous

time slot (lag=1) and 3 (0.9%) with a dependency

with time slots with lag equals to 2.

The Breusch-Pagan test is used to understand if

the series is heteroscedastic, that is, if mean and stan-

dard deviation change over time. We found 137 TS

(38.9%) having this behavior.

These results suggest there is no single algorithm

able to forecast accurately all TS. For each series mul-

tiple schemes must be tested in order to select the best

candidate.

5 ALGORITHMS AND

METHODOLOGY

5.1 Algorithms

In a previous article, we used statistical/regression

models. In this set of experiments, we have used the

algorithms in Table 3: the statistical models are used

for the comparisons, while the rest are based on neu-

ral networks:

1. tabular models Linear and KNN, used as reference

2. statistical models SARIMAX and GARCH, used

as reference

3. simple NN model composed by one or two dense

layers

4. Recurrent Neural Networks, followed by a simple

dense layer (RNN, GRU, LSTM)

5. models based on CNN (CNN, TCN)

6. Transformer architectures (Transformer, TFT)

7. models that extract temporal correlations at differ-

ent time resolutions (N-HiTS, N-BEATS)

8. encoder/decoder architectures with simple linear

blocks (TiDE, TSMixer)

All algorithms are part of, or integrated into, the

Python library sktime (L

oning et al., 2019). We

have included SARIMAX and GARCH strategies

(in 2 variants) from sktime, 10 NN models imple-

mented in-house (simple NN based on RNN, GRU,

LSTM, CNN layers followed by a dense layer, a lin-

ear model with a single layer and another one with 2

dense layers), and 12 NN from Darts library (Herzen

et al., 2022). All NN are implemented with PyTorch

(Paszke et al., 2023). The tabular schemes (Linear and

KNN) are part of scikit-learn (Pedregosa et al.,

2011) library and wrapped in such a way that they

can be used with TS. In total, there are 25 different

models.

• Linear regression, KNN regression are two clas-

sical algorithms used to approximate the function

Y = F(X). They can be used as TS model trans-

forming the TS data in tabular format following

one of the strategies described in Section 3

A Comparison of Advanced Machine Learning Models for Food Import Forecasting

571

Table 3: List of models speciﬁc for time series, used in ex-

periments.

name algo article

Linear regression lin

KNN regression knn (Bentley, 1975)

SARIMAX arima (Hyndman et al., 2008)

GARCH garch (Bollerslev, 1986)

One Linear Layer lnnlin (in-house)

Two Linear Layers lnnlin2 (in-house)

DLinear dlinear (Zeng et al., 2023)

NLinear nlinear (Kim et al., 2021)

GRU gru (Chung et al., 2014)

LSTM lstm (Chung et al., 2014)

RNN rnn (Chung et al., 2014)

CNN cnn (Liu et al., 2019)

TCN tcn (Hewage et al., 2020)

Transformer transf. (Ahmed et al., 2023)

N-BEATS nbeats (Oreshkin et al., 2019)

N-HITS nhits (Challu et al., 2023)

TFT tft (Lim et al., 2021)

TiDE tide (Das et al., 2023)

TSMixer tsmixer (Ekambaram, 2023)

• SARIMAX (Seasonal ARIMA with eXogenous

variables) is a linear model considering the time

series composed by two major components (the

seasonal component and the stationary compo-

nent) and each major component composed by 3

parts: a Moving Average part, an Autoregressive

part and an Integrated differencing step, used to

convert a polynomial behavior in a stationary one

• GARCH (Generalized Autoregressive Condi-

tional Heteroscedasticity) is another linear model,

similar to ARIMA, but it is used when mean and

variance of a TS changes (in a autoregressive way)

with the time

• One Linear Layer, Two Linear Layers, DLin-

ear are simple NN models composed by 1 or 2

dense layers. In the article (Zeng et al., 2023) it

was observed that if a simple dense layer works

well, more complex models do not necessarily

work better

• NLinear can be considered the NN version of

GARCH: to handle the distribution shift, a sim-

ple linear model is integrated a learnable (and

reversible) module with the responsibility to re-

move, and to re-add, the TS heteroscedasticity

• RNN, GRU, LSTM are Recurrent Neural Net-

works, used in Natural Language Processing area,

applied to TS analysis for the correspondence be-

tween a sentence (a sequence of words) and a TS

(a sequence of values). The have some limits: the

model is able to handle only values in the range

[0, 1], for each element in the sequence, it consid-

ers only the previous one, and the sequence must

be processed sequentially

• CNN (Convolutional Neural Network 1-

dimensional) is a classical NN used in signal

processing. The main difference from a RNN

is that, for each element in the channel (the

equivalent of the sequence), it is considered just

a small number of elements before and after the

current one

• TCN (Temporal Convolutional Neural Network)

is a model composed by multiple CNN layers

where in each layer, for each element in the chan-

nel, it is considered some elements before and af-

ter the current one, but at distance k2

where l is

the index layer. This approach permits to consider

long-range temporal effects

• Transformer is the current replacement for all

RNN models: it permits to process the sequence

in parallel, and it learns the best correlation be-

tween all elements in the sequence against them-

selves

• N-BEATS is a model organized into 3 levels. The

ﬁrst one, the basic block, with the responsibility

to receive in input the past data or the backcast

from the previous block, and to emit the back-

cast and the forecast. The second level, the stack

block, put in sequence multiple basic blocks, con-

nected using the backcast and adding, between

the block’s input and backcast’s output, a resid-

ual link. The stack block has two outputs: the

residual output from the last basic block, and the

stack forecast (sum of forecasts output from inter-

nal basic blocks). The third level put in sequence

multiple stack blocks and emits the prediction as

sum of internal stack forecasts

• N-HiTS it is an improvements of N-BEATS. It ex-

tends the previous basic block adding a sampling

layer. In this way, each block in the stack block,

analyzes the data at a different frequency

• TFT (Temporal Fusion Transformer) is a complex

architecture, composed by a RNN layer, with out-

put enriched by a residual links, a Multi-head At-

tention layer, with the responsibility to identify

the more relevant information, and a ﬁnal set of

normalization and dense layers, used to generate

the predictions

• TiDE has an encoder-decoder architecture where

encoders and decoders are composed by a stack

of simple building blocks. Each building block

comprises: 2 dense layers, separated by a ReLU,

a Dropout layer and a ﬁnal normalization layer.

As in previous models, the output of the Dropout

layer is enriched with a residual link. The out-

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

572

put of the decoder is the output of a Temporal De-

coder, a simple residual block with the responsi-

bility to convert the bi-dimensional tensor emitted

by the decoder in the uni-dimensional predicted

target

• TSMixer is another model based on simple dense

layers, but using a patch-based strategy to enrich

the input. A patch-strategy consists of covering

each target’s value at time slot t into a small vector

composed by the values at time slots t, t + 1, . . . ,t

(the patch).

Except for SARIMAX and GARCH, Linear and

KNN models and those based on NN require speci-

fying the number of past lags to use and how many

future lags to predict. In the experiments, we used 24

months for the past and 12 months as FH. The pre-

diction can be performed with a window of 1,3,6,12

months. Cases with windows shorter than one year

use the recursive method to cover the entire horizon.

In total, we have 97 experiments for each TS, for a

total of 34144 (= 97 × 352) experiments.

5.2 Methodology

Many NN models coming from the Natural Language

Processing world (RNN, GRU, LSTM, Transformer),

cannot handle values outside the range [0, 1]. To ob-

tain a comparable behavior between all models, all

TS are normalized using the following rules: all tar-

get values that exceed 4

standard deviations above or

below the mean, are replaced with the median value

and all values are scaled in the range [0, 1].

We have used algorithms with minimal tuning be-

cause they work well with the default parameters.

For all NN models, we have used a maximum of

100 training epochs, integrated with an early stop-

ping mechanism: this reduces the training time if the

model reaches a conﬁguration with a stable loss. The

loss metric used is the mean square error.

5.3 Prediction Quality

To evaluate the quality of the prediction, we have used

the WAPE score, deﬁned as:

WAPE =

∑

− ˆy

∑

where i is the forecasting time slot, y

the actual

value and ˆy

the predicted one.

When applied to the entire data set D, y

and ˆy

are

computed as

This is the standard value used in our system

Table 4: Forecasting horizon length in the best predictions.

pos fh length freq

1 1 116

2 3 85

3 12 81

4 6 70

∑

ˆy

∑

ˆy

that is, the dataset is considered as a single TS

where the monthly import (y

) is the sum of the im-

ports in the same month from all TS (y

). The same

rule is applied to the predicted values (ˆy

, ˆy

The global score, the prediction quality, is deﬁned

as:

PQ = 1 − WAPE

6 EXPERIMENTAL RESULTS

The questions are: is it true that by predicting the

complete FH we get better predictions? Are NN mod-

els really better than statistical or regression ones?

Table 4 shows that it is not always necessary to use

a FH longer than a single time slot. In fact, in 116 of

352 cases (33.0%) we obtain the best prediction using

only a single future time slot. Longer horizons work

well for the remaining cases, but there is no second

better choice.

Table 5 shows that the LSTM model delivers

the best prediction for the highest number of cases

(56 times, 15.9%), followed by the Transformer (48

times, 13.6%). In third position we found a sim-

ple NN model based on two dense layers (lnnlin2,

36 times, 10.2%). The most advanced NN models

(nbeats, tft, etc) trail the simple CNN model. The

worst results come from Linear Regression, KNN,

SARIMAX and GARCH, with the last two never de-

livering the best result.

If we consider the algorithms and the FH length

(Table 6), we ﬁnd Transformer architectures 3 times

in the ﬁrst 10 positions. We also ﬁnd lnnlin2 (lin-

ear NN model with 2 layers), lstm and cnn, simple

models, based on the LSTM and CNN layers, in the

top ten. In the last 3 positions, we ﬁnd linear (ﬂat-

ten) (the only case where we obtain the best prediction

from a dedicated model for each time step), KNN and

N-HITS with 12 months. The other 3 variants of N-

HITS (1,3,6 months) perform better but do not reach

the top positions.

Compared to the work (Mio et al., 2023), where

the statistical and regression models achieved a pre-

A Comparison of Advanced Machine Learning Models for Food Import Forecasting

573

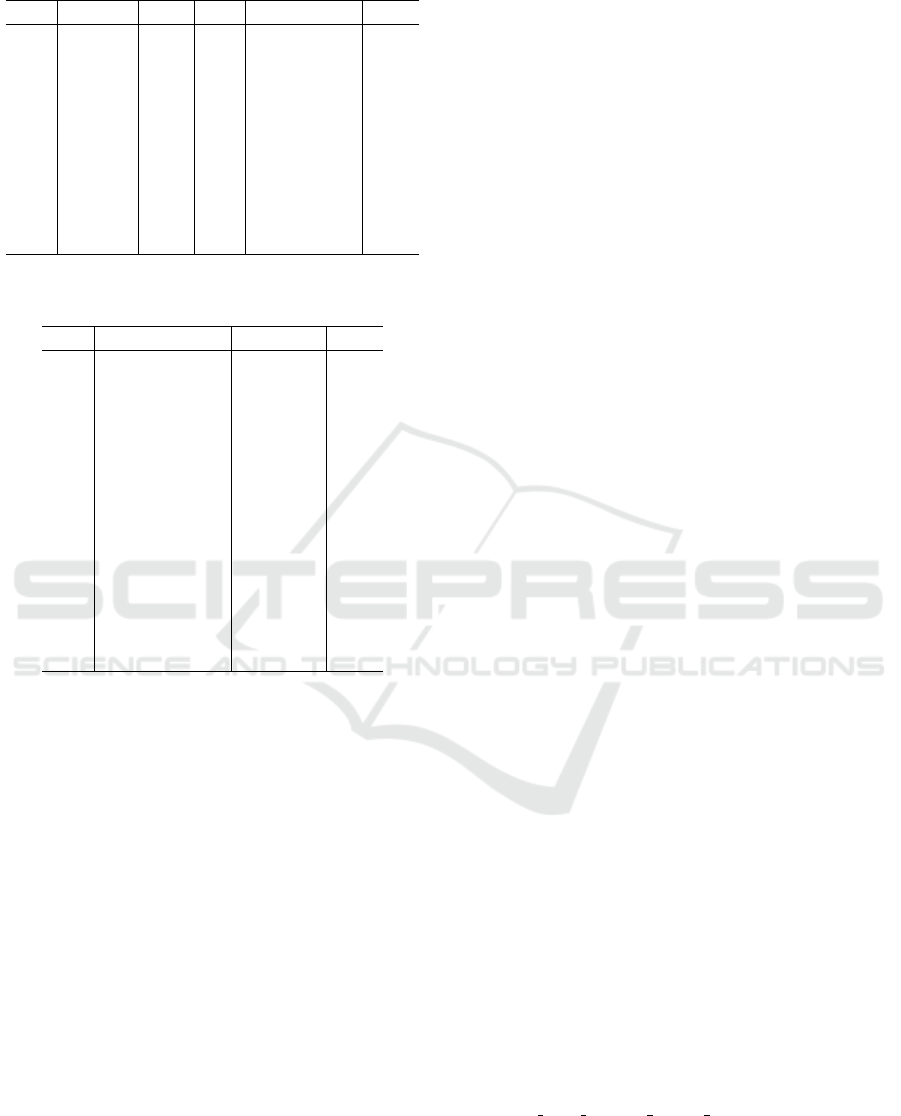
Table 5: Algorithms yielding the best predictions.

pos algo freq pos algo freq

1 lstm 56 2 transformer 48

3 lnnlin2 36 4 rnn 32

gru 32 5 cnn 21

6 nbeats 20 tsmixer 20

tft 20 7 tcn 18

8 tide 10 nlinear 10

9 nhits 8 10 lnnlin 7

11 knn 6 12 dlinear 5

13 lin 3 14 arima 0

garch 0

Table 6: Algorithms and forecasting horizon giving the best

predictions.

pos algo fh length freq

1 transformer 1 19

2 transformer 3 14

3 lnnlin2 1 11

4 txmixer 1 10

5 lstm 3 10

6 lnnlin2 12 10

7 transformer 12 9

8 cnnlin 1 9

9 tcn 1 9

10 nbeats 1 9

...

75 linear (ﬂatten) 12 6

76 knn 12 3

77 nhits 12 3

diction quality of 88.6%, using for each TS the best

model (selected between the models used in this

work) this value reached 96.5%.

7 CONCLUSIONS

The objective is to create a framework that can auto-

mate the forecasting of expected imports for our part-

ner organizations. This system analyzes the received

TSs using a set of models, identiﬁes the best model

for each TS, then uses these models for predictions.

To this end, we continue to improve our infrastruc-

ture and analyze the quality of the models proposed

in the literature on a controlled set of real data.

In this new set of experiments, we have found that:

1) 1-step ahead forecasting is much closer to model-

ing than to prediction, 2) models based on Transform-

ers work well, 3) simple NN models, based on LSTM

and CNN, perform better than more complex ones,

and 4) NN schemes can deliver better predictions than

statistical/regression ones.

Future lines of improvement include autotuning,

based on some advanced tuning strategy (for exam-

ple using the Bayesian Optimization) and investigat-

ing the Fundation Time Series Models, NN models

pretrained on thousands of TS, which may be able to

generate good predictions without additional training.

REFERENCES

Ahmed, S., Nielsen, I. E., Tripathi, A., Siddiqui, S., Ra-

machandran, R. P., and Rasool, G. (2023). Trans-

formers in time-series analysis: A tutorial. Circuits,

Systems, and Signal Processing, 42(12):7433–7466.

Alkaabi, N. and Shakya, S. (2022). Comparing ml mod-

els for food production forecasting. In Artiﬁcial Intel-

ligence XXXIX: 42nd SGAI International Conference

on Artiﬁcial Intelligence, AI 2022, Cambridge, UK,

December 13–15, 2022, Proceedings, pages 303–308.

Springer.

Alzaidi, A., Shakya, S., and Khargharia, H. S. (2022). In-

vestigating prediction models for vehicle demand in a

service industry. In IJCCI, pages 359–366.

Bentley, J. L. (1975). Multidimensional binary search trees

used for associative searching. Communications of the

ACM, 18(9):509–517.

Bollerslev, T. (1986). Generalized autoregressive condi-

tional heteroskedasticity. Journal of econometrics,

31(3):307–327.

Challu, C., Olivares, K. G., Oreshkin, B. N., Ramirez, F. G.,

Canseco, M. M., and Dubrawski, A. (2023). Nhits:

Neural hierarchical interpolation for time series fore-

casting. In Proceedings of the AAAI conference on

artiﬁcial intelligence, volume 37, pages 6989–6997.

Choiriyah, E., Syaﬁtri, U. D., and Sumertajaya, I. M.

(2020). Pengembangan model peramalan space time:

Studi kasus: Data produksi padi di sulawesi selatan.

Indonesian Journal of Statistics and Its Applications,

4(4):579–589.

Chung, J., Gulcehre, C., Cho, K., and Bengio, Y.

(2014). Empirical evaluation of gated recurrent neu-

ral networks on sequence modeling. arXiv preprint

arXiv:1412.3555.

Das, A., Kong, W., Leach, A., Mathur, S., Sen, R.,

and Yu, R. (2023). Long-term forecasting with

tide: Time-series dense encoder. arXiv preprint

arXiv:2304.08424.

Ekambaram, V. e. a. (2023). Tsmixer: Lightweight mlp-

mixer model for multivariate time series forecasting.

In Proceedings of the 29th ACM SIGKDD Conference

on Knowledge Discovery and Data Mining, pages

459–469.

FAO (2006). Food security. https://www.fao.org/

ﬁleadmin/templates/faoitaly/documents/pdf/

pdf Food Security Cocept Note.pdf. Accessed:

2023-06-14.

Fattah, J., Ezzine, L., Aman, Z., El Moussami, H., and

Lachhab, A. (2018). Forecasting of demand using

arima model. International Journal of Engineering

Business Management, 10:1847979018808673.

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

574

Herzen, J., L

A¤ssig, F., Piazzetta, S. G., Neuer, T.,

Tafti, L., Raille, G., Pottelbergh, T. V., Pasieka,

M., Skrodzki, A., Huguenin, N., Dumonal, M.,

cisz, J., Bader, D., Gusset, F., Benheddi,

M., Williamson, C., Kosinski, M., Petrik, M.,

and Grosch, G. (2022). Darts: Time series

made easy in python. https://unit8.com/resources/

darts-time-series-made-easy-in-python/. Accessed:

2024-07-04.

Hewage, P., Behera, A., Trovati, M., Pereira, E., Ghahre-

mani, M., Palmieri, F., and Liu, Y. (2020). Tempo-

ral convolutional neural (tcn) network for an effec-

tive weather forecasting using time-series data from

the local weather station. Soft Computing, 24:16453–

16482.

Hyndman, R. J., Khandakar, Y., and Khandakar, Y. (2008).

Automatic time series forecasting: the forecast pack-

age for r. Journal of statistical software, 27:1–22.

Khargharia, H. S., Shakya, S., Sharif, S., Ainslie, R., and

Owusu, G. (2022). On predicting the work load for

service contractors. In Artiﬁcial Intelligence XXXIX:

42nd SGAI International Conference on Artiﬁcial In-

telligence, AI 2022, Cambridge, UK, December 13–

15, 2022, Proceedings, pages 223–237. Springer.

Kim, T., Kim, J., Tae, Y., Park, C., Choi, J.-H., and Choo,

J. (2021). Reversible instance normalization for accu-

rate time-series forecasting against distribution shift.

In International Conference on Learning Representa-

tions.

Lim, B., Arık, S.

O., Loeff, N., and Pﬁster, T. (2021).

Temporal fusion transformers for interpretable multi-

horizon time series forecasting. International Journal

of Forecasting, 37(4):1748–1764.

Liu, S., Ji, H., and Wang, M. C. (2019). Nonpooling convo-

lutional neural network forecasting for seasonal time

series with trends. IEEE transactions on neural net-

works and learning systems, 31(8):2879–2888.

Liu, Y., Hu, T., Zhang, H., Wu, H., Wang, S., Ma, L., and

Long, M. (2023). itransformer: Inverted transformers

are effective for time series forecasting. arXiv preprint

arXiv:2310.06625.

oning, M., Bagnall, A., Ganesh, S., Kazakov, V., Lines,

J., and Kir

aly, F. J. (2019). sktime, a library for time

series analysis in python. http://www.sktime.net/en/

latest/. Accessed: 2023-06-14.

Mahajan, S., Sharma, M., and Gupta, A. (2020). Arima

modelling for forecasting of rice production: A case

study of india. Agricultural Science Digest-A Re-

search Journal, 40(4):404–407.

Mahalakshmi, G., Sridevi, S., and Rajaram, S. (2016). A

survey on forecasting of time series data. In 2016

International Conference on Computing Technolo-

gies and Intelligent Data Engineering (ICCTIDE’16),

pages 1–8. IEEE.

Mahmoud, A. and Mohammed, A. (2021). A survey on

deep learning for time-series forecasting. Machine

Learning and Big Data Analytics Paradigms: Anal-

ysis, Applications and Challenges, pages 365–392.

Mio, C., Shakya, S., Khargharia, H., Ruta, D., Den-

gur, S., Al Shamisi, A. A. S., and Alawneh, A.

(2023). Strengthening food security: A comparison

of food import forecasting models. In Proceedings

of the IEEE/ACM 10th International Conference on

Big Data Computing, Applications and Technologies,

pages 1–6.

Oreshkin, B. N., Carpov, D., Chapados, N., and Bengio, Y.

(2019). N-beats: Neural basis expansion analysis for

interpretable time series forecasting. arXiv preprint

arXiv:1905.10437.

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,

Chanan, G., Killeen, T., Lin, Z., Gimelshein, N.,

Antiga, L., Desmaison, A., Kopf, A., Yang, E., De-

Vito, Z., Raison, M., Tejani, A., Chilamkurthy, S.,

Steiner, B., Fang, L., Bai, J., and Chintala, S. (2023).

Pytorch, a python library for neural networks. https:

//pytorch.org/. Accessed: 2023-11-24.

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P.,

Weiss, R., Dubourg, V., et al. (2011). scikit-learn,

machine learning in python. https://scikit-learn.org/

stable/. Accessed: 2023-06-14.

Rathod, S., Singh, K., Patil, S., Naik, R. H., Ray, M., and

Meena, V. S. (2018). Modeling and forecasting of

oilseed production of india through artiﬁcial intelli-

gence techniques. Indian J. Agric. Sci, 88(1):22–27.

Sharma, P. K., Dwivedi, S., Ali, L., and Arora, R. (2018).

Forecasting maize production in india using arima

model. Agro-Economist, 5(1):1–6.

Shaw, D. J. (1996). Rome declaration on world food se-

curity. https://www.fao.org/3/w3613e/w3613e00.htm.

Accessed: 2023-06-14.

Sheng, Y. and Song, L. (2019). Agricultural production and

food consumption in china: A long-term projection.

China Economic Review, 53:15–29.

Song, F., Liu, J., Zhang, T., Guo, J., Tian, S., and Xiong, D.

(2020). The grey forecasting model for the medium-

and long-term load forecasting. In Journal of Physics:

Conference Series, volume 1654, page 012104. IOP

Publishing.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I.

(2017). Attention is all you need. Advances in neural

information processing systems, 30.

Wen, Q., Zhou, T., Zhang, C., Chen, W., Ma, Z., Yan, J.,

and Sun, L. (2022). Transformers in time series: A

survey. arXiv preprint arXiv:2202.07125.

Zeng, A., Chen, M., Zhang, L., and Xu, Q. (2023). Are

transformers effective for time series forecasting? In

Proceedings of the AAAI conference on artiﬁcial intel-

ligence, volume 37, pages 11121–11128.

A Comparison of Advanced Machine Learning Models for Food Import Forecasting

575