Sampling in CMA-ES: Low Numbers of Low Discrepancy Points

Jacob de Nobel

, Diederick Vermetten

, Thomas H. W. B

ack

and Anna V. Kononova

LIACS, Leiden University, Leiden, Netherlands

{j.p.de.nobel, d.l.vermetten, t.h.w.baeck, a.kononova}@liacs.leidenuniv.nl

Keywords:

Benchmarking, CMA-ES, Derandomization, Low Discrepancy Samples.

Abstract:

The Covariance Matrix Adaptation Evolution Strategy (CMA-ES) is one of the most successful examples of

a derandomized evolution strategy. However, it still relies on randomly sampling offspring, which can be

done via a uniform distribution and subsequently transforming into the required Gaussian. Previous work

has shown that replacing this uniform sampling with a low-discrepancy sampler, such as Halton or Sobol

sequences, can improve performance over a wide set of problems. We show that iterating through small,

ﬁxed sets of low-discrepancy points can still perform better than the default uniform distribution. Moreover,

using only 128 points throughout the search is sufﬁcient to closely approximate the empirical performance

of using the complete pseudorandom sequence up to dimensionality 40 on the BBOB benchmark. For lower

dimensionalities (below 10), we ﬁnd that using as little as 32 unique low discrepancy points performs similar or

better than uniform sampling. In 2D, for which we have highly optimized low discrepancy samples available,

we demonstrate that using these points yields the highest empirical performance and requires only 16 samples

to improve over uniform sampling. Overall, we establish a clear relation between the L

discrepancy of the

used point set and the empirical performance of the CMA-ES.

1 INTRODUCTION

Optimization techniques play a crucial role in var-

ious scientiﬁc and engineering applications. Exact

methods systematically explore the parameter space

but often suffer from inefﬁciency due to their exhaus-

tive nature. For example, it has been shown that ran-

domized search is superior to grid search for hyperpa-

rameter tuning (Bergstra and Bengio, 2012). This is

because, especially in higher dimensions, a random-

ized process will provide better coverage of sample

points in the domain than an exhaustive search, given

a limited evaluation budget. While samples generated

uniformly at random provide an improvement in ex-

ploring the search space, such samples can still be

quite suboptimal in covering the domain. Given a

limited number of samples, uniform samples can be

distributed very unevenly (Halton, 1960). This no-

tion of evenly spreading points across a given do-

main motivates the research into Low-Discrepancy

Sequences. These are sequences of pseudo-randomly

generated points that are designed to minimize the

https://orcid.org/0000-0003-1169-1962

https://orcid.org/0000-0003-3040-7162

https://orcid.org/0000-0001-6768-1478

https://orcid.org/0000-0002-4138-7024

gaps and clusters that often occur in uniform random

sampling, providing more uniform coverage of the

search space. Speciﬁcally, discrepancy measures are

designed to measure how regularly a given point set

is distributed in a given space (Cl

ement et al., 2023b).

While early work with low discrepancy point sets

focuses on Monte Carlo integration (Halton, 1960;

Sobol’, 1967), they have subsequently been used in

various domains, such as computer vision (Paulin

et al., 2022) and ﬁnancial modeling (Galanti and Jung,

1997). Low Discrepancy point sets have been used in

the optimization domain to set up the Design of Ex-

periments (DoE) within a constrained budget (Sant-

ner et al., 2003). One application of particular in-

terest in our context is one-shot optimization, where

low-discrepancy sequences have been shown to out-

perform more traditional uniform sampling (Bous-

quet et al., 2017). Moreover, random search us-

ing quasi-random points has been shown to outper-

form traditional random search (Niederreiter, 1992).

In metaheuristics, randomized search is employed by

many different algorithms, such as Evolution Strate-

gies (ES) (Beyer, 2001). In ES, quasi-random point

sets have been used as an alternative sampling strat-

egy to pure random sampling (Teytaud and Gelly,

2007), speciﬁcally for the CMA-ES (Hansen and Os-

120

de Nobel, J., Vermetten, D., Bäck, T. and Kononova, A.

Sampling in CMA-ES: Low Numbers of Low Discrepancy Points.

DOI: 10.5220/0013000900003837

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 120-126

ISBN: 978-989-758-721-4; ISSN: 2184-3236

termeier, 2001). Simpliﬁed, the procedure of the

CMA-ES can be divided into two steps, which are re-

peated until convergence:

• Sample λ points from a multivariate normal dis-

tribution N (m,C).

• Adjust the parameters of the multivariate normal

distribution to move towards the µ points with the

highest ﬁtness.

Modifying the sampling step to use points from a

pseudo-random sequence (Teytaud, 2015) demon-

strated increased performance and stability on bench-

mark functions. Moreover, this furthers derandom-

ization, which aims to achieve self-adaptation with-

out any independent stochastic variation of the strat-

egy parameters (B

ack et al., 2023). This paper aims to

extend this work by focusing on the number of sam-

ples drawn from a (pseudo) random sampling strategy

speciﬁcally for the CMA-ES. Speciﬁcally, we inves-

tigate if repeatedly reusing small subsets of pseudo-

random sequences in a deterministic manner can be

an effective sampling strategy for the CMA-ES. We

provide an analysis for several well-known low dis-

crepancy point sets to investigate the relation between

discrepancy and empirical performance on the BBOB

benchmark functions.

2 PRELIMINARIES

2.1 Low-Discrepancy Sequences

The discrepancy of a set of points quantiﬁes how reg-

ularly they are spaced in the domain. One of the

most common discrepancy measures of a point set

P ⊆ [0,1]

is the L

∞

star discrepancy (Cl

ement et al.,

2023a), which is deﬁned as follows:

∗

∞

(P) = sup

q∈[0,1]



|P ∩[0, q)|

|P|

−λ(q)



(1)

Here, λ(q) is the Lebesgu measure of the box [0,q)

and d

∗

∞

(P) measures the worst absolute difference be-

tween λ(q) of a d-dimensional box anchored at the

origin and the proportion of points that fall inside

this box. Note that this measure should be mini-

mized to evenly space points in the domain. Since the

∞

star discrepancy can be computationally expen-

sive (Cl

ement et al., 2023b), we can also consider the

star discrepancy, which is deﬁned as follows (Zhou

et al., 2013):

∗

(P) =



[0,1]



|P ∩[0, q)|

|P|

−λ(q)





1/2

(2)

Several pseudo-random sequences have lower star

discrepancies than corresponding uniform sequences.

These methods include Latin Hypercube Sam-

pling (Loh, 1996), Jittered sampling (Pausinger

and Steinerberger, 2016), and Hammersly se-

quences (Peart, 1982). Our work considers the Hal-

ton (Halton, 1960) and Sobol (Sobol’, 1967) se-

quences.

2.2 Derandomization and CMA-ES

While Evolution Strategies (Beyer, 2001) depend

on a random process to sample candidate solutions,

the internal parameter update has been derandom-

ized in state-of-the-art implementations of the algo-

rithm. Derandomization ensures self-adaptation hap-

pens without any independent stochastic variation of

the strategy parameters (Ostermeier et al., 1994). Ef-

fectively, this means the update of the strategy param-

eters is decoupled from the sampling of candidate so-

lutions, moving away from the notion that ‘good so-

lutions have good parameters’ of traditional ES. This

allows modern ES, such as the CMA-ES, to be more

robust and learn good strategy parameters while using

relatively small population sizes (Hansen and Oster-

meier, 2001). Within the CMA-ES, the sampling pro-

cedure is the only remaining source of stochasticity.

At every generation, λ individuals are sampled from

the d-dimensional Gaussian distribution N (m,σ

C).

Where m is the mean of the sampling distribution, σ

is the global step size, and C is the covariance matrix.

In practice, C is spectrally decomposed into two ma-

trices, B and D, representing the eigenvectors and in-

verse square root of the eigenvalues of C, respectively.

This allows the sampling of points in the CMA-ES to

happen in a three-stage process:

1. z

∼ N (0, 1)

2. y

= BDz

∼ N (0,C)

3. x

= m + σy

∼ N (m,σ

Given this decomposition, the ﬁrst step of the sam-

pling process can be practically achieved by sampling

from a uniform distribution u ∼ U(0,1)

, and trans-

forming each coordinate u

of the sample by:

−1

) =

√

2erf

−1

(2u

−1) (3)

which is the inverse of the cumulative density func-

tion for a standard Gaussian distribution.

Since the sampling procedure in CMA-ES can

be seen as sampling in [0, 1]

, replacing the uniform

sampling with a low-discrepancy sequence is a natural

step. Previous work has shown that scrambled Halton

sequences can improve performance over the standard

sampling procedure on most considered benchmark

problems (Teytaud and Gelly, 2007; Teytaud, 2015).

Sampling in CMA-ES: Low Numbers of Low Discrepancy Points

121

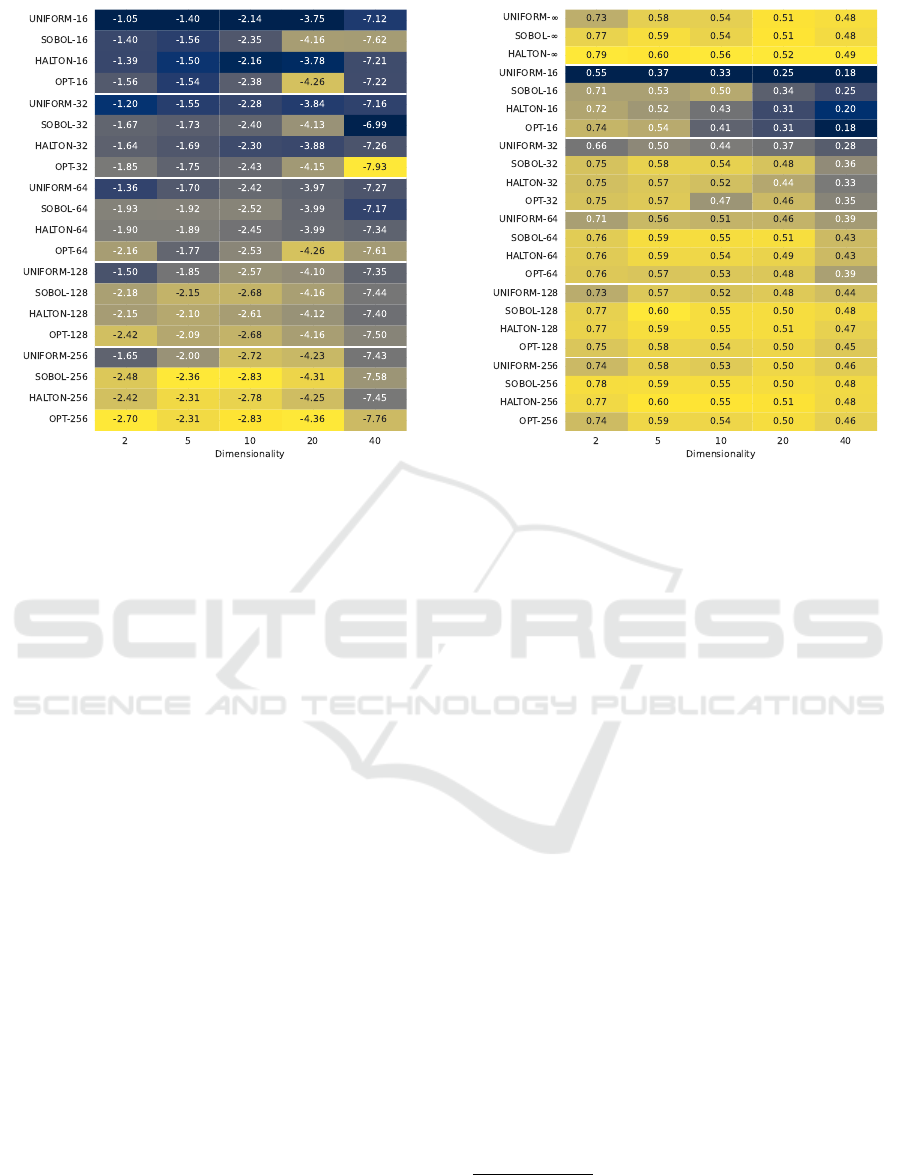
Figure 1: (Average) log

∗

) star discrepancy for the gen-

erated ﬁxed-size point sets across all dimensionalities. Col-

ors are (min-max) normalized on a per-dimensionality ba-

sis; darker colors indicate a worse (higher) d

∗

value.

3 METHODS

3.1 Point Set Generation

For our experiments, we modify how the CMA-ES

samples from a normal distribution by exchanging the

uniform number generator with a selection of points

from a ﬁxed point set stored in a cache. The cache

is randomly permuted once, at the beginning of an

optimization run, and cycled through in steps of size

λ. The permutation is performed to break the bias that

might be present in the ordering of the point set.

We consider four methods for generating point

sets: Sobol, Halton, uniform, and ‘optimized’. Hal-

ton sequences are known to have unwanted correla-

tions in higher dimensional spaces, and as such, we

employ a scrambling method to prevent this (Braaten

and Weller, 1979). For the Sobol sequences, its bal-

ance properties require that the number of points gen-

erated is equal to a power of 2, so we always round

up our number of points sampled to the closest power

of 2. Finally, our ‘optimized’ method for generat-

ing low-discrepancy point sets is split into two parts

based on search space dimensionality. When d =

2, we use optimized Fibonacci sets (Cl

ement et al.,

2023a), considered among the best low-discrepancy

point sets available. However, these are only available

for 2D since generating optimized low-discrepancy

Figure 2: Average area under the EAF curve for each

sampling method on the BBOB benchmark, grouped by

dimension. Colors are (min-max) normalized on a per-

dimensionality basis; darker colors indicate a worse (lower)

EAF value.

point sets is a very hard computational problem. We

use the improved Threshold Accepting subset selec-

tion heuristic from (Cl

ement et al., 2024) for higher

dimensionalities, using Sobol sequences as the base

sets.

We create point sets of sizes k ∈

{16,32,64,128,256} for each generation mech-

anism and calculate their L

star discrepancy

Figure 1 shows how the discrepancy changes with

increasing dimensionality and size of the point sets.

We observe that, as expected, the standard uniform

sampling has a noticeably higher discrepancy than

both Halton and Sobol sequences, with the optimized

method usually having the lowest discrepancy.

Note that for the optimized method, the relative

difference in discrepancy is largest when d = 2 due

to the different generation mechanism used for this

dimensionality.

3.2 Experimental Setup

To gauge the impact of our derandomization, we

run the Modular CMA-ES (de Nobel et al., 2021)

with each of the generated point sets on the single-

We use L

instead of L

∞

star discrepancy for computa-

tional reasons.

For the uniform points sets, we calculate the average

over 100 samples.

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

122

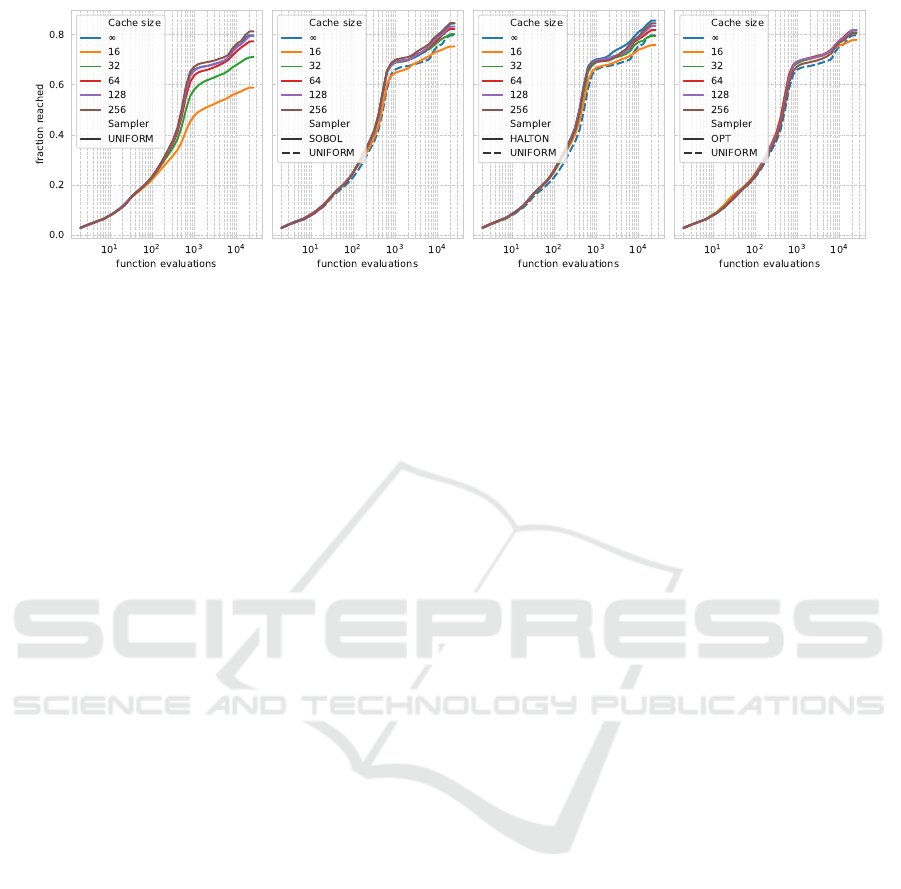
Figure 3: Empirical Attainment Function aggregated over all 24 BBOB functions for dimensionality 2. The methods are

shown in color for each sampling strategy, with cache size indicating the number of points in the cache and ∞ indicating no

caching; every sample is unique. From left to right, the subﬁgures show results using a uniform sampler, a Sobol sequence,

a scrambled Halton sequence, and the optimized point sets. Note that in the three rightmost ﬁgures, the default CMA-ES

sampling strategy, UNIFORM-∞, is included for comparison.

objective, noiseless BBOB suite (Hansen et al., 2009).

This suite consists of 24 functions, of which we use

100 different instances (generated by transformations

such as rotation and translation) in dimensionalities

d ∈ {2, 5, 10, 20,40}. We set our evaluation budget at

B = d ·10000. By using only a single run on each

instance, we only need to generate a single point set

for each (d, N)-pair, while the fact that we use 100 in-

stances ensures a large enough sample size for each

function. Additionally, we benchmark the default

sampling mechanism, UNIFORM-∞, and sampling

from arbitrarily long scrambled Halton and Sobol se-

quences, denoted by the ∞ sufﬁx in our results. No

caching is applied in these cases, and each generated

sample in the optimization process is unique.

To measure performance, we consider the

attainment-based cumulative distribution func-

tion (L

opez-Ib

nez et al., 2024), with bounds 10

and

−8

for the log-scaled precision values.

Reproducibility

All used point sets, the full experimental code, and

data are in our reproducibility repository (de Nobel

et al., 2024).

4 RESULTS

Figure 2 shows each sampling method’s normalized

area under the EAF curve. Without caching, we

observe that both low-discrepancy sequences outper-

form the uniform sampler, and overall, the scram-

bled Halton shows the highest empirical performance.

Note that the differences tend to decrease with dimen-

sionality. When comparing the results within each

ﬁxed point set size, the uniform sampler often per-

forms notably worse than any of the low-discrepancy

sets. This effect is especially noticeable for smaller

set sizes (lower values of k) but remains observable

for all cache sizes. Interestingly, the optimized point

sets only seem to bring performance beneﬁts in low

dimensionalities and using smaller cache sizes. For

higher dimensionalities, they often perform similarly

to uniform sampling. Overall, increasing the size of

the cached point set increases performance, and using

the complete sequence (∞) yields the highest perfor-

mance for each method. Interestingly, point sets of

only 64 to 128 samples are often enough to get very

close in performance to using the complete sequence

as a sampling strategy. Moreover, we ﬁnd that such

sequences still outperform the default sampling strat-

egy of the CMA-ES, i.e., UNIFORM-∞, especially in

lower dimensions. In 2D, we can observe that only

using 16 optimized samples can outperform the de-

fault sampling strategy.

When looking at the performance of the algorithm

variants over time, as visualized in Figure 3, we no-

tice that the differences between the different sam-

pling methods occur rather early in the search. While

the used set does not have a noticeable impact on the

initialization, soon after, the small sets with low dis-

crepancy are seen to stagnate, resulting in the much

worse anytime performance observed in Figure 2. By

comparing the different sampler to the dashed line of

the default uniform sequence, we note that all sets

of size 32 and higher outperform this baseline at the

end of the optimization. Additionally, we should note

that the optimized sets perform best among the small-

est sample sizes, but the Halton and Sobol sequences

beneﬁt more from increasing their size. Plots for other

dimensionalities are available in the appendix. Fi-

nally, we show the relation between discrepancy and

performance in Figure 4, where we observe a clear

Sampling in CMA-ES: Low Numbers of Low Discrepancy Points

123

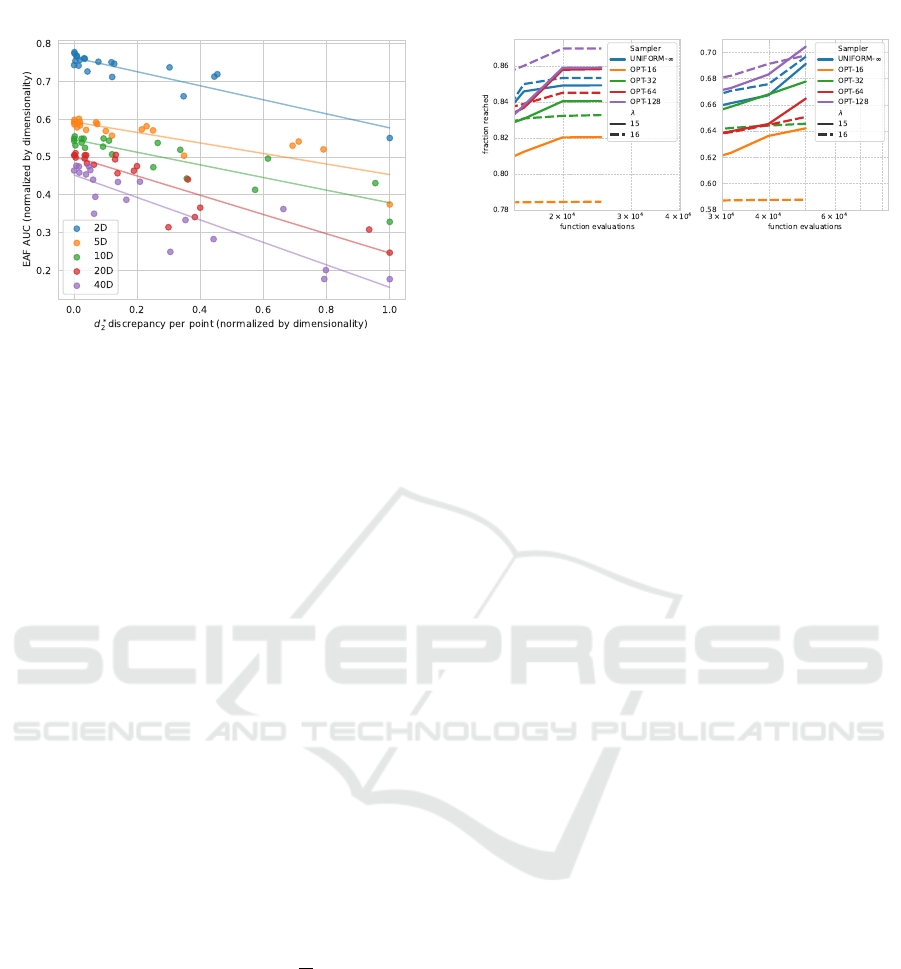
Figure 4: Average area under the Empirical Attainment

Function over all BBOB functions, grouped by dimension

vs. the L

star discrepancy, normalized by dimensionality

and the number of points. Lines indicate a linear (least-

squares) model for each dimensionality.

correlation between these two measures. This sup-

ports our previous observation that low discrepancy

point sets are beneﬁcial to the performance of the

CMA-ES.

4.1 Multiples of λ

Since the CMA-ES only requires λ points at every

iteration, a natural assumption would be that only λ

unique points would be required for an effective sam-

pling strategy, given that these points cover the do-

main sufﬁciently. In our previous experiments, we

have used the default setting for λ, i.e., 4 + ⌊3 +

ln(d)⌋, which is strictly less than 16, the smallest

tested cache size k. This causes the sampler to cy-

cle through the point set, causing variance between

the samples used in each generation. Here, we inves-

tigate this effect using either a population size λ of 15

or 16. In the latter case, λ is a multiple of the cache

size, and for k = 16, this ensures that every genera-

tion uses exactly the same samples. For k < 16, this

causes a cyclic pattern, where every

-th generation

has the same samples. In ﬁgure 5, the empirical per-

formance of this experiment is visualized. The ﬁgure

shows that when using the default sampling strategy,

i.e., UNIFORM-∞, using a λ = 16 is better than using

λ = 15. This is reversed for a cache size k = 16, where

there is no variance between the samples in subse-

quent generations. For larger k, this performance of

λ = 15 becomes closer to λ = 16. This indicates

there must be variation between generations, not only

between the samples within each generation, which

aligns with (Teytaud and Gelly, 2007). Intuitively,

this makes sense, as the strategy parameters are be-

ing averaged over multiple generations, making diver-

Figure 5: Empirical Attainment Function aggregated over

all 24 BBOB functions for dimensionality 2 (left) and 5

(right), zoomed to ﬁnal fraction reached. The default sam-

pling strategy of the CMA-ES, UNIFORM-∞, is shown in

comparison to using a cached sampling strategy, which uses

the ‘OPT’ samples for a cache size k ∈ {16,32,64, 128}.

The solid lines represent λ = 15 and the dashed lines λ = 16.

sity between subsequent populations important. No-

tably, though, using only 4-8 unique populations dur-

ing the entire optimization procedure already yields

higher performance than the UNIFORM-∞ sampling

strategy (for d = 2 and d = 5).

5 CONCLUSIONS AND FUTURE

WORK

In this paper, we have shown that replacing the uni-

form sampling with low discrepancy samples in the

offspring generation of the CMA-ES can yield clear

beneﬁts in performance on commonly used bench-

marks. While this matches previous observations

on the advantage of low-discrepancy sequences (Tey-

taud, 2015), our experiments on repeatedly (re-)using

small sets of points show that we don’t necessarily

need to rely on generators when sampling with the

CMA-ES. While we note that, in general, sampling

from an arbitrarily long low discrepancy sequence

is better than using a ﬁxed point set, such sets re-

main competitive when using only 128 points. In

fact, on the two-dimensional problems, where our L

∞

optimized point sets can be considered state-of-the-

art (Cl

ement et al., 2023a), a cached set consisting of

only 16 samples is enough to outperform the default

sampling strategy of the CMA-ES.

However, our results in higher dimensionalities

show that while there is a clear correlation between

the discrepancy of a point set and the performance

of the CMA-ES using it, this correlation is not per-

fect. While our optimized sets generated by im-

proved Threshold Accptance (Cl

ement et al., 2024)

have lower discrepancy than the corresponding Hal-

ton and Sobol sets, their anytime performance is

slightly worse, indicating that there might be other as-

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

124

pects of the point sets we should take into account.

We have shown that not only does the discrepancy

of samples within a single generation impact perfor-

mance, but the diversity between subsequent genera-

tions also has an impact. Future work might focus on

diving deeper into the relationship between point set

size, discrepancy, diversity, and performance.

ACKNOWLEDGEMENTS

We want to thank Franc¸ois Cl

ement and Carola Doerr

for providing us with the optimized low-discrepancy

point sets used in this paper.

REFERENCES

Bergstra, J. and Bengio, Y. (2012). Random search for

hyper-parameter optimization. Journal of machine

learning research, 13(2).

Beyer, H. (2001). The theory of evolution strategies. Natural

computing series. Springer.

Bousquet, O., Gelly, S., Kurach, K., Teytaud, O., and Vin-

cent, D. (2017). Critical hyper-parameters: No ran-

dom, no cry. arXiv preprint arXiv:1706.03200.

Braaten, E. and Weller, G. (1979). An improved low-

discrepancy sequence for multidimensional quasi-

monte carlo integration. Journal of Computational

Physics, 33(2):249–258.

ack, T. H. W., Kononova, A. V., van Stein, B., Wang,

H., Antonov, K. A., Kalkreuth, R. T., de Nobel, J.,

Vermetten, D., de Winter, R., and Ye, F. (2023).

Evolutionary Algorithms for Parameter Optimiza-

tion—Thirty Years Later. Evolutionary Computation,

31(2):81–122.

ement, F., Doerr, C., Klamroth, K., and Paquete, L.

(2023a). Constructing optimal l

∞

star discrepancy

sets. arXiv preprint arXiv:2311.17463.

ement, F., Doerr, C., and Paquete, L. (2024). Heuristic

approaches to obtain low-discrepancy point sets via

subset selection. Journal of Complexity, 83:101852.

ement, F., Vermetten, D., De Nobel, J., Jesus, A. D., Pa-

quete, L., and Doerr, C. (2023b). Computing star dis-

crepancies with numerical black-box optimization al-

gorithms. In Proceedings of the Genetic and Evolu-

tionary Computation Conference, pages 1330–1338.

de Nobel, J., Vermetten, D., Kononova, A. V., and B

ack, T.

(2024). Reproducibility ﬁles and additional ﬁgures.

de Nobel, J., Vermetten, D., Wang, H., Doerr, C., and B

ack,

T. (2021). Tuning as a means of assessing the ben-

eﬁts of new ideas in interplay with existing algorith-

mic modules. In Krawiec, K., editor, GECCO ’21:

Genetic and Evolutionary Computation Conference,

Companion Volume, Lille, France, July 10-14, 2021,

pages 1375–1384. ACM.

Galanti, S. and Jung, A. (1997). Low-discrepancy se-

quences: Monte carlo simulation of option prices. The

Journal of Derivatives, 5(1):63–83.

Halton, J. H. (1960). On the efﬁciency of certain quasi-

random sequences of points in evaluating multi-

dimensional integrals. Numerische Mathematik, 2:84–

90.

Hansen, N., Finck, S., Ros, R., and Auger, A. (2009).

Real-parameter black-box optimization benchmark-

ing 2009: Noiseless functions deﬁnitions. Research

Report RR-6829, INRIA.

Hansen, N. and Ostermeier, A. (2001). Completely deran-

domized self-adaptation in evolution strategies. Evo-

lutionary computation, 9(2):159–195.

Loh, W.-L. (1996). On latin hypercube sampling. The an-

nals of statistics, 24(5):2058–2080.

opez-Ib

nez, M., Vermetten, D., Dr

eo, J., and Doerr, C.

(2024). Using the empirical attainment function for

analyzing single-objective black-box optimization al-

gorithms. CoRR, abs/2404.02031.

Niederreiter, H. (1992). Random number generation and

quasi-Monte Carlo methods. SIAM.

Ostermeier, A., Gawelczyk, A., and Hansen, N. (1994). A

derandomized approach to self-adaptation of evolu-

tion strategies. Evolutionary Computation, 2(4):369–

380.

Paulin, L., Bonneel, N., Coeurjoly, D., Iehl, J.-C.,

Keller, A., and Ostromoukhov, V. (2022). Mat-

Builder: Mastering sampling uniformity over projec-

tions. ACM Transactions on Graphics (proceedings of

SIGGRAPH).

Pausinger, F. and Steinerberger, S. (2016). On the dis-

crepancy of jittered sampling. Journal of Complexity,

33:199–216.

Peart, P. (1982). The dispersion of the hammersley se-

quence in the unit square. Monatshefte f

ur Mathe-

matik, 94(3):249–261.

Santner, T., Williams, B., and Notz, W. (2003). The De-

sign and Analysis of Computer Experiments. Springer

Series in Statistics, Springer.

Sobol’, I. M. (1967). On the distribution of points in a cube

and the approximate evaluation of integrals. Zhurnal

Vychislitel’noi Matematiki i Matematicheskoi Fiziki,

7(4):784–802.

Teytaud, O. (2015). Quasi-random numbers improve the

CMA-ES on the BBOB testbed. In Bonnevay, S.,

Legrand, P., Monmarch

e, N., Lutton, E., and Schoe-

nauer, M., editors, Artiﬁcial Evolution - 12th Inter-

national Conference, Evolution Artiﬁcielle, EA 2015,

Lyon, France, October 26-28, 2015. Revised Selected

Papers, volume 9554 of Lecture Notes in Computer

Science, pages 58–70. Springer.

Teytaud, O. and Gelly, S. (2007). DCMA: yet another

derandomization in covariance-matrix-adaptation. In

Lipson, H., editor, Genetic and Evolutionary Compu-

tation Conference, GECCO 2007, Proceedings, Lon-

don, England, UK, July 7-11, 2007, pages 955–963.

ACM.

Zhou, Y.-D., Fang, K.-T., and Ning, J.-H. (2013). Mixture

discrepancy for quasi-random point sets. Journal of

Complexity, 29(3-4):283–301.

Sampling in CMA-ES: Low Numbers of Low Discrepancy Points

125

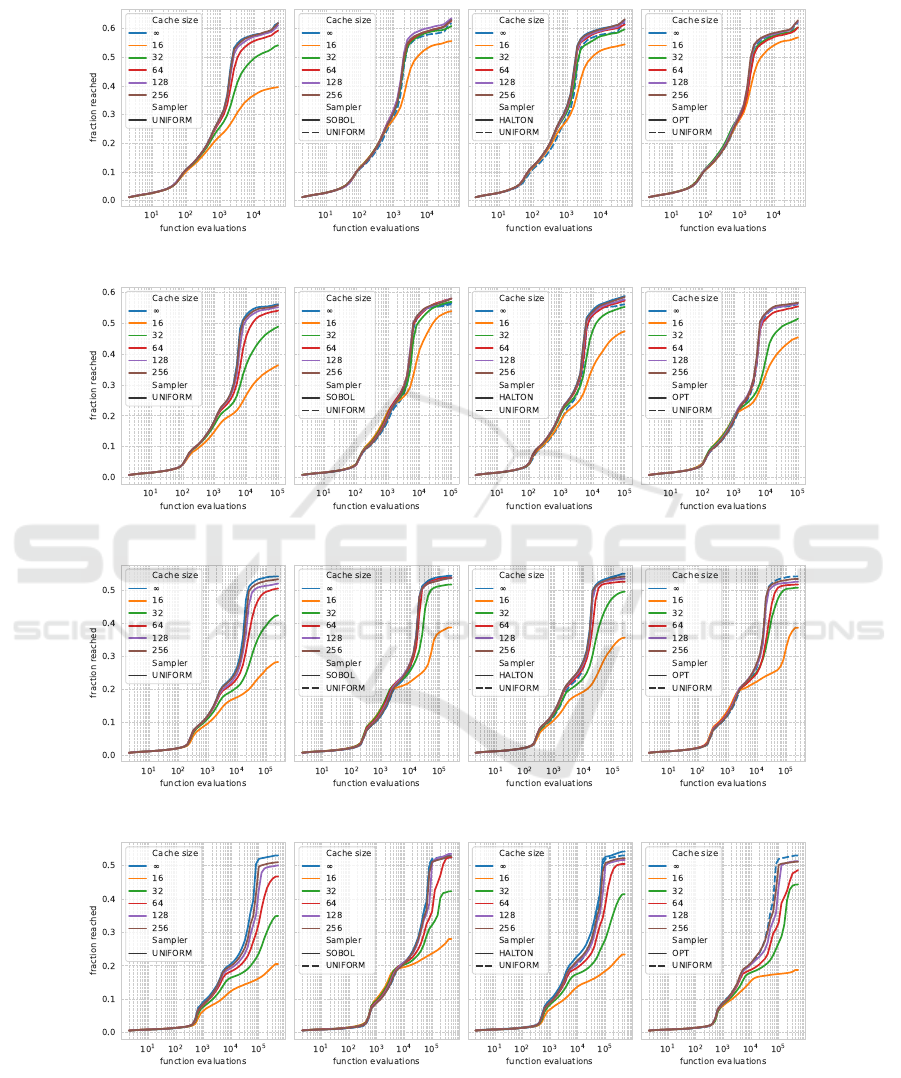
APPENDIX

(a) Dimensionality 5

(b) Dimensionality 10

(d) Dimensionality 40

Figure 6: Empirical Attainment Function aggregated over all 24 BBOB functions for dimensionalities 5, 10, 20, and 40 (from

top to bottom). The methods are shown in color for each sampling strategy, with cache size indicating the number of points in

the cache and ∞ indicating no caching; every sample is unique. From left to right, the subﬁgures show results using a uniform

sampler, a Sobol sequence, a scrambled Halton sequence, and the optimized point sets. Note that in the three rightmost

ﬁgures, the default CMA-ES sampling strategy, UNIFORM-∞, is included for comparison.

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

126