
Decision of Production Combinations Based on Cournot Model and
Linear Programming
Hanyang Li
1, *
, Yuxuan Li
2
and Xiaoti Wu
3
1
College of Liberal Arts and Sciences, University of Illinois at Urbana-Champaign, Champaign, 61820, U.S.A.
2
School of Business Administration, South China University of Technology, Guangzhou, 510641, China
3
School of Arts and Sciences, Syracuse University, Syracuse, NY,13202, U.S.A.
Keywords: Cournot Model, Linear Programming, Market Competition, Strategic Decisions.
Abstract: This paper explores production strategies for micro electric vehicle manufacturers in small cities using a
revised Cournot model and linear programming. Focusing on cities like Liuzhou, Nanyang, and Shangqiu,
where market dynamics favour oligopolies, the traditional Cournot model is adapted to emphasize cost-based
strategies. By integrating unit costs as variables representing service levels, the model examines competition
among manufacturers providing different service levels within the same market. A payoff matrix and linear
programming determine optimal strategies for maximizing profits while maintaining market stability. The
study highlights the importance of strategic decisions in cost control, brand positioning, and supply chain
management. Results indicate that both firms should adopt mixed strategies to enhance competitiveness and
profitability. The paper suggests future research to refine the model for more complex market scenarios,
including additional competitors and dynamic market conditions. This research provides insights into market
competition strategies and lays the groundwork for more nuanced economic and mathematical analyses.
1 INTRODUCTION
In recent years, the surge in popularity of micro
electric vehicles in smaller cities has presented a
unique set of market dynamics, particularly evident in
cases such as Liuzhou, Nanyang and Shangqiu, which
usually emerges in small cities. From 9.7% in 2017 to
53.3% in 2022, Liuzhou's new energy vehicle market
penetration rate has been steadily increasing
(Yunjing, 2023). Where a monopolistic trend is
emerging. In many of these cities, oligopoly and even
monopoly market is observed.
This phenomenon has sparked interest among
researchers aiming to understand the implications of
such market structures. On the on hand, for
companies, which strategies they should adopt to
achieve their goals, like maximize their profits and
put the competitors at a disadvantage, need to be
clarified. On the other hand, for the market, whether
a stable state, or technically, a Nash equilibrium exist
is essential to define whether this market is efficient.
The Cournot model, a classic economic
framework for analyzing oligopoly markets, becomes
highly relevant in this context. The Cournot duopoly
model, or Duopoly model, is another name for the
Cournot model. An early example of an oligopoly is
the Cournot model. The French economist Cournot
first put up the idea in 1838 (Yan, Da and Pei, 2013).
The first use of the Nash equilibrium is the Cournot
model, which is frequently utilized as a jumping off
point for oligopoly theory study (Tang, 1997).
According to the Cournot model, there are just two
sellers of a product in the market, and they don't
cooperate with one another. Instead, they anticipate
each other's actions and decide on the best output to
maximize profits (Du, 2005). The Cournot model's
conclusions can be applied with ease to situations
involving three or more oligopolistic manufacturers
(Zhang and Xiao, 2003). Studies such as those by
prominent scholars have applied it to similar markets,
emphasizing the strategic behaviors of oligopolies.
Given the niche nature of micro electric vehicle
markets in smaller cities, the sales volume tends to be
relatively stable due to the limited market size.
Despite the homogeneity in product characteristics,
manufacturers can still strategize by varying the level
of services provided with their products. For example,
in the case of similar models, companies can achieve
product differentiation by providing customization
service, such as customized auto parts. Shortening
Li, H., Li, Y. and Wu, X.
Decision of Production Combinations Based on Cournot Model and Linear Programming.
DOI: 10.5220/0013001000004601
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Innovations in Applied Mathematics, Physics and Astronomy (IAMPA 2024), pages 119-125
ISBN: 978-989-758-722-1
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
119

delivery time can also enhance the competitiveness of
enterprises. However, higher service level requires
higher cost. These costs will be shared into the cost of
every car. Hence, the service level is quantified in
terms of cost. It suggests a significant shift in market
modeling, moving from quantity-based variables to
cost-based ones. In the traditional Cournot model,
two producers have identical items with linear
demand curves, and one decides how to maximize
profit by varying the volume of sales dependent on
the other's actions (Yuan et al., 2003). Thus, the
traditional Cournot model with sales volume as
variable is no longer applicable. A research based on
revised Cournot model is both necessary and timely,
aiming to delve deeper into how these cost-based
strategies affect market dynamics and competition
among few but powerful players in small yet pivotal
market segments.
Actually, the researchers have noticed these cases
and made some attempts. A famous model named the
Bertrand model was proposed by French economist
Joseph Bertrand in 1883. Unlike the Cournot model,
the Bertrand model describes price competition rather
than quantity competition (Tremblay and Tremblay,
2019). In this model, it is assumed that there are two
or more firms selling identical or non-differentiated
products and that they compete on price. When
setting prices, firms must consider their competitors'
reactions and anticipate their potential pricing
strategies. Consumers will buy from the firm offering
the lowest price. In equilibrium, each firm's price
equals its marginal cost. If a firm's price is above its
marginal cost, it will lose market share.
There are also researchers combines the Cournot
model with Bertrand model. They believe that firms
can decide to compete in both cost and quantity. It
appeared in early studies as “mixed oligopoly", a
model with a “mixed equilibrium”, or a “mixed
strategy setting" (Bylka and Komar, 1976 & Singh
and Vives, 1084). In some later studies, it is referred
as “Cournot–Bertrand Model” discussed a duopoly
where competitors can adjust their output or price
(Sato, 1996 & Correa-Lopez, 2007). However, these
models do not fit the market discussed by this paper
very well, either. On the one hand, customers’ choices
are not always the products with the lowest price.
Customers have various preference based on the
quality and the brand of the products. On the other
hand, to maintain the brand image, there exists a
satisfied threshold of customers a firm should keep.
Therefore, a revised model is needed (Maggi, 1996).
The objective of this paper is to build a revised
model based on Cournot model model to calculate the
best strategies for companies in a market segment and
analyze the Nash equilibrium of it. In this model, Unit
costs of the products are regarded as variables, which
is able to measure the service level of similar
products. To achieve this goal, a payoff matrix of a
firm in this market is derived first based on the revised
model. Then, a linear programming model is built,
considering the satisfaction constraints. To solve this
model, duality theory is considered. The dual problem
not only ensures the primal problem can be solved,
but at the same time derives a Nash equilibrium.
Finally, examples which are closed to reality, related
data and python algorithms will be used to assess the
validity and reliability of the models. The model can
help provide valuable advice and insights for
companies to make informed decisions and estimate
the final balance of a certain market segment.
2 METHODOLOGY
2.1 Data Source
There are many factors in the market model that are
difficult to analyze with available data. It is difficult
to do regression analysis to obtain continuous
quantified factors. Thus, to facilitate the
establishment of mathematical models and
calculations, this paper quantifies the factors involved
in this model based on the basic rule of the market,
instead of using certain direct data. To ensure the
authority and accuracy of the data, current prices and
strategies in the market are also considered as
reference (Ma et al., 2018). This paper especially
refers to the markets of Liuzhou and Nanyang, and
get the picture in Figure1 after investigation, the top
two brands, which are the blue and orange parts,
occupy the majority of the market share in both
Liuzhou and Nanyang.
IAMPA 2024 - International Conference on Innovations in Applied Mathematics, Physics and Astronomy
120
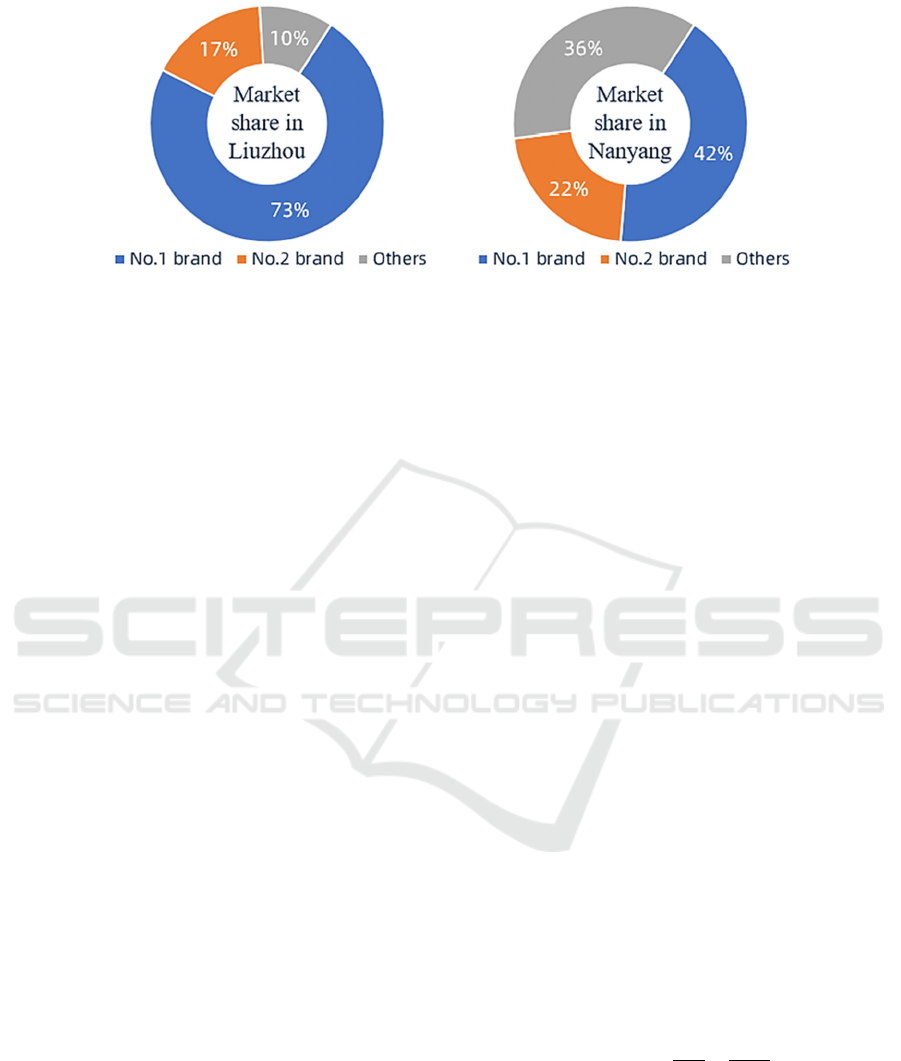
Figure 1: Market Shares in Liuzhou and Nanyang.
2.2 Variable Introduction
Firstly, In the oligopolistic market, similar but
different products are selling. The differences
between these products are not indicated in the
product itself, but in the related service level. For
instance, the products with higher level of
customization, quick response and excellent after-
sales service will be the high-end product in this
market. In this model, there are two firms. Firm 1
focuses on high-end products while Firm 2 focuses
on the low-end ones. The firm's investment in
service levels is spread over each product.
Therefore, the service level of the product is
measured by the unit product cost.
Secondly, due to the different positioning of the
firms, customers have certain expectations for the
strategies adopted by the firm. Part of that
expectation is not adjustable. The non-adjustable
part represents the bottom line of the company's
image maintenance, which the company must meet.
For example, once a company with a high-end
positioning sells a product with a very low
positioning, old customers who pursue high quality
will be disappointed and stop buying the company's
products. The other part of expectations is elastic.
Although the company will face the loss of certain
expectations that are not met, the company can
make up for the loss with the profit resulting from
this adjustment. In addition, the budgets of the firms
are different since the sizes of them are different.
2.3 Method Introduction
To make the description clear, the example of Firm
1 producing Product 1 is considered. Since the
objective of a firm is to maximize their profit, a
system of functions needs to be built. The
researchers considered different parameters for the
firm and the product, such as the firm's production
budget, the product's unit price, and the market
expectation.
For Firm 1, the budget 𝑏 that it has for
production is a constant. If it only produces Product
1, the relation between the cost of Product 1 and the
quantity of them can be represented as below. In the
equation (1), 𝑐
is the cost of Product 1. The
quantity of Product 1 is 𝑞
.
𝑏=𝑐
𝑞
(1)
The price of Product 1 (𝑃
) is affected by its unit
cost 𝑐
and its expected production 𝑞
. Specifically,
if the firm produced more products than it is
expected, the price of the product will drop, and vice
versa. The researchers consider these effects to be
linear, respectively controlled by two coefficients
𝜆
and 𝑘
.
𝑃
=𝜆
𝑐
−𝑘
𝑞
−𝑞
(2)
The profit of the firm by selling only Product 1(𝜋
)
can be calculated as below.
𝜋
=𝑃
𝑞
−𝑐
𝑞
(3)
Then, by solving the simultaneous equations, the
final expression of 𝜋
is obtained.
𝜋
=𝑏𝜆
−
+
−𝑏 (4)
The profit function is of unit cost. Thus, the
researchers set the derivative of the function equal
to zero to find the optimal unit cost that maximizes
profit. This represents the optimal pure strategy for
Product 1. The whole process is shown in Figure 2.
Decision of Production Combinations Based on Cournot Model and Linear Programming
121
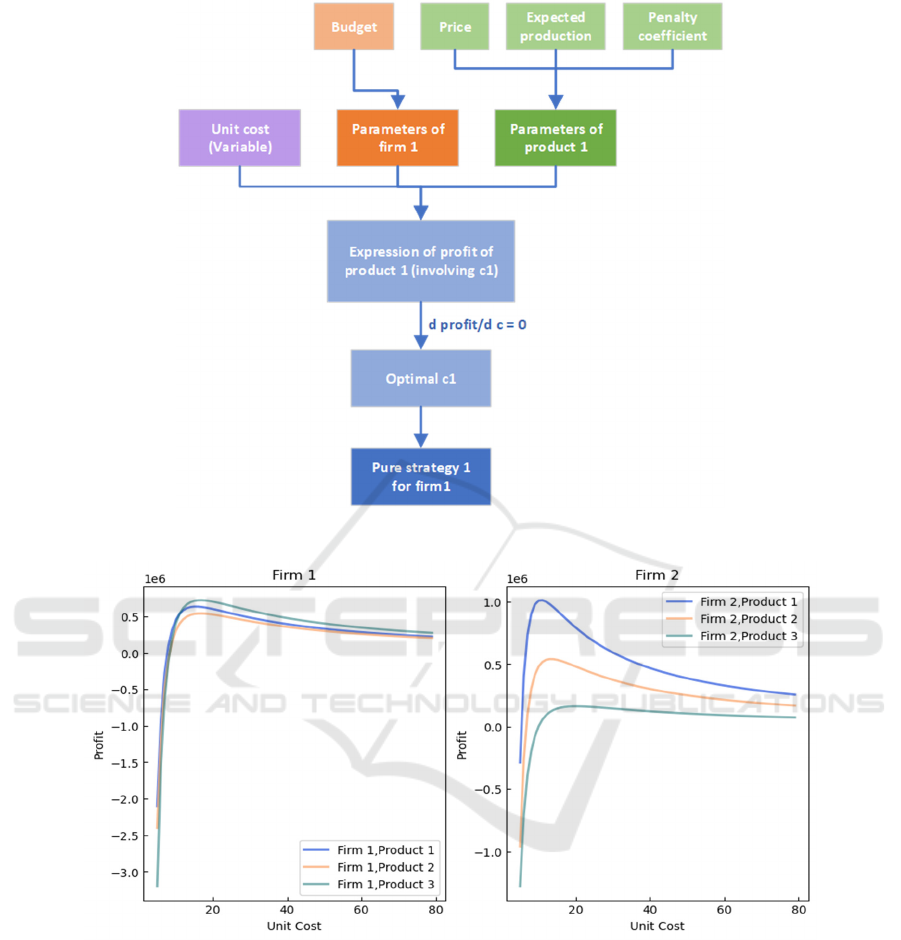
Figure 2: Pure Strategy Model.
Figure 3. Relationship Between Unit Cost and Profit.
3 RESULTS AND DISCUSSION
3.1 Preliminary Work
Similarly, other pure strategies can be calculated. In
the model, Firm 1 is high-end and Firm 2 is low-end.
The differences between them are reflected in the
parameter. For instance, the budgets of the firms are
different since the volume of them are different. The
customers’ expectation of different products is
different since the firm’s image determines their
market. By changing the parameters, the pure
strategies for Firm 2 can be found. How the profits of
companies producing different products vary with
changes in cost are shown by Figure 3. For a certain
product, the cost that corresponds to the highest profit
point is the best pure strategy.
Recognizing that a company wouldn't produce
just one type of product, the researchers mixed these
pure strategies in proportion to form mixed strategies.
IAMPA 2024 - International Conference on Innovations in Applied Mathematics, Physics and Astronomy
122

The proportions of the mixed strategies are shown in
Table 1. The first row indicates that in strategy 1, 20%
of the budget is allocated to producing Product 1,
40% to Product 2, and the remaining 40% to Product
3. Similar for the rest.
It is important to point out that the unit cost of
Product 1 is the lowest, Product 2’s is middle and
Product 3’s is the highest. This means that the quality
of the products is higher with the increase of their
index. Thus, mixed strategy 1 with emphasis on
production of Product 2 and Product 3 is a high-end
strategy.
Table 1: Mixed Strategy.
Product 1 Product 2 Product 3
Strategy 1 0.2 0.4 0.4
Strategy 2 0.3 0.5 0.2
Strategy 3 0.5 0.3 0.2
As mentioned earlier, a firm's goal is to maximize
profits while putting their competitors at a
disadvantage. The payoff is defined as their profit
minus the competitor's profit.
𝑃𝑎𝑦𝑜𝑓𝑓 𝑜𝑓 𝐹𝑖𝑟𝑚 1 = 𝜋
−𝜋
(5)
With the previously derived profit expression, the
payoff matrix of Firm 1 is obtained.
Table 2: Payoff Matrix.
Strategy 1 Strategy 2 Strategy 3
Strategy 1 1484540 254760 -689600
Strategy 2 1214890 -14890 -959250
Strategy 3 1401590 171810 -772500
Using the data above, the researchers came up
with the following linear programming model (Table
2). 𝐴
is the payoff matrix of Firm 1. By pre-
multiplying transpose of Firm 1’s strategy vector 𝑥
and post-multiplying Firm 2’s strategy vector 𝑦, the
payoff of Firm 1( 𝑢 ) under certain strategies are
determined.
For Firm 2, not knowing which strategy Firm 1
will take, it also in the face of determine a strategy-
choosing problem. For a given 𝑥, Firm 2 will take the
strategy that minimizes 𝑢 to put Firm 1 at
disadvantage. Thus, the objective of Firm 2 is to
minimize 𝑢 by choosing 𝑦.
𝑀𝑖𝑛𝑖𝑚𝑖𝑧𝑒 𝑢 = 𝑥
𝐴
𝑦 (6)
In addition, 𝑦 is under several constraints:
Summation of the proportions of the strategies equals
1. The strategy Firm 2 take should meet the
satisfaction constraint. The proportions of the
strategies should be greater than or equal to 0.
The satisfaction matrix of Firm 2 is 𝑆
. The
satisfied threshold of customers for Firm 2 is 𝑐
. Then
the constrains of the linear programming model can
be written as, subject to:
∑
𝑦
=1 (7)
𝑆
𝑦≥𝑐
(8)
𝑦≥0 (9)
For Firm 1, it will choose the strategy that will
maximize its payoff. With the model above, 𝑥 can be
estimated. However, 𝑢 is not a linear function. To
solve the problem, linear programming duality is
used.
The dual problem is obtained by using linear
programming duality as below:
𝑀𝑎𝑥𝑖𝑚𝑖𝑧𝑒 𝑣 = 𝑥
+𝑐
𝑥
(10)
Subject to,
⎣
⎢
⎢
⎢
⎡
00111
1𝑆
_
−𝐴
_,
−𝐴
_,
−𝐴
_,
1𝑆
_
−𝐴
_,
−𝐴
_,
−𝐴
_,
1𝑆
_
−𝐴
_,
−𝐴
_,
−𝐴
_,
00 𝑆
_
𝑆
_
𝑆
_
⎦
⎥
⎥
⎥
⎤
⎣
⎢
⎢
⎢
⎡
𝑥
𝑥
𝑥
𝑥
𝑥
⎦
⎥
⎥
⎥
⎤
=
≥
≥
≥
≥
⎣
⎢
⎢
⎢
⎡
1
0
0
0
𝑐
⎦
⎥
⎥
⎥
⎤
(11)
𝑥
≤0 (12)
𝑥
,,
≥0 (13)
In the dual problem, Firm 1 maximizes its own payof
f while meeting its own market satisfaction criteria, r
epresented by the satisfaction matrix 𝑆
. 𝑆
_
represe
nts the 𝑗𝑡ℎ element in 𝑆
. 𝐴
_,
represents the elemen
t in 𝐴
that is in the 𝑖𝑡ℎ row and the 𝑗𝑡ℎ column. No
w, the problem can be solved by calling linprog in
Python.
3.2 Sensitivity Analysis
In this analysis, researchers performed a sensitivity
analysis on a Cournot competition model
implemented using linear programming. The primary
goal was to understand how small changes in key
parameters affect the model's outcomes. Specifically,
researchers increased and decreased certain
parameters by 10% to observe the impact on the
model's results.
Decision of Production Combinations Based on Cournot Model and Linear Programming
123

After adjusting the parameters and rerunning the
model, the results showed minimal changes in the
outcomes. Below are the comparative results for the
original parameters, +10% adjustment, and -10%
adjustment. The Cournot competition model used
here is a linear programming model, which means it
optimizes a linear objective function subject to linear
constraints. Linear models tend to be more stable and
less sensitive to small parameter changes compared to
non-linear models. Adjusting parameters by 10%
might not be significant enough to push the system
into a different region of the feasible solution space.
In other words, the feasible region defined by the
constraints may not change much with these small
adjustments, resulting in similar optimal solutions.
The Nash equilibrium in the Cournot model
represents a stable state where firms have optimized
their strategies given the strategies of their
competitors. This equilibrium tends to be robust to
small perturbations in parameters, meaning that small
changes in costs or budget do not significantly alter
the strategic interactions and outcomes.
3.3 Payoff Matrix and Mixed Strategy
Solving the problem with the payoff matrix and
mixed strategy, the final strategies are shown in Table
3. As a result, Firm 1 will choose mixed strategy 2,
and Firm 2 will choose mixed strategy 1.
3.4 Competitive Strategies Analysis
In today's fiercely competitive business environment,
companies employ well-crafted competitive
strategies to enhance their market position and
profitability. These strategies not only impact a
company's immediate benefits but also shape its long-
term development. For example, Firm 1 employs a
Cost Leadership and Price War Strategy, which has
its advantages and disadvantages. The advantages
include economies of scale, where scaling production
spreads fixed costs over more units, reducing the cost
per unit and gaining a competitive edge in price-
sensitive markets, and rapid market penetration,
where lower price points attract a large customer base
quickly, effectively expanding market share.
However, the risks involve profit margin
compression, as long-term low pricing can lead to
sustained decreases in profit margins, especially
when raw material or production costs rise, and brand
value dilution, where continuous price wars may
degrade the brand's perceived value, making it
difficult to raise prices or expand into higher-end
product lines later.
On the other hand, Firm 2's Brand Positioning and
Customer Loyalty Strategy also comes with its own
set of advantages and risks. The advantages include
the ability to charge a premium for products due to
strong brand influence, achieving higher profit
margins, and enhanced customer retention, where
increased customer satisfaction and emotional
connection lead to repeat purchases and new
customer referrals. However, the risks include high
costs associated with maintaining a brand image and
improving customer service, involving significant
marketing and advertising expenses, and poor market
adaptability, where an overemphasis on a specific
brand position may limit the company's ability to
adapt to market changes.
Lastly, the importance of supply chain
management cannot be overlooked. Advantages
include cost efficiency, where optimized supply chain
operations reduce the cost of acquiring raw materials
and enhance production efficiency, and market
responsiveness, where a flexible and efficient supply
chain allows for quick adaptation to market demand
changes, reducing inventory backlog and increasing
customer satisfaction. However, risks include supply
chain disruptions, where dependence on single or key
suppliers includes risks of production halts and
logistical delays, and raw material price volatility,
where uncertainty in raw material costs can lead to
budget overruns.
Table 3: Final Strategies.
𝑥
𝑥
Mixed Strategy 1Mixed Strategy 2Mixed Strategy 3
Firm1
1.22 × 10
0 0 1 0
Firm2
1.95 × 10
−3.15 × 10
1 0 0
IAMPA 2024 - International Conference on Innovations in Applied Mathematics, Physics and Astronomy
124

4 CONCLUSION
This research provides a comprehensive examination
of strategic approaches within micro electric vehicle
markets, utilizing a modified Cournot model
alongside linear programming to assess competition
dynamics in small cities. By integrating service levels
and costs into the Cournot framework, researchers
reveal that firms can enhance their competitive edge
and profitability through strategic diversification. The
study confirms that both high-end and low-end
market strategies can coexist successfully by
balancing service quality and cost-effectiveness. This
paper’s findings also suggest that mixed strategies,
blending different levels of service and pricing, allow
firms to optimize their market presence and financial
performance effectively. Looking ahead, further
refinement of this model is recommended to include
a broader range of competitors and dynamic market
conditions, which would provide deeper insights into
the complexities of market competition and strategy
optimization. This research not only underscores the
utility of advanced economic and mathematical tools
in market analysis but also sets the stage for future
studies aimed at evolving these methodologies for
more comprehensive market scenarios.
AUTHORS CONTRIBUTION
All the authors contributed equally and their names
were listed in alphabetical order.
REFERENCES
Yunjing C 2023 Research on the Competitiveness
Evaluation of New Energy Vehicle Industry in Liuzhou
City. Master's thesis Guangxi University of Science and
Technology.
Yan A, Da Q L and Pei F 2013 Research on long-term
output solution of dynamic Cournot model for
simultaneous game of multiple firms. Journal of
Management Engineering 27(001) 94-98.
Tang XW 1997 Cournot model study under the condition
of two manufacturers. Journal of University of
Electronic Science and Technology of China 26(1) 83-
88.
Du D C 2005 Integrated application of Cournot model.
Journal of Jianghan University: Natural Science
Edition 33(1) 3.
Zhang M S He D Q and Xiao F P 2003 Dynamic Cournot
model analysis for multiple manufacturers. Journal of
Southwest University for Nationalities: Natural Science
Edition 29(1) 9.
Yuan ZQ, Hou Z J, Jiang C W N and Tai N L 2003
Equilibrium analysis of Cournot model of power
market. Power Grid Technology 27(12) 4.
Tremblay C H and Tremblay V J 2019 Oligopoly games
and the Cournot-A survey. Journal of Economic
Surveys 33(5) 1555-1577.
Bylka S and Komar J 1976 Cournot-Bertrand mixed
oligopolies. In M.W, Los, J. Los and A. Wieczorek(eds),
Warsaw Fall Seminars in Mathematical Economics.
22-33.
Singh N and Vives X 1984 Price and quantity competition
in a differentiated duopoly. Journal of Economics 15(4)
546-554.
Sato T 1996 On Cournot-Bertrand mixed duopolies.
Japanese Economic Review 47(4) 412-420.
Correa-Lopez M 2007 Price and quantity competition in a
differentiated duopoly with upstream suppliers. Journal
of Economics and Management Strategy 16(2) 469-505.
Maggi G 1996 Strategic trade policies with endogenous
mode of competition. American Economic Review
86(1) 237-258.
Ma J, et al. 2018 Complexity study on the Cournot –
Bertrand mixed duopoly game model with market share
preference. Chaos: An Interdisciplinary Journal of
Nonlinear Science 28(2) 23101.
Decision of Production Combinations Based on Cournot Model and Linear Programming
125
