Transmission Analysis and Future Trend Prediction of Deyr City's
B1H3 Virus by SIR Modelling
Ziyi Zhao
Faculty of Sciences, Engineering and Technology, University of Adelaide, SA, 5000, Australia
Keywords: SIR Model, Virus Transmission, Future Trend Prediction.
Abstract: This study analysed the transmission dynamics of a virus using data from bat monitoring and hospital testing.
This research investigated the positivity rate and infection spread in bat populations and human patients. The
study employed a Poisson distribution model to evaluate bat infection rates and a linear regression model to
estimate the virus's doubling time and basic reproduction number 𝑅

Additionally, an epidemic branching
process simulation was conducted to predict future virus transmission paths. The Susceptible-Infectious-
Recovered (SIR) model was utilized to understand and predict epidemic dynamics. The results indicate a
moderate transmission potential with a doubling time of 41.6232 days and 𝑅

of 1.1665. The simulation
emphasized the importance of early detection and intervention, providing valuable insights for public health
strategies. By integrating various statistical and mathematical models, this research offers a comprehensive
approach to understanding the transmission mechanisms of the virus. The findings highlight the
interconnectedness of bat and human infections, underscoring the necessity of a holistic approach that
considers the health of humans, animals, and the environment. The methodology in this research can also be
applied to other zoonotic diseases, aiding in the development of robust monitoring and response systems.
Future research should focus on refining models with more granular data and exploring the impacts of
different intervention strategies on controlling virus spread.
1 INTRODUCTION
In December 2019, a novel strain of Coronavirus
(SARS-CoV-2) was identified. This virus led to a
severe and potentially deadly respiratory syndrome
called COVID-19. As it spread rapidly worldwide,
the World Health Organization (WHO) declared it a
pandemic on March 11, 2020 (Xing et al., 2024; Zhen
and Sun, 2020 & Chen et al., 2023). The unparalleled
global impact of the COVID-19 pandemic has
highlighted the essential need for early detection and
effective management of infectious diseases. Since
the onset of COVID-19, various mathematical
modelling approaches have been utilized to simulate
the disease's progression. Although artificial
intelligence-based models are promising, their
reliability can be questioned without sufficient
training datasets due to their dependency on extensive
learning processes. Another method, day-level
forecasting based on time-series data, merely follows
previous patterns and fails to predict trend changes
(Zhou and Huang, 2024). In response to the ongoing
threat of new zoonotic diseases, particularly in
regions with dense wildlife populations, enhanced
surveillance systems have been established. One such
initiative is the sentinel system in Deyr, a city in the
Bergia region of Sordland, known for its significant
bat population and frequent zoonotic spillovers.
The mathematical modelling of epidemics has
been extensively studied over the past century
(Diekmann and Heesterbeek, 2000). This paper aims
to apply epidemiological models to predict and
manage potential outbreaks resulting from these
interactions. The main goal of this research is to use
mathematical modeling to analyze and forecast the
transmission dynamics of diseases in Deyr.
Specifically, the study employs methods to calculate
the early infection growth rate, which is crucial for
understanding the initial stages of an outbreak.
Additionally, the Susceptible-Infected-Recovered
(SIR) model, a well-established tool in epidemiology,
will be utilized to project the potential spread of the
disease within the human population (Wang, Luo and
Hu, 2020). Among the significant mathematical
models for epidemics, the SIR model, originally
proposed by Kermack and McKendrick, holds great
historical importance.
Zhao, Z.
Transmission Analysis and Future Trend Prediction of Deyr City’s B1H3 Virus by SIR Modelling.
DOI: 10.5220/0013001500004601
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Innovations in Applied Mathematics, Physics and Astronomy (IAMPA 2024), pages 131-135
ISBN: 978-989-758-722-1
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
131

This research builds on the foundational work in
epidemiological modelling, which dates back to the
early 20th century (Mao and Liu, 2023). The use of
models such as the SIR model has evolved
significantly, providing insights into the mechanisms
of disease spread and the effectiveness of control
measures (Satsuma et al., 2004). In Deyr, the recent
increase in cases detected through the sentinel system
has raised concerns about a possible escalation into a
more severe outbreak. This situation mirrors
historical precedents where initial outbreaks were
either contained or evolved into widespread
epidemics based on the interactions between
susceptible and infected populations. By calculating
the early growth rate and applying the SIR model, this
study aims to provide actionable insights that can
inform public health strategies. These models will
help predict the trajectory of the outbreak and assess
the potential impact of intervention measures. The
analysis will also consider the accuracy of the models
and the reliability of the data from the sentinel
system, ensuring that the predictions are both
scientifically robust and practically applicable.
The findings from this research are intended to
guide public health decisions in Deyr and could serve
as a reference for other regions facing similar
challenges. By advancing the application of
epidemiological models in real-world scenarios
(Rodrigues, 2016). This study contributes to the
broader field of public health, enhancing the ability to
respond effectively to emerging infectious diseases.
2 METHODOLOGY
2.1 Data Sources and Description
This study utilizes two primary databases:
`bat_monitoring.db` and `hospital_testing.db`. The
`bat_monitoring.db` contains data on bat monitoring
at different stations, including station names,
monitoring dates, total bats detected, and the number
of positive bats. The `hospital_testing.db` includes
data on positive patients detected in hospitals, such as
detection dates and patients' dates of birth. Relevant
data were extracted from these databases for
subsequent processing and analysis.
2.2 Indicator Description
The positivity rate in bat monitoring data was
calculated as the ratio of positive bats to the total
number of bats detected at each station. The positivity
rate in hospital testing data was calculated as the ratio
of positive patients to the total number of patients
tested in hospitals. The virus transmission rate 𝑅

was calculated based on detection data and
epidemiological models to evaluate the virus's
potential spread within the population. The duration
of illness was estimated by analyzing the duration of
symptoms in positive patients. The doubling time was
calculated using a linear regression model to evaluate
the speed of virus spread within the population.
2.3 Method Description
Data were extracted from `bat_monitoring.db` and
`hospital_testing.db` using SQLite.Date fields were
converted to standard date formats for time series
analysis. Data were sorted and filtered to ensure
completeness and consistency. Histograms and time
series plots were used to visualize bat monitoring data
and hospital testing data. The positivity rate in bat
monitoring data was calculated and the data were
fitted using a Poisson distribution model. A weekly
analysis of hospital testing data was performed to
calculate the trend in the number of positive patients
detected each week. Based on hospital testing data, a
linear regression model was used to calculate the
doubling time and basic reproduction number 𝑅

of
the virus. Bat monitoring data and hospital testing
data were combined to evaluate the virus's
transmission characteristics in different populations.
To understand and predict the dynamics of
epidemic spread, the article employed the
Susceptible-Infectious-Recovered model. The
simplicity and robustness of the model make it an
ideal choice for simulating epidemic processes and
understanding the underlying mechanisms of disease
transmission.
The dynamics of the SIR model can be defined by
these ODEs:


= −𝛽𝑆𝐼 (1)


= 𝛽𝑆𝐼 − 𝛾𝐼 (2)


= 𝛾𝐼 (3)
In these equations: equation (1) represents the
changing rate of the susceptible population, which
decreases as susceptible individuals become infected.
Equation (2) represents the rate of change of the
infectious population, which increases as susceptible
individuals become infected and decreases as infected
individuals recover. Equation (3) represents the rate
of change of the recovered population, which
increases as infected individuals recover. Moreover,
the key parameters in the model are the infection rate
( 𝛽) and the recovery rate ( 𝛾). As for the Infection
IAMPA 2024 - International Conference on Innovations in Applied Mathematics, Physics and Astronomy
132

Rate ( 𝛽) , this parameter indicates how many
susceptible individuals get infected per infectious
individual per unit time. It is influenced by factors
such as the transmission rate of the disease and the
contact rate between individuals. This parameter
Recovery Rate represents the rate at which infectious
individuals recover and move to the recovered
category. It is the inverse of the average infectious
period. The infection rate can be further detailed as:
β = γ +


(4)
where ( 𝑟 ) is the rate of new infections per week. The
basic reproduction number (𝑅

), a critical threshold
parameter, is defined as:
𝑅

=


(5)
The equation (5) represented the average number of
secondary infections produced by a single infectious
individual in a completely susceptible population. If
𝑅

>1, the disease is expected to spread; if 𝑅

<1,
the disease will eventually die out.
To simulate the epidemic process, the paper
initialized the model with a predefined number of
infected individuals. The simulation ran for 100
repetitions over 60 times steps, capturing the
stochastic nature of disease transmission. Besides,
each simulation iteration involved the following
steps:
First was to set initial values for S, I, and R. Then
this paper updated the values of S, I, and R at each
time step using the SIR equations. Finally, the basic
reproduction number 𝑅

and doubling time were
calculated and provided a measure of the disease's
transmissibility and a forecast over next 60 days will
be beneficial to understand the spread of the virus
more intuitively.
3 RESULTS AND DISCUSSION
The research extracted the monitoring data for station
H1, converting the dates to a standard format and
sorting the data by date. This allowed us to visualize
the detected bats and positive bats over time. The plot
showed fluctuations in these numbers, which
provided a basis for further analysis.
3.1 Positivity Rate Analysis
By analysing the monitoring data of station H1 from,
then the following figure was plotted:
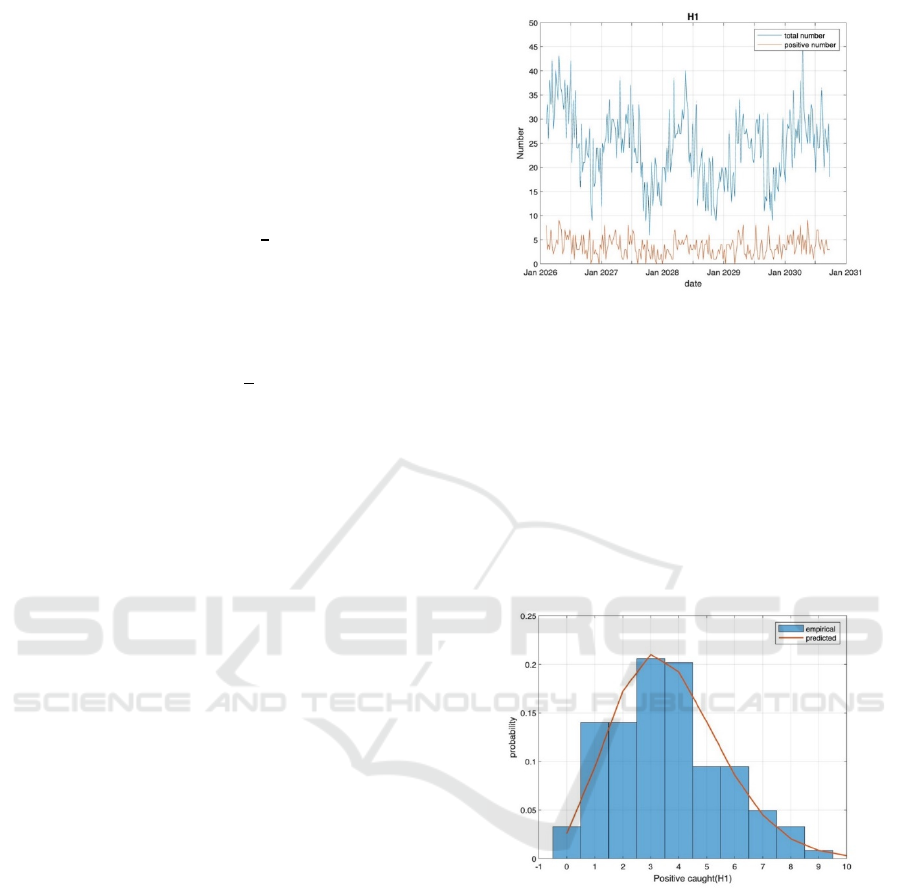
Figure 1. Positive number and total number of bats.
The results of Figure 1 showed fluctuations in the
total number of bats detected and the number of
positive bats over time at station H1. Then, to analyse
the positivity rate, the distribution of positive bats was
plotted and fitted a Poisson distribution model. The
positivity rate p was calculated as the ratio of the total
positive bats to the total number of bats detected. The
Poisson model helped to understand the expected
distribution of positive bats and evaluate the infection
spread in the bat population in Figure 2.
Figure 2. Positive caught and probability.
The analysis shows that the distribution of
positive bats at station H1 fits well with the Poisson
distribution, with a positivity rate of p.
3.2 Hospital Testing Data Analysis
Next, the research focused on analysing the hospital
testing data from the `hospital_testing.db` database.
Here are the steps and explanations: By analysing the
hospital testing data from the hospital_testing.db
database, then the number of positive cases detected
each week was calculated and plotted the following
Figure 3:
Transmission Analysis and Future Trend Prediction of Deyr City’s B1H3 Virus by SIR Modelling
133

Figure 3. Weekly number of detected cases.
The result showed a clear temporal trend in the
number of positive cases detected each week.
3.3 Simulation of Epidemic Branching
Process
Using a linear regression model, the research fitted
the data to calculate the virus's doubling time and
basic reproduction number 𝑹
𝟎
shown in Figure 4.
Figure 4. Reproduction number and doubling time.
The analysis of bat monitoring data and hospital
testing data provided insights into the virus's
transmission dynamics. The positivity rate and the
distribution of positive cases in bats helped us
understand the infection spread in wildlife, while the
hospital data gave a clear picture of human infections.
The epidemiological modelling revealed the virus's
potential to spread, as indicated by the 𝑹
𝟎
value and
the doubling time. The doubling time was found to be
41.6232 days, and 𝑹
𝟎
was calculated as 1.1665,
indicating a moderate transmission potential.
The following Figure 5 presented the forecast
with the mean and 90% prediction intervals over the
next 60 days.
Figure 5. Forecast over the next 60 days.
The simulation of the epidemic branching process
further illustrated the possible trajectories of virus
transmission, highlighting the importance of early
detection and intervention. These results are crucial
for informing public health strategies and mitigating
the impact of future outbreaks.
4 CONCLUSION
This paper conducted a comprehensive analysis of the
transmission dynamics of the B1H3 virus in Deyr
City, revealing the complex patterns of infection
IAMPA 2024 - International Conference on Innovations in Applied Mathematics, Physics and Astronomy
134

spread between wildlife and human populations, and
highlighting the importance of wildlife as reservoirs
and vectors of disease. The positivity rates and case
distribution in bats indicated heterogeneity in
infection across different locations, possibly due to
ecological factors, which is crucial for preventing
potential spillovers to humans. Meanwhile, the
analysis of hospital data provided a clear view of
infection trends in humans, identifying patterns
critical for early detection and intervention through
the statistical data of weekly positive cases.
Additionally, the SIR model was used to predict the
disease's potential spread with considerable accuracy
by calculating 𝑹
𝟎
and doubling time, quantifying the
virus's transmission potential. The model highlighted
the effectiveness of potential intervention strategies.
The calculated 𝑹
𝟎
value of 1.1665 indicated a
moderate potential for transmission, while a doubling
time of 41.6232 days provided a critical window for
implementing public health measures. The paper's
simulation predicted the possible trajectory of the
disease over the next 60 days, providing guidance for
public health strategies. In summary, the study,
through exhaustive methodologies and empirical
analysis, offered valuable insights for addressing
similar infectious threats and underscored the
importance of continuous monitoring and timely
intervention to effectively manage future outbreak.
REFERENCES
Xing Y, Meng W, Zhou J and Nie Z 2024 Research on key
nodes in fire causal network of self-built houses
based on TOPSIS-SIR model. Safety (04), 48-56.
Zhen W and Sun S W 2020 Improved SIR model for virus
propagation dynamics analysis. Journal of Tianjin
University of Technology.
Chen W, Wang Y and Liu X Y 2023 A secondary infection
SIR model for stock market risk contagion. Journal of
Systems Engineering (06), 791-811.
Zhou Q and Huang Z 2024 Improvement of classical SIR
model and its application. Industry and Technology
Forum (04), 45-47.
Diekmann O and Heesterbeek J A P 2000 Mathematical
epidemiology of infectious diseases: model building,
analysis and interpretation. John Wiley & Sons.
Wang Y, Luo X and Hu J 2020 Research on the prediction
of new coronavirus pneumonia epidemic and
preventive and control measures based on SIR model.
Journal of Qiannan Nationalities Normal College (04),
58-63.
Mao Y C and Liu X B 2023 Exit problem of stochastic SIR
model with limited medical resource. Theoretical &
Applied Mechanics Letters (01), 8-13.
Satsuma J, et al. 2004 Extending the SIR epidemic model.
Physica A: Statistical Mechanics and its Applications,
336(4), 369-375.
Kang G and Liu B 2020 Predictive analysis of novel
coronavirus pneumonia. Sino-Arabic Science and
Technology Forum (06), 151-153.
Rodrigues H S 2016 Application of SIR epidemiological
model: new trends. Theoretical & Applied Mechanics
Letters.
Transmission Analysis and Future Trend Prediction of Deyr City’s B1H3 Virus by SIR Modelling
135