Local Motion Planning for Overtaking Maneuvers in a Rural Road

Environment

aniel Losonczi

1 a

Arp

ad Feh

2 b

, Szil

ard Aradi

2 c

and L

aszl

o Palkovics

3 d

Systems and Control Laboratory, HUN-REN Institute for Computer Science and Control (SZTAKI),

Kende utca 13-17., H-1111 Budapest, Hungary

Department of Control for Transportation and Vehicle Systems, Faculty of Transportation Engineering and Vehicle

Engineering, Budapest University of Technology and Economics, M

uegyetem rkp. 3., H-1111 Budapest, Hungary

echenyi Istv

an University, Egyetem t

er 1., H-9026 Gy

or, Hungary

Keywords:

Local Motion Planning, Overtaking Maneuvers, Rural Road Environment, Autonomous Vehicles, Frenet

Frame.

Abstract:

This paper introduces an application of local motion planning designed explicitly for overtaking maneuvers in

a rural road environment. The approach integrates multiple driving strategies for enhanced passenger comfort,

including the fastest path and minimum jerk trajectory. A robust trajectory planner technique is developed

using the Frenet frame, effectively considering real trafﬁc situations, curves, and moving obstacles. Compre-

hensive analyses are performed on vehicle dynamics, individual cost function components, and planning and

tracing times to assess the performance and computational efﬁciency of the proposed methods. The simulation

results highlight the approach’s strengths in maintaining dynamic feasibility, ensuring safety, and enhancing

passenger comfort while identifying areas for potential improvements, such as computational overhead in

complex scenarios.

1 INTRODUCTION

Autonomous vehicle systems must reliably and accu-

rately plan trajectories in real-time within dynamic

and changing environments, considering obstacles

and moving goals. Achieving this requires a compre-

hensive, hierarchical software system that integrates

multiple layers (Paden et al., 2016), each essential for

ensuring the vehicle’s safe and efﬁcient navigation.

As the ﬁrst step in the motion planning process,

observing the vehicle’s environment and representing

it as a map is necessary (Bresson et al., 2017). Subse-

quently, the vehicle must determine a global route that

avoids static obstacles while considering various con-

straints, such as the vehicle’s kinematic limitations

and the road’s geometry. While traversing the global

path, the vehicle has to make decisions at speciﬁc

points and then plan its local trajectories (Schwart-

ing et al., 2018). In the process of doing so, the ve-

hicle must generate and periodically update a local

https://orcid.org/0009-0007-5053-1714

https://orcid.org/0000-0002-9491-4211

https://orcid.org/0000-0001-6811-2584

https://orcid.org/0000-0001-5872-7008

path that follows the global route as a reference, con-

sidering real-time constraints, the vehicle’s dynamics,

and dynamically moving objects. The term ”local”

indicates that this path is short-term, and the planning

occurs in the vehicle’s local coordinate system. The

vehicle must follow the planned local path using con-

trol algorithms that determine longitudinal and lateral

control inputs. All of this must be performed in real-

time, accounting for uncertainties and the vehicle’s

continuously changing environment.

This paper presents a method for local trajec-

tory planning in a Frenet frame to implement a lane-

keeping and overtaking maneuver.

1.1 Related Work

The problem of trajectory planning and control for

autonomous vehicles, particularly in overtaking sce-

narios, has been addressed through various innova-

tive approaches. These efforts balance multiple ob-

jectives, such as safety, smoothness, and efﬁciency,

while considering practical constraints and dynamic

environments.

Several methodologies illustrate these concepts.

220

Losonczi, D., Fehér, Á., Aradi, S. and Palkovics, L.

Local Motion Planning for Overtaking Maneuvers in a Rural Road Environment.

DOI: 10.5220/0013001600003822

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 2, pages 220-227

ISBN: 978-989-758-717-7; ISSN: 2184-2809

For instance, (You et al., 2015) proposed a coop-

erative vehicle infrastructure system for improving

lane change maneuvers through real-time adjustments

based on vehicle dynamics. Similarly, (Palatti et al.,

2021) developed a risk assessment and decision-

making framework using a ﬁnite state machine to en-

hance overtaking safety. During motion planning for

overtaking situations, the authors used a graph-based

method in (Heged

us et al., 2020) that reduces com-

plexity by clustering and predicts the movement of

surrounding vehicles with density functions, ensuring

a safe and comfortable trajectory.

Model Predictive Control (MPC) has been ex-

tensively applied to autonomous vehicle overtaking.

Studies by (Li et al., 2023) and (Batkovic et al., 2022)

demonstrate MPC’s real-time optimization of trajec-

tories, accounting for dynamic road conditions. Addi-

tionally, (Dixit et al., 2020) integrated potential ﬁelds

and reachability sets with MPC for high-speed over-

taking on highways.

Distributed motion planning techniques also show

promise. (Wu et al., 2021) and (Kala and Warwick,

2014) emphasize decentralizing decision-making to

improve trafﬁc safety and system responsiveness.

(Xie et al., 2022) extended this approach with the Ar-

tiﬁcial Potential Field method for multi-vehicle envi-

ronments.

Reinforcement learning (RL) is another advanced

methodology. A continuous reinforcement learning

method was developed to determine the trajectory of

the double lane change maneuver (Feh

er et al., 2020).

The real-time solution was compared with the per-

formance of human drivers. In (Lelk

o and N

emeth,

2024), the authors present a control framework that

combines a robust H

∞

controller and an RL agent

to ensure the safe movement of autonomous vehi-

cles. (Kulathunga, 2022) and (Wang et al., 2023)

highlighted RL’s effectiveness in improving decision-

making and trajectory planning, with signiﬁcant suc-

cess in the Frenet coordinate system. Similarly,

(Huang et al., 2023) proposed a multiobjective op-

timization algorithm within the Frenet frame to en-

hance driving comfort and safety.

Virtual target-based algorithms are also notable.

(Chae and Yi, 2020) developed a method incorporat-

ing human driving behavior for improved driver ac-

ceptance and safety. (Ghumman et al., 2008) pro-

posed a rendezvous guidance-based trajectory gener-

ation approach for real-time safety and comfort.

Dynamic trajectory planning within the Frenet

coordinate system remains crucial. (Wang et al.,

2019) and (Paden et al., 2016) explored compre-

hensive surveys and hierarchical urban and highway

driving frameworks, focusing on safety and consis-

tency. (Moghadam and Elkaim, 2021) further devel-

oped a hierarchical framework combining long-term

and short-term trajectory optimization.

For speciﬁc scenarios involving frequent accel-

eration and deceleration, (Zhang et al., 2019) pre-

sented an optimal trajectory generation method con-

sidering centripetal acceleration constraints, beneﬁ-

cial for curvy roads.

1.2 Contributions of the Paper

As a contribution, we propose a method to plan an

optimal local trajectory for lane-keeping and overtak-

ing maneuvers in a rural road environment. In each

planning step, the planner generates several alterna-

tive trajectories in the feasible range and assigns a cost

to each of them. The optimization objective can be

multiple and is achieved by weighting the cost func-

tion. The method is designed to be easily integrated

into a hierarchical approach to vehicle decision con-

trol structure. In order to demonstrate and test the

method, a local planning solution was integrated into

a self-developed simulation environment.

Section 2 offers a detailed formulation of the prob-

lem and essential topological information pertinent to

the task. In Section 3, we introduce the Hierarchi-

cal Control Structure utilized in the construction of

our system. Following this, Section 4 outlines the

local trajectory generation process within the Frenet

Frame, conducted in the Simulation Environment de-

scribed in Section 5. Finally, Section 6 discusses the

results of the successful maneuver, highlighting the

cost function-based driving style management and the

decision-making and control strategies employed for

maneuver handling.

2 LOCAL MOTION PLANNING

AND FRENET FRAME

Local trajectory planning focuses on generating a fea-

sible and safe trajectory for a vehicle over a short time

horizon, typically in response to dynamic changes in

the environment. This includes continuously updat-

ing the planned trajectory based on new sensor data

and the vehicle’s current state. Unlike route planning,

which provides a static sequence of points describing

a plan, trajectory planning also includes additional ve-

locity proﬁles.

Trajectory planning in dynamic environments is

inherently complex and is considered PSPACE-hard

(Paden et al., 2016). This complexity increases in dy-

namic settings, where previously manageable prob-

lems become intractable. As exact algorithms for

Local Motion Planning for Overtaking Maneuvers in a Rural Road Environment

221

non-trivial trajectory planning in autonomous driv-

ing are unavailable, numerical methods are often em-

ployed. These methods address trajectory planning

by utilizing variational methods within the time do-

main or by transforming the problem into a path plan-

ning challenge within a conﬁguration space that in-

corporates a time dimension. The path planning solu-

tion accommodates differential constraints and is then

transformed back into a trajectory.

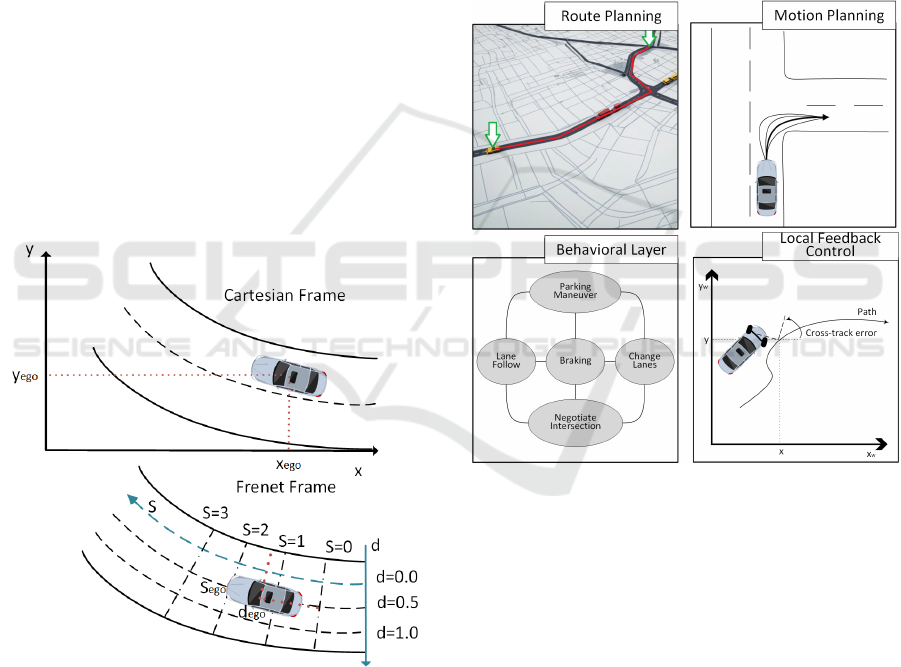
The Frenet-Serret (FS) frame (Werling et al.,

2010) is a powerful mathematical tool also used in ve-

hicle dynamics and path planning to describe vehicle

motion along a planned trajectory. This frame deﬁnes

a moving reference frame with tangential and normal

vectors at a certain point on a curve, called the center

line. This center line can be an ideal path on a free

road, the center of the road, or a path planned by an

algorithm. In this paper, the reference line will be the

center of the right-hand lane. As shown in Figure 1,

the s-axis runs parallel to the lane line, and the d-axis

is perpendicular to the reference line. This simpliﬁca-

tion makes it easier to plan within the proposed frame

as the local coordinate system moves with the vehicle,

and constraints such as lane boundaries and obstacles

are easier to handle.

Figure 1: Frenet Frame Coordinate System.

Given the initial and ﬁnal states of the vehicle

along the d-axis (d

, d

), six equations can

be formed to determine the polynomial coefﬁcients,

representing the d-axis trajectory with a quintic poly-

nomial. For the s-axis, using its start and end states

, ˙s

, ¨s

, ˙s

, ¨s

), a quartic polynomial represents the

trajectory. The planning period t ranges from 0 to

T , creating a time series [0, ∆t, . . . , T ], which is ap-

plied to both axes’ trajectory equations to calculate

each trajectory point’s coordinates. This will be fur-

ther discussed in Section 4.

3 HIERARCHICAL CONTROL

APPROACH

Several advanced methodologies for controlling

highly automated vehicles have been developed re-

cently. One prevalent approach is the hierarchical

structure (Paden et al., 2016), which consists of four

levels, each with a speciﬁc role in the vehicle’s oper-

ation, as illustrated in Fig. 2

Figure 2: Hierarchical Control Structure.

At the ﬁrst level, autonomous vehicles plan a

global route within a given road network to reach

their destination from the current position. The road

network is represented as a directed graph, where

weighted edges determine the cost of traversing the

network. These weights can represent various fac-

tors such as distance, travel time, trafﬁc density, and

road conditions. Standard algorithms used for global

route planning include Dijkstra’s algorithm and the

A* search algorithm.

Once a global route plan is selected, the vehicle

must navigate the route and interact with other road

users according to trafﬁc conditions and rules. The

behavioral layer is responsible for selecting the ap-

propriate driving behavior at any given time, consid-

ering the actions of other road users, road conditions,

and infrastructure signals. This decision-making pro-

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

222

cess can be automated using ﬁnite state machines and

probabilistic planning formalisms, such as Markov

Decision Processes (MDPs) and their generalizations.

After the behavioral layer decides on the driving

behavior, the local motion planning layer deﬁnes the

vehicle’s trajectory. This trajectory must be dynami-

cally feasible, ensuring passenger comfort and avoid-

ing obstacles detected by onboard sensors. Numerical

approximation methods are commonly used to solve

the motion planning problem. The solution discussed

in this article focuses on this layer.

At the fourth level, the planned path and trajec-

tory are executed. The feedback controller calculates

the corresponding actuator inputs for driving, steer-

ing, and braking to execute the planned movement

and reduce tracking errors. This layer relies on well-

established algorithms that emphasize robustness and

stability.

4 LOCAL TRAJECTORY

PLANNING IN FRENET FRAME

Local trajectory planning and tracking are conducted

within a simulation environment that adheres to real-

world trafﬁc restrictions. The global path is deﬁned

as the centerline of the right lane of the road, serv-

ing as our reference route within the Frenet frame, as

previously discussed.

In the Frenet frame coordinate system, the lateral

displacement d is zero when the vehicle is on the ref-

erence path. The value of d increases as the vehi-

cle moves towards the left edge of the road and de-

creases (becoming negative) as it approaches the right

edge. The longitudinal position s represents the vehi-

cle’s position along the local trajectory, reset to zero

at each planning interval.

The vehicle is initialized on this global trajectory

at the start, with a planning interval of T = 3 sec-

onds. This planning interval allows the vehicle to

plan ahead for 41.6 meters at a target speed of

3.6

m/s,

which is deemed safe for dynamic obstacle detection

and avoidance.

4.1 Planning Process

During the planning process of the local trajectory (as

shown in Fig. 4a), several possible route alternatives

are planned. To ensure thorough exploration of the

available space, the alternatives are generated at ev-

ery 0.1-meter point along the full width of the road.

These trajectories are described with different poly-

nomials in the lateral and longitudinal directions. The

polynomials give the deviation from the global path.

Firstly, the lateral characteristics are determined by

quintic polynomial ﬁtting, where the 1st, 2nd, 3rd,

and 4th derivatives describe the lateral characteristics

of the trajectory at each time step. The quintic poly-

nomial is expressed as:

d(t) = a

+ a

t + a

+ a

(1)

where d(t) represents the lateral position at time

t. The coefﬁcients a

, a

, and a

are deter-

mined based on boundary conditions such as initial

and ﬁnal positions, velocities, and accelerations.

The ﬁrst derivative represents the rate of change

of the lateral position with respect to time, indicating

how fast the vehicle is moving laterally at any given

moment. The second calculates the rate of change of

lateral velocity, providing information about the lat-

eral forces acting on the vehicle. The third derivative

represents the rate of change of lateral acceleration,

which is important for determining ride comfort.

The longitudinal characteristics are deﬁned at

each time step using a quartic polynomial given by:

s(t) = b

+ b

t + b

+ b

(2)

where s(t) represents the longitudinal position at time

The ﬁrst derivative represents the rate of change

of the longitudinal position with respect to time. The

second measures the rate of change of longitudinal

velocity. The third represents the rate of change of

longitudinal acceleration.

4.2 Combining Proﬁles and Cost

Function

Once the longitudinal and lateral proﬁles are gener-

ated, they are combined. A cost function is used to

select the appropriate trajectory for the given objec-

tive. The function includes jerk, deviation from the

reference path, lane change, and costs for weight-

ing the fastest trajectory and shortest trajectory. By

weighting these factors differently, trajectory designs

for various purposes can be implemented. The results

of these designs are presented in the following sec-

tions. Each trajectory’s costs are combined and nor-

malized, and the trajectory with the lowest total cost

is selected. In the case of obstacle detection, the ac-

tual trajectory encountering an obstacle is prohibited

rather than penalized by cost.

The elements of the cost function can be calcu-

lated as follows:

J(t) =

∑

t=0



′′′

(t)



(3)

Local Motion Planning for Overtaking Maneuvers in a Rural Road Environment

223

The jerk cost J(t) is calculated by summing the

squares of the third derivatives of the lateral position

with respect to time. This represents the cumulative

lateral acceleration change over the planning horizon.

ref

∑

t=0



d(t) − x

target



(4)

The deviation from the reference route D

ref

is calcu-

lated by summing the squared differences between the

actual lateral position d(t) and the target lane center

target

over the planning horizon.

Dist =

(GlobalRouteEnd

− TrajectoryEnd

)

(5)

The distance cost Dist is calculated as the Euclidean

distance between the planned trajectory endpoint and

the global route endpoint.

change



− x

target



(6)

The lane change cost L

change

is calculated as the abso-

lute difference between the lateral displacement d

the trajectory and the target lane center x

target

Table 1: Cost Function Parameters.

Cost Function Parameters

Penalized

Weights

Comfort

stlye

Sporty

stlye

Jerk 10.0 1.3

Speed 1.3 10.0

Deviation 3.0 3.0

Distance 0.01 0.01

Lane

Change

3.0 3.0

Finally, the resulting trajectories are transformed

from the Frenet frame to the global Cartesian coordi-

nate system for visualization and tracking. The trans-

formation from Frenet to global coordinates involves

mapping a local position (given by s and d) on a ref-

erence path to its corresponding global position by

calculating the global coordinates for the given arc

length, applying the lateral offset to these coordinates,

determining the orientation and segment lengths, and

deriving the curvature from changes in orientation.

5 SIMULATION ENVIRONMENT

For the development and testing of the local trajec-

tory planning method, a unique simulation environ-

ment was developed, which consists of the following

components:

• A road generator that meets standard road design

guidelines. It builds up the track from straight,

curved, and clothoid transitional curves. The ru-

ral road environment was created by deﬁning two

lanes. The global path is the center line of the

right lane in the direction of travel.

• A nonlinear planar single-track vehicle model

containing a dynamic wheel model (Heged

et al., 2020) is also applied as an EGO vehicle to

provide accurate behavior prediction.

• Lateral MPC controller running a linear dynamic

model. The model states that there are tracking

errors, which the controller aims to minimize. The

yaw-rate proﬁle is deﬁned as a constraint.

• Longitudinal PID controller. The speed reference

is determined by the speed proﬁle.

• Transformation solutions that facilitate planning

in the Frenet frame. Simpliﬁed trafﬁc simulation.

• 2D graphical interface see in Fig. 3

Figure 3: Simulation Environment.

6 RESULTS

As a result of this study, we present a local trajec-

tory planning method speciﬁcally designed for over-

taking maneuvers in rural environments. A compre-

hensive software architecture was used for validation,

including global route planning, a decision-making

layer, local motion planning, and local feedback con-

trol. As mentioned in Section 4, the global route has

been aligned and ﬁtted to the reference path.

The maneuvering scenarios were tested in the

presented simulation environment. Personalized

decision-making was implemented using a ﬁnite-state

machine based on a simpliﬁed version of the MO-

BIL (Minimizing Overall Braking Induced by Lane

changes) model (Kesting et al., 2007), which is a lane-

changing algorithm that assesses the advantages and

consequences of a lane change for the ego vehicle

and the vehicles around it. The model consists of an

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

224

incentive criterion that promotes lane changes bene-

ﬁting trafﬁc ﬂow and a safety criterion that prevents

lane changes from posing a risk to other vehicles. Our

simpliﬁed MOBIL model deﬁnes three states, which

maneuvers are shown in Figure 4:

• Free-Driving State: The ego vehicle remains in or

returns to this state if there is no preceding vehi-

cle. The primary operations involve controlling

speed and following the reference route with the

speciﬁed driving style. In this state, trajectories

crossing into the opposite lane are strictly prohib-

ited to ensure safety and compliance with trafﬁc

rules.

• Tracking State: This state occurs when another

vehicle is in front of the ego vehicle, prevent-

ing a safe overtake. Here, Adaptive Cruise Con-

trol (ACC) is realized, allowing the ego vehicle

to adapt to the speed of the preceding vehicle and

maintain a safe distance. The Intelligent Driver

Model (IDM) (Kesting et al., 2010) is utilized

to calculate the desired acceleration based on the

current speed, the distance and relative speed be-

tween the two vehicles.

• Overtaking State: This state is triggered when the

decision-making process deems overtaking feasi-

ble, and the driver approves it. The steps involved

in this maneuver are swerving, overtaking, and re-

turning to the original lane.

6.1 Cost Function Based State

Management

During the planning process, two distinct settings

were identiﬁed beside the decision-based states: jerk

minimization (comfort setting) and fastest trajectory

execution (sporty setting). In the comfort setting, the

cost function heavily weights the variation in lateral

acceleration, whereas, in the sporty setting, the ex-

ecution time is prioritized, as shown in Table 1. A

comparative cost function diagram pair can be found

in Figure 5.

The driving style can be customized using the cost

parameters outlined above. For example, trajectories

with lower lateral acceleration can be selected for a

smoother ride, while a faster method yields sportier

trajectories with higher jerks. This customization

is reﬂected in the decision-making layer, where a

sportier setting may lead to riskier decisions due to

shorter trajectory execution times. For this, detailed

maximum lateral slip values corresponding to differ-

ent road IDs, which denote varying levels of curve

difﬁculties in both comfort and sporty styles, are pro-

vided in Table 2.

(a) Free-Driving / Tracking. (b) Swerving.

Figure 4: Local Trajectories during maneuvers.

6.2 Control Strategies

The accurate and safe lateral tracking of planned tra-

jectories is managed by an MPC (Model Predictive

Controller) that handles the lateral and angular er-

ror. Meanwhile, the speed is maintained by a PID

(Proportional-Integral-Derivative) controller. The tar-

get speed for the PID controller is determined by

the motion planner and is maximized by the decision

layer. These velocity proﬁles of the optimal trajectory

are assigned to the control at each time step, tracing

75% of the trajectory before the next planning. By

default, the vehicle plans and proceeds free-driving

along the trajectory in one of the operationally switch-

able driving styles (comfort or sporty). If a vehicle is

detected ahead within a safe braking distance, the be-

havioral layer switches to the tracking state, and the

vehicle adaptively matches its speed to the preceding

vehicle and maintains a safe distance until the over-

taking maneuver is triggered. Upon activation, the

vehicle switches to the overtaking state, increases its

speed, and selects trajectories that allow for a quick

and safe overtaking. Once the maneuver is complete,

the vehicle returns to the previous state and continues

free-driving on its path.

Table 2: Maximum lateral slip values for comfort and sporty

styles across different difﬁculty of road sections.

Road ID Comfort stlye Sporty style

1 0.00772 0.01056

2 0.00171 0.01195

3 0.00746 0.01466

4 0.00838 0.01706

5 0.00996 0.01192

The driving style inﬂuences the lateral and longi-

tudinal characteristics of the maneuvers. These trajec-

tories are selected by the designer using the associated

cost functions, ensuring the vehicle’s behavior aligns

with the desired performance and safety criteria.

Local Motion Planning for Overtaking Maneuvers in a Rural Road Environment

225

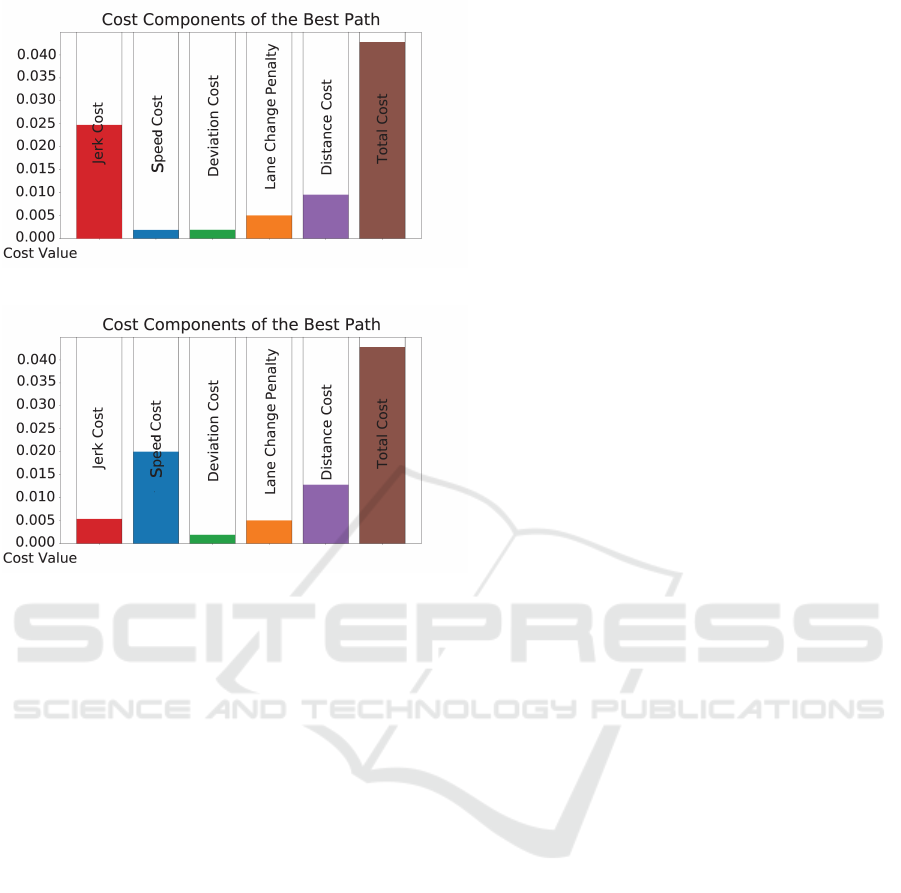
(a) Cost Function Diagram of Comfort setting

(b) Cost Function Diagram of Sporty setting

Figure 5: Different Driving Styles given the same planning

conditions.

7 CONCLUSIONS

In this paper, we presented a comprehensive approach

to local motion planning for autonomous vehicles,

with a particular focus on overtaking maneuvers in

rural road environments. Our method demonstrated

effectiveness, safety, and reliability, proving easy to

tune for various driving styles. Currently, our sim-

ulation includes two vehicles, and we aim to expand

this to incorporate trafﬁc scenarios, allowing for over-

taking in more complex environments. Our immedi-

ate goal is to implement real vehicle tests in a known

environment to validate our approach further. Ad-

ditionally, we aim to replace the polynomial ﬁt de-

sign with a classical trajectory design method. This

transition will allow us to determine curvature points

and trajectory orientation more precisely, enabling

the creation of unique, parameterizable trajectories.

Such advancements will facilitate the design of opti-

mized paths, including speciﬁc apex points of curves,

thereby enhancing the versatility and performance of

autonomous vehicle motion planning.

ACKNOWLEDGEMENTS

The research was supported by the European Union

within the framework of the National Laboratory for

Autonomous Systems. (RRF-2.3.1-21-2022-00002)

REFERENCES

Batkovic, I., Zanon, M., and Falcone, P. (2022). Model

predictive control for safe autonomous driving appli-

cations. In AI-enabled Technologies for Autonomous

and Connected Vehicles, pages 255–282. Springer.

Bresson, G., Alsayed, Z., Yu, L., and Glaser, S. (2017).

Simultaneous localization and mapping: A survey of

current trends in autonomous driving. IEEE Transac-

tions on Intelligent Vehicles, 2(3):194–220.

Chae, H. and Yi, K. (2020). Virtual target-based overtaking

decision, motion planning, and control of autonomous

vehicles. IEEE Access, 8.

Dixit, S., Montanaro, U., Dianati, M., Oxtoby, D., Mizu-

tani, T., Mouzakitis, A., and Fallah, S. (2020). Trajec-

tory planning for autonomous high-speed overtaking

in structured environments using robust mpc. IEEE

Transactions on Intelligent Transportation Systems,

21.

Feh

er,

A., Aradi, S., and B

ecsi, T. (2020). Hierarchical eva-

sive path planning using reinforcement learning and

model predictive control. IEEE Access, 8:187470–

187482.

Ghumman, U., Kunwar, F., and Benhabib, B. (2008).

Guidance-based on-line motion planning for au-

tonomous highway overtaking. International Journal

on Smart Sensing and Intelligent Systems, 1.

Heged

us, T., N

emeth, B., and G

asp

ar, P. (2020). Design

of a low-complexity graph-based motion-planning al-

gorithm for autonomous vehicles. Applied Sciences,

10(21):7716.

Huang, J., He, Z., Arakawa, Y., and Dawton, B. (2023). Tra-

jectory planning in frenet frame via multi-objective

optimization. IEEE Access, 11:70764–70777.

Kala, R. and Warwick, K. (2014). Dynamic distributed

lanes: motion planning for multiple autonomous ve-

hicles. Applied intelligence, 41:260–281.

Kesting, A., Treiber, M., and Helbing, D. (2007). General

lane-changing model mobil for car-following models.

Transportation Research Record, 1999:86–94.

Kesting, A., Treiber, M., and Helbing, D. (2010). Enhanced

intelligent driver model to access the impact of driv-

ing strategies on trafﬁc capacity. Philosophical trans-

actions. Series A, Mathematical, physical, and engi-

neering sciences, 368:4585–4605.

Kulathunga, G. (2022). A reinforcement learning based

path planning approach in 3d environment. In Pro-

cedia Computer Science, volume 212.

Lelk

o, A. and N

emeth, B. (2024). Optimal motion design

for autonomous vehicles with learning aided robust

control. IEEE Transactions on Vehicular Technology.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

226

Li, G., Zhang, X., Guo, H., Lenzo, B., and Guo, N. (2023).

Real-time optimal trajectory planning for autonomous

driving with collision avoidance using convex opti-

mization. Automotive Innovation, 6(3):481–491.

Moghadam, M. and Elkaim, G. H. (2021). An autonomous

driving framework for long-term decision-making and

short-term trajectory planning on frenet space. In

IEEE International Conference on Automation Sci-

ence and Engineering, volume 2021-August, pages

1745–1750. IEEE Computer Society.

Paden, B.,

ap, M., Yong, S. Z., Yershov, D., and Fraz-

zoli, E. (2016). A survey of motion planning and con-

trol techniques for self-driving urban vehicles. IEEE

Transactions on intelligent vehicles, 1(1):33–55.

Palatti, J., Aksjonov, A., Alcan, G., and Kyrki, V. (2021).

Planning for safe abortable overtaking maneuvers in

autonomous driving. In 2021 IEEE International In-

telligent Transportation Systems Conference (ITSC),

pages 508–514. IEEE.

Schwarting, W., Alonso-Mora, J., and Rus, D. (2018). Plan-

ning and decision-making for autonomous vehicles.

Annual Review of Control, Robotics, and Autonomous

Systems, 1(1):187–210.

Wang, J., Chu, L., Zhang, Y., Mao, Y., and Guo, C.

(2023). Intelligent vehicle decision-making and tra-

jectory planning method based on deep reinforcement

learning in the frenet space. Sensors, 23.

Wang, M., Zhang, L., Wang, Z., Sai, Y., and Chu, Y.

(2019). A real-time dynamic trajectory planning for

autonomous driving vehicles. In 3rd Conference on

Vehicle Control and Intelligence, CVCI 2019.

Werling, M., Ziegler, J., Kammel, S., and Thrun, S. (2010).

Optimal trajectory generation for dynamic street sce-

narios in a frenet frame. In 2010 IEEE international

conference on robotics and automation, pages 987–

993. IEEE.

Wu, J., Wang, Y., Shen, Z., Wang, L., Du, H., and Yin, C.

(2021). Distributed multilane merging for connected

autonomous vehicle platooning. Science China Infor-

mation Sciences, 64(11):212202.

Xie, S., Hu, J., Bhowmick, P., Ding, Z., and Arvin, F.

(2022). Distributed motion planning for safe au-

tonomous vehicle overtaking via artiﬁcial potential

ﬁeld. IEEE Transactions on Intelligent Transporta-

tion Systems, 23.

You, F., Zhang, R., Lie, G., Wang, H., Wen, H., and Xu, J.

(2015). Trajectory planning and tracking control for

autonomous lane change maneuver based on the coop-

erative vehicle infrastructure system. Expert Systems

with Applications, 42(14):5932–5946.

Zhang, Y., Sun, H., Zhou, J., Hu, J., and Miao, J. (2019).

Optimal trajectory generation for autonomous vehi-

cles under centripetal acceleration constraints for in-

lane driving scenarios. In 2019 IEEE Intelligent

Transportation Systems Conference, ITSC 2019.

Local Motion Planning for Overtaking Maneuvers in a Rural Road Environment

227