
AI-Based Preliminary Modeling for Failure Prediction of Reactor
Protection System in Nuclear Power Plants
Hye Seon Jo
a
, Ho Jun Lee
b
, Ji Hun Park
c
and Man Gyun Na
d
Department of Nuclear Engineering, Chosun University, 10, Chosundae 1-gil, Dong-gu, Gwangju, Republic of Korea
Keywords: Failure Prediction, Reactor Protection System, Nuclear Power Plants.
Abstract: Nuclear power plants (NPPs), which generate electricity through nuclear fission energy, are crucial for safe
operation due to the potential risk of exposure to radioactive materials. NPPs contain a variety of safety
systems, and this study aims to develop an artificial intelligence-based failure prediction model that can
predict and prevent potential failures in advance by targeting the reactor protection system (RPS). Currently,
failure data for RPS are being collected through a testbed, so we conducted preliminary modeling using open-
source data due to insufficient data acquisition. The applied open-source data are the accelerated aging data
of insulated gate bipolar transistors (IGBTs), and the remaining useful life of IGBT was predicted using long
short-term memory and Monte Carlo dropout technology. Also, physical rules were applied to improve their
prediction performance and their applicability was confirmed through performance evaluation. Through
performance evaluation of the developed prediction models, we explored the optimal model and confirmed
the applicability of the applied methodologies and technologies.
1 INTRODUCTION
A nuclear power plant (NPP) is a facility that
produces electricity by turning a turbine with steam
generated through nuclear fission energy. NPPs have
hundreds of systems with different functions,
including several safety and control systems to ensure
the safe operation of the NPP, even in the event of an
accident. Among them, the reactor protection system
(RPS) monitors safety-related variables and trips the
reactor when the monitored variables reach the set
values. The instrumentation and control system,
including the RPS, consists of various electronic
components and circuits, such as analog and digital.
The instrumentation and control system checks its
integrity through self-diagnostics at the system level
or periodical tests. However, self-diagnostics is
performed only for limited functionalities, or in the
case of the periodical tests, it is difficult to check
integrity during normal operation. In NPP,
malfunction of the RPS is directly related to plant
safety, so the prognostics and health management
a
https://orcid.org/0000-0002-4413-5244
b
https://orcid.org/0009-0001-5155-9483
c
https://orcid.org/0000-0001-6225-5621
d
https://orcid.org/0000-0003-0097-3403
(PHM) technology that can prevent potential
component failures during normal operation is
required. It can be achieved through fault diagnosis
and estimation of the remaining useful life (RUL) for
major electronic components that are vulnerable to
failure.
Currently, for the PHM of electronic components,
many studies are being conducted to predict the RUL
of electronic components using a data-driven
approach in various fields, such as hard disks
(Coursey et al., 2021), lithium-ion batteries (Rouhi
Ardeshiri et al., 2021), and insulated gate bipolar
transistors (IGBTs) (Lu et al., 2023). Through these
studies, the effectiveness of data-driven approaches in
the PHM field has been confirmed. Therefore, this
study proposes a framework for predicting the RUL
of electronic components in the RPS using artificial
intelligence (AI) technology. Due to limitations in
obtaining failure data on electronic components of the
RPS in actual NPPs, accelerated aging tests are being
conducted on major components by establishing a test
bed. Accordingly, this study performed a preliminary
Jo, H., Lee, H., Park, J. and Na, M.
AI-Based Preliminary Modeling for Failure Prediction of Reactor Protection System in Nuclear Power Plants.
DOI: 10.5220/0013006000003837
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 593-599
ISBN: 978-989-758-721-4; ISSN: 2184-3236
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
593
modeling using open-source data to predict the RUL
of electronic components. The preliminary modeling
involves exploring and confirming methodologies
using open-source data before developing a failure
prediction model for electronic components within
RPS. This process can identify effective approaches
and derive a more optimal model for developing a
failure prediction model based on actual data in the
future. The open-source data utilized in this study are
the IGBT accelerated aging data provided by NASA
(Celaya et al., 2009). Previous studies (Ismail et al.,
2020; Lu et al., 2023; Chen et al., 2024; He et al.,
2021) on predicting the RUL of IGBTs have
primarily used neural networks, such as feedforward
neural networks, long short-term memory (LSTM),
and random forest methods. So, this study utilized
LSTM (Hochreiter & Schmidhuber, 1997) and Monte
Carlo (MC) dropout (Gal & Ghahramani, 2016) based
on these studies. RUL prediction was performed
using LSTM, and uncertainty about the prediction
results was estimated through MC dropout. Also, to
enhance the performance of the LSTM, physical rules
reflecting the characteristics of RUL were added to
the loss function during model training.
The developed IGBT RUL prediction model was
compared in performance with the basic LSTM with
dropout, which does not include physical rules. It
evaluates the applicability of the proposed method for
the failure prediction model of RPS to be developed
in the future.
2 METHODS
This section describes the AI method and
optimization used in this study. The AI method
applied to predict RUL was LSTM, and MC dropout
technology was used to estimate uncertainty. Then,
the optimization procedure of the RUL prediction
model was explained.
2.1 LSTM with MC Dropout
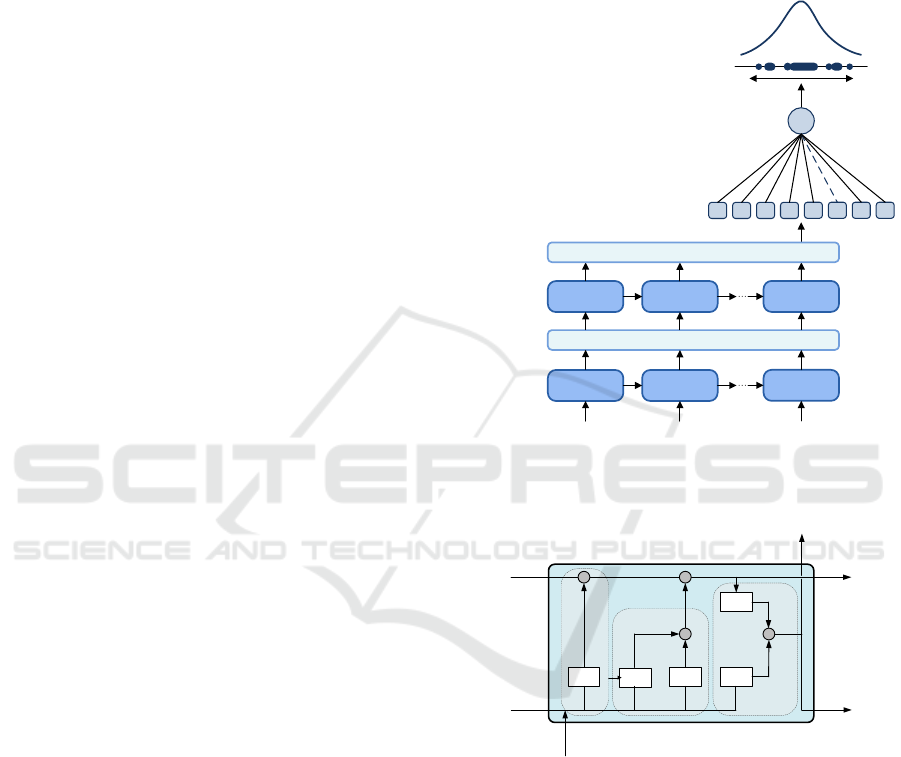
Figure 1 shows the structure of LSTM with MC
dropout for RUL prediction of IGBT in this study.
LSTM (Hochreiter & Schmidhuber, 1997) is a
modified recurrent neural network-based
methodology that can learn information about long
sequences as well as short sequences. LSTM
regulates the flow of information through gates within
its memory cells. Figure 2 shows the LSTM cell at the
t-13 step, and the gates include the input, forget, and
output gates. These gates determine how to reflect
new information, whether to maintain or discard
previous cell state information, and ultimately, how
to derive the final output based on input data and the
cell state. In other words, LSTM learns the input
sequence data and derives results. In this study, the
time sequence of the LSTM model was empirically
set to 15.
Input X
t-14
Input X
t-13
Input X
t
LSTM
Layer 1
LSTM
Layer 2
Dropout
Layer
Dropout
Layer
Fully-connected
Layer
ˆ
Output
t
y
Figure 1: Model structure for RUL prediction of IGBT.
sigmoid
tanh
13t
F
−
13t
I
−
13t
O
−
13
Input X
t−
14t
C
−
14t
h
−
12t
h
−
12t
C
−
12t
h
−
sigmoid
sigmoid
tanh
+
Figure 2: LSTM cell structure at the t-13 step.
Also, the MC dropout (Gal & Ghahramani, 2016)
technology was used to estimate the uncertainty in the
prediction results. MC dropout involves applying the
dropout technique to neural networks during training
and keeping the dropout active during evaluation,
thereby producing prediction results in the form of a
distribution for the same input data. The mean and
standard deviation values of the predicted distribution
are used to perform the prediction value and
uncertainty estimation, respectively. Applying MC
dropout to the neural networks enhances
NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications
594

generalization performance and allows for the
assessment of the reliability of the prediction results.
In this study, the dropout rate was set to 0.1 to
estimate uncertainty, and the results were derived 100
times for the same input data. The dropout rate was
experimentally applied to various values, with 0.1
identified as the optimal value, so this study presented
the RUL prediction results applying that value.
As a result, RUL prediction using LSTM with MC
dropout proceeds through the following steps. First,
the LSTM with MC dropout model is trained based
on the train data. Second, 100 prediction results are
generated for the same input data using the trained
model. At this time, dropout is also activated. Finally,
the mean and standard deviation of the prediction
results for the same input data are calculated. This
allows for the evaluation of the final predicted RUL
value and its uncertainty.
2.2 Optimization of the RUL
Prediction Model
Hyperparameter optimization was performed to
develop an optimal RUL prediction model using
LSTM with MC dropout. The hyperparameters of the
model are listed in Table 1, which indicates the
specific ranges for each hyperparameter. Network
training and comparative evaluation were performed
for all hyperparameter combinations. Here, RUL
prediction is a regression problem and generally uses
mean squared error (MSE) as the loss function. In
addition, based on a previous study (Lu et al., 2023)
where physics-informed regularization was applied to
improve RUL prediction performance, it was also
used in this study.
Table 1: Model hyperparameters and value ranges.
Hyperparameters
Value ranges
Number of units
[16, 32, 64, 128]
Number of layers
[2, 3]
Batch size
[8, 16, 32, 64]
In this study, model development was performed
individually using four different loss functions, and
performance was compared for each applied loss
function. Among these, two loss functions utilized
were MSE and a scoring function. When MSE and
scoring functions are used as loss functions, the
model is trained to ensure that these values converge
to lower values. The scoring function is an evaluation
metric related to RUL prediction proposed at the
International Conference on Prognostics and Health
Management (PHM08) Data Challenge (Saxena &
Goebel, 2008). In the case of the scoring function, a
larger penalty is imposed when the RUL prediction is
higher than the real value in terms of maintenance.
That is, if the predicted RUL is lower than the real
RUL, the failure can be prevented in advance through
preventive maintenance, but if not, the failure cannot
be prevented. The other two loss functions were based
on them and included physical rules. The four loss
functions are shown in Eqs. (1) to (4). In Eqs. (3) and
(4),
represents the monotonic decreasing
condition for the RUL prediction. Here, the rectified
linear unit (ReLU) is a function that outputs the input
value as is if it is greater than 0, and outputs 0 if it is
less than 0. Considering that the RUL value typically
decreases over time,
imposes a penalty when
the difference between the current predicted RUL (
)
and the previously predicted RUL (
) is positive.
This ensures that the RUL prediction adheres to the
natural characteristic of decreasing over time.
represents the boundary condition that the normalized
RUL cannot be less than 0 or greater than 1. Also,
and are constants that adjust the proportions of
each term. These values were the same as those used
in the previous study (Lu et al., 2023). By applying
various hyperparameters and loss functions, the RUL
prediction model for IGBT was developed, and the
performance of each was evaluated.
(1)
(2)
(3)
(4)
where
: Real RUL values
: Predicted RUL values
: Constants
AI-Based Preliminary Modeling for Failure Prediction of Reactor Protection System in Nuclear Power Plants
595

3 DATA PREPARATION
The IGBT accelerated aging data provided by the
NASA Ames Laboratory Prognostics Center of
Excellence were used (Celaya et al., 2009). The data
were obtained by performing accelerated aging under
thermal overstress conditions with a square signal
bias at the gate. That is, accelerated aging was
performed as temperature and voltage conditions
changed over time until failure occurred. The failure
criterion in IGBT accelerated aging data is defined by
the occurrence of the transistor latch-up phenomenon.
This phenomenon is confirmed based on the
characteristic that the collector-emitter voltage of the
provided data drops rapidly. In this study, IGBT
accelerated aging data for 4 devices with supply and
measurement information were used. It includes
supply temperature and voltage, collector-emitter
current and voltage, etc.
The failure time is determined based on the time
of latch-up occurrence, and the difference between
the current time and the failure time is calculated as
the RUL value. This is expressed in Eq. (5).
(5)
where
and
represent the failure time and current
time, respectively.
As input variables, environmental variables that
were considered to be obtainable were selected
because it is difficult to acquire information on
electronic components within the RPS in actual
NPPs. Environmental variables include operation
time, temperature, and voltage. Also, mean and
weighted average values were utilized as additional
input variables. The input variable groups are divided
into three groups as follows:
1. Operation time, Temperature, and Voltage
2. Operation time, Temperature, Voltage, and
Mean Temperature/Voltage
3. Operation time, Temperature, Voltage, Mean
Temperature/Voltage, Weighted Average
Temperature/Voltage
The data were divided into train, validation, and
test datasets. Three devices (Device 2, 3, and 4) were
used as train and validation datasets, and the
remaining device (Device 5) was used as test datasets.
The data for the selected input variables were
transformed into a normal distribution using a
standardization method. The data for the output
variable (i.e., RUL value) were normalized to a value
between 0 and 1 to apply physical rules.
4 RESULTS
Using the LSTM with MC dropout method, the RUL
prediction models for IGBT were developed
according to the input variable group and applied loss
function. A total of 12 prediction models were
developed, and for each model, the combination of
hyperparameters that exhibited the best performance
was selected as the final model for each model. Mean
absolute error (MAE) and R-square (R
2
) were used as
prediction performance evaluation metrics, which are
calculated as Eqs. (6) and (7). MAE indicates better
performance as its value decreases, while R
2
indicates
better performance as it approaches 1.
(6)
(7)
Table 2 shows the RUL prediction results of IGBT
according to all input variable groups and applied loss
functions. The performance was progressively
improved in the order of input variable groups 1, 2,
and 3. It indicates that utilizing mean and weighted
average values when predicting RUL is more
meaningful than using only temperature and voltage
values. Based on the applied loss functions, the
prediction performance on the train and validation
datasets was similar for the other three models, except
for the LSTM (MSE) model. However, the prediction
performance on the test datasets was relatively better
for the LSTM (MSE) model.
Figure 3 shows the RUL prediction results
according to the input variables. The prediction error
decreases as the input variable group number
increases from 1 to 3. Figure 4 shows the prediction
results with confidence intervals for input variable
group 3. This demonstrates that a model
incorporating physical rules exhibits lower
uncertainty in predictions than a model that does not
incorporate physical rules. This study reviewed the
input variables and AI methods to be applied as
preliminary modeling of the failure prediction model
for RPS in the future. So, we expect to utilize these
input variables and methods when developing failure
prediction models in practice.
NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications
596
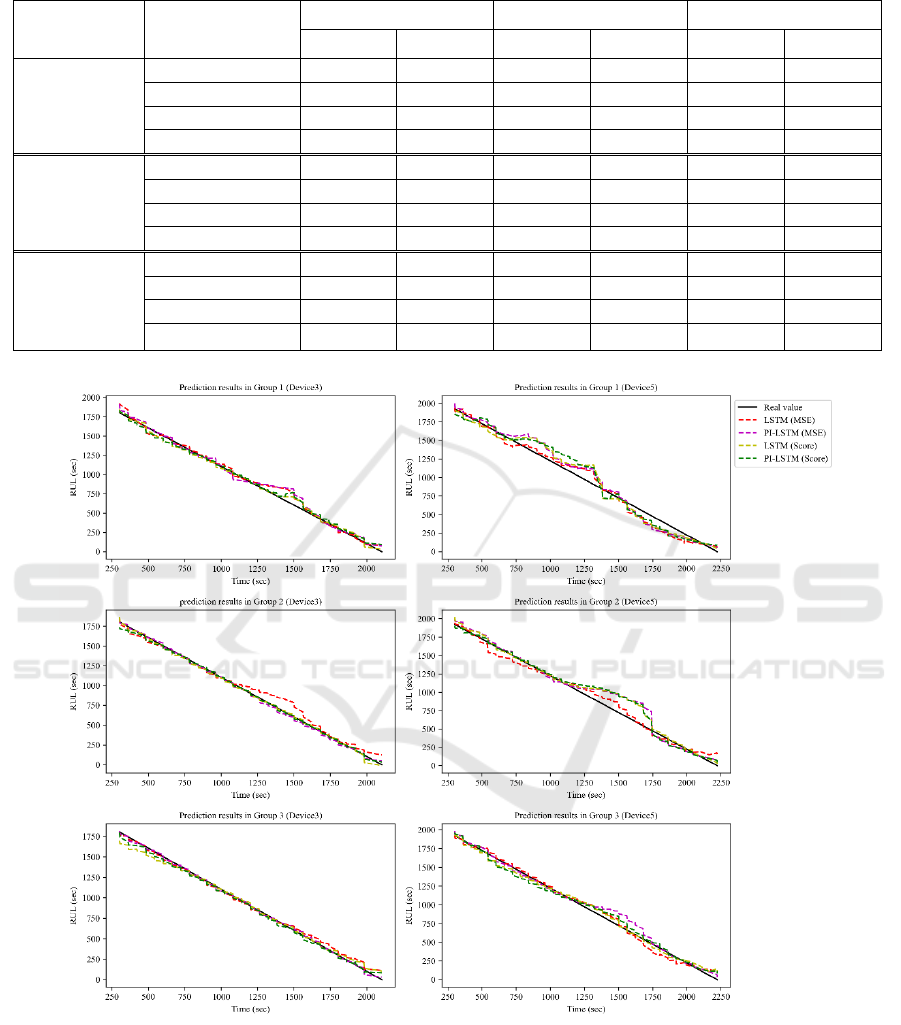
Table 2: Prediction results for all input variable groups.
Input variable
group
Model
Train datasets
Validation datasets
Test datasets
MAE
R
2
MAE
R
2
MAE
R
2
Group 1
LSTM (MSE)
50.73
0.9856
44.54
0.9888
65.04
0.9788
PI-LSTM (MSE)
40.36
0.9903
36.64
0.9920
80.14
0.9681
LSTM (Score)
31.88
0.9924
25.08
0.9962
85.64
0.9625
PI-LSTM (Score)
37.34
0.9919
35.81
0.9942
93.99
0.9587
Group 2
LSTM (MSE)
56.82
0.9835
54.27
0.9863
53.54
0.9854
PI-LSTM (MSE)
20.49
0.9981
23.49
0.9975
83.50
0.9523
LSTM (Score)
23.49
0.9973
19.50
0.9977
71.59
0.9606
PI-LSTM (Score)
24.57
0.9965
24.83
0.9967
78.15
0.9555
Group 3
LSTM (MSE)
33.24
0.9946
31.22
0.9952
43.58
0.9909
PI-LSTM (MSE)
21.51
0.9978
22.77
0.9978
47.99
0.9838
LSTM (Score)
35.56
0.9936
36.62
0.9933
54.58
0.9850
PI-LSTM (Score)
35.76
0.9939
37.31
0.9938
46.56
0.9893
Figure 3: IGBT RUL prediction results according to input variable groups.
AI-Based Preliminary Modeling for Failure Prediction of Reactor Protection System in Nuclear Power Plants
597
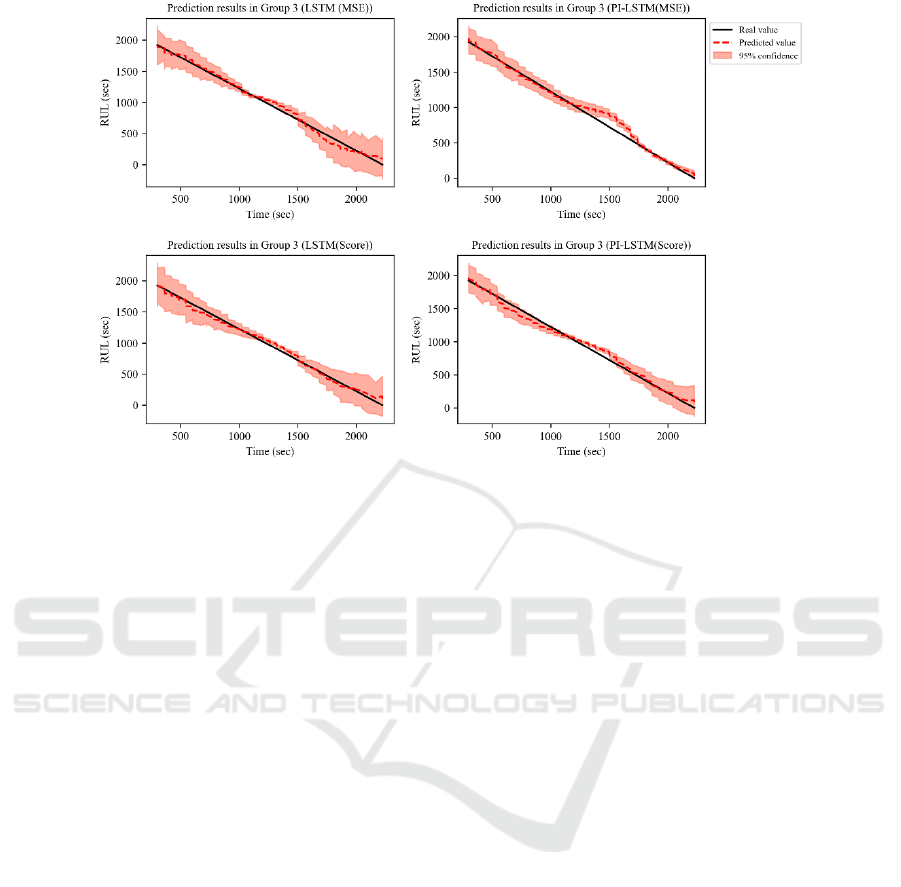
Figure 4: Prediction results for device 5 in input variable group 3.
5 CONCLUSIONS
In this study, prior to developing a failure prediction
model for RPS, a preliminary modeling was
performed using IGBT accelerated aging data to
develop a failure prediction model and evaluate its
performance. In the IGBT accelerated aging data, the
failure point is defined based on the occurrence of the
transistor latch-up phenomenon, and the RUL value
was calculated based on this. In addition, variables
that were judged to be obtainable in real NPPs, such
as operation time, temperature, and voltage, were
selected as input variables. Based on the selected
environmental variables, model development and
performance evaluation were conducted by dividing
into three input variable groups. RUL prediction was
performed through a combination of LSTM and MC
dropout technology. Additionally, to enhance
prediction performance, the model development
incorporated physical rule constraints into the loss
function for RUL prediction. As a result, using mean
and weighted average values, rather than just
temperature and voltage values, led to better RUL
prediction performance. Among these, the
performance of the model developed using a loss
function including physical rules was slightly better.
The results of preliminary modeling are expected to
be useful when developing fault prediction models
based on accelerated aging data for major electronic
components within the RPS in the future.
ACKNOWLEDGEMENTS
This work was supported by the Korea Institute of
Energy Technology Evaluation and Planning
(KETEP) grant funded by the Korea government
(MOTIE) (20224B10100120, Development of
commercialization technology for failure diagnosis of
reactor control and digital I&C systems) and the
National Research Council of Science & Technology
(NST) grant by the Korea government (MSIT) (No.
GTL24031-000).
REFERENCES
Celaya, J. R., Wysocki, P., & Goebel, K. (2009). IGBT
Accelerated Aging Data Set, NASA Prognostics Data
Repository, NASA Ames Research Center, Moffett
Field, CA.
Chen, Z., Dai, M., Liu, J., Jiang, W., & Min, Y. (2024). Life
prediction of IGBT module for nuclear power plant rod
position indicating and rod control system based on
SDAE-LSTM. Nuclear Engineering and Technology.
Coursey, A., Nath, G., Prabhu, S., & Sengupta, S. (2021,
December). Remaining useful life estimation of hard
disk drives using bidirectional lstm networks. In 2021
IEEE International Conference on Big Data (Big Data)
(pp. 4832-4841). IEEE.
Gal, Y., & Ghahramani, Z. (2016, June). Dropout as a
bayesian approximation: Representing model
uncertainty in deep learning. In international
NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications
598

conference on machine learning (pp. 1050-1059).
PMLR.
He, C., Yu, W., Zheng, Y., & Gong, W. (2021, October).
Machine learning based prognostics for predicting
remaining useful life of IGBT–NASA IGBT
accelerated ageing case study. In 2021 IEEE 5th
Information Technology, Networking, Electronic and
Automation Control Conference (ITNEC) (Vol. 5, pp.
1357-1361). IEEE.
Hochreiter, S., & Schmidhuber, J. (1997). Long short-term
memory. Neural computation, 9(8), 1735-1780.
Ismail, A., Saidi, L., Sayadi, M., & Benbouzid, M. (2020).
A new data-driven approach for power IGBT remaining
useful life estimation based on feature reduction
technique and neural network. Electronics, 9(10), 1571.
Lu, Z., Guo, C., Liu, M., & Shi, R. (2023). Remaining
useful lifetime estimation for discrete power electronic
devices using physics-informed neural network.
Scientific Reports, 13(1), 10167.
Rouhi Ardeshiri, R., & Ma, C. (2021). Multivariate gated
recurrent unit for battery remaining useful life
prediction: A deep learning approach. International
Journal of Energy Research, 45(11), 16633-16648.
Saxena, A., & Goebel, K. (2008). PHM08 Challenge Data
Set. NASA Ames Prognostics Data Repository, NASA
Ames Research Center, Moffett Field, CA.
AI-Based Preliminary Modeling for Failure Prediction of Reactor Protection System in Nuclear Power Plants
599
