Temporal Complexity of a Hopﬁeld-Type Neural Model in Random and

Scale-Free Graphs

Marco Caﬁso

1,2 a

and Paolo Paradisi

2,3 b

Department of Physics ’E. Fermi’, University of Pisa, Largo Bruno Pontecorvo 3, I-56127, Pisa, Italy

Institute of Information Science and Technologies ‘A. Faedo’, ISTI-CNR, Via G. Moruzzi 1, I-56124, Pisa, Italy

BCAM-Basque Center for Applied Mathematics, Alameda de Mazarredo 14, E-48009, Bilbao, Basque Country, Spain

ﬁ

Keywords:

Bio-Inspired Neural Networks, Temporal Dynamics, Self-Organization, Connectivity, Intermittency,

Complexity.

Abstract:

The Hopﬁeld network model and its generalizations were introduced as a model of associative, or content-

addressable, memory. They were widely investigated both as an unsupervised learning method in artiﬁcial

intelligence and as a model of biological neural dynamics in computational neuroscience. The complex-

ity features of biological neural networks have attracted the scientiﬁc community’s interest for the last two

decades. More recently, concepts and tools borrowed from complex network theory were applied to artiﬁcial

neural networks and learning, thus focusing on the topological aspects. However, the temporal structure is

also a crucial property displayed by biological neural networks and investigated in the framework of systems

displaying complex intermittency. The Intermittency-Driven Complexity (IDC) approach indeed focuses on

the metastability of self-organized states, whose signature is a power-decay in the inter-event time distribu-

tion or a scaling behaviour in the related event-driven diffusion processes. The investigation of IDC in neural

dynamics and its relationship with network topology is still in its early stages. In this work, we present the

preliminary results of an IDC analysis carried out on a bio-inspired Hopﬁeld-type neural network comparing

two different connectivities, i.e., scale-free vs. random network topology. We found that random networks

can trigger complexity features similar to that of scale-free networks, even if with some differences and for

different parameter values, in particular for different noise levels.

1 INTRODUCTION

The Hopﬁeld model is the ﬁrst example of a recur-

rent neural network deﬁned by a set of linked two-

state McCulloch-Pitts neurons evolving in discrete

time. The Hopﬁeld model is similar to the Ising model

(Ernst, 1925) describing the dynamics of a spin sys-

tem in a magnetic ﬁeld, but with all-to-all connec-

tivity among neurons instead of local spin-spin in-

teractions. More importantly, in his milestone pa-

per (Hopﬁeld, 1982), Hopﬁeld ﬁrst introduced a rule

for changing the topology of network connections

based on external stimuli. Hopﬁeld ﬁrst proposed

and investigated the properties of this network model

in (Hopﬁeld, 1982) and in successive works (Hop-

ﬁeld, 1984; Hopﬁeld, 1995). In particular, he also

proposed an extension of the original 1982 model

https://orcid.org/0009-0004-9519-1221

https://orcid.org/0000-0002-1036-4583

to a continuous-time leaky-integrate-and-ﬁre neuron

model (Hopﬁeld, 1984), also considering the case of

neurons with graded response, i.e., with a sigmoid

function mediating the voltage inputs from upstream

neurons. The main property of the Hopﬁeld model

is that the connectivity matrix is allowed to change

according to a Hebbian rule (Hebb, 1949), which is

often summarised in the statement: “(neuron) cells

that ﬁre together wire together” (L

owel and Singer,

1992). To our knowledge, with this rule, the Hopﬁeld

neural network model results in being the ﬁrst model

used for the investigation of associative, or content-

addressable, memory. In the Artiﬁcial Intelligence

(AI) jargon, external stimuli correspond to the cases

of a training dataset that trigger the changes in the

connectivity matrix. This process involves decoding

the input data into a map of neural states (see, e.g.,

(Hopﬁeld, 1995)).

The Hopﬁeld neural model, as such and its varia-

tions, belong to the class of Spiking Neural Networks

438

Caﬁso, M. and Paradisi, P.

Temporal Complexity of a Hopﬁeld-Type Neural Model in Random and Scale-Free Graphs.

DOI: 10.5220/0013007600003837

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 438-448

ISBN: 978-989-758-721-4; ISSN: 2184-3236

(SNNs). SSNs are still attracting considerable atten-

tion due to energy efﬁciency and high sensitivity to

temporal features of data and, even if they are nowa-

days less efﬁcient concerning the classical deep neu-

ral networks, are thought to have great potential in

the context of neuromorphic computing (Davies et al.,

2018).

An interesting aspect studied by Hopﬁeld is the

emergence of collective, i.e., self-organizing be-

haviour in relation to the stability of memories in the

network model. In this framework, Grinstein et al.

(Grinstein and Linsker, 2005) investigated the role

of topology in a neural network model extending the

Hopﬁeld model to a more biologically plausible one,

but partially maintaining the computational advantage

of two-state McCulloch-Pitts neurons with respect to

continuous-time extension of the model. This was

achieved by introducing a maximum ﬁring time and

a refractory time in the single neuron dynamics.

Since the last two decades, the interest towards the

complex topological features of neural networks has

gained momentum in many scientiﬁc ﬁelds involv-

ing concepts and tools of computational neuroscience

and/or AI (see, e.g., (Kaviani and Sohn, 2021) for a

survey). In particular, neural networks with complex

topologies, such as random (Erd ¨os-R

enyi) (Erd ¨os and

enyi, 1959), (Gros, 2013), small-world or scale-

free networks (Boccaletti et al., 2006), were shown

to outperform artiﬁcial neural networks with all-to-all

connectivity (McGraw and Menzinger, 2003; Torres

et al., 2004; Lu et al., 2006; Shaﬁee et al., 2016; Ka-

viani and Sohn, 2020; Adjodah et al., 2020; Kaviani

and Sohn, 2021).

Complexity is a general concept related to the

ability of a multi-component system to trigger self-

organizing behaviour, a property that is manifested

in the generation of spatio-temporal coherent states

(Paradisi et al., 2015; Grigolini, 2015; Paradisi and

Allegrini, 2017). Interestingly, in many research

ﬁelds, many authors consider the complexity of a sys-

tem as a concept essentially referring to its topolog-

ical structure, which is an approach borrowed from

graph theory and complex networks (Watts and Stro-

gatz, 1998; Barab

asi and Albert, 1999; Albert and

Barab

asi, 2002; Barab

asi and Oltvai, 2004). How-

ever, another aspect, which is often overlooked and

instead is typically a crucial feature of complex self-

organizing behaviour, is the temporal structure of the

system. This is intimately related not only to the

topological/geometrical structure of the network but

also to its dynamical properties, both at the level of

single nodes, of clusters of nodes, and as a whole.

Hereafter we refer to Temporal Complexity (TC),

or Intermittency-Driven Complexity (IDC), as the

property of the system to generate metastable self-

organized states, the duration of which is marked by

rapid transition events between two states (Grigolini,

2015). The underlying theories of TC/IDC refer

to Cox’s renewal theory (Cox, 1970), Cox’s failure

events are reinterpreted in a temporal sense, that is,

precisely as rapid transitions or jumps in the sys-

tem’s observed variables. The rapid transitions can

occur between two self-organized states or between a

self-organized state and a disordered or non-coherent

state. The sequence of transition events is then de-

scribed as a point process and the ideal condition for

TC/IDC is the renewal one (Cox, 1970; Bianco et al.,

2007; Paradisi et al., 2009), which is not easily de-

termined being mixed to spurious effects such as sec-

ondary events and noise (Paradisi and Allegrini, 2017;

Paradisi and Allegrini, 2015). The self-organizing be-

haviour can be detected by the recognition of given

patterns in the system’s variables, e.g., eddies in a tur-

bulent ﬂow or synchronization epochs in neural dy-

namics, and the identiﬁcation of events is achieved

by means of proper event detection algorithm in sig-

nal processing (Paradisi and Allegrini, 2017; Paradisi

and Cesari, 2023).

A general concept commonly accepted in the

complex system research ﬁeld is that complexity fea-

tures are related to the power-law behaviour of some

observed features, e.g.: space and/or time correlation

functions, the distribution of some variables such as

the sequence of inter-event times and the size of neu-

ral avalanches (Beggs and Plenz, 2003). In TC/IDC a

crucial feature to be evaluated is the probability den-

sity function (PDF) of inter-event times, or Waiting

Times (WT). However, the WT-PDF is often blurred

by secondary events related to noise or other side ef-

fects (Allegrini et al., 2010; Paradisi and Allegrini,

2015). A more reliable analysis relies on diffusion

processes derived by the sequence of events and on

their scaling analysis (Akin et al., 2009).

This approach involves several scaling analyses

widely investigated in the literature that were inte-

grated in the Event-Driven Diffusion Scaling (ED-

DiS) algorithm (Paradisi and Allegrini, 2017; Paradisi

and Allegrini, 2015). This approach was also success-

fully applied in the context of brain data, being able to

characterize different brain states from wake, relaxed

condition to the different sleep stages (Paradisi et al.,

2013; Allegrini et al., 2013; Allegrini et al., 2015).

At present, the relationships between network

connectivity and temporal complexity by one hand

and the complexity of connectivity matrix and learn-

ing efﬁciency are still not clear. In this work, we

present some preliminary results regarding the ﬁrst

aspect, having in mind the potential applications

Temporal Complexity of a Hopﬁeld-Type Neural Model in Random and Scale-Free Graphs

439

regarding the second aspect, i.e., connectivity vs.

learning efﬁciency. Along this line, an IDC anal-

ysis is carried out on a bio-inspired Hopﬁeld-type

neural network comparing two different connectivi-

ties, i.e., scale-free vs. random network topology.

In Section 2 we introduce the methods to generate

the network topologies and the details of the bio-

inspired Hopﬁeld-type neural network model. Sec-

tion 3 brieﬂy describes the event-based scaling anal-

yses. In Section 4 we describe the results of numeri-

cal simulations and of their IDC analyses that are dis-

cussed in Section 5. Finally, we sketch some conclu-

sions in Section 6.

2 MODEL DESCRIPTION

2.1 Network Topology: Scale-Free vs.

Erd ¨os-R

enyi

We here consider two types of networks, both with

N number of nodes

. Our networks are constrained

to have the same minimum number k

of links for

each neuron and the same average number of links

⟨k⟩. In both cases, self-loops and multiple directed

edges from one node to another are excluded, fol-

lowing the methodology outlined in (Grinstein and

Linsker, 2005). The ﬁrst class of networks is that

of Scale-Free (SF) graphs, characterized by a power-

law node out-degree distribution. The probability of a

node i to have k

outgoing links is given by:

∀i = 1, ...,N : P

) =

(1)

m =

α − 1

(1−α)

− (N − 1)

(1−α)

(2)

For the construction of SF networks, we used a

power-law exponent α = 2.5.

The second class of networks is that of Erd ¨os-

enyi (ER) graphs, which are random graphs where

each pair of distinct nodes is connected with a prob-

ability p. In an ER network with N nodes and with-

out self-loops, the average degree is simply given by:

⟨k⟩

= p

(N − 1). Then, from the equality of de-

gree averages: ⟨k⟩

= ⟨k⟩

we simply derive:

⟨k⟩

N − 1

(3)

Let us recall that the degree of a node in the network is

the number of links of the node itself. In a directed network,

each node has an out-degree, given by the number of outgo-

ing links, and an in-degree, given by the number of ingoing

links.

The theoretical mean out-degree of the SF network is

approximated by the following formula:

⟨k⟩ ≃ m

2−α

− (N − 1)

2−α

α − 2

α − 1

α − 2

2−α

− (N − 1)

2−α

1−α

− (N − 1)

1−α

that is obtained by considering k as a continuous ran-

dom variable. However, due to the large variability

of SF degree distribution, different statistical samples

drawn from P

can have very different mean outde-

grees. Thus, we have chosen to numerically evalu-

ate the mean out-degree associated with the sample

drawn from P

and to use this value instead of the

theoretical one to deﬁne P

The algorithm used to generate the two network

topologies is as follows:

(SF)(a) For each node i, choose the out-degree k

the nearest integer of the real number deﬁned

by:

= (((N − 1)

(1−α)

− k

(1−α)

)ξ

+ k

(1−α)

)

1−α

(4)

being ξ a random number uniformly dis-

tributed in [0,1]. This formula is obtained by

the cumulative function method. The drawn

are within the range [k

,N − 1].

(b) Given k

for each node i, the target nodes

are selected by drawing k

integer numbers

{ j

,..., j

} uniformly distributed in the set

{1,..., i − 1,i + 1,..., N}.

is deﬁned as:

i j



1 if j ∈ T

= { j

,..., j

}

0 otherwise

(5)

With this choice, the in-degree distribution

results in a mono-modal distribution similar

to a Gaussian distribution.

(ER)(a) From the adjacency matrix A

i j

the actual

mean out-degree ⟨k⟩

is computed.

(b) For each couple of nodes (i, j) with j ̸= i a

random number ξ

i, j

is drawn from a uniform

distribution in [0,1].

i j



1 if ξ

i, j

< p

0 otherwise

(6)

where p

is given by Eq. (3).

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

440

2.2 The Grinstein Hopﬁeld-Type

Network Model

Grinstein et al. (Grinstein and Linsker, 2005) mod-

ify the Hopﬁeld network by adding three elements:

(i) a random endogenous probability of ﬁring p

endo

for each node; (ii) a maximum ﬁring duration, thanks

to which the activity of a node shuts down after t

max

time steps; (iii) a refractory period such that a node,

once activated and subsequently deactivated, must re-

main inactive for at least t

re f

consecutive time-steps.

Each neuron i has two states: S

= 0 (”not ﬁring”)

and S

= 1 (”ﬁring at maximum rate”). The weight of

link from j to i is given by J

i j

(Nonconnected neurons

have J

i j

= 0). The network is initialized at time t = 0

by randomly setting each neuron state S

(0) equal to

1 with a probability p

init

that we chose equal to the

endogenous ﬁring probability. At each time step the

weighted input to node i is deﬁned:

(t) =

∑

i j

(t) (7)

as in the Hopﬁeld network dynamics. The state of

the node i evolves with t according to the following

algorithm:

1. If S

(τ) for all τ = t,t − 1,· · · ,t − t

max

+ 1, then

(t + 1) = 0 (maximum ﬁring duration rule).

2. If S

(t) = 1 and S

(t + 1) = 0 then S(τ) = 0 for

(t + 1) < τ ≤ (t +t

re f

) (refractory period rule).

3. If neither rule 1 nor rule 2 applies, then

(a) If I

(t) ≥ b

then S

(t + 1) = 1;

(b) If I

(t) < b

then S

(t + 1) = 1 with a probability

equal to p

endo

otherwise S

(t + 1) = 0.

where b

is the ﬁring threshold of neuron i.

In our study, unlike Grinstein and colleagues, the

link’s weights and the ﬁring thresholds are taken uni-

formly throughout the network: J

i j

= J and b

= b.

3 EVENT-DRIVEN DIFFUSION

SCALING ANALYSIS

The diffusion scaling analysis is a powerful method

for scaling detection and, when applied to a se-

quence of transition events, can give useful informa-

tion on the underlying dynamics that indeed gener-

ate the events. The complete IDC analysis involves

the Event-Driven Diffusion Scaling (EDDiS) algo-

rithm (Paradisi and Allegrini, 2015; Paradisi and Al-

legrini, 2017) with the computation of three different

random walks generated by applying three walking

rules to the sequence of observed transition events

and the computation of the second moment scaling

and the similarity of the diffusion PDF. The gen-

eral idea is based on the Continuous Time Random

Walk (CTRW) model (Montroll, 1964; Weiss and Ru-

bin, 1983), where a particle moves move only at the

event occurrence times. Here we limit to the so-called

Asymmetric Jump (AJ) walking rule (Grigolini et al.,

2001), which simply consists of making a unitary

jump ahead when an event occurs and, thus, corre-

sponds to the counting process generated by the event

sequence:

X(t) = #{n : t

< t}. (8)

The method used to extract events from the sim-

ulated data and the scaling analyses are described in

the following.

3.1 Neural Coincidence Events

The IDC features here investigated are applied to

coincidence events that are deﬁned as the events at

which a minimum number N

of neuron ﬁres at the

same time. Then, given the global set of single neu-

ron ﬁring times, the coincidence event time is deﬁned

as the occurrence time of more than N

nodes ﬁr-

ing simultaneously, i.e., in a tolerance time interval

of duration ∆t

. Hereafter we always set ∆t

equal

to a sampling time, i.e., ∆t

= 1, which is equiva-

lent to look for simultaneous events. The total ac-

tivity distribution of the network corresponds to the

size distribution of coincidences with minimum num-

ber N

= 1: P(n

= 1). The actual threshold N

here applied is deﬁned by computing the 35th per-

centile of P(n

= 1). Then, each n-th coincidence

event is described by its occurrence time t

(n) and its

size S

(n).

3.2 Detrended Fluctuation Analysis

(DFA)

DFA is a well-known algorithm (see, e.g., (Peng et al.,

1994)) that is widely used in the literature for the eval-

uation of the second-moment scaling H deﬁned by:

(∆t) = ⟨(∆X(∆t) − ∆X

trend

(∆t))

⟩ ∼ t

(9)

F(∆t) = a · ∆t

⇒

⇒ log(F(∆t)) = log(a) + H · log(∆t) (10)

being ∆X(t,∆t) = X(t + ∆t) − X (t). We use the no-

tation H as this scaling exponent is essentially the

same as the classical Hurst similarity exponent (Hurst,

1951). X

trend

(∆t) is a proper local trend of the time

series. The DFA is computed over different values of

the time lag ∆t and the statistical average is carried

Temporal Complexity of a Hopﬁeld-Type Neural Model in Random and Scale-Free Graphs

441

out over a set of time windows of duration ∆t into

which the time series is divided. In the EDDiS ap-

proach, DFA is applied to different event-driven dif-

fusion processes (see, e.g., (Paradisi et al., 2012; Par-

adisi and Allegrini, 2017)). To check the validity of

Eq. (10) on the data and evaluate the exponent H is

it sufﬁcient to carry out a linear best ﬁt in the loga-

rithmic scale. To perform the DFA we employed the

function MFDFA of package MFDFA of Python (Ry-

din Gorj

ao et al., 2022).

3.3 Diffusion Entropy

The Diffusion Entropy (DE) is deﬁned as the Shannon

entropy of the diffusion process X(t) and was exten-

sively used in the scaling detection of complex time

series (Grigolini et al., 2001; Akin et al., 2009). The

DE algorithm is the following:

1. Given a time lag ∆t, split the time series X(t)

into overlapping time windows of duration ∆t and

compute: ∆X(t,∆t) = X (t + ∆t) − X (t), ∀ t ∈

[0,t − ∆t].

2. For each time lag ∆t, evaluate the distribution

p(∆x,∆t).

3. Compute the Shannon entropy:

S(∆t) = −

+∞

−∞

p(∆x,∆t)log p(∆x,∆t)dx (11)

If the probability density function (PDF) is self-

similar, i.e., p(∆x,∆t) = f (∆x/∆t

)/∆t

, it re-

sults:

S(∆t) = A + δlog(∆t + T ) (12)

To check the validity of Eq. (12) on the data and

evaluate the exponent δ is it sufﬁcient to carry out

a linear best ﬁt with a logarithmic scale on the

time axis.

4 NUMERICAL SIMULATIONS

AND RESULTS

We performed a comprehensive parametric analysis

with a ﬁxed t

max

value of 3, while systematically vary-

ing the other parameters. These include J which was

constrained to integer values ranging from 1 to 4,

endo

set to 0.001, 0.01 and 0.1, k

limited to integers

spanning from 1 to 5, b with two options of either 2

or 3, and t

re f

set at 0, 4, 6, 8 and 10. For dimen-

sional reasons, the model’s dynamics depend only on

the adimensional parameter π =

, which is conve-

niently used in the plots summarising the parametric

analysis, i.e. Figs. 1 and 2. The simulations were car-

ried out for 20000 time steps within networks com-

prising N = 1000 neurons. We analyzed the network

behaviours by examining two key metrics: the total

activity distribution P(n

= 1) and the average ac-

tivity over time. The parametric analysis results are

reported in Fig. 1 and Fig. 2. For the ER networks

we have identiﬁed the following qualitative behaviors

in the total activity distributions:

1. Asymmetric Bell Curve distribution

2. Symmetric Bell Curve distribution

3. Bell curve and transition to multi-modal distribu-

tion

4. Cycle distribution

5. Mono-modal at zero distribution

6. Multi-modal distribution

7. Peak with Power-Law distribution

8. Peak with Power-Law and transition to multi-

modal distribution

9. Power-Law distribution

10. Power-Law with Multiple Peaks distribution

For the SF networks we have identiﬁed the follow-

ing qualitative behaviors in the total activity distribu-

tions:

1. Asymmetric Bell Curve distribution

2. Symmetric Bell Curve distribution

3. Cycle distribution

4. Mono-modal at zero distribution

5. Multi-modal distribution

6. Peak with Power-Law distribution

7. Peak with Power-Law and transition to multi-

modal distribution

8. Power-Law distribution

9. Power-Law and transition to cycle distribution

Figures 4 and 5 report the results for ER and SF

networks, respectively.

We selected speciﬁc cases for further investigation us-

ing TC/IDC analysis. Speciﬁcally, we analyzed the

WTs between successive coincidence events by ap-

plying the DFA and DE analyses. We report some

of the results in Fig. 3, where a few relevant cases

involving power-law behaviour were selected. The

best-ﬁt values of the scaling exponents H and δ are

reported in Table 1.

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

442

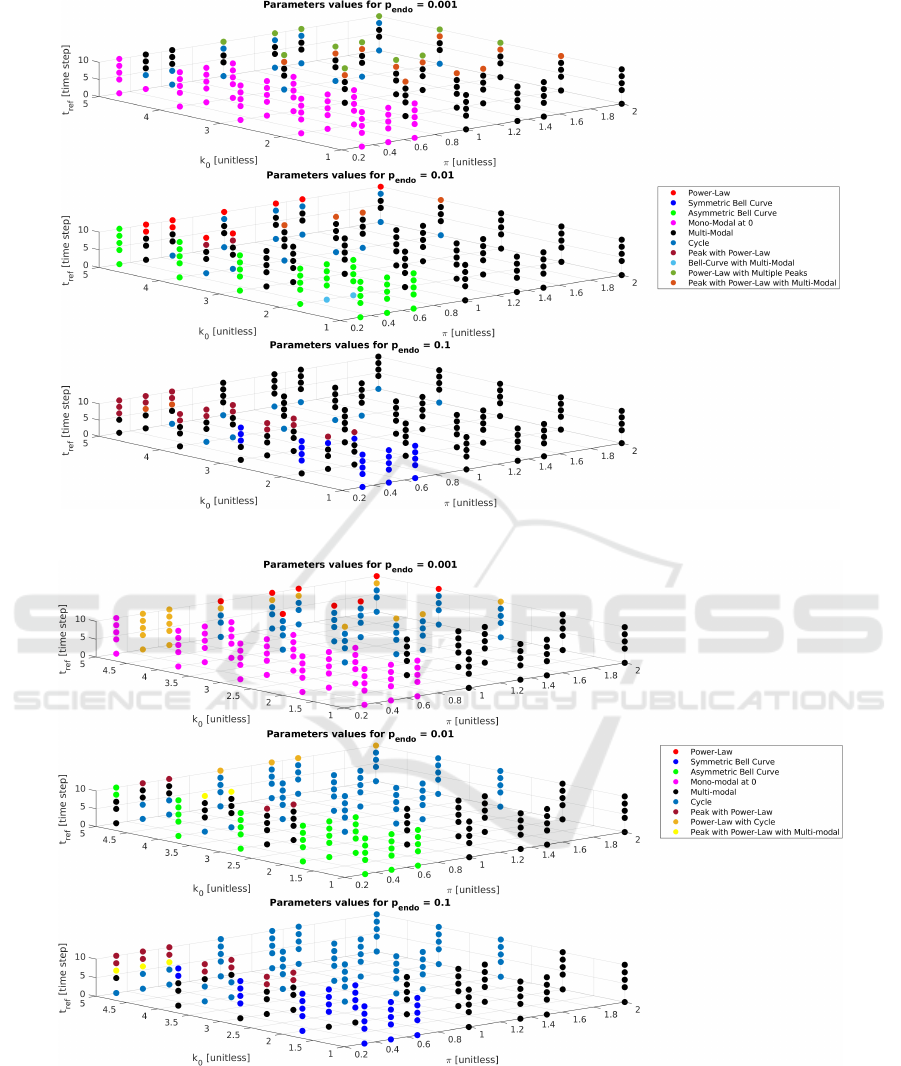
Figure 1: Results of parameter analysis derived from the behaviour of the total activity distribution in ER networks.

Figure 2: Results of parameter analysis derived from the behaviour of the total activity distribution in SF network.

5 DISCUSSION

Our numerical simulations showed a large variety of

behaviours in the Hopﬁeld-type network in both net-

work topologies, i.e., random (ER) and scale-free

(SF). As can be seen from Figs. 4 and 5, most quali-

tative behaviors can be found in both network topolo-

gies, but with different sets of parameters. However,

some differences can be seen: (i) “bell curve with

multimodal” and “power-law with multiple peaks”

Temporal Complexity of a Hopﬁeld-Type Neural Model in Random and Scale-Free Graphs

443

Table 1: Result of ﬁts for DFA and DE. For the “Power-Law with Cycle (SF)” row: Power-Law part is indicated with (PL), and

Cycle part is indicated with (C). In the “Power-Law (SF)” case, the ﬁt δ = 0.184 for DE in the time range ∆t ∼ 10

− 3 · 10

was not reported.

DFA (H) DE (δ)

Short-Time Long-Time Short-Time Long-Time

Power-Law (ER) 0.061 1.164 / 0.352

Power-Law (SF) 0.070 1.061 / 0.382

Power-Law with Multiple Peaks (ER) 0.084 1.075 / 0.407

Power-Law with Cycle (SF) 0.105 (PL) 1.138 (PL) / /

0.078 (C) 1.327 (C) / /

(a) DFA (b) DE

Figure 3: DFA and DE analyses. Panels (1) and (2) same parameter set k

= 5, t

re f

= 10, b = 2, J = 3 and p

endo

= 0.01 (same

as panels (9) of Fig. 4 and (9) of Fig. 5). Panels (3) and (4) same as before but with different noise level p

endo

= 0.001 (same

as panels (10) of Fig. 4 and (8) of Fig. 5).

behaviours appear only in the ER network topology

(panels (3) and (10) in Fig. 4), while (ii) “power-

law with cycle” behaviour is exclusive of the SF net-

work topology (panels (9) of Fig. 5). Interestingly, all

other behaviours are seen in both topologies, even if

with slight differences. In particular, the emergence

of power-law behaviour in the total activity distribu-

tion (compare, e.g., panel (9) of Fig. 4 with panel

(8) of Fig. 5). It is worth noting that different kinds

of power-law behaviours are seen in both topologies

(panels (7-10) of Fig. 4 and panels (6-9) of Fig. 5).

As can be seen also from Figs. 1 and 2, for the pure

power-law behaviour (red dots) the main difference

seems to lie in the different noise levels: p

endo

= 0.01

for ER and p

endo

= 0.001 for SF.

Another remarkable observation regards the abrupt

transition among different behaviours seen in some

speciﬁc cases. In particular, some cases display a ini-

tial power-law behaviour that can persist for a very

long time, but then it is followed by an unexpected

transition to multimodal or cycle behaviour (panels

(8) in Fig. 4 and panels (7) and (9) in Fig. 5). Only

in ER networks, it is also seen a transition between

a mono-modal to a multi-modal distribution where

maxima are shifted towards higher values of total ac-

tivity (panels (3) of Fig. 4 ).

Fig. 3 shows some relevant behaviours in both DE

and DFA functions. In particular, we chose to an-

alyze: (i) pure power-law behavior in both topolo-

gies (panels (1) and (4)), which surprisingly arises

for similar parameter sets apart from the noise level;

(ii) power-law with multiple peaks in ER (panel (3))

and (iii) power-law with a transition to a cycle for SF

(panel (2)). Regarding “power-law with cycle” (panel

(2)), due to the rapid transition from the power-law

to the cycle behaviour, DFA and DE were applied

separately to the two regimes. Surprisingly, the cy-

cle regimes gives a pattern of DFA and DE similar to

that of the power-law regime, even if with different

slopes. Reliable ﬁt values for H and δ are reported

in Table 1. It can be seen that the qualitative be-

haviour of DFA are essentially the same in the differ-

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

444

(a)

(b)

Figure 4: (a) Average Activity plots over time and (b) Histograms of Total Activity for all the qualitative behaviours found in

ER networks. Parameters for each panel: (1) k

= 1, t

re f

= 4, b = 2, p

endo

= 0.01, and J = 1; (2) k

= 1, t

re f

= 4, b = 2, p

endo

0.1, and J = 1; (3) k

= 2, t

re f

= 0, b = 2, p

endo

= 0.01, and J = 1; (4) k

= 4, t

re f

= 0, b = 2, p

endo

= 0.01, and J = 1; (5) k

1, t

re f

= 4, b = 2, p

endo

= 0.001, and J = 1; (6) k

= 3, t

re f

= 6, b = 3, p

endo

= 0.1, and J = 2; (7) k

= 5, t

re f

= 6, b = 3, p

endo

0.1, and J = 1; (8) k

= 5, t

re f

= 6, b = 3, p

endo

= 0.1, and J = 2; (9) k

= 5, t

re f

= 10, b = 2, p

endo

= 0.01, and J = 3; (10) k

5, t

re f

= 10, b = 2, p

endo

= 0.001, and J = 3.

ent cases. All the investigated cases have the same pa-

rameters, except for the noise level, which is given by

endo

= 0.01 for the top panels and 0.001 for the bot-

tom panels. In summary, we have: (i) short-time with

very low H, associated with highly anti-persistent cor-

relations; (ii) long-time with very high H ∼ 1, except

in panel (3) where H > 1, associated with highly per-

sistent correlations and superdiffusion. Interestingly,

Temporal Complexity of a Hopﬁeld-Type Neural Model in Random and Scale-Free Graphs

445

(a)

(b)

Figure 5: (a) Average Activity plots over time and (b) Histograms of Total Activity for all the qualitative behaviours found in

SF networks. Parameters for each panel: (1) k

= 1, t

re f

= 0, b = 2, p

endo

= 0.01, and J = 1; (2) k

= 1, t

re f

= 0, b = 2, p

endo

0.1, and J = 1; (3) k

= 5, t

re f

= 0, b = 3, p

endo

= 0.01, and J = 2; (4) k

= 1, t

re f

= 0, b = 2, p

endo

= 0.001, and J = 1; (5) k

3, t

re f

= 0, b = 3, p

endo

= 0.1, and J = 1; (6) k

= 3, t

re f

= 10, b = 3, p

endo

= 0.1, and J = 2; (7) k

= 5, t

re f

= 10, b = 3, p

endo

0.1, and J = 2; (8) k

= 5, t

re f

= 10, b = 2, p

endo

= 0.001, and J = 3; (9) k

= 5, t

re f

= 10, b = 2, p

endo

= 0.01, and J = 3.

we get H ≃ 1 for p

endo

= 0.001 in both topologies,

while the pure power-law, which occurs for different

noise levels in the two topologies gives a larger value

of H for the ER network (H ≃ 1.16). The DE dis-

plays a power-law only in the long-time regime that

is, at variance with the DFA, in agreement with a sub-

diffusive behaviour. This is not directly related to the

persistence of correlations, but directly to the shape

of the diffusion PDF. In summary, in the long-time

regime of time lags, the diffusion generated by the

coincidence events, which are a manifestation of self-

organizing behaviour, shows highly persistent corre-

lations, as revealed by DFA, associated with a subd-

iffusive behaviour in the DE analysis. This could be

compatible with a very slow power-law decay in the

WT-PDF, i.e., ψ(τ) ∼ τ

with µ < 2.

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

446

6 CONCLUDING REMARKS

Here we have investigated a Hopﬁeld-type model

and, in particular, the model proposed in (Grinstein

and Linsker, 2005), being a simple prototype of bio-

inspired neural model. This includes bio-inspired

features, such as the refractory time and the maxi-

mum ﬁring time that can be tuned and interpreted,

in the context of AI, as hyper-parameters. A partic-

ularly interesting bio-inspired feature is also encoded

in the learning mechanism of Hopﬁeld-type networks,

which is exactly the Hebbian bio-inspired, unsuper-

vised, learning. The network topology is recognized

to also play a central role in both global network dy-

namics and learning efﬁciency. This last feature is of

particular interest in the AI ﬁeld.

In particular, some authors focused on the effect

of topological structure on learning features (Kaviani

and Sohn, 2021), in some cases ﬁnding a better learn-

ing performance associated with speciﬁc topologies,

e.g., scale-free and/or small-world (Lu et al., 2023).

The present work represents a preliminary investiga-

tion of the relationships among connectivity features

and temporal complexity of a simple spiking neural

network without learning algorithms. Interestingly,

different topological structures can give similar dy-

namical behaviours and complexity features (see, e.g,

Fig. 4b, panel (9), with Fig. 5b, panel (8), and Fig.

3a, panels (1) and (4)).

Regarding the relationship between connectivity

and temporal complexity, further investigations are

needed to better understand the reason why very dif-

ferent topologies can give similar complexity. We ex-

pect these further investigations to deepen the under-

standing of the relationship between dynamical fea-

tures of the network, e.g., temporal complexity, con-

nectivity structure and learning features, such as stor-

age capacity.

We also plan future investigations regarding the re-

lationship between connectivity structure and learn-

ing algorithms, to study how the performance mea-

sures, jointly with the evaluation of complexity in-

dices, change with the number of stored patterns (e.g.,

in the Hopﬁeld model).

7 FUNDING

This work was supported by the Next-Generation-

EU programme under the funding schemes PNRR-

PE-AI scheme (M4C2, investment 1.3, line on AI)

FAIR “Future Artiﬁcial Intelligence Research”, grant

id PE00000013, Spoke-8: Pervasive AI.

REFERENCES

Adjodah, D., Calacci, D., Dubey, A., Goyal, A., Krafft,

P., Moro, E., and Pentland, A. (2020). Leveraging

communication topologies between learning agents in

deep reinforcement learning. volume 2020-May, page

1738 – 1740.

Akin, O., Paradisi, P., and Grigolini, P. (2009).

Perturbation-induced emergence of poisson-like be-

havior in non-poisson systems. J. Stat. Mech.: Theory

Exp., page P01013.

Albert, R. and Barab

asi, A.-L. (2002). Statistical mechanics

of complex networks. Reviews of Modern Physics,

74(1):47 – 97.

Allegrini, P., Menicucci, D., Bedini, R., Gemignani, A., and

Paradisi, P. (2010). Complex intermittency blurred

by noise: theory and application to neural dynamics.

Phys. Rev. E, 82(1 Pt 2):015103.

Allegrini, P., Paradisi, P., Menicucci, D., Laurino, M., Be-

dini, R., Piarulli, A., and Gemignani, A. (2013). Sleep

unconsciousness and breakdown of serial critical in-

termittency: New vistas on the global workspace.

Chaos Solitons Fract., 55:32–43.

Allegrini, P., Paradisi, P., Menicucci, D., Laurino, M., Pi-

arulli, A., and Gemignani, A. (2015). Self-organized

dynamical complexity in human wakefulness and

sleep: Different critical brain-activity feedback for

conscious and unconscious states. Phys. Rev. E Stat.

Nonlin. Soft Matter Phys, 92(3).

Barab

asi, A.-L. and Albert, R. (1999). Emergence of scal-

ing in random networks. Science, 286(5439):509 –

512.

Barab

asi, A.-L. and Oltvai, Z. N. (2004). Network biology:

Understanding the cell’s functional organization. Na-

ture Reviews Genetics, 5(2):101 – 113.

Beggs, J. M. and Plenz, D. (2003). Neuronal avalanches

in neocortical circuits. Journal of neuroscience,

23(35):11167–11177.

Bianco, S., Grigolini, P., and Paradisi, P. (2007). A ﬂuctu-

ating environment as a source of periodic modulation.

Chem. Phys. Lett., 438(4-6):336–340.

Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., and

Hwang, D.-U. (2006). Complex networks: Structure

and dynamics. Phys. Rep., 424(4-5):175–308. DOI:

10.1016/j.physrep.2005.10.009.

Cox, D. (1970). Renewal Processes. Methuen & Co., Lon-

don. ISBN: 0-412-20570-X; ﬁrst edition 1962.

Davies, M., Srinivasa, N., Lin, T.-H., Chinya, G., Cao, Y.,

Choday, S. H., Dimou, G., Joshi, P., Imam, N., Jain,

S., Liao, Y., Lin, C.-K., Lines, A., Liu, R., Math-

aikutty, D., McCoy, S., Paul, A., Tse, J., Venkatara-

manan, G., Weng, Y.-H., Wild, A., Yang, Y., and

Wang, H. (2018). Loihi: A neuromorphic many-

core processor with on-chip learning. IEEE Micro,

38(1):82 – 99.

Erd ¨os, P. and R

enyi, A. (1959). On random graphs i. Pub-

licationes Mathematcae, 6(3-4):290–297.

Ernst, I. (1925). Beitrag zur theorie des ferromag-

netismus. Zeitschrift f

ur Physik A Hadrons and Nu-

clei, 31(1):253–258.

Temporal Complexity of a Hopﬁeld-Type Neural Model in Random and Scale-Free Graphs

447

Grigolini, P. (2015). Emergence of biological complexity:

Criticality, renewal and memory. Chaos Solit. Frac-

tals, 81(Part B):575–88.

Grigolini, P., Palatella, L., and Raffaelli, G. (2001). Asym-

metric anomalous diffusion: an efﬁcient way to detect

memory in time series. Fractals, 9(04):439–449.

Grinstein, G. and Linsker, R. (2005). Synchronous neural

activity in scale-free network models versus random

network models. Biological Sciences, 102(28):9948–

9953.

Gros, C. (2013). Complex and adaptive dynamical systems:

A primer, third edition.

Hebb, D. O. (1949). The Organization of Behavior: A Neu-

ropsychological Theory. Wiley & Sons, New York.

Hopﬁeld, J. (1982). Neural networks and physical systems

with emergent collective computational abilities. Pro-

ceedings of the National Academy of Sciences of the

United States of America, 79(8):2554 – 2558.

Hopﬁeld, J. (1984). Neurons with graded response have

collective computational properties like those of two-

state neurons. Proceedings of the National Academy

of Sciences of the United States of America, 81(10

I):3088 – 3092.

Hopﬁeld, J. (1995). Pattern recognition computation us-

ing action potential timing for stimulus representation.

Nature, 376(6535):33 – 36.

Hurst, H. (1951). Long-term storage capacity of reservoirs.

Trans. Am. Soc. Civil Eng., 116(1):770–799. DOI:

10.1061/TACEAT.0006518.

Kaviani, S. and Sohn, I. (2020). Inﬂuence of random topol-

ogy in artiﬁcial neural networks: A survey. ICT Ex-

press, 6(2):145 – 150.

Kaviani, S. and Sohn, I. (2021). Application of complex

systems topologies in artiﬁcial neural networks opti-

mization: An overview. Expert Systems with Applica-

tions, 180.

owel, S. and Singer, W. (1992). Selection of intrinsic hor-

izontal connections in the visual cortex by correlated

neuronal activity. Science, 255(5041):209 – 212.

Lu, J., He, J., Cao, J., and Gao, Z. (2006). Topology inﬂu-

ences performance in the associative memory neural

networks. Physics Letters A, 354(5-6):335 – 343.

Lu, L., Gao, Z., Wei, Z., and Yi, M. (2023). Working

memory depends on the excitatory–inhibitory balance

in neuron–astrocyte network. Chaos: An Interdisci-

plinary Journal of Nonlinear Science, 33(1):013127.

McGraw, P. N. and Menzinger, M. (2003). Topology and

computational performance of attractor neural net-

works. Physical Review E, 68(4 2):471021 – 471024.

Montroll, E. (1964). Random walks on lattices. Proc. Symp.

Appl. Math., 16:193–220.

Paradisi, P. and Allegrini, P. (2015). Scaling law of diffusiv-

ity generated by a noisy telegraph signal with fractal

intermittency. Chaos Soliton Fract, 81(Part B):451–

62.

Paradisi, P. and Allegrini, P. (2017). Intermittency-driven

complexity in signal processing. In Barbieri, R.,

Scilingo, E. P., and Valenza, G., editors, Complex-

ity and Nonlinearity in Cardiovascular Signals, pages

161–195. Springer, Cham.

Paradisi, P., Allegrini, P., Gemignani, A., Laurino, M.,

Menicucci, D., and Piarulli, A. (2013). Scaling and in-

termittency of brain events as a manifestation of con-

sciousness. AIP Conf. Proc, 1510:151–161. DOI:

10.1063/1.4776519.

Paradisi, P. and Cesari, R. (2023). Event-based complex-

ity in turbulence. Cambridge Scholar Publishing. In

Paolo Grigolini and 50 Years of Statistical Physics

(edited by B.J. West and S. Bianco), ISBN: 1-5275-

0222-8.

Paradisi, P., Cesari, R., Donateo, A., Contini, D., and Alle-

grini, P. (2012). Scaling laws of diffusion and time in-

termittency generated by coherent structures in atmo-

spheric turbulence. Nonlinear Proc. Geoph., 19:113–

126. P. Paradisi et al., Corrigendum, Nonlin. Processes

Geophys. 19, 685 (2012).

Paradisi, P., Cesari, R., and Grigolini, P. (2009). Superstatis-

tics and renewal critical events. Cent. Eur. J. Phys.,

7:421–431.

Paradisi, P., Kaniadakis, G., and Scarfone, A. M. (2015).

The emergence of self-organization in complex sys-

tems - preface. Chaos Soliton Fract, 81(Part B):407–

11.

Peng, C.-K., Buldyrev, S. V., Havlin, S., Simons, M., Stan-

ley, H. E., and Goldberger, A. L. (1994). Mosaic or-

ganization of dna nucleotides. Phys Rev E, 49:1685–

1689.

Rydin Gorj

ao, L., Hassan, G., Kurths, J., and Witthaut, D.

(2022). Mfdfa: Efﬁcient multifractal detrended ﬂuc-

tuation analysis in python. Computer Physics Com-

munications, 273:108254.

Shaﬁee, M. J., Siva, P., and Wong, A. (2016). Stochasticnet:

Forming deep neural networks via stochastic connec-

tivity. IEEE Access, 4:1915 – 1924.

Torres, J., Mu

noz, M., Marro, J., and Garrido, P. (2004).

Inﬂuence of topology on the performance of a neural

network. Neurocomputing, 58-60:229 – 234.

Watts, D. J. and Strogatz, S. H. (1998). Collective dynamics

of ’small-world9 networks. Nature, 393(6684):440 –

442.

Weiss, G. H. and Rubin, R. J. (1983). Random walks: the-

ory and selected applications. Advances in Chemical

Physics, 52:363–505.

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

448