A Vector Autoregression-Based Algorithm for Dynamic Many-Objective

Optimization Problems

Kalthoum Karkazan

, Haluk Rahmi Topcuoglu

and Shaaban Sahmoud

Faculty of Engineering, Computer Engineering Department, Marmara University, Istanbul, Turkey

Faculty of Engineering, Computer Engineering Department, Fatih Sultan Mehmet Vakif University, Istanbul, Turkey

Keywords:

Dynamic Many-Objective Optimization, Many-Objective Evolutionary Algorithms, Change Detection,

Prediction-Based Optimization.

Abstract:

Dynamic Many-Objective Optimization Problems (DMaOPs) represent a signiﬁcant challenge due to their

inherent dynamism and the presence of a large number of objectives. In addressing this complexity, this paper

proposes a new prediction-based strategy tailored to managing detected changes in such problems, which is

one of the ﬁrst attempts to address the DMaOPs. Our proposed algorithm constructs a Vector Autoregressive

(VAR) model within a dimensionality-reduced space. This model effectively captures the mutual relationships

among decision variables and enables an accurate prediction of the initial positions for the evolving solutions

in dynamic environments. To accelerate the convergence process, the algorithm demonstrates adaptability

by responding multiple times to the same detected change. In our empirical study, the performance of the

proposed algorithm is evaluated using four selected test problems from various benchmarks. Our proposed

approach shows competitive results compared to the other algorithms in most test instances.

1 INTRODUCTION

Many-objective optimization problems (MaOPs) are

deﬁned as optimization problems that have four or

more conﬂicting objectives to be optimized simulta-

neously (Farina and Amato, 2002). Many real-world

problems from diverse domains belong to this type of

optimization problem where they sometimes involve

up to 15 objectives or more (Coello and Lamont,

2004). One illustrative example is explored in (Zhu

et al., 2019), where the authors argue that the evolv-

ing societal landscape necessitates increasing demand

for high-quality power. Recognizing the limitations

of single-objective economic optimization, there is

a persistent need for a shift toward many-objective

power ﬂow optimization. These objectives primar-

ily encompass economic, environmental, reliability,

and stability factors, aiming for comprehensive mod-

ern power system management. Another instance is

presented in (Li et al., 2008), where the authors in-

vestigate the power generation loading optimization

problem with four objectives: minimize total cost,

minimize fuel consumption, minimize emissions, and

maximize output.

The primary distinction between a dynamic opti-

mization problem (DOP) and a stationary optimiza-

tion problem lies in the presence of dynamism within

the environment (Jin and Branke, 2005). Dynamism

can manifest in various forms, encompassing changes

in one or more objective functions, modiﬁcations

in constraints, and/or shifts in problem parameters

across time (Jin and Branke, 2005). Solutions deemed

optimal or the best before a change may not retain

their optimality or superiority in the new environ-

ment. Consequently, the main objective of a dynamic

optimization problem is to track the global optima

closely. This dynamic nature presents additional com-

plexities when dealing with such problems.

While most of the current research on MaOPs

assumes that the environment is stationary, in real-

world scenarios, many factors can affect the environ-

ment or the optimization problem objectives and vari-

ables (Gupta and Nanda, 2021). To the best of our

knowledge, this paper is one of the ﬁrst to try to han-

dle this type of optimization problem called Dynamic

Many-Objective Optimization Problems (DMaOPs).

The complexity of dynamic many-objective op-

timization problems requires advanced optimiza-

tion algorithms and strategies to explore the high-

dimensional solution space efﬁciently and quickly

adapt to new environmental changes. Therefore, the

algorithms designed for static many-objective prob-

Karkazan, K., Topcuoglu, H. and Sahmoud, S.

A Vector Autoregression-Based Algorithm for Dynamic Many-Objective Optimization Problems.

DOI: 10.5220/0013009200003837

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 279-287

ISBN: 978-989-758-721-4; ISSN: 2184-3236

279

lems are not adequate for handling the changing na-

ture of DMaOPs. As a result, these problems need

the development of adaptive algorithms that can con-

sistently update the estimated Pareto-optimal front

(POF) to align it as quickly, accurately, and uniformly

diversiﬁed as possible to the actual POF.

In this paper, we present the design and develop-

ment of a dynamic many-objective evolutionary al-

gorithm (DMaOEA) that effectively solves dynamic

many-objective optimization problems (DMaOPs).

Our algorithm adapts to changes in the problem en-

vironment and efﬁciently handles the trade-offs be-

tween multiple conﬂicting objectives over time to en-

sure the attainment of an accurately estimated Pareto-

optimal front (POF). The proposed DMaOEA consis-

tently tracks the shifting Pareto-optimal fronts (POFs)

and produces a widely spread set of solutions across

it. The algorithm’s effectiveness is assessed using dif-

ferent metrics that measure the estimated POFs’ con-

vergence and diversity.

The rest of this paper is organized as follows: Sec-

tion 2 deﬁnes the dynamic many-objective optimiza-

tion problem and summarizes the related work. Sec-

tion 3 describes and explains the proposed algorithm

in detail. Experimental settings and results are given

in Section 4. Section 5 concludes the paper and pro-

poses some future research directions.

2 DYNAMIC MANY-OBJECTIVE

OPTIMIZATION

In this section, we focus on many-objective opti-

mization and dynamic multi-objective optimization

because they are considered the two origins from

which Dynamic Many-Objective Optimization Prob-

lems (DMaOPs) are derived. A DMaOP is an opti-

mization problem characterized by two merged key

attributes: the existence of dynamism within the prob-

lem environment and the involvement of many con-

ﬂicting objectives.

As in dynamic multi-objective optimization prob-

lems, the dynamism of DMaOP is exempliﬁed by

variations over time in one or more aspects of the op-

timization problem, such as alterations in objective

functions, constraints, or problem parameters. Con-

currently, the optimization problem is more complex

by the inclusion of a signiﬁcant number of conﬂict-

ing objectives, typically exceeding four. As a result of

this large number of objectives, the Pareto-dominance

becomes ineffective in differentiating between indi-

viduals.

In MaOPs, obtaining a well-distributed set of non-

dominated solutions on the POF becomes increas-

ingly challenging as the number of objectives rises.

Moreover, the visualization for this type of prob-

lem is complicated as the traditional graphical meth-

ods struggle to represent high-dimensional Pareto

fronts (Deb and Jain, 2014). In addition, evaluat-

ing many-objective optimization problems is compu-

tationally expensive since the performance metrics re-

quire larger computational effort as the number of ob-

jectives increases (C.M. Fonseca and Lopez-Ibanez,

2006).

Although the performance of the existing MOEAs

has dropped dramatically when handling MaOPs due

to the difﬁculties mentioned above, they can be used

as a baseline to develop effective MaOEAs. Many

successful MOEAs have been adapted in literature

and have proven their effectiveness in solving vari-

ous real-world MaOPs such as the NSGA-III (Deb

and Jain, 2014) and the MOEA/D (Zhang and Li,

2007). The main idea in these two algorithms is to

divide the search space into predeﬁned multiple tar-

geted searches. As a result, an individual will com-

pete with only the individuals that are associated with

its search target rather than compete with all the other

individuals in the population. Consequently, optimal

points corresponding to each targeted search task are

identiﬁed, easing the difﬁculty associated with han-

dling a large non-dominated set as well as maintain-

ing a good level of diversity in the population. Un-

fortunately, most MaOEAs are not directly applicable

to DMaOPs because of the existence of various forms

of dynamism which dramatically degrade the perfor-

mance.

In the literature, there are many approaches have

been proposed to solve DMOPs including diversity-

based (Deb et al., 2007), problem type-based (Sah-

moud and Topcuoglu, 2018), memory-based (Sah-

moud and Topcuoglu, 2020), and prediction-

based (Azzouz et al., 2017; Karkazan et al., 2023).

On the other hand, there are many attempts to

beneﬁt from Machine Learning models to improve

the prediction results such as using Support Vector

Machine (SVM) (Weizhen et al., 2019) and trans-

fer learning (Jiang et al., 2017). In a recent re-

search work, the authors of (Jiang et al., 2023) in-

troduced an algorithm called Vector Autoregressive

Evolution (VARE), which combines Vector Autore-

gression (VAR) and environment-aware hypermuta-

tion (EAH) techniques to track the changing POFs in

DMOPs. The VARE constructs a VAR model that

captures the mutual relationships between decision

variables, enabling accurate prediction of the loca-

tions of new solutions in the evolving environment.

Additionally, the VARE incorporates environment-

aware hypermutation techniques to enhance popu-

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

280

lation diversity and improve the algorithm’s perfor-

mance in cases where the prediction approach is un-

suitable.

3 A NEW PREDICTION-BASED

ALGORITHM

Our proposed algorithm utilizes the NSGA-III algo-

rithm (Deb and Jain, 2014) as a baseline, enhancing

its ability to deal with environmental changes. It also

applies the Principle Component Analysis (PCA) for

constructing a Vector Auto Regression (VAR) model.

In the following subsections, the VAR and the PCA

are explained brieﬂy, which is followed by the steps

of our algorithm.

3.1 Vector Auto Regression

Multivariate time series is a special case of time se-

ries where multiple variables are recorded over time,

creating a sequence of data points. These variables

can be interrelated and impact each other’s values. In

other words, each variable is inﬂuenced not only by its

past values but also by other variables. This interde-

pendency is utilized to predict future values. Analyz-

ing those time series and creating models from them

opens doors to comprehending and predicting trends

and patterns effectively (Jonathan D. Cryer, 2008).

Vector Auto Regression (VAR) is a widely uti-

lized approach for forecasting multivariate time series

data. This technique has consistently demonstrated

its effectiveness across various ﬁelds by capturing in-

tricate relationships among multiple time series vari-

ables and accurately predicting future values. Some

of its applications include but are not limited to eco-

nomic forecasting, ﬁnancial market analysis, climate

and environmental studies, and social sciences. In a

VAR model, each variable is modeled as a linear com-

bination of its past values as well as the past values of

other variables in the system (Jin and Chen, 2013).

According to (S. Huband and While, 2006), the

decision variables in a MOP/MaOP are often cor-

related and interrelated. This characteristic makes

VAR models a highly suitable technique to address

these problems. However, there is a critical consid-

eration before applying VAR to MaOPs. Although

VAR models deliver accurate prediction results, their

performance can be signiﬁcantly impacted when deal-

ing with high-dimensional problems, as in the case

of MaOP decision variables. To mitigate this effect,

a dimension reduction technique is employed as ex-

plained in the following section.

3.2 Principal Component Analysis

Principal Component Analysis (PCA) is a statisti-

cal method used for dimensionality reduction, out-

liers detection, data analysis, and graphical clustering

or classiﬁcation (Geladi and Linderholm, 2020). It

identiﬁes the most signiﬁcant patterns in a dataset by

transforming the original variables into a new set of

uncorrelated variables called principal components.

These components capture the maximum variance in

the data, allowing for a reduction in dimensional-

ity while retaining essential information. Principal

Component Analysis (PCA) is a commonly employed

technique in multivariate data analysis (Geladi and

Linderholm, 2020).

Figure 1 provides a simple example illustrating the

process of dimensionality reduction using PCA. The

ﬁrst sub-ﬁgure on the left shows the position of the

data points in the original space. PCA identiﬁes the

best-ﬁtting lower-dimensional surface in which the

projection error is minimized, as demonstrated in the

middle sub-ﬁgure. The ﬁnal sub-ﬁgure represents the

points in the new surface after the reduction process.

Figure 1: Converting 2-D space to a 1-D space using PCA.

Let POP

= x

, x

, ..., x

(where each x

is a D×1

vector) represent all archived solutions up to the cur-

rent environment. We aim to map any data point

∈ pop

from the D − Dimentions space to a much

lower k − Dimentions (k ≪ n) space, namely,

= (x

, x

, ..., x

) ⇒ y

= (y

, y

, ..., y

) (1)

One advantage of the PCA algorithm is the abil-

ity to reconstruct the points in the original space (i.e.

from y

back to x

), as demonstrated in Figure 2. This

feature is essential in the context of our algorithm and

makes PCA a good choice for dimensionality reduc-

tion.

3.3 Non-Dominated Sorting Genetic

Algorithm III (NSGA-III)

The NSGA-III (Deb and Jain, 2014) algorithm is

an extension of the popular NSGA-II algorithm to

adapt for many-objective optimization problems. The

fundamental structure remains same to the original

NSGA-II algorithm, with substantial modiﬁcations in

A Vector Autoregression-Based Algorithm for Dynamic Many-Objective Optimization Problems

281

Figure 2: Reconstruction of 2-D space using PCA.

its selection mechanism which is designed to over-

come the main difﬁculty mentioned in Section 2. This

new approach also helps in maintaining a diverse set

of solutions. The main idea behind the modiﬁcations

in NSGA-III is to initialize the algorithm with refer-

ence points (RPs) at the start of the run. The positions

of individuals concerning these RPs serve as the foun-

dation for the selection process, diverging from the

approach of using crowding distance as in NSGA-II.

3.4 Change Response Strategy

To effectively characterize changes in dynamic multi-

objective optimization problems, it is vital to both

detect the changes and evaluate their severity. The

severity of a change typically refers to the magni-

tude or extent of modiﬁcations made to the prob-

lem’s parameters, constraints, or objective function.

When a dynamic multi-objective evolutionary algo-

rithm incorporates a precise mechanism for detecting

the severity of changes, it becomes beneﬁcial to en-

hance the algorithm with dynamic and efﬁcient mech-

anisms to appropriately respond to the detected sever-

ity of change (Sahmoud and Topcuoglu, 2019). In this

paper, we will adapt the same strategy for dynamic

many-objective optimization problems.

When a change is detected, the severity of change

is calculated according to Equation 2. It is important

to highlight that employing this equation for calcu-

lating the severity of change resolves issues encoun-

tered when determining the overall severity of change

(SC) by choosing the maximum value among the cal-

culated severities for each objective function indepen-

dently (Sahmoud and Topcuoglu, 2019).

∑

i=1

i, j

(t) − F

i, j

(t − 1)

i, j

(t) + s

SC = λ × max(SC

, SC

, ..., SC

)

(2)

In this equation, SC

denotes the severity of change

for the objective function j, and S represents the num-

ber of selected indicators for detecting environmen-

tal changes. F

i, j

(t) and F

i, j

(t − 1) signify the val-

ues of objective function j for sensor i in the current

and previous generations, respectively. The term s

is a small constant utilized to prevent undeﬁned re-

sults when F

i, j

(t) is zero. Additionally, λ is employed

to adapt the equation for varying numbers of objec-

tive functions. In this study, it is set to M − 1 as

recommended by the reference study (Sahmoud and

Topcuoglu, 2019), where M represents the objectives

of the given problem.

If the severity of change is greater than or equal

to the average value, ε% of the population is replaced

by randomly generated individuals. Otherwise, the

algorithm will replace ε% of the population with mu-

tated solutions. It is noteworthy that this technique

is employed because a signiﬁcant change suggests

that the new POF’s location is likely far from the old

POF’s position. Hence, to explore new locations in

the search space, the re-initialization procedure is im-

plemented. Conversely, a small severity of change

value indicates a slight shift in the new POF’s loca-

tion, and the mutation operation is sufﬁcient to track

it. In our empirical study, ε% is equal to 20% of the

population.

In the predetermined number of generations fol-

lowing the detected change, the algorithm systemati-

cally archives the decision variable values of the clos-

est individual associated with each reference point,

if there are any, for subsequent usage. These val-

ues serve as training samples when constructing the

vector autoregression model. In this study, we collect

samples for ﬁve generations after each change. After

that, the collected training data are used to construct

and train a vector autoregression model. The process

for doing that is explained in detail in the following

subsection. Algorithm 1 explains how the proposed

algorithm reacts to a detected change.

3.5 Prediction Strategies for Individuals

After collecting a sufﬁcient number of training sam-

ples, our algorithm utilizes these samples to construct

a vector autoregression model. In the preparatory

phase, the algorithm employs PCA for dimensional-

ity reduction, constructing a VAR model within the

reduced space of time series solutions. Subsequently,

this VAR model is utilized to predict new individu-

als, and these newly predicted individuals are recon-

structed with PCA to revert to the original number

of dimensions before being added to the population.

To maintain a high level of diversity in the popula-

tion, a ﬁxed percentage of the population is substi-

tuted with randomly generated individuals. In this

empirical study, a 5% of the population is replaced

each time the algorithm responds.

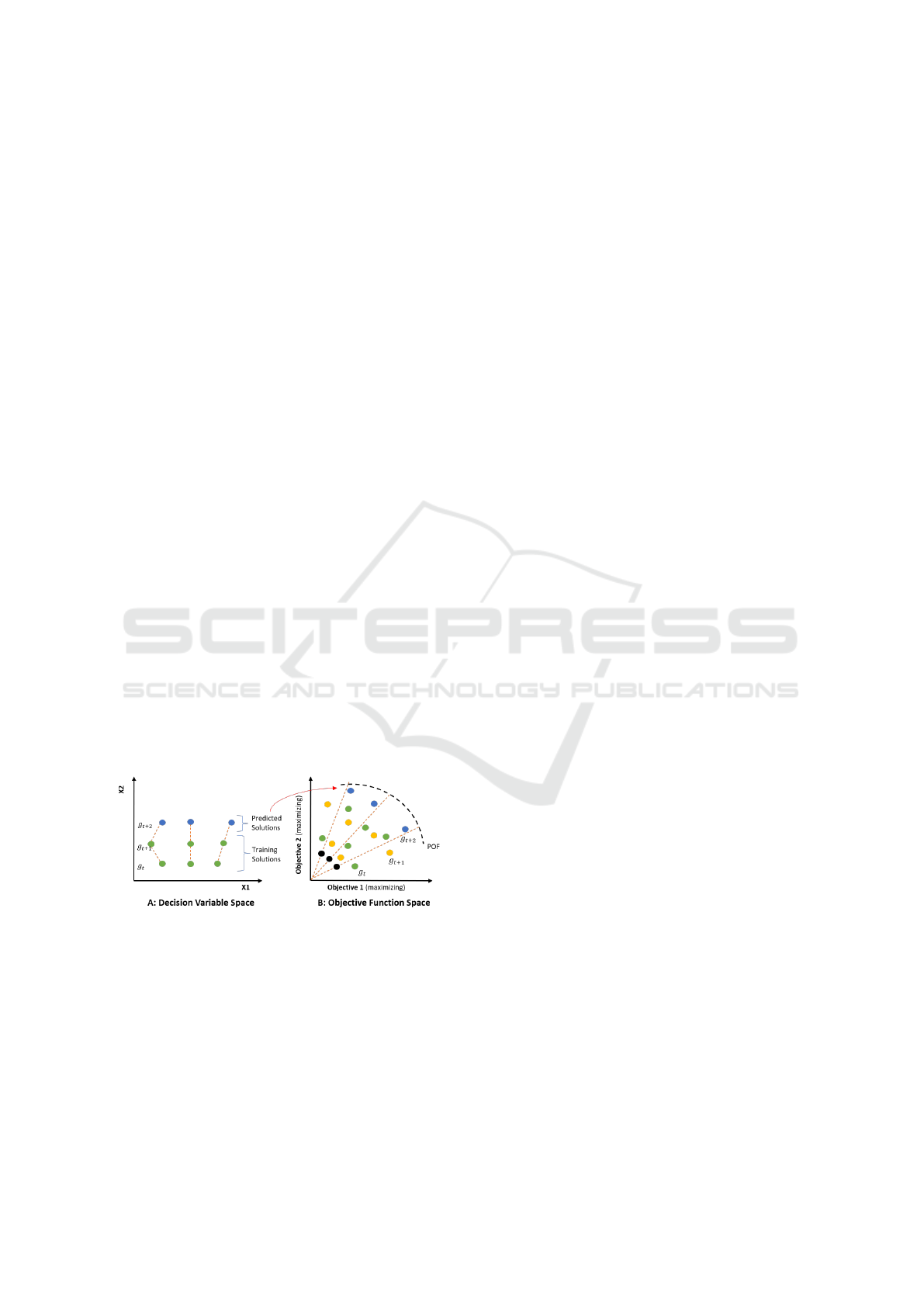
The visualization in Figure 3 illustrates the con-

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

282

if ChangeDetected then

Calculate the SeverityO f Change

if SeverityO fChange >= AvgSeverityO fChange

then

Reinitialize ε% of the population

else

Mutate ε% of the population

end if

Update AvgSeverityO fChange

count ← 0

end if

if count <= T S then

Store the closest individual of each reference

point in the archive

else

if T S mod λ ≡ 0 then

Reinitialize α% of the population

Construct VAR and employ it to forecast new

population members

end if

count ← count + 1

Algorithm 1: The Change Reaction Strategy.

cept. The black points represent the reference points

generated by the NSGA-III algorithm at the begin-

ning of the run. Within the objective function space,

the green points denote the selected individuals to be

stored in the archive and utilized as training samples.

When a point is chosen for archiving, values of its

decision variables are stored and all of the archived

information is employed to construct a model that

predicts new individuals, which is indicated by the

green points in the decision variable space in Figure3.

The resulting individuals predicted by the VAR model

are represented as blue points in the decision variable

space.

Figure 3: The proposed prediction strategy for individuals

in the new detecting environments.

3.6 Considering Multiple Reactions

Finally, periodic reactions are applied after the new

environment has been running for a speciﬁc number

of generations. In our empirical study, the algorithm

reacts periodically after every ﬁve generations. This

step helps accelerate the convergence process and pre-

vents the solutions from sticking to the local opti-

mum. This step is very important for the performance

of the algorithm. After each generation more infor-

mation is collected about the new environment and

the prediction process will be more accurate, which

can help catch up any error in the previous prediction

process.

Figure 4 summarizes the proposed algorithm in

a ﬂowchart. As depicted in the ﬂowchart, the al-

gorithm initiates by randomly initializing individuals

for the ﬁrst generation, conﬁguring the algorithm’s

parameters, and generating reference points. Sub-

sequently, the environment is sensed at the incep-

tion of each generation. If no change is detected,

the static MOEA, speciﬁcally NSGA-III, is activated,

and the population evolves through its genetic oper-

ators. Conversely, upon detecting a change, the al-

gorithm computes the severity of the change and up-

dates a portion of the population accordingly. Si-

multaneously, it begins collecting training samples by

storing the closest individual for each reference point

(RP) in the archive. When the number of genera-

tions used for collecting training samples reaches a

speciﬁc threshold called T S, the algorithm employs

the dimensional reduction technique, namely Princi-

ple Component Analysis (PCA) on the training sam-

ples. The output of PCA is then used to construct a

VAR model, which is used to predict the new individ-

uals that are injected into the population.

4 EXPERIMENTAL DESIGN

This section outlines the experimental design, encom-

passing information about the test problems, perfor-

mance evaluation metrics, and the algorithms in our

comparative study.

4.1 Test Problems

The performance of algorithms is evaluated using

a total of four test instances. Two of these prob-

lems, FDA4 and FDA5, are from the FDA test prob-

lems (Farina et al., 2004), and the other two, SJY4

and SJY5, are from the SJY test problems (Jiang and

Yang, 2014). These speciﬁc test instances were se-

lected because they are among the limited number of

scalable test instances available in the literature. Due

to their scalability, these instances can be tested with

more than 3-objective functions, making them suit-

able for evaluating Dynamic Many-Objective Prob-

lems (DMaOPs).

These test suites encompass all types of DMOPs,

based on the classiﬁcation presented by Farina et

al. (Farina et al., 2004). Notably, these instances, fea-

A Vector Autoregression-Based Algorithm for Dynamic Many-Objective Optimization Problems

283

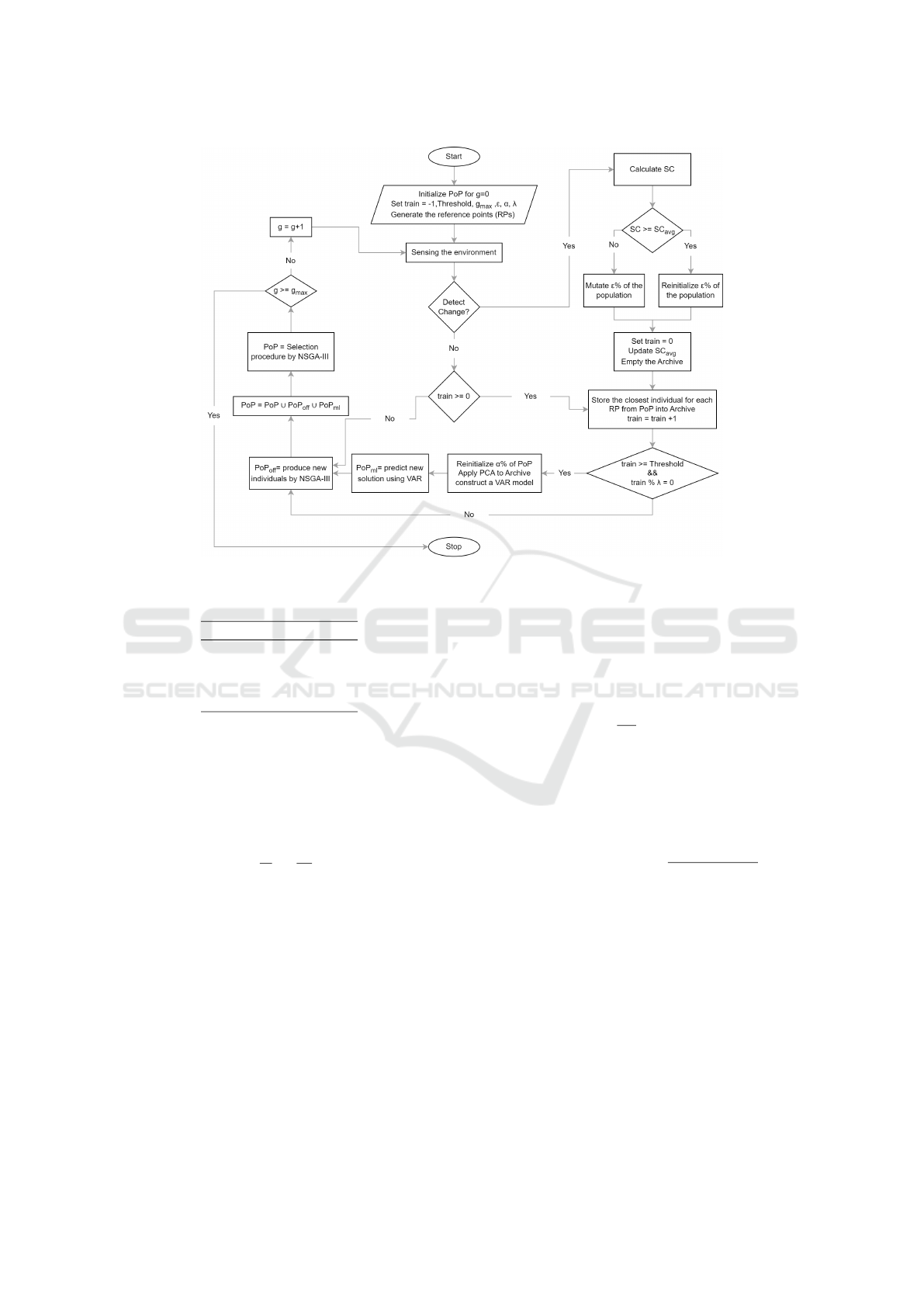
Figure 4: The ﬂowchart of the proposed algorithm for DMaOPs.

Table 1: The used benchmarks types.

Problem Type

FDA4 Type 1

FDA5 Type 2

SJY4 Type 3

SJY5 Type 4

turing known Pareto-optimal fronts, are speciﬁcally

designed to assess the performance of algorithms de-

signed to react to the dynamic changes in many-

objective optimization problems.

The details of the selected test problems are sum-

marized in Table 1, where the time used in these tests

is deﬁned as

t =

∗



f r



(3)

where f r is the change frequency, τ is the generations

counter, and n

is the severity of change.

4.2 Performance Metrics

Within this section, the deﬁnitions of the utilized

metrics are introduced, clarifying their importance in

evaluating the outcomes of the developed algorithms.

Two of the extensively acknowledged performance

metrics are used and their overviews are presented be-

low.

• Mean Inverted Generational Distance (mIGD):

This metric is a modiﬁed form of the inverted gen-

erational distance (IGD) (Li and Zhang, 2009). In

this approach, the mean value of the IGD metric

across all generations is computed, as illustrated

below.

mIGD =

|T |

∑

t∈T

IGD(PF

, PF

∗

) (4)

The IGD metric (Coello and Cortes, 2005) is em-

ployed to assess the diversity and convergence of

algorithms designed for static multi-objective op-

timization problems.

IGD(PF

, PF

∗

) =

∑

v∈PF

d(v, PF

∗

)

|PF

(5)

In this context, PF

denotes the set represent-

ing uniformly distributed points in the true Pareto

front and PF

∗

is the set comprising the estimated

Pareto optimal front generated by the algorithm at

the t-th time step. The minimum Euclidean dis-

tance between a point v in PF

and the points in

∗

is expressed as d(v, PF

∗

• Average Maximum Spread (aMS): This metric

quantiﬁes the diversity of the estimated Pareto op-

timal front by assessing its dispersion across the

true Pareto optimal front. Originally designed for

application in steady-state multi-objective envi-

ronments, it is adjusted for dynamic environments

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

284

by computing the average of its values across

all generations, as demonstrated below (Goh and

Tan, 2009):

aMS =

∑

k=1

min

[

POF

,POF

∗

]

−max

POF

,POF

∗

POF

−POF

(6)

In this equation, POF

∗

denotes the minimum

value of the k-th objective in the estimated Pareto

optimal front. M denotes the count of ﬁtness func-

tions, and POF

refers to the maximum value of

the k-th objective in the true Pareto optimal front.

4.3 Algorithms in the Empirical Study

Two DMaOEAs are used in the comparison study: the

dynamic version of the NSGA-III algorithm (NSGA-

III-Reinitialize), and the Dynamic non-dominated

sorting genetic algorithm III (DNSGA-III) (Gupta

and Nanda, 2021).

• NSGA-III-Reinitialize: This algorithm is adapted

for dynamic problems by introducing new indi-

viduals when a change in the environment is de-

tected. The newly introduced solutions are chosen

to be 20% of the population size and they are gen-

erated by random initialization.

• Dynamic Non-dominated Sorting Genetic Algo-

rithm III (DNSGA-III): The only reference al-

gorithm found in the literature proposed to han-

dle DMaOPs is the DNSGA-III, which is adapted

from the NSGA-III algorithm. To address the

dynamism in the problem, the authors suggested

using machine learning (ML) techniques to pre-

dict the initial location of individuals in future

environments (Gupta and Nanda, 2021). The

authors studied the effect of applying differ-

ent ML techniques for the prediction process.

Those techniques include support vector regres-

sion (SVR) with linear kernel and radial basis

function (RBF) kernel, polynomial interpolation,

and cubic spline-based prediction. According to

the authors, the algorithm delivers its best results

when the prediction is conducted using the sup-

port vector regression with radial basis function

(SVR-RBF) kernel ML technique. Consequently,

this technique was utilized during the simulation

of this algorithm in our empirical study.

4.4 Parameters Setting

Following are the values for some of the key parame-

ters as been set in the experiment:

• Number of Objectives (M): Three different

values have been chosen to effectively test the al-

gorithms’ ability to deal with MaOPs.

• Number of Reference Points (H): This

value has been calculated according to the num-

ber of objectives as suggested by the authors of

NSGA-III (Deb and Jain, 2014).

• Population size (N): This value is set for each

test case as the smallest multiple of four greater

than H (Deb and Jain, 2014).

• Number of Decision Variables (D): The

No. of decision variable is suggested in (Deb

and Jain, 2014) to be calculated by the following

equation:

D = M + k − 1 (7)

where M is the number of objectives, and k = 10

for the problems extended from DTLZ2, namely,

FDA4 and FDA5.

• Change Frequency: For each test instance, each

algorithm has been tested with three different val-

ues for change frequency τ

, those values are 10,

20, and 30.

• Number of Generations: At each run, the num-

ber of generations has been speciﬁed according

to the change frequency for that run. 10 gener-

ations have been given between each two consec-

utive changes to give the algorithms the chance to

converge to the real POF. This is represented by,

10 ∗ τ

• Number of Executions: Each algorithm was

executed 30 independent times on each test in-

stance.

4.5 Experimental Results

In this section, the effectiveness of our algorithm is

evaluated and compared with other DMaOEAs within

the context of our experimental framework. All of

the experiments ran on the same experimental plat-

form PlatEMO (Tian et al., 2017). This platform

is an evolutionary multi-objective optimization plat-

form developed in MATLAB for free use in research

and educational purposes. It supports diverse bench-

mark problems, performance metrics, and visualiza-

tion tools.

Table 2 shows the results of the mIGD metric. The

best results from each of the three algorithms are de-

noted in bold. As seen in Table 2, the proposed algo-

rithm outperforms the other algorithms in most of the

test instances (23 out of 36 cases). The mIGD metric

evaluates both convergence and diversity when mea-

suring an algorithm’s performance, so getting com-

petitive results in this metric means that the proposed

A Vector Autoregression-Based Algorithm for Dynamic Many-Objective Optimization Problems

285

Table 2: Mean inverted generational distance values of al-

gorithms.

Problem M tau Proposed NSGA-III DNSGA-

Algorithm -Reinitialize III

FDA4

10 1.28E-01 1.31E-01 1.34E-01

20 1.23E-01 1.21E-01 1.21E-01

30 1.10E-01 1.11E-01 1.12E-01

10 2.18E-01 2.13E-01 2.11E-01

20 1.91E-01 1.93E-01 1.92E-01

30 1.77E-01 1.77E-01 1.76E-01

10 2.76E-01 2.95E-01 2.91E-01

20 2.20E-01 2.26E-01 2.25E-01

30 2.04E-01 2.08E-01 2.06E-01

FDA5

10 2.61E-01 2.70E-01 2.74E-01

20 2.39E-01 2.43E-01 2.44E-01

30 2.23E-01 2.22E-01 2.26E-01

10 4.52E-01 4.48E-01 4.50E-01

20 3.95E-01 3.92E-01 3.92E-01

30 3.58E-01 3.57E-01 3.55E-01

10 6.20E-01 6.62E-01 6.47E-01

20 4.59E-01 4.79E-01 4.68E-01

30 4.18E-01 4.27E-01 4.22E-01

SJY4

10 1.12E-01 1.13E-01 1.12E-01

20 1.08E-01 1.08E-01 1.09E-01

30 1.08E-01 1.08E-01 1.08E-01

10 1.65E-01 1.63E-01 1.63E-01

20 1.59E-01 1.59E-01 1.59E-01

30 1.59E-01 1.59E-01 1.58E-01

10 1.78E-01 1.78E-01 1.78E-01

20 1.73E-01 1.73E-01 1.72E-01

30 1.72E-01 1.72E-01 1.72E-01

SJY5

10 9.48E-02 8.95E-02 9.56E-02

20 8.21E-02 8.20E-02 8.25E-02

30 8.17E-02 8.17E-02 8.24E-02

10 1.39E-01 1.42E-01 1.43E-01

20 1.26E-01 1.26E-01 1.26E-01

30 1.25E-01 1.25E-01 1.25E-01

10 1.50E-01 1.48E-01 1.52E-01

20 1.39E-01 1.39E-01 1.40E-01

30 1.38E-01 1.38E-01 1.38E-01

algorithm is able to converge successfully to the true

POF quickly and maintains the diversity, as well.

Table 3 shows the results of the aMS metric which

evaluates the diversity level of the obtained solutions.

Although the proposed algorithm obtains the best re-

sults, the other algorithms provide competitive re-

sults. When those results are compared, it can be ob-

served that there is no signiﬁcant difference for most

of the test instances.

5 CONCLUSION AND FUTURE

WORK

The primary objective of this paper is to create an

algorithm capable of effectively tackling dynamic

many-objective optimization problems. This algo-

rithm adaptively responds to the change according to

the severity of the detected change by either mutat-

ing or re-initializing a portion of the population. It

then preserves the Pareto-optimal front (POF) for cer-

tain subsequent populations, utilizing them as training

samples to construct a VAR model. This VAR model

is then used to predict new individuals that are sup-

posed to be closer to the real POF. The algorithm re-

sponds multiple times for the same change to speed

up the convergence process. Our algorithm demon-

Table 3: Mean average maximum spread values of algo-

rithms.

Problem M tau Proposed NSGA-III DNSGA-

Algorithm -Reinitialize III

FDA4

10 1.00E+00 9.99E-01 9.99E-01

20 9.92E-01 9.93E-01 9.85E-01

30 9.99E-01 9.99E-01 9.99E-01

10 1.00E+00 1.00E+00 1.00E+00

20 9.94E-01 9.91E-01 9.94E-01

30 9.95E-01 9.96E-01 9.97E-01

10 1.00E+00 1.00E+00 1.00E+00

20 9.98E-01 9.98E-01 9.96E-01

30 9.98E-01 9.99E-01 9.98E-01

FDA5

10 9.98E-01 9.99E-01 9.99E-01

20 9.95E-01 9.93E-01 9.88E-01

30 9.97E-01 9.97E-01 9.96E-01

10 1.00E+00 1.00E+00 1.00E+00

20 9.91E-01 9.93E-01 9.90E-01

30 9.92E-01 9.95E-01 9.93E-01

10 1.00E+00 1.00E+00 1.00E+00

20 9.98E-01 9.98E-01 9.98E-01

30 9.96E-01 9.97E-01 9.96E-01

SJY4

10 9.97E-01 9.94E-01 9.94E-01

20 9.96E-01 9.95E-01 9.94E-01

30 9.96E-01 9.96E-01 9.95E-01

10 1.00E+00 9.97E-01 9.96E-01

20 9.94E-01 9.94E-01 9.93E-01

30 9.94E-01 9.94E-01 9.93E-01

10 1.00E+00 1.00E+00 1.00E+00

20 9.96E-01 9.96E-01 9.96E-01

30 9.95E-01 9.95E-01 9.95E-01

SJY5

10 9.92E-01 9.90E-01 9.90E-01

20 9.96E-01 9.94E-01 9.94E-01

30 9.95E-01 9.95E-01 9.94E-01

10 9.99E-01 9.90E-01 9.85E-01

20 9.93E-01 9.93E-01 9.93E-01

30 9.94E-01 9.93E-01 9.94E-01

10 9.99E-01 9.99E-01 9.99E-01

20 9.93E-01 9.94E-01 9.95E-01

30 9.95E-01 9.95E-01 9.94E-01

strates better performance results in comparison with

the other algorithms utilized in this study.

It is evident that Dynamic Many-Objective Prob-

lems (DMaOPs) are relatively new and remain under-

explored. Therefore, exploring this area represents a

potential research direction. This exploration process

may involve proposing new scalable and dynamic test

instances, devising more effective performance mea-

sures, developing efﬁcient algorithms, and studying

the effectiveness of proposed methodologies on real-

world problems.

REFERENCES

Azzouz, R., Bechikh, S., and Ben Said, L. (2017). Dynamic

multi-objective optimization using evolutionary algo-

rithms: a survey. Recent advances in evolutionary

multi-objective optimization, pages 31–70.

C.M. Fonseca, L. P. and Lopez-Ibanez, M. (2006). An

improved dimension-sweep algorithm for the hyper-

volume indicator. In 2006 IEEE International Con-

ference on Evolutionary Computation, pages 1157–

1163.

Coello, C. A. and Cortes, N. C. (2005). Solving multiob-

jective optimization problems using an artiﬁcial im-

mune system. Genetic Programming and Evolvable

Machines, 6(2):163–190.

Coello, C. A. C. and Lamont, G. B. (2004). Applications

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

286

of multi-objective evolutionary algorithms, volume 1.

World Scientiﬁc.

Deb, K., Bhaskara Rao N., U., and Karthik, S. (2007).

Dynamic multi-objective optimization and decision-

making using modiﬁed nsga-ii: A case study on

hydro-thermal power scheduling. In International

Conference on Evolutionary Multi-Criterion Opti-

mization, pages 803–817. Springer.

Deb, K. and Jain, H. (2014). An evolutionary many-

objective optimization algorithm using reference-

point-based nondominated sorting approach, part i:

Solving problems with box constraints. IEEE Trans-

actions on Evolutionary Computation, 18(4):577–

601.

Farina, M. and Amato, P. (2002). On the optimal solution

deﬁnition for many-criteria optimization problems. In

2002 Annual Meeting of the North American Fuzzy In-

formation Processing Society Proceedings. NAFIPS-

FLINT 2002 (Cat. No. 02TH8622), pages 233–238.

Farina, M., Deb, K., and Amato, P. (2004). Dynamic multi-

objective optimization problems: Test cases, approxi-

mations, and applications. Evolutionary Computation,

IEEE Transactions on, 8:425 – 442.

Geladi, P. and Linderholm, J. (2020). 2.03 - principal com-

ponent analysis. In Brown, S., Tauler, R., and Wal-

czak, B., editors, Comprehensive Chemometrics (Sec-

ond Edition), pages 17–37. Elsevier, Oxford, second

edition edition.

Goh, C.-K. and Tan, K. C. (2009). A competitive-

cooperative coevolutionary paradigm for dynamic

multiobjective optimization. IEEE Transactions on

Evolutionary Computation, 13(1):103–127.

Gupta, R. and Nanda, S. J. (2021). Solving dynamic many-

objective tsp using nsga-iii equipped with svr-rbf ker-

nel predictor. In 2021 IEEE Congress on Evolutionary

Computation (CEC), pages 95–102.

Jiang, M., Huang, Z., Qiu, L., Huang, W., and Yen, G. G.

(2017). Transfer learning-based dynamic multiobjec-

tive optimization algorithms. IEEE Transactions on

Evolutionary Computation, 22(4):501–514.

Jiang, S., Wang, Y., Hu, Y., Zhang, Q., and Yang, S. (2023).

Vector autoregressive evolution for dynamic multi-

objective optimisation.

Jiang, S. and Yang, S. (2014). A framework of scalable dy-

namic test problems for dynamic multi-objective opti-

mization. In 2014 IEEE Symposium on Computational

Intelligence in Dynamic and Uncertain Environments

(CIDUE), pages 32–39.

Jin, J. and Chen, Y. (2013). Var-based research on energy

consumption in china. In 2013 International Con-

ference on Computational and Information Sciences,

pages 1746–1749.

Jin, Y. and Branke, J. (2005). Evolutionary optimization in

uncertain environments-a survey. Trans. Evol. Comp,

9(3):303–317.

Jonathan D. Cryer, K.-S. C. (2008). Introduction, pages 1–

10. Springer New York, New York, NY.

Karkazan, K., Topcuoglu, H. R., and Sahmoud, S. (2023).

A new prediction-based algorithm for dynamic multi-

objective optimization problems. In International

Conference on the Applications of Evolutionary Com-

putation (Part of EvoStar), pages 194–209. Springer.

Li, H. and Zhang, Q. (2009). Multiobjective optimization

problems with complicated pareto sets, moea/d and

nsga-ii. IEEE Transactions on Evolutionary Compu-

tation, 13(2):284–302.

Li, L. D., Li, X., and Yu, X. (2008). Power generation load-

ing optimization using a multi-objective constraint-

handling method via pso algorithm. In 2008 6th IEEE

International Conference on Industrial Informatics,

pages 1632–1637.

S. Huband, P. Hingston, L. B. and While, L. (2006). A

review of multiobjective test problems and a scalable

test problem toolkit. IEEE Transactions on Evolution-

ary Computation, 10(5):477–506.

Sahmoud, S. and Topcuoglu, H. R. (2018). A type detec-

tion based dynamic multi-objective evolutionary algo-

rithm. In International Conference on the Applica-

tions of Evolutionary Computation, pages 879–893.

Springer.

Sahmoud, S. and Topcuoglu, H. R. (2019). Exploiting

characterization of dynamism for enhancing dynamic

multi-objective evolutionary algorithms. Applied Soft

Computing, 85:105783.

Sahmoud, S. and Topcuoglu, H. R. (2020). Memory-

assisted dynamic multi-objective evolutionary algo-

rithm for feature drift problem. In 2020 IEEE

Congress on Evolutionary Computation (CEC), pages

1–8. IEEE.

Tian, Y., Cheng, R., Zhang, X., and Jin, Y. (2017).

PlatEMO: A MATLAB platform for evolutionary

multi-objective optimization. IEEE Computational

Intelligence Magazine, 12(4):73–87.

Weizhen, H., Jiang, M., Gao, X., Tan, K. C., and Cheung,

Y.-m. (2019). Solving dynamic multi-objective opti-

mization problems using incremental support vector

machine. In 2019 IEEE Congress on Evolutionary

Computation (CEC), pages 2794–2799. IEEE.

Zhang, Q. and Li, H. (2007). Moea/d: A multiob-

jective evolutionary algorithm based on decomposi-

tion. IEEE Transactions on Evolutionary Computa-

tion, 11(6):712–731.

Zhu, X., Zhang, J., and Wu, Z. (2019). Many-objective

power ﬂow optimization problems based on an im-

proved moea/d with dynamical resource allocation

strategy. In 2019 Chinese Automation Congress

(CAC), pages 3680–3685.

A Vector Autoregression-Based Algorithm for Dynamic Many-Objective Optimization Problems

287