Identifying Kinetic Model Parameters and Implementing 3-DOF Control
for a Dual-Thruster USV: A Case Study Using the VRX Simulation
Environment
Jungeun Yoon
a
and Rockwon Kim
b
ETRI, South Korea
Keywords:
Unmanned Surface Vehicle, Dual Thrust, 3-DOF Model, Parameter Identification, Gazebo Simulation.
Abstract:
This study addresses the challenge of creating accurate kinetic model-based simulations for Unmanned Sur-
face Vehicles (USVs) that replicate the VRX simulation environment. Without precise parameter estimation,
discrepancies arise between kinetic model-based position predictions and the USV’s position in the VRX sim-
ulation. We propose a comprehensive method for parameter estimation to bridge this gap, coupled with a
Dynamical PD+LOS controller to further minimize operational differences. In the control using the kinetic
model with the best fit thrust parameters and drag coefficients, the turning radius may vary depending on these
parameters. To handle this, it not only calculates the thrust difference based on the heading error but also
dynamically adjusts the base thrust according to the speed and distance to the target. This approach prevents
over-correction and ensures better alignment between the kinetic model prediction path and VRX movement.
The proposed methodology was validated through circle and zigzag path tests. Results demonstrated high
fidelity, with position errors of 2% and time errors of 0.37% between the VRX and kinetic model.
1 INTRODUCTION
Unmanned surface vehicles (USVs) have recently
gained significant attention due to their diverse ap-
plications in marine engineering. To effectively op-
erate USV systems, it is crucial to accurately under-
stand each vessel’s kinetic and dynamic characteris-
tics. Specifically, quantitatively analyzing and con-
trolling USVs requires precise identification of their
dynamic equations and physical parameters. How-
ever, when adding autonomous navigation capabili-
ties to remotely controlled small boats designed for
rivers, lakes, and coastal areas, we often encounter
situations where the kinetic model parameters are un-
known. In such scenarios, parameter estimation and
the subsequent use of kinetic model-based path gen-
eration simulations become critical prerequisites for
USV control.
Traditionally, parameter estimation has heavily re-
lied on methods such as the Kalman filter (Yoon and
Rhee, 2003) and recursive least squaress (Nguyen,
2008). More recently, modern artificial intelligence
techniques have been employed to identify the dy-
a
https://orcid.org/0009-0006-3461-0693
b
https://orcid.org/0009-0007-7329-9401
namic models of ships (Wang et al., 2019; Woo et al.,
2018). Wirtensohn et al. conducted a quality evalua-
tion of parameter identification for small USVs and
performed sensitivity analysis using the Fisher in-
formation matrix. During the identification process,
all parameters were estimated simultaneously, and a
correlation matrix was used to analyze interdepen-
dencies among parameters. Eigenvalue and eigen-
vector analyses were also performed to avoid over-
parameterization (Wirtensohn et al., 2015). Xu et al.
proposed a method for identifying the dynamic model
of USVs that discretizes the Abkowitz model and
utilizes a Cuckoo Search (CS) algorithm-enhanced
Support Vector Machine (SVM) method. This ap-
proach achieves more accurate identification of the 3-
degree-of-freedom (3-DOF) dynamic model of USVs
and was validated through experimental tests and data
analysis conducted on the Qinghuai River (Xu et al.,
2020).
In this study, we propose a method for parameter
estimation and control using the OpenRobotics’ Vir-
tual RobotX (VRX) simulation environment instead
of a physical USV. VRX offers extensive capabilities
for research in USV control system design. VRX en-
ables the attachment and data collection from diverse
sensors such as GPS, IMU, LiDAR, and cameras on
368
Yoon, J. and Kim, R.
Identifying Kinetic Model Parameters and Implementing 3-DOF Control for a Dual-Thruster USV: A Case Study Using the VRX Simulation Environment.
DOI: 10.5220/0013010600003822
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 368-375
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

ships, and as a ROS environment simulator, it facili-
tates the easy addition or removal of USV sensors and
motors (Bayrak and Bayram, 2023; Li et al., 2023;
Wu and Wei, 2023; Chu et al., 2024). This allows for
replicating the thruster configuration of real USVs in
a virtual environment, enabling the modeling of vari-
ous USV motions. VRX simulation offers advantages
in terms of cost and time compared to real experi-
ments, allowing for efficient and safe testing under
various environment conditions (Huang et al., 2023;
Bingham et al., 2019; Paravisi et al., 2019).
The 3-DOF kinetic model can predict and gener-
ate paths quickly by setting the time interval as a vari-
able and using iterative loops. The generated paths
vary depending on kinetic model parameters, such as
drag coefficients, inertia, and thrust. Based on previ-
ous studies (Li et al., 2019), we estimated the USV
parameters in the VRX simulator. However, the ki-
netic model failed to generate the correct path to reach
the target in the VRX simulation. The reason is that
incorrect thrust parameters and drag coefficients were
identified, which resulted from incorrectly determin-
ing the point at which the USV reaches a steady state
in the VRX simulation. This issue will be discussed in
detail in Section 2.3. Therefore, this study refines the
parameter estimation methods from previous research
to improve accuracy in VRX simulations. When ap-
plying the correctly identified parameters to the ki-
netic model to generate paths, an issue arose where
the turning radius became larger. To resolve this, we
propose a control algorithm that enables the USV to
reach the target point more quickly with a smaller
turning radius. To address these issues, our study fo-
cuses on the following:
• First, unlike previous studies, we aim to simulta-
neously identify the propulsion force parameters
and surge-direction drag coefficients by applying
an iterative optimization method. To achieve this,
we use velocity variation data from multiple lin-
ear motion tests under different thrust conditions.
(While the propulsion parameters are unknown,
we can control certain conditions, such as revo-
lutions per second.)
• Second, We propose a new thrust control algo-
rithm for USVs. This algorithm addresses the
challenge of controlling USVs with large turning
radius, which can lead to inefficient navigation.
Our approach considers not only heading error
but also velocity and distance to the target. This
comprehensive control strategy enables more effi-
cient path planning and optimized navigation, es-
pecially in situations where the turning radius in-
creases. Furthermore, this thrust control approach
contributes to minimizing the gap between the tra-
jectory and timing predicted by the kinetic model
and the behavior of the USV controlled by the ki-
netic model within the VRX simulator.
The structure of this paper is as follows: Section 2.1
provides a brief introduction to the VRX simulation
environment and the specifications of the USV. Sec-
tion 2.2 describes the dynamics of the USV. Sec-
tion 2.3 proposes a parameter identification procedure
for the dual thruster model using the Nelder-Mead al-
gorithm. Section 2.4 identifies the drag matrix pa-
rameters through VRX simulation driving tests and
performs corrections to enhance the accuracy of the
kinetic model. Section 2.5 proposes a USV control
system applying the improved PD controller and vali-
dates it through circle and zigzag simulations. Finally,
Section 3 summarizes the conclusions.
2 METHODOLOGY
2.1 Simulation Environment
In this study, we identify the kinetic model parameters
using the VRX ROS2 package from Open Robotics
and the Gazebo simulator environment. The USV
model supported by VRX is the WAM-V (Bingham
et al., 2019), with its specifications listed in Table 1.
Experiments were conducted in the Sydney Regatta
world, one of the various environments provided by
VRX. To eliminate the effects of external forces, both
wind and wave parameters were set to zero. Addition-
ally, to focus on the validity of the parameter extrac-
tion method, GPS and IMU sensor errors were also
set to zero.
Figure 1: Parameter estimation to minimize and control dis-
crepancies between VRX and Kinetic Model trajectories.
2.2 3-DOF Kinetic Model for Dual
Thruster USV
The 3-DOF mathematical model of USV is used to
mathematically represent the position and physical
motion of the vehicle, reflecting the characteristics of
Identifying Kinetic Model Parameters and Implementing 3-DOF Control for a Dual-Thruster USV: A Case Study Using the VRX
Simulation Environment
369

Table 1: Physical characteristics of the WAM-V USV.
Parameter Value
Length overall (LO) 4.00 m
Waterline length (L) 3.21 m
Draft (D) 0.089 m
Beam overall (W) 2.44 m
Distance between two propellers (B) 2.01 m
Mass (m) 180 kg
USV velocity (max) 1.5 m/s
the USV and optimizing its driving control. As ex-
plained in (Fossen, 2011), the 3-DOF mathematical
model of USV can be described as follows:
˙
η =


˙x
˙y
˙
ψ


= R(ψ)v =


cosψ −sinψ 0
sinψ cosψ 0
0 0 1




u
v
r


(1)
M
˙
v +C(v)v + D(v)v = τ (2)
η =

x y ψ

, where η
t
= η
t−1
+
˙
η∆t, is a vector
that defines the position and orientation of the USV.
Here, x and y are the position coordinates in the plane,
ψ is the heading angle, η
t
and η
t−1
represent the cur-
rent and previous states respectively,
˙
η
t
is the rate of
change, and ∆t is the time interval between states.
v =

u v r

is a vector consisting of the linear veloc-
ities (u,v) in the surge and sway directions and the
rotational velocity (r). R(ψ) is a rotation matrix that
transforms from the fixed body frame to the earth-
fixed frame.
In Equation (2), M, C(v), and D(v) represent the
mass matrix, the Coriolis and centripetal matrix, and
the drag matrix, respectively. τ is a vector represent-
ing the force generated by the thruster, where T
1
is
the force of the port thruster and T
2
is the force of the
starboard thruster.
The matrix M accounts for both the rigid-body
mass and the hydrodynamic added mass effects in
surge, sway, and yaw motions. For notational con-
venience, m −X
˙u
, m −Y
˙v
, and I
z
−N
˙r
are denoted as
m
11
, m
22
, and m
33
respectively, where m
11
and m
22
represent the total mass (including added mass) in the
surge and sway directions respectively, and m
33
rep-
resents the total moment of inertia (including added
moment) about the z-axis.
The following describes the vectors and matrices
of the kinetic model, which can be simplified under
the following conditions (Li et al., 2019):
• Low USV velocity: In this study, the maximum
velocity is 1.5 m/s.
• Negligible Effect of Off-Diagonal Terms on USV
Dynamics: The off-diagonal terms of M and D
can be neglected.
• Assuming the USV sails in a calm environment.
M =


m
11
0 0
0 m
22
0
0 0 m
33


(3)
C(v) =


0 0 −m
22
v
0 0 m
11
u
m
22
v −m
11
u 0


(4)
D(v) = D = −


X
u
0 0
0 Y
v
0
0 0 N
r


(5)
τ =

T
1
+ T
2
0 (T
1
−T
2
) ·d
P

T
(6)
Therefore, the 3-DOF model of a USV with dual
thrusters without a rudder can be expressed as Equa-
tion (7), in which d
p
represents half the distance be-
tween the two propellers. This model enables us to
iteratively generate a movement path by calculating
the necessary corrective thrust at each subsequent po-
sition, accounting for positional errors and continu-
ously adjusting the control inputs. In actual VRX
movement, GPS and IMU yaw data are utilized for
navigation. To reduce the difference between these
two, we must estimate the parameters of the thrust
equation and the drag coefficients X
u
, Y
v
, and N
u
with
a certain degree of precision.
m
11
˙u −m
22
˙vr + X
u
u = T
1
+ T
2
m
22
˙v + m
11
ur +Y
v
v = 0
m
33
˙r −(m
11
−m
22
)uv + N
r
r = (T
1
−T
2
) ·d
P
(7)
2.3 Identification of Thrust Coefficients
The thrust of a dual-thruster USV is determined by
both the propeller and the hull velocity is described
by Equation (8)(Mu et al., 2018). In this equation,
n represents the propeller’s rotational speed in revo-
lutions per second (RPS), and V =
√
u
2
+ v
2
denotes
the total velocity of the USV. c and d are the key pa-
rameters of the thrust model. The coefficient c reflects
the interaction between the hull velocity and propeller
rotation, while d represents the thrust generation char-
acteristics of the propeller itself.
T
i
= cV n
i
+ d|n
i
|n
i
(8)
To achieve accurate velocity and position estima-
tion, it is essential to determine the coefficients c
and d that closely approximate the actual thrust. To
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
370

achieve this, we can approximate the coefficients c
and d by utilizing the straight-line motion equation
from the kinetic model, which allows us to reduce the
number of variables. In a straight-line motion, the
Coriolis force is canceled as v = r = 0, and the ve-
locity only has a surge component. Consequently, the
model can be simplified to a 1-DOF model, only in-
cluding surge velocity, as follows:
Li et al. collected velocity, acceleration, and RPS
data for a stationary USV to estimate the coefficients
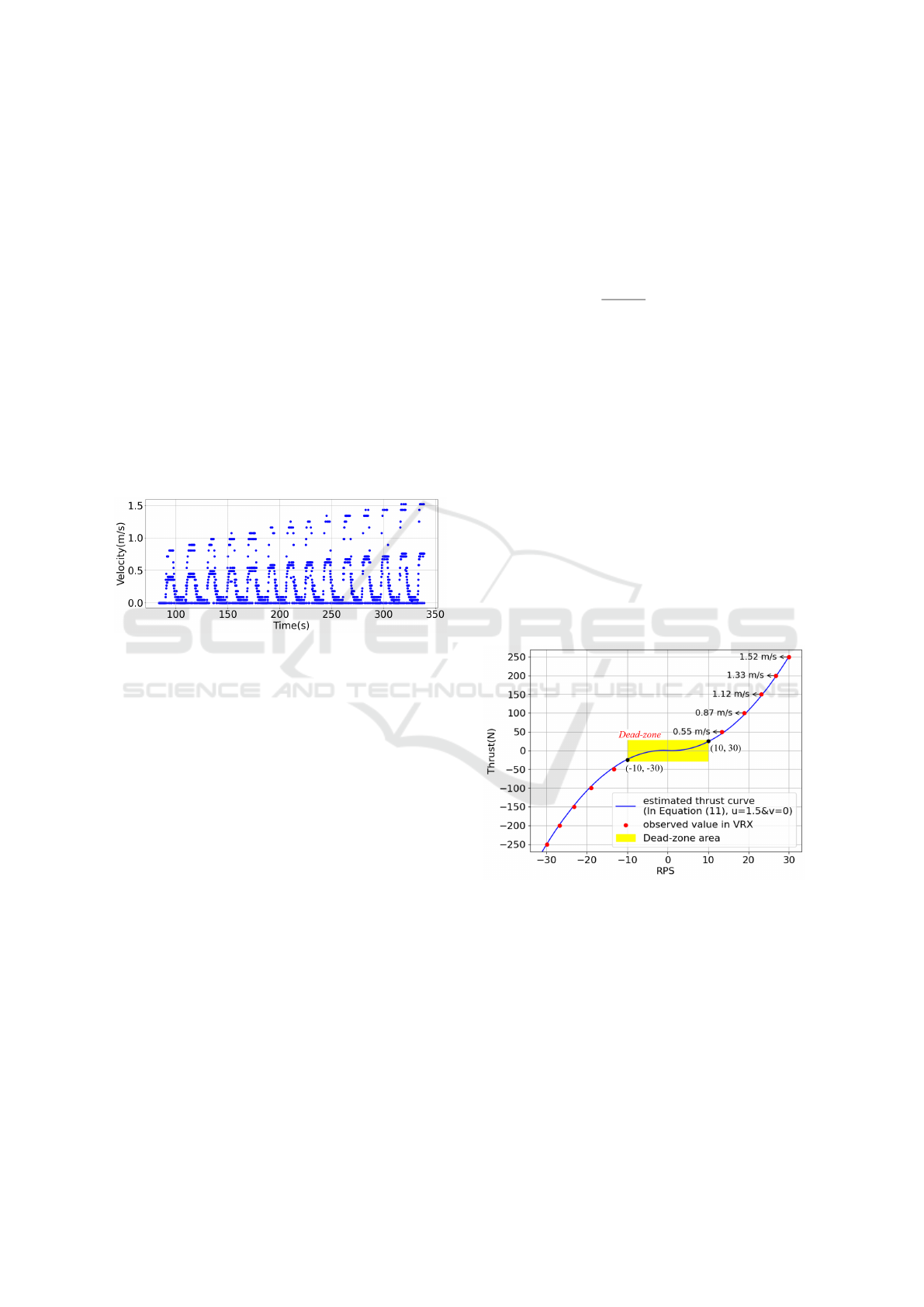
c and d (Li et al., 2019). However, as shown in Fig. 2,
the data collected from the VRX sensor exhibited sig-
nificant instability and fluctuations. This instability
made it ambiguous to determine a reliable point for
calculating initial acceleration when estimating the c
and d values for the VRX thrust equation using Li’s
method. Consequently, to minimize potential errors,
we propose estimating the c and d values without con-
sidering the acceleration value.
Figure 2: Visualization of velocity data collected using
VRX.
When the USV maintains a constant surge ve-
locity, the surge acceleration becomes zero. Conse-
quently, the thrust model can be simplified, as shown
in Equation (9). Using the Nelder-Mead algorithm,
we estimate the values of c, d, and X
u
in this sim-
plified model. This is especially important because
the velocity data exhibits high nonlinearity, irregu-
lar variability, and clear discontinuities, suggesting a
complex, non-differentiable objective function. The
Nelder-Mead algorithm is well-suited to handle such
nonlinear optimization problems effectively without
requiring derivatives, thanks to its robustness to noise
and ability to manage discontinuities. Additionally,
the simplicity and computational efficiency of the al-
gorithm make it advantageous in this situation, where
a large number of data points must be processed.
X
u
u = 2(cun + d|n|n),n = n
1
= n
2
(9)
Data for estimating the values of c, d, and X
u
are
collected through straight-line motion experiments.
The procedure is as follows: First, the USV is brought
to a complete stop to stabilize its state before each
run. Then, the thrust value is adjusted. Once the USV
reaches the point where the speed oscillates with the
same amplitude between increasing and decreasing,
velocity and propeller RPS data are collected.
Based on the collected data, we can estimate the
values as c = −0.397956, d = 0.299914, and X
u
=
145.75. Substituting these values into Equation (9),
we can calculate the thrust value of the USV as shown
in Equation (10).
T
i
= −0.397956
p
u
2
+ v
2
·n
i
+0.299914|n
i
|·n
i
(10)
As shown in Fig 3, repeated experiments on the
relationship between thrust and velocity in the VRX
simulator revealed that the USV reached a maximum
speed of 1.5 m/s at the highest thrust value of 250. It
was observed that the USV would not move when the
thrust was below 30 due to resistance. Considering
these characteristics, the effective thrust range for the
simulation was set between 30 and 250.
The blue curve in the Fig 3 is the estimated thrust
curve fitted based on Equation (10) with a maximum
surge velocity of 1.5m/s and sway velocity of 0m/s.
The red dots represent the RPS values observed in
VRX by inputting thrust values to the port and star-
board thrusters, with the USV velocity at that time
indicated by arrows. The fact that the two sets of val-
ues coincide suggests that the thrust parameters c and
d have been correctly estimated.
Figure 3: The relationship between RPS and thrust.
2.4 Identification of Drag Coefficients
To identify N
r
and Y
v
, experiments were conducted
with zero-radius rotation (r ≈ 0) and non-zero radius
turning (r > 0) respectively, by configuring different
RPS values for the port and starboard thrusters of the
USV. Velocity vector v data was collected from these
experiments and then used to estimate the parameters
using the Nelder-Mead algorithm.
To achieve zero-radius rotation, the USV’s port
and starboard thruster revolutions per second (RPS)
Identifying Kinetic Model Parameters and Implementing 3-DOF Control for a Dual-Thruster USV: A Case Study Using the VRX
Simulation Environment
371

were set to -30 and 30 respectively for 30 seconds.
This configuration caused the USV to rotate around
its center of gravity while minimizing surge and sway
velocities. Under these conditions, where ˙r ≈u ≈v ≈
0, the rotation drag coefficient N
r
could be estimated
using Equation (11).
N
r
r = (T
1
−T
2
) ·d
P
(11)
Similarly, for the sway direction drag coefficient
Y
v
, by running the thrusters with an RPS of 0 and 30
for 60 seconds, the USV travels with a larger non-zero
radius turning maneuver. Y
v
can be estimated based
on Equation (12).
m
22
˙v + m
11
ur +Y
v
v = 0 (12)
The mass matrix M can be calculated as fol-
lows according to the USV specifications in Ta-
ble 1 (Muske et al., 2008).
m
11
≈ m + 0.05m = 189 (13)
m
22
≈ m + 0.5(ρπD
2
L) = 229 (14)
m
33
≈
m(L
2
+W
2
) +
1
2
(0.1mB
2
+ ρπD
2
L
3
)
12
= 333
(15)
Therefore, the drag coefficients were estimated as
X
u
= 145, Y
v
= 56, and N
r
= 1023. When these drag
parameter values were applied to the kinetic model, a
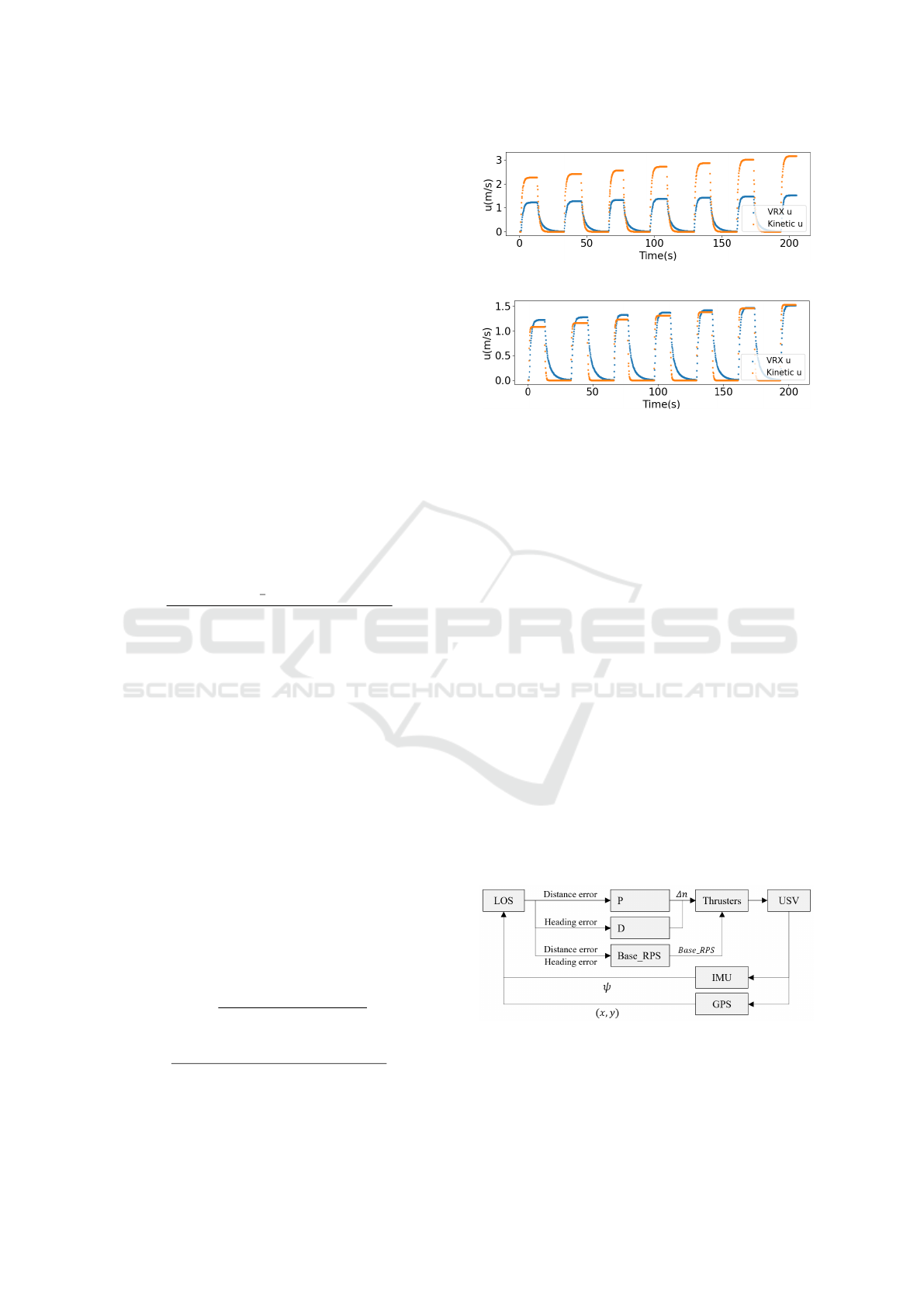
problem arose where the surge velocity calculated by
the kinetic model was faster than the VRX simulation,
as shown in Fig. 4a. This resulted in a mismatch be-
tween the VRX and kinetic model. This discrepancy
suggests that there is an error in the kinetic model pa-
rameters.
The method presented in Section 2.3 requires
reaching a state of constant acceleration, but the dif-
ficulty in clearly distinguishing the point of constant
acceleration led to an incorrect identification. To ad-
dress this, the acceleration calculated from the exper-
imental data set used to estimate c and d is compared
to the acceleration calculated from Equation (16), and
the error is used to re-adjust the X
u
value for correc-
tion. Similarly, N
r
can also be corrected using the
same approach.
˙u =
(T
1
+ T
2
) + m
22
vr −X
u
u
m
11
(16)
˙r =
(T
1
−T
2
)d
p
+ (m
11
−m
22
)uv −N
r
r
m
33
(17)
Since the drag parameters do not have a significant
impact at low velocities, data corresponding to more
(a)
(b)
Figure 4: VRX-collected and kinetic model-calculated ve-
locity: (a) Before correction and (b) After correction.
than 70% of the maximum velocity was collected and
used for the correction. As a result, the values of X
u
and N
r
were re-identified as X
u
= 340 and N
r
= 1012,
and as shown in Fig 4b, the velocity was improved
compared to Fig 4a when applied to the kinetic model.
2.5 USV Motion Control System
In USV motion control systems, the design of path-
following controllers plays a crucial role in enabling
real-world navigation. Proportional-Derivative (PD)
control is widely used in autonomous navigation due
to its simple structure and high stability, while the
Line of Sight(LOS) algorithm offers the advantages
of low computational complexity and ease of imple-
mentation (Mu et al., 2017; Sarda et al., 2015). In this
study, we utilized a USV control system that com-
bines PD control and the LOS algorithm. As shown
in the Fig 5, the LOS algorithm calculates the error
between the current position and the target position,
and PD control determines the thrust of the port and
starboard thrusters based on the error.
Figure 5: The USV motion control system.
The LOS algorithm guides the USV to navigate
along the line connecting the target points on the
tracking path. As the USV approaches the desired
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
372

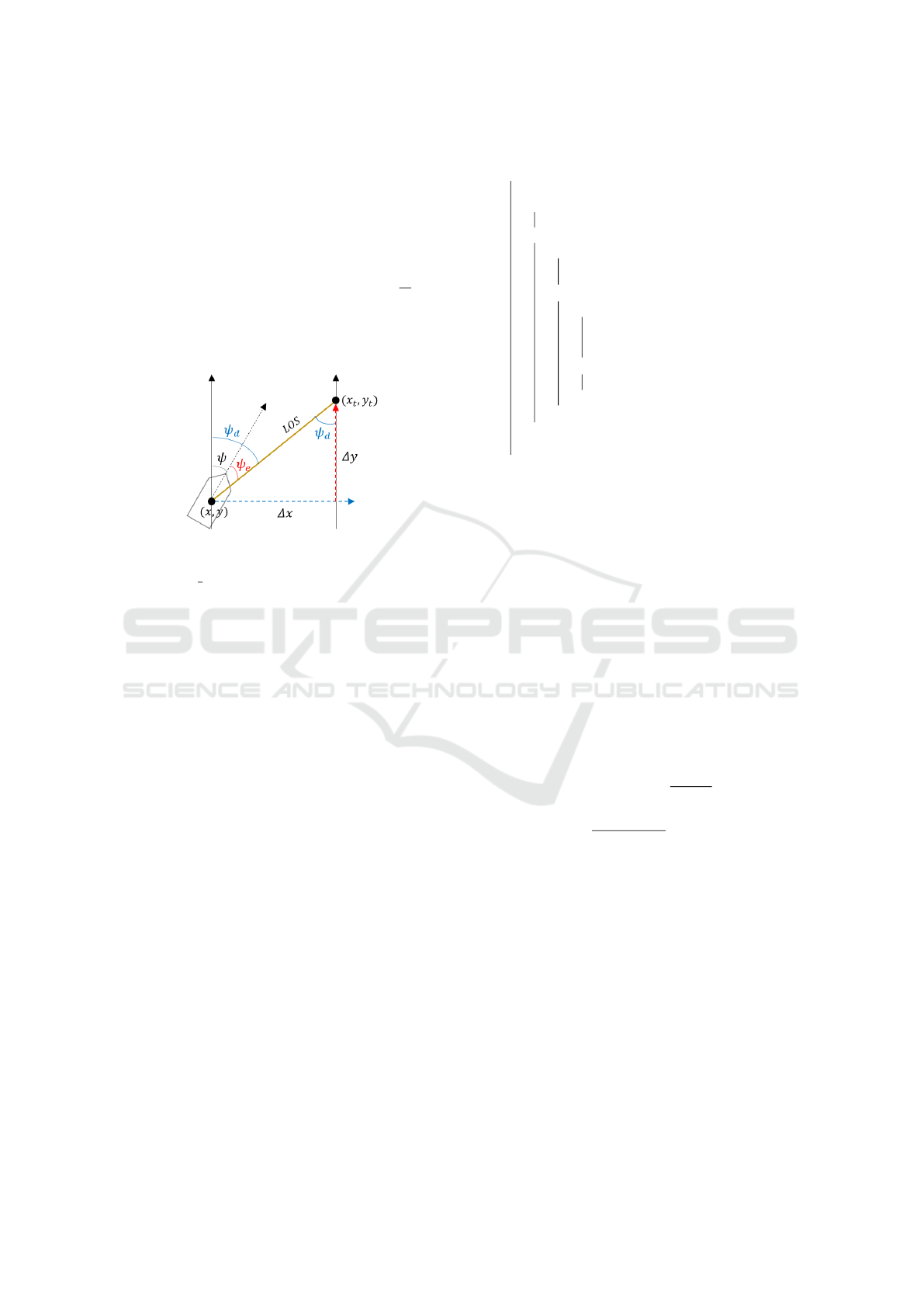
path, the distance gradually decreases, allowing it to
follow the desired path (Lekkas and Fossen, 2012).
In Fig 6, (x,y) represents the coordinates of the cur-
rent position, and ψ represents the heading value of
the USV at the current position. (x
t
,y
t
) represents the
coordinates of the target position, and ψ
d
represents
the target heading value for reaching the target point.
In this case, ψ
d
can be calculated as arctan

∆y
∆x

, as
shown in Fig 6. The heading error between the cur-
rent position and the target position can be obtained
as ψ
e
= ψ −ψ
d
.
Figure 6: The principle of the LOS guidance algorithm.
The Base RPS in the Fig 5 represents the base
value for the RPS. It is dynamically adjusted based
on the distance error, which is the distance between
the current and target positions, and the value of e
t
according to the algorithm 1. When the distance is
less than dis
min
and the e
t
is small, indicating prox-
imity to the target position, the base value is set to
the minimum value. When the distance is less than
dis
min
but the e
t
is large, a constant velocity must be
maintained to enable rotation. therefore, the midpoint
between dis
min
and dis
max
becomes the base value. If
the distance falls between dis
min
and dis
max
, linear in-
terpolation is used to determine the base value based
on the distance ratio. In other cases, when the dis-
tance is large, the maximum velocity is set as the base
value.
The output of the PD controller is ∆n, which is
the difference in rotation velocity between the port
and starboard thrusters, thrust values of the port and
starboard thrusters are set combine basen and ∆n.The
derivative part is sensitive to noise, and a first-order
low-pass filter is added, as expressed in Equation (18).
Here, T
f
is the time constant of the filter, and d f
t−1
is
the differential output value of the previous moment.
T is the period of the PD controller.
Conventional PD controllers utilize fixed constant
values for their gain parameters, K
p
and K
d
. The
gains K
p
and K
d
of the PD controller were experimen-
tally tuned through kinetic model, with values gradu-
ally adjusted from small to large until the USV could
accurately follow the target points. This approach has
Procedure GetDynamicBaseN(
ψ
e
t
,dis
t
,dis
min
,dis
max
,base
min
,base
max
):
n ← 0;
if dis
t
< dis
min
∧ψ
e
t
< 10
◦
then
n ← base
min
;
else
if dis
t
< dis
min
∧ψ
e
t
≥ 10
◦
then
n ←
base
min
+(base
max
−base
min
)×0.5;
else
if dis
t
≥ dis
min
∧dis
t
≤ dis
max
then
n ←
base
min
+ (base
max
−base
min
)×
(dis
t
−dis
min
)/(dis
max
−dis
min
);
else
n ← base
max
;
end
end
end
return n;
Algorithm 1: Dynamic Base RPS Calculation.
the drawback of an increased turning radius, as shown
by the orange dotted line in Fig 7. To reach the tar-
get point more quickly with a smaller turning radius,
we dynamically adjusted the gain value based on the
current position using Equation (18). Consequently,
it is able to reduce the turning radius, as shown by the
blue line.
K
p
is a proportional control variable that reflects
the distance between two points, providing a larger
control signal as the distance increases. K
d
is a differ-
ential control variable that reflects the ψ
e
value, de-
signed to respond more sensitively as the error rate in-
creases. To prevent the values of each control variable
from changing abruptly, the log function is applied.
∆n = K
p
·log(dis
t
) ·ψ
e
t
+

T
f
T
f
+ T

·d f
t−1
+

K
d
·log(ψ
e
)
T
f
+ T

·(ψ
e
t
−ψ
e
t−1
)
(18)
The USV motion control system calculates the
thrust values of the port and starboard thrusters by
considering both distance error and heading error, en-
abling precise navigation.
The circle and zigzag driving tests were conducted
to estimate kinetic model parameters and validate
control algorithms. The kinetic model and VRX sim-
ulation were set up under the same conditions. Fig 8
shows the experimental results for tests. While each
path does not perfectly match, it can be confirmed that
the vehicle follows a similar path. The time error for
the circle test was about 2%, and there was no error in
the zigzag test. The distance error showed low errors
of about 0.37% for both circle and zigzag tests.
Identifying Kinetic Model Parameters and Implementing 3-DOF Control for a Dual-Thruster USV: A Case Study Using the VRX
Simulation Environment
373

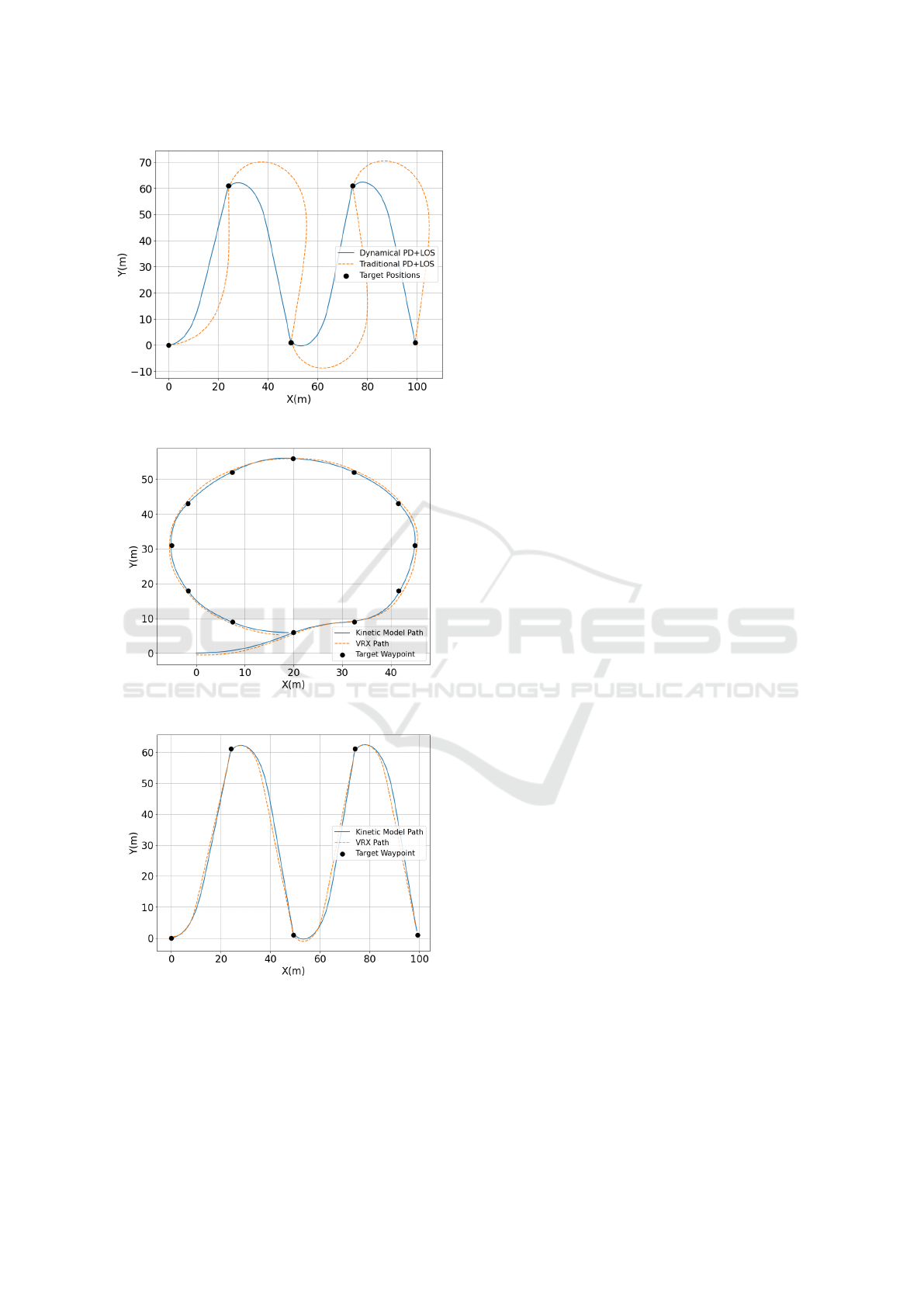
Figure 7: The simulation results of the kinetic-model.
(a)
(b)
Figure 8: The simulation results of the kinetic-model and
VRX path: (a) circle path and (b) zigzag path.
3 CONCLUSION
This paper addressed the development of a control
method using a 3-DOF kinetic model in the VRX sim-
ulation environment, as well as the accurate identifi-
cation of the necessary parameters for this model.
We proposed a method for determining propul-
sion force parameters and drag coefficients using the
Nelder-Mead algorithm.
This method simultaneously estimates the values
of propulsion force parameters and surge-direction
drag coefficients using a simplified surge motion
equation, based on linear motion velocity data ob-
tained under various thrust speeds.
Additionally, we developed a dynamical PD+LOS
control algorithm that minimizes position and time
discrepancies between movement in VRX and the ki-
netic model prediction path. This algorithm does not
provide a fixed differential thrust for heading errors;
instead, it offers varying differential thrust even for
the same heading error by considering the current ve-
locity and distance to the target point. This method
enables the generation of optimized paths, effectively
adapting to changes in velocity and turning radius
in response to thrust, which may vary based on the
identified parameters. The validity of the proposed
methodology was verified through circle and zigzag
path tests. Results demonstrated high fidelity, with
position errors of 2% and time errors of 0.37% be-
tween the movement in the VRX simulation and the
kinetic model-generated path.
This study contributes to enhancing the learning
value of the open-source VRX simulator for under-
standing 3-DOF control of small USVs’ kinetic mod-
els. While VRX is a well-designed simulator that of-
fers a cost-effective alternative to real-world experi-
ments, its utility for educational purposes was lim-
ited by discrepancies between simulated and theoret-
ical behaviors. Our work addresses these inconsis-
tencies, potentially improving VRX’s effectiveness as
a learning tool for small USV dynamics and control.
By refining the parameter estimation and control algo-
rithms, we aim to bridge the gap between simulation
and theoretical models, thus supporting more accu-
rate and reliable learning experiences in USV control
systems.
Future research could focus on testing the model’s
performance under various maritime environmental
conditions and extending the methodology to more
complex path and mission scenarios. Additionally,
validation experiments in real marine environments
could further strengthen the practicality of the pro-
posed method.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
374

ACKNOWLEDGEMENTS
This work was supported by SME ICT convergence
technologies project in Andong-si [24AD1100]. This
work was supported by Electronics and Telecommu-
nications Research Institute(ETRI) grant funded by
the Korean government. [24ZD1110, Regional Indus-
try ICT Convergence Technology Advancement and
Support Project in Daegu-Gyeongbuk].
REFERENCES
Bayrak, M. and Bayram, H. (2023). Colreg-compliant sim-
ulation environment for verifying usv motion planning
algorithms. In OCEANS 2023-Limerick, pages 1–10.
IEEE.
Bingham, B., Aguero, C., McCarrin, M., Klamo, J., Malia,
J., Allen, K., Lum, T., Rawson, M., and Waqar,
R. (2019). Toward maritime robotic simulation in
gazebo. In Proceedings of MTS/IEEE OCEANS Con-
ference, Seattle, WA.
Chu, Y., Wu, Z., Zhu, X., Yue, Y., Lim, E. G., and Pao-
letti, P. (2024). Self-supervised dock pose estimator
for unmanned surface vehicles autonomous docking.
In 2024 10th International Conference on Mechatron-
ics and Robotics Engineering (ICMRE), pages 189–
194. IEEE.
Fossen, T. I. (2011). Handbook of marine craft hydrody-
namics and motion control. John Wiley & Sons.
Huang, F., Chen, X., Xu, Y., Yang, X., and Chen, Z. (2023).
Immersive virtual simulation system design for the
guidance, navigation and control of unmanned surface
vehicles. Ocean Engineering, 281:114884.
Lekkas, A. M. and Fossen, T. I. (2012). A time-varying
lookahead distance guidance law for path following.
IFAC Proceedings Volumes, 45(27):398–403. 9th
IFAC Conference on Manoeuvring and Control of Ma-
rine Craft.
Li, C., Jiang, J., Duan, F., Liu, W., Wang, X., Bu, L., Sun,
Z., and Yang, G. (2019). Modeling and experimental
testing of an unmanned surface vehicle with rudder-
less double thrusters. Sensors, 19(9).
Li, J., Chavez-Galaviz, J., Azizzadenesheli, K., and Mah-
moudian, N. (2023). Dynamic obstacle avoidance for
usvs using cross-domain deep reinforcement learning
and neural network model predictive controller. Sen-
sors, 23(7):3572.
Mu, D., Wang, G., Fan, Y., Sun, X., and Qiu, B. (2017).
Adaptive los path following for a podded propulsion
unmanned surface vehicle with uncertainty of model
and actuator saturation. Applied Sciences, 7(12).
Mu, D., Wang, G., Fan, Y., Sun, X., and Qiu, B. (2018).
Modeling and identification for vector propulsion of
an unmanned surface vehicle: Three degrees of free-
dom model and response model. Sensors, 18(6).
Muske, K. R., Ashrafiuon, H., Haas, G., McCloskey, R., and
Flynn, T. (2008). Identification of a control oriented
nonlinear dynamic usv model. In 2008 American Con-
trol Conference, pages 562–567.
Nguyen, H. D. (2008). Recursive identification of ship
manoeuvring dynamics and hydrodynamics. In Mer-
cer, G. N. and Roberts, A. J., editors, Proceedings of
the 8th Biennial Engineering Mathematics and Ap-
plications Conference, EMAC-2007, volume 49 of
ANZIAM J., pages C717–C732.
Paravisi, M., H. Santos, D., Jorge, V., Heck, G., Gonc¸alves,
L. M., and Amory, A. (2019). Unmanned surface
vehicle simulator with realistic environmental distur-
bances. Sensors, 19(5).
Sarda, E. I., Bertaska, I. R., Qu, A., and von Ellenrieder,
K. D. (2015). Development of a usv station-keeping
controller. In OCEANS 2015-Genova, pages 1–10.
IEEE.
Wang, Z., Zou, Z., and Guedes Soares, C. (2019).
Identification of ship manoeuvring motion based on
nu-support vector machine. Ocean Engineering,
183:270–281.
Wirtensohn, S., Wenzl, H., Tietz, T., and Reuter, J. (2015).
Parameter identification and validation analysis for a
small usv. In 2015 20th International Conference
on Methods and Models in Automation and Robotics
(MMAR), pages 701–706.
Woo, J., Park, J., Yu, C., and Kim, N. (2018). Dynamic
model identification of unmanned surface vehicles us-
ing deep learning network. Applied Ocean Research,
78:123–133.
Wu, X. and Wei, C. (2023). Drl-based motion control for
unmanned surface vehicles with environmental distur-
bances. In 2023 IEEE International Conference on
Unmanned Systems (ICUS), pages 1696–1700. IEEE.
Xu, P.-F., Cheng, C., Cheng, H.-X., Shen, Y.-L., and Ding,
Y.-X. (2020). Identification-based 3 dof model of un-
manned surface vehicle using support vector machines
enhanced by cuckoo search algorithm. Ocean Engi-
neering, 197:106898.
Yoon, H. K. and Rhee, K. P. (2003). Identification of hydro-
dynamic coefficients in ship maneuvering equations
of motion by estimation-before-modeling technique.
Ocean Engineering, 30(18):2379–2404.
Identifying Kinetic Model Parameters and Implementing 3-DOF Control for a Dual-Thruster USV: A Case Study Using the VRX
Simulation Environment
375