
A Decoupled Graph Convolutional Network with Dual Adaptive
Propagation Mechanism for Homophily and Heterophily
Haoran Zhang
1
, Yan Yang
1,2,*
and YingLi Zhong
1,*
1
School of Computer Science and Technology, Heilongjiang University, Harbin, China
2
Key Laboratory of Database and Parallel Computing of Heilongjiang Province, Harbin, China
*
Keywords: Graph Neural Networks, Graph Representation Learning, Heterophily, Over-Smoothing.
Abstract: Despite the rapid development of graph neural networks (GNNs) for graph representation learning, there are
still problems, such as the most classical model GCN and its variants, which is based on the assumption of
homophily is proposed, making it difficult to perform well in heterophilic graphs. To solve this problem, we
propose a decoupled graph convolutional network DAP-GCN with dual adaptive propagation mechanism. It
learns node representations from two perspectives: attribute and topology, respectively. In heterophilic
graphs, connected nodes are more likely to belong to different classes. To avoid aggregating to irrelevant
information, we introduce a class similarity matrix for more accurate aggregation based on the similarity
between nodes. In addition, we incorporate the class similarity matrix into the propagation and perform the
aggregation in an adaptive manner to further alleviate the over-smoothing issue. Experiments show that DAP-
GCN has significant performance improvement in both homophilic and heterophilic datasets, especially in
heterophilic datasets.
1 INTRODUCTION
In recent years, many researchers have worked on
developing new GNNs methods. However, these
methods largely ignore the limitations of the
implicitly existing assumption of homophily,
including the widely used Graph Convolutional
Network (T. N. Kipf, 2016) and its variants, which
assumes that most of the connections occur between
nodes of the same class or with similar features. In
fact, heterophily is also prevalent, connected nodes
are more likely to belong to different classes.
Therefore, simple aggregation introduces noise
information. These GNNs are not applicable to
heterophilic networks. In addition, multiple
aggregation of GCNs creates over-smoothing issues
(Chen, 2020): after multiple iterations of GCNs, the
nodes representation tends to be consistent.
Many scholars have proposed different methods
to resolve the above issues. For example, H2GCN
(Zhu, 2020) uses higher-order neighborhoods and
intermediate representations as outputs to solve the
above problem. Geom – GCN(Pei, 2020) proposes a
new geometric aggregation method, which
aggregates nodes that have similarity to the target
node. However, the above methods do not distinguish
the homophily among nodes more accurately, and the
aggregation may absorb useless information or noise.
Therefore, we aim to compute similarity between
nodes and thus modeling the homophily more
accurately between nodes. In addition, there are a
number of methods that have been used to solve the
problem of over-smoothing. For example, DropEdge
(Rong, 2019) increases the diversity of input data by
reducing a certain percentage of edge weights to zero.
However, due to its high sensitivity to the dropout
rate, it may lead to loss of information in the graph.
APPNP (Gasteiger, 2019) uses personalized
PageRank to iteratively update by combining its own
features with neighbors.
To solve the above issues, we present a
decoupling graph neural network DAP-GCN with a
dual adaptive propagation mechanism. DAP-GCN
learns the class similarity between nodes from
attribute and topological information. Each element
in the class similarity matrix describes the degree to
which the classes are the identical between the nodes.
Specifically, DAP-GCN can extract class-aware
information from the nodes and adaptively change the
propagation of the nodes. On the one hand, compared
to previous models, our method has a guiding role in
the propagation process and nodes are more likely to
130
Zhang, H., Yang, Y. and Zhong, Y.
A Decoupled Graph Convolutional Network with Dual Adaptive Propagation Mechanism for Homophily and Heterophily.
DOI: 10.5220/0013010800004536
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Data Mining, E-Learning, and Information Systems (DMEIS 2024), pages 130-136
ISBN: 978-989-758-715-3
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

aggregate useful information. On the other hand, it
considers similarity not only from attribute
information but also from topological information,
which is a more comprehensive consideration.
Finally, we aggregate information from different
layers by setting adaptive weights, which effectively
mitigates over-smoothing.
Our major contributions are as follows:
• We propose a dual adaptive decoupling
model (DAP-GCN), which mainly deals with
the heterophilic problem of networks while
effectively mitigating over-smoothing.
• DAP-GCN learns the class similarity
between nodes through attributes and
topological information, which models the
homophily among nodes. In addition, we
design adaptive propagation and adaptive
layer aggregation.
Experiments show that DAP-GCN outperforms
other methods on almost all datasets. It is even more
significant in heterophilic datasets.
2 PRELIMINARIES
2.1 Problem Setup
Given an unoriented, non-weighted graph 𝐺
=(𝑉, 𝐸, 𝑿), where 𝑉 ={𝑣
,𝑣
,𝑣
,…,𝑣
}is the set of
nodes, 𝐸 represents the set of edges between node 𝑖
and node 𝑗, and 𝑿∈𝑅
×
is the node features matrix.
The 𝑖-th row of 𝑿 denotes the attributes of node 𝑖.
The topology of 𝐺 is represented by the adjacency
matrix 𝑨 = [𝑎
]∈𝑅
×
, which is 𝑎
=1 when the
node 𝑣
is connected to 𝑣
and 𝑎
=0 otherwise.
2.2 Homophily & Heterophily &
Homophily Ratio
Homophily: given a graph, interconnected nodes
usually belong to the same class or have similar
features, e.g. papers are more likely to cite papers
from the same field.
Heterophily: interconnected nodes in a network may
be of different classes or have different features, e.g.
Most people prefer to connect with the other sex in a
dating network. Importantly, heterophily emphasizes
the diversity of features.
Homophily Ratio(Tang, 2009): given a graph 𝐺
= ( 𝑉, 𝐸, 𝑿 ), the homophily ratio ℎ =
|
,
:
,
∈∧
|
||
, ℎ ∈ [0,1], ℎ denotes the overall
level of homophily in the graph, and |𝐸| is the
number of edges connected between nodes of the
same class. When ℎ is closer to 1, homophily is
stronger; graphs with ℎ approaching 0 have stronger
heterophily.
2.3 Decoupling Methods
Some researchers have demonstrated that the
coupling of transformations and propagation during
message passing affects network performance. Over-
smoothing can be effectively mitigated by separating
the two operations, transformation and propagation.
One of the most classical neural network models,
GCN, follows the pattern of neighbor aggregation (or
message passing). The general 𝑙-th layer of graph
convolution is expressed as:
𝒂
= PROPAGATION
𝒙
, 𝒙
⌊
𝑗∈𝒩
𝒙
= TRANSFORMATION
𝒂
. (1)
The forward propagation process of a typical
representative GCN can be expressed as:
𝑿
(
)
= 𝜎𝑨
𝑿
(
)
𝑾
(
)
(
2
)
In traditional message passing mechanisms,
transformation and propagation are intertwined. That
is, each transformation bridges the propagation
operation. As the sensory domain increases, the node
representations are propagated repeatedly over many
iterations. The node representations converge, i.e., the
over-smoothing.
𝒁 =MLP
(
𝑿
)
∈ℝ
×
𝑯
= 𝑨
𝒁, 𝑙 =1,2,⋯, 𝑘 ∈ℝ
×
(
3
)
The idea of decoupling is to separate
transformation and propagation. 𝑿 is first
downscaled by MLP to obtain 𝒁, and 𝒁 is propagated
many times to obtain 𝑯
.
3 THE FRAMEWORK
We first give an overview and then describe the
design approach and the details of specific modules
3.1 Overview
We bring the class similarity matrix into the message
passing process of GCN and develop a graph
convolutional network with homogeneity and
heterogeneity. The framework consists of three parts,
A Decoupled Graph Convolutional Network with Dual Adaptive Propagation Mechanism for Homophily and Heterophily
131
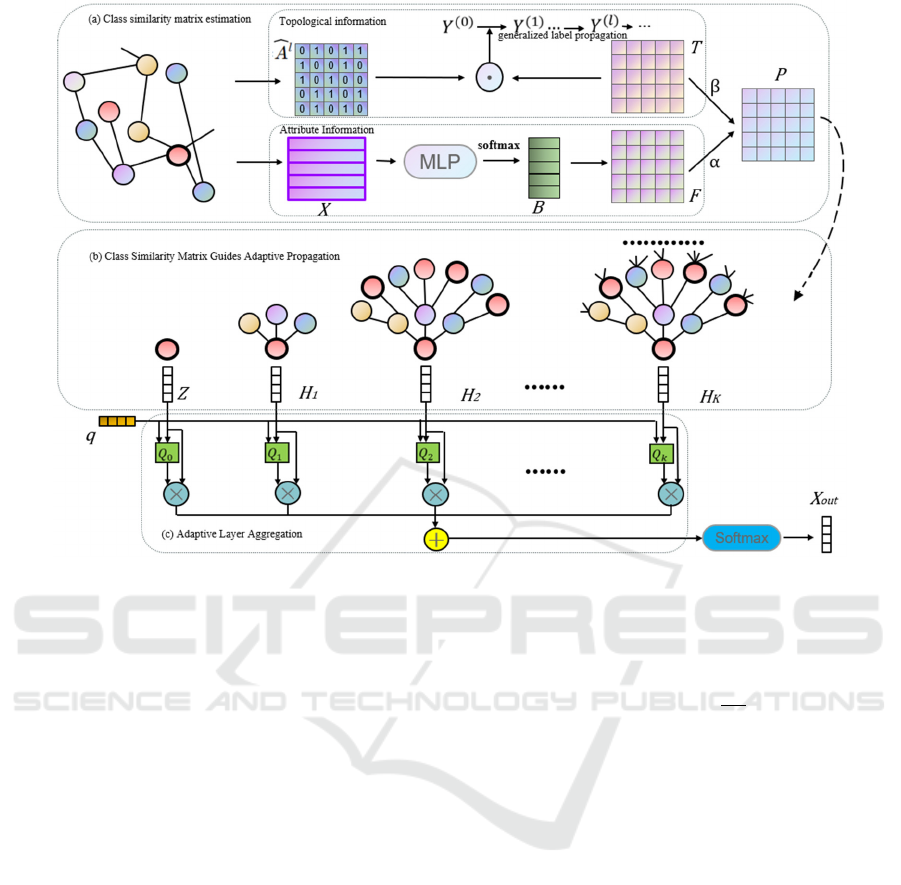
Figure 1: The structure of DAP-GCN, consisting of (a) class similarity matrix estimation, (b) class similarity matrix guided
adaptive propagation and (c) adaptive layer aggregation.
(1) the learning process of class similarity matrix, (2)
adaptive propagation guided by class similarity
matrix, and (3) adaptive layer aggregation.
3.2 Similarity Matrix Estimation
We extract class-aware information from both
attribute information and topological information.
First Angle: From attribute. It has been shown that a
MLP considering only features performs better in
heterophilic graphs. Therefore we use it as a
component of this module to compute the attribute-
based class similarity matrix. The 𝑙-th layer of the
MLP is indicated as:
𝒁
(
)
= 𝜎
𝒁
(
)
𝑾
(
)
∈ ℝ
×
(
4
)
where 𝒁
()
=
𝑿 , 𝑾
()
is the learnable parameter
matrix of MLP and σ(·) used is a sigmoid function.
The output of the 𝑙-th layer of mlp is 𝒁
(
)
. The soft
labeling matrix 𝑩 ∈ 𝑅
×
is the can be obtained as
follows:
𝑩 =softmax𝒁
(
)
(
5
)
where the matrix 𝑩 contain the factors symbolized by
𝑩
. Each factor 𝑩
indicates the probability that
node 𝑣𝑖 belongs to class 𝑐. Let 𝜃
indicate the
parameters in the MLP. We predict the labels by
minimizing the loss of the MLP to get the best 𝜃
∗
.
Θ
∗
=argmin
ℒ
=argmin
1
|
𝑉
|
∈
𝐽𝑏
, 𝑦
(
6
)
where 𝐽 is the cross-entropy loss, 𝑏
is the forecast
labeling of the node 𝑣
passing through the MLP, and
𝑦
is true one-hot label. 𝑉
denotes the labeled nodes
in the training set. The class similarity matrix 𝑭 based
on attribute considerations, can be characterized as
follows.
𝑭 = 𝑩𝑩
(
7
)
where 𝐹
= 𝑏
𝑏
denotes the degree to which node 𝑣
and node 𝑣
belong to the identical class.
Second Angle: From topological. Network
topologies contain a large amount of useful
information. We need as much labelled information
as possible to capture class similarity in the topology
space. However, labels are scarce and difficult to
obtain in semi-supervised node classification tasks.
Therefore, a generalized label propagation algorithm
with a learnable edge weight matrix is used to assign
pseudo-labels to unlabelled nodes in the form of
topological information that can respond to the edge
weights between nodes during label propagation, and
DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems
132

then the edge weights are used to compute the class
similarity matrix.
First, we introduce the classical label
propagation algorithm. It usually assumes that two
linked nodes are more likely to have the identical
class. Therefore, the labels are iteratively propagating
between neighbors nodes. This is formalized as 𝒀
()
= [𝒚
()
, 𝒚
()
,...,𝒚
()
]
, ∈ 𝑅
×
denote the soft label
matrix of the iterative 𝑙-layer ( 𝑙 > 0), where 𝒚
denotes the predicted label distribution of node 𝑣
in
the 𝑙-layer. The label propagation of the 𝑙-th layer is
defined as follows:
𝒀
(
)
= 𝑫
𝑨𝒀
(
)
,
𝒚
(
)
= 𝒚
(
)
, ∀𝑣
∈𝑉
(
8
)
The degree matrix is represented by 𝑫 and
𝑫
= ∑
𝑨
. However, classical label propagation
techniques assume homophily and cannot be adapted
to networks with heterophily. To address this, Guided
by the labels, we improve the classical labeling
propagation by means of a learnable weight matrix.
The degree to which two nodes belong to the same
class is represented by the learned weight matrix. To
capture more homophily nodes, label propagation is
performed on the 𝑘-order structure of the network,
due to the network having varying degrees of
heterophily. The 𝑘-order formalized as 𝑴 is defined
as.
𝑴 = 𝑨+ 𝑨
+ ⋯+ 𝑨
(
9
)
The iterative l-layer's generalized label propagation is
defined as.
𝒀
(
)
= 𝑫
(
𝑴⊙𝑻
)
𝒀
(
)
(
10
)
The diagonal matrix of matrix 𝑴⊙𝑻 is represented
by 𝑫
. In this equation, nodes use learnable edge
weights as propagation instructions to propagate
labels to their 𝑘-hop neighborhoods. Finally, we
minimize the loss in a run of the generalized label
propagation algorithm, which in turn learns the
optimal edge weights 𝑇
∗
.
𝑇
∗
=argmin
ℒ
=argmin
1
|
𝑉
|
∈
𝐽
𝒚
𝒂
𝒍𝒑
, 𝒚
𝒂
(
11
)
where 𝒚
𝒂
𝒍𝒑
is the label distribution of 𝑣
predicted by
generalized label propagation. We continuously
optimize the loss and thus obtain the best 𝑇
∗
which
maximizes the probability of correctly propagating
labels among nodes. It reflects the extent to which
two node classes are identical. The weight matrix 𝑻 is
used as the class similarity matrix for topological
space estimation. Finally, we combine the similarity
matrices estimated in attribute and topological spaces
using adjustable parameters.
𝑷 = 𝛼𝑭+ 𝛽𝑻
(
12
)
where 𝛼 and 𝛽 are hyperparameter.
3.3 Adaptive Guidance Dissemination
After obtaining the class similarity matrix 𝑷. We
introduce the learnable 𝑷 into the propagation
process. The propagation weights between neighbors
are adaptively changed according to the class
similarity between nodes. This distinguishes the
degree of homophily between nodes. To capture more
homophilic nodes, we use feature propagation on 𝑘-
hop neighborhoods. The feature propagation process
of DAP-GCN at iteration 𝑙-th layer is.
𝑯
= 𝑨
⊙𝑷𝒁, 𝑙 = 1,2,3, … , 𝑘
∈ℝ
×
(
13
)
We use a symmetric normalized propagation
mechanism 𝑨
= 𝑫
𝑨
𝑫
, where 𝑨
= 𝑨+ 𝑰, and 𝑘
is a hyperparameter of the number of propagation
layers. Here, 𝑐 represents the amount of node classes.
3.4 Adaptive Guidance Dissemination
According to Eq. (13), we obtain the node
representations (𝑯
,
𝑯
,
𝑯
,…,𝑯
) for the different
layers in the model graph by multiple propagation.
We should treat different layers of information
differently. Because each layer contains a different
amount of useful information. Therefore, we
adaptively aggregate information from different
layers based on the learned weights. We use a
learnable projection vector 𝒒 with 𝑯
to compute the
corresponding weight 𝑸
. Based on 𝑸
(𝑘=0, 1, 2, 3,
...), we obtain the useful information retained by 𝑯
.
Finally, we splice and integrate each layer of
representation.
𝑯 =stack
(
𝒁, 𝑯
, ⋯, 𝑯
)
∈ℝ
×
(
)
×
𝑸 = 𝜎
(
𝑯𝒒
)
∈ℝ
×
(
)
×
𝑸
=reshape
(
𝑸
)
∈ℝ
××
(
)
𝑿
=softmax
squeeze𝑸
𝑯
∈ℝ
×
,
(
14
)
where 𝒁 is obtained by applying the MLP
network to the original feature matrix. The trainable
projection vector 𝒒 is of size 𝑅
×
and σ ( · ) is a
sigmoid function. The data sizes are adjusted using
stacking, reshaping, and squeezing to ensure
compatibility during computation.
A Decoupled Graph Convolutional Network with Dual Adaptive Propagation Mechanism for Homophily and Heterophily
133

4 EXPERIMENTS
4.1 Datasets
We selected three homophily graphs and four
heterophily graphs for the semi-supervised node
classification (Gao, 2018) task. The datasets used for
the task include three homophilic graphs (Cora,
Citeseer, and Pubmed)(Namata, 2012) and three
heterophilic graphs (Cornell, Texas, and Wisconsin)
representing web pages and hyperlinks. Additionally,
the participant co-occurrence network dataset for
films is included, where nodes denote actors and
edges denote actors appearing in the same movie.
Table 1 shows the statistical information for each
dataset, with R representing the heterophily ratio of
the graph.
4.2 Baseline
We compared DAP-GCN with the following
approaches: (1) MLP, which consider only features;
(2) DeepWalk (Perozzi, 2014), which randomizes the
walk but considers only network topology
information; and (3) the classical GNN models: GCN
and GAT (Veličković, 2017). (4) Graph neural
network models dealing with heterophily graph
include Geom-GCN, H2GCN , GPR-GNN (Chien,
2021), and AM-GCN (Wang, 2020).
4.3 Overall Results
Ensure fair and valid experimental results. In the
homophilic dataset, we take 20 labeled nodes in each
class to be used as training set, 500 nodes to be used
as validation set and 1000 nodes to be used as test set
and run a fixed training/validation/testing of 100 runs
separated from (Liu, 2020). In the heterophilic
dataset, the Geom-GCN setup is used. For the above
comparisons, we use the optimal parameters
originally set by the authors. In DAP-GCN, a two-
layer MLP is utilized to estimate the class similarity
matrix. Two layer graph convolution operation is
utilized to propagate the class similarity. The Adam
optimizer (Kingma, 2014), and the default
initialization in PyTorch are used.
4.4 Node Classification
Tables 2 and 3 display the results of node
classification for both homophily and heterophily,
and they both use the average accuracy as a metric.
Significantly, bolded text indicates optimal
performance, underlining indicates second highest
performance. The analysis shows that DAP-GCN
outperforms all other methods, particularly in
heterophilic graphs. This demonstrates the
importance of applying a class similarity matrix based
on the graph convolution framework in heterophilic
graphs. Among the four heterophilic graphs, DAP-
GCN's performance is almost always the best. For
example, in Wisconsin, DAP-GCN improves 36.37%
Table 1: Mean and standard deviation of node classification in
homophiy.
Datasets/Accuracy(%) Cora CiteSeer PubMed
MLP 61.65±0.61 61.12±1.09 74.24±0.73
ChebNet 80.51±1.13 69.65±1.43 78.17±0.66
GCN 81.41±0.80 71.14±0.72 78.84±0.64
GAT 83.13±0.45 70.82±0.53 79.17±0.45
APPNP 83.32±0.52 71.85±0.45 80.16±0.27
SGC 81.74±0.11 71.38±0.26 78.91±0.16
JK-Net 81.83±0.56 70.75±0.74 78.81±0.72
DAGNN 84.51±0.53
73.46±0.55 80.53±0.44
Ours (DAP-GCN) 85.32±0.28 74.23±0.28 81.16±0.45
Table2:Statistics of datasets.
Datasets Texas Wisconsin Cornell Film Cora CiteSeer PubMed
Nodes 183 251 183 7600 2708 3327 19717
Edges 309 499 295 33544 5429 4732 44338
Features 1703 1703 1703 931 1433 3703 500
Classes 5 5 5 5 7 6 3
R 0.09 0.19 0.3 0.22 0.81 0.74 0.8
DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems
134
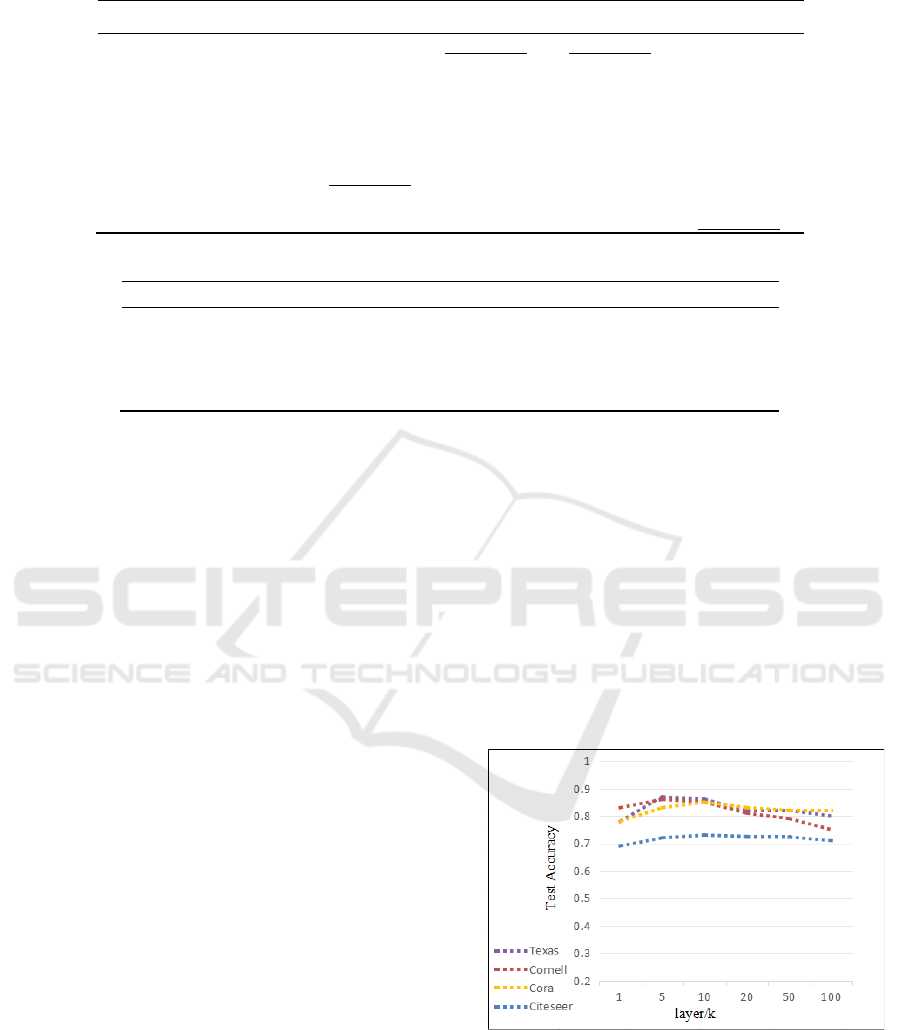
Table 3: Mean and standard deviation of node classification in heterophiy.
Datasets/Accuracy(%) Texas Wisconsin Cornell Film
MLP
GCN
GAT
DeepWalk
Geom-GCN
H2GCN
GPR-GNN
AM-GCN
80.98±4.69
53.86±4.45
57.28±3.26
49.19±3.45
66.35±6.42
79.68±7.23
84.62±4.34
78.42±7.32
85.35±3.47
50.42±7.32
54.36±5.48
53.42±5.13
62.44±5.36
82.54±4.35
83.86±3.23
81.74±4.86
83.39±7.42
54.12±8.75
54.62±7.19
44.15±9.14
55.68±8.15
78.45±4.55
82.96±5.62
78.37±4.98
36.35±1.55
28.36±1.56
29.15±1.54
23.78±0.64
32.39±1.46
36.83±1.36
36.45±1.42
33.61±1.12
Ours (DAP-GCN) 85.45±4.46 86.79±3.86 84.65±4.29 36.82±0.93
Table 4: Ablation study of DAP-GCN.
Method Texas Wisconsin Cornell Film
w/o F、T 80.23±3.56 82.36±2.69 82.15±4.23 32.36±2.36
w/o F 83.36±5.32 84.76±4.68 83.45±3.43 34.85±4.63
w/o T 82.72±3.78 82.63±3.25 83.37±2.36 35.44±5.74
Our(F+T) 85.45±4.46 86.79±3.86 84.65±4.29 36.82±0.93
and 32.43% on average over the traditional GNN
models GCN and GAT, respectively. Compared to
other approaches to heterophily, such as H2GCN,
Geom-GCN and GPR-GNN, DAP-GCN improves
the average accuracy by 2.93% to 24.35%. These
results demonstrate the reliability of DAP-GCN in
heterophilic graphs. The performance of the
homophily network improves to varying degrees. For
example, in Cora, The average performance of DAP-
GCN was 3.91% and 2.19% better than that of GCN
and GAT, respectively, which are assumed to be
strongly homophilic. DAP-GCN performs
exceptionally well in both heterophily and homophily
networks, further validating the method's
effectiveness homophily network improves to
varying degrees. For example, in Cora, The average
performance of DAP-GCN was 3.91% and 2.19%
better than that of GCN and GAT, respectively, which
are assumed to be strongly homophilic. DAP-GCN
performs exceptionally well in both heterophily and
homophily networks, further validating the method's
effectiveness.
4.5 Ablation Experiments
Table 4 shows the ablation experiments on each of the
four heterophilic datasets, using the average accuracy
as the metric. The necessity of these two components
in the class similarity matrix estimation module is
verified. Classification accuracy is used as a metric.
Four cases are given in the table:(1) calculation of
similarity matrix without attribute and topology
information; (2) similarity matrix with topology
information only; (3) similarity matrix with attribute
information only; and (4) the model used in this paper
that considers both attributes and topology. The
experimental results show that the performance
decreases when different components are removed. It
shows that each component plays a role as well as the
necessity of considering both attributes and topology.
Secondly, in the first three datasets, the performance
of w/o T is slightly higher compared to w/o F,
indicating that attribute information is slightly more
influential than topology information in small and
medium-sized graphs. In the film dataset, w/o F is
higher, suggesting that on large graphs, it is likely that
topology information has more influence.
Figure 2: Results of DAP-GCN with different depths.
4.6 Over-Smoothing Analysis
Figure 2 shows the performance of four datasets at
different aggregation levels (number of hops). We
used two homophilic datasets (Cora, Citeseer) and
two heterophilic datasets (Cornell, Texas) to test our
A Decoupled Graph Convolutional Network with Dual Adaptive Propagation Mechanism for Homophily and Heterophily
135

method's reliability. We verified accuracy for 1 to 100
layers. It can be concluded that our model's
performance remains stable even when increasing the
number of layers. Additionally, there is no
representation convergence due to the increase in the
number of layers, which is the opposite of GCN. This
demonstrates that decoupling the propagation from
the transformation can alleviate the over-smoothing
problem.
5 CONCLUSIONS
We propose a decoupled graph convolutional
network DAP-GCN with a dual adaptive propagation
mechanism. It can be applied to both homophilic and
heterophilic networks. DAP-GCN extracts class-
aware information by learning class similarity
matrices from attribute information and topological
information. The matrix adaptively changes the
propagation process of the network based on the class
similarity between nodes. Finally, the information is
extracted adaptively in different layers. DAP-GCN
mainly solves the heterophilic problem and also
effectively mitigates the over-smoothing problem.
Experiments on real datasets show that DAP-GCN
provides better performance than current methods
under both homophilic and heterophilic graphs.
REFERENCES
T. N. Kipf and M. Welling, 2016. Semi-supervised
classification with graph convolutional networks.
arXiv:1609.02907.
Chen. D, Lin. Y, Li. W, Li. P, Zhou. J, and Sun. X, 2020.
Measuring and relieving the over-smoothing problem
for graph neural networks from the topological view, in
Proc. AAAI Conf. Artif. Intell., vol. 34, no. 4, pp. 3438–
3445.
M. Liu, H. Gao, and S. Ji . 2020. Towards deeper graph
neural networks.In Proc. 26th ACM SIGKDD Int. Conf.
Knowl. Discovery Data Mining,Aug. pp. 338–348.
J. Zhu, Y. Yan, L. Zhao, M. Heimann, L. Akoglu, and D.
Koutra, 2020. Beyond homophily in graph neural
networks: Current limitations and effective designs. In
Advances in Neural Information Processing Systems 33.
H. Pei, B. Wei, K. C. Chang, Y. Lei and B. Yang, 2020.
Geom-GCN: Geometric graph convolutional networks.
In Proceeding of the 8th International Conference on
Learning Representations.
Y. Rong,W. Huang, T. Xu, and J. Huang, 2019. DropEdge:
Towards deep graph convolutional networks on node
classification. arXiv:1907.10903.
J. Gasteiger, A. Bojchevski, and S. Günnemann, 2018.
Predict then propagate: Graph neural networks meet
personalized PAGERANK. arXiv:1810.05997.
J. Tang, J. Sun, C. Wang and Z. Yang, 2009. Social
influence analysis in large-scale networks. In
Proceedings of the 15th ACMSIGKDD International
Conference on Knowledge Discovery & Data Mining,
pp. 807–816.
G. M. Namata, B. London, L. Getoor and B. Huang, 2012 .
Query-driven active surveying for collective
classification. In 10th International Workshop on
Mining and Learning with Graphs, pp. 8.
B. Perozzi, R. Al-Rfou and S. Skiena, 2014 . DeepWalk:
Online learning of social representations. In
Proceedings of the 20th ACMSIGKDD International
Conference on Knowledge Discovery & Data Mining.
pp. 701–710.
P. Veličković, G. Cucurull, A. Casanova, A. Romero, P.
Liò, and Y. Bengio, 2017. Graph attention networks.
arXiv:1710.10903.
E. Chien, J. Peng, P. Li and O. Milenkovic, 2021. Adaptive
universal generalized pagerank graph neural network.
In Proceeding of the 9th International Conference on
Learning Representations.
X. Wang, M. Zhu, D. Bo, P. Cui, C. Shi and J. Pei, 2020.
AM-GCN: Adaptive multi-channel graph
convolutional networks. In Proceedings of the 26th
ACM SIGKDD International Conference on
Knowledge Discovery & Data Mining, pp. 1243–1253.
D. P. Kingma and J. Ba, 2015. Adam: A Method for
stochastic optimization. In Proceedings of the 3rd
International Conference on Learning Representations.
H. Gao, Z. Wang, and S. Ji, 2018. Large-scale learnable
graph convolutional networks. In Proceedings ofthe
24th ACM SIGKDD International Conference on
Knowledge
Discovery & Data Mining, pp. 1416–1424.
DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems
136
