
Identification of Piezoelectric Actuator
Using Bayesian Approach and Neural Networks
Lenka Kukli
ˇ
sov
´
a Pavelkov
´
a
a
and Kv
ˇ
etoslav Belda
b
Department of Adaptive Systems,
The Czech Academy of Sciences, Institute of Information Theory and Automation,
Pod Vod
´
arenskou v
ˇ
e
ˇ
z
´
ı 4, CZ-182 00, Prague 8, Czech Republic
Keywords:
Piezoceramic Actuator, Hammerstein Model, Hysteresis, ARX Model, Bounded Noise, Bayesian Estimation,
Physical Modelling, Continuum Mechanics, Euler–Bernoulli Beam Theory.
Abstract:
The paper deals with a modelling and identification of a class of piezoelectric actuators intended for mecha-
tronic and bio-inspired robotic applications. Specifically, a commercial piezoelectric bender PL140 from
Physik Instrumente Co. is used. Considering catalogue/datasheet parameters, a physical model of PL140 is
derived using Euler-Bernoulli beam theory. This model serves as a substitution of reality to generate proper
data without potentially damaging the real actuator. However, due to its complex structure, this model cannot
be used for control design. For this purpose, a Hammerstein model is proposed. It consists of a static nonlin-
ear part describing the hysteresis and a dynamic linear part that is represented by the auto-regressive model
with exogenous input (ARX model). The nonlinear part of the Hammerstein model is identified by a neural
network. The Bayesian approach is used for the estimation of the ARX model parameters.
1 INTRODUCTION
Continuous progress in science and technology stim-
ulates the demand for novel materials and devices.
Piezoelectric actuators represent such a device. They
have great potential in various fields such as micro-
robotics, precision instruments or biomedicine (Gao
et al., 2024).
Piezoelectric actuator (PEA) uses electro-
mechanical coupling (inverse piezoelectric effect)
to convert input electrical energy into output force
or motion. Piezoelectric materials can be classified
into single crystals, piezoelectric ceramics (PZT) and
polymers. For a precision positioning, PZT is mostly
used (Zhou et al., 2024). However, the accuracy of
the generated motion is significantly impacted by the
intrinsic non-linearity of PEAs under dynamic work-
ing conditions. This non-linearity arises mainly from
hysteresis. Therefore, suitable modeling approaches
that are able to model this nonlinearity are required
to achieve higher motion accuracy (Kanchan et al.,
2023).
The mechanical behavior of materials can be mod-
elled by means of continuum mechanics. Never-
a
https://orcid.org/0000-0001-5290-2389
b
https://orcid.org/0000-0002-1299-7704
theless, the respective partial differential equations
are too complex to be solved analytically. There-
fore, a numerical technique called the finite element
method (FEM) is used to solve these equations for
complex systems in a computationally feasible man-
ner (Hughes, 2003). However, the obtained model is
still too complex for the control tasks. Thus, alterna-
tive models are used for nonlinear modeling of PZT
actuators. They incorporate a black-box modeling to-
gether with a physical understanding of the hysteretic
system (Ismail et al., 2009).
A hysteresis can by modelled either by using op-
erator superposition or by differential equations (Dai
et al., 2023). In the context of piezo actuators, the
Bouc-Wen (BW) model, which belongs to the second
group, is often used (Ismail et al., 2009).
However, the BW model only provides a static
description, so it is often supplemented with a dy-
namic linear part such as auto-regressive model with
exogenous input (ARX model). This combination of
static non-linear and dynamic linear parts corresponds
to the concept of Hammerstein’s model (Dai et al.,
2023).
Currently, the required control model is also of-
ten identified by artificial neural networks (ANNs)
(Uralde et al., 2023).
Kuklišová Pavelková, L. and Belda, K.
Identification of Piezoelectric Actuator Using Bayesian Approach and Neural Networks.
DOI: 10.5220/0013011700003822
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 591-599
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)
591
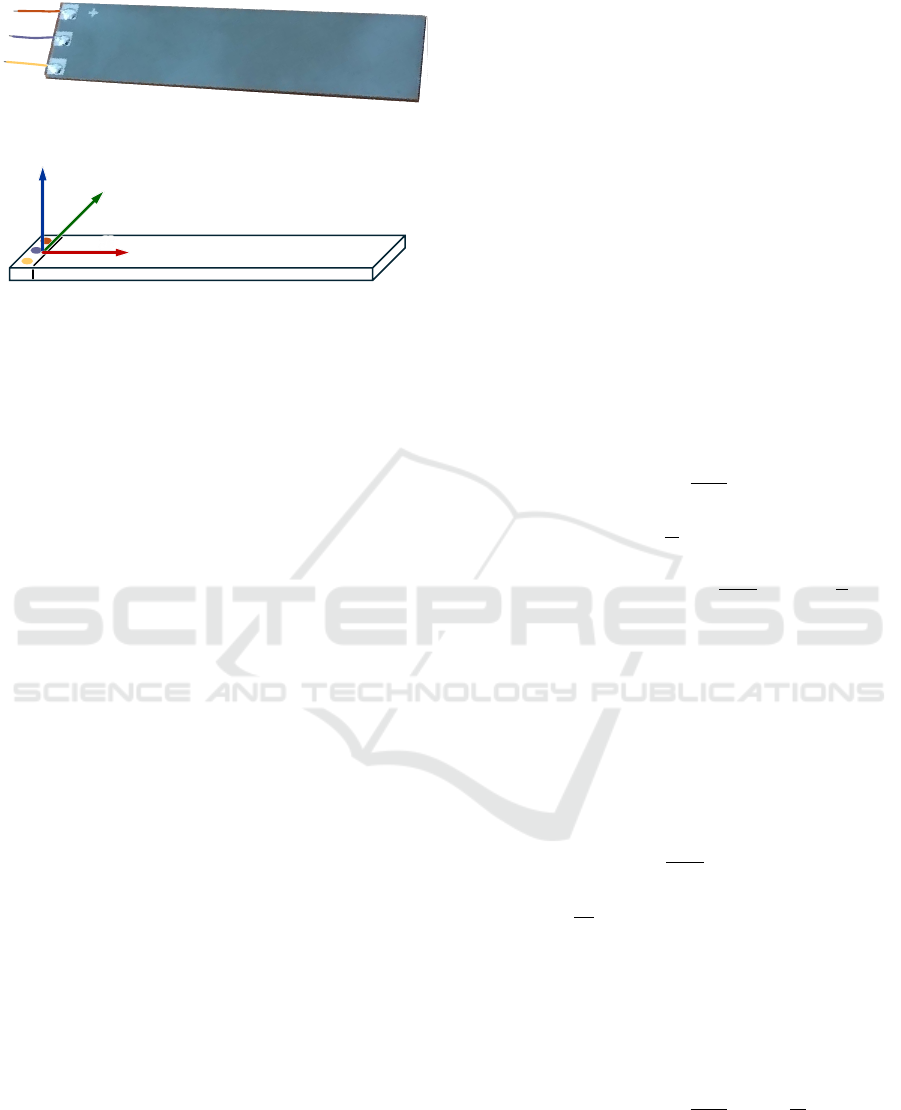
Figure 1: PEA bender PL140.
L
a
b
z
y
x
Figure 2: Main dimensions of PEA bender PL140.
This paper aims to provide a nonlinear data-driven
model of the commercial piezoelectric bender PL140
of Physik Instrumente (PI) Co. The model is intended
for a subsequent use in the micro-position control
tasks. The proposed model will be based on a Ham-
merstein model.
Simultaneously, a physically based model is de-
veloped as a substitute of the real piezo bender.
It is meant to simulate data for the identification
of the above mentioned data-driven model with-
out the need for an actual piezoelectric actuator.
The paper is organized as follows. In Section 2,
a physical model of the piezoelectric bender PL140
is introduced. In Section 3, a relevant data-driven
model is presented and the estimation of its param-
eters is proposed. The simulation experiments using
both physical and data-driven models are described in
Section 4.
2 PHYSICAL MODEL
This section summarises physical model of the PEA
including the related theory. Namely the PICMA
Bender PL140 is considered, see Figure 1. The simu-
lation model is realized using MATLAB/Simulink en-
vironment and serves as a substitute for the real PEA.
2.1 Beam Theory for Piezo Bender
Physical bodies can be described using the gen-
eral theory of continuum mechanics (Bruno et al.,
2018). In the case of a prism-shaped piezo bender,
i.e. a beam, a simplification in the form of Euler-
Bernoulli beam theory can be used (Tadmor and
K
´
osa, 2003). This theory will be considered and ap-
plied to model construction in this section. The ob-
tained model is considered as a model substitut-
ing a real piezo ceramic beam. We consider that
used piezo bender actuator is built from a homo-
geneous isotropic linear elastic piezoceramic mate-
rial. Its stress σ is related to the strain ε by σ = E ε,
where E is the Young’s modulus. Then, general con-
stitutive equations (Bruno et al., 2018) considering
strains in space are as follows
σ = C ε− e
T
E
◦
(1)
d = e ε + ϵ E
◦
(2)
where E
◦
, C, ε, e, d and ϵ are the electric field,
compliance tensor, strain field, electric displacement
field, piezo stress coefficient tensor and permittivity
tensor at constant or zero strain, respectively. The re-
quired beam equations can be separated from (1) and
(2). Let us proceed from strain along axis x (simpli-
fying a general three-dimensional problem to a one-
dimensional one, ◦ → (x ∧ z), i.e. corresponding di-
rections):
ε → ε
xx
(x,z) = −z
dφ
y
dx
(x) (3)
E
◦
→ E
z
=
u
b
(4)
σ → σ
xx
(x,z) = −c
11
z
dφ
y
dx
(x) − e
31
u
b
(5)
where c
11
= E and E
z
is electric field perpendic-
ular to plane xy and u is input voltage between
surface electrodes of PEA. Then, bending moment
from the stress field is
M
y
(x) = −
¨
z σ
xx
(x,z) dS (6)
By performing a double integral in (6), the bending
moment is expressed as follows
M
y
(x) = E I
dφ
y
dx
(x) + abe
31
u (7)
where I =
1
12
ab
3
is the second moment of area
of the rectangular cross-section.
Let us continue by developing the equation
for electric displacement (2), again simplifying
to the relevant one-dimensional subspace, as:
d
z
(x,z) = e
31
ε
xx
(x,z) + ϵE
z
(8)
d
z
(x,z) = −e
31
z
dφ
y
dx
(x) + ϵ
u
b
(9)
dq =
"
d
z
dS = e
31
a b dφ
y
(10)
where dq is infinitesimal accumulated charge
at a bend characterized by a bend angle change.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
592

Thus, the charge q for a specific bend can be ex-
pressed as follows
q = e
31
ab(φ
y
(x
k+1
) − φ
y
(x
k
)) (11)
Then, the resulting Euler-Bernoulli beam equations
for torque and charge are as follows
M
y
(x) = E I
dφ
y
dx
(x) + abe
31
u (12)
q = e
31
ab(φ
y
(x
k+1
)−φ
y
(x
k
))+
ϵaℓ
b
u (13)
The set of equations (7)-(13) leads to the state-space
finite-element form (16) of one element of the mod-
elled beam divided into n elements:
F
C
τ
C
F
R
τ
R
= K
z
C
φ
C
z
R
φ
R
(14)
¯
M 0
0 0
¨
x
0
+
K υ
piezo
−υ
T
piezo
δ
piezo
x
u
=
f
q
(15)
where
K =
E I
ℓ
3
12 6ℓ −12 6ℓ
6ℓ 4ℓ
2
−6ℓ
2
2ℓ
2
−12 −6ℓ 12 −6ℓ
6ℓ 2ℓ
2
−6ℓ 4ℓ
2
¯
M =
m
420
156 22ℓ 54 −13ℓ
22ℓ 4ℓ
2
13ℓ −3ℓ
2
54 13ℓ 156 −22ℓ
−13ℓ −12ℓ −22 ℓ 4 ℓ
2
υ
piezo
= [ 0 e
31
ab 0 − e
31
ab]
T
δ
piezo
=
ϵaℓ
b
with added dumping matrix B, the final form is
M
¨
x
0
+ B
˙
x
0
+
¯
K
x
u
=
f
q
(16)
where m = ρabℓ is the element mass with den-
sity ρ and ℓ as element length and L = nℓ total
beam length, a and b are cross-sectional parameters
– width and thickness respectively (see Figure 2),
x = [z
C
φ
C
z
R
φ
R
]
T
is generalized coordinate vector,
e
31
is a piezoelectric stress-charge coupling element
and ϵ is electrical permittivity.
The set (16) can be numerically solved in n-
element chain, where terms K, M, B (= zero matrix
but b
11
̸= 0), q and f = [F
C
τ
C
F
R
τ
R
]
T
are stiffness
matrix, mass matrix, stiffness finite element matrix,
damping matrix, accumulated charge trough PEA and
generalized force effects, respectively, with right di-
mensions (Benjeddou et al., 1997).
The relations between available datasheet
parameters and material parameters, which can
be equally used in the equations and MAT-
LAB/Simulink/Simscape blocks for Piezo Bender
simulation, are summarised as follows (Tadmor and
K
´
osa, 2003)
e
31
= −
2ℓF
block
3ab u
rated
(17)
E = −
4F
block
ℓ
3
y
free
ab
(18)
ϵ =
b
aℓ
C
piezo
+
4F
block
y
free
y
free
ab
3
(19)
where parameters on the right side of equations:
F
block
, a, b, u
rated
, y
free
and C
piezo
– blocking force,
dimensions, rated drive voltage and free deflection
at u
rated
, beam capacitance, respectively – can be
found in specific datasheet of PI Co.
The following section will focus on the modelling
based on Simulink block models that can consider
both the parameter types above.
2.2 Simscape Model
In the context of physical analysis above, to construct
a suitable simulation model representing a real beam,
MATLAB/Simulink with Simscape block libraries of-
fers a simple start (user-friendly pre-arranged alterna-
tive to programming the mathematical equations de-
fined in Section 2.1) for experimental research and
development, see Figure 3. This model has several
advantages such as structural clarity, fast implemen-
tation considering real physical parameters and con-
stants contained in data sheets of producers.
Identification of Piezoelectric Actuator Using Bayesian Approach and Neural Networks
593
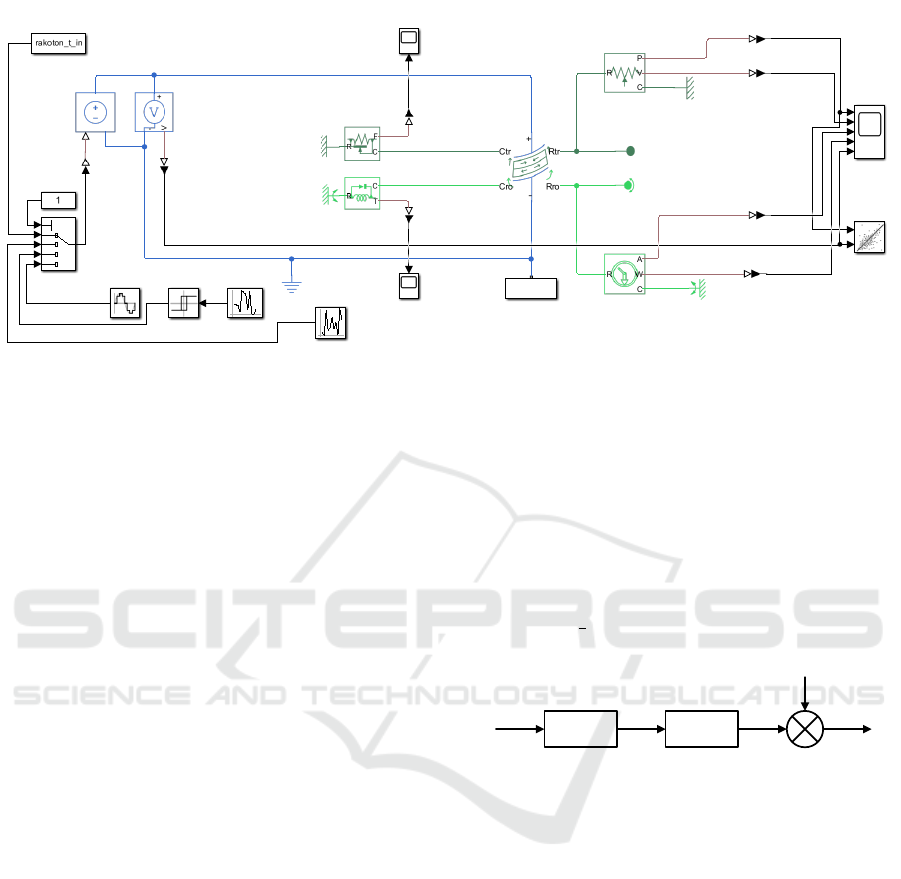
Piezo Bender Actuator
f(x) = 0
Solver
Configuration
Electrical
Reference
Rotational
Free End
Piezo Bender
PS-Simulink
Converter z = z(t)
Translational
Free End
Mechanical
Rotational
Reference
Mechanical
Translational
Reference
Ideal
Translational
Motion Sensor
Mechanical
Translational
Reference1
PS-Simulink
Converter
v = v(t) = dz/dt
Voltage
Sensor
PS-Simulink
Converter u [V]
Controlled
Voltage
Source
Simulink-PS
Converter
Ideal
Rotational
Motion Sensor
Mechanical
Rotational
Reference1
PS-Simulink
Converter fi = fi(t)
PS-Simulink
Converter
omg = dfi/dt
Scope:
Piezo
Ideal
Force Sensor
PS-Simulink
Converter F = F(t)
Scope:
Force Fr
Ideal
Torque Sensor
PS-Simulink
Converter T = T(t)
Scope:
Torque Tr
XY Graph
Sine Wave
Uniform Random
Number
From
Workspace
Multiport
Switch
Random
Number
Relay
Constant
z
dz
voltage
dphi
phi
F
T
Figure 3: Simulink model comprising Simscape blocks.
The Simulink model can be described as fol-
lows. The main block is Piezo Bender block (Math-
Works, 2021). It represents piezoelectric bimorph
beam of rectangular cross-section that is connected
trough mechanical translational and rotational refer-
ence via ideal force and torque sensors to the ground
on one side and on other side leaved free via transla-
tional and rotational free ends. They are connected
with ideal translational and rotational motion sen-
sors. Input voltage of PEA is provided by controlled
voltage source.
The function of Piezo bender block is as follows:
it bends when an electrical potential is applied across
its layers. Conversely, when a piezo bender is bended,
it generates an electrical potential.
3 DATA DRIVEN MODEL
This section presents a data-driven model of the piezo
bender PL140 that is aimed to be used in microposi-
tion control tasks.
3.1 Hammerstein Model
The Hammerstein model describes a dynamics of
nonlinear systems by combining a static nonlinearity
followed by a linear dynamic model. In the context
of PEA, it concatenates various basic (static) hystere-
sis models with dynamic transfer functions, giving the
model better dynamic description ability (Dai et al.,
2023). Using the Hammerstein model for a descrip-
tion of a PZT actuator simplifies the analysis because
it separates the nonlinear hysteresis component from
the linear dynamic behavior. It is also easy to use in a
various control algorithms and simulation tools (Gao
et al., 2015).
A block diagram of the model is shown in Fig-
ure 4. The block NLS describes the rate-independent
(static) hysteresis nonlinearity and the block LD de-
scribes rate-dependent (dynamic) linear part charac-
teristic of the piezoelectric actuator. The involved sig-
nals u
t
, z
t
, ν
t
, and y
t
represents an input, hidden un-
measurable variable, noise, and output, respectively;
t∈ {1,2,·· · ,t} denotes a discrete time.
NLS LD
u
t
z
t
y
t
ν
t
+
+
y
t
~
Figure 4: Block diagram of Hammerstein model
Generally, there is a coupling between the lin-
ear part and the nonlinear part of Hammerstein
model. Nevertheless, under certain conditions, the lin-
ear part can be separated from the nonlinear one dur-
ing the identification.
The paper (Bai, 2004) proposes such an identifica-
tion algorithm. In the first step, the system is excited
by the pseudo-random binary sequences (PRBS) in-
put. Under this input, the nonlinearity will not appear
as it is not excited. Then, z
t
= u
t
and the linear part
LD can be identified independently of the non-linear
one.
On the other side, to identify the nonlinear part
NLS, the input has to be sufficiently rich. There-
fore, a new input–output data set {u
t
, y
t
} needs to
be generated. We consider that NLS is unknown but
static. Therefore, if u
t
and z
t
are available (see Fig-
ure 4), the structural information on the unknown
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
594

NLS can be derived from their graphical representa-
tion (Bai, 2004). We will estimate the unmeasurable
z
t
using the mentioned rich input–output data set and
already identified linear part LD.
3.2 Uniform ARX Model
The LD part of Hammerstein model (Figure 4) is of-
ten represented by an ARX model (Dai et al., 2023).
Here, we will consider the ARX model with an adi-
tive bounded noise, as it is suitable for real application
(d’Onofrio, 2013). Namely, we will consider a uni-
formly distributed noise. When considering a model
with uniform noise, we do not need to know the sta-
tistical properties of the noise, but only its bounds.
The ARX model with a uniform noise is defined
as follows
y
t
= ψ
T
t
θ + ν
t
, ν
t
∼ U
ν
(−r, r) (20)
where
y
t
is an observable output,
u
t
is an optional known input,
ψ
t
is a finite-dimensional regression vector,
ψ
t
= [y
t−1
,.. .,y
t−m
, u
t−1
,.. .,u
t−m
]
T
,
θ is a vector of unknown regression coefficients,
θ = [a
1
,.. .,a
m
,b
1
,.. .,b
m
]
T
, m is model order,
T denotes the transposition,
ν
t
is a uniformly distributed i.i.d. white noise, i.e.,
zero mean and uncorrelated with older observa-
tions,
U
ν
(−r, r) denotes a uniform distribution of ν; r > 0
is a noise range.
To estimate the regression coefficients of ARX
model (20), we use the Bayesian framework (K
´
arn
´
y
et al., 2006). There, a system of interest is described
by the following probability density functions (pdfs):
prior pdf f(Θ) ≡ f(Θ|d(0)),
observation model f(y
t
|u
t
,d(t − 1), Θ),
(21)
where Θ is an unknown parameters vector.
Bayesian parameter estimation consists in the re-
cursive evolution of the posterior pdf f(Θ|d(t)) that
starts from the prior pdf f(Θ):
f(Θ|d(t))∝ f(y
t
|u
t
,d(t−1),Θ)f(Θ|d(t−1)) (22)
where d(t) = [d
t
,d
t−1
,.. .,d
1
], t = 1,2,.. .,
t, is a se-
quence of observed data records, d
t
= (y
t
,u
t
), ∝
means the equality up the normalising constant. Note
that here is no formal distinction of a random variable,
its realization and pdf argument.
Considering the ARX model (20) in the role of
the observation model (21) with Θ comprising both
θ and r, then the use of (22) leads to the increasing
complexity of the support of f(Θ|d(t)) ≡ f(Θ|ψ
t
).
In (Pavelkov
´
a and K
´
arn
´
y, 2012), the approximate
estimation is proposed that recursively circumscribe
this complex support by a feasible set. The follow-
ing expected values of both the model parameters θ
and the noise bound r are provided:
ˆ
θ = ˆrv
−1
ψ
[I
n−1
,0]
u + l
2
− v
−1
ψ
v
y
, (23)
v =
v
ψ
v
y
0 1
ˆr =
ν + 1
ν
1 − γ
ν
1 − γ
ν+1
u
−1
n
, γ =
max(l
n
,0)
u
n
.
where ν corresponds to the number of processed data,
[I
n−1
,0] denote n − 1 rows of unit n matrix,
column vectors l, u and the square matrix v are the ap-
proximate statistics that define the approximate sup-
port
ˆ
S
t
of f(Θ|d(t)) as follows:
ˆ
S
t
= {Θ : Θ
n
> 0, l ≤ v Θ ≤ u}, (24)
Θ
n
= 1/r is the n-th entry of the vector Θ, Θ =
[−θ
T
Θ
n
, Θ
n
]. The matrix v has the upper triangu-
lar form with unit diagonal.
The update of
ˆ
S
t
includes extension of v by one
row corresponding to the vector Ψ
t
= [ψ
T
,y
t
] and ex-
tension of l by −1 and u by 1 followed by the orthog-
onal rotation that zeroes the last rows of l, v, u and
keep the triangular form of v (Pavelkov
´
a and K
´
arn
´
y,
2012).
Note that we do not need to know the noise range
r because it is estimated together with the model pa-
rameters.
3.3 Static Nonlinearity
To identify NLS, the static nonlinear part of the Ham-
merstein model, we need a data set of u
t
and z
t
, see
Figure 4. The inputs u
t
are available. The hidden
variables z
t
can be estimated using the inverse esti-
mated ARX model representing LD part and from the
known y
t
generated by the Simscape model, Figure 3.
Considering that LD is represented by the ARX
model (20), the inverse model with input y
t
and out-
put z
t
has the following form:
z
t
= ˆz
t
−
1
b
1
v
t+1
=
=
1
b
1
(y
t+1
− a
1
y
t
− · ·· − a
m
y
k−m+1
−
−b
2
z
t−1
− · ·· − b
m
z
t−m+1
) −
1
b
1
v
t+1
(25)
Identification of Piezoelectric Actuator Using Bayesian Approach and Neural Networks
595
where a
i
, b
i
, i = 1,2,.. .,m, corresponds to the pa-
rameters of the ARX model (20). Considering the
noise v
t+1
, z
t
is uniformly distributed on the support
[ˆz
t
− r/b
1
, ˆz
t
+ r/b
1
] with the mean ˆz
t
.
To identify the NLS block of Hammerstein model,
we use the generated inputs u
t
together with es-
timated means ˆz
t
of hidden variable z
t
(25). As
a mapping function, a neural network idNeuralNet-
work from MATLAB was chosen. This function
is designed to identify nonlinear ARX models and
Hammerstein-Wiener models and requires Statistics
and Machine Learning Toolbox or Deep Learning
Toolbox (MathWorks, 2023).
Mathematically, idNeuralNetwork is a function
that maps vector of regressors X
t
to a single scalar
output y
t
using the relationship
y
t
= S(X
T
t
Q) (26)
where X
t
= [ψ
T
1
,.. .,ψ
T
t
]
T
, Q is a projection ma-
trix, S(.) represents a neural network object. This
object is defined by the number of hidden layers in-
cluding number of nodes and activation function for
each layer.
3.4 Identification Procedure
Consider the Hammerstein model in Figure 4. Then,
the identification of data-driven model of PL140 is as
follows:
a) generate PRBS data using Simscape model de-
picted in Figure 3
b) estimate the parameters of the block LD
in Hammerstein model represented by the ARX
model (20) according to (23) using the generated
PRBS data
c) generate new rich data (with sin waveform, ran-
dom or (Rakotondrabe, 2021) inputs)
d) estimate the z
t
in Hammerstein model as the out-
put of inverse ARX model (25) where the gener-
ated outputs y
t
from c) serve as inputs
e) identify the NLS block in Hammerstein model as
described in Subsection 3.3 using input data u
t
from c) and output data ˆz
t
from d) together with
the mapping function (26)
f) generate new rich data set as described in c) to test
the identified Hammerstein model accuracy.
4 EXPERIMENTS
This section presents a performance of the proposed
identification scheme, Subsection 3.4, applied to the
piezoelectric bender PL140.
The real-like data are generated by the Simscape
model of piezoelectric bender PL140, see Figure
3. The following input sources corresponding the ap-
plied voltage are available:
PRBS - pseudorandom binary sequence with param-
eter C
P
, i.e. sequence of random numbers from
the set {−C
P
,C
P
}
RAND - data uniformly distributed within a given in-
terval [−C
R
,C
R
]
SINE - sine wave signal of tunable amplitude and fre-
quency
RAKO - input data from the Matlab example “Piezo-
electric Actuator Model Identification Using Ma-
chine Learning” (Rakotondrabe, 2021)
The experiments were performed in accordance
with the proposed identification scheme (Subsection
3.4) with the sampling frequency T
s
= 10
−3
s.
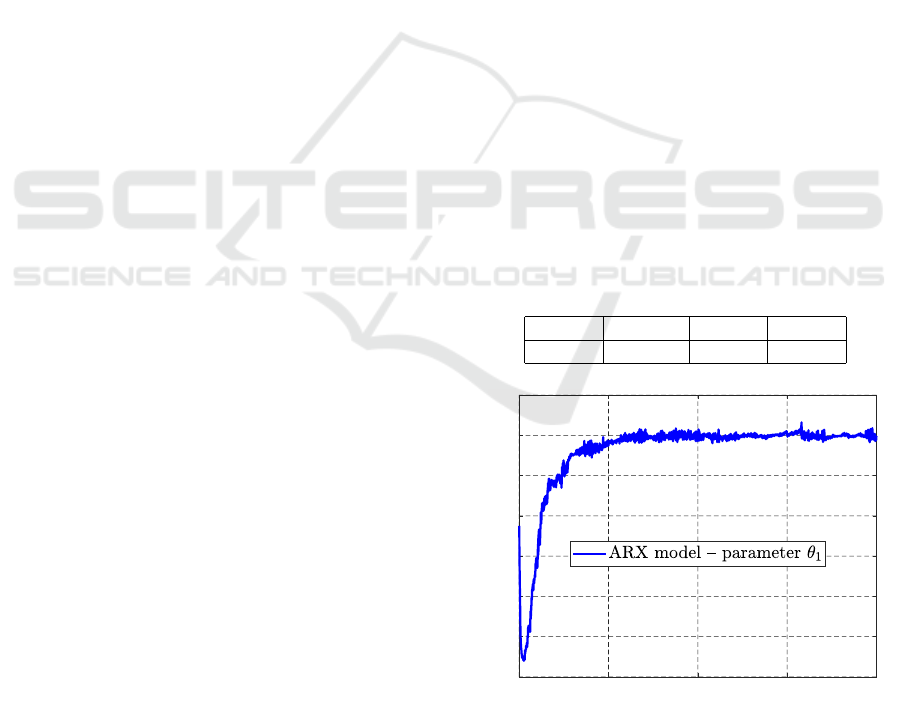
First, the PRBS data with C
P
= 1 were generated
and subsequently used to estimate the parameters of
the ARX model (20). The time course of the regres-
sion coefficients estimates are depicted in Figures 5
– 8. It can be seen that although the estimates con-
verge to a particular values, they do not stabilize and
oscillate around these values.
For further use, we set the point parameter esti-
mates as the mean values from the steady-state part
of the relevant time courses. The estimates are shown
in the Table 1.
Table 1: Point estimates of the ARX model (20).
a
1
a
2
b
1
b
2
1.1980 -0.9719 0.0042 0.0021
0 1000 2000 3000 4000
0
0.2
0.4
0.6
0.
8
1
1.2
1.
4
Figure 5: Time course (in 10
−3
s) of the parameter estimate
θ
1
= a
1
in ARX model (20).
Then, the new input-output data with SINE input
was generated to be used for estimating the hidden
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
596
0 1000 2000 3000 4000
-1
-0.5
0
0.5
1
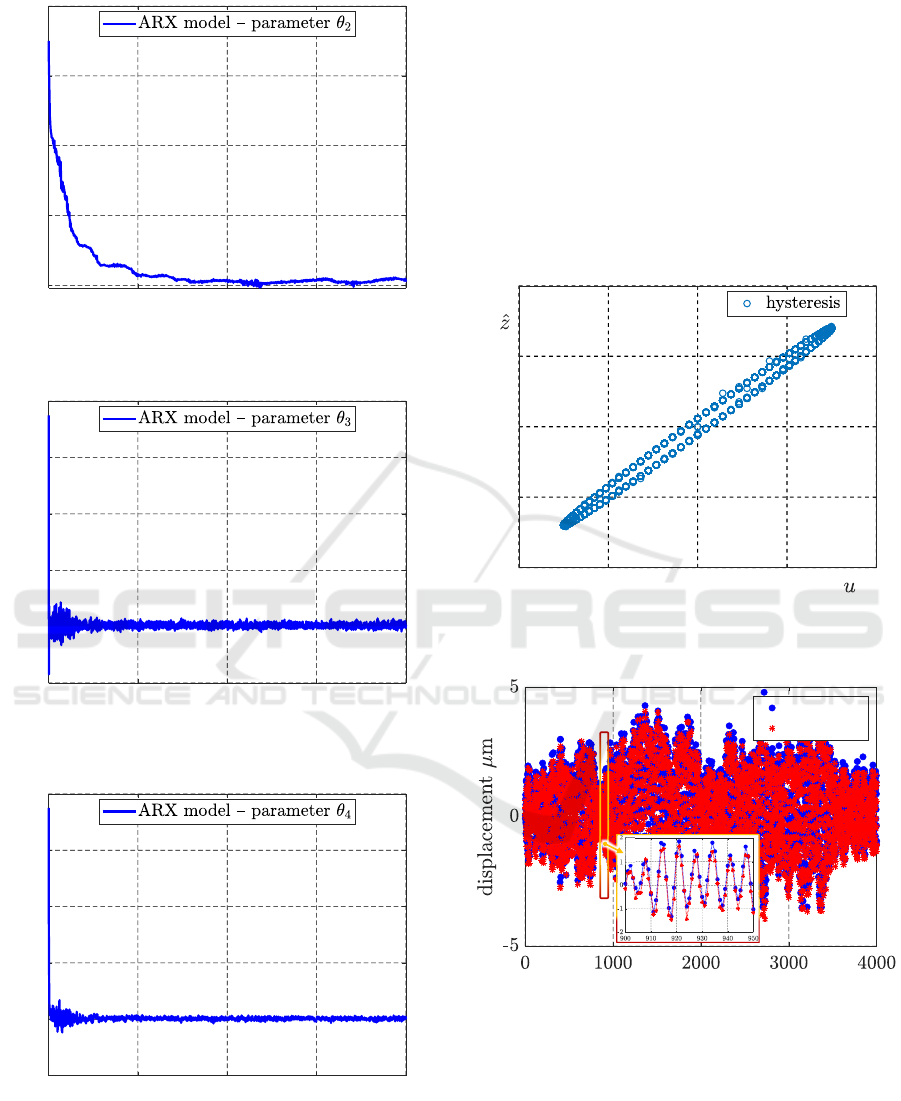
Figure 6: Time course (in 10
−3
s) of the parameter estimate
θ
2
= a
2
in ARX model (20).
0 1000 2000 3000 4000
-0.2
0
0.2
0.4
0.6
0.
8
Figure 7: Time course (in 10
−3
s) of the parameter estimate
θ
3
= b
3
in ARX model (20).
0 1000 2000 3000 4000
-0.2
0
0.2
0.4
0.6
0.
8
Figure 8: Time course (in 10
−3
s) of the parameter estimate
θ
4
= b
4
in ARX model (20).
variable z
t
and the subsequent identification of the
nonlinear part NLS represented by (26). In the exper-
iment, we have used neural network with three hid-
den layers and the hyperbolic tangent activation func-
tion. Model parameters were obtained using the Mat-
lab function nlarx. The estimated hysteresis curve,
i.e. relationship between the applied input voltage
u and the mean of the hidden variable ˆz is depicted
in Figure 9.
To test the performance of identified Hammerstein
model, we generated another rich input-output data
sets with RAND inputs and used them for the predic-
tion task. A sample example of the simulated outputs
and their predictions is shown in Figure 10.
-40 -20 0 20 40
-100
-50
0
50
100
Figure 9: NLS part of Hammerstein model – identified hys-
teresis between u and ˆz.
simulated
predicted
Figure 10: Time course (in 10
−3
s) of predicted (red) and
simulated (blue) outputs with a zoomed part for the Ham-
merstein model excited by random inputs.
5 CONCLUSION
This paper deals with the construction of a physical
model of the commercial piezoelectric bender PL140
as well as with the identification of the correspond-
ing data-driven model. Nevertheless, the presented re-
sults can be easily adapted to other beam PZT actua-
Identification of Piezoelectric Actuator Using Bayesian Approach and Neural Networks
597

tors. The explanation of these models provides inter-
ested readers with the necessary background to carry
out their own experiments.
The Simscape model is based on a physical anal-
ysis and it is intended as a substitute for the real
piezoelectric actuator. It serves as an experimental
data source. It has the advantage that various experi-
ments can be performed without expensive measuring
equipment and without the risk of damaging the real
actuator.
The identified data-driven model is intended for
a subsequent model-based micro-positioning control
design. This control design will be tuned on the de-
veloped Simulink model and then verified on a real
bender PL140.
The used identification scheme, i.e. Hammerstein
model, with an independent estimation of the linear
dynamic and the nonlinear static parts, offers freedom
in the choice of both the linear model and a function
representing the nonlinear static part.
Our choice of uniform ARX model was motivated
by the facts that models with a bounded noise are suit-
able for a real applications, and that the estimation al-
gorithm is simple and not time-consuming. Moreover,
we do not need to know the noise bound r, because it
is estimated together with the model parameters.
A function representing the nonlinear static part
was conveniently identified by the means of a neural
network MATLAB toolbox.
The proposed model offers a good prediction re-
sults with isolated outliers. The achieved result could
be further improved by tuning the network param-
eters. Another increase in model accuracy can be
achieved by a creep modelling. After hysteresis, the
creep is another factor responsible for nonlinearity in
the piezoelectric actuator. It is a time-dependent ef-
fect that causes a slow drift of the output displacement
when the input voltage changes suddenly (Kanchan
et al., 2023).
Future research will focus on incorporating
the proposed data-driven model into a model predic-
tive control task and on a testing the developed algo-
rithms on a real piezo actuator.
ACKNOWLEDGEMENTS
This work was supported by The Czech Academy
of Sciences, Institute of Information Theory
and Automation under the project No. 23-04676J
of the Czech Science Foundation: Controllable
Gripping Mechanics: Modelling, Control and
Experiments.
REFERENCES
Bai, E.-W. (2004). Decoupling the linear and nonlinear
parts in Hammerstein model identification. Automat-
ica, 40(4):671–676.
Benjeddou, A., Trindade, M. A., and Ohayon, R. (1997).
A unified beam finite element model for extension
and shear piezoelectric actuation mechanisms. Jour-
nal of Intelligent Material Systems and Structures,
8(12):1012–1025.
Bruno, B. P., Fahmy, A. R., St
¨
urmer, M., Wallrabe, U.,
and Wapler, M. C. (2018). Properties of piezoceramic
materials in high electric field actuator applications.
Smart Materials and Structures, 28(1):015029.
Dai, Y., Li, D., and Wang, D. (2023). Review on the non-
linear modeling of hysteresis in piezoelectric ceramic
actuators. Actuators, 12(12).
d’Onofrio, A. (2013). Bounded Noises in Physics, Biology,
and Engineering. Springer.
Gao, T., Liao, Q., Si, W., Chu, Y., Dong, H., Li, Y., Liao,
Y., and Qin, L. (2024). From fundamentals to future
challenges for flexible piezoelectric actuators. Cell
Reports Physical Science, 5(2):101789.
Gao, X., Ren, X., Zhu, C., and Zhang, C. (2015). Iden-
tification and control for Hammerstein systems with
hysteresis non-linearity. IET Control Theory & Appli-
cations, 9(13):1935–1947.
Hughes, T. J. (2003). The finite element method: linear
static and dynamic finite element analysis. Courier
Corporation.
Ismail, M., Ikhouane, F., and Rodellar, J. (2009). The hys-
teresis Bouc-Wen model, a survey. Archives of com-
putational methods in engineering, 16:161–188.
Kanchan, M., Santhya, M., Bhat, R., and Naik, N. (2023).
Application of modeling and control approaches of
piezoelectric actuators: A review. Technologies,
11(6):155.
K
´
arn
´
y, M., B
¨
ohm, J., Guy, T. V., Jirsa, L., Nagy, I., Ne-
doma, P., and Tesa
ˇ
r, L. (2006). Optimized Bayesian
Dynamic Advising: Theory and Algorithms. Springer,
London.
MathWorks (2021). Piezo bender. www.mathworks.com/
help/sps/ref/piezobender.html. Accessed: 2024-06-
30.
MathWorks (2023). Available mapping functions for non-
linear ARX models. www.mathworks.com/help/ident/
ref/idneuralnetwork.html. Accessed: 2024-06-30.
Pavelkov
´
a, L. and K
´
arn
´
y, M. (2012). Approxi-
mate Bayesian recursive estimation of linear model
with uniform noise. IFAC Proceedings Volumes,
45(16):1803–1807.
Rakotondrabe, M. (2021). Piezoelectric actuator
model identification using machine learning.
www.mathworks.com/help/ident/ug/machine-
learning-based-identification-of- piezoelectric-
actuator.html. Accessed: 2024-02-08.
Tadmor, E. B. and K
´
osa, G. (2003). Electromechanical cou-
pling correction for piezoelectric layered beams. Jour-
nal of Microelectromechanical Systems, 12(6):899–
906.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
598

Uralde, J., Artetxe, E., Barambones, O., Calvo, I.,
Fernandez-Bustamante, P., and Martin, I. (2023). Ul-
traprecise controller for piezoelectric actuators based
on deep learning and model predictive control. Sen-
sors, 23(3).
Zhou, X., Wu, S., Wang, X., Wang, Z., Zhu, Q., Sun, J.,
Huang, P., Wang, X., Huang, W., and Lu, Q. (2024).
Review on piezoelectric actuators: materials, classifi-
cations, applications, and recent trends. Frontiers of
Mech. Engin., 19(1):6.
Identification of Piezoelectric Actuator Using Bayesian Approach and Neural Networks
599
