Alternative Step-Size Adaptation Rule for the Matrix Adaptation
Evolution Strategy
Eryk Warchulski
a
and Jarosław Arabas
b
Institute of Computer Science, Warsaw University of Technology, Warsaw, Poland
Keywords:
Evolution Strategies, Step-Size Adaptation, Optimization.
Abstract:
In this paper, we present a comparison of various step-size adaptation rules for the Matrix Adaptation Evolu-
tion Strategy (MA-ES) algorithm, which is a lightweight version of the Covariance Matrix Adaptation Evo-
lution Strategy (CMA-ES). In contrast to CMA-ES, MA-ES does not require to invoke numerically complex
covariance matrix factorization. We take a step further in this direction and provide a quantitative assessment
of alternative step-size rules to Cumulative Step Adaptation (CSA), which is considered to be a state-of-the-art
method. Our study shows that generalized 1/5-th success rules like the Previous Population Midpoint Fitness
rule (PPMF) or Population Success Rule (PSR) exhibit comparable or superior performance to the CSA rule
on standard benchmark problems, including the CEC benchmark suites.
1 INTRODUCTION
The Covariance Matrix Adaptation Evolution Strat-
egy (CMA-ES) (Hansen et al., 2003) exhibits out-
standing performance on various optimization prob-
lems and is considered a state-of-the-art method in
the evolution strategy algorithms family. However, its
performance is occupied by the high numerical com-
plexity associated with matrix factorization. There
have been attempts to decrease its complexity over
the years, which led to the development of the Matrix
Adaptation Evolution Strategy (MA-ES) (Beyer and
Sendhoff, 2017). MA-ES takes radical steps to de-
crease the computational time and memory demands
of CMA-ES by excluding the need for the covari-
ance matrix factorization in the process of sampling
the new points. In consequence, the evolution path
is no longer needed. Such design decisions result in a
lightweight version of CMA-ES with only slightly de-
teriorated performance. Still, the authors of MA-ES
equipped introduced optimizer with the Cumulative
Step-Size Adaptation (CSA) (Hansen and Ostermeier,
2001) rule to adapt the mutation strength. While it is a
standard and highly performant method to control the
mutation step, it exhibits certain limitations like sam-
ple distribution dependency, sensitivity to the popula-
tion size, and complexity due to reliance on the evo-
a
https://orcid.org/0000-0003-1416-7031
b
https://orcid.org/0000-0002-5699-947X
lution path (Ait Elhara et al., 2013), (Hansen, 2008).
We demonstrate that equipping MA-ES with sim-
pler and less demanding rules to control mutation
strength could be beneficial in terms of performance
and simplicity. We provide an experimental study to
compare CSA with other alternative step-size adapta-
tion rules.
The paper is organized as follows. Section 2 out-
lines the MA-ES algorithm and compares it to the
CMA-ES. In section 3, we introduce and describe
step-size adaptation mechanisms considered in this
paper. Section 4 contains the empirical evaluation of
different step-size adaptation rules combined with the
MA-ES algorithm. We perform experiments using the
set of simple functions adopted from (Hansen et al.,
2014) and (Krause et al., 2017), and additionally, we
perform benchmarking using the CEC 2017 test suite
(Awad et al., 2016). Section 5 concludes the paper.
2 MATRIX ADAPTATION
STRATEGY
The MA-ES algorithm is outlined in Alg.1 while Alg.
2 shows the canonical version of CMA-ES. The con-
secutive steps of MA-ES resemble the classical ver-
sion of CMA-ES (Hansen, 2023). The state of the
algorithm consists of three parameters which are up-
dated in every iteration t: the expectation vector m
t
,
Warchulski, E. and Arabas, J.
Alternative Step-Size Adaptation Rule for the Matrix Adaptation Evolution Strategy.
DOI: 10.5220/0013012800003837
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 151-158
ISBN: 978-989-758-721-4; ISSN: 2184-3236
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
151

the matrix M
t
, and the evolution path vector s
t
used
for the step-size adaptation. After initialization of pa-
rameters (line 2), the algorithm samples in every iter-
ation the set of λ difference vectors d
t
(line 3), which
are utilized to define points in the search space x
t
(line
4). The sets of search points X
t
1: λ
and difference vec-
tors D
t
1: λ
are sorted according to their fitness. The
fraction of µ points with the best fitness and their cor-
responding difference vectors are used to update the
expectation vector m
t
(line 10), the evolution path
vector s
t
(line 11) and the matrix M
t
(line 12). Sim-
ilarly to CMA-ES, the step-size multiplier σ
t
is up-
dated according to the CSA rule (line 13).
The significant difference between MA-ES and
CMA-ES is expressed in the form of matrix M
t
and
the absence of evolution path p
t
. In contrast to CMA-
ES, the matrix M
t
is updated by taking into account
two summands: the outer product of the step-size evo-
lution path s
t
and the outer products of weighted dif-
ference vectors.
Due to limited space, we cannot rephrase the
derivation of the matrix M
t
from the covariance ma-
trix C
t
and removal of its evolution path p
t
. Interested
readers are referred to the original work of Beyer
(Beyer and Sendhoff, 2017).
Algorithm 1: Outline of MA-ES considered in the paper.
1: t ← 1
2: initialize(m
1
,σ
1
,λ, .. .)
3: s
1
← 0, M
1
← I
D
4: while !stop do
5: for i = 1 to λ do
6: d
t
i
∼ N(0,M
t
)
7: x
t
i
← m
t
+ σ
t
d
t
i
8: end for
9: evaluate (X
t
)
10: m
t+1
← ⟨X
t
⟩
µ
w
where
⟨X
t
⟩
µ
w
=
∑
µ
i=1
w
i
X
t
i:µ
11: s
t+1
← (1 −c
s
)s
t
+
p
µc
s
(2 −c
s
) ·⟨D
t
⟩
µ
w
12: M
t+1
← M
t
[I
n
+
c
1
2
(M
t
s
−I
n
) +
c
w
2
(M
t
D
−I
n
)]
where
M
t
s
= s
t
(s
t
)
T
M
t
D
= ⟨D
t
(D
t
)
T
⟩
µ
w
13: σ
t+1
← σ
t
exp

c
s
d
σ

∥s
t+1
∥
E∥N(0,I)∥
−1

14: t ←t + 1
15: end while
Algorithm 2: Outline of classic CMA-ES.
1: t ← 1
2: initialize(m
1
,σ
1
,C
1
)
3: p
1
← 0, s
1
← 0
4: while !stop do
5: for i = 1 to λ do
6: d
t
i
∼ N(0,C
t
)
7: x
t
i
← m
t
+ σ
t
d
t
i
8: end for
9: evaluate (X
t
)
10: m
t+1
← ⟨X
t
⟩
w
11: s
t+1
← (1 − c
s
)s
t
+
p
µc
s
(2 −c
s
) ·
(C
t
)
−
1
2
⟨D
t
⟩
µ
w
12: p
t+1
← (1 −c
p
)p
t
+
p
µc
p
(2 −c
p
) ·⟨D
t
⟩
µ
w
13: C
t+1
← (1 −c
1
−c
µ
)C
t
+ c
1
C
t
1
+ c
µ
C
t
µ
where
C
t
µ
=
1
µ
eff
⟨D
t
⟩
µ
w
, µ
eff
=
∑
µ
i=1
(w
i
)
2
C
t
1
= p
t
(p
t
)
T
14: σ
t+1
← σ
t
exp

c
s
d
σ

∥s
t+1
∥
E∥N(0,I)∥
−1

15: t ←t + 1
16: end while
3 STEP-SIZE ADAPTATION
The control of mutation strength in evolution strate-
gies proved to be a crucial mechanism for the conver-
gence of evolution strategy optimizers (Hansen and
Auger, 2014). In this study, we want to take a step
further toward a less numerically demanding CMA-
ES-based method by assessing lightweight alternative
step-size adaptation methods to the CSA. Although
the CSA derived in (Beyer and Sendhoff, 2017) does
not require computing inversion of
√
C as in the clas-
sic CMA-ES (line 11 in Algorithm 2), it still in-
volves vector operations and inherits all drawbacks of
the CSA pointed in (Beyer and Arnold, 2003), and
(Hansen, 2008). Therefore, we will only consider
methods based on the Rechenberg’s 1/5-th success
rule (Rechenberg, 1994) or techniques derived from
line-search methods (Salomon, 1998). Naturally, we
must exclude from our study methods like xNES-SA
(Glasmachers et al., 2010) or its derivations proposed
in (Krause et al., 2017) which are based on matrix
computations.
3.1 Cumulative Step-Size Adaptation
The core mechanism of CSA (Hansen and Oster-
meier, 2001) focuses on the norm of evolution path
s
t
which accumulates over iterations the values of ex-
pectation vectors m
t
scaled by ⟨D
t
⟩
µ
w
— see Algo-
rithm 3.
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
152

Algorithm 3: Cumulative Step-Size Adaptation (CSA).
1: s
t+1
← (1 −c
s
)s
t
+ c
s
√
µ
eff
⟨D
t
⟩
µ
w
2: σ
t+1
← σ
t
exp

c
s
d
σ

∥s
t+1
∥
E∥N(0,I)∥
−1

The philosophy behind CSA is based on the fol-
lowing two phenomena. The first phenomenon is re-
lated to the distance between the expectation vector
m
t
and the optimum of the fitness function. If they are
close, then the optimum is surrounded by the popula-
tion of points. Then, the selection will prefer shorter
difference vectors d
t
i
, reducing the length of s
t
. Thus,
it will also effect in reducing the value of σ
t
. The fur-
ther the expectation vector m
t
from the optimum, the
longer difference vectors will be selected, which will
result in the opposite effect, i.e., values of s
s
and of
σ
t
will be increased. The second phenomenon is the
correlation between consecutive evolution paths s
t
. If
the correlation is positive, then the values of σ
t
will be
increased. Otherwise, a negative correlation will lead
to decreased values of σ
t
.
3.2 Previous Population Midpoint
Fitness
Previous Population Midpoint Fitness (PPMF)
(Warchulski and Arabas, 2021) was introduced as
an attempt to generalize the Rechenberg’s 1/5-th
success rule for (µ/µ
w
,λ)-ES algorithms. The PPMF
is depicted on Algorithm 4.
Algorithm 4: Previous Population Midpoint Fitness
(PPMF).
1: m
t−1
←
1
λ
∑
λ
i=1
X
t−1
i
2: evaluate (m
t−1
)
3: p
t
s
←


{i : q(X
t
i
) < q(m
t−1
)}


/λ
4: σ
t+1
← σ
t
exp

1
d
σ
·
p
t
s
−p
t
1−p
t

The method is inspired by the step-size adaptation
mechanism employed in (1 + 1)-CMA-ES (Arnold
and Hansen, 2010) and utilizes the observations made
in (Arabas and Biedrzycki, 2017) about the posi-
tive impact of the midpoint on the evolution algo-
rithms performance. In each iteration, PPMF esti-
mates the success probability p
t
s
by calculating the
ratio of points from the current generation with bet-
ter fitness value than the arithmetic midpoint from the
previous generation m
t−1
. The step-size is adapted in
an exponential fashion. The method is controlled via
damping factor d
σ
and target probability p
t
parame-
ters.
3.3 Median Success Rule
Another attempt to generalize the 1/5-th success rule
for (µ/µ
w
,λ)-ES is the Median Success Rule (MSR)
(Ait Elhara et al., 2013) — see Algorithm 5.
Algorithm 5: Median Success Rule (MSR).
1: K
s
←
|
{i : q(X
t
i
) < q(X
k:λ−1
)}
|
/λ
2: z
t
←
2
λ
·

K
s
−
λ+1
2

3: p
t+1
s
← (1 −c
σ
)p
t
s
+ c
σ
·z
t
4: σ
t+1
← σ
t
exp

p
s
d
σ

The core idea of MSR is to compare the current
generation’s fitness values to the chosen k-th per-
centile of fitness values from the previous genera-
tion. The method estimates the success probability
p
s
, which is used to calculate normalizing statistic z
t
.
The step-size is adapted exponentially according to
the smoothed value of z
t
and damping factor d
σ
. Pa-
rameters of MSR are the percentile k, the smoothing
factor c
σ
, and the dumping factor d
σ
.
3.4 Population Success Rule
The Population Success Rule (PSR), which was in-
troduced in (Loshchilov, 2015), is presented as Algo-
rithm 6.
Algorithm 6: Population Success Rule (PSR).
1: r
t
,r
t−1
← ranks of q
t
,q
t−1
in q
t
∪q
t−1
2: z
t
psr
←
∑
λ
i=1
r
t−1
(i)−r
t
(i)
λ
2
−z
⋆
3: z
t+1
← (1 −c
σ
)z
t
+ c
σ
z
t
psr
4: σ
t+1
← σ
t
exp

z
t+1
d
σ

The PSR is derived from the MSR with the as-
sumption that the base method may be enhanced if
the success probability p
t
s
is calculated by taking into
account fitness values from the previous and current
generations. In each iteration, the PSR constructs
rank r
t
and r
t−1
of points from current and previ-
ous generations using the set of mixed fitness values
q
t
∪q
t−1
. Then, ranks are used to calculate enhanced
z
t
statistics. Further steps are the same as in the MSR
method. The PSR is controlled by target probabil-
ity z
⋆
, damping factor d
σ
, and exponential smoothing
factor c
σ
.
Alternative Step-Size Adaptation Rule for the Matrix Adaptation Evolution Strategy
153

3.5 Two-Point Adaptation
The Two-point Adaptation (TPA) rule was introduced
in (Hansen, 2008). In contrast to CSA or generalized
versions of the 1/5-th success rule, TPA relies solely
on the optimizer runtime trajectory and does not as-
sume an internal model of optimality regarding the
step-size values. Algorithm 7 outlines the TPA.
Algorithm 7: Two-point adaptation (TPA).
1: q
+
← q(m
t
+ α
′
σ
t
⟨D
t
⟩
µ
w
)
2: q
−
← q(m
t
−α
′
σ
t
⟨D
t
⟩
µ
w
)
3: α
act
← I
q
−
<q
+
{−α + β < 0}+ I
q
−
≥q
+
{α > 0}
4: α
s
← (1 −c
α
)α
s
+ c
α
α
act
5: σ
t+1
← σ
t
exp(α
s
)
The method requires computing fitness of two ad-
ditional points, i.e., q
−
and q
+
. These values are
used to calculate the α
s
parameter employed to update
step-size σ
t
values exponentially. The TPA relies on
the following parameters: smoothing factor c
σ
, test
width coefficient α
′
, changing factor α, and update
bias β.
4 NUMERICAL VALIDATION
We performed two types of numerical experiments to
assess the overall dynamic of MA-ES equipped with
different step-size adaptation mechanisms.
The convergence rates were evaluated by running
each optimizer on a set of basic optimization prob-
lems with different properties. As a well-conditioned
problem, we used the sphere function. For ill-
conditioned problems, we selected cigar and ellip-
soid functions. The ellipsoid function was parame-
terized by the condition coefficient k. We also in-
cluded the Rosenbrock function as an example of a
non-convex problem, which is challenging for solvers
to optimize due to the narrow valley. Equations 1-
4 present the set of considered functions. For each
problem and optimizer, we ran 50 runs independently
and recorded the best-so-far value for the following
dimensions: D = 10,50,100, 200. Each optimizer
was terminated after 100·D iterations and was started
in point x
0
= [100, .. ., 100]
D
. The results from exper-
iments were averaged and presented as convergence
curves.
The second type of experiment was the bench-
marking using the standard CEC’2017 suite of prob-
lems. We investigated the performance of MA-ES,
coupled with considered step-size adaptation, on dif-
ferent classes of optimization functions with different
Optimization problems used to assess the convergence dy-
namics of different MA-ES variants: (1) Sphere (2) Ellip-
soid (3) Cigar (4) Rosenbrock.
q(x) =
D
∑
i=1
x
2
i
(1)
q(x) =
D
∑
i=1
k
i−1
D−1
x
2
i
(2)
q(x) = x
2
1
+ 10
6
D
∑
i=2
x
2
i
(3)
q(x) =
D−1
∑
i=1
h
100

x
i+1
−x
2
i

2
+ (1 −x
i
)
2
i
(4)
difficulty and dimension numbers. The CEC’2017
benchmark suite is split into four classes of opti-
mization problems: unimodal (F1-F3), multimodal
(F4-F10), hybrid functions (F11-F20), and composi-
tion functions (F21-F30). Hybrid and complex func-
tions are the product of composing selected unimodal
and multimodal functions in two different manners.
To resemble real-world problems, the hybrid func-
tions divide the decision variables into components
with different properties. In contrast, the composition
functions merge the properties of selected component
(unimodal or multimodal) functions. Additionally,
each function is geometrically transformed by shift-
ing, rotating, or scaling. We conducted numerical ex-
periments on CEC’2017 following the rules specified
in (Awad et al., 2016). The only difference between
the official specification and our setup was that we
did not exclude the sum of different powers functions
from the benchmark set. The specification authors re-
moved this function after the competitions, although
most software libraries implement or re-implement
CEC functions with the mentioned function. The re-
sults of the experiments are demonstrated as ECDF
plots (Hansen, 2018) aggregated over each problem
class.
4.1 Parameter Setup
Each MA-ES variant shares the same standard values
for general parameters like the population size λ, or
matrix update coefficients c
1
,c
w
suggested in (Beyer
and Sendhoff, 2017). The initial value for step-size
σ
0
was set to 1.
Specific parameters of step-size adaptation rules
were set to the values recommended by their authors.
We treat each adaptation rule as a drop-in replace-
ment, so we perform no parameter tuning. Contrary
to the opinion expressed in (Krause et al., 2017), we
do not believe that experiments on non-tunned meth-
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
154

ods may lead to biases and unfair comparisons. Each
considered step-size adaptation mechanism was in-
troduced with the recommended parameter values.
We assume that the authors investigated their meth-
ods and recommended values shall ensure satisfactory
performance on various optimization problems.
The parameters for step-size adaptation mecha-
nisms used to conduct numerical experiments are
listed below:
1. CSA: following the (Beyer and Sendhoff, 2017),
we set the damping factor to
d
σ
= 1 + c
s
+ 2max(0,
q
µ
eff
−1
D+1
−1) where c
s
=
µ
eff
+2
µ
eff
+D+5
2. TPA: following the (Hansen, 2008), we set α
′
=
0.5, α = 0.5, β = 0, and c
σ
= 0.3
3. MSR: following the (Ait Elhara et al., 2013), we
set k = 0.3λ, c
σ
= 0.3, and damping factor to d
σ
=
2D−2
D
4. PPMF: following the (Warchulski and Arabas,
2021), we set d
σ
= 0.2, and p
t
= 0.1
5. PSR: following the (Loshchilov, 2015), we set
z
⋆
= 0.25, c
σ
= 0.3, d
σ
= 1.
All performed experiments can be reproduced by us-
ing source code and containerized environment avail-
able in the repository https://github.com/ewarchul/
maes-2024.
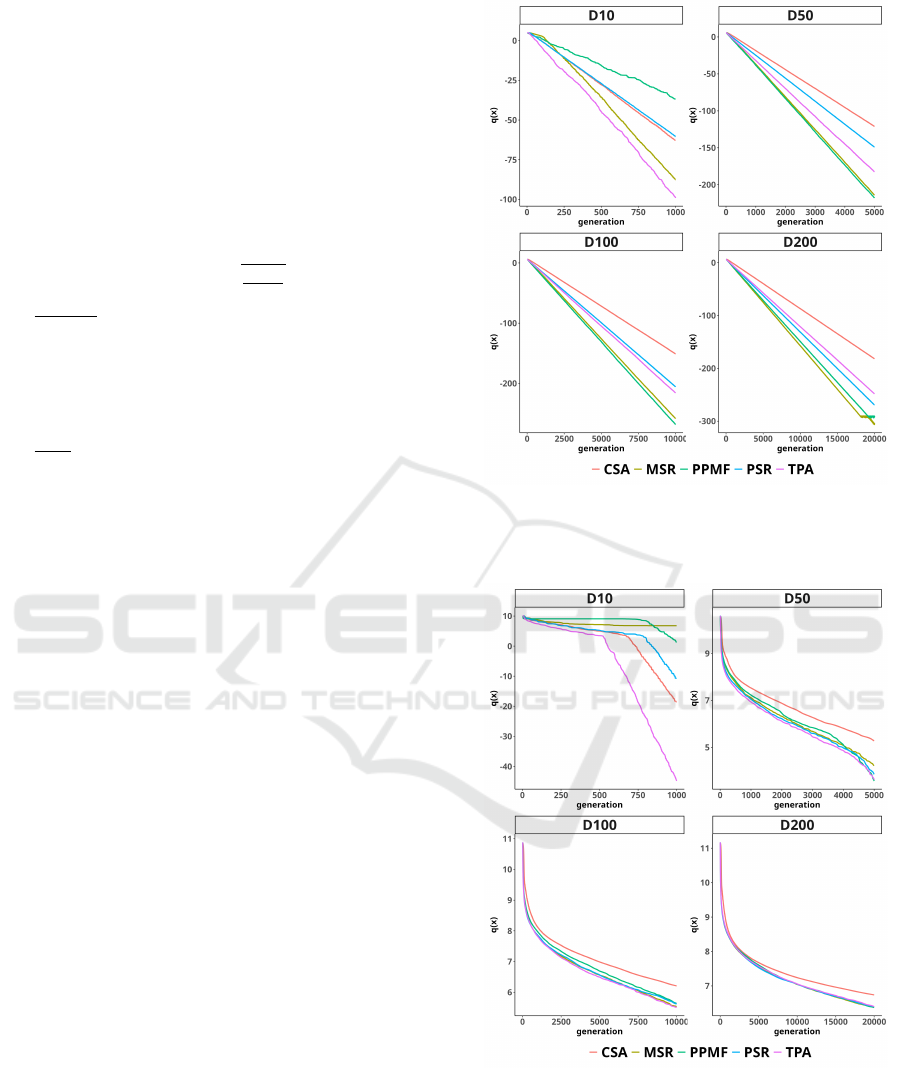
4.2 Convergence Dynamics
The convergence curves obtained for the sphere func-
tion are presented in Fig. 1. The results show that
alternative methods exhibit faster convergence for al-
most every dimension than CSA. For dimension D =
10, the PPMF is the slowest method, but its dynamic
differs for greater dimensions where it, together with
MSR, outperforms other methods. Such behavior
may indicate too aggressive step-size reduction, lead-
ing to premature convergence on multimodal func-
tions. On both ellipsoid functions and the cigar func-
tion depicted respectively in Fig. 5, Fig. 2, and Fig. 4
similar effects can be observed. The 1/5-th success
rule variants and TPA rapidly reduce step-size, but
the gap between them and CSA decreases with the
growing dimension. The performance of each MA-
ES variant is similar on the Rosenbrock function in
Fig 3. In 10 dimensions, the PPMF reveals the worst
convergence, but with increasing dimensions - the gap
between variants diminishes.
Figure 1: Semi-log convergence plot of the best-so-far solu-
tion for MA-ES coupled with different step-size adaptation
rules on the sphere function in 10, 50, 100, and 200 dimen-
sions.
Figure 2: Semi-log convergence plot of the best-so-far so-
lution for MA-ES coupled with different step-size adapta-
tion rules on the ellipsoid function with condition coeffi-
cient k = 10 in 10, 50, 100, and 200 dimensions.
4.3 CEC’2017 Benchmarking
According to the benchmark results for problems in
10 dimensions depicted in Fig. 6, on unimodal prob-
Alternative Step-Size Adaptation Rule for the Matrix Adaptation Evolution Strategy
155

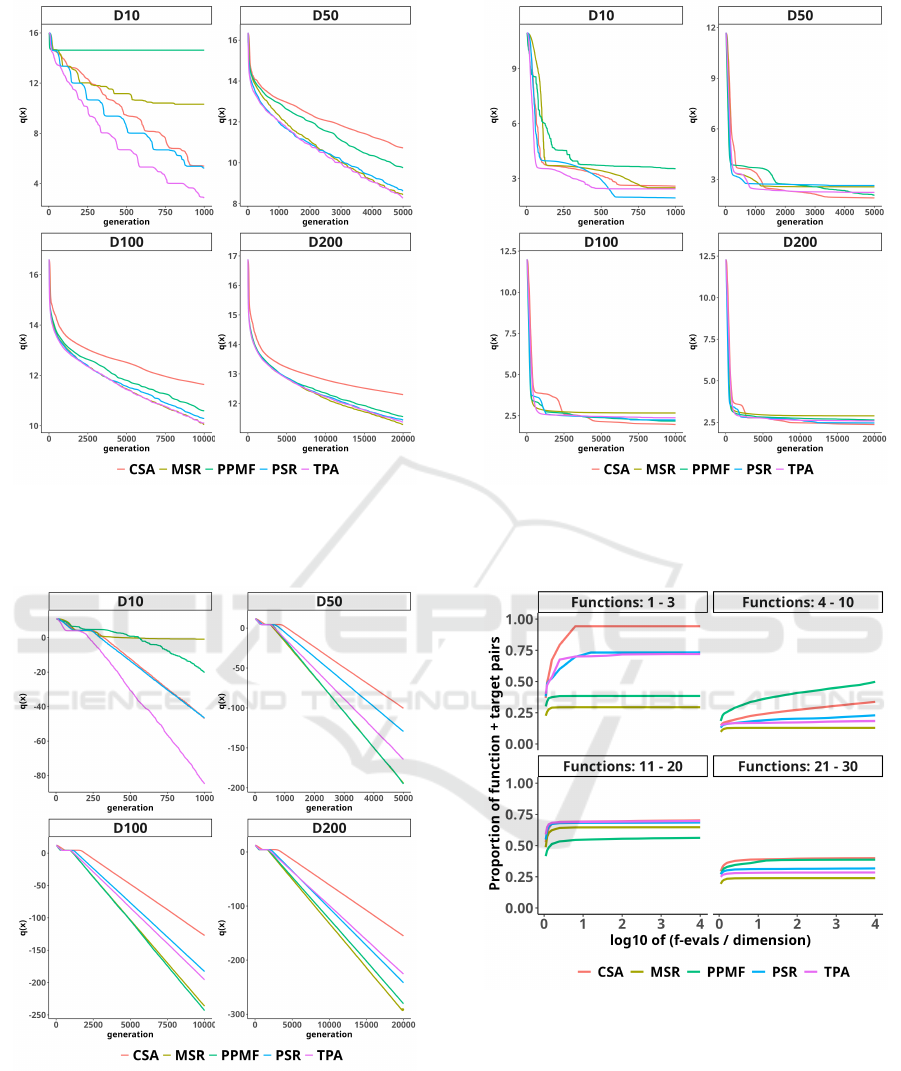
Figure 3: Semi-log convergence plot of the best-so-far so-
lution for MA-ES coupled with different step-size adapta-
tion rules on the ellipsoid function with condition coeffi-
cient k = 100 in 10, 50, 100, and 200 dimensions.
Figure 4: Semi-log convergence plot of the best-so-far solu-
tion for MA-ES coupled with different step-size adaptation
rules on the cigar function in 10, 50, 100, and 200 dimen-
sions.
lems, the MA-ES coupled with CSA outperformed
each alternative method. However, the performance
on more complex functions is comparable between
Figure 5: Semi-log convergence plot of the best-so-far solu-
tion for MA-ES coupled with different step-size adaptation
rules on the Rosenbrock function in 10, 50, 100, and 200
dimensions.
Figure 6: Results for MA-ES coupled with different step-
size adaptation rules on CEC’2017 in 10 dimensions.
each method. On multimodal functions, the PPMF
achieved better performance than other variants. The
same effect can be observed for problems in 30 di-
mensions presented in Fig. 7, i.e., CSA is superior
only on unimodal functions. In 50 dimensions shown
in Fig. 8, the performance gap on basic multimodal
and composition functions between PPMF and other
methods increases in favor of PPMF. The method with
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
156

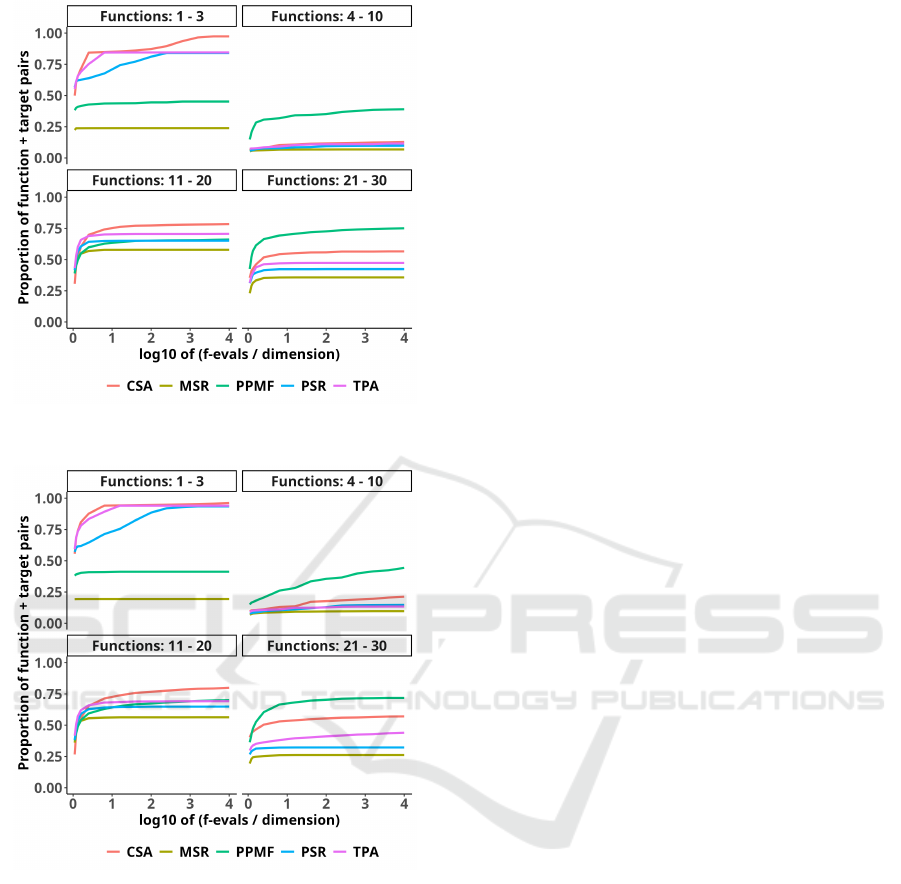
Figure 7: Results for MA-ES coupled with different step-
size adaptation rules on CEC’2017 in 30 dimensions.
Figure 8: Results for MA-ES coupled with different step-
size adaptation rules on CEC’2017 in 50 dimensions.
the worst performance for each dimension is MSR,
which may indicate sensitivity to the parameters setup
or recommended values not being generic enough to
combine well with MA-ES. The TPA and PSR vari-
ants reveal almost identical performance, which was
slightly worse than CSA.
5 CLOSING REMARKS
We demonstrate that the MA-ES algorithm can be ac-
companied with different cumulative step-size adap-
tation techniques that involve different mechanisms
than CSA. For specific optimization problems, MA-
ES coupled with the alternative methods performs
more efficiently than CSA. Among the analyzed step-
size adaptation methods, PPMF is quite competitive,
particularly in higher dimensions and when the opti-
mization problem is highly multimodal.
REFERENCES
Ait Elhara, O., Auger, A., and Hansen, N. (2013). A me-
dian success rule for non-elitist evolution strategies:
study of feasibility. In Proceedings of the 15th An-
nual Conference on Genetic and Evolutionary Com-
putation, GECCO ’13, page 415–422, New York, NY,
USA. Association for Computing Machinery.
Arabas, J. and Biedrzycki, R. (2017). Improving evolution-
ary algorithms in a continuous domain by monitoring
the population midpoint. IEEE Transactions on Evo-
lutionary Computation, 21(5):807–812.
Arnold, D. V. and Hansen, N. (2010). Active covari-
ance matrix adaptation for the (1+1)-cma-es. In Pro-
ceedings of the 12th Annual Conference on Genetic
and Evolutionary Computation, GECCO ’10, page
385–392, New York, NY, USA. Association for Com-
puting Machinery.
Awad, N. H., Ali, M., Liang, J., Qu, B., and Suganthan,
P. N. (2016). Problem definitions and evaluation cri-
teria for the CEC 2017 special session and competi-
tion on real-parameter optimization. Technical report,
Nanyang Technol. Univ., Singapore and Jordan Univ.
Sci. Technol. and Zhengzhou Univ., China.
Beyer, H.-G. and Arnold, D. (2003). Qualms regarding
the optimality of cumulative path length control in
csa/cma-evolution strategies. Evolutionary computa-
tion, 11:19–28.
Beyer, H.-G. and Sendhoff, B. (2017). Simplify
your covariance matrix adaptation evolution strat-
egy. IEEE Transactions on Evolutionary Computa-
tion, 21(5):746–759.
Glasmachers, T., Schaul, T., Yi, S., Wierstra, D., and
Schmidhuber, J. (2010). Exponential natural evolution
strategies. In Proceedings of the 12th Annual Con-
ference on Genetic and Evolutionary Computation,
GECCO ’10, page 393–400, New York, NY, USA. As-
sociation for Computing Machinery.
Hansen, N. (2008). Cma-es with two-point step-size adap-
tation.
Hansen, N. (2018). A practical guide to experimentation.
In Proceedings of the Genetic and Evolutionary Com-
putation Conference Companion, GECCO ’18, page
432–447, New York, NY, USA. Association for Com-
puting Machinery.
Hansen, N. (2023). The cma evolution strategy: A tutorial.
Hansen, N., Atamna, A., and Auger, A. (2014). How to as-
sess step-size adaptation mechanisms in randomised
search. In Bartz-Beielstein, T., Branke, J., Filipi
ˇ
c, B.,
and Smith, J., editors, Parallel Problem Solving from
Alternative Step-Size Adaptation Rule for the Matrix Adaptation Evolution Strategy
157

Nature – PPSN XIII, pages 60–69, Cham. Springer In-
ternational Publishing.
Hansen, N. and Auger, A. (2014). Principled Design of
Continuous Stochastic Search: From Theory to Prac-
tice, pages 145–180. Springer Berlin Heidelberg,
Berlin, Heidelberg.
Hansen, N., Müller, S. D., and Koumoutsakos, P. (2003).
Reducing the time complexity of the derandomized
evolution strategy with covariance matrix adaptation
(cma-es). Evolutionary Computation, 11(1):1–18.
Hansen, N. and Ostermeier, A. (2001). Completely deran-
domized self-adaptation in evolution strategies. Evol.
Comput., 9(2):159–195.
Krause, O., Glasmachers, T., and Igel, C. (2017). Quali-
tative and quantitative assessment of step size adapta-
tion rules. In Proceedings of the 14th ACM/SIGEVO
Conference on Foundations of Genetic Algorithms,
FOGA ’17, page 139–148, New York, NY, USA. As-
sociation for Computing Machinery.
Loshchilov, I. (2015). Lm-cma: An alternative to l-bfgs
for large-scale black box optimization. Evolutionary
computation, 25.
Rechenberg, I. (1994). Evolutionsstrategie. Arbeitstagung
der Freien Akademie Berlin,.
Salomon, R. (1998). Evolutionary algorithms and gradient
search: similarities and differences. IEEE Transac-
tions on Evolutionary Computation, 2(2):45–55.
Warchulski, E. and Arabas, J. (2021). A new step-size adap-
tation rule for cma-es based on the population mid-
point fitness. In 2021 IEEE Congress on Evolutionary
Computation (CEC), pages 825–831.
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
158