Step Size Control in Evolutionary Algorithms for Neural

Architecture Search

Christian Nieber

1 a

, Douglas Mota Dias

2 b

, Enrique Naredo Garcia

3 c

and Conor Ryan

1 d

Department of Computer Science and Information Systems, University of Limerick, Limerick, Ireland

Department of Computer Science & Applied Physics, Atlantic Technological University, Galway, Ireland

Departamento de Ciencias Básicas, Universidad del Caribe, Cancun, Mexico

Keywords: Step Size Control, Evolutionary Algorithms, Neural Architecture Search, Lightweight CNNs, MNIST, LeNet.

Abstract: This work examines how evolutionary Neural Architecture Search (NAS) algorithms can be improved by

controlling the step size of the mutation of numerical parameters. The proposed NAS algorithms are based on

F-DENSER, a variation of Dynamic Structured Grammatical Evolution (DSGE). Overall, a (1+5)

Evolutionary Strategy is used. Two methods of controlling the step size of mutations of numeric values are

compared to Random Search and F-DENSER: Decay of the step size over time and adaptive step size for

mutations. The search for lightweight, LeNet-like CNN architectures for MNIST classification is used as a

benchmark, optimizing for both accuracy and small architectures. An architecture is described by about 30

evolvable parameters. Experiments show that with step size control, convergence is faster, better performing

neural architectures are found on average, and with lower variance. The smallest architecture found during

the experiments reached an accuracy of 98.8% on MNIST with only 5,450 free parameters, compared to the

62,158 parameters of LeNet-5.

1 INTRODUCTION

1.1 Neural Architecture Search

Deep Convolutional Neural Networks (CNNs) are

used for state-of-the-art (SOTA) image classification

and segmentation tasks, like recognizing objects in a

street scene. Designing and optimizing CNNs and

other high-performing neural architectures is

challenging and requires expert knowledge. Hence,

there is great interest in automating the search for a

well-performing neural architecture for a given

problem. An extensive overview of current NAS

methods was conducted by (White et al., 2023).

Search spaces used for NAS can be conceptually

grouped as narrow or wide. A narrow search space is

one with few free variables, often of a single type

(numeric or topological), where layer arrangement

constraints, variables and their ranges are chosen to

closely match architectures known to work well.

https://orcid.org/0009-0002-6208-4097

https://orcid.org/0000-0002-1783-6352

https://orcid.org/0000-0001-9818-911X

https://orcid.org/0000-0002-7002-5815

Numeric parameters are often constrained to a small

set of values. In this work, a wide search space is

understood as one using a wider range of layer

arrangements, more parameters of more varied types,

larger numeric ranges, and continuous values. A wide

search space can also be characterized as one

containing only a small proportion of high-

performing architectures.

(Yang et al., 2019) and (Yu et al., 2020) have

shown that several state-of-the-art NAS methods like

DARTS, PNAS and ENAS do not perform much

better than randomly sampling their search space:

“the small range of accuracies obtained [by random

sampling] hints at narrow search spaces, where even

the worst architectures perform reasonably well”

(Yang et al., 2019)

This paper proposes using relatively wide search

spaces on lightweight CNNs as a benchmark so that

NAS methods can be compared more reliably.

288

Nieber, C., Dias, D., Garcia, E. and Ryan, C.

Step Size Control in Evolutionary Algorithms for Neural Architecture Search.

DOI: 10.5220/0013013800003837

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 288-295

ISBN: 978-989-758-721-4; ISSN: 2184-3236

1.2 Contribution

We explore the question of how step size control can

improve evolutionary NAS algorithms. In this work,

step size control is understood as the algorithmic

control of the magnitude of mutations of numeric

parameters and, in some cases, the probability of

mutations of network topology or categorical

parameters. We propose two simple methods of step

size control, which we call Stepper algorithms. In

Stepper-Decay, a single global step size parameter

decays over time. In Stepper-Adaptive, a step size

parameter is associated with each individual and is

subject to mutation and selection so that the step size

can slowly be adapted towards an optimal value.

To assess the effectiveness of these algorithms,

we developed a benchmark using lightweight CNN

architectures that is relatively fast to compute, has, on

average, about 30 evolvable parameters, and a wider

search space than almost any published NAS

benchmark. The Stepper algorithms are compared to

the F-DENSER algorithm, which they are based on

(which has no step size control), and additionally to

Random Search. The fitness function is chosen so that

the search optimizes for 1) low error rate and 2) small

architectures.

The experiments show that with these simple

methods of step size control, convergence is faster,

better performing neural architectures are found on

average, and with lower variance.

2 BACKGROUND AND RELATED

WORK

2.1 Evolution Strategies and Step Size

Control

Evolution Strategies (ES) are robust optimization

algorithms often used for black box optimizations on

real-valued parameter spaces (Rechenberg, 1994;

Schwefel, 1995). They were originally developed

mainly for engineering problems.

While step size control is rarely used with Genetic

Algorithms (Holland, 1992), it is widely used with

ESs, starting with Rechenberg’s 1/5

rule

(Rechenberg, 1965). Many variations were explored,

including Self-adaptive ES (Schwefel, 1995) and

Differential Evolution (Storn & Price, 1997). CMA-

ES (Hansen & Ostermeier, 2001) is a SOTA

optimizer for continuous black-box functions. It can

be interpreted as controlling a step size not only for

each parameter but also for each pair of parameters.

(Loshchilov et al., 2013) showed that CMA-ES

performed best out of more than 100 classic and

modern optimizers on a wide range of black-box

benchmark functions.

(Droste & Wiesmann, 2000) and (Li et al., 2013)

suggest guidelines for the choice of mutation

operators, including Locality (Solutions can be

gradually improved, and mutations can generate

similar solutions) and Scalability (An efficient

method should be used to control the strength of the

impact of the mutation operator on the fitness values).

2.2 Genetic Algorithms and

F-DENSER

Genetic Algorithms apply mutation, recombination

and selection on a bit string representing an individual

(Holland, 1992). Genetic Programming is an

extension of this concept to the evolution of functions

built from inputs, constants, and operators (Cramer,

1985; Koza, 1989). Grammatical Evolution (GE) is a

genetic algorithm that evolves programs that conform

to context-free grammar (Ryan et al., 1998).

The search algorithm used in this work is based

on Fast DENSER, also called F-DENSER (Assunção

et al., 2019). DENSER (Assunção et al., 2018) is an

extension of Dynamic Structured Grammatical

Evolution (DSGE) (Assunção et al., 2017). DENSER

used a population of 100 for 100 generations. F-

DENSER introduced a



  



 ES and removed

crossover. Instead of using DSGE mutations, specific

probabilities of 15-25% are used for the different

kinds of layer mutations. This reduced the number of

evaluations drastically without compromising the

performance of generated solutions.

3 THE BENCHMARK PROBLEM

A benchmark problem for NAS algorithms should

have the following properties:

Rapid Evaluation: an evaluation means the

complete training of an architecture on the training

data and the measurement of the classification error

rate on test data.

Relatively Wide, Realistic Search Space: the search

space and fitness function should have properties

similar to those of hard SOTA problems.

Reproducibility of Evaluations: the fitness function

should have a low noise-to-signal ratio.

MNIST classification is an easy problem by today’s

standards. We decided to use it for benchmarking at

this early stage, because models can be trained

relatively quickly. As a starting point, we used A

Step Size Control in Evolutionary Algorithms for Neural Architecture Search

289

modernized Variant of LeNet-5 from Kaggle (Sultan,

2022) that can be fully trained on a GPU in 10-20

seconds.

It is easy to reach error rates below 1.5% on

MNIST with variants of LeNet. There are various

techniques to reduce the error rate further, like data

augmentation, dropout regularization or using

ensembles. We didn’t find these useful for a

benchmark because they increase training time.

3.1 The Fitness Function

We chose to optimize neural architectures for both

accuracy (low error rate) and small network size (low

number of trainable parameters) to make NAS on

MNIST more challenging and to reduce training times.

There are two common approaches to optimize

for two objectives: multi-objective optimization and

using a penalty function that combines multiple

objectives into a single fitness function. Multi-

objective optimization may be interesting to explore

in future research. However, this cannot be done with

an unmodified



  



 ES.

The fitness function is:

  

















(1)

 is usually computed after training on

53,000 images for ten epochs.

 is the number of free trainable

parameters in the neural network model.

The rationale is that a low error rate is more

important than minimizing parameters, so the error

rate is squared. The constants were chosen so that (i)

the fitness of A Modern Variant of Lenet-5 is near

zero (this has 62,158 parameters and an error rate of

1.25%), and (ii) halving the original number of

parameters compensates an increase in the error rate

from 1% to 



.

Any fitness above zero is considered an

improvement. The best-observed fitness was 2.2.

3.2 The Grammar and Search Space

The grammar used in the experiments describes

LeNet/AlexNet/VGG-like architectures. It uses

extensions to the BNF for numeric and categorical

variables, for example

[num-filters,int,2,256]

defines an integer variable num-filters with a

range from 2 to 256, and

[act:linear/relu/elu/sigmoid]

defines a categorical variable act that can assume

four values. Boolean variables are treated like

categoricals with two values.

Here is the grammar used in the experiments:

| <pooling>

<convolution> ::= layer:conv

[num-filters,int,2,256]

[filter-shape,int,2,5]

[stride,int,1,3]

[act:linear/relu/elu/sigmoid]

[padding:same/valid]

[bias:True/False]

[batch-norm:True/False]

<pooling> ::= layer:pooling

[pooling-type:avg/max]

[kernel-size,int,2,5]

[stride,int,1,3]

[padding:same/valid]

<classification> ::= layer:fc

[act:linear/relu/elu/sigmoid]

[num-units,int,64,2048]

[bias:True/False]

[batch-norm:True/False]

<output> ::= layer:output num-units:10

bias:True

[batch_size,int,50,2048]

| <rmsprop>

[batch_size,int,50,2048]

| <adam> [batch_size,int,50,2048]

<gradient-descent> ::=

learning:gradient-descent

[lr,float,0.0001,0.1]

[momentum,float,0.68,0.99]

[nesterov:True/False]

<rmsprop> ::= learning:rmsprop

[lr,float,0.0001,0.1]

[rho,float,0.5,1]

<adam> ::= learning:adam

[lr,float,0.0001,0.1]

[beta1,float,0.5,1]

[beta2,float,0.5,1]

The symbols shown in bold are top-level symbols

corresponding to layer groups. There are 1 to 10

layers in the feature group (of type convolution or

pooling), followed by one to five layers in the

classification group. Finally, a fixed output layer of

ten units is added. A dummy layer group learning

defines the learning optimizer that applies to the

whole architecture.

An equivalent grammar was used in the

experiments with F-DENSER. We estimate the size

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

290

of the relevant search space

to be 10

combinations.

According to the overview of NAS benchmarks in

(White et al., 2023), most search spaces used for

benchmarks are much smaller.

4 THE NAS ALGORITHMS

4.1 Mutation Operators for NAS

For each generated offspring, only a few variables

and topological parameters are chosen for mutation.

The probability of mutating a variable or a layer

group is 0.15 in Stepper so that only a few parameters

(usually 2 to 5) are mutated for each new individual.

Special mutation operators are applied to layers in

the features and classification groups. For each of the

following operators, a layer group is selected, and

then a layer in it is chosen at random.

Copy Layer: a layer is copied and inserted at a

random position in the layer group.

Add Layer: a new layer with random type and

parameters is created and inserted at a random

position in the layer group.

Remove Layer: a layer is deleted from the group.

Change Layer Type: the type of a layer is changed;

all its parameters are randomly reset.

If a mutation would violate the minimum or

maximum constraint of layers per group, another

mutation operator is randomly chosen instead. The

number of layer mutations in a group is chosen

randomly so that at least one mutation is applied, two

mutations are relatively common, and three happen

occasionally.

Individuals had, on average, about five layers and

four variables per layer. This results in about 0.75

layer mutations and three variable mutations per

offspring generated.

When mutations result in an invalid individual

(e.g., Keras error), offspring generation will start

over.

4.2 Mutation Step Size Control

This work introduces algorithmic control of the

mutation step size to NAS. Step size control is widely

used in ES. ES is usually applied to search spaces

where all parameters are real-valued. However, most

parameters describing neural architecture are

integers, categorical values, or layer architecture

parameters. In the experiments, the architectures had

about ten integers, 14 categorical and two real-valued

parameters (the exact number depends on the number

and type of layers). Real value calculations can be

adapted to integers by rounding the result. This

approach was followed by (Loshchilov & Hutter,

2016), where step size control in the form of CMA-

ES was extended to integer parameters but only to

those with a large range.

Table 1 shows the mutation operators of the Stepper

algorithms in comparison to F-DENSER.

is the

algorithmically controlled step size, which is

associated with a generation for Stepper-Decay and

with an individual in Stepper-Adaptive. 







is a

Gaussian-distributed random variable with a mean 

and standard deviation , and the range of a mutable

variable is max  min.

Special care must be taken if a mutated numerical

value falls outside the allowed interval. If values were

simply clipped to the interval, this would introduce an

additional bias into the distribution. To minimize this

bias, the interval transformation described in (Li et

al., 2013) is used. Intuitively, it reflects values outside

of the interval back into the interval.

4.3 Initialization of Individuals

The number of feature layers is chosen at random to

be two, three, or four, followed by one classification

layer. The layer type is chosen at random, and the

layer is initialized with random values within the

parameter’s ranges. The same applies to the learning

pseudo-layer.

Table 1: Mutation operators in F-DENSER and the Stepper Algorithms. is the algorithmically controlled step size, and

Range max  min is the range of a mutable variable.

Type of mutation

F-DENSER

Stepper-Decay and Stepper-Adaptive

copy layer, remove layer

fixed probability

add layer, change layer type

fixed probability

probability proportional to 

Floating point

add 







 Range

add 







 Range

Integer

random resetting

Add 











 Range+1



Categorical value

random resetting

Assuming 1000 significant discrete values for

continuous values, and a maximum of 3 convolutional, 3

pooling and 2 fully connected layers. A larger number of

layers was almost never reached during searches.

Step Size Control in Evolutionary Algorithms for Neural Architecture Search

291

5 EXPERIMENTAL SETUP

5.1 MNIST Dataset

MNIST consists of 60,000   grey level

pictures in the training set and 10,000 in the test set.

The training set is triple split into 53,000 training (for

training architectures), 3,500 validation (to calculate

the loss during training) and 3,500 test samples (for

calculating the error rate of a trained model). The

10,000 test set is only used to calculate the final error

rate for the results of the NAS search.

Preliminary NAS searches were run with ten and

30 training epochs. We observed no significant

difference in the behavior; even the final error rate

was similar. Ten training epochs were used in the

experiments to minimize computation time.

5.2 Implementation

The Python code of this work started with the F-

DENSER code. The main author rewrote most of it

and added the collection of more statistics, caching of

results, and recording of the evolutionary history

Experiments were run with Keras/TensorFlow on

an NVIDIA GeForce RTX 2070 Super from 2019.

5.3 Benchmark Experiments

All NAS algorithms use a



  



 ES for 200

generations, so one run evaluates 1,000 architectures.

F-DENSER is used as a baseline, with the

modification that batch normalization is applied after

the activation function. The original paper about

batch normalization proposed this (Ioffe & Szegedy,

2015), and it appears to be more effective.

For comparison, a Random Search is run. It’s

limited to five feature layers and one classification

layer because nearly all best-performing architectures

were observed in this subspace.

5.4 Experiment 1: Stepper-Decay

As a simple way of controlling a global step size, we

introduce the Stepper-Decay algorithm, which

reduces the step size over time. The rationale is that

NAS should initially explore large sections of the

search space and be able to jump out of a local

optimum; later, when it has found a reasonably good

solution, large steps will probably lead it away from

Source code and additional materials for this article

are available on https://github.com/ChristianNieber/

nas_on_cnns

the (local) optimum, while small steps can bring it

closer to it.

 is the standard deviation of a normal distribution of

random values that generate the mutation steps. 

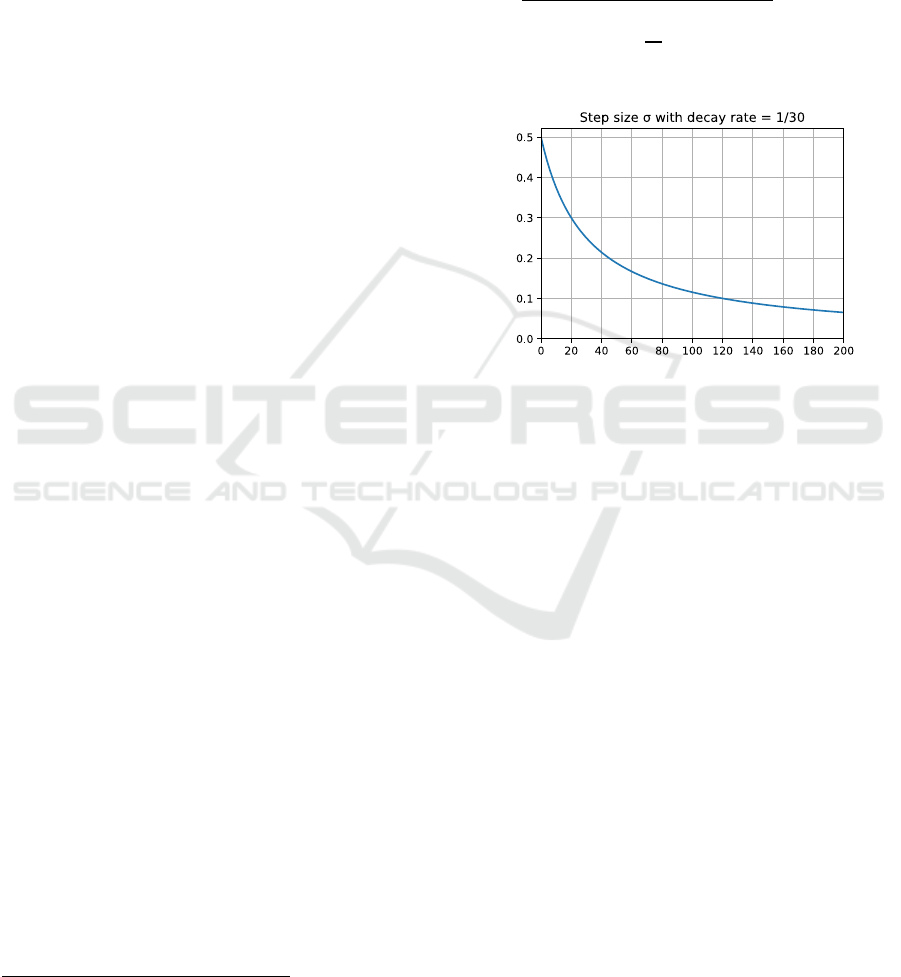
starts at 0.5 in the first generation and decays to 

in the 200th generation. The decay function (shown

in Figure 1) is:













  

  

(2)

where  





, which was determined in a

few experiments.

Figure 1: Decay of the step size  over generations in the

Stepper-Decay experiment.

The mutation operations add layer and change

layer type that randomly reset parameters are

subjected to an analog decay of their probabilities.

Other layer mutations and categorical values are not

affected.

5.5 Experiment 2: Stepper-Adaptive

As a more refined method of step size control, we

propose the Stepper-Adaptive algorithm, where every

individual carries its own mutation step size. This is

based on Derandomized Self-Adaptation of Evolution

Strategies (Hansen & Ostermeier, 2001; Ostermeier

et al., 1994), but modified so that only a few of the

possible variables (usually 2 to 5) are mutated to

generate each offspring.

For each offspring, a new mutation step size is

generated from the parent’s step size:





















(3)

Where 









is the step size or standard deviation

used to generate mutations of individual  in

generation , 







is the step size associated with the

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

292

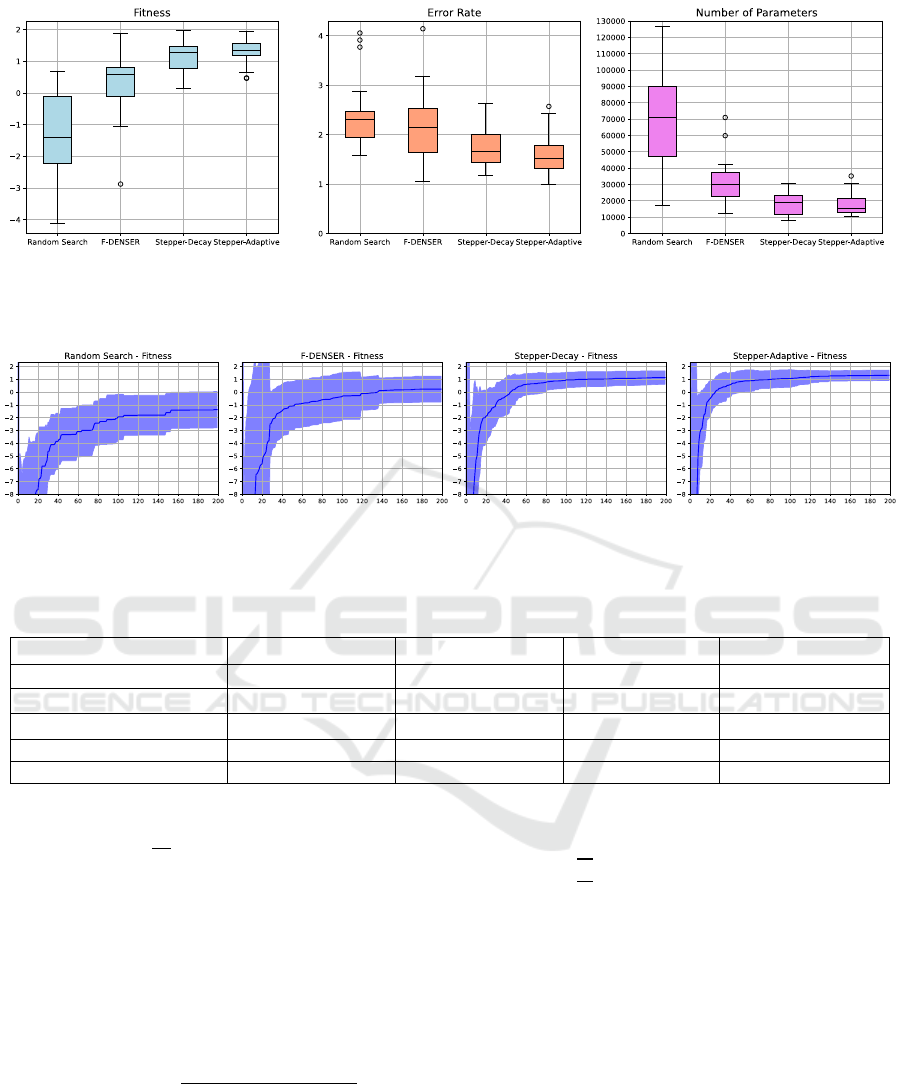
Figure 2: Box plots with the distribution of quartiles and outliers of metrics of the best (highest fitness) architecture found in

each run for 20 runs of 200 generations. The square of the error rate and the number of parameters negatively affect fitness.

0 is the fitness of an expert-optimized LeNet-like architecture, the best observed fitness was 2.2.

Figure 3: Fitness of the best individual of each generation, averaged over 20 runs of 200 generations. The darker line shows

the mean, the filled area the standard deviation.

Table 2: Mean and standard deviations of metrics of the best individuals found, summarized over 20 runs of each NAS

algorithm. The most relevant results are in bold.

Metric

Random Search

F-DENSER

Stepper-Decay

Stepper-Adaptive

Fitness

-1.38  1.42

0.23  1.02

1.13  0.52

1.31  0.41

Final test fitness

-1.38  1.35

-0.06  1.06

1.00  0.59

1.13  0.58

Error rate

2.41  0. 71

2.17  0. 75

1.78  0.45

1.59  0.39

Final test error rate

2.41  0.67

2.41  0.79

1.92  0.48

1.79  0.44

Number of parameters

73,669 37,066

31,690 14,663

  

  7,287

parent of generation , and  is a random variable

distributed as 





with a probability of 0.5 each.

Then, the variable values chosen for mutation for the

new individual are generated with the step size 









If an individual is selected as a new parent for the next

generation, the step size associated with this

individual is recalculated as the standard deviation

that has the highest likelihood of generating the step

that was taken. This is the concept of

derandomization.





























 

















(4)

where 



is the vector of the random numbers used to

mutate the  variables that were chosen to mutate the

individual,  is the unity matrix of rank ,  is a

dampening factor  that reduces the change rate of

the step size so that step size does not change too

randomly from one generation to the next. According

to (Ostermeier et al., 1994),  should be proportional

to the square root of the number of variables.  was

chosen as 







, where 25 is the expected

number of numeric variables per individual and 8 is a

reduction factor.

6 RESULTS

Table 2 summarizes the metrics of the best individual

over 20 runs of each NAS algorithm. Figure 2 shows

box plots of fitness, error rate and number of

parameters. Figure 3 shows the convergence behavior

of each algorithm.

Step Size Control in Evolutionary Algorithms for Neural Architecture Search

293

7 DISCUSSION

The error rate has an observed standard deviation on

k-folds of ~ , resulting in a standard deviation

of the fitness of ~ 0.



  



ES only selects individuals as new

parents that have better fitness than the previous best.

Because of this noise in the measurement, selected

individuals are often those that “got lucky” and have

a fitness significantly above the mean k-folds fitness

of the architecture. This appears to strongly influence

the behavior of the search.

To check for statistical significance in a pair-wise

comparison of the algorithms, we used a one-sided

Mann-Whitney U test on the 20 fitness values from

the 20 runs. For Stepper-Decay vs. F-DENSER, this

found p = 0.000813, for Stepper-Adaptive vs. F-

DENSER p = 0.000052. Since p < 0.05, they perform

significantly better than F-DENSER. Stepper-

Adaptive is not significantly better than Stepper-

Decay (p = 0.130808).

Stepper-Decay and Stepper-Adaptive converge

faster than F-DENSER, find better average solutions,

and have a lower variance.

All algorithms find architectures with a similar

error rate to LeNet-5 and with less than a quarter of

the free parameters.

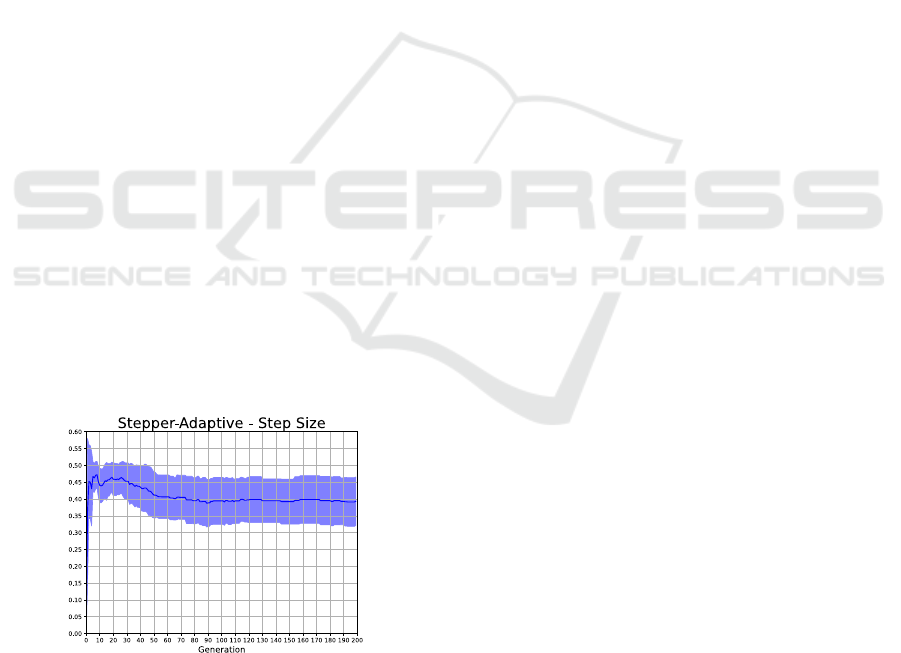
Figure 4 shows the evolution of the step size in

Stepper-Adaptive. After initial adaptations, the

average step size hovers near 0.4. If the step size were

regulated effectively, it should decrease continuously

in later generations. Presumably, evolutionary

pressure keeps the step size at a compromise value,

where a larger step size would be optimal for some

variables and a lower one for others.

Figure 4: The evolution of the global step size

 over 20

runs of Stepper-Adaptive is shown as the mean and standard

deviation.

8 CONCLUSIONS AND FUTURE

WORK

Compared to F-DENSER, two different simple

methods of controlling the step size resulted in faster

convergence, better average fitness, and lower

variance.

The search for architectures to classify MNIST

data is an effective way to compare the performance

of NAS algorithms operating on wide search spaces.

Twenty runs of a



  



 ES for 200 generations

gave a good indication of the relative performance of

the algorithms, requiring 10,000 architecture

evaluations that took about 28 hours on a single GPU.

Noise caused by training data randomization and

random initialization is significant compared to the

low error rates of <1.5% that were easily reached; we

conjecture that perhaps MNIST is too easy. This

could be remedied by using a harder-to-classify

MNIST replacement like Fashion-MNIST or

Kuzushiji-MNIST, where error rates are generally

higher, so noise is less significant.

The methods of step size control studied here are

rather crude for three reasons. First, a global step size

is unlikely to be adequate for all numeric parameters.

Secondly, step size control currently does not apply

to categorical parameters, which in the studied

problem represent about half the parameters of an

architecture. The third point applies to Stepper-

Adaptive. The step size is only adapted when a new

individual is selected as a parent, which happens quite

rarely in a



  



ES. So, the algorithm cannot

learn from the >  of non-selected individuals and

ignores most of the available information about the

search space.

In principle, these kinds of step size control can

be applied to any problem where solution candidates

are described by a grammar-conforming expression

containing numerical values. This research could be

useful in other domains that have this kind of

optimization problem, like Operations Research.

Future work will go into two separate directions:

(i) perform experiments with a wider set of

benchmarks and datasets and more complex

architectures (e.g., including skip connections), and

compare it to the best applicable published methods.

(ii) explore how step size can be adapted in a more

fine-grained way, with separate step size for single

parameters or groups of parameters, and how it can

be changed based on more of the existing knowledge

about the search space.

The smallest architecture found in the

experiments had 5,450 trainable parameters and

reached an accuracy of 98.8% on MNIST. It

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

294

contained an unusual stack of three convolutional

filter layers that use ELU, linear and linear activation

functions, and only one fully connected classification

layer. This example suggests that a NAS working on

a wider search space can find interesting designs that

the experimenters had not considered before.

There is a large potential for future improvement

by exploring variations of step size control and

mutation operators. This is a step towards more

general and more efficient NAS methods. If NAS can

be improved further and applied to even wider search

spaces, perhaps in the future, it can find surprising

new architectural improvements.

REFERENCES

Assunção, F., Lourenço, N., Machado, P., & Ribeiro, B.

(2017). Towards the evolution of multi-layered neural

networks: A dynamic structured grammatical evolution

approach. 393–400. https://doi.org/10.1145/

3071178.3071286

Assunção, F., Lourenço, N., Machado, P., & Ribeiro, B.

(2018). Evolving the Topology of Large Scale Deep

Neural Networks (pp. 19–34).

https://link.springer.com/chapter/10.1007/978-3-319-

77553-1_2

Assunção, F., Lourenço, N., Machado, P., & Ribeiro, B.

(2019). Fast DENSER: Efficient Deep NeuroEvolution.

In Lecture Notes in Computer Science (pp. 197–212).

Springer International Publishing.

https://dx.doi.org/10.1007/978-3-030-16670-0_13

Cramer, N. L. (1985). A Representation for the Adaptive

Generation of Simple Sequential Programs. In

Proceedings of the First International Conference on

Genetic Algorithms and their Applications. Psychology

Press.

Droste, S., & Wiesmann, D. (2000). Metric Based

Evolutionary Algorithms. 29–43.

Hansen, N., & Ostermeier, A. (2001). Completely

Derandomized Self-Adaptation in Evolution Strategies.

Evolutionary Computation, 9(2), 159–195.

https://doi.org/10.1162/106365601750190398

Holland, J. H. (1992). Adaptation in Natural and Artificial

Systems: An Introductory Analysis with Applications to

Biology, Control, and Artificial Intelligence. The MIT

Press. https://direct.mit.edu/books/book/2574/

Adaptation-in-Natural-and-Artificial-SystemsAn

Ioffe, S., & Szegedy, C. (2015). Batch Normalization:

Accelerating Deep Network Training by Reducing

Internal Covariate Shift. arXiv Pre-Print Server.

https://arxiv.org/abs/1502.03167

Koza, J. R. (1989). Hierarchical genetic algorithms

operating on populations of computer programs.

Proceedings of the 11th International Joint Conference

on Artificial Intelligence - Volume 1, 768–774.

Li, R., Emmerich, M., Eggermont, J., Bäck, T., Schütz, M.,

Dijkstra, J., & Reiber, J. (2013). Mixed Integer

Evolution Strategies for Parameter Optimization.

Evolutionary Computation.

https://doi.org/10.1162/EVCO_a_00059

Loshchilov, I., & Hutter, F. (2016). CMA-ES for

Hyperparameter Optimization of Deep Neural

Networks.

Loshchilov, I., Schoenauer, M., & Sèbag, M. (2013). Bi-

population CMA-ES agorithms with surrogate models

and line searches. Proceedings of the 15th Annual

Conference Companion on Genetic and Evolutionary

Computation, 1177–1184.

https://doi.org/10.1145/2464576.2482696

Ostermeier, A., Gawelczyk, A., & Hansen, N. (1994). A

derandomized approach to self-adaptation of evolution

strategies. Evolutionary Computation, 2(4), 369–380.

Rechenberg, I. (1965). Cybernetic solution path of an

experimental problem. Roy. Aircr. Establ., Libr.

Transl., 1122. https://cir.nii.ac.jp/crid/

1570291225013966592

Rechenberg, I. (1994). Evolutionsstrategie. Frommann-

Holzboog.

Ryan, C., Collins, J., & Neill, M. O. (1998). Grammatical

evolution: Evolving programs for an arbitrary language.

In W. Banzhaf, R. Poli, M. Schoenauer, & T. C. Fogarty

(Eds.), Genetic Programming (pp. 83–96). Springer.

https://doi.org/10.1007/BFb0055930

Schwefel, H.-P. (1995). Evolution and optimum seeking.

Sixth-generation computer technology series.

Storn, R., & Price, K. (1997). Differential evolution–a

simple and efficient heuristic for global optimization

over continuous spaces. Journal of Global

Optimization, 11(4), 341–359.

https://doi.org/10.1023/A:1008202821328

Sultan, A. (2022). A Modern Variant of LeNet by TF.keras

on MNIST. https://www.kaggle.com/code/abedsultan/

a-modern-variant-of-lenet-by-tf-keras-on-mnist

White, C., Safari, M., Sukthanker, R., Ru, B., Elsken, T.,

Zela, A., Dey, D., & Hutter, F. (2023). Neural

Architecture Search: Insights from 1000 Papers

(arXiv:2301.08727). arXiv. https://doi.org/10.48550/

arXiv.2301.08727

Yang, A., Esperança, P., & Carlucci, F. (2019). NAS

evaluation is frustratingly hard.

Yu, K., Suito, C., Jaggi, M., Musat, C.-C., & Salzmann, M.

(Eds.). (2020). Evaluating the search phase of neural

architecture search. ICRL 2020 Eighth International

Conference on Learning Representations.

Step Size Control in Evolutionary Algorithms for Neural Architecture Search

295