
Approaches for Extending Recommendation Models for Food
Choices in Meals
Nguyen Thi Hong Nhung
1,2
, Dao Khoa Nguyen
1,2
, Tiet Gia Hong
1,2,*
and Thi My Hang Vu
1,2
1
Faculty of Information Technology, University of Science, Ho Chi Minh City, Vietnam
2
Vietnam National University, Ho Chi Minh City, Vietnam
Keywords: Food Recommender System, Neighbor-Based Recommendation, Latent Factor-Based Recommendation.
Abstract: In this paper, we propose food recommender systems based on users' historical food choices. Their advantage
lies in providing personalized food suggestions for each user considering each meal. These systems are
developed using two popular recommendation principles: neighbor-based and latent factor-based. In the
neighbor-based model, the system aggregates the food choices of neighboring users to recommend food
choices for the active user during the considered meal. In contrast, the latent factor-based model constructs
and optimizes an objective function to learn positive representations of users, foods, and meals. In this new
space, predicting users' food choices during meals becomes straightforward. Experimental results have
demonstrated the effectiveness of the proposed models in specific cases. However, in a global statistical
comparison, the latent factor-based model has proven to be more effective than the neighbor-based model.
1 INTRODUCTION
Recommender systems are increasingly playing an
important role on digital platforms. On YouTube and
Netflix, they help suggest videos that match users'
past viewing experiences (Amatriain and Basilico,
2015; Hong and Kim, 2016). Users on social
networks are assisted by recommender systems in
finding suitable friends (Ahmadian et al., 2020). On
Amazon, thanks to recommender systems, users can
quickly and accurately find desired items (Smith and
Linden, 2017). Moreover, researchers are expanding
traditional recommender systems to provide
recommendations for groups of users (Nam, 2021a).
As a result, recommender systems can fully meet
users' needs, from individual preferences to group
preferences.
In this study, we focus on a specific domain of
recommender systems, which is food
recommendation. Many previous food recommender
systems have aimed to provide the most optimal
recommendations by suggesting foods that users are
predicted to like after trying them (Twomey et al.,
2020; Jia et al., 2022; Hamdollahi et al., 2023;
Bondevik et al., 2023). Such recommender systems
are trained using preference data, which consists of
*
Corresponding Author
ratings given by users after trying the foods. The
rating scale is typically diverse, ranging from "dislike
very much" to "like very much". Therefore, it is
difficult for users to provide ratings that accurately
reflect their feelings about foods (Shen et al., 2019;
Vy et al., 2024). Collecting a large and accurate
number of ratings for food recommender systems
requires significant cost and time. Hence, our study
aims to propose a more neutral recommendation
solution by suggesting foods that users are likely to
choose. For these systems, the underlying training
data is much easier to collect, as it consists of users'
food choice history.
Within the scope of this study, the distinguishing
feature is considering meal information in the food
recommendation process. Meal information directly
influences users' food choices; for instance, users
might choose a pastry for breakfast but not for lunch.
Therefore, taking into account the user-food-meal
correlation is more suitable for food recommendation
systems compared to traditional models such as
neighbor-based (Aggarwal, 2016) and latent factor-
based recommendations (Nam, 2021b), which only
address the user-product correlation during the
recommendation process.
Nhung, N., Nguyen, D., Hong, T. and Vu, T.
Approaches for Extending Recommendation Models for Food Choices in Meals.
DOI: 10.5220/0013014000003838
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2024) - Volume 1: KDIR, pages 113-121
ISBN: 978-989-758-716-0; ISSN: 2184-3228
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
113
Specifically, our contributions are as follows:
• We extend two typical user-product
recommendation models, namely neighbor-
based and latent factor-based models, to
achieve user-food-meal recommendation
models.
• We conduct experiments to conclude the
suitability of the neighbor-based and latent
factor-based models for the user-food-meal
recommendation problem.
The structure of the paper is as follows. In section
2, we analyze some limitations of previous studies on
food recommendation. In section 3, we propose
approaches to address these limitations. In section 4,
experiments are conducted to evaluate the proposed
approaches. Finally, we present the conclusions and
future works.
2 RELATED WORKS
The core of food recommender systems is predicting
a user's preference for a food, and then recommending
the foods predicted to be the most liked. To achieve
this, previous studies (Twomey et al., 2020; Jia et al.,
2022) have utilized the user's past food preferences
and the descriptions of the foods to estimate how
much the user would like a particular food.
(Hamdollahi et al., 2023) also incorporate user
descriptions and food images to predict food
preferences.
One approach defines a similarity measure
between the user vector and the food vector,
recommending the food most similar to the user. To
design this similarity measure, some studies use TF-
IDF and cosine measures (Chhipa et al., 2022;
Padmavathi et al., 2023), while others use Positive
Pointwise Mutual Information (PPMI) (Teng et al.,
2012; Zhang et al., 2022). Another approach
(Mokdara et al., 2018) applies matrix factorization to
learn features for representing both foods and users.
This feature space facilitates the estimation of the
compatibility between users and foods. Researchers
improve the quality of this feature learning process by
incorporating user tags (Ge et al., 2015). Another
approach to matching users and foods is to use health
rules combined with users' past preferences in certain
contexts (Agapito et al, 2018; Vairale and Shukla,
2021).
It can be seen that previous studies have relied on
users' past food preferences, typically indicated by a
rating score ranging from 1 to 5, collected after users
have experienced the foods. Due to this nature, the
number of ratings collected is often very low, and the
accuracy of these ratings is frequently not high (Vy et
al., 2024). Evidence of this is apparent on platforms
like Amazon, where users may leave highly positive
textual reviews about an item but assign a low rating
score, and vice versa (Shen et al., 2019). This
discrepancy arises because users may not fully grasp
the correlation between their preferences and the
numerical rating scale, leading to ratings that do not
accurately depict their true experience with the foods.
Furthermore, a variety of additional information
is utilized to enhance the accuracy of predicting users'
food preferences. This includes food descriptions,
nutritional principles, health considerations, and
more (Gao et al, 2019; Zhang et al., 2022; Oskouei
and Hashemzadeh, 2023). However, it is not always
feasible to comprehensively collect all such
information. Moreover, the use of excessive
additional information can also reduce the flexibility
of the system.
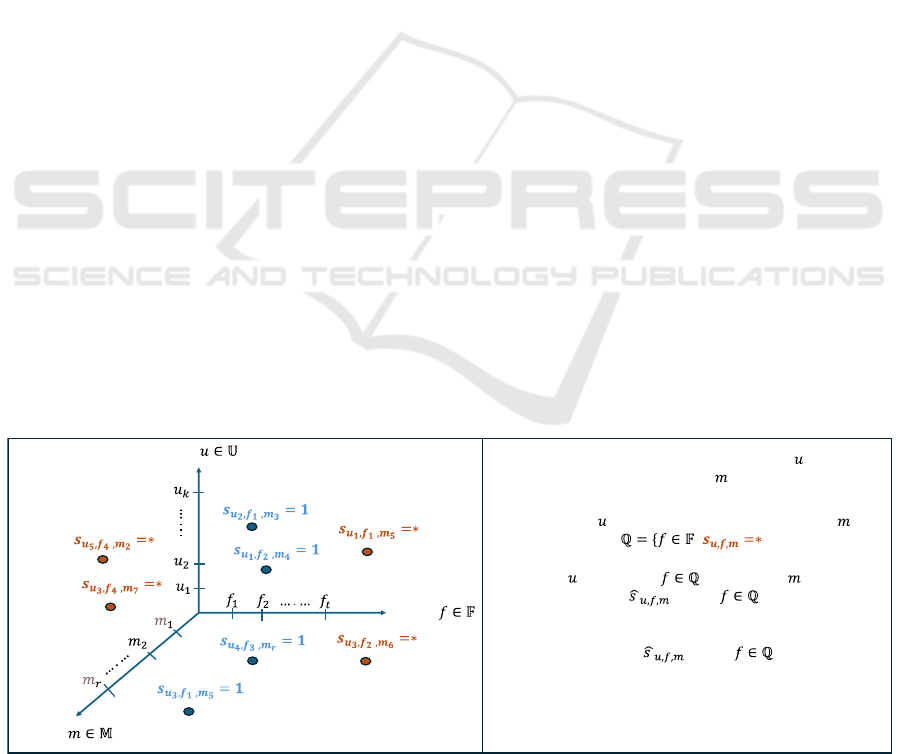
Figure 1: The user-food-meal recommendation problem.
Foods
Users
Meals
The food recommendation for a user
during a meal
-The foods that has not experienced during meal
| }
-Predicting
's choice of during meal
where
-Foods predicted to be chosen by u will be recommended
Top
where
KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval
114

Given the limitations identified above, this paper
proposes food recommendation models that rely
solely on the easiest-to-collect information: users'
food choice history. To better reflect real-world
scenarios, users' food choices will be detailed for each
meal. Detailed descriptions of the user-food-meal
recommendation problem are provided in Subsection
3.1.
Collaborative filtering is one of the effective
models for achieving good recommendations. The
term "collaborative" means utilizing community data
to provide recommendations of items to users. Its two
typical models are neighbor-based (Aggarwal, 2016)
and latent factor-based (Nam, 2021b). As mentioned
earlier, our recommendation model not only involves
users and foods but also meals. Therefore, our
motivation is to extend these two user-product
collaborative filtering models to user-food-meal
recommendation models. Details of this extension
will be presented in Subsections 3.2 and 3.3
3 OUR PROPOSED
APPROACHES
3.1 User-Food-Meal Recommendation
Problem
Fig. 1 illustrates the user-food-meal recommendation
problem addressed in this paper. Specifically, data on
users' food choices during meals is collected. If a user
𝑢∈𝕌={𝑢
,𝑢
,…,𝑢
} chooses a food 𝑓∈𝔽=
{𝑓
,𝑓
,…,𝑓
} during a meal 𝑚∈𝕄=
{𝑚
,𝑚
,…,𝑚
}, the corresponding value is 1,
denoted by 𝑠
,,
=1. For an active user 𝑢 seeking
food recommendations during a meal 𝑚, the choices
of 𝑢 for foods 𝑓 not yet experienced in meal 𝑚 need
to be predicted (𝑠
,,
=∗). Foods predicted to be
chosen by the active user will be recommended. Table
1 presents the symbols used to describe the proposed
approaches in Subsections 3.2 and 3.3.
3.2 Neighbor-Based Model for
User-Food-Meal Recommendation
(NUFM)
The principle of the neighbor-based model is to
recommend products that users similar to the active
user have liked in the past (Aggarwal, 2016; Vy et al,
2024). In this section, we refine this principle to
address the problem of recommending foods to users
during meals, namely NUFM.
Table 1: The symbols.
Symbol Description
𝑢∈𝕌={𝑢
,𝑢
,…,𝑢
}
User
𝑓∈𝔽={𝑓
,𝑓
,…,𝑓
}
Food
𝑚∈𝕄={𝑚
,𝑚
,…,𝑚
}
Meal
𝑠
,,
=1
User 𝑢 has chosen
food
𝑓
during meal 𝑚
𝑠
,,
=∗
User 𝑢 has not chosen
food
𝑓
during meal 𝑚
𝑠
,,
Predicting user 𝑢 's
choice of food 𝑓
during meal 𝑚
𝑠𝑖𝑚(𝑢
()
,𝑢′
()
)
The similarity
between user 𝑢 in
meal 𝑚 and user 𝑢′ in
meal 𝑚′
𝑘
The number of
selected neighbors in
neighbor-based
models
ℕ
Top 𝑘 𝑢′
()
similar
to 𝑢
(
)
ℍ
Set of 𝑢′
()
who
have chosen 𝑓 in the
pas
t
𝑧
The number of latent
factors in latent-
facto
r
-
b
ased models
𝑎
,
, 𝑎
,
,…,𝑎
,
Representations of
user 𝑢∈𝕌 under 𝑧
latent factors
𝑏
,
, 𝑏
,
,…,𝑏
,
Representation of
food 𝑓∈𝔽 under 𝑧
latent factors
𝑐
,
, 𝑐
,
,…,𝑐
,
Representations of
meal 𝑚∈𝕄 under 𝑧
latent factors
𝜆
Tikhonov
regularization weigh
t
𝜑
,
, 𝜑
,
,…,𝜑
,
Learning rates of user
𝑢∈𝕌 under 𝑧 latent
factors
𝜑
,
, 𝜑
,
,…,𝜑
,
Learning rates of food
𝑓∈𝔽 under 𝑧 latent
factors
𝜑
,
, 𝜑
,
,…,𝜑
,
Learning rates of meal
𝑚∈𝕄 under 𝑧 latent
factors
Specifically, for the offline phase, we implement
the calculation of the similarity in food choices
between each pair of users 𝑢∈𝕌={𝑢
,𝑢
,…,𝑢
}
considering each pair of meals 𝑚∈𝕄=
{𝑚
,𝑚
,…,𝑚
}. With collected data on food choices
during meals, a Jaccard similarity (Bag et al., 2019)
is suitable for this case. Accordingly, the more
common food choices user 𝑢 in meal 𝑚 (𝑢
()
) and
user 𝑢′ in meal 𝑚′ (𝑢′
()
), the higher their similarity
Approaches for Extending Recommendation Models for Food Choices in Meals
115

( 𝑠𝑖𝑚(𝑢
()
,𝑢′
()
). Specifically, the formula is
implemented as follows:
𝑠𝑖𝑚
𝑢
(
)
,𝑢
(
)
=
𝑓
|𝑠
,,
=1 ∧𝑠
,,
=1
𝑓
|𝑠
,,
=1 ∨𝑠
,,
=1
(1)
In the online phase, the prediction of user 𝑢's
choice of food 𝑓 during meal 𝑚 is as follows:
• Based on the similarity scores computed
during the offline phase, the set of top 𝑘
𝑢′
()
similar to 𝑢
(
)
: ℕ
(
)
⬚
.
• Get the set of 𝑢′
()
who have chosen 𝑓: ℍ
⬚
• Predicting user 𝑢's choice of food 𝑓 during
meal 𝑚 ( 𝑠
,,
) by computing the sum of
similarities between 𝑢′
()
(𝑢
∈
ℕ
(
)
⬚
∩ ℍ
⬚
) and 𝑢
(
)
, as follows:
𝑠
,,
=𝑠𝑖𝑚(𝑢′
()
,𝑢
()
)
⬚
()
∈ ℕ
(
)
⬚
∩ℍ
⬚
(2)
If 𝑠
,,
is higher, it indicates that users similar to 𝑢
often choose food 𝑓 for meal 𝑚.
The drawback of the above approach is the high
computation time required for calculating similarities
in the offline phase, especially as the number of users
and meals grows. Consequently, we propose parallel
computation using Hadoop for the similarity
calculation described above. Specifically, on Hadoop,
the users' food choice data will be partitioned into
smaller fragments corresponding to each food 𝑓∈
𝔽={𝑓
,𝑓
,…,𝑓
}, as follows:
𝑓
;𝑢
(
)
,𝑢
(
)
,𝑢
(
)
𝑓
;𝑢
(
)
,𝑢
(
)
,𝑢
(
)
𝑓
;𝑢
(
)
,𝑢
(
)
,𝑢
(
)
…….
(3)
where the right side represents 𝑢
(
)
chosen the left
food 𝑓∈𝔽={𝑓
,𝑓
,…,𝑓
}.
In each partitioned fragment, parallel
computations are executed using mapping functions.
Specifically, the mapping function generates (key;
value) elements where the keys represent pairs of
users who have both selected the food (denoted as
_𝑞), pairs where only one user has selected the food
(denoted as _𝑝), and the values are set to 1. For
example, with the fragment corresponding to food 𝑓
(𝑓
;𝑢
(
)
,𝑢
(
)
,𝑢
(
)
) , (key; value) elements
after the mapping function will be as follows:
(𝑢
(
)
_
𝑢
(
)
_𝑞;1)
(𝑢
(
)
_
𝑢
(
)
_𝑞;1)
(𝑢
(
)
_𝑢
(
)
_𝑞;1)
(𝑢
(
)
_𝑢
(
)
_𝑝;1)
(𝑢
(
)
_𝑢
(
)
_𝑝;1)
(𝑢
(
)
_
𝑢
(
)
_𝑝;1)
…….
(4)
After all mapping functions are completed, a
reducing function is executed to compute the sum of
values with the same key. For example, to compute
𝑠𝑖𝑚(𝑢
()
,𝑢′
()
) as in Eq. (1), the sum of values
with the same key 𝑢
()
_𝑢′
()
_𝑞 serves as the
numerator, while the sum of values with the same key
𝑢
()
_𝑢′
()
_𝑝 serves as the denominator.
3.3 Latent-Factor-Based Model for
User-Food-Meal Recommendation
(LUFM)
The latent factor model aims to find the compatibility
between users and products in a latent factor space to
decide whether to recommend products to users (Shen
et al., 2019; Nam, 2021a). Accordingly, given that the
entities involved in our problem are users, foods, and
meals, our model, namely LURM, needs to learn their
representations under 𝑧 latent factors,
denoted as 𝑎
,
,
𝑎
,
,…,𝑎
,
for each user 𝑢∈𝕌, 𝑏
,
, 𝑏
,
,…,𝑏
,
for
each food 𝑓∈𝔽, and 𝑐
,
, 𝑐
,
,…,𝑐
,
for each meal
𝑚∈𝕄. At this point, user 𝑢's choice of food 𝑓 during
meal 𝑚 ( 𝑠
,,
) will depend on the alignment of three
latent-factor-based representations, as follows:
𝑠
,,
=𝑎
,
.𝑏
,
+𝑎
,
.𝑐
,
+𝑐
,
.𝑏
,
(5)
Fig. 2 illustrates the process in LUFM.
In the LUFM, the latent-factor-based
representations for users, foods, and meals are
optimized to minimize the distance between actual
and predicted values, as follows:
𝑚𝑖𝑛
⬚
1
2
𝑠
,,
−𝑠
,,
,,
⬚
⇔
𝑚𝑖𝑛
⬚
1
2
𝑎
,
.𝑏
,
+𝑎
,
.𝑐
,
+𝑐
,
.𝑏
,
− 𝑠
,,
,,
(6)
KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval
116
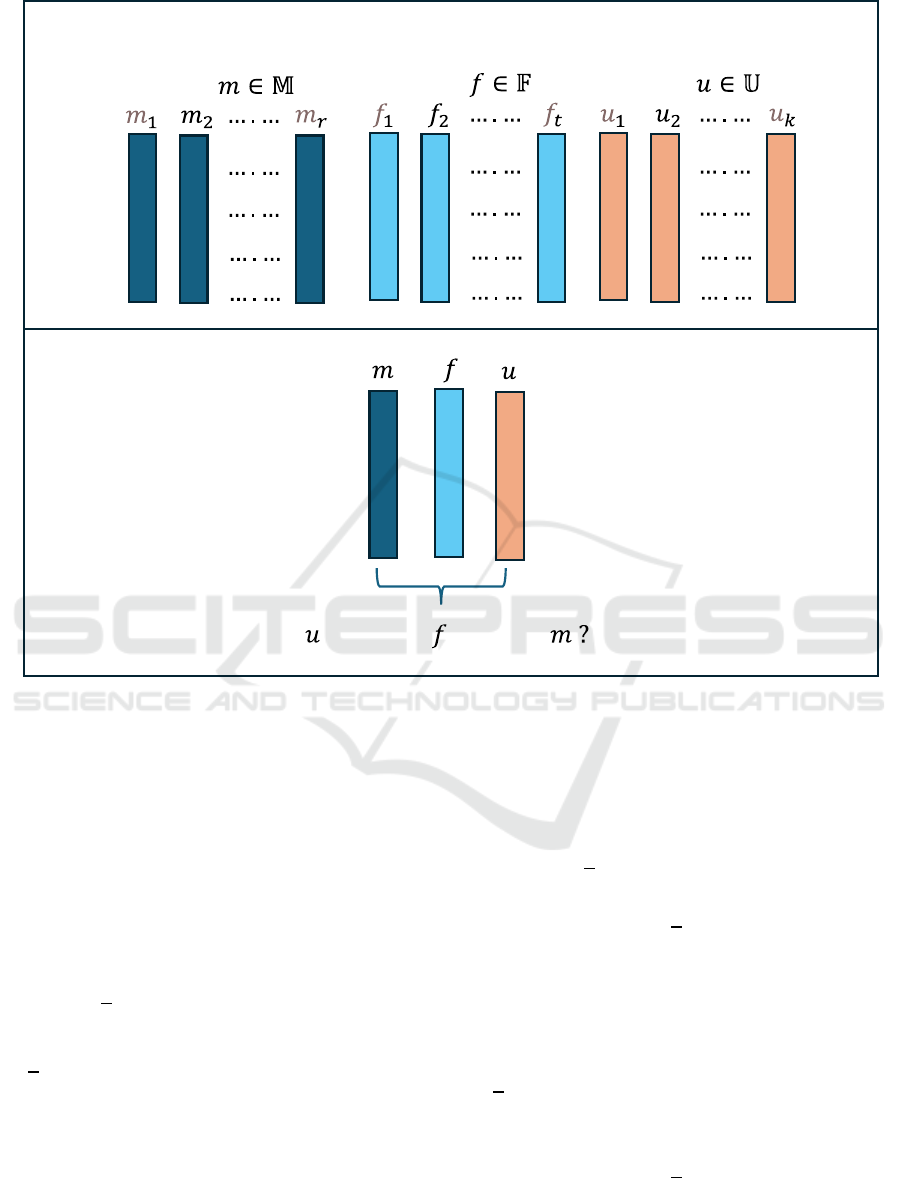
Figure 2: Our proposed approach, LUFM.
To enhance the semantic meaning of the latent-
factor-based presentations, we enforce a constraint
that their components are always positive. This
constraint creates a meaningful part-based
representation (Chen et al., 2021; Salahian et al.,
2023). Additionally, to prevent overfitting, we add a
Tikhonov regularization term (Nam, 2021a; Vy et al.,
2024) to the objective function with a weight 𝜆.
Finally, the objective function will be rewritten as
follows:
𝑚𝑖𝑛
⬚
1
2
𝑠
,,
− 𝑠
,,
,,
+
𝜆
2
𝑎
,
⬚
∈𝕌
+𝑏
,
⬚
∈𝔽
+𝑐
,
⬚
∈𝕄
Subject to positive parameters:
𝑎
,
≥0,𝑏
,
≥0,𝑐
,
≥0
∀
𝑗
=1…𝑧, ∀𝑢∈𝕌, ∀
𝑓
∈𝔽, ∀𝑚∈𝕄
(7)
To optimize Eq. (7), this paper employs
Stochastic Gradient Descent (SGD). Specifically,
SGD first sets up the objective function at a data point
𝑠
,,
, denoted by 𝑉
(
𝑢,𝑓,𝑚
)
. Subsequently, partial
derivatives of 𝑉
(
𝑢,𝑓,𝑚
)
concerning each parameter
will be computed as follows:
𝑉
(
𝑢,
𝑓
,𝑚
)
=
1
2
𝑠
,,
−𝑠
,,
+
𝜆
2
𝑎
,
+𝑏
,
+𝑐
,
⇔
𝑉
(
𝑢,𝑓,𝑚
)
=
1
2
𝑎
,
.𝑏
,
+𝑎
,
.𝑐
,
+𝑐
,
.𝑏
,
− 𝑠
,,
+
𝜆
2
𝑎
,
+𝑏
,
+𝑐
,
(8)
Meals
Foods
Users
Latent factors
Latent factors
The training
The prediction
chooses for meal
Approaches for Extending Recommendation Models for Food Choices in Meals
117

∀
𝑗
=1…𝑧:
𝜕𝑉
(
𝑢,
𝑓
,𝑚
)
𝜕𝑎
,
=
𝑏
,
+𝑐
,
𝑠
,,
− 𝑠
,,
+𝜆.𝑎
,
(9)
𝑗
=1…𝑧:
𝜕𝑉
(
𝑢,
𝑓
,𝑚
)
𝜕𝑏
,
=
𝑎
,
+𝑐
,
𝑠
,,
− 𝑠
,,
+𝜆.𝑏
,
(10)
𝑗
=1…𝑧
𝜕𝑉
(
𝑢,
𝑓
,𝑚
)
𝜕𝑐
,
=
𝑎
,
+𝑏
,
𝑠
,,
− 𝑠
,,
+𝜆.𝑐
,
(11)
These partial derivatives will be used to update the
corresponding parameters with learning rates 𝜑
,
,
𝜑
,
, 𝜑
,
𝑗=1…𝑧, as follows:
∀
𝑗
=1…𝑧: 𝑎
,
← 𝑎
,
−𝜑
,
.
𝜕𝑉
(
𝑢,
𝑓
,𝑚
)
𝜕𝑎
,
𝑎
,
← 𝑎
,
+ 𝜑
,
.𝑏
,
+𝑐
,
.𝑠
,,
− 𝜑
,
.
𝑏
,
+𝑐
,
. 𝑠
,,
+𝜆.𝑎
,
(12)
∀
𝑗
=1…𝑧: 𝑏
,
← 𝑏
,
−𝜑
,
.
𝜕𝑉
(
𝑢,
𝑓
,𝑚
)
𝜕𝑏
,
𝑏
,
← 𝑏
,
+ 𝜑
,
.𝑎
,
+𝑐
,
.𝑠
,,
−𝜑
,
.
𝑎
,
+𝑐
,
. 𝑠
,,
+𝜆.𝑏
,
(13)
∀
𝑗
=1…𝑧: 𝑐
,
← 𝑐
,
−𝜑
,
.
𝜕𝑉
(
𝑢,
𝑓
,𝑚
)
𝜕𝑐
,
𝑐
,
← 𝑐
,
+ 𝜑
,
.𝑎
,
+ 𝑏
,
.𝑠
,,
− 𝜑
,
.
𝑎
,
+𝑏
,
. 𝑠
,,
+𝜆.𝑐
,
(14)
To ensure all parameters remain positive, the
learning rates 𝜑
,
, 𝜑
,
, 𝜑
,
𝑗=1…𝑧 must be set
to eliminate negative components from Eqs. (12-14),
as in (Luo et al., 2014), as follows:
∀
𝑗
=1…𝑧: 𝜑
,
=
𝑎
,
𝑏
,
+𝑐
,
. 𝑠
,,
+𝜆.𝑎
,
(15)
∀
𝑗
=1…𝑧: 𝜑
,
=
𝑏
,
𝑎
,
+𝑐
,
. 𝑠
,,
+𝜆.𝑏
,
(16)
∀
𝑗
=1…𝑧:𝜑
,
=
𝑐
,
𝑎
,
+𝑏
,
. 𝑠
,,
+𝜆.𝑐
,
(17)
Based on Eqs. (15-17), the update process Eqs.
(12-14) can be rewritten as follows:
∀
𝑗
=1…𝑧:𝑎
,
← 𝜑
,
.𝑏
,
+𝑐
,
.𝑠
,,
(18)
∀
𝑗
=1…𝑧:𝑏
,
←𝜑
,
.𝑎
,
+𝑐
,
.𝑠
,,
(19)
∀
𝑗
=1…𝑧:𝑐
𝑚,
𝑗
← 𝜑
𝑚,
𝑗
.
𝑎
𝑢,
𝑗
+ 𝑏
𝑓,
𝑗
.𝑠
𝑢,𝑓,𝑚
(20)
Algorithm 1 presents a detailed description of
LFUM
Algorithm 1: The LUFM training and prediction.
The training
Initialize 𝑎
,
≥0,𝑏
,
≥0,𝑐
,
≥0
∀
𝑗
=1…𝑧, ∀𝑢∈𝕌, ∀
𝑓
∈𝔽, ∀𝑚∈𝕄
While (Not satisfying the convergence criterion):
Randomly shuffle (𝑢∈𝕌,
𝑓
∈𝔽,𝑚∈𝕄)
For each pair (𝑢,𝑓,𝑚):
∀𝑗=1…𝑧: Compute 𝜑
,
, 𝜑
,
, 𝜑
,
b
ased on
Eqs. (15-17), respectively.
∀
𝑗
=1…𝑧: Update the latent representations o
f
𝑢,
𝑓
,𝑚 based on based on Eqs. (18-20), respectively
The prediction
𝑠
,,
=𝑎
,
.𝑏
,
+𝑎
,
.𝑐
,
+𝑐
,
.𝑏
,
4 EXPERIMENT
4.1 Experiment Setup
In this section, we compare our approaches with a
recent approach designed for the user-food-meal
recommendation problem, as follows:
• NUFM: The neighbor-based model
proposed in subsection 3.2 uses the Jaccard
similarity between each pair of users
considering each pair of meals.
• LUFM: The latent factor model proposed in
section 3.3 learns positive latent factors
representing users, foods, and meals.
• PPMI: The model for the Positive Pointwise
Mutual Information between meals and
foods is proposed by (Zhang et al., 2022).
For a fair comparison between approaches NUFM
and LUFM, we set the number of neighbors in NUFM
equal to the number of latent factors in LUFM. The
KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval
118
regularization weight is set to 0.01. The convergence
condition in LUFM is set to 500 updates.
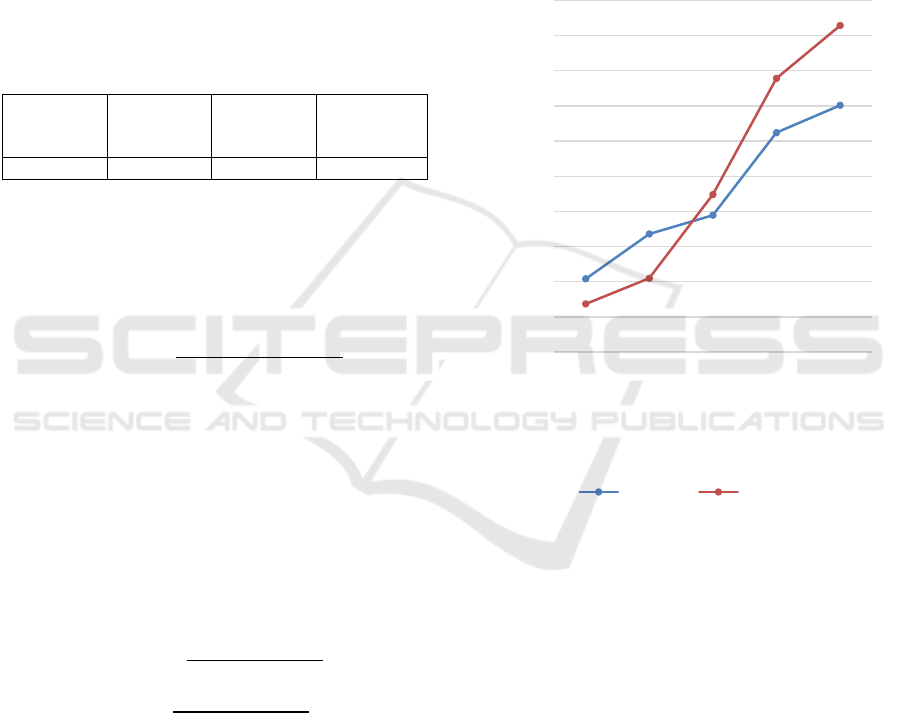
4.2 Dataset
The experimental dataset was gathered from
MyFitnessPal (MFP), a health and body management
application. It details the specific food items chosen
by each user for their daily meals. This dataset are
presented in Table 2. 80% of the dataset is allocated
for training, and the remaining 20% is used for testing
to evaluate the system recommendations.
Table 2: Experimental dataset, MyFitnessPal
https://www.kaggle.com/datasets/zvikinozadze/myfitnessp
al-dataset.
Number of
meals
Number of
users
Number of
foods
Number of
food
choices
6 9873 953296 5411275
4.3 Measurement
The F1-score is used to evaluate the accuracy of the
recommendation results. It is calculated based on
precision and recall as follows:
𝐹1 − 𝑠𝑐𝑜𝑟𝑒=
2.𝑃𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛.𝑅𝑒𝑐𝑎𝑙𝑙
𝑃𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 + 𝑟𝑒𝑐𝑎𝑙𝑙
(21)
To calculate precision and recall, the
recommendation set ( 𝕋
) and the correct set
( ℂ
) must be formed. The recommendation set
consists of the top foods with the highest predicted
values, while the correct set consists of the foods that
users have chosen in the test set. Precision is the ratio
of correct recommendations to the total number of
recommended foods. Recall is the ratio of correct
recommendations to the total number of correct
foods, as follows:
𝑝𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛=
∑|
𝕋
∩ ℂ
|
∑|
𝕋
|
𝑟𝑒𝑐𝑎𝑙𝑙=
∑|
𝕋
∩ ℂ
|
∑
|ℂ
|
(22)
4.4 Experiment Result and Discussion
Fig. 3 shows the comparison results between NUFM
and LUFM. It can be seen that the neighbor-based
model (NUFM) performs better than the latent factor-
based model (LUFM) when the number of neighbors
(which is also the number of latent factors) is set to a
small value. This is because, with a small number of
latent factors, the latent vectors are insufficient to
fully represent the characteristics of users, foods, and
meals. However, the performance of the latent factor-
based model improves significantly as the number of
latent factors increases. Evidence of this is that the
recommendation performance of LUFM not only
improves but also gradually surpasses that of NUFM.
In practice, the number of neighbors or latent factors
is determined by the computational power of the
device. When computational capacity is limited and
high accuracy is not required, these numbers are
usually kept small, and vice versa.
Figure 3: F1-score with a recommendation set size of 15.
Next, we fixed LUFM and NUFM at 45 latent
factors and neighbors. As shown in Fig. 4, LUFM and
NUFM consistently provide better recommendation
results than PPMI across all sizes of the
recommendation set. Specifically, when the size of
the recommendation set is 10, the F1-score of LUFM
and NUFM increases by 0.139 and 0.074 over PPMI,
respectively.
Finally, to achieve more convincing conclusions,
we conducted statistical t-test comparisons. The input
sample for these comparisons consists of the F1-score
results measured at the individual user level, instead
of a single F-score result at the system level as shown
in the previous experiments. The results in Table 3
indicate that LUFM provides the best statistical
outcome compared to NUFM and PPMI, as all p-
values are less than 0.05. Additionally, for LUFM, in
0.2
0.22
0.24
0.26
0.28
0.3
0.32
0.34
0.36
0.38
0.4
10 20 30 40 50
F1-score
The number of latent factors
(The number of neighbors)
NUFM LUFM
Approaches for Extending Recommendation Models for Food Choices in Meals
119
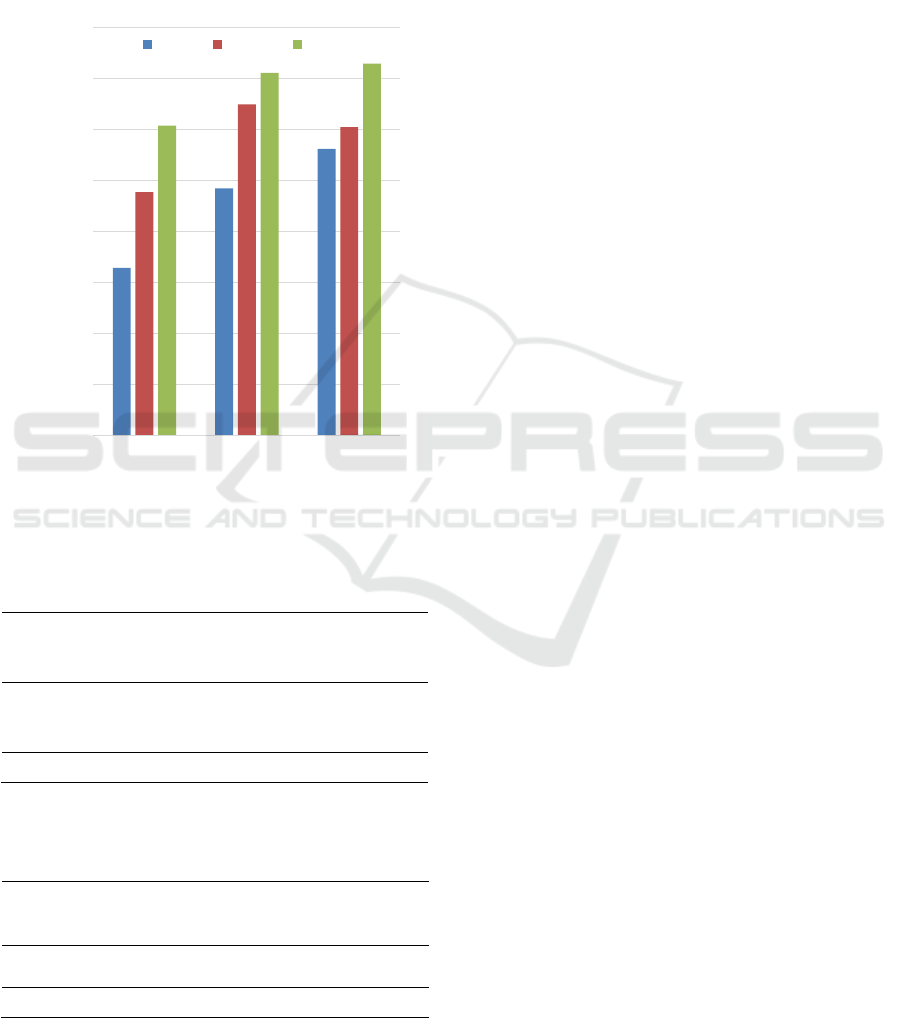
Table 4, we also performed a statistical comparison
between it and a version of it that excludes positive
constraints during training. In this comparison, the
lack of positive constraints reduced the F1-score
compared to when positive constraints were applied.
This demonstrates that the positive constraints and the
optimization method with these constraints are
reasonable and suitable for the problem.
Figure 4: F1-score at 45 latent factors (neighbors).
Table 3: The t-test comparison between NUFM, LUFM,
and PPMI.
Approach
NUFM
>>
PPMI
LUFM
>>
PPMI
LUFM
>>
N
UFM
Sample
mean
0.296
>>
0.270
0.337
>>
0.270
0.337
>>
0.296
p-value 0.0049 0.0001 0.0068
Table 4: The t-test comparison between LUFM with
positive constraints and LUFM without positive
constraints.
Approach
LUFM with positive constraints
>>
LUFM without positive constraints
Sample
mean 0.337 >> 0.308
p-value
0.0072
5 CONCLUSION
In this paper, we extend two typical recommendation
models, namely the neighbor-based model and the
latent-factor-based model, to address the user-food-
meal recommendation problem. Specifically, for the
neighbor-based model, a similarity measure between
pairs of users for each pair of meals is proposed using
the Jaccard principle, while the positive latent-factor-
based model for the user-food-meal
recommendations is also implemented. Experiments
have shown that the neighbor-based model performs
better than the latent-factor-based model when the
number of neighbors, which is also the number of
latent factors, is set to a low value. As this number
increases, the latent-factor-based model yields better
results.
However, overall, the latent factor-based
model provides statistically better results than the
neighbor-based model.
Our research focuses solely on the most basic
data, which is users' food choice history. However,
food choices also depend on various other factors
such as nutrition, health, and so forth. Accurate
recommendations based on food choice data are a
crucial foundation for integrating additional factors in
building a comprehensive method in the future.
ACKNOWLEDGEMENTS
This research is funded by University of Science,
VNU-HCM under grant number CNTT 2024-05.
REFERENCES
Agapito, G., Simeoni, M., Calabrese, B., Caré, I.,
Lamprinoudi, T., Guzzi, P. H., ... & Cannataro, M.
(2018). DIETOS: A dietary recommender system for
chronic diseases monitoring and management.
Computer methods and programs in biomedicine, 153,
93-104.
Aggarwal, C. C. (2016). Neighborhood-based collaborative
filtering. Recommender Systems: The Textbook, 29-
70.
Ahmadian, S., Joorabloo, N., Jalili, M., Ren, Y., Meghdadi,
M., & Afsharchi, M. (2020). A social recommender
system based on reliable implicit relationships.
Knowledge-Based Systems, 192, 105371.
Amatriain, X., & Basilico, J. (2015). Recommender
systems in industry: A netflix case study. In
Recommender systems handbook (pp. 385-419).
Boston, MA: Springer US.
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
10 15 20
F1-score
The size of recommendation set
PPMI NUFM LUFM
KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval
120

Bag, S., Kumar, S. K., & Tiwari, M. K. (2019). An efficient
recommendation generation using relevant Jaccard
similarity. Information Sciences, 483, 53-64.
Bondevik, J. N., Bennin, K. E., Babur, Ö., & Ersch, C.
(2023). A systematic review on food recommender
systems. Expert Systems with Applications, 122166.
Chen, Z., Jin, S., Liu, R., & Zhang, J. (2021). A deep non-
negative matrix factorization model for big data
representation learning. Frontiers in Neurorobotics, 15,
701194.
Chhipa, S., Berwal, V., Hirapure, T., & Banerjee, S. (2022).
Recipe recommendation system using TF-IDF. In ITM
web of conferences (Vol. 44, p. 02006). EDP Sciences.
Gao, X., Feng, F., He, X., Huang, H., Guan, X., Feng, C.,
... & Chua, T. S. (2019). Hierarchical attention network
for visually-aware food recommendation. IEEE
Transactions on Multimedia, 22(6), 1647-1659.
Ge, M., Elahi, M., Fernaández-Tobías, I., Ricci, F., &
Massimo, D. (2015, May). Using tags and latent factors
in a food recommender system. In Proceedings of the
5th international conference on digital health 2015 (pp.
105-112).
Hamdollahi Oskouei, S., & Hashemzadeh, M. (2023).
FoodRecNet: a comprehensively personalized food
recommender system using deep neural networks.
Knowledge and Information Systems, 65(9), 3753-
3775.
Hong, S. E., & Kim, H. J. (2016, July). A comparative study
of video recommender systems in big data era. In 2016
Eighth International Conference on Ubiquitous and
Future Networks (ICUFN) (pp. 125-127). IEEE.
Jia, N., Chen, J., & Wang, R. (2022). An attention-based
convolutional neural network for recipe
recommendation. Expert Systems with Applications,
201, 116979.
Luo, X., Zhou, M., Xia, Y., & Zhu, Q. (2014). An efficient
non-negative matrix-factorization-based approach to
collaborative filtering for recommender systems. IEEE
Transactions on Industrial Informatics, 10(2), 1273-
1284.
Mokdara, T., Pusawiro, P., & Harnsomburana, J. (2018,
July). Personalized food recommendation using deep
neural network. In 2018 Seventh ICT international
student project conference (ICT-ISPC) (pp. 1-4). IEEE.
Nam, L. N. H. (2021a). Latent factor recommendation
models for integrating explicit and implicit preferences
in a multi-step decision-making process. Expert
Systems with Applications, 174.
Nam, L. N. H. (2021b). Towards comprehensive profile
aggregation methods for group recommendation based
on the latent factor model. Expert Systems with
Applications, 185.
Padmavathi, A., & Sarker, D. (2023, July). RecipeMate: A
Food Media Recommendation System Based on
Regional Raw Ingredients. In 2023 14th International
Conference on Computing Communication and
Networking Technologies (ICCCNT) (pp. 1-6). IEEE.
Salahian, N., Tab, F. A., Seyedi, S. A., & Chavoshinejad, J.
(2023). Deep autoencoder-like NMF with contrastive
regularization and feature relationship preservation.
Expert Systems with Applications, 214, 119051.
Shen, R. P., Zhang, H. R., Yu, H., & Min, F. (2019).
Sentiment based matrix factorization with reliability for
recommendation. Expert Systems with Applications,
135, 249-258.
Smith, B., & Linden, G. (2017). Two decades of
recommender systems at Amazon. com. Ieee internet
computing, 21(3), 12-18.
Teng, C. Y., Lin, Y. R., & Adamic, L. A. (2012, June).
Recipe recommendation using ingredient networks. In
Proceedings of the 4th annual ACM web science
conference (pp. 298-307).
Twomey, N., Fain, M., Ponikar, A., & Sarraf, N. (2020,
September). Towards multi-language recipe
personalisation and recommendation. In Proceedings of
the 14th ACM conference on recommender systems
(pp. 708-713).
Vairale, V. S., & Shukla, S. (2021). Recommendation of
food items for thyroid patients using content-based knn
method. In Data Science and Security: Proceedings of
IDSCS 2020 (pp. 71-77). Springer Singapore.
Vy, H. T. H., Pham-Nguyen, C., & Nam, L. N. H. (2024).
Integrating textual reviews into neighbor-based
recommender systems. Expert Systems with
Applications, 249, 123648.
Zhang, J., Li, M., Liu, W., Lauria, S., & Liu, X. (2022).
Many-objective optimization meets recommendation
systems: A food recommendation scenario.
Neurocomputing, 503, 109-117.
Approaches for Extending Recommendation Models for Food Choices in Meals
121
