Tangled Program Graphs with Indexed Memory in Control Tasks with
Short Time Dependencies
Tanya Djavaherpour
a
, Ali Naqvi
b
and Stephen Kelly
c
Department of Computing and Software, McMaster University, Hamilton, On, Canada
Keywords:
Evolutionary Reinforcement Learning, Genetic Programming, Partially Observable Environments.
Abstract:
This paper addresses the challenges of shared temporal memory for evolutionary reinforcement learning agents
in partially observable control tasks with short time dependencies. Tangled Program Graphs (TPG) is a genetic
programming framework which has been widely studied in memory intensive tasks from video games, time
series forecasting, and predictive control domains. In this study, we aim to improve external indexed memory
usage in TPG by minimizing the impact of destructive agents during cultural transmission. We test various
memory resetting strategies—per agent, per episode, and a no-memory control group—and evaluate their
effectiveness in mitigating destructive effects while maintaining performance. Results from Acrobot, Pen-
dulum, and CartPole tasks show that resetting memory more often can significantly boost TPG performance
while preserving computational efficiency. These findings highlight the importance of memory management
in Reinforcement Learning (RL) and suggest opportunities for further optimization for more complex visual
RL environments, including adaptive memory resetting and evolved probabilistic memory operations.
1 INTRODUCTION
Reinforcement Learning (RL) agents learn through
trial-and-error interaction with their environment
(Sutton and Barto, 2018). Deep Reinforcement
Learning (DRL), with its capacity to decompose sen-
sor inputs and build hierarchical representations of
sensor data, has significantly expanded the capabili-
ties of autonomous agents operating within complex
environments (Mnih et al., 2015). Despite these ad-
vancements, DRL agents often encounter formidable
obstacles in tasks necessitating robust memory func-
tionalities (Pleines et al., 2023). This paper inves-
tigates these challenges and proposes simple strate-
gies to enhance temporal memory capabilities in the
recently-proposed genetic programming framework
known as Tangled Program Graphs (TPG) (Kelly and
Heywood, 2018).
Effective memory management is crucial for en-
suring that agents can retain and utilize relevant in-
formation over time, particularly in environments that
are only partially observable or which require long
term planning. We explore various strategies for en-
a
https://orcid.org/0009-0002-3585-1262
b
https://orcid.org/0009-0009-5735-4313
c
https://orcid.org/0000-0002-6071-4705
hancing the efficiency of indexed memory in TPG,
with the goal of minimizing the negative impact of
destructive agents and improving overall system per-
formance. Through a series of experiments, we eval-
uate different memory management approaches, in-
cluding probabilistic methods for writing into mem-
ory shared among a population of agents, and inves-
tigate their impact on the performance of TPG agents
in partially observable benchmark RL environments
with short time dependencies. This study focuses
on comparing memory management strategies within
TPG, using the original version of PyTPG (Amaral,
2019) as the baseline. Our results demonstrate that
clearing shared temporal memory before each evalua-
tion episode improves agent performance by reducing
the negative impact of destructive agents and lowering
decision-making complexity.
2 BACKGROUND
Genetic Programming (GP) is an Evolutionary
Computation paradigm that evolves computer pro-
grams using evolutionary algorithms (Brameier and
Banzhaf, 2007). RL agents evolved with GP can
model their environment over time through the use of
temporal memory. In Linear Genetic Programming
296
Djavaherpour, T., Naqvi, A. and Kelly, S.
Tangled Program Graphs with Indexed Memory in Control Tasks with Short Time Dependencies.
DOI: 10.5220/0013016800003837
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 296-303
ISBN: 978-989-758-721-4; ISSN: 2184-3236
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

(LGP) (Brameier and Banzhaf, 2007), programs are
represented a sequence of instructions which read and
write from memory registers. LGP supports a sim-
ple form of recursive temporal memory simply by al-
lowing registers to maintain state between sequential
program executions. More generally, GP can support
indexed memory by augmenting agents with a linear
memory array and adding specialized read and write
operations to the GP function set (Teller, 1994). If
indexed memory is shared among agents in a pop-
ulation, it can also support the transmission of in-
formation between individuals by non-genetic means.
Spector’s (Spector and Luke, 1996b), “Culture” al-
lows all individuals to share the same memory, sim-
ilar to societal interactions, where each individual is
affected by others in a shared environment, but risks
“pollution” of the memory matrix by agents that per-
form badly.
In Visual RL, observable states are high-
dimensional matrices such as video frames. TPG can
directly process high-dimensional video inputs and
has been tested in various gaming scenarios, outper-
forming traditional deep neural network RL methods
in multi-task learning (Kelly and Heywood, 2018).
These TPG agents were also more computationally
efficient, requiring fewer calculations per action than
other approaches. Their efficiency is primarily due to:
1) the hierarchical complexity of each entity evolving
based on its interaction with the problem domain, un-
like the fixed complexity in conventional Deep Learn-
ing (Mnih et al., 2015); and 2) within a TPG entity,
subsystems often focus on different segments of the
visual input, meaning only certain components are ac-
tive at any specific moment (Kelly et al., 2020).
Despite visual RL providing high-resolution in-
put, individual frames often lack the complete infor-
mation required to select the best action. This par-
tial observability significantly limits the agent’s per-
ception of the environment and implies that tempo-
ral memory must be available for the agent to build a
mental model of its environment. TPG has success-
fully used emergent modularity combined with reg-
ister memory and indexed memory to evolve prob-
lem solvers for memory-intensive tasks (Kelly et al.,
2021). In short, TPG agents are composed of teams
of linear genetic programs which share a single mem-
ory data structure and cooperatively manage a model
of the environment which enables operation in par-
tially observable RL tasks. In this work, we aim to en-
hance the effectiveness of indexed memory usage by
minimizing the effects of destructive individuals dur-
ing the cultural transmission of information through
shared memory, advancing our understanding of the
“culture” of digital organisms.
3 METHODOLOGY
3.1 Environments
The environments used in this work are partially-
observable versions of the widely-studied RL bench-
marks Acrobot, Pendulum, and Cartpole (Sutton and
Barto, 2018), Figure 1. These tasks are selected for
their high level of challenge, extensive comparative
results available in the literature, and computational
simplicity resulting in fast experiments.
3.1.1 Acrobot
The Acrobot task is a dynamical system involving a
double pendulum with 6 observation variables, indi-
cated in Table 1, and 500 time steps. The control task
involves swinging up the lower link of the double pen-
dulum to reach a specified target height. As shown in
Figure 1, the state of the Acrobot at every time step is
given by the cosine and sine of the angles of the two
links in radians (θ
1
, θ
2
) and their angular velocities.
The action space is discrete and consists of three ac-
tions: applying +1 torque, -1 torque, or no torque (0)
to the second joint.
Table 1: Acrobot observation space.
Num Observation Min Max
0 Cos(θ
1
) -1 1
1 Sin(θ
1
) -1 1
2 Cos(θ
2
) -1 1
3 Sin(θ
2
) -1 1
4 θ
1
Angular Velocity -4π 4π
5 θ
2
Angular Velocity -9π 9π
The reward function is −t
end
, which is reached
when the free end hits the target height (−cos(θ
1
) −
cos(θ
2
+ θ
1
) > 1.0) or when the episode exceeds 500
steps. The goal is to reach the target in as few steps
as possible, with each step incurring a -1 reward, and
reaching the target ending with a reward of 0.
3.1.2 Pendulum Task
The Pendulum task, shown in Figure 1, is a control
problem with 3 observation variables and 200 time
steps. This task involves swinging up a pendulum to
an upright position and keeping it balanced. The ac-
tion space consists of a single continuous control vari-
able, representing the torque applied to the joint. The
observation space consists of three elements which
are indicated in Table 2.
The reward function is as follows:
t
max
∑
t=1
−(φ(θ)
2
+ 0.1 ×
˙
θ
2
+ 0.001 × Torque
2
) (1)
Tangled Program Graphs with Indexed Memory in Control Tasks with Short Time Dependencies
297

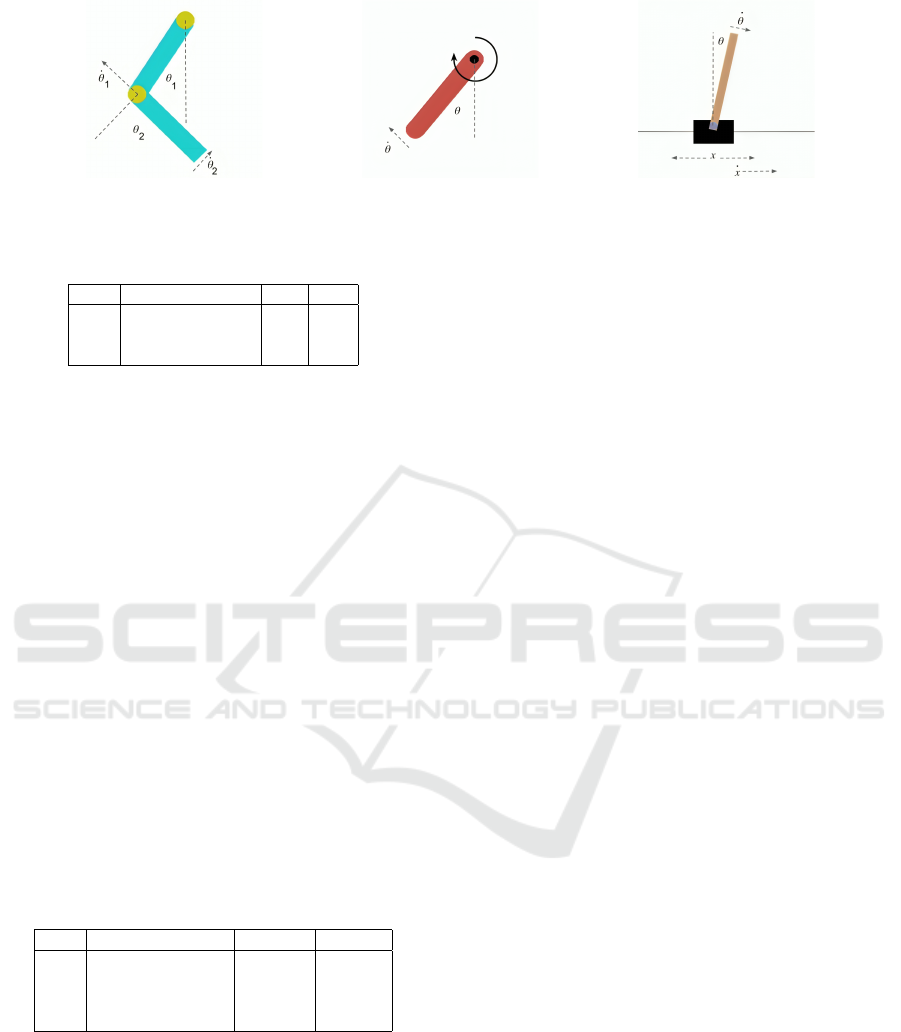
a Acrobot. b Pendulum. c Cartpole.
Figure 1: Problem environments used in this work. See (Brockman et al., 2016) for a detailed description of control tasks.
Table 2: Pendulum observation space.
Num Observation Min Max
0 x = cos(θ) -1.0 1.0
1 y = sin(θ) -1.0 1.0
2
˙
θ = Angular Velocity -0.8 0.8
In this reward function, φ(θ) is the difference be-
tween the current angle θ and the upright position
angle, and torque is the control input applied to the
pendulum. The term φ(θ)
2
penalizes deviation from
the upright position, 0.1 ×
˙
θ
2
penalizes high angu-
lar velocities to encourage smoother movements, and
0.001 × Torque
2
penalizes large control inputs to pro-
mote energy efficiency.
3.1.3 Cartpole Task
The Cartpole task involves balancing a pole on a cart
by applying force to the cart to keep the pole upright.
This task has 4 observation variables given by cart po-
sition (x), cart velocity ( ˙x), pole angle (θ), and pole
velocity at the tip (
˙
θ). As shown in Figure 1, the state
of the Cartpole at every time step is given by the cart
position and velocity, pole angle in radians (θ), and
pole angular velocity. The action space is discrete and
consists of two actions, which represent pushing the
cart to the left or right. The observation space consists
of four elements which are indicated in Table 3.
Table 3: Cartpole observation space.
Num Observation Min Max
0 Cart Position -4.8 4.8
1 Cart Velocity -Inf Inf
2 Pole Angle (θ) -0.418 rad 0.418 rad
3 Pole Angular Velocity -Inf Inf
The reward function is t
end
, with +1 awarded for
each time step the pole remains upright. t
end
is
reached when the pole falls, the cart moves out of
bounds, or the max number of steps is reached. The
goal is to maximize the number of time steps the pole
stays upright.
In all tasks, agent training fitness is its mean re-
ward over 20 episodes, where each episode begins
with random initial conditions and ends with success,
failure, or reaching a time constraint. Post-evolution,
the single training champion is reloaded and evalu-
ated in 100 test episodes with initial conditions not
seen during training.
Velocity state variables describe how the system
is changing over time. To make these environments
partially observable, we remove velocity state vari-
ables from the observation space. In order to con-
trol the systems without this information, agents must
use temporal memory to store sequential observations
over time and integrate this data to predict the velocity
of the system. Note that predicting system velocities
only requires short-term memory.
3.2 Tangled Program Graphs
Tangled Program Graphs (TPG) is a hierarchical al-
gorithm for evolving teams of programs. The basic
building block in TPG is a team of programs (see Fig-
ure 2). Each team represents a stand-alone decision-
making entity (agent) in this framework. Each pro-
gram is a linear structure consisting of registers and
instructions that operate on observation inputs and in-
ternal memory registers. Programs return two val-
ues: a bid value and an action value. Teams follow
a first-placed sealed bid auction method where the
highest bidding program at each timestep wins the
right to decide the action. This action could be a dis-
crete value (directional forces in Figure 2), continuous
value (contents of scalar register s[1] in Figure 2), or
a pointer to another team. If the action is atomic (i.e.
discrete or continuous) it is returned to the task envi-
ronment as the control output for the current timestep.
If the action is a team pointer, then decision-making is
delegated and the bidding process repeats at this team
for the same timestep and observation. The process
repeats recursively until an atomic action is reached.
3.3 Memory
The TPG model introduced in (Smith and Heywood,
2019) features an external shared memory accessible
to all agents. Each agent consists of several teams and
programs, and each program has its own private reg-
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
298

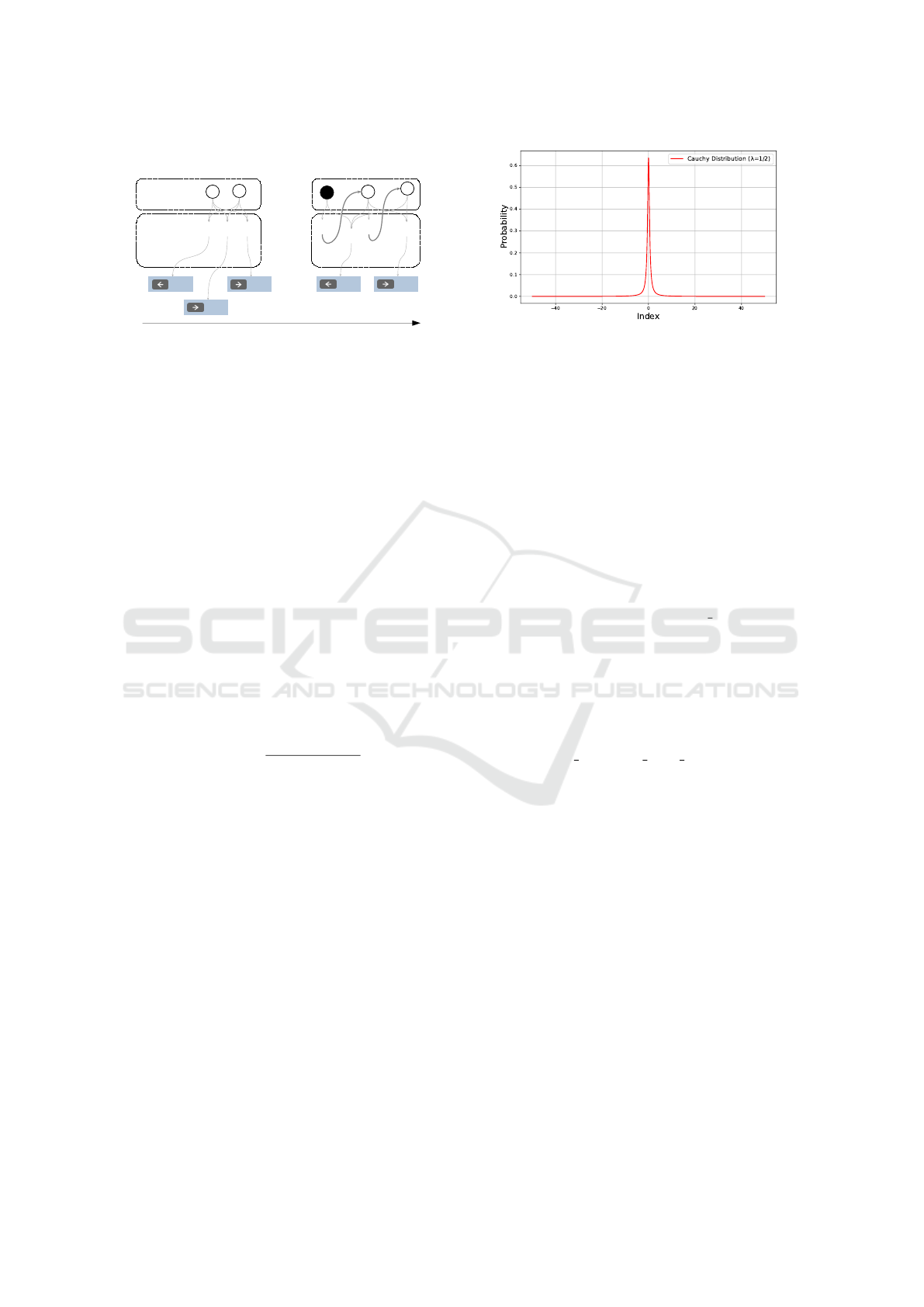
Time (generations)
t
1
Team
Populaon
Program
Populaon
{ }{ } { }
t
2
t
1
{ }
{ }
{ }
t
2
t
3
{ }
Program Graphs Emerge
s[1]
s[1]
s[1]
s[1]s[1]
Inial Populaons
Figure 2: Tangled Program Graphs’ hierarchical decision-
making structure in which teams of programs predict dis-
crete and continuous actions.
isters, which are inaccessible to other programs. Pro-
gram registers are stateful, and thus provide a simple
form of recurrent temporal memory. Furthermore, all
programs have access to the shared external memory
for reading and writing operations. This memory is
not reset between training episodes or the evaluation
of different agents, ensuring continuity and allowing
for cumulative knowledge building.
Indexed memory operations are handled proba-
bilistically to manage both short-term and long-term
retention. The write operations distribute the con-
tent of a program’s registers across the external mem-
ory in a probabilistic manner, with locations in the
middle of the memory being updated more frequently
(short-term memory) and those towards the ends be-
ing updated less frequently (long-term memory). This
study uses the following probability definition, which
is shown in Figure 3, and where i corresponds to the
index:
P
write
(i) =
0.25
0.5π(i
2
+ 0.25)
(2)
This function provides a heavy-tailed distribution,
allowing writing across a wide range of memory lo-
cations, the probability is sharply peaked at the center
and rapidly decreases as the offset increases.
Read operations use indexing, allowing programs
to locate regions of external memory characterized by
specific temporal properties. This approach allows
programs to interact during each generation or across
different generations, facilitating more sophisticated
decision-making strategies.
4 EXPERIMENTS
The experiments detailed in this section are designed
to evaluate our TPG shared temporal memory im-
plementations in mitigating the negative impact of
destructive agents while maintaining system perfor-
mance and efficiency. We used TPG as implemented
Figure 3: Probability function for memory write operations.
in (Amaral, 2019). The culture method discussed in
(Spector and Luke, 1996a) highlights the negative im-
pact of destructive agents, noting that while positive
ideas from individuals can be preserved for collective
benefit, negative actions by a single agent can destroy
valuable information. To reduce this negative impact,
we study the effect of clearing memory at different
stages and compare the results with the original ver-
sion of shared memory in TPG.
We assess three strategies: resetting memory for
each agent (Section 4.1), resetting memory for each
episode (Section 4.2), and a no-memory condition
(Section 4.3). Algorithm 1 details the implemen-
tation of these strategies. The following terms are
used in the pseudocode: execute frames() exe-
cutes a set of frames where the agent takes an ac-
tion based on observations and receives feedback
from the environment for each frame. Lock pool-
ing and release pooling manage parallelism, with
lock pooling preventing other agents from inter-
acting with memory and release pooling restoring
parallelism after the agent completes its interac-
tions. execute episodes with frames() runs mul-
tiple episodes.
4.1 Reset Memory for Each Agent
In this case, the external memory and registers are
cleared and set to zero at the beginning of evaluating
each agent in each generation. This method ensures
that each agent can independently build its own mem-
ory model at run time and removes the possibility of
negative impact from other agents. Each agent essen-
tially has its own indexed memory which is shared
among its programs, resembling a smaller society. In
this case, the agent’s memory maintains state over all
training episodes, during which time the agent is free
to gradually develop its mental model of the environ-
ment. While each agent interacts with memory, it is
essential to restrict others’ access to it. In our current
implementation, this requires blocking the paralleliz-
ing system, which increases experiment run time.
Tangled Program Graphs with Indexed Memory in Control Tasks with Short Time Dependencies
299

Algorithm 1: Agent execution with memory resetting
conditions.
for generation in generations do
run agent with pooling
if original version then
execute episodes with frames()
else
if reset for each agent then
lock pooling
reset external memory
reset agent’s registers
execute episodes with frames()
release pooling
else
if reset for each episode then
for episode in episodes do
lock pooling
reset external memory
reset agent’s registers
execute frames()
release pooling
end
else
for episode in episodes do
for frame in frames do
reset agent’s registers
act and get feedback
end
end
end
end
end
end
Function execute frames():
for frame in frames do
act and get feedback
end
Function
execute episodes with frames():
for episode in episodes do
execute frames();
end
4.2 Reset Memory for Each Episode
This approach also removes potential negative impact
of other agents. In this version, we reset the external
memory and all the agent’s registers at the beginning
of each episode. This tests the agents’ ability to build
their memory quickly during a single episode. Again,
when one agent interacts with memory, it is essential
to restrict others’ access to it.
4.3 No Memory
In this version, we do not use any external indexed
memory and we clear all the agent’s registers to zero
at the beginning of each time step, implying the
agent’s behaviour is entirely stateless. This is a con-
trol experiment to confirm that all partially observable
task configurations absolutely require stateful agents
with temporal memory capabilities.
4.4 Experimental Parameters
Evolutionary hyper-parameters follow previous TPG
work in RL tasks (Smith and Heywood, 2019). The
initial root team population is set at 360 and remains
static throughout evolution. We utilize “Cauchy Half”
(Equation 2) for memory distribution in scenarios in-
volving memory. The operation set includes: “ADD”,
“SUB”, “MULT”, “DIV”, “NEG”, “COS”, “LOG”,
“EXP”, “MEM READ”, and “MEM WRITE” allow-
ing complex interactions without any task-specific
functions. To constrain model complexity and com-
putational cost of decision-making, we set the proba-
bility of acting atomic to be 1.0, meaning no programs
point to another team.
4.5 Results
Experiments reveal that the reset memory for each
episode strategy (Section 4.2) improves the score and
performance of TPG agents across all the control
problems mentioned in Section 3.1, as shown in Fig-
ure 5. This memory configuration also results in the
lowest solution complexity, as indicated in Figure 6.
We conduct experiments for all the cases detailed
in Section 4 as well as the original version of PyTPG
(Amaral, 2019), using the Cauchy Half distribution
for memory writing probability. We ran 10 repeats
with unique random seeds for Pendulum task and
CartPole task, and 8 repeats for Acobot task. Each
experiment was run using multiple cores to manage
the computational load efficiently: 30 hours with 30
cores for Acrobot, 48 hours with 10 cores for Pendu-
lum, and 72 hours with 20 cores for CartPole. The
results were compared based on the achieved score
during the same running period (Figure 4), reached
score based on the number of generations (Figure 5),
and their complexity (Figure 6). The complexity is
characterized by average number of instructions exe-
cuted per action decision.
To plot Figures 5 and 4, we determined the min-
imum number of generations across all experiments.
According to Figure 5, for all three environments, the
approach of resetting memory for each episode has
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
300

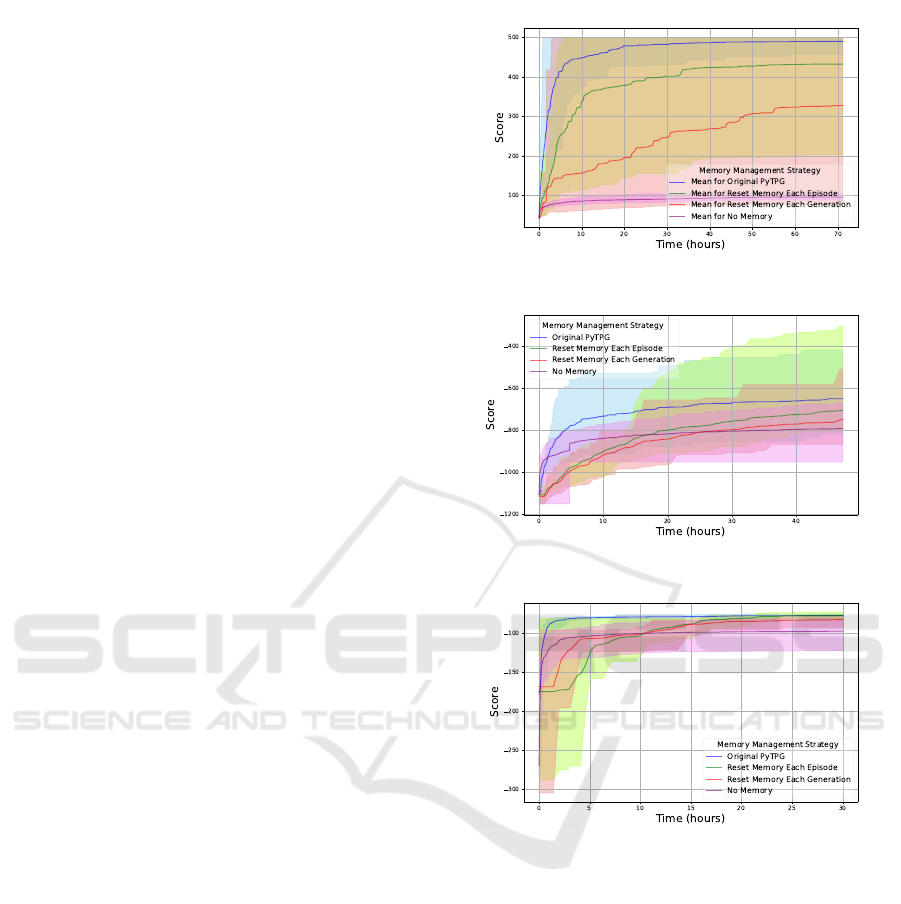
the best average score after the 5
th
generation.
In Figure 6, the complexity over the minimum
number of generations across all experiments is re-
ported. This figure demonstrates that resetting mem-
ory and registers for each episode reduces complexity.
Interestingly, in all three environments, although the
no memory version has the worst score over genera-
tions, it exhibits the highest complexity. This indi-
cates that agents are struggling to improve by making
more complex decisions. On the other hand, the ver-
sion with resetting memory for each episode, which
has the highest score, also exhibits less computational
complexity than the original PyTPG.
Execution speed varied across tasks: the no mem-
ory version consistently ran the most generations, in-
dicating the fastest execution speed. The original ver-
sion performed at an intermediate speed, while both
the reset memory for each agent and reset memory
for each episode versions were the slowest, running
significantly fewer generations across all tasks due to
the blocking of parallelism as discussed in Section 4.
The blocking mechanism is further illustrated in Al-
gorithm 1. The running time explains the original ver-
sion’s superior results over the same amount of time
as indicated in Figure 4. However, since this version
runs more generations in the same amount of time as
reset for each episode, it achieves a better score. Still,
based on Figure 5, it would perform worse if it oper-
ated at the same speed as the reset memory for each
episode case.
These results support our hypothesis that, for tasks
without long term state dependencies, resetting mem-
ory before each episode can reduce the effect of nega-
tive agents and improve results over the same number
of generations. As expected, the no memory version
cannot solve these partially observable tasks.
After training, we reloaded and tested the cham-
pion of the last common generations for each case
across all seeds. We applied the Mann-Whitney U test
to compare each case with the reset memory for each
episode case, confirming the results in Figure 5 with
p-values less than 0.05. In Acrobot, the reset memory
for each agent and reset memory for each episode ver-
sions showed no significant differences due to simi-
lar scores. However, both versions showed significant
differences (p-value<0.05) compared to the original
and no-memory versions. Readers interested in fur-
ther details about TPG and visualizations of evolved
graphs of teams are referred to (Djavaherpour et al.,
2024), (Smith and Heywood, 2024), (Kelly et al.,
2021).
a Cartpole environment.
b Pendulum environment.
c Acrobot environment.
Figure 4: Scores achieved in different memory strategy ex-
periments over 48 hours in various environments.
5 CONCLUSION
This study explored the effectiveness of different
memory management strategies in enhancing the per-
formance of Tangled Program Graphs in partially ob-
servable Reinforcement Learning environments. We
experimented with TPG’s original shared indexed
memory formulation, resetting memory for each
agent, resetting memory for each episode, and a no-
memory condition across three benchmark tasks: Ac-
robot, Pendulum, and CartPole.
The results show that resetting memory for each
episode improves the performance of TPG agents
across all tasks. This strategy led to the highest av-
Tangled Program Graphs with Indexed Memory in Control Tasks with Short Time Dependencies
301

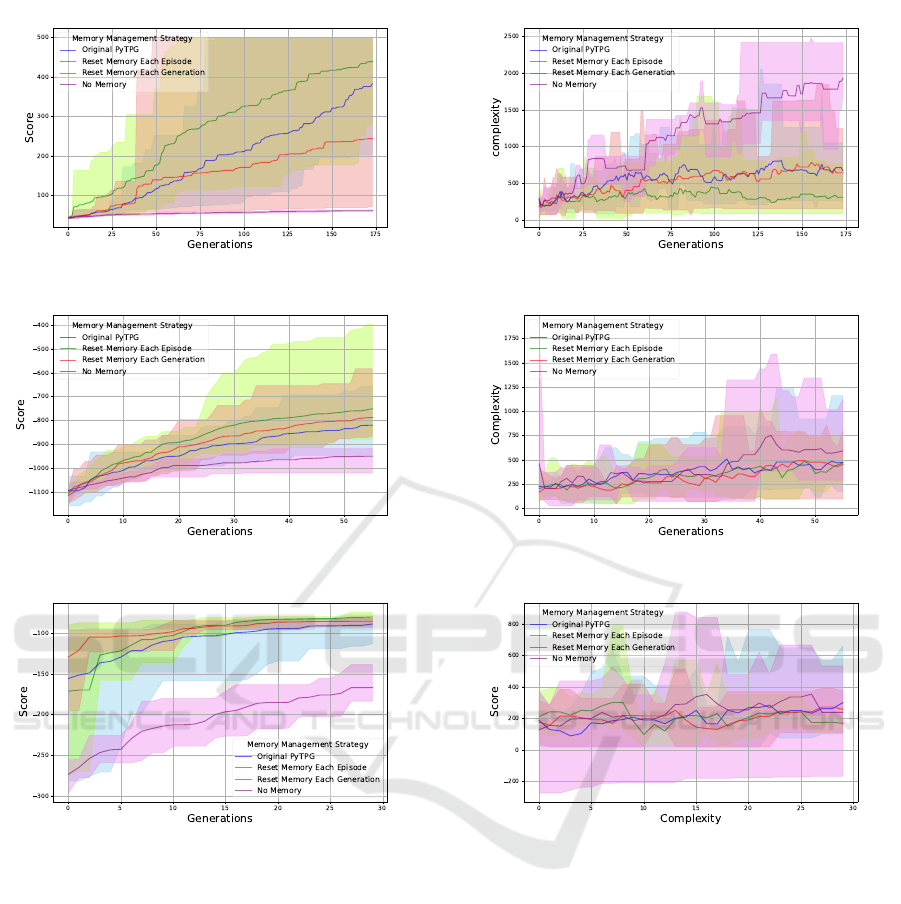
a Cartpole environment.
b Pendulum environment.
c Acrobot environment.
Figure 5: Scores achieved in different memory strategy ex-
periments over 48 hours, based on the minimum number of
generations run in various environments.
erage scores after the initial few generations and re-
duced the complexity of decision-making processes.
In contrast, the no-memory version, although capable
of running more generations, struggled to solve the
partially observable tasks effectively, exhibiting the
highest complexity and lowest performance.
Interestingly, while the reset memory for each
agent and reset memory for each episode strategies
showed similar performance, both were significantly
better than the original and no-memory versions in
terms of robustness and reliability, demonstrating
consistency of the agents’ performance across differ-
ent runs with a tighter distribution of scores over the
repeats. In contrast, the reset memory for each gen-
a Cartpole environment.
b Pendulum environment.
c Acrobot environment.
Figure 6: Complexity in different memory strategy exper-
iments over 48 hours, based on the minimum number of
generations run in the different environment.
eration case failed to perform better than the original
version in CartPole only. The Mann-Whitney U test
confirmed these findings, with p-values less than 0.05,
indicating significant differences.
These findings suggest that shared memory and
“culture” can have a negative impact on the perfor-
mance of TPG agents in partially observable tasks
with no long term temporal dependencies. Resetting
memory before each episode can mitigate these neg-
ative effects, improving agent performance and re-
ducing decision-making complexity. However, the
primary drawback of the memory reset strategies is
the increased runtime due to the blocking of paral-
lelism. Implementing a dedicated memory for each
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
302

agent could potentially mitigate this issue, allowing
parallel execution without interference and maintain-
ing computational efficiency.
Overall, effective memory management strate-
gies are crucial in reinforcement learning tasks. By
carefully selecting and optimizing memory resetting
strategies, significant improvements can be achieved
in the efficiency and effectiveness of TPG in challeng-
ing control environments.
6 FUTURE WORK
Future work will scale these experiments to more
complex environments, such as Memory Gym
(Pleines et al., 2023), in order to validate the meth-
ods’ robustness and explore their adaptability to tasks
with long and short time dependencies. The current
memory strategies help agents quickly build mental
models without directly sharing information. How-
ever, this may not be suitable in complex tasks where
global memory is beneficial (e.g. (Smith and Hey-
wood, 2019)). For such cases, we envision a dynamic
method, such as resetting memory based on real-time
performance metrics (e.g., wiping memory if median
score drops below that of the previous generation),
could provide a more adaptive approach. Addition-
ally, investigating other probabilistic memory func-
tions and their combinations could provide further in-
sights into optimizing agent’s memory use. For exam-
ple, rather than manually resetting memory, it might
be possible to evolve customized memory manage-
ment rules for each agent which automatically min-
imize negative effects on shared memory. Finally,
integrating advanced parallelization techniques could
mitigate the runtime overhead caused by memory re-
sets, improving their practicality in real-world appli-
cations. Since this paper incurred significant wall
clock run time, faster TPG frameworks, such as those
from (Djavaherpour et al., 2024), will be considered
for use in future work.
Overall, studying the long-term evolutionary im-
pacts of different memory strategies could provide
deeper insights into the development of more sophis-
ticated and adaptive agents in partially observable en-
vironments.
REFERENCES
Amaral, R. (2019). Pytpg: Tangled program graphs
in python. https://github.com/Ryan-Amaral/PyTPG/
tree/7295f90ececbfc34fdbc1d73e032a9c2407a182c.
Brameier, M. and Banzhaf, W. (2007). Linear Genetic Pro-
gramming. Springer.
Brockman, G., Cheung, V., Pettersson, L., Schneider, J.,
Schulman, J., Tang, J., and Zaremba, W. (2016). Ope-
nAI Gym. arXiv, 1606.01540.
Djavaherpour, T., Naqvi, A., Zhuang, E., and Kelly, S.
(2024). Evolving Many-Model Agents with Vector
and Matrix Operations in Tangled Program Graphs.
In Genetic Programming Theory and Practice XXI.
Springer (AD).
Kelly, S. and Heywood, M. I. (2018). Emergent Solutions
to High-Dimensional Multitask Reinforcement Learn-
ing. Evolutionary Computation, 26(3):347–380.
Kelly, S., Newsted, J., Banzhaf, W., and Gondro, C. (2020).
A modular memory framework for time series predic-
tion. In Proceedings of the 2020 Genetic and Evolu-
tionary Computation Conference, GECCO ’20, page
949–957, New York, NY, USA. Association for Com-
puting Machinery.
Kelly, S., Smith, R. J., Heywood, M. I., and Banzhaf, W.
(2021). Emergent tangled program graphs in partially
observable recursive forecasting and vizdoom naviga-
tion tasks. ACM Trans. Evol. Learn. Optim., 1(3).
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Ve-
ness, J., Bellemare, M. G., Graves, A., Riedmiller,
M. A., Fidjeland, A. K., Ostrovski, G., Petersen, S.,
Beattie, C., Sadik, A., Antonoglou, I., King, H., Ku-
maran, D., Wierstra, D., Legg, S., and Hassabis, D.
(2015). Human-level control through deep reinforce-
ment learning. Nature, 518:529–533.
Pleines, M., Pallasch, M., Zimmer, F., and Preuss, M.
(2023). Memory gym: Partially observable challenges
to memory-based agents. In The Eleventh Interna-
tional Conference on Learning Representations.
Smith, R. J. and Heywood, M. I. (2019). A model of
external memory for navigation in partially observ-
able visual reinforcement learning tasks. In Genetic
Programming: 22nd European Conference, EuroGP
2019, Held as Part of EvoStar 2019, Leipzig, Ger-
many, April 24–26, 2019, Proceedings, page 162–177,
Berlin, Heidelberg. Springer-Verlag.
Smith, R. J. and Heywood, M. I. (2024). Interpreting tan-
gled program graphs under partially observable dota 2
invoker tasks. IEEE Transactions on Artificial Intelli-
gence, 5(4):1511–1524.
Spector, L. and Luke, S. (1996a). Cultural transmission of
information in genetic programming. In Proceedings
of the 1st Annual Conference on Genetic Program-
ming, page 209–214, Cambridge, MA, USA. MIT
Press.
Spector, L. and Luke, S. (1996b). Culture enhances the
evolvability of cognition. In Cottrell, G., editor, Cog-
nitive Science (CogSci) 1996 Conference Proceed-
ings, pages 672–677, Mahwah, NJ, USA. Lawrence
Erlbaum Associates.
Sutton, R. and Barto, A. (2018). Reinforcement Learning:
An Introduction. The MIT Press, Cambridge, MA,
2nd edition.
Teller, A. (1994). The evolution of mental models, page
199–217. MIT Press, Cambridge, MA, USA.
Tangled Program Graphs with Indexed Memory in Control Tasks with Short Time Dependencies
303