Does Path Tracking Benefit from Sequential or Simultaneous
RL Speed Controls?
Jason Chemin, Eric Lucet and Aur
´
elien Mayoue
Institut LIST, CEA, Universit
´
e Paris-Saclay, F-91120, Palaiseau, France
Keywords:
Path Tracking, Reinforcement Learning, Speed Control.
Abstract:
Path tracking is a critical component of autonomous driving, requiring both safety and efficiency through
improved tracking accuracy and appropriate speed control. Traditional model-based controllers like Pure
Pursuit (PP) and Model Predictive Control (MPC) may struggle with dynamic uncertainties and high-speed
instability if not modeled accurately. While advanced MPC or Reinforcement Learning (RL) can enhance path
tracking accuracy via steering control, speed control is another crucial aspect to consider. We explore various
RL speed control approaches, including end-to-end acceleration, acceleration correction, and target speed
correction, comparing their performance against simplistic model-based methods. Additionally, the impact
of sequential versus simultaneous control architectures on their performance is analyzed. Our experiments
reveal that RL methods can significantly improve path tracking accuracy by balancing speed and lateral error,
particularly for poorly to moderately performing steering controllers. However, when used with already well-
performing steering controllers, they performed similarly or slightly worse than simple model-based ones,
raising questions about the utility of RL in such scenarios. Simultaneous RL control of speed and steering is
complex to learn compared to sequential approaches, suggesting limited utility in simple path tracking tasks.
1 INTRODUCTION
Steering and speed controls for path tracking are
essential for autonomous driving systems, requiring
vehicles to accurately navigate predetermined paths
while maintaining safe speeds. This task is challeng-
ing due to uncertainties such as control delays, vehicle
dynamics, inaccurate localization, or road sliding.
Various steering controllers have been developed
to minimize lateral error and keep vehicles on desired
paths (Paden et al., 2016). Traditional controllers like
Pure Pursuit, Stanley or PID (Coulter, 1992; Hoff-
mann et al., 2007; Normey-Rico et al., 2001) are
widely used due to their simplicity. Model-Predictive
Controllers (MPC) (Stano et al., 2022) can predict the
vehicle’s future actions and states, considering system
dynamics over time. However, tuning their gains be-
comes more intricate as their complexity grows.
Reinforcement Learning (RL) has emerged as a
promising approach for control, improving through
interactions with the environment (Faust et al., 2017;
Vollenweider et al., 2023). In a prior work (Chemin
et al., 2024), several RL strategies were evaluated for
steering control. In the experiments, vehicle speeds
1
This work was supported by the OTPaaS project. This
project has received funding from the French government
as part of the “Cloud Acceleration Strategy”.
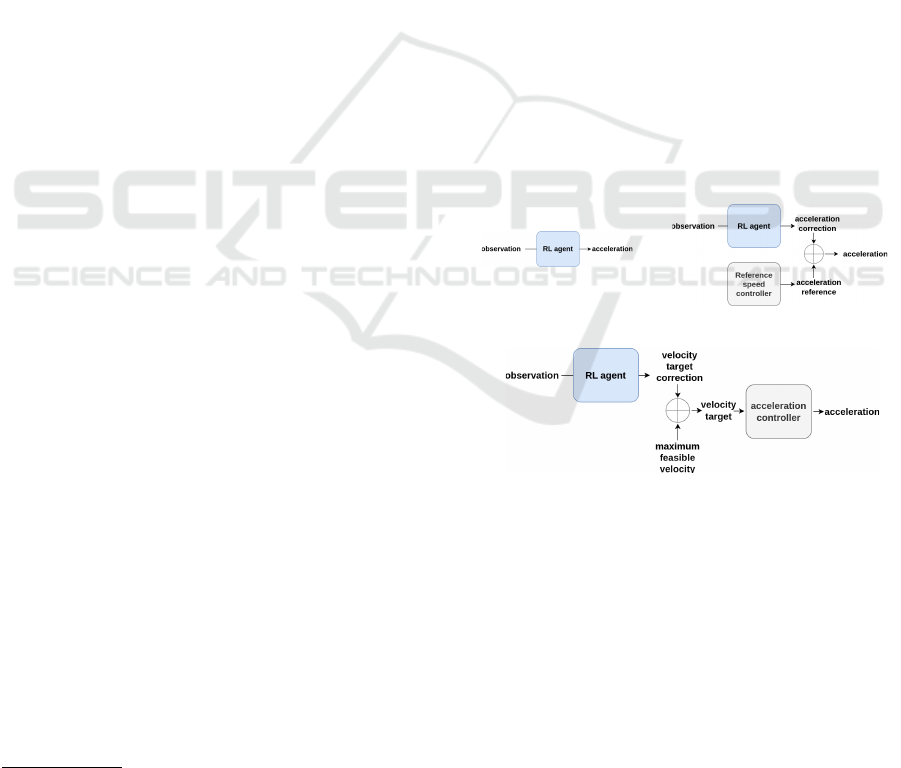
(A).
(AC).
(VC).
Figure 1: Design of three RL speed controllers: end-to-end
acceleration (A), acceleration correction (AC), and target
velocity correction (VC).
varied randomly along the path and the RL agents
learned to steer accordingly. However, real-world ap-
plications of learning methods may encounter diffi-
culties related to safety, stability, and explainability,
which are areas of ongoing research (Gangopadhyay
et al., 2022; Xu et al., 2023).
To further enhance path tracking, we now focus
on more complex speed control strategies. Human
drivers typically slow down before entering a corner,
adjusting speed based on the sharpness of the turn,
274
Chemin, J., Lucet, E. and Mayoue, A.
Does Path Tracking Benefit from Sequential or Simultaneous RL Speed Controls?.
DOI: 10.5220/0013017800003822
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 2, pages 274-281
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

which is measured by the path curvature k. The max-
imum feasible speed for a given vehicle can be esti-
mated using either physical formulas, fuzzy logic or
data-driven approaches. In (Zhou et al., 2021), an
MPC computes optimal acceleration controls to bet-
ter anticipate corners and improve driving comfort
and safety. Additionally, a sophisticated controller
in (Serna and Ruichek, 2017) uses GPS data to ad-
just speed based on road curvature and speed lim-
its. While model-based approaches can be effective,
learning approaches offer the potential to further en-
hance speed control performance by learning to cope
with unknown factors. Trained models can adapt to
these factors, improving the robustness and effective-
ness of the speed control (Gauthier-Clerc et al., 2021).
In (Geng et al., 2016; Cheng et al., 2017), a network is
trained to predict longitudinal control using data from
various driving profiles, achieving more human-like
behaviors. While these works estimate well the max-
imum feasible velocity, this paper aims to address:
How to balance tracking accuracy (safety) with max-
imum vehicle speed (time efficiency)?
Another question addressed is: Should speed con-
trol be computed simultaneously with steering, or se-
quentially? In most prior works, speed and steering
controls are decoupled. Intuitively, such a speed con-
trol could involve slowing down before entering a cor-
ner, maintaining a constant speed through the corner,
then re-accelerating, considering only future curva-
tures. In parallel, given the current vehicle speed, the
driver controls the steering to follow the path ahead.
However, in more complex scenarios, a coupled con-
trol architecture could be beneficial to enhance safety
and performance (Macadam, 2003). In (Attia et al.,
2014), a coupled strategy is implemented using a non-
linear MPC for highway exit scenarios. Using deep
learning in (Devineau et al., 2018), a coupled control
agent is trained for enhanced tracking accuracy. The
seminal research (Kendall et al., 2019) learns cou-
pled RL control, observing cameras and other sensors.
They demonstrate the first deep RL agent driving a car
in the real world. In (Cai et al., 2020), highly chal-
lenging drifting scenarios are solved through coupled
RL control, where coordination between acceleration
and steering is critical.
This study extends upon prior works (Hill, 2022)
and (Chemin et al., 2024). Our contributions include:
• RL Speed Control: Several RL designs are pro-
posed to balance tracking accuracy and speed.
• Evaluation: The potential benefits of RL tech-
niques for speed control are evaluated, either in si-
multaneous control or when decoupled to enhance
performance of a given steering controller.
• Comparison: A comprehensive comparison is
made using speed and lateral error metrics for
quantitative performance evaluation.
Finally, the RL speed agents are compared with sim-
plified model-based speed controllers, which serve as
a reference. This study focuses on evaluating RL ar-
chitectures for steering and speed control, to provide
insights. While the methods may not be fully opti-
mized, the results could offer valuable guidance on
what works well and under what conditions, even if
not directly benchmarked against the latest research.
2 PATH TRACKING PROBLEM
Path tracking is a fundamental challenge in au-
tonomous navigation, aiming to guide a vehicle along
a predefined trajectory. The path tracking and speed
problem can be summarized in three main objectives:
1. Minimizing the lateral error (e
lat
) by controlling
the vehicle’s steering (δ).
2. Aligning the vehicle’s direction with the desired
path’s direction.
3. Adapting the longitudinal velocity (v
vehicle
) to bal-
ance safe tracking and time efficiency.
This study focuses on car-like vehicles, addressing (1)
and (2) mainly through steering. However, increasing
speed (3) inherently challenges these objectives.
The control policy is a function π(obs) = u, where
obs are the observations and u is the action computed
by the agent, which is detailed in this section.
2.1 Steering: Model-Based and RL
In this paper, we use two model-based path tracking
controllers to control the steering. The well-known
”Pure Pursuit” (PP) controller is a simple geometric
approach that guides the vehicle towards a point on
the path ahead, ensuring it follows the desired tra-
jectory. We also use an MPC, named EBSF (Lenain
et al., 2021). EBSF considers a simplified dynamic
model, performing well at low to medium speeds (< 4
m/s). However, it can become unstable at higher
speeds, making it an interesting baseline for evalu-
ating how different speed controllers can mitigate its
issues. Geometric controllers like PP are straightfor-
ward but may lack performance. MPCs can be effec-
tive depending on model complexity, but may become
unstable under unknown or strong external forces.
To address these problems, we investigated sev-
eral RL methods for steering control in (Chemin et al.,
2024). We now use two of the best-performing RL
steering controllers: (S) learning to steer, and (SC)
Does Path Tracking Benefit from Sequential or Simultaneous RL Speed Controls?
275

correcting the steering of a given controller. For (S),
the action is u = [δ], where δ is the steering control.
For (SC), the action is u = [∆δ], where ∆δ is the cor-
rection added to the reference steering. The reference
steering, corrected by (SC), is provided by the model-
based controllers, PP and EBSF.
2.2 Speed: Model-Based
The maximum feasible speed is computed for a given
curvature as v
f easible
= f (k), where k is the curvature
and f (k) is a linear interpolation from [k
min
,k
max
] to
[v
min
,v
max
]. This heuristic, denoted A
re f
, provides a
good approximation for our scenarios, where values k
are found empirically. While more precise mathemat-
ical models exist, they can be complex due to depen-
dencies on vehicle characteristics and other factors.
Additionally, the lateral error value is used to de-
crease speed when deviations from the desired path
occur. While this method, denoted A
lateral
, reacts
to the current lateral error, it does not anticipate fu-
ture errors. Although methods like MPC can predict
future lateral errors, this work only investigates RL
techniques for speed control to address these issues.
The goal is to evaluate whether these RL methods are
beneficial in all cases.
2.3 Sequential or Simultaneous Speed
and Steering Controls
A key question in path tracking is whether to con-
trol speed and steering sequentially or simultaneously.
The core of the problem lies in the interaction be-
tween these two controls, which is not trivial. In the
study (Macadam, 2003), it is found that while speed
and steering are often decoupled in simpler driving
situations, an integrated control system is required for
more complex maneuvers. In these cases, humans
naturally coordinate both controls, often leading to si-
multaneous adjustments during demanding tasks like
cornering or obstacle avoidance. This approach be-
comes even more critical in highly complex scenarios
such as drifting (Weber and Gerdes, 2023).
This paper evaluates the benefits and limitations of
both sequential and simultaneous control approaches.
Based on the literature, we hypothesize that simul-
taneous control may offer better performance in the
challenging scenarios we address. Our study also in-
directly assesses whether these scenarios are complex
enough to justify the use of simultaneous control.
3 LEARNING SPEED CONTROL
In this section, the approach to learning speed control
for path tracking is described. The goal is to compute
the optimal acceleration to ensure efficient and safe
navigation along a predefined path.
3.1 Actions
Three different RL speed controls are explored:
• End-to-End Acceleration (A): The output is the
acceleration control u = [a], where a is the accel-
eration in m/s
2
.
• Acceleration Correction (AC): The output is a
correction u = [∆a] to a reference acceleration
a
re f
. The final acceleration is u = a
re f
+ ∆a.
• Speed target Correction (VC): The output is
a correction u = [∆v] to a reference speed tar-
get v
re f
. The corrected speed target is v
target
=
v
re f
+ ∆v, which is then used by any acceleration
controller to achieve the desired speed.
3.2 Observations
Similar observations than in prior work are used, with
a few additions depending on the RL speed controller.
3.2.1 Common Observations
The common observations are defined as:
o
present
= {e
lat
,e
head
,c f
cr,δ
real
,v, v
f easible
}
where e
lat
is the lateral error, e
head
is the heading er-
ror, c f cr represents the cornering stiffness for both
front and rear, δ
real
is the orientation of the front
wheel, v is the vehicle speed, and v
f easible
is the max-
imum feasible speed at the estimated path curvature.
These observations differ from the prior work as we
now train a speed controller specific to a given steer-
ing controller. The aim here is for the agent to rely
more on the global tracking performance, rather than
on small details useful for computing the steering.
The future path is discretized in 12 points, with
a full time horizon H = 6s. This empirical value is
sufficient to anticipate future path curves and con-
trol delays. Therefore, the time separating each point
is ∆T = H/12 = 0.5s, which in distance is equal to
∆D = 0.5 ∗ v.
o
path
= {c
i
,...,c
i+11
} (1)
One critique is that if the vehicle velocity is jerky,
the observations will also be jerky, complicating the
agent’s understanding and training. Despite this,
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
276

our discretization worked adequately, but a distance-
based approach may be preferred for speed control.
Additionally, we include past observations to cope
with control delays. These help the agent understand
the impact of previous actions:
o
past
= {δ
i
,...,δ
i−N
,a
i
,...,a
i−N
}
where δ
i
is the steering control and a
i
is the accelera-
tion control at frame i. We observe N = 4 previous
frames to cover possible control delays, which can
have a maximum value of 0.4s, considering a timestep
T = 0.1s between each RL agent step.
3.2.2 Additional Observations
Additional observations are required for AC and VC,
defined as o
add
= {u
i
,...,u
i−N
}, with u
i
being the ac-
tion performed at frame i. The past actions help the
agent produce smooth actions and understand their
impact on the system due to delay. These additional
observations are not used for method A as u
i
= a
i
.
3.3 Rewards
We employ a reward design in the shape:
R = w
track
· r
track
+ w
vel
· r
vel
+ w
smooth
· r
smooth
+ w
minimize
· r
minimize
The reward r
smooth
is common to all RL speed con-
trollers. It aims to reduce large action variations to
avoid ”bang-bang” strategies (rapidly switching be-
tween minimum and maximum action values):
r
smooth
= −(u
i−1
− u
i
)
2
The reward r
minimize
is used by AC and VC to re-
duce correction aggressiveness and stay close to the
reference, but it can also be used in A to punish overly
strong acceleration or steering:
r
minimize
= −u
2
i
3.3.1 Tracking Reward
The main positive reward, r
track
, minimizes the lateral
error e
lat
between the vehicle and the path. We use a
Gaussian function bounded in [0,1]:
r
track
= e
−
(e
lat
)
2
2·(c)
2
with a standard deviation c = 0.3, the Gaussian func-
tion strongly encourages lateral errors to be less than
0.2 meters, and results in a null reward for errors ex-
ceeding 1 meter. If the tracking is perfect, r
track
at
each step should be close to 1.
In situations where localization suffers from sig-
nificant inaccuracies, ∆GPS set to 10 cm maximum
in our study, a lateral error plateau is set up within the
range of [−∆GPS,∆GPS]:
e
lat
= max(0,|e
lat
| − ∆GPS)
During training, any lateral error falling within this
range is treated as zero, resulting in r
track
= 1. While
this approach helps mitigate instability issues due to
localization inaccuracy, it also introduces a trade-off,
potentially affecting the overall tracking performance.
3.3.2 Acceleration Reward
A positive reward r
vel
encourages the agent to acceler-
ate towards the estimated maximum feasible velocity
v
f easible
. It is also a Gaussian, similar to r
track
. The
velocity error is e
vel
= v
f easible
− v and the standard
deviation of the Gaussian is c = 3, which is arbitrarily
set and is 10 times larger than that of r
track
.
To strike a balance between r
track
and r
vel
, r
track
for lateral errors of [0.1,0.2,0.3,...]m is nearly equal
to r
vel
for velocity errors of [1,2, 3, ...]m/s, respec-
tively. Balancing the standard deviation of each term
is crucial if the task requires prioritizing lateral error
over velocity error minimization.
Similar to e
lat
, a margin is used on vehicle speed
error e
vel
. The velocity must be as close as possible
to v
f easible
, but not strictly equal. Therefore, we set
e
vel
= max(0,|e
vel
| − v
margin
), with v
margin
= 0.5 m/s.
During training, an episode terminates when the
lateral error norm |e
lat
| goes over 1.5 meters. The
value was chosen empirically to allow for sufficient
exploration. The agent must learn to maximize the
rewards R without prematurely ending the episode.
3.4 Simultaneous RL Steering and
Speed Controls
In our work, decoupled speed controls is also com-
pared to coupled RL steering and speed controls,
where both controls are output by the same agent.
Observations are the concatenation of all obser-
vations required for each steering and speed method,
with redundant observations removed.
Rewards are the concatenation of all reward terms,
with r
smooth
and r
minimize
being added for both steering
and speed controls. To maintain a balance between
positive rewards, r
track
and r
vel
, and negative rewards,
r
smooth
and r
minimize
, the reward weights is set such that
w
track
+ w
vel
= 1. It ensures that the final reward will
always be equal to 1 in the best-case scenario.
Does Path Tracking Benefit from Sequential or Simultaneous RL Speed Controls?
277

4 TRAINING AND
HYPERPARAMETERS
We train our agents using PPO on Stable Baselines3
(Raffin et al., 2021). Hyperparameters are set as
follows: Number of parallel workers: 16, learn-
ing rate: linear schedule(3e-4, 3e-5) over the full
training, n steps: 1024, batch size: 256, n epochs:
10, gamma: 0.96, gae lambda: 0.98, clip range:
0.2, normalize advantage: True, ent coef: 0.001,
vf coef: 0.5, max grad norm: 0.5, use sde: True,
sde sample freq: 4.
4.1 Random Path Generation
Paths are generated using a kinematic car model that
randomly oscillates its steering angle. Velocity pa-
rameters are v
min
= 1.5 and v
max
= 9.5 meters per
second, with the maximum curvature set accordingly.
To simulate diverse driving conditions, the slipping
coefficient (c f cr) is also randomized after a random
number of steps. Such paths allows to test the agent’s
ability to adapt controls under varying conditions.
4.2 Reward Weights
We define the reward weights for each control
method: A, AC, and VC. The weights determine the
balance between reward components, such as track-
ing accuracy, smoothness, and action magnitude.
End-to-End Acceleration Controller (A):
w
track
= 1.0, w
vel
= 1.0, w
smooth
= 2.0, w
minimize
= 0.1.
Acceleration Correction Controller (AC):
w
track
= 1.0, w
vel
= 1.0, w
smooth
= 3.0, w
minimize
= 0.1.
Speed Target Correction Controller (VC):
w
track
= 1.0, w
vel
= 1.0, w
smooth
= 1.0, w
minimize
= 0.1.
If used, the rewards for RL steering controllers,
whether decoupled or simultaneous, are as defined in
prior work (Chemin et al., 2024).
5 RESULTS: SPEED
CONTROLLER EVALUATION
ACROSS DIFFERENT
STEERING METHODS
The RL speed controllers are evaluated on various
steering methods to understand when RL is beneficial
for speed control. Around 100 random trajectories
are generated, with varying slipping conditions and
v
f easible
changes based on the curvature. The evalua-
tions focus on three criteria:
1. Average lateral error: The average distance be-
tween the vehicle and the trajectories.
2. Average diff vel: The difference between v
f easible
and v, indicating the discrepancy from the maxi-
mum feasible velocity at each step.
3. Average score: A metric balancing lateral
error and velocity, calculated as score =
max(lateral error,
di f f vel
10
). Velocity error is di-
vided by 10 to align r
vel
with the r
track
for the
given standard deviations.
All steering controls are tested with several speed
control strategies:
1. Two simple model-based strategies: A
re f
and
A
lateral
as described in Section 2.2.
2. Three RL speed controllers described in Section
3: A (end-to-end acceleration), AC (acceleration
correction), and VC (target speed correction).
When using RL speed and steering, we test both se-
quential and simultaneous approaches. In this section,
the figures show the boxplot results, where the X-axis
labels indicate the speed control tested. If ”Sim:” is
specified, it means that Steering and Speed Controls
are simultaneous, otherwise, they are decoupled. Cat-
egories of controllers are indicated by boxplot col-
ors: blue is model-based speed, green is sequential
RL speed, and purple is simultaneous controls.
The optimal lateral error expected is around 10cm
which is equal to the maximum GPS error, ∆GPS, as
specified in Section 3.3.1. As for the velocity error,
there is no specific requirement, but the goal is for the
RL agents to achieve a balance between errors, such
that the overall score is minimized.
5.1 Combined with Model-Based
Steering
We first evaluate our methods using the two model-
based controllers PP and EBSF.
Pure Pursuit (PP) in Figure 2a: This straight-
forward controller provides simple steering control
but does not consider vehicle dynamics and can suf-
fer from artifacts like corner cutting. Using PP with
A
re f
, which accelerates up to near the maximum fea-
sible speed v
f easible
(di f f vel near 0), results in high
lateral errors and poor score. Using PP with A
lateral
alleviates this issue by slowing down when lateral er-
ror is high, trading speed for improved accuracy.
RL methods improved tracking overall, but with
varied results. The RL method AC (3) has the low-
est improvement. While it can adjust the acceleration
controls produced by A
re f
, it does not significantly re-
duce the speed compared to other RL methods and it
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
278

(a) Pure Pursuit.
(b) EBSF.
Figure 2: Results of different combinations between model-
based steering and speed controllers. Boxplots are shown
for several metrics, where the smaller the value, the better.
stays close to the reference speed. We observed simi-
lar difficulty in our prior work with RL Gain Correc-
tion (GC), where determining the maximum correc-
tion magnitude is challenging. A small value keeps
the system close to the reference, which may limit
potential improvements. Conversely, a larger value
allows for greater deviation from the reference, which
could improve performance but also reduce stabil-
ity. Therefore, to improve performance of (AC), in-
creasing the correction, currently set at ±30% of the
maximum acceleration, could be considered. How-
ever, this suggestion requires further validation to en-
sure meaningful improvements. This problem does
not occur with (VC), despite it also being a correc-
tion method. Indeed, small variations of ±30% of
the maximum speed (v
max
= 9.5m/s) do result in more
substantial variations of the final acceleration.
The two other RL methods, A and VC, efficiently
balance speed and lateral error on Pure Pursuit. They
sacrifice speed, as indicated by the higher average
di f f vel, to greatly reduce lateral errors. Conse-
quently, their balance score are better than those of
other speed controllers, showing their efficacy in en-
hancing PP for path tracking through speed control.
EBSF in Figure 2b: Similar results to PP are
observed, with the MPC struggling for stability with
A
re f
at high speeds. Using the lateral error to reduce
speed in A
lateral
greatly helps to stabilize it. A sim-
ilar conclusion is drawn for the RL methods, where
AC slightly decrease lateral error but still underper-
forms compared to A and VC. Overall, the RL meth-
ods demonstrate a better ability to balance both error
metrics, hence leading to a score improvement.
Conclusion: For model-based steering con-
trollers, RL approaches A and VC effectively trade
off speed for increased safety by reducing lateral er-
ror. However, it is worth questioning whether learning
such a speed controller is more beneficial than simply
tuning A
lateral
, and more evaluation using more com-
plex model-based speed controllers is required.
In the next section, we will evaluate whether sim-
ilar conclusions can be drawn for better-performing
RL steering methods developed in our prior work.
5.2 Combined with RL Steering
Speed agents are evaluated with pretrained RL steer-
ing agents, sequentially (training RL steering on A
re f
,
then the speed agent on the RL steering) or simulta-
neously (learning both controls on the same agent).
End-to-End Steering (S) in Figure 3c: Re-
sults differ significantly from those with model-based
steering. Method (S) performs very well with A
re f
,
achieving low lateral errors (mostly below 10cm)
and near-maximum feasible speeds, resulting in near-
optimal scores, and A
lateral
has minimal impact as the
lateral error remains small. Interestingly, training RL
speed methods (A,AC,VC) using (S) sequentially re-
sults in slightly worse performance than A
re f
. We hy-
pothesize it may be due to (S) being optimized for
the predictable A
re f
, allowing efficient anticipation of
future accelerations. This predictability is lost when
training RL speed agent sequentially with (S), caus-
ing (S) to struggle with anticipation and control qual-
ity. Similarly, method (S) being a neural network out-
putting steering control using complex observations,
the RL speed agents seem to struggle to enhance it.
Surprisingly, simultaneous training with (S) per-
formed worse than expected. Re-training with var-
ied parameters revealed that this approach was sensi-
tive and required longer training times. This sensitiv-
ity likely stems from the agent needing to learn the
complex interplay between speed and steering, com-
pounded by random slipping, localization inaccura-
cies, and control delays.
Steering Correction on PP and EBSF in Fig-
ures 3a and 3b: Similar results are observed with RL
steering correction methods. Using A
re f
and A
lateral
,
we can retrieve results of our prior work: PP is simple
and predictable, so it can be more efficiently corrected
by RL agents with (SC) than the complex EBSF MPC.
This relates to our earlier discussion where (S) per-
Does Path Tracking Benefit from Sequential or Simultaneous RL Speed Controls?
279

forms efficiently if the speed controller is predictable.
For the decoupled approaches, RL speed control sac-
rifices speed but does not significantly improve lat-
eral error, suggesting they found a control strategy in-
ferior to A
re f
in both (SC PP) and (SC EBSF). This
is reflected in the average score, where both steer-
ing methods perform better with the simple A
re f
they
were trained on. Here as well, simultaneous control
did not achieve the expected improvement.
(a) SC with Pure Pursuit.
(b) SC with EBSF.
(c) S.
Figure 3: Results of different combinations between RL
steering and speed controllers.
5.3 Conclusion
When combined with model-based steering con-
trollers, the RL speed controllers (A) and (VC) suc-
cessfully balance vehicle speed and tracking accu-
racy. Method (AC) on the other hand does not correct
the reference sufficiently to notice any big improve-
ment, which may imply greater acceleration correc-
tion magnitude may be necessary. However, reducing
the correction amplitude could also be another benefi-
cial strategy for both (AC) and (VC). If the reference
already performs well, minor adjustments to speed
or acceleration might help maintain close adherence
to this reference and potentially enhance performance
by narrowing the exploration space.
When combined with RL steering methods, RL
speed agents do not perform as well as the reference
A
re f
. Indeed, the predictability of A
re f
aids the RL
steering method, but this advantage is lost with RL
speed controls, hence degrading performance. Ad-
ditionally, simultaneous learning of both speed and
steering did not perform as expected. These results
highlight that more advanced training techniques or
RL designs may be required, such as in prior work on
simultaneous control for drifting by (Cai et al., 2020).
However, within the context of our study, the utility
of simultaneous control appears limited, as shown by
the consistent under-performance across the results.
6 DISCUSSION
6.1 RL, Predictability and Simplicity
Our findings suggest that for our tracking scenarios,
a divide-and-conquer strategy may be more effective
than using a single complex RL model. For each
RL control, whether speed or steering, predictabil-
ity of other components was key to achieving op-
timal performance. While this was confirmed in
our experiments, it may not hold true for complex
scenarios like drifting, where simultaneous control
is required. Additionally, simultaneous approaches
performed slightly worse on average than sequential
ones, but they may have the potential to achieve the
same optimal performance for both tracking accuracy
and speed given sufficient training time, better hyper-
parameter tuning, or improved learning algorithms.
7 CONCLUSION
This study explored the effectiveness of various RL
speed controllers combined with both model-based
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
280

and RL steering methods for path tracking. The goal
was to determine whether RL speed control could
enhance and balance tracking accuracy (safety) and
speed (time efficiency) compared to simpler model-
based speed controllers. We also evaluated whether
there was any benefit in performing speed control si-
multaneously with steering control, rather than se-
quentially, in our scenarios. Results revealed several
key insights depending on the steering controls used:
• Model-Based Steering: A and VC demonstrated
significant improvements in reducing lateral er-
rors when combined with Pure Pursuit (PP) and
EBSF, but at the cost of reduced speed. The pre-
dictability of the model-based steering was crucial
for the RL speed agents to perform effectively.
• RL Steering: Sequentially with RL steering,
methods (A,AC,VC) underperformed compared
to A
re f
. The predictability of A
re f
aided RL steer-
ing, but this advantage was lost with RL speed
controls. Similarly, learning of simultaneous con-
trols proved challenging, indicating the need for
further refinement for effective joint control.
In summary, while RL speed controllers can en-
hance safety and reduce lateral errors when combined
with model-based steering, their benefits may be lim-
ited for simple tracking scenarios. However, using
RL to learn acceleration control remains interesting,
especially when requiring an additional safety layer
on poorly performing steering controllers. In future
work, we will focus on real-world testing and explore
fine-tuning the agent to address sim-to-real issues.
REFERENCES
Attia, R., Orjuela, R., and Basset, M. (2014). Combined
longitudinal and lateral control for automated vehicle
guidance. Vehicle System Dynamics.
Cai, P., Mei, X., Tai, L., Sun, Y., and Liu, M. (2020). High-
speed autonomous drifting with deep reinforcement
learning. IEEE-RAL.
Chemin, J., Hill, A., Lucet, E., and Mayoue, A. (2024).
A study of reinforcement learning techniques for path
tracking in autonomous vehicles. In IEEE-IV.
Cheng, Z., Chow, M.-Y., Jung, D., and Jeon, J. (2017).
A big data based deep learning approach for vehicle
speed prediction. In IEEE-ISIE.
Coulter, C. (1992). Implementation of the pure pursuit path
tracking algorithm.
Devineau, G., Polack, P., Altch
´
e, F., and Moutarde, F.
(2018). Coupled longitudinal and lateral control of
a vehicle using deep learning. CoRR.
Faust, A., Ramirez, O., Fiser, M., Oslund, K., Francis,
A. G., Davidson, J., and Tapia, L. (2017). PRM-
RL: long-range robotic navigation tasks by combining
reinforcement learning and sampling-based planning.
CoRR.
Gangopadhyay, B., Dasgupta, P., and Dey, S. (2022). Safe
and stable rl (s2rl) driving policies using control bar-
rier and control lyapunov functions. IEEE-IV.
Gauthier-Clerc, F., Hill, A., Laneurit, J., Lenain, R., and
Lucet, E. (2021). Online velocity fluctuation of off-
road wheeled mobile robots: A reinforcement learn-
ing approach. IEEE-ICRA.
Geng, X., Liang, H., Xu, H., Yu, B., and Zhu, M. (2016).
Human-driver speed profile modeling for autonomous
vehicle’s velocity strategy on curvy paths. In IEEE-IV.
Hill, A. (2022). Adaptation du comportement sensori-
moteur de robots mobiles en milieux complexes. Phd
thesis, Universite - Clermont-Ferrand.
Hoffmann, G. M., Tomlin, C. J., Montemerlo, M., and
Thrun, S. (2007). Autonomous automobile trajectory
tracking for off-road driving: Controller design, ex-
perimental validation and racing. In American Control
Conference.
Kendall, A., Hawke, J., Janz, D., Mazur, P., Reda, D., Allen,
J. M., Lam, V. D., Bewley, A., and Shah, A. (2019).
Learning to drive in a day. In IEEE-ICRA.
Lenain, R., Thuilot, B., Cariou, C., and Martinet, P. (2021).
Accurate autonomous navigation strategy dedicated to
the storage of buses in a bus center. Robotics and Au-
tonomous Systems.
Macadam, C. (2003). Understanding and modeling the hu-
man driver. Vehicle system dynamics.
Normey-Rico, J. E., Alcal
´
a, I., G
´
omez-Ortega, J., and Ca-
macho, E. F. (2001). Mobile robot path tracking using
a robust pid controller. Control Engineering Practice.
Paden, B.,
ˇ
C
´
ap, M., Yong, S. Z., Yershov, D., and Frazzoli,
E. (2016). A survey of motion planning and control
techniques for self-driving urban vehicles. IEEE-IV.
Raffin, A., Hill, A., Gleave, A., Kanervisto, A., Ernestus,
M., and Dormann, N. (2021). Stable-baselines3: Reli-
able reinforcement learning implementations. Journal
of Machine Learning Research.
Serna, C. G. and Ruichek, Y. (2017). Dynamic speed adap-
tation for path tracking based on curvature informa-
tion and speed limits. Sensors, 17(6):1383.
Stano, P., Montanaro, U., Tavernini, D., Tufo, M., Fiengo,
G., Novella, L., and Sorniotti, A. (2022). Model pre-
dictive path tracking control for automated road vehi-
cles: A review. Annual Reviews in Control.
Vollenweider, E., Bjelonic, M., Klemm, V., Rudin, N., Lee,
J., and Hutter, M. (2023). Advanced skills through
multiple adversarial motion priors in reinforcement
learning. In IEEE-ICRA.
Weber, T. and Gerdes, J. C. (2023). Modeling and control
for dynamic drifting trajectories. IEEE-IV.
Xu, Z., Liu, B., Xiao, X., Nair, A., and Stone, P. (2023).
Benchmarking reinforcement learning techniques for
autonomous navigation. In IEEE-ICRA.
Zhou, H., Gao, J., and Liu, H. (2021). Vehicle speed
preview control with road curvature information for
safety and comfort promotion. Proceedings of the In-
stitution of Mechanical Engineers.
Does Path Tracking Benefit from Sequential or Simultaneous RL Speed Controls?
281