L-SAGA: A Learning Hyper-Heuristic Architecture for the Permutation
Flow-Shop Problem
Younes Boukacem
1 a
, Hatem M. Abdelmoumen
1 b
, Hodhaifa Benouaklil
1 c
, Samy Ghebache
1
,
Boualem Hamroune
1
, Mohammed Tirichine
1 d
, Nassim Ameur
1 e
and Malika Bessedik
1,2
1
Ecole Nationale Sup
´
erieure d’Informatique (ESI), BP 68M - 16270 Oued Smar, Algiers, Algeria
2
Laboratoire des M
´
ethodes de Conception de Syst
`
emes (LMCS), Ecole Nationale Sup
´
erieure d’Informatique (ESI),
BP 68M - 16270 Oued Smar, Alger, Algeria
Keywords:
Flow-Shop Permutation Problem, Hyper-Heuristic, Simulated Annealing, Genetic Algorithm.
Abstract:
The permutation flow-shop problem or PFSP consists in finding the optimal launching sequence of jobs to be
sequentially executed along a chain of machines, each job having different execution times for each machine,
in order to minimize the total completion time. As an NP-hard problem, PFSP has significant applications
in large-scale industries. In this paper we present L-SAGA, a generative hyper-heuristic designed for finding
optimal to sub-optimal solutions for the PFSP. L-SAGA combines a high level simulated annealing with a
learning component and a low level PFSP adapted genetic algorithm. The performed tests on various bench-
marks indicate that, while our method had competitive results on some small and medium size benchmarks
thus showing interesting potential, it still requires further improvement to be fully competitive on larger and
more complex benchmarks.
1 INTRODUCTION
The Permutation Flow Shop Problem (PFSP) con-
sists in finding an optimal schedule for executing jobs
along a chain of machines under a set of constraints
(see Section 2), with the aim to minimize the total
completion time also known as the makespan. This
NP-hard problem is vital in most industries, where ef-
ficient scheduling boosts productivity and can induce
major cost savings.
Early works addressed the PFSP using heuris-
tics such as the NEH (Nawaz et al., 1983), the CDS
(Campbell et al., 1970), and Palmer’s (Palmer, 1965)
heuristics. More recent works used metaheuristics
like the immunity-based hybrid genetic algorithm
(Bessedik et al.2016), the improved genetic immune
algorithm with vaccinated offspring (Tayeb et al.,
2017), the hybrid genetic algorithm and bottleneck
shifting (Gao et al., 2007), and the iterated greedy
algorithm (Ruiz and Stutzle, 2007). While heuris-
a
https://orcid.org/0009-0001-5896-3227
b
https://orcid.org/0009-0006-1459-2723
c
https://orcid.org/0009-0002-1239-2606
d
https://orcid.org/0009-0003-9205-6158
e
https://orcid.org/0009-0009-1120-6286
tics are often instance-specific and may not general-
ize well across instances, metaheuristics are adaptable
but sensitive to hyperparameters, affecting their abil-
ity and usability to solve complex problems.
Hyper-heuristics offer higher abstraction and
adaptability than traditional (meta)heuristics. They
can either be selective, i.e. select appropriate heuris-
tics from a set, or generative, i.e. generate new ones
by combining existing components, see (Burke et al.,
2010). We chose hyper-heuristics for their scalability
and potential to improve performance across diverse
problem instances.
In recent years, hyper-heuristics have gained at-
tention for addressing NP-hard optimization prob-
lems, including the PFSP. (Garza-Santisteban et al.,
2019) highlights the effectiveness of Simulated An-
nealing (SA) in training selection hyper-heuristics
through stochastic optimization to boost performance.
Additionally, (Garza-Santisteban et al., 2020) incor-
porates feature transformations to improve the train-
ing phase, enhancing state differentiation while also
using SA in perturbative selection hyper-heuristics. A
new hyper-heuristic method, HHGA, was introduced
by (Bacha et al., 2019), which applies genetic algo-
rithms to dynamically generate customized configura-
tions for each PFSP instance. Moreover, (Alekseeva
Boukacem, Y., Abdelmoumen, H., Benouaklil, H., Ghebache, S., Hamroune, B., Tirichine, M., Ameur, N. and Bessedik, M.
L-SAGA: A Learning Hyper-Heuristic Architecture for the Permutation Flow-Shop Problem.
DOI: 10.5220/0013020000003837
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th Inter national Joint Conference on Computational Intelligence (IJCCI 2024), pages 321-329
ISBN: 978-989-758-721-4; ISSN: 2184-3236
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
321

et al., 2017) proposed a parallel multi-core hyper-
heuristic based on the Greedy Randomized Adaptive
Search Procedure (GRASP), automatically evaluating
315 configurations to identify the best one, with par-
allel computing improving efficiency.
This paper introduces L-SAGA (Learning
Simulated Annealing Genetic Algorithm): a gener-
ative hyper-heuristic designed to efficiently explore
the solution space of the PFSP. L-SAGA combines
a PFSP-specific genetic algorithm for the low level,
with a simulated annealing hyperparameter tuner
equipped with a learning component for the high
level. The hybrid use of these two metaheuristics has
shown promising results on some small and medium
size benchmarks, but still requires improvement
for larger and more complex instances to be fully
competitive.
The rest of the paper is organized as follows: Sec-
tion 2 formulates the PFSP. Section 3 describes the
L-SAGA architecture. Section 4 presents a perfor-
mance comparison between L-SAGA and state-of-
the-art methods, along with an empirical analysis of
L-SAGA’s behavior in different testing scenarios. The
paper concludes in Section 5, discussing L-SAGA’s
limitations and potential areas for improvement.
2 FORMAL PROBLEM
DEFINITION
The PFSP with the objective of minimizing the
makespan can be formally defined as follows. A fi-
nite set J consisting of n jobs J = {J
1
, J
2
, . . . , J
n
} need
to be processed on a finite set M of m machines M =
{1, 2, . . . , m} in a sequential manner. The sequence in
which jobs are processed is consistent across all ma-
chines; thus, the processing order on the first machine
is maintained throughout the remaining machines.
Several standard assumptions are made regarding
this problem (Pinedo, 2012):
• All n jobs are independent and available for pro-
cessing at time zero.
• All m machines are continuously available with-
out any interruptions.
• Each machine can process at most one job at a
time, and each job can be processed on only one
machine at a time (capacity constraints).
• The processing of any given job J
i j
cannot be in-
terrupted, implying no preemption is allowed.
• Setup and removal times of jobs on machines are
included in the processing times or negligible.
• If a machine required for the next operation of a
job is busy, the job can wait in an unlimited queue.
The objective of the PFSP is to find a sequence,
i.e., a permutation of job indices {1, 2, . . . , n}, that
minimizes the makespan C
max
(Miller et al., 1967).
The makespan is the total time required to complete
all jobs on all machines. This problem is commonly
denoted as n|m|P|C
max
or F
m
|prmu|C
max
(Pinedo,
2012), where n and m represent the number of jobs
and machines respectively, prmu indicates that only
permutation schedules are allowed, and C
max
refers to
the criterion of makespan minimization. Notably, the
problem F
m
|prmu|C
max
is known to be NP-complete
in the strong sense when m > 3 (Garey et al., 1976).
Consider a permutation π = {π
1
, π
2
, . . . , π
n
}
where n jobs are sequenced through m machines, and
π
j
denotes the j-th job in the sequence. Let p
i j
repre-
sent the processing time of job j on machine i, and c
i j
the time at which machine i finishes processing job j.
The mathematical model for the completion time of
the sequence π is formulated as follows:
c
1,π
1
= p
1,π
1
(1)
c
1,π
j
= c
1,π
j−1
+ p
1,π
j
for j = 2, . . . , n (2)
c
i,π
1
= c
i−1,π
1
+ p
i,π
1
for i = 2, . . . , m (3)
c
i,π
j
= max(c
i,π
j−1
, c
i−1,π
j
) + p
i,π
j
for j = 2, . . . , n and i = 2, . . . , m (4)
Thus, the makespan C
max
of a permutation π can
be formally defined as:
C
max
(π) = c
m,π
n
(5)
Therefore, the PFSP with the makespan criterion
aims to find the optimal permutation π
∗
within the set
of all permutations Π such that:
C
max
(π
∗
) ≤ C
max
(π) ∀π ∈ Π (6)
In this study, we consider a flexible flowshop con-
figuration that can adapt to different numbers of ma-
chines and jobs. The setup ensures compatibility with
various problem sizes and maintains adherence to the
aforementioned constraints.
3 MODEL ARCHITECTURE
As a generative hyper-heuristic, L-SAGA general ar-
chitecture is composed of two levels as depicted in
Figure 1: A low level which comprises a genetic al-
gorithm (GA) specifically designed for exploring the
space of the PFSP job launching sequences, and a
high level which comprises a simulated annealing al-
gorithm (SA) that will explore the space of hyperpa-
rameters of the low level’s genetic algorithm with the
help of a top level learning component (LC) whose
main data structure is a ”podium bank” which is de-
scribed further.
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
322

Figure 1: L-SAGA general architecture.
3.1 Low-Level Genetic Algorithm
We designed a PFSP-adapted GA for the low level
where each chromosome (or individual) of the pop-
ulation is a scheduling sequence of the jobs. Each
gene represents a job in the sequence with the posi-
tions of the genes determining the jobs order. An in-
dividual’s fitness is computed as its makespan. The
architecture and operational mechanisms of the GA,
which include initialization, selection, crossover, mu-
tation, and replacement strategies, make the popu-
lation evolve towards optimal solutions, as visually
summarized in Figure 2.
1. Initialization. Multiple techniques are possible
for initialization to ensure diversity and quality.
Methods like the NEH, CDS, and Palmer heuris-
tics, as well as combinations of these, are used.
Full random initialization is also an option. Each
technique generates job sequences (chromosomes)
that are evaluated by their makespan.
2. Selection: The selection process determines
which individuals from the current population are
chosen to form a mating pool for the next gener-
ation. Various strategies are available, including
roulette wheel, rank-based, elitist, tournament, and
random selection. These methods ensure a diverse
and high-quality mating pool by favoring better-
performing solutions while maintaining genetic di-
versity.
3. Crossover. Crossover is the primary genetic oper-
ator that combines pairs of parents to produce off-
spring. The algorithm supports uniform crossover
and k-point crossover. Each technique involves
swapping job sequences between parents at spe-
cific points, generating new candidate solutions
that inherit characteristics from both parents as de-
picted in Figure 3. The crossover rate (P
c
) controls
the likelihood of crossover events, thereby influ-
encing the genetic diversity and convergence rate
of the population.
4. Mutation. Mutation introduces genetic variation
into the population by randomly altering genes
in the offspring. This operator helps to maintain
genetic diversity and prevents premature conver-
gence and local optima trapping. Permutation-
based mutation is employed, where jobs within a
sequence are swapped, ensuring feasibility of the
solutions. The mutation rate (P
m
) defines the prob-
ability of mutation for each chromosome, balanc-
ing the need for exploration of new solutions and
the preservation of high-quality individuals.
5. Replacement. The replacement strategy governs
how the new generation is formed from the current
population and the newly created offspring. This
step ensures that the population evolves toward
better solutions while maintaining necessary ge-
netic diversity to avoid stagnation. Various meth-
ods are employed, including replacing all parents
with offspring, replacing the worst solutions in the
population, or selecting the best individuals be-
tween parents and offspring. Moreover, all selec-
tion methods mentioned in the selection phase can
be used here to ensure a diverse and high-quality
population for the next generation.
The genetic algorithm iterates through successive
generations until one of the termination criteria is met.
These criteria include a predefined number of itera-
tions or maximum stagnation, defined as the number
of consecutive generations without improvement. The
solution with the best makespan identified through-
out the iterations is ultimately returned as the optimal
schedule.
3.2 High-Level Simulated Annealing
with a Learning Component
3.2.1 Simulated Annealing
As depicted in Figure 1, L-SAGA’s high-level SA will
explore the hyperparameters space for the low level
GA, requiring an appropriate encoding of the search
space. A natural encoding was adopted, represent-
ing each hyperparameter as a dimension in a vector
called HPS for HyperParameter State, with two types
of dimensions: qualitative (Qual.Dims) and quanti-
tative (Quant.Dims). The general SA algorithm, as
shown in Figure 4, begins by receiving key hyperpa-
rameters:
• T. The initial temperature of the simulated anneal-
ing.
L-SAGA: A Learning Hyper-Heuristic Architecture for the Permutation Flow-Shop Problem
323

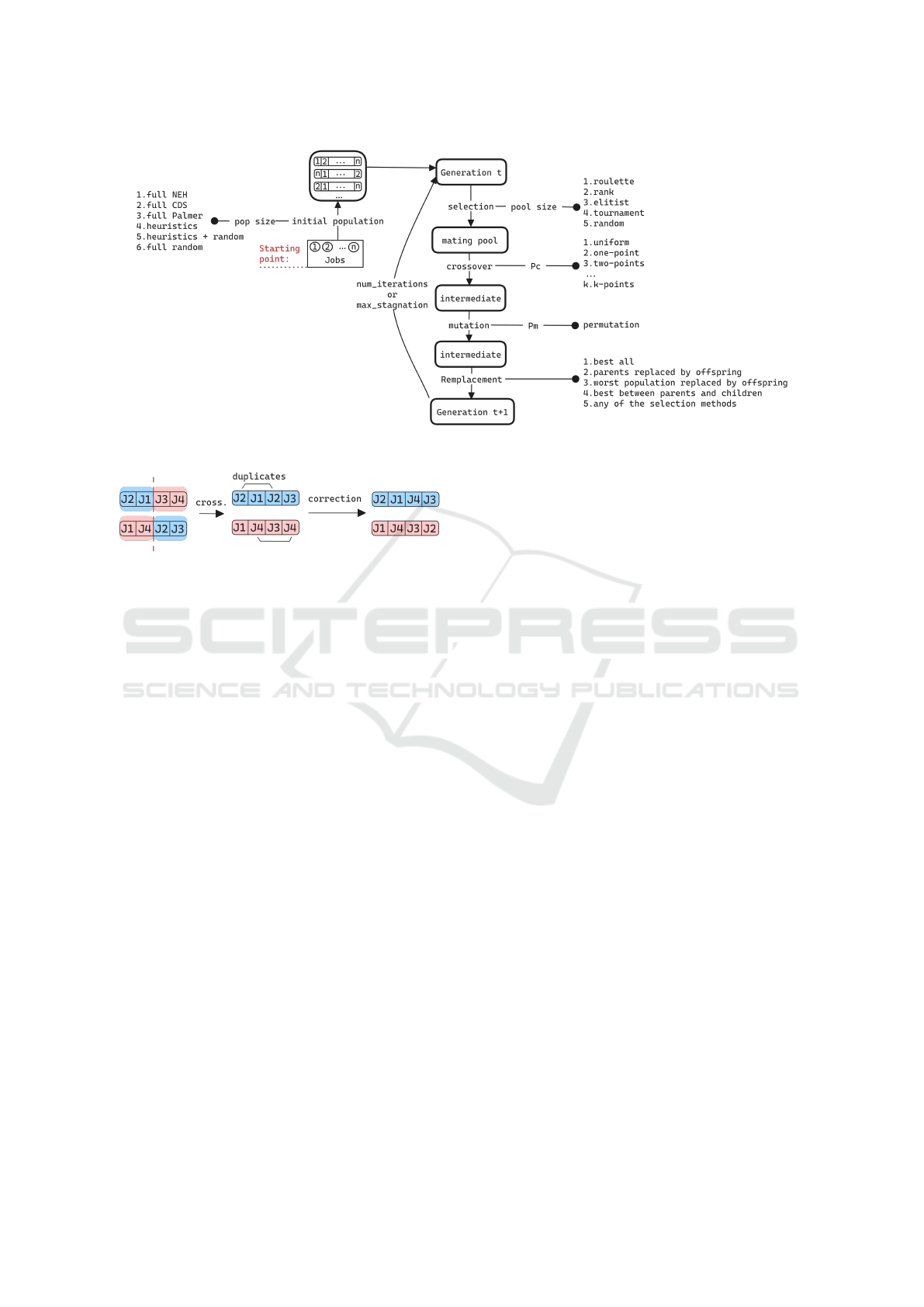
Figure 2: Low Level Genetic Algorithm.
Figure 3: Crossover operator on job sequences.
• Tmin. The minimum temperature under which the
algorithm stops.
• α
α
α. The geometric decay (< 1) coefficient for the
temperature.
• TemperatureSession. The number of iterations
during which the temperature remains fixed.
• JumpRate. The probability of increasing the tem-
perature (jumping) instead of decreasing it at the
end of a ’TemperatureSession’.
• JumpRatio. The geometric jump coefficient (> 1)
for the temperature in case of jumping at the end of
a ’TemperatureSession’.
• RetentionRate. The percentage of population to
pass from the previous execution of the GA to the
next iteration.
Starting from a randomly generated HPS, the SA
component generates a neighboring HPS at each iter-
ation, passes it to the genetic algorithm, and records
the resulting makespan. The neighbor HPS and
makespan are added to the podium bank for future
iterations. If the makespan improves, the neighbor
HPS becomes the current HPS; otherwise, it may be
accepted with a probability that decreases as the tem-
perature lowers and makespan degradation increases.
The temperature adjusts based on the JumpRate prob-
ability and the TemperatureSession counter and the
process ends when the temperature falls below a min-
imum or after a set number of iterations, returning the
best makespan found.
3.2.2 Learning Component
L-SAGA proposes a learning component that can be
used to help the high level’s SA component in the
search process of the optimal HPS. This add-on learn-
ing component is centered around the podium bank
data structure which, in conjunction with a selection
algorithm, aims at improving the exploitation capac-
ity of the SA component during the neighbor HPS
generation step which, in the vanilla simulated an-
nealing algorithm, is completely random during the
whole search process. The architecture of the LC is
depicted in Figure 5.
The podium bank is a finite size priority queue
data structure which will store during the whole
search process the top P (P being a hyperparameter)
encountered HPS’s according to their makespan, thus
constituting a memory of the HPS configurations that
provided the best results. When generating a neigh-
bor HPS, a number ”variety degree” of dimensions
in the current HPS will be marked as to ”forcibly
change” in the neighborhood space i.e. : their val-
ues won’t remain in the possible neighbors. The di-
mensions that will be marked so are randomly cho-
sen. Then the set of all possible neighbors (consider-
ing the variety degree) is generated: Each qualitative
dimension is randomly swapped with a given number
(Qual. Dim. Neighbor Window) of other possible val-
ues, and in the same way each quantitative dimension
will be swapped with the other possible values in a
given neighborhood window (Quant. Dim. Neighbor
Window). While the variety degree helps in augment-
ing the exploration potential of the algorithm, the two
latter hyperparameters helps in controlling the size of
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
324

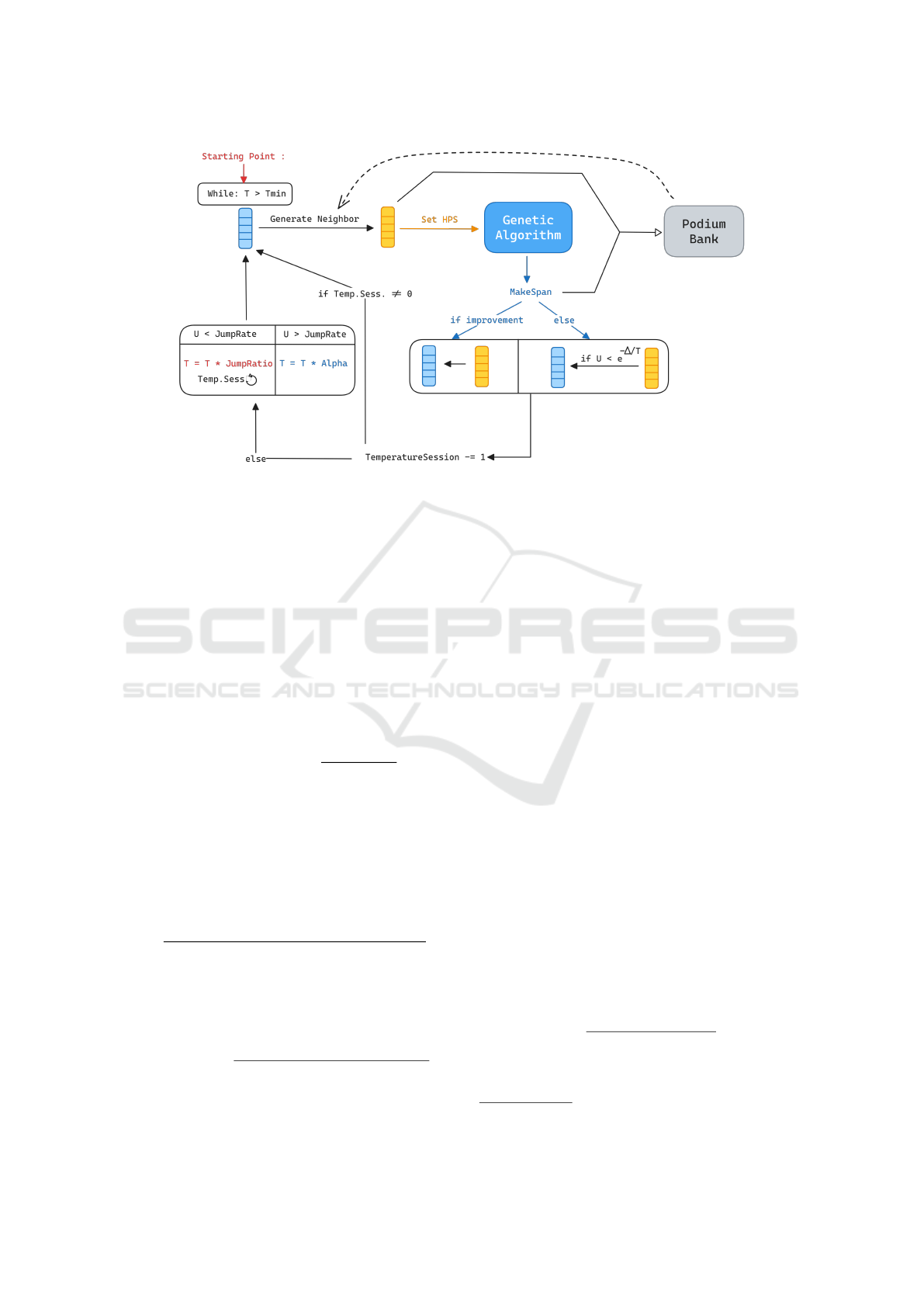
Figure 4: Top level simulated annealing component with the podium bank add-on.
the explored neighborhood which may help in explo-
ration if large but at the cost of performance overhead.
Once the neighbor set is generated, two scenar-
ios are possible: either a neighbor is chosen randomly
according to a uniform distribution, this scenario hap-
pens with a probability that decreases as tempera-
ture decreases and is controlled by the beta hyperpa-
rameter (which when increased increases the uniform
choice probability for more exploration). Otherwise
the podium bank will be used to attribute a score to
each neighbor which will determine its probability of
being chosen according to equation 7:
P(choosing neighbor
i
) =
Score
i
∑
k
n=1
Score
n
(7)
The score of each neighbor represents its quality
in the sense of the proximity it has with the previ-
ously best observed HPSs stored in the podium bank.
The formula for calculating the said ”proximity” is a
weighted average of the ”similarities” of the neighbor
with the various podium bank HPSs.
Score
i
= (8)
∑
P
p=1
makespan
−1
p
.e
Sim(neighbor
i
,PodiumHPS
p
)
∑
P
p=1
makespan
−1
p
Sim(neighbor
i
, PodiumHPS
p
) = (9)
−
∑
d∈Qual.Dims
δ(neighbor
i
[d] = PodiumHPS
p
[d])
−
∑
d∈Quant.Dims
|neigbor
i
[d] − PodiumHPS
p
[d]|
MaxVal[d] − MinVal[d]
where the δ function returns 0 in case of equality and
1 otherwise.
4 RESULTS
We present here various results obtained from the ex-
ecution of L-SAGA on the Taillard benchmarks (Tail-
lard, 1993). The executions were all performed using
manually tuned hyper-parameters for the high level
such as a podium bank size of 5, a variety degree of
5, an initial and final temperature of 1 and .008 re-
spectively, and a maximum number of iterations of
170. These values were chosen accounting for both
solutions quality and available hardware resources at
the time of this publication. More implementation
details are available on the dedicated GitHub repos-
itory
1
. The testing computer had an intel i5 11th gen-
eration with 16 GB of RAM.
4.1 Performance Comparison of
L-SAGA with State-of-the-Art
Methods
The Taillard benchmark for the PFSP presents with
12 configurations of number of jobs × number of
machines, each of which has 10 different instances.
For each instance, we measure the performance of
L-SAGA using the Relative Percentage Deviations
(RPD) presented in equation 10:
RPD
i
=
C
max
− UpperBound
i
UpperBound
i
× 100 (10)
Where C
max
is the makespan of the best solution
found by L-SAGA and UpperBound
i
is the makespan
1
https://github.com/YounesBoukacem/L-SAGA
L-SAGA: A Learning Hyper-Heuristic Architecture for the Permutation Flow-Shop Problem
325

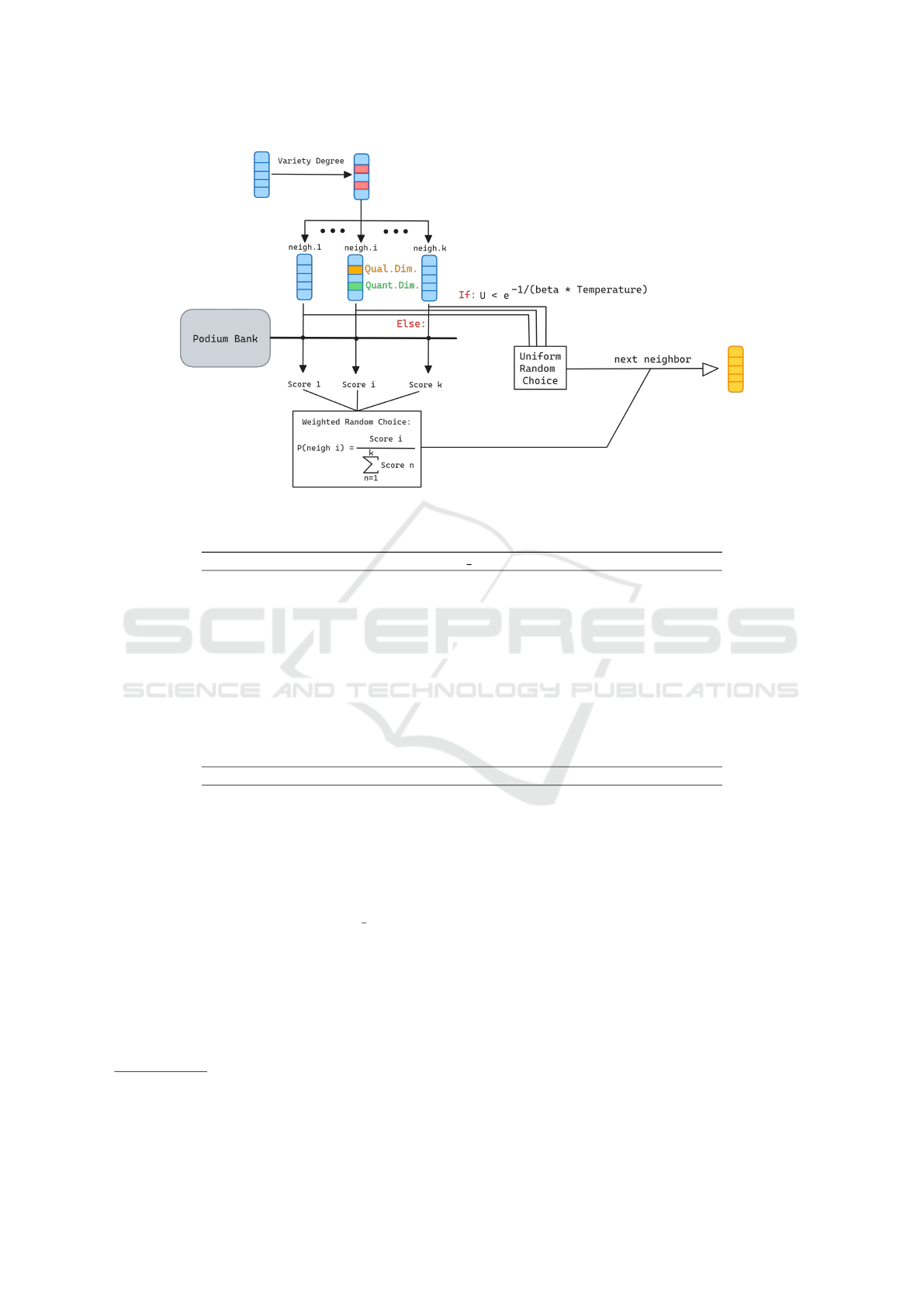
Figure 5: High level’s learning component architecture.
Table 1: Comparison of different approaches with makespan objective.
Benchmark PACO HGA RMA IG RS LS PSO
vns
HHGA L-SAGA
20 × 5 0.18 0.04 0.04 0.03 0.04 0.03
20 × 10 0.24 0.02 0.06 0.02 0.00 1.03
20 × 20 0.18 0.05 0.03 0.05 0.00 0.00
50 × 5 0.05 0.00 0.00 0.00 0.00 0.00
50 × 10 0.81 0.72 0.56 0.57 0.62 1.47
50 × 20 1.41 0.99 0.94 1.36 1.03 3.19
100 × 5 0.02 0.01 0.01 0.00 0.00 0.00
100 × 10 0.29 0.16 0.20 0.18 0.08 1.17
100 × 20 1.93 1.30 1.30 1.45 1.30 3.14
200 × 10 0.23 0.14 0.12 0.18 0.12 1.04
200 × 20 1.82 1.26 1.26 1.35 1.26 2.50
Average 0.65 0.42 0.41 0.47 0.4 1.23
of the best-known solution for the instance i as indi-
cated in the benchmark data.
For each instance we execute L-SAGA from 1
to 3 times and report the minimum found RPD. We
compared L-SAGA with several state-of-the-art ap-
proaches such as PACO (Ruiz et al., 2006), HGA
RMA (Rajendran and Ziegler, 2004), IG RS LS (Ruiz
and St
¨
utzle, 2007), PSO
vns
(Tasgetiren et al., 2007),
and HHGA (Bacha et al., 2019). Table 1 presents
the average Relative Percentage Deviation (ARPD)
for the ten instances of the first 11 configurations with
the best performing results for each benchmark high-
lighted in bold
2
.
By analyzing these observations, we can see that
2
The last configuration of 500×20 was not yet tested
at the time of this publication and is postponed for future
research.
L-SAGA had no difficulty in handling increasing
number of jobs as long as the number of machines
remained small (in this case 5 machines); it indeed
ranked first for the 20 × 5, 50 × 5 and 100 × 5 con-
figurations. But as the number of machines increases,
L-SAGA was systematically the least performant in-
dependently of the number of jobs, at the intrigu-
ing exception of the 20 × 20 configuration where
it also ranked first. Further analysis, presented in
Section 4.2 on the final HPSs generated by L-SAGA
and Section 4.3 on the influence of the podium bank
size, seem to provide plausible explanations of this
behavior revealing potential avenues of improvement
for further research. Still, immediate solutions for im-
provement can be thought of, such as allowing for
the parallel execution of multiple low level GAs for a
given HPS during exploration; as this would allow for
better statistical estimation of an HPS ability to pro-
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
326

Figure 6: Percentage distribution of various initialization, selection, crossover, and replacement methods across different
benchmark configurations.
duce good results (given that the low level GA rely on
random processes) while maintaining minimum ex-
ecution times. Also the current similarity measure
used in the learning component could be improved by
the online computation of correlation coefficients be-
tween the different hyperparameters of the HPS and
the obtained makespans to give more weight to the
more correlated dimensions when computing the sim-
ilarity measure presented in equation 9.
4.2 Analysis of L-SAGA’s Generated
Low Level Hyperparameters
In order to gain some insight on the behavior of our
method, we examined for each instance a selected set
of hyperparameters in the final HPS generated by L-
SAGA when producing the results in Section 4.1 and
aggregated the results for analysis.
4.2.1 Qualitative Hyperparameters
For each configuration, we count, over the instances,
the number of times a particular value of a qualitative
hyperparameter appeared in the final HPS. The per-
centages are graphically represented in Figure 6 for
initialization, selection, crossover, and replacement
methods.
1. Initialization. The ’NEH’ method is widely used,
proving effective for generating good initial solu-
tions. ’Full-random’ and ’heuristics-random’ are
also popular for providing diverse starting points,
while the ’Palmer’ method sees higher use in spe-
cific benchmarks (e.g., 100×20 and 200×20).
2. Selection. The ’random’ selection method is most
common, followed by ’roulette,’ highlighting a
balance between selection pressure and population
diversity. The ’elitist’ method, though less com-
mon, plays a crucial role in retaining top solutions.
3. Crossover. ’Uniform’ crossover dominates most
benchmarks, with ’k-points’ crossover being pre-
ferred in cases like 20×5 and 200×20.
4. Replacement. There’s a balanced use of re-
placement methods, with ’best-all’ slightly more
favored in benchmarks like 50×10 and 100×20,
while ’roulette’ replacement is used less, showing
it to be less effective in this role.
From these observations it appears that L-SAGA
does attempt to adapt to the different instances across
different configurations. While this is indeed the de-
sired behavior starting from the principle that no HPS
configuration could fit all possible instances, the re-
sults presented in Section 4.1 show that L-SAGA still
has difficulty in efficiently identifying the optimal
combinations of qualitative hyperparameters. A pos-
sible explanation could be a local optimum stagnation
caused by a too small beta value which would induce
an early exploitation, or a too small podium bank size
(see Section 4.3) which could cause a lack of variabil-
ity during exploitation itself. Experimenting with dif-
ferent values of these two hyperparameters in a more
extensive setup than manual fine tuning, along with
analyzing the content of the whole podium bank at the
end of the execution (instead of the final HPS only),
could provide better insight and potentially a solution
to this problem.
4.2.2 Quantitative Hyperparameters
1. Average Crossover Rate (ACR) and Average
Mutation Rate (AMR): for each configuration, we
average over the instances the values of the CR and
the MR that appears in the final HPSs. The analysis
of Figure 7 reveals important adaptive mechanisms
L-SAGA: A Learning Hyper-Heuristic Architecture for the Permutation Flow-Shop Problem
327

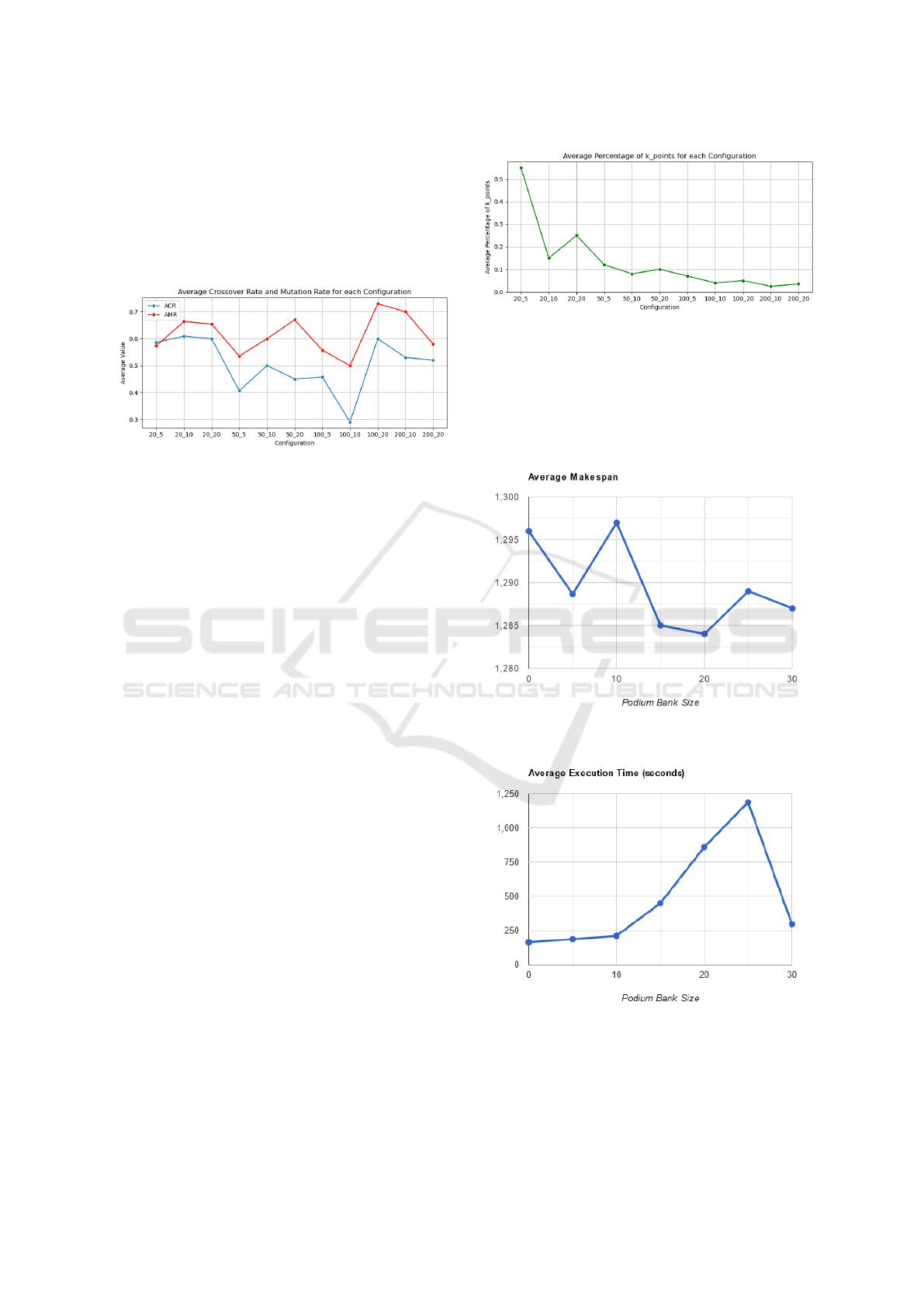
found by the algorithm: The AMR consistently sur-
passes the ACR, emphasizing the importance of mu-
tation for enhancing exploration and discovering new
solution areas, and both rates fluctuate in tandem, in-
dicating a coordinated approach that balances explo-
ration (through mutation) and exploitation (through
crossover).
Figure 7: Behavior of the Average Crossover Rate (ACR)
and Average Mutation Rate (AMR) across different config-
urations.
2. Average Relative K-Point Crossover Value: we
also examined, among the instances on which L-
SAGA execution led to a k-point crossover type in the
final HPS, the evolution of the value of k across con-
figurations. More specifically we compute for each
instance the percentage of k relatively to the job se-
quence length i.e. the number of jobs (since 1 < k <
number of jobs in the sequence - 1), and we then com-
pute a per-configuration average. Observing this aver-
age in Figure 8 reveals a clear trend; as the number of
jobs and machines increases, the average percentage
of k-points decreases. This reduction suggests that
L-SAGA tends towards less a fragmented approach
to genetic material exchange for larger problem con-
figurations. Analyzing this graph reveals an interest-
ing fact: the only configuration with more than 5 ma-
chines (in this case 20 × 20) in which L-SAGA actu-
ally ranked first displays a peak on the relative k-point
crossover value where it reaches 25%. This could
indicate that large values of k-point crossover are ac-
tually preferable. We suspect that one of the reasons
that L-SAGA didn’t evolve towards larger values of k-
point crossover for other configurations is that the ex-
ploration window length that we set to 4 was not suf-
ficient to allow for an effective exploration of this low
level hyperparameter which worsened as the number
of jobs increased. This suggests that experimenting
with larger values of the exploration window, espe-
cially for this low level hyperparameter, should be a
next step for further research.
Figure 8: Average percentage of k-points in crossover oper-
ations across different problem configurations.
4.3 Effect of the Podium Bank Size
We studied the impact of the podium bank size on
both the quality of the solutions and the execution
time.
Figure 9: Study of the Average Makespan against Podium
Bank Size.
Figure 10: Study of the Average Execution Time against
Podium Bank Size.
The experimentation was done by performing
three L-SAGA executions for each podium bank
size on the first instance of the 20 jobs by 5 ma-
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
328

chines configuration, and then averaging the obtained
makespans and execution times. From Figure 9 it ap-
pears that an increase in the podium bank size tends
to provide better results as the average makespan de-
creases, but at the price of an increase in the execution
time as shown in Figure 10 which can be explained by
the necessity to perform more calculations for com-
puting the podium scores during search. The exe-
cution time could be reduced by implementing par-
allelization during the scores computation as these
don’t depend on each other. Also, the sudden drop
in execution time noticed at the podium bank size of
30 is explained by the early stopping of the execu-
tion due to a stagnation in the makespan, which when
correlated with the relatively low average makespan
value at this podium bank size could support the idea
that the algorithm finds better optimum more quickly.
5 CONCLUSION
In this work we have presented L-SAGA, a generative
hyper-heuristic conceived for finding near optimal so-
lutions to the PFSP. L-SAGA, by combining a simu-
lated annealing backed by a specially designed learn-
ing component for the high level, and a PFSP adapted
version of the genetic algorithm for the low level,
managed to give competitive results on some specific
small to medium size benchmarks. Still, as of this pa-
per’s results, the execution of L-SAGA shows a lack
of performance on larger and more complex instances
when compared to the state of the art. The results
obtained by analyzing L-SAGA behavior suggest that
the most important next step in improving its perfor-
mance would be to perform a more extensive high
level hyperparameters fine-tuning that would leverage
the insights found in this first study, such as those con-
cerning the effect of the podium bank size, the relative
k-point crossover value, or the beta hyperparameter
of the learning component. Coupled with an auto-
mated setup, and along some additional implementa-
tions such as multiple GA executions per HPS and a
refined similarity measure, we expect this fine-tuning
to allow L-SAGA to significantly improve on more
complex instances. This shall be our next step.
REFERENCES
Alekseeva, E., Mezmaz, M., Tuyttens, D., and Melab,
N. (2017). Parallel multi-core hyper-heuristic grasp
to solve permutation flow-shop problem. Concur-
rency and Computation: Practice and Experience,
29(9):e3835.
Bacha, S. Z. A., Belahdji, M. W., Benatchba, K., and Tayeb,
F. B.-S. (2019). A new hyper-heuristic to generate ef-
fective instance ga for the permutation flow shop prob-
lem. Procedia Computer Science, 159:1365–1374.
Burke, E. K., Hyde, M., Kendall, G., Ochoa, G.,
¨
Ozcan,
E., and Woodward, J. R. (2010). A classification of
hyper-heuristic approaches. Handbook of metaheuris-
tics, pages 449–468.
Garey, M. R., Johnson, D. S., and Sethi, R. (1976).
The complexity of flowshop and jobshop scheduling.
Mathematics of Operations Research, 1(2):117–129.
Garza-Santisteban, F., Amaya, I., Cruz-Duarte, J., Ortiz-
Bayliss, J. C.,
¨
Ozcan, E., and Terashima-Mar
´
ın, H.
(2020). Exploring problem state transformations to
enhance hyper-heuristics for the job-shop scheduling
problem. In 2020 IEEE Congress on Evolutionary
Computation (CEC), pages 1–8. IEEE.
Garza-Santisteban, F., S
´
anchez-P
´
amanes, R., Puente-
Rodr
´
ıguez, L. A., Amaya, I., Ortiz-Bayliss, J. C.,
Conant-Pablos, S., and Terashima-Mar
´
ın, H. (2019).
A simulated annealing hyper-heuristic for job shop
scheduling problems. In 2019 IEEE Congress on Evo-
lutionary Computation (CEC), pages 57–64. IEEE.
Miller, L. W., Conway, R. W., and Maxwell, W. L. (1967).
Theory of Scheduling.
Pinedo, M. L. (2012). Scheduling: Theory, Algorithms, and
Systems. Springer Science & Business Media.
Rajendran, C. and Ziegler, H. (2004). Ant-colony algo-
rithms for permutation flowshop scheduling to mini-
mize makespan/total flowtime of jobs. European Jour-
nal of Operational Research, 155(2):426–438.
Ruiz, R., Maroto, C., and Alcaraz, J. (2006). Two new ro-
bust genetic algorithms for the flowshop scheduling
problem. Omega, 34(5):461–476.
Ruiz, R. and St
¨
utzle, T. (2007). A simple and effective
iterated greedy algorithm for the permutation flow-
shop scheduling problem. European Journal of Op-
erational Research, 177(3):2033–2049.
Taillard, E. (1993). Benchmarks for basic scheduling prob-
lems. European Journal of Operational Research,
64(2):278–285.
Tasgetiren, M. F., Liang, Y.-C., Sevkli, M., and Gencyilmaz,
G. (2007). A particle swarm optimization algorithm
for makespan and total flowtime minimization in the
permutation flowshop sequencing problem. European
Journal of Operational Research, 177(3):1930–1947.
L-SAGA: A Learning Hyper-Heuristic Architecture for the Permutation Flow-Shop Problem
329