META: Deep Learning Pipeline for Detecting Anomalies on Multimodal

Vibration Sewage Treatment Plant Data

Simeon Krastev

, Aukkawut Ammartayakun

, Kewal Jayshankar Mishra

, Harika Koduri

Eric Schuman

, Drew Morris

, Yuan Feng

, Sai Supreeth Reddy Bandi

, Chun-Kit Ngan

Andrew Yeung

, Jason Li

, Nigel Ko

, Fatemeh Emdad

, Elke Rundensteiner

, Heiton M. H. Ho

T. K. Wong

and Jolly P. C. Chan

Data Science Program, Worcester Polytechnic Institute, 100 Institute Rd., Worcester, MA, U.S.A.

XTRA Sensing Limited, Wan Chai, Hong Kong Island, Hong Kong SAR

Drainage Services Department, The Government of the Hong Kong Special Administrative Region, Wanchai,

Hong Kong Island, Hong Kong SAR

{sdkrastev, aammartayakun, kmishra1, hkoduri, demorris, erschuman, yfeng8, sbandi, cngan, femdad, rundenst}@wpi.edu,

Keywords:

Predictive Maintenance, Anomaly Detection, Signal Averaging, Data Fusion, Multimodal Feature Extraction,

Autoencoder, Transformer Model, Sewage Treatment Plants.

Abstract:

In this paper, we propose a hybrid anomaly detection pipeline, META, which integrates Multimodal-feature

Extraction (ME) and a Transformer-based Autoencoder (TA) for predictive maintenance of sewage treatment

plants. META uses a three-step approach: First, it employs a signal averaging method to remove noise and

improve the quality of signals related to pump health. Second, it extracts key signal properties from three

vibration directions (Axial, Radial X, Radial Y), fuses them, and performs dimensionality reduction to create

a reﬁned PCA feature set. Third, a Transformer-based Autoencoder (TA) learns pump behavior from the PCA

features to detect anomalies with high precision. We validate META with an experimental case study at the

Stonecutters Island Sewage Treatment Works in Hong Kong, showing it outperforms state-of-the-art methods

in metrics like MCC and F1-score. Lastly, we develop a web-based Sewage Pump Monitoring System hosting

the META pipeline with an interactive interface for future use.

1 INTRODUCTION

A sewage treatment plant (STP) is a critical infras-

tructure designed to process wastewater from residen-

tial, commercial, and industrial sources. Its objective

is to remove contaminants, ensuring the treated water

is safe and suitable for reuse before releasing it back

to the environment. This process is essential for pro-

tecting public health and preserving the natural envi-

ronment by adhering to water quality standards.

STPs support a sustainable environment and pos-

itively impact human life in several ways. For exam-

ple, advanced sewage treatment, such as Singapore’s

NEWater program, signiﬁcantly reduces the risk of

waterborne diseases (Lee and Tan, 2016). By convert-

ing treated wastewater into ultra-clean, high-quality

water, Singapore meets up to 40% of its water de-

mand with NEWater, demonstrating a commitment to

public health and environmental sustainability. The

Groundwater Replenishment System (GWRS) in Or-

ange County, California, demonstrates the poten-

tial of STPs in supporting sustainable agriculture

and conserving freshwater resources (Ormerod and

Silvia, 2017). By purifying treated wastewater to

potable standards, GWRS provides a reliable water

supply, reducing dependence on imported water. In

Namibia, Windhoek Goreangab Operating Company

(WINGOC) provides treated wastewater which is ex-

tensively used for agricultural irrigation (Lahnsteiner

and Lempert, 2007). This approach not only con-

serves freshwater resources but also supports sustain-

able agriculture by providing a reliable water source

for irrigation.

The Stonecutters Island Sewage Treatment Works

(SCISTW) is one of the most efﬁcient chemical treat-

ment plants in the world, removing 70% of the or-

ganic pollutants in terms of biochemical oxygen de-

mand; 80% of the suspended solids; and 50% of

sewage pathogens in terms of Escherichia coli (E.

Krastev, S., Ammartayakun, A., Mishra, K., Koduri, H., Schuman, E., Morris, D., Feng, Y., Bandi, S., Ngan, C., Yeung, A., Li, J., Ko, N., Emdad, F., Rundensteiner, E., Ho, H., Wong, T. and

Chan, J.

META: Deep Learning Pipeline for Detecting Anomalies on Multimodal Vibration Sewage Treatment Plant Data.

DOI: 10.5220/0013031600003837

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 461-474

ISBN: 978-989-758-721-4; ISSN: 2184-3236

461

Figure 1: Stonecutters Island Sewage Treatment Works is located in Victoria Harbour and collects sewage from the Hong

Kong region for processing. The project is focused on the main pumping stations (3) that pump the ﬁltered sewage up to the

chemical processing tanks (Drainage Services Department, 2009b).

coli) level, which is an indicator of disease causing

microorganisms. In addition, the levels of key pol-

lutants in the harbour-area waters have generally de-

creased. Ammonia, which is toxic to marine life, de-

clined by 25%; nutrients, in terms of total inorganic

nitrogen and phosphorus, have reduced by 16% and

36%, respectively; and the overall E. coli level has

reduced by around 50% (Drainage Services Depart-

ment, 2009a).

The current strategy to prevent failures in large-

scale industrial pumps like those found in STPs is

to follow a routine maintenance schedule. This ap-

proach involves servicing the pumps at regular inter-

vals and replacing parts that cannot be repaired over

the life of the pump. For example, the bearings may

be repacked with grease annually until they reach

their rated life, at which point the entire bearing as-

sembly must be replaced. This approach is relatively

simple to implement and does prevent failures due to

wear and age, but it is not able to capture failures due

to incorrect installation or operation. Another issue

with this approach is that parts may be prematurely

replaced, which increases part cost and may unneces-

sarily bring about machine downtime (Carson, 2011).

Predictive maintenance, also referred to as

condition-based maintenance, enhances routine main-

tenance by continuously monitoring the condition of

system components, replacing those that exhibit signs

of impending failure. A primary beneﬁt of such an ap-

proach is that a broader range of causes of failure can

be prevented. For example, an incorrectly installed

component would start to show signs of wear that the

predictive model could detect and signal a need for re-

placement despite the service life not being reached.

However, this approach requires a more complex

system to predict and identify potential failures before

they occur. A traditional approach for doing this usu-

ally requires the development of hard-coded rules and

algorithms to deﬁne and then detect abnormal opera-

tion. This can easily grow exponentially in cost and

complexity to implement (Newton, 2021); addition-

ally, it requires prior knowledge and deﬁnition of all

possible anomalies. An alternative approach, which

this paper proposes, is to instead leverage state-of-

the-art deep learning techniques and neural networks

to automatically learn data-driven strategies that char-

acterize abnormal operation (Faisal et al., 2023).

Such a technique requires the fusion of multiple

sources of pump vibration data (Diez-Olivan et al.,

2019). If intelligently fused, the anomaly detection

model can then learn from a much broader space in-

stead of just learning one source of vibration data.

For example, fusing three directions of pump vibra-

tion data together may pick up anomalous behavior

that does not arise in just one direction. In addition,

the data dimensions can be reduced through model-

ing techniques such as Autoencoders and Principal

Component Analysis (PCA). These techniques can re-

move noise and redundant information from the data

streams, resulting in a cleaner signal for the anomaly

detection models to work on.

Thereafter, the multi-modal preprocessed data can

be used as the input to modern deep learning meth-

ods such as transformer models. Transformers learn

complex possibly non-linear relationships in data

through a deep neural network architecture and atten-

tion mechanisms (Vaswani et al., 2017), which focus

on different aspects of the data to understand normal

pump behavior. Combining this feature with an abil-

ity to track changes over time, the models can tell

when the pump is deviating from normal activity.

In the literature, hybrid machine learning (ML)

models and neural networks have been used to diag-

nose power transformers using acoustic signals (Yu

et al., 2023), while transformer models have been uti-

lized for fault detection and classiﬁcation in manu-

facturing (Wu et al., 2023). However, research on the

applications of these models remains limited. In ad-

dition, a few studies (Diez-Olivan et al., 2019) have

explored leveraging multiple input data formats and

combining data from various sources to enhance de-

tection performance.

To leverage the strengths of these methodologies

for predictive maintenance of STPs, we propose a in-

novative anomaly detection platform, called META,

which integrates Multimodal-feature Extraction (ME)

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

462

and a Transformer-based Autoencoder (TA) solution.

Our contributions to this work are ﬁve-fold:

1. We develop a signal averaging method to remove

unrelated noise from the raw sensor data and im-

prove the quality of signals related to the pump

health and operations.

2. We extract the meaningful signal properties from

three vibration signal directions (i.e., Axial, Ra-

dial X, and Radial Y) using multimodal-feature

extraction methods. We then fuse these proper-

ties together and reduce data dimensionality using

PCA to generate a reﬁned PCA feature set.

3. We apply a Transformer-based Autoencoder (TA)

model to learn pump behavior from the extracted

PCA feature set to detect anomalous behavior.

4. We conduct an extensive experimental case study

on the SCISTW, located in Hong Kong, in which

we reconstruct the vibration signals of the pumps

and set a threshold to detect anomalies based

on reconstruction error. Having labeled data

on the dates in which the pumps were oper-

ating abnormally, we are able to obtain accu-

racy metrics on the performance of the META

pipeline. META achieves MCC/F1 scores of

0.966/0.995 in anomaly detection, a percent-

age increase of 4.89%/2.47% compared to the

state-of-the-art anomaly detection performance

by (Yu et al., 2023), and a percentage increase of

2.77%/3.977% compared to (Wu et al., 2023).

5. We create a web prototype for a Sewage Pump

Monitoring System hosting the META pipeline,

providing an interactive interface for future use.

The rest of the paper is organized as follows. In

Section 2, we review the previous work and litera-

ture on anomaly detection methods and explore the

existing data fusion techniques and transformer-based

models in predictive maintenance. In Section 3, we

provide an overview of the SCISTW. In Section 4,

we introduce our META framework, broadly describ-

ing its core components. Starting in Section 4.1, we

examine each of its components, beginning with the

Signal Averaging method. In Section 4.2, we explain

our ME approach. In Section 4.3, we present our

TA Model, explaining its architecture and the mech-

anism that it uses to detect anomalies. In Section 5,

we conduct an extensive experimental study and an-

alyze the performance of the META platform in de-

tecting anomalies at the SCISTW. In Section 6, we

describe the development of our GUI-based applica-

tion for monitoring sewage pumps and visualizing the

analysis results. Finally, in Section 7, we conclude the

paper and outline the potential future work to enhance

our META framework’s performance and explore its

application in other types of industrial machinery.

2 RELATED WORK

The development of anomaly detection methods for

rotating machinery is an active area. Three data fu-

sion techniques are reviewed and explored for rotat-

ing machinery. In Yuan et al.’s work, a ﬂexible frame-

work is proposed to fuse multiple sources together

to detect abnormal operation. Multiple 1-d and 2-d

signals are ﬁrst individually passed through convolu-

tional neural networks and subsequently joined using

t-distributed Stochastic Neighbor Embedding (tSNE)

(Yuan et al., 2018). The beneﬁt of this approach is

the ﬂexibility in its application which would allow it

to be adapted to other domains. Pang et al.’s work

proposes a model that applies Stacked Denoising Au-

toEncoders (SDAEs) to the individual data sources

and fuses these sources together via Local and Global

Principal Components Analysis (LGPCA) with the

aim of improving the representation of the signal.

The SDAEs remove the uncorrelated noise from the

source signal and the LGPCA combines the signals

together across different scales to ensure that the tem-

poral relationships are preserved (Pang et al., 2020).

Finally, in Wang et al.’s work, the authors propose

a method of incorporating feature selection into the

model training processing by computing the Mean

Impact Value (MIV) and Within-class and Between-

class Discriminant Analysis (WBDA) to dynamically

select features. The approach uses traditional mea-

sures to assess the health of rotating machinery and

aims to combine these features so that a greater repre-

sentation and context is achieved while reducing data

redundancy and noise (Wang et al., 2021).

Two transformer models are reviewed and ex-

plored in predictive maintenance of rotating machin-

ery. In Yu et al.’s work, the authors propose a hybrid

anomaly detection model that combines a convolu-

tional neural network and a recurrent neural network

with the attention mechanism found in a transformer.

This approach uses the CNN to extract relevant pat-

terns from the input signals and the recurrent layer to

capture the long-running state of the system and feeds

this information into the attention mechanism to de-

tect anomalous operation (Yu et al., 2023). In Wu et

al.’s work, the authors adapt a traditional transformer

to work in the classiﬁcation setting for the purpose of

detecting abnormal operation of the pump. The trans-

former is used as an encoder to embed the input data

and generate a classiﬁcation by passing the embed-

ding to a fully connected network (Wu et al., 2023).

META: Deep Learning Pipeline for Detecting Anomalies on Multimodal Vibration Sewage Treatment Plant Data

463

Figure 2: The motor that drives one of the pumps in main

pumping station 2.

3 BACKGROUND:

STONECUTTERS ISLAND

SEWAGE TREATMENT

The SCISTW in Hong Kong is a core infrastructure

that makes every effort to minimize unplanned inter-

ruptions in service. It is one of the largest and the

most compact sewage treatment works of its type in

the world, occupying 10 hectares of reclaimed land,

and is designed to provide Chemically Enhanced Pri-

mary Treatment for an average ﬂow of 1.7 million cu-

bic meters per day (Drainage Services Department,

2009a). The overall process of treating sewage is

shown in Figure 1. In order to pump 1.7 million cubic

meters of sewage per day, the SCISTW has two main

pumping facilities that run continuously. Both pump-

ing stations are comprised of eight sewage pumps that

are able to be independently driven at a range of fre-

quencies or completely shutdown in order to maintain

a target ﬂow rate into the treatment pools. Direct-

drive pumps pump sewage approximately 40 meters

up from the collection tunnels to the treatment pools.

The AC induction motor used to drive the pump is

shown in Figure 2; the main pump body is shown

in Figure 3. The sewage pumps that move the raw

Figure 3: Main pump body that transfers sewage from the

collection tunnels to the treatment pools 40 meters above.

sewage from the collection tunnels up to the treat-

ment tanks are critical to the operation of the treat-

ment plant. The current regime for failure preven-

tion at the SCISTW is largely based on preventative

maintenance, relying on the excess pumping capac-

ity available in the plant by using working pumps

to handle the load when pumps fail. Shifting to a

condition-based maintenance approach would allow

the SCISTW to prevent pumps from failing unexpect-

edly and enable the plant to treat a greater load of

sewage as a result.

The primary hurdle to the SCISTW adopting a

condition-based maintenance approach is the cost and

complexity of implementing a hard-coded approach

to the pumps. While the design of those pumps is rel-

atively simple, the number of failure modes is high,

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

464

and the interaction between failure modes increases

the complexity of creating logic that may not accu-

rately detect when a pump is about to fail. Fur-

thermore, the pumps are controlled and monitored

through several disparate systems, making it difﬁ-

cult to create a holistic anomaly detection system that

can integrate all the data coming from the different

sources. As a solution, the SCISTW is looking to-

wards implementing an independent monitoring sys-

tem capable of detecting abnormalities autonomously,

without the need to tap into each system individually.

4 META OVERVIEW: ANOMALY

DETECTION PLATFORM

Our pipeline for anomaly detection incorporates a

method of fusing multi-directional raw acceleration

time waveform data (Axial, Radial X, and Radial Y)

and using the resultant product as an input for a trans-

former model architecture. This pipeline, shown in

Figure 4, consists of three core components, including

Signal Averaging (SA), Multimodal-feature Extrac-

tion, and a Transformer-based Autoencoder Model.

The purpose of the SA module is to process the

three time waveform signals (Axial, Radial X, and

Radial Y) collected from the accelerometer. These

signals are ﬁrst split into time segments based on

the shaft periods and then averaged to preserve the

segment signals speciﬁc to each individual pump,

effectively removing unrelated noise. After that,

the cleaned signals are sent to the ME module that

summarizes the speciﬁc aspects of the data by us-

ing statistical measures, empirical mode decomposi-

tion (EMD), entropy measures, wavelet packet de-

composition (WPD), and frequency domain analysis

(FDA), respectively. The summarized data of each

time waveform signal are then further processed us-

ing Mean Impact Value (MIV) and Within-class and

Between-class Discriminant Analysis (WBDA) for

feature selection. The ﬁnal selected feature set is then

fused by PCA. Those PC features are combined for

each time waveform signal and then further concate-

nated from all these three directions to form the ﬁ-

nal feature set that is then sent to the TA model for

the anomaly detection. This model processes the ﬁnal

feature set through ﬂattening, patching, and positional

encoding layers, before going through a multi-head

attention encoder. The output is then sent through

several dense layers to reconstruct the signal. Once

trained, this model architecture is used to classify

pump behavior as normal or anomalous based on re-

construction error. Once the error threshold is deter-

mined, any major deviation from the reconstruction

error of a model trained on normal data, i.e., above

the error threshold, could be a potential anomaly.

4.1 META Signal Averaging Strategy

The data that is analyzed by the META framework

to detect abnormal pump operations is collected from

various locations on the pumps using a three-axis ac-

celerometer. The data is collected in two seconds ev-

ery four hours in all three directions, yielding 25,600

data points per two-second recording. The accelerom-

eter is able to record all frequencies between 0.5 and

5,000 Hz. A two-second recording is long enough to

record several full rotations of the pump so that pump

health can be determined.

While the ability to record such a large range of

signals has the beneﬁt of being able to detect multi-

ple types of failures like shaft imbalances at the low

Figure 4: META Framework.

META: Deep Learning Pipeline for Detecting Anomalies on Multimodal Vibration Sewage Treatment Plant Data

465

Figure 5: 1) The raw time-based signal is ﬁrst used to determine the rotation period of the pump. 2) The extracted period is

then used to segment the raw time-based signal into windows equal to the rotation period. This aligns the angle of rotation

for elements across windows. 3) The segmented windows are then averaged across the segments to generate a new segment

which should reduce the uncorrelated noise while preserving the relevant signals.

end and seized bearings at the high end, it also has the

drawback of capturing a lot of information in the pro-

cess. In fact, the system’s broadband noise is so sig-

niﬁcant that it poses substantial challenges for many

anomaly detection algorithms, making it difﬁcult to

distinguish between signals from a healthy pump and

an unhealthy one. Our META framework can address

this issue by incorporating signal averaging as a pre-

processing step to improve the signal-to-noise ratio.

Signal averaging is applied to the raw time wave-

form signal in an attempt to improve the signal-to-

noise ratio of the captured signal. At its core, the

pumps are rotating machinery, and that means the ma-

jority of vibration signals relevant to the operation

of the pump is periodic in nature. Furthermore, the

short duration of the recording means the speed of the

pumps can be assumed to be steady-state. Exploiting

this fact allows the original time waveform signal to

Figure 6: Top) The original time waveform data. Middle)

The original time waveform data segmented into windows

of time that match the period of rotation. Bottom) Resulting

signal averaged data.

be split into time segments equal to the rotation pe-

riod of the pump and then averaged together. Aver-

aging these segments together is expected to preserve

the signals speciﬁc to the pump because they ”con-

structively” overlap. However, the random noise not

related to the operation of the pump is expected to

”destructively” overlap, as it is assumed that the noise

has a mean of 0. By averaging multiple segments to-

gether, the signals related to the pump are elevated

above the noise providing a cleaner signal to the work

downstream. Signal averaging is implemented in our

META framework shown in Figure 5.

Applying signal averaging as a preprocessing step

makes the assumption that the noise that is uncorre-

lated to the rotation is of less importance than the sig-

nals and the noise that is correlated to the rotation.

The rotation of the shaft is the sole energizing com-

ponent of the system, making this a safe assumption.

Furthermore, while signal averaging reduces the noise

ﬂoor of the resulting signal, it does not remove the

noise from the signal altogether. This provides some

protection against the assumption proving to be false.

One notable issue with applying signal averaging to

the data is that it may greatly diminish transient sig-

nals that do not repeatedly appear across multiple ro-

tations of the pump. An example of passing the data

through signal averaging is shown in Figure 6.

4.2 META Multimodal Feature

Extraction

In the context of enhancing anomaly detection mecha-

nisms for pump systems, the presented method adopts

a multimodal feature extraction approach, leveraging

the tri-axial nature of pump operation—Radial X, Ra-

dial Y, and Axial. This approach facilitates a com-

prehensive analysis by considering the acceleration

data across each dimension, enabling the capture of a

full spectrum of potential anomalies. The engineering

process produces an initial robust set of features in-

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

466

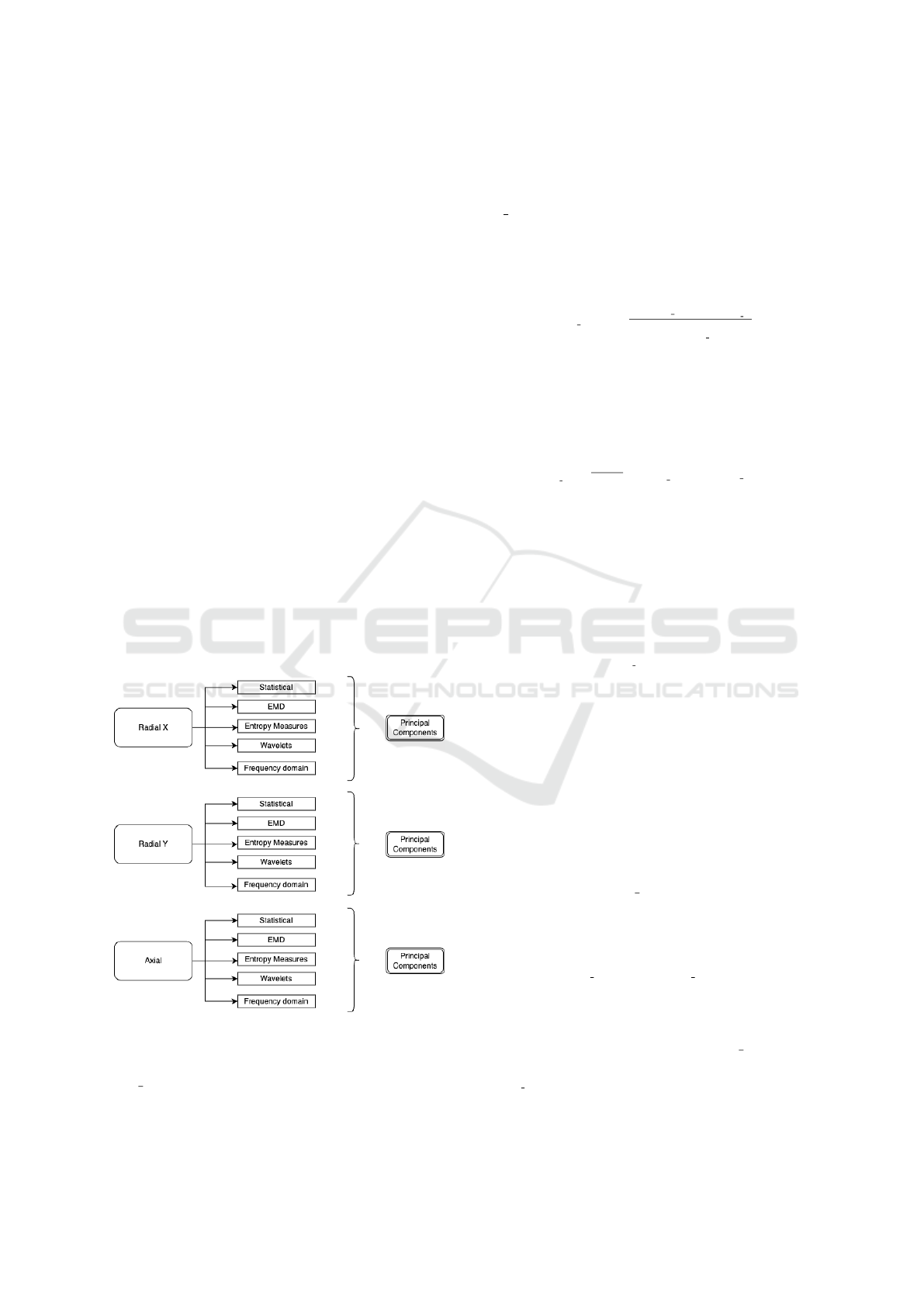
corporating time-domain statistics, frequency-domain

characteristics, and time-frequency domain features.

These features, which are meticulously named to re-

ﬂect their source and extraction method, shown in

Figure 7, range from basic statistical measures, such

as mean, standard deviation, skewness, and kurtosis,

to more complex analyses including empirical mode

decomposition (EMD) (i.e., energy and entropy), en-

tropy measures (i.e., permutation and dispersion),

wavelet packet decomposition, and frequency mea-

sures (i.e., sum amplitude, average spectrum, standard

deviation spectrum, and integral spectrum).

The ME approach therefore offers a comprehen-

sive analysis of the pump system’s operational data.

The concatenation of these features enables a robust

anomaly detection system that can accurately detect

and characterize a wide range of anomalous behav-

iors unique to each axis of operation, thereby enabling

more reliable predictive maintenance. Additionally, it

caters to the detection of complex, non-linear interac-

tions within pump mechanics, thereby broadening the

scope of detectable anomalies.

Following the feature selection process by MIV

and WBDA, PCA is applied to each directional fea-

ture set independently. PCA, as a dimensionality

reduction technique, identiﬁes the principal compo-

nents that encapsulate the maximum variance within

the data, thus preserving essential information while

reducing the data’s complexity.

Figure 7: Multimodal-Feature Extraction.

For the PCA method explanation, we use Ra-

dial X as an example. When PCA is applied to this

signal, the process involves the following steps:

Standardization

The features extracted by each method from the Ra-

dial X, shown in Figure 7, are standardized. This in-

volves subtracting the mean of each feature and then

dividing by the standard deviation. Standardization

ensures that each feature contributes equally to the

analysis.

Radial X, std

Radial X

−µ

Radial X

(1)

Covariance Matrix Calculation

The covariance matrix of the standardized features is

computed. The covariance matrix provides a measure

of how much the features vary together.

Radial X

n −1

⊤

Radial X, std

(2)

Eigenvalue and Eigenvector Computation

The eigenvalue equation is solved to obtain the eigen-

values and eigenvectors of the covariance matrix.

The eigenvalues represent the amount of variance ex-

plained by each principal component, and the eigen-

vectors represent the direction of the principal com-

ponents.

Radial X

= λ

(3)

Principal Component Selection

The top k principal components are selected by the

eigenvectors corresponding to the largest eigenvalues.

This step reduces the dimensionality of the data while

retaining the most important information.

= [v

, v

, . . . , v

] (4)

Data Transformation

The standardized Radial X data is transformed into

the principal component space. This transformation

projects the original data onto the new basis formed

by the selected principal components.

Radial X, PCA

= X

Radial X, std

(5)

Principal Components Concatenation

The same process is applied to the Radial Y and Ax-

ial signals, resulting in the transformed data matrices

Radial Y, PCA

and X

Axial, PCA

. The principal compo-

nents from all three directions are then concatenated

META: Deep Learning Pipeline for Detecting Anomalies on Multimodal Vibration Sewage Treatment Plant Data

467

to form the ﬁnal feature set, ensuring that the multi-

directional information is integrated into a compre-

hensive analysis.

Radial X, PCA

, X

Radial Y, PCA

, X

Axial, PCA

]

PCA Example

Let’s assume that we have the following data for Ra-

dial

X, Radial Y, and Axial signals:

Radial X





1 2 3

4 5 6

7 8 9





Radial Y





2 3 4

5 6 7

8 9 10





Axial





3 4 5

6 7 8

9 10 11





Standardization

We standardize the features by subtracting the mean

and dividing by the standard deviation using Equation

(1). This step ensures that the data has zero mean and

unit variance, which is necessary for PCA. The mean

and standard deviation for X

Radial X

are:

Radial



4 5 6



Radial X



2.449 2.449 2.449



Standardized X

Radial X, std

Radial X

−µ

Radial X





−1.224 −1.224 −1.224

0 0 0

1.224 1.224 1.224





Covariance Matrix Calculation

We then compute the covariance matrix of the stan-

dardized features by using Equation (2). The covari-

ance matrix helps in understanding the relationships

between different features.

Radial X

n −1

⊤

Radial X, std





1.5 1.5 1.5





Eigenvalue and Eigenvector Computation

After that, we solve the eigenvalue equation to obtain

eigenvalues and eigenvectors by using Equation (3).

The eigenvalues indicate the variance explained by

each principal component, and the eigenvectors pro-

vide the directions of these components. Assume that

the eigenvalues are λ

= 4.5 and λ

= λ

= 0, with

corresponding eigenvectors:

√









with v

, v

as any orthogonal vectors in the null space

Principal Component Selection

We then select the top k principal components in

Equation 4 (let’s choose k = 1). This step simpliﬁes

the data by reducing its dimensions while retaining

the most signiﬁcant variance.







√







Data Transformation

Finally, we transform the standardized Radial X data

into the principal component space using Equation

(5). This transformation projects the data onto the se-

lected principal components, resulting in a new repre-

sentation of the data.

Radial X, PCA

= X

Radial X, std





−1.224 −1.224 −1.224

0 0 0

1.224 1.224 1.224











√











−2.121

2.121





The resulting X

Radial X, PCA

matrix represents the

data projected onto the principal component, captur-

ing the most signiﬁcant variance in the data.

The cluster heatmap in Figure 8 derived from the

Radial X direction employs hierarchical clustering to

group features with respect to the principal compo-

nents, with the color-coding representing the degree

of correlation. It corroborates the PCA’s ability to

concentrate variance and provides a visual interpre-

tation tool to assess how different features inform the

principal components. That results in showing that

the multimodal feature extraction and the PCA di-

mension reduction offer a data-efﬁcient, informative

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

468

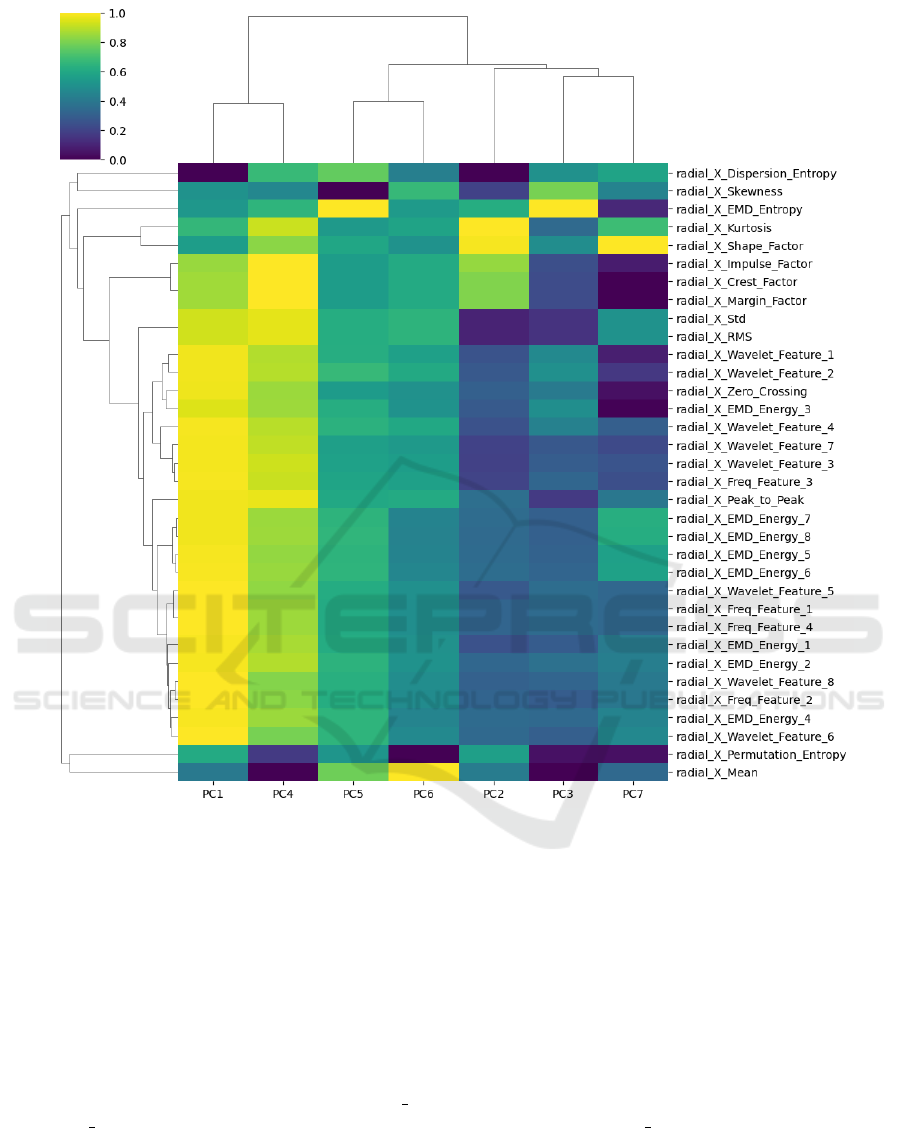
Figure 8: PCA Cluster Map.

foundation for transformer-based algorithms to detect

and predict anomalies in pump systems. The visual

representation through the cluster map further assists

in interpreting the data, ensuring that the most signif-

icant features for anomaly detection are highlighted

and utilized in predictive maintenance models.

When concatenating PCA features, we make the

distinction between PCA Directions and PCA groups.

The Directions approach involves applying PCA sep-

arately to features extracted from different measure-

ment directions of vibration signals (Axial, Radial X,

and Radial Y). Each direction’s features result in dis-

tinct sets of principal components for each direction.

This approach allows for a detailed examination of

how different directions contribute to the overall con-

dition or behavior being studied. On the other hand,

the Feature Groups approach groups features based

on their calculation methods or characteristics and

then applies PCA to each group separately. The fea-

ture groups considered are statistical, EMD-Based,

entropy measures, wavelet packet features, and fre-

quency domain features. Each group’s features are

scaled and PCA is applied independently, resulting in

distinct sets of principal components for each group.

This method allows for a more nuanced understand-

ing of the variability within each feature group and

can highlight important patterns within those groups.

In both cases, the resulting datasets include meta-

data columns (Sensor ID, Datetime, label) along with

the PCA components for each group/direction.

META: Deep Learning Pipeline for Detecting Anomalies on Multimodal Vibration Sewage Treatment Plant Data

469

4.3 Meta Transformer-Based

Autoencoder

4.3.1 Transformer-AutoEncoder Anomaly

Detection (TrAEAD)

In this model, shown in Figure 9, the input data in the

form of a sequence of the PC vectors is used. The

preprocessing and positional encoding are used to in-

corporate the positional relationship into the model

and make the data in a format that is suitable for the

model. This model aims to learn and enhance the dis-

crimination of the representation of the data if the data

is under the normal operation (denoted by D

). After

the training on the normal operation data is done, the

reconstruction of this model should be the version of

the normal operation of the input. If the difference

between the input and the reconstruction input of the

model is high, that implies that the input data is in

a different distribution of the reconstruction data. In

other words, the input data is anomalous.

This model achieves the task by using the concept

of autoencoder where we aim to reconstruct any input.

The green block is used for the encoding part, and the

red-pink block is the fully-connected neural network

blocks that are used for the reconstruction of the in-

put. In the encoder block, the multi-head attention

and fully-connected layers are used along with layer

normalization and dropout. This is repeated N times

for the scalability of the complexity of the model.

Mathematically, suppose we have a data input x ∈

(or its isomorphic form like x ∈ R

a×b×c

∼

abc

)

from the dataset D = {(x

, y

), . . . (x

, y

)}, y

∈{0, 1}

that includes training data D

⊂ {(x, y) ∈ D|y = 0}

and validation data D

= D \D

and assume that la-

tent space from the embedding function f : R

→ R

is separable for each input x

given the label y

, that is,

data from both classes are discriminative or distinct

enough.

We can assume that the normal operation data

is mostly deterministic with recognizable stochastic

elements. Suppose the normal operation signal is

φ(t). Then, the sensor, if perfect, should be able to

fully capture the signal φ(t). However, as the sen-

sor is not perfect, we can model this as φ(t) + ε(t)

for measurement noise ε(t) ∼ T (θ, t) for some dis-

tribution T (θ, t). However, the faulty operation will

look different in either one of those as it will be

φ(t) + ω(t) + ε(t), which will have a different distri-

bution for the faulty condition if ω(t) has enough im-

pact. The assumption of discrimination can be used.

Now, suppose we create a model M that consists

of two parts: an embedding function f and a recon-

struction function g : R

→ R

. Given the training

data D

⊂ D where D

= {(x

, y

) | y

= 0}, the em-

bedding function f maps this data to the latent space:

= {f (x

) | (x

, y

) ∈ D

} ⊂ R

Let ˆz ∈Z

be a sample from the region in the latent

space that is concentrated with normal operation data.

The reconstruction function g then maps ˆz back to the

input space: ˆx = g(ˆz)

Since ˆz is from the image of f given the training

data D

, the reconstruction ˆx should be similar to the

original data x in D

. Mathematically, this implies

that:

ˆx = g( f (x

)) ≈ x

for (x

, y

) ∈ D

(6)

Furthermore, we assume that normal operation

data x outside of the training set D

will be mapped

by f to a neighborhood of Z

in the latent space. De-

ﬁne the ε-neighborhood of Z

as:

) = {z ∈ R

| ∃z

∈ Z

such that ∥z −z

∥ < ε} (7)

We assume that for normal operation data x out-

side of D

f (x) ∈ N

) for some ε > 0 (8)

This implies that for new normal operation data x,

the embedding f (x) lies within an ε-distance of the

region Z

in the latent space, ensuring that the recon-

struction g( f (x)) is similar to normal operation data.

This is possible due to our assumption that normal op-

eration data is mostly deterministic with predictable

stochastic elements. If the data is from the normal

operation, the difference should be mostly on the de-

terministic part, and if f is good enough, the distance

between the slight changes in value should be pre-

served.

Given the versatility and SOTA performance of

transformer models in various domains (Vaswani

et al., 2017; Raffel et al., 2020), it is reasonable to

explore the possibility that f can be implemented as

a transformer model. Transformers are capable of

generating high-quality embeddings due to their self-

attention mechanisms, which capture complex rela-

tionships and patterns in data (Vaswani et al., 2017).

Input

Preprocessing

Positional Encoding

Encoder

Decoder

Reconstruction

Multi-head

Attention

Fully

Connected

Fully

Connected

×N

×M

Figure 9: Architecture of TrAEAD Model.

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

470

However, it is important to note that while transform-

ers have shown surprising empirical results, claiming

that they will always preserve the distance for slight

alterations of data points in the embedding space is an

assumption that warrants further investigation. The

empirical result later from (Wu et al., 2023) shows

that the transformer model is a good ﬁt for this task.

The transformer architecture is mainly drawn

from (Wu et al., 2023). The basic fully connected lay-

ers are linked with multi-head attention to form a ba-

sic transformer model. While the authors use classiﬁ-

cation head on top of the transformer model to make

it a classiﬁcation task, in this work, the alteration has

been done to make it a generative model to follow our

previous assumption about the behavior of our input.

For the reconstruction part g, the primary require-

ment is that the reconstruction error with respect to

the original data should be minimal. A simple neu-

ral network, such as a fully connected network, can

be used with an objective function to minimize this

reconstruction error. Given that our training data is

a subset of the dataset containing only normal op-

eration samples, the reconstruction error becomes a

key factor in anomaly classiﬁcation. Speciﬁcally, if

the reconstruction error is high, it can imply that the

data point is out of the training distribution and, thus,

further from the neighborhood of the normal opera-

tion distribution. Therefore, it can be classiﬁed as an

anomaly. In this study, the mean squared error (MSE):

Error

∑

)∈D

||x

−M(x

)||

(9)

is used as the reconstruction error. The deﬁnition

of ”high” can be determined in the model selection

phase, where metrics like Matthews’ correlation co-

efﬁcient (MCC) can be used as the cutting point.

Speciﬁcally, the classiﬁcation threshold that maxi-

mizes this metric would be the optimal threshold for

classiﬁcation. In other words, the threshold T is given

by:

T = arg max

T ∈R

MCC(I(Error(x, M(x)) > T )) (10)

where the indicator function I classiﬁes whether the

error between the true value x and the model’s predic-

tion M(x) exceeds the threshold T .

4.3.2 Model Inference Example

Here is a simple example to illustrate the idea of how

the model works. Suppose our input data is 3-axis

accelerations from the accelerometer. For the sake of

visualization, suppose we have a random vector R

for three-dimensional signals with four samples. Here

we have x ∈ R

3×4

data.

Preprocessing

This data is then fed to the pipeline as 4 data points

with three features each. That is for the signal

X =





1 0 1 1

1 1 0 1

0 1 1 1





is treated as



1 1 0



⊤



0 1 1



⊤



1 0 1



⊤



1 1 1



⊤

That is, we have three series of four or four lengths

with three features. Then, for the ﬁxed length size l,

which is one of the hyperparameters of the prepro-

cessing, the preprocessing will process a token as a

group of vector (x

, . . . , x

), (x

l+1

, . . . , x

), . . . . Sup-

pose that l = 2, then the ﬁrst token for the model is

, x

), and the second token of the model is (x

, x

It then will provide the positional encoding to each of

the tokens. Speciﬁcally,

PE(i, j) =











sin

10000

model

⌊

⌋

if j is even

cos

10000

model

⌊

⌋+

model

if j is odd

for the position i at dimension j = 0, . . . , d

model

. Here,

model

= 3. For the ﬁrst token,

PE(1) =



0 1 0



⊤

PE(2) =



0.84147098 0.54030231 0.00215443



⊤

and second token

PE(3) =



0.90929743 −0.41614684 0.00430886



⊤

PE(4) =



0.14112001 −0.9899925 0.00646326



⊤

The ﬁrst input token to the transformer then is (x

PE(1), . . . , x

+ PE(l)).

Classiﬁcation

After getting the reconstruction M(X) = R

(Z)),

given that the model is trained on the normal oper-

ation signal, the difference in input would be pro-

nounced if the input and reconstruction are from dif-

ferent distributions. In this case, the MSE between

M(X) and X deﬁned in Equation (9) is 0.38840. If

the threshold from the training is larger than 0.38840,

then this would mean X is under normal operation.

However, if it is otherwise greater than the threshold,

it is an abnormally.

META: Deep Learning Pipeline for Detecting Anomalies on Multimodal Vibration Sewage Treatment Plant Data

471

Transformer Model (Encoder)

Suppose that N = 1; this input will then pass through

the multi-head attention layer as outlined in (Vaswani

et al., 2017). This attention is then combined with

the input and passes through the fully connected layer.

Note that the fully connected network works for each

data point within the token. In other words, this fully

connected layer works with the R

vector for our ex-

ample. For the simplicity of explanation, let the out-

put for this model be the embedding in R

and let

p = 5. Suppose that the output for this encoder model

Z =



0.144 0.213 −0.115 0.821 1.110



Reconstruction (Decoder)

The series of fully connected networks in the decoder

will map R

→R

model

for n data points. In this case,

it will map the embedding in R

to R

which is iso-

morphic with R

3×4

which is the original data dimen-

sion. Suppose our N = 2 and we have R

: R

→ R

then R

: R

→ R

For the sake of space, the R

will

be written as R

2×4

matrix and R

will be written as

3×4

The reconstruction will look like this

(Z) =



0.811 0.911 0.314 0.112

0.000 0.213 0.981 −0.772



(Z)) =





0.811 0.591 0.994 0.991

−0.012 0.818 0.011 −0.772

0.012 0.995 0.892 0.742





5 EXPERIMENTAL STUDY

In these experiments, we are attempting to compare

the performance of reconstruction anomaly detection

from the (Wu et al., 2023) and (Yu et al., 2023)

models to various data fusion methods paired with

the TrAEAD model. These variations include test-

ing the raw time wave-form data, the PCA Groups

and PCA Directions methods, and the signal-averaged

PCA Groups and PCA Directions approaches. For

this comparison, we are focusing on metrics such as

MCC score, Accuracy, Precision, Recall, F1 Score,

Negative Predictive Value (NPV), and Speciﬁcity.

The assumption for the reconstruction approach

is that the input data from the anomalous and non-

anomalous sources should look different and signiﬁ-

cant enough to deﬁne a threshold of the reconstruction

error to make a good classiﬁcation decision. Using la-

beled data from the pumps at SCISTW, we are able to

assess the performance of anomaly detection.

Since the accuracy of our models is based on the

reconstruction error of the signals surpassing a prede-

ﬁned threshold to label a vibration reading as anoma-

lous, the training set for this task only consists of data

from the normally operating pumps (Pumps 5 and 6).

This data was split into 80% training and 20% test-

ing data, consisting of the ﬁrst and last 10% by date

recorded. The anomalous pump data from Pump 2

was reserved for testing.

The TrAEAD model reconstructs the signal well,

with an overall reconstruction error from all the test

signals of 0.01. However, the anomalous data has the

tendency to be reconstructed with the wrong ampli-

tude level. For the normal signal, the reconstruction

fails to match some of the ground truth signals but

manages to get the amplitude range correct.

As a baseline for comparison with the TrAEAD

model, the data was reconstructed using a hybrid re-

current layer structure such as the model introduced

by (Yu et al., 2023), originally intended for voiceprint

anomaly detection, adapted to work with the time-

waveform and spectrogram data, and the same recon-

struction error threshold was used to label anomalies.

Furthermore, the same experiment was repeated with

the original model proposed by (Wu et al., 2023).

Table 1 shows that while all models perform

well, the TrAEAD model with multimodal-feature

extraction tends to perform better overall compared

to the models by (Wu et al., 2023) and (Yu et al.,

2023). Though these other models slightly outper-

form TrAEAD in Precision, NPV, and Speciﬁcity, the

differences are marginal and don’t signiﬁcantly affect

Table 1: Performance Comparison of Various Models.

Data Fusion Model MCC Acc. Prec. Rec. F1 NPV Spec.

Wavelet Scaleogram Wu et al. (2023) 0.940 0.978 1.000 0.919 0.957 0.971 1.000

Raw Data Yu et al. (2023) 0.921 0.962 1.000 0.943 0.971 0.898 1.000

Raw Data TrAEAD 0.945 0.978 1.000 0.919 0.958 0.971 1.000

PCA Groups TrAEAD 0.923 0.978 0.988 0.988 0.988 0.902 0.958

PCA Groups Sig. Avg. TrAEAD 0.955 0.993 0.993 0.993 0.993 0.958 0.958

PCA Directions TrAEAD 0.944 0.991 0.991 0.991 0.991 0.939 0.958

PCA Directions Sig. Avg. TrAEAD 0.966 0.995 0.995 0.995 0.995 0.959 0.979

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

472

the model’s overall value. TrAEAD’s higher Recall

and F1-score suggest it is better at identifying true

anomalies and reducing false negatives, with the PCA

Directions and Signal Averaging method producing

the best results.

6 SEWAGE PUMP MONITORING

SYSTEM PROTOTYPE

In order to host our META pipeline as well as visu-

alize the output of analyzing pump vibration data, a

web-based Sewage Pump Monitoring System was de-

signed and built.

The system’s backend was developed using Flask,

a lightweight WSGI web application framework that

provides tools for URL routing, request handling, and

template rendering (Grinberg, 2018). For this appli-

cation, Flask handles the upload and preprocessing of

sensor data ﬁles, performs feature extraction on the

raw sensor data, and exposes RESTful API endpoints

that the frontend can interact with.

The frontend of the application, on the other hand,

was built with React, a component-based JavaScript

library for building user interfaces (Banks and Por-

cello, 2017). It integrates the backend APIs using

asynchronous HTTP requests through libraries like

Axios, and allows for the incorporation of visualiza-

tion libraries such as Chart.js to display sensor data.

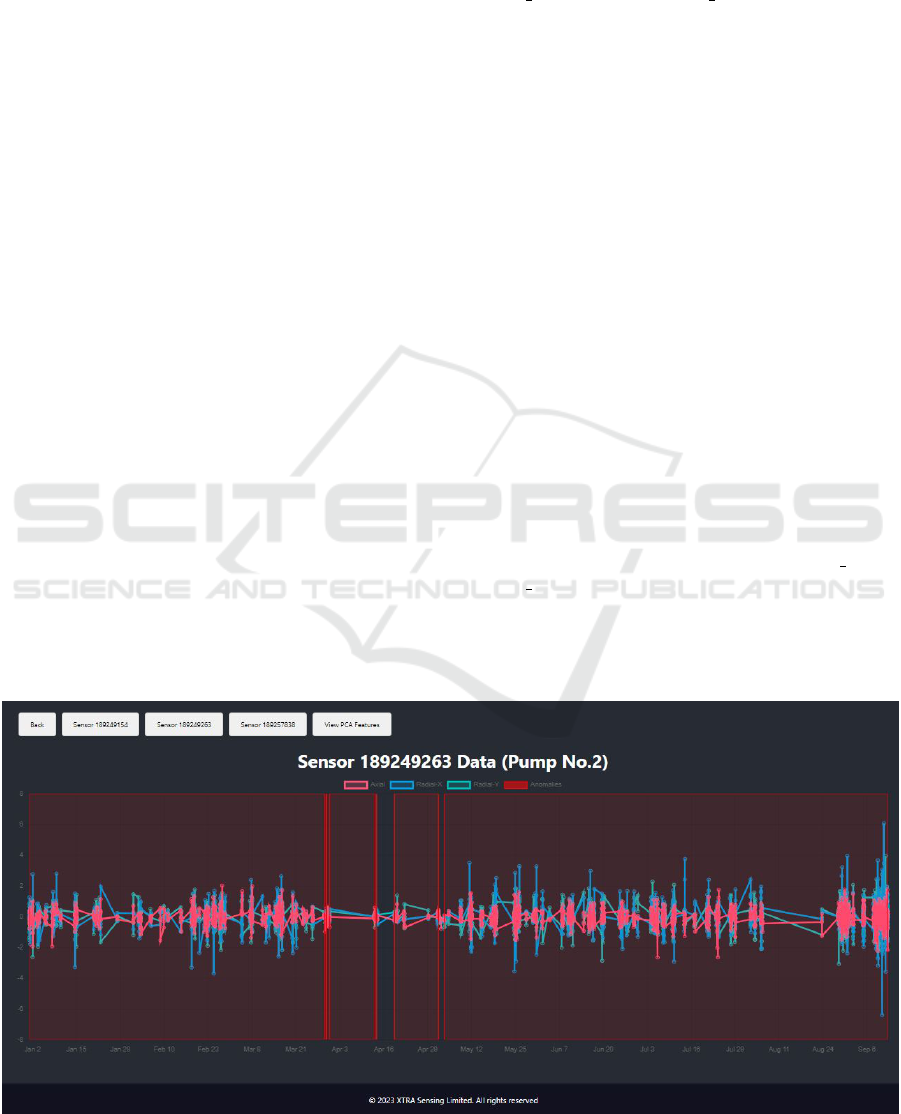
In this interface, the user is able to select and up-

load sensor data ﬁles with vibration data. This data is

then processed through the META pipeline, from sig-

nal averaging, to multimodal feature extraction, and

ﬁnally passed through the transformer-based autoen-

coder model. The output of this process is then dis-

played visually, organized by sensor, in a graph of

amplitude versus time that shows three different lines

for each dimension of the original data (Axial [pink],

Radial X [blue], and Radial Y [green]) and marks

the dates in which anomalies in the operation of the

pumps are detected. The spans of consecutive data

entries with anomalous data points are marked in a

bright red color, which is toggle-able alongside the

individual data from each of the input dimensions. A

sample output for this process is shown in Figure 10.

7 CONCLUSION AND FUTURE

WORK

In this paper, we propose a hybrid anomaly

detection platform, called META, which inte-

grates Multimodal-feature Extraction (ME) and a

Transformer-based Autoencoder (TA) to leverage the

strengths of the existing methodologies for predic-

tive maintenance of sewage treatment plants. We

ﬁrst developed a signal averaging method that can

preprocess the raw data using the signal processing

algorithms to remove unrelated noise and improve

the quality of signals related to the pump health and

operations. Second, we enhanced the existing ME

method to extract the meaningful signal properties on

three vibration signal directions (Axial, Radial X, and

Radial Y), respectively, by using ﬁve computational

methods and measures and then fusing them together

using PCA to generate PCA feature sets. Third, we

enhanced a TA model to learn pump behavior from

the extracted PCA feature sets to detect anomalous

Figure 10: Sample GUI Output for the anomalous data, marked in red, from Pump No.2.

META: Deep Learning Pipeline for Detecting Anomalies on Multimodal Vibration Sewage Treatment Plant Data

473

behavior over time with high precision. Fourth, we

conducted an extensive experimental case study on

the SCISTW, located in Hong Kong, to demonstrate

that our META platform achieves SOTA performance

in terms of MCC, F1-score, Accuracy, Precision, Re-

call, Negative Predictive Value, and Speciﬁcity. Fi-

nally, we built a prototype web-based Sewage Pump

Monitoring System hosting the entire pipeline, pro-

viding an interactive user interface for future use.

Further research is needed to validate the versa-

tility and robustness of the META framework. As-

sessing META’s performance in anomaly detection

for other types of industrial machinery as well as ex-

ploring different types of data fusion techniques could

increase conﬁdence in such a hybrid platform. For

instance, examining late fusion techniques, in which

the feature integration occurs at a later stage, right

before the model makes a decision, could yield in-

teresting insights into the system’s performance. Fur-

thermore, investigating the incorporation of other ma-

chine learning models with transformers and examin-

ing their impact on anomaly detection could lead to

the development of more robust and scalable predic-

tive maintenance approaches.

REFERENCES

Banks, A. and Porcello, E. (2017). Learning React:

Functional Web Development with React and Redux.

O’Reilly Media, Inc.

Carson, S. (2011). Best practice for lift stations:

predictive maintenance or ”run to fail”? On-

line: https://www.pumpsandsystems.com/

best-practice-lift-stations-predictive-maintenance-or-run-fail.

Diez-Olivan, A., Ser, J. D., Galar, D., and Sierra, B. (2019).

Data fusion and machine learning for industrial prog-

nosis: Trends and perspectives towards industry 4.0.

Information Fusion, 50:92–111. Full Length Article.

Drainage Services Department (2009a). Stonecutters

Island Sewage Treatment Works. Online: https:

//www.dsd.gov.hk/TC/Files/publications publicity/

publicity materials/leaﬂets booklets factsheets/

Stonecutter.pdf. Last accessed on January 27, 2024.

Drainage Services Department (2009b). Stonecutters

Island Sewage Treatment Works under Harbour

Area Treatment Scheme Stage 2A. Online: https:

//www.dsd.gov.hk/EN/Files/publications publicity/

publicity materials/leaﬂets booklets factsheets/

HATS2A Brochure REV15.pdf. Last accessed on

January 27, 2024.

Faisal, M., Muttaqi, K. M., Sutanto, D., Al-Shetwi, A. Q.,

Ker, P. J., and Hannan, M. (2023). Control technolo-

gies of wastewater treatment plants: The state-of-the-

art, current challenges, and future directions. Renew-

able and Sustainable Energy Reviews, 181:113324.

Available online 3 May 2023, Version of Record 3

May 2023.

Grinberg, M. (2018). Flask Web Development: Developing

Web Applications with Python. O’Reilly Media, Inc.

Lahnsteiner, J. and Lempert, G. (2007). Water management

in windhoek, namibia. Water Science and Technology,

55(1-2):441–448.

Lee, H. and Tan, T. P. (2016). Singapore’s experience with

reclaimed water: Newater. International Journal of

Water Resources Development, 32(4):611–621.

Newton, E. (2021). Predictive maintenance for pump oper-

ations — modern pumping today.

Ormerod, K. J. and Silvia, L. (2017). Newspaper cov-

erage of potable water recycling at orange county

water district’s groundwater replenishment system,

2000–2016. Water, 9(12):984. This article belongs

to the Special Issue Development of Alternative Wa-

ter Sources in the Urban Sector.

Pang, S., Yang, X., Zhang, X., and Lin, X. (2020). Fault

diagnosis of rotating machinery with ensemble ker-

nel extreme learning machine based on fused multi-

domain features. ISA Transactions, 98:320–337.

Raffel, C., Shazeer, N., Roberts, A., Lee, K., Narang, S.,

Matena, M., Zhou, Y., Li, W., and Liu, P. J. (2020).

Exploring the limits of transfer learning with a uniﬁed

text-to-text transformer. J. Mach. Learn. Res., 21(1).

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, Ł. and Polosukhin, I.

(2017). Attention is all you need. In Proceedings

of the 31st International Conference on Neural Infor-

mation Processing Systems (NIPS 2017), Long Beach,

CA, USA. Curran Associates Inc. [Google Scholar].

Wang, G., Zhao, Y., Zhang, J., and Ning, Y. (2021). A novel

end-to-end feature selection and diagnosis method for

rotating machinery. Sensors, 21(6).

Wu, H., Triebe, M. J., and Sutherland, J. W. (2023). A

transformer-based approach for novel fault detection

and fault classiﬁcation/diagnosis in manufacturing: A

rotary system application. Journal of Manufacturing

Systems, 67:439–452.

Yu, D., Zhang, W., and Wang, H. (2023). Research on trans-

former voiceprint anomaly detection based on data-

driven. Energies, 16(5).

Yuan, Z., Zhang, L., and Duan, L. (2018). A novel fu-

sion diagnosis method for rotor system fault based on

deep learning and multi-sourced heterogeneous mon-

itoring data. Measurement Science and Technology,

29(11):115005.

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

474