Precise Estimation of Urban Vegetation Carbon Stock Using Multi-

Source LiDAR: A Case Study of East China Normal University

Haoyang Song

School of Geographic Sciences, East China Normal University, Shanghai, China

Keywords: LiDAR. Carbon Stock, Tree Segmentation, Average Biomass Method

Abstract: With the intensification of global climate change, accurately estimating vegetation carbon stock has become

one of the keys to achieving carbon neutrality. This study combines multi-source LiDAR data and empirical

carbon stock formulas to propose a comprehensive and reliable technical framework for the fine estimation

of urban vegetation carbon stock. This framework includes: LiDAR data preprocessing, shrub extraction and

volume calculation, tree segmentation, and carbon stock calculation. In particular, the study compares various

commonly used tree segmentation algorithms and uses the layer stacking algorithm for tree segmentation in

the study area, ultimately obtaining the total carbon stock in the study area to be 2,677,442.666 kg. Overall,

this technical framework can effectively improve the accuracy and efficiency of traditional urban vegetation

carbon stock estimation, providing technical support and data foundation for achieving carbon neutrality.

1 INTRODUCTION

Research on the carbon cycle in urban ecosystems has

become a focal point in climate change mitigation

strategies. Urban carbon storage is primarily

composed of trees and shrubs, both playing an

irreplaceable role in improving the living

environment, maintaining ecological security, and

achieving sustainable urban development (Creutzig et

al., 2016). Traditionally, estimation of urban carbon

stocks relied on field measurements. However, this

method is highly subjective and laborious (Zhang et

al., 2015). Meanwhile, although high-resolution

satellite remote sensing images have significant

spectral characteristics and rich texture information,

they failed to provide data below the canopy and

neglected the vertical spatial structure differences of

vegetation, resulting in a lower accuracy in carbon

stock estimation.

The rise of LiDAR (Light Detection and Ranging)

technology has provided robust technical support for

fine carbon stock estimation. LiDAR is characterized

by its high resolution, strong penetrative ability, and

high efficiency, allowing for the convenient

acquisition of accurate three-dimensional structural

information of urban vegetation. Additionally,

https://orcid.org/0009-0000-5656-1649

LiDAR operates effectively under various

environmental conditions and offers high precision

and high-density data collection capabilities.

Since the majority of urban carbon storage comes

from trees. Therefore, the accuracy of carbon stock

estimation based on LiDAR largely depends on the

precision of tree segmentation (Mei and Durrieu,

2004). Current tree segmentation algorithms can be

primarily divided into two categories: tree

segmentation based on Canopy Height Model(CHM)

or point clouds.

For CHM-based tree segmentation, Hyyppä et al.

(2001) were the first to apply the region-growing

algorithm to the segmentation of LiDAR data in

Nordic coniferous forests. Mei & Durrieu (2004)

achieved a 90% accuracy using the watershed

algorithm for tall and regularly spaced trees, but faced

challenges of over-segmentation or under-

segmentation in complex and dense forests. Koch et

al. (2006) employed the flooding algorithm to

segment coniferous and deciduous forests in

Germany, achieving an accuracy of 61.7%. Chen et

al. (2006) proposed a marker-controlled watershed

tree segmentation algorithm, tested with an accuracy

of 64.1% in the savannas of California, USA.

Khosravipour et al. (2014) enhanced upon Chen et

al.'s algorithm by removing CHM pits through

Song, H.

Precise Estimation of Urban Vegetation Carbon Stock Using Multi-Source LiDAR: A Case Study of East China Normal University.

DOI: 10.5220/0013035300004601

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Innovations in Applied Mathematics, Physics and Astronomy (IAMPA 2024), pages 201-208

ISBN: 978-989-758-722-1

201

overlapping point cloud subsets, achieving a

segmentation accuracy of 74.2%. Besides, Kaartinen

et al. (2012) introduced two new methods: multi-scale

Gaussian Laplacian segmentation and CHM

minimum curvature segmentation. Overall, CHM-

based tree segmentation runs fast, although the

interpolation process and canopy cover of tall trees

can affect the results.

Tree segmentation algorithms based on point

clouds are more straightforward, avoiding potential

errors that may arise during CHM generation.

Nevertheless, these methods require substantial

computational resources and high-performance

hardware. Early studies such as Morsdof et al. (2004)

were the first to apply k-means clustering for tree

segmentation, demonstrating the feasibility of this

approach. Li et al. (2012) introduced a region-

growing algorithm combined with threshold

judgment, achieving an accuracy of 0.9 in California,

USA, but the segmentation accuracy of this algorithm

in deciduous forests was lower. Lu et al. (2014)

introduced a bottom-up region-growing algorithm

that marked trunk points and allocated distances

topologically, achieving a recall rate of 0.84 and an

accuracy of 0.97 in the deciduous forests of

Pennsylvania, USA. Lin et al. (2017) used circle

detection theory to extract individual tree locations,

heights, and diameters at breast height, achieving an

accuracy of over 90%. Aryey et al. (2017) developed

layer stacking algorithm that clusters point clouds at

1-meter intervals, performing better than traditional

algorithms in deciduous or leafless conditions. Paris

et al. (2016) explored a combined method using CHM

and point cloud space, accurately segmenting

dominant trees by analyzing horizontal and vertical

profiles of the point cloud, achieving an accuracy

exceeding 92%.

This study utilizes multi-source LiDAR data to

test and compare several commonly used tree

segmentation algorithms, with the aim of proposing a

comprehensive and reliable technical process for fine

estimation of urban vegetation carbon stock. The

results aim to serve as a guideline for future urban

planning and sustainable development endeavors.

This article is organized as follows: Section 2 will

show the materials and methods in this research,

Section 3 will display all the results and analysis, and

Section 4 will provide the discussion and conclusions.

2 MATERIALS AND METHODS

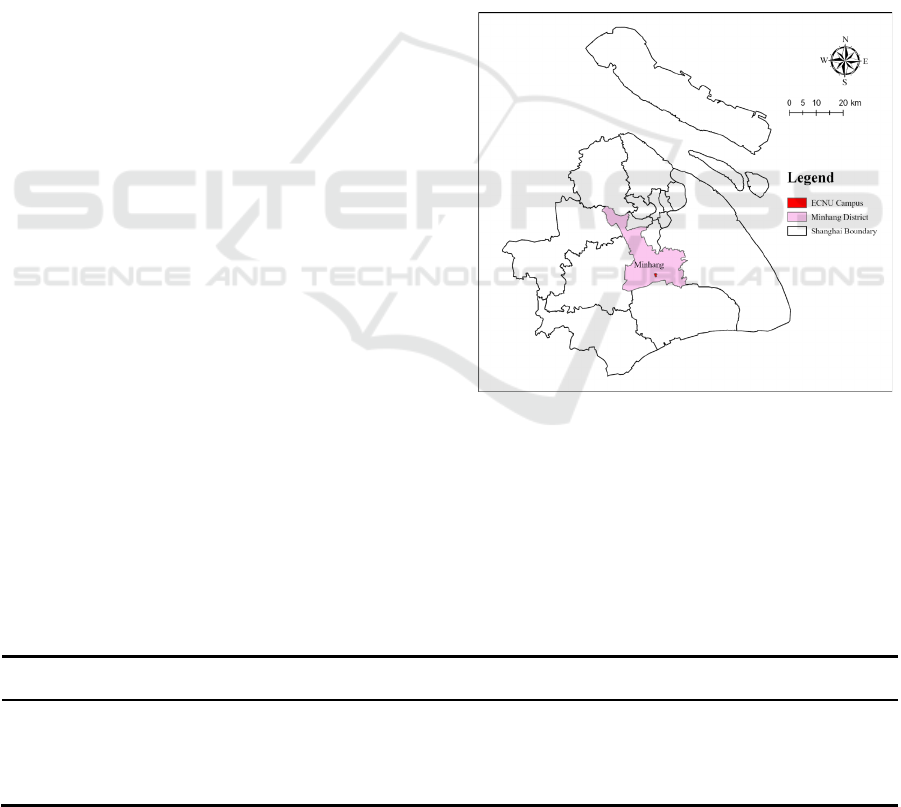
2.1 Study Area

Study area in this research is East China Normal

University (Minhang Campus), which is located on

No. 500 Dongchuan Rd., Minhang District, Shanghai,

China(Figure 1). Due to the large size of the study

area, the campus is divided into eight zones based on

the road, river, and vegetation characteristics. The

campus is rich in tree species, dominated by camphor,

bellflower, ginkgo, and luan. Also, it contains a

variety of deciduous small trees. In terms of shrubs,

they mainly composed of buxus sinica and

rhododendron.

Figure 1: Study area (Picture credit: Original)

2.2 Data Source

This study contains three parts of LiDAR data,

namely airborne, vehicle-mounted and backpack

LiDAR. The detailed information of each data type is

shown in Table 1 and data samples are shown in

Figure 2.

Table 1: Detailed information of different types of LiDAR data

Data Type

Acquisition

Device

Coordinate

System

Point

Density

File

Format

File

Size(G)

Range

Airborne

ECNU-ULS

UTM Zone 51N

Low

las

3.1

Entire campus

Vehicle-

mounted

ECNU-MLS UTM Zone 51N High las 13.7

Main roads

only

Backpack LiBackpack C50

Relative

coordinates

High ply 19.8 Entire campus

IAMPA 2024 - International Conference on Innovations in Applied Mathematics, Physics and Astronomy

202

(a) (b) (c)

Figure 2: Sample LiDAR data: (a) Airborne LiDAR

(entire campus area); (b) Vehicle- mounted

LiDAR(main roads only); (c) Backpack LiDAR(part

of Zone 5) (Picture credit: Original)

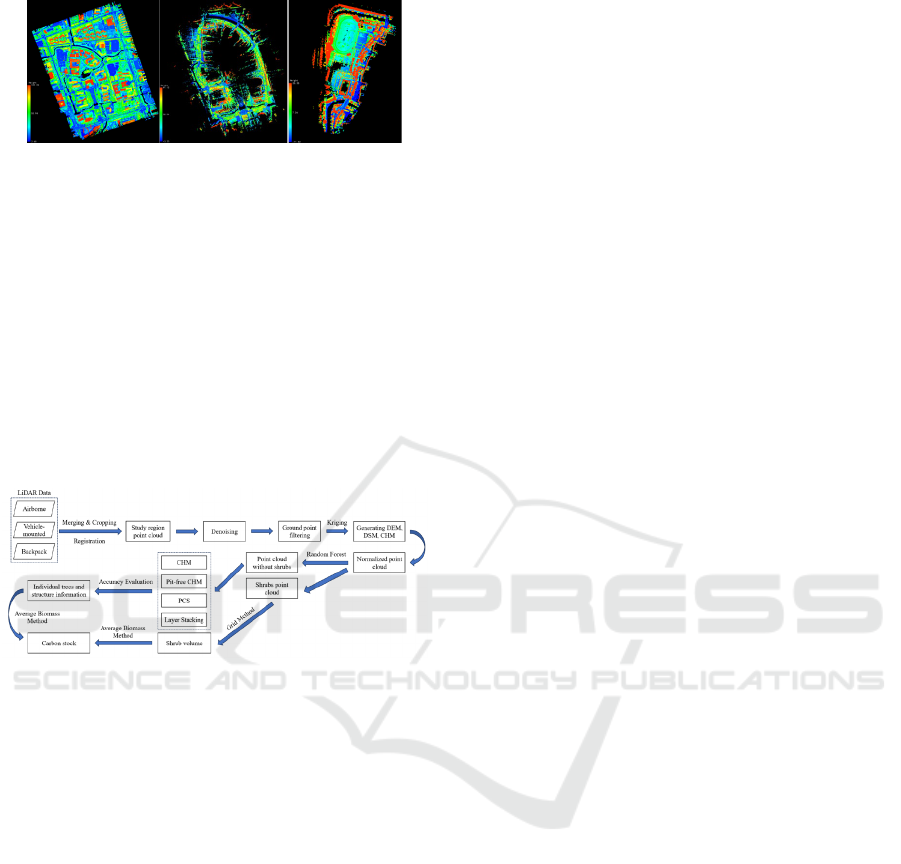
2.3 Technical Framework

The study harnesses multi-source LiDAR data and

proposes a reliable technical framework for fine

estimation of urban carbon stock. Four steps are

involved in the technical framework (Figure 3),

namely LiDAR data preprocessing, shrub extraction

and volume calculation, tree segmentation methods

and carbon stock calculation.

Figure 3: Techinical framework of the research

(Picture credit: Original)

2.4 LiDAR Data Preprocessing

The LiDAR data preprocessing includes: 1) Multi-

source data registration to UTM Zone 51N coordinate

system, 2) Data merging and cropping, 3) LiDAR

denoising, 4) Ground point filtering, 5) Kriging

interpolation to generate DEM, DSM and CHM with

the pixel size of 0.1m, 6)Point cloud normalization.

In this study, traditional automatic registration

methods(e.g. Iterative Closest Point) are less effective

due to the disparity in point density between aerial

LiDAR data and other two forms of data. Therefore,

in this study, a stepwise minimum spanning tree

matching algorithm based on quadrant search is

utilized for point cloud registration.

The algorithm primarily involves of three steps:

extraction of tree locations, quadrant search-based

minimum spanning tree matching, and registration.

As the airborne and vehicle-mounted LiDAR data

already had UTM coordinates, only the

transformation matrix from backpack LiDAR data to

UTM coordinates needs to be calculated. Firstly, the

tree location points collected from the three LiDAR

data are extracted, and then matched based on the

topological similarity of the minimum spanning tree

connected into a quadrant search, and matched by

stepwise search, finally realizing the fusion of the

LiDAR data collected by three different sensors.

2.5 Shrub Extraction and Volume

Calculation

Shrubs constitute a crucial component of urban

vegetation, playing an essential role in the calculation

of urban carbon stock. The extraction of shrubs from

the point cloud data was accomplished using the

random forest algorithm, integrated within the

LiDAR360 software. By manually selecting a small

number of representative shrub point clouds to train

the model and applying the model to the remaining

data, all shrubs in the point cloud can be obtained.

This approach substantially reduces the labor-

intensive and time-consuming nature of manual

selection.

The calculation of shrub volume uses the grid

method, which is conceptually similar to calculus.

Specifically, the process begins by projecting 3D

point cloud data onto a 2D plane Then, the 2D plane

is divided into small cells using a grid structure. The

tallest point in each grid is recorded, multiplying by

the grid cell size gives the volume of the shrub within

that cell. The overall volume of shrub is calculated by

adding the volumes of all the grid cells.

Therefore, the choice of grid size largely

determines the accuracy of the result volume. If the

grid is too small, many grid cells might fall into gaps

between point cloud data points, leading to an

underestimated volume, and vice versa. Thus, the

selection of grid size should primarily be based on

point density. Since shrubs in LiDAR data are

primarily detected by high-density backpack LiDAR

and vehicle-mounted LiDAR, a grid size of 0.1m is

chosen for this study.

2.6 Tree Segmentation Methods

This study evaluated and compared four common tree

segmentation methods: two region-based

segmentation methods using CHM and pit-free CHM,

region-growing and threshold judgment algorithm

(PCS), and Layer Stacking algorithm which both

directly based on point cloud.

1) CHM (Chen et al., 2006)

The Watershed Algorithm is used for CHM based

segmentation (Figure 4). It is mainly based on the

concept of immersion simulation. It first takes the

Precise Estimation of Urban Vegetation Carbon Stock Using Multi-Source LiDAR: A Case Study of East China Normal University

203

complement of the CHM, where each local minimum

represents a tree height point, and its influence area is

called a catchment basin (the extent of the tree crown).

At the junction of catchment basins, a dam is

constructed to form the watershed that segments the

tree crowns, thereby isolating individual trees.

Figure 4: Watershed Algorithm (Picture credit:

Original)

2) Pit-free CHM (Khosravipour et al., 2014)

However, black holes can form in the CHM as a

result of some laser pulses passing through the tree

crowns and reflecting back from the ground due to

LiDAR's great penetration into the canopy. This

phenomenon leads to an incomplete canopy surface

and is referred to as pits.

Khosravipour et al. (2014) introduced a technique

for generating pit-free CHM (Figure 5): First, an

initial CHM (CHM00) is established. The normalized

point cloud is then vertically stratified according to

the ASPRS point cloud classification standards: low

vegetation (0.5m < h ≤ 2.0m), medium vegetation

(2.0m < h ≤ 5.0m), and high vegetation (h > 5.0m).

For high vegetation, further stratification is done at 5-

meter intervals. This results in the construction of

CHMs for each layer (CHM02, CHM05, CHM10, ...).

Finally, the CHMs of all layers are stacked, with each

pixel in the result taking the maximum value of the

corresponding x, y pixel position from all the layers,

thereby generating a pit-free CHM and using the

Watershed Algorithm for tree segmentation.

Figure 5: Methods for generating Pit-free CHM

Picture credit: Khosravipour et al., 2014

3) PCS (Li et al., 2012)

PCS algorithm makes the assumption that the tree

apex is the local highest point in the LiDAR data. This

point is used as a seed for region growing through

iterative expansion. During each iteration, a threshold

is used to determine whether a point belongs to an

existing tree or represents a new tree apex. Points

farther from the existing tree than the threshold are

assigned to a new tree; points closer are categorized

under the existing tree.

4) Layer Stacking (Ayrey et al., 2017)

Main steps of the Layer Stacking Algorithm are

shown in Figure 6: (a) Vertically segment the point

cloud starting from 0.5 meters with a certain interval

(generally 1m) up to the highest point. (b) Applying

K-means clustering algorithm to each layer. (c)

Creating a 0.5m buffer polygon around each cluster.

(d) Overlaying polygons of each layers. (e)

Smoothing the overlap result using a window size of

1.5m. (f) Detecting the local maxima, which represent

the center of the tree.

Figure 6: Main steps of Layer Stacking algorithm

Picture credit: Ayrey et al., 2017

There are three types of segmentation results

(Figure 7): 1) True Positive (TP): The quantity of

properly segmented trees. 2) False Positive (FP): The

quantity of excessively segmented trees. 3) False

Negative (FN): The quantity of unsegmented trees

that are wrongly believed to be a component of other

trees. To evaluate the accuracy of various tree

segmentation methods on sample plots, the study

used the following formulas to compute recall(r),

precision(p), and F-score(F).

Figure 7: Three different types of segmentation

results: (a) TP, (b) FP, (c) FN

Picture credit: Original

IAMPA 2024 - International Conference on Innovations in Applied Mathematics, Physics and Astronomy

204

 =





(1)

 =





(2)

 = 2 ×

×



(3)

2.7 Carbon Stock Calculation

After the tree segmentation process is finished,

LiDAR360 may use the segmentation data to

automatically determine each tree's diameter at breast

height (DBH), crown width, tree height, and crown

volume.

Carbon stock was calculated using the average

biomass method of the sample plot inventory method,

which is suitable for small to medium-scale plant

biomass calculation in this study. Meanwhile, the

anisotropic biomass growth equation is crucial for the

measurement of carbon stock in trees. In order to

guarantee the scientific validity of the carbon stock

findings, the study selected common tree species in

the campus, and constructed the biomass model of

each tree species according to the local and adjacent

areas of Shanghai. The carbon content coefficient was

selected based on the average carbon content

coefficient for forest trees, which is 0.5, as published

by the IPCC. Finally, the following formulas were

derived for calculating carbon stock in an individual

tree (Zhong et al, 2019).

Soft broadleaf trees:

 = 0.01901

.

(4)

Hard broadleaf trees:

 = 0.10387

.

(5)

Coniferous:

 = 0.01639

.



.

0.06539

.



.

(6)

Carbon stock of trees:

 = 

(7)

In the formula, C, W, D, H, α respectively

represent the carbon stock of trees, biomass, DBH,

tree height and carbon content coefficient (0.5).

For the calculation of shrub carbon stock,

considering that the distribution of shrubs on the

campus is heterogeneous and difficult to distinguish,

this study referenced the optimal models from

previous research on the relationship between canopy

volume and annual branch biomass of different

shrubs in Shanghai. The study chose the common

shrubs on the campus (Buxus sinica and

Rhododendron) as the representative shrubs and

averaged their carbon stock models to calculate the

carbon stock of all shrubs on the campus (Fang, 2013).

Shrubs:

 =



.×

.

.×

.



 × 0.5

(8)

Carbon stock of shrubs:

 = 

(9)

In the formula, C, W, V, α respectively represent

the carbon stock of shrubs, biomass, shrub volume

and carbon content coefficient (0.5).

3 RESULTS

3.1 Selecting the Best Tree

Segmentation Method

A total of six sample plots (four broadleaf and two

coniferous) were selected in this research to evaluate

the four segmentation methods’ accuracy, and the

results are shown in Table 2.

Table 2: Accuracy evaluation results of different segmentation algorithms (Picture credit: Original)

Sample plot

Segmentation

algorithm

Actual

trees

Segment

Trees

TP FN FP r p F

Broadleaf

Layer stacking

.825

.788

.805

PCS

.675

.540

.600

CHM

.550

.423

.478

Pit-free CHM

.775

.660

.713

Broadleaf

Layer stacking

.741

.811

.775

PCS

.672

.591

.629

CHM

.569

Pit-free CHM

.672

.765

.716

Broadleaf

Layer stacking

.800

.780

.790

PCS

.500

.588

.541

CHM

.625

.581

.602

Pit-free CHM

.700

.683

.691

Precise Estimation of Urban Vegetation Carbon Stock Using Multi-Source LiDAR: A Case Study of East China Normal University

205

Broadleaf

Layer stacking

.787

.814

.800

PCS

.672

.683

.678

CHM

.541

.465

.500

Pit-free CHM

.623

.594

.608

Coniferous

Layer stacking

100

.880

.926

.903

PCS

.329

.434

.374

CHM

113

.840

.743

.789

Pit-free CHM

101

.910

.901

.905

Coniferous

Layer stacking

.889

.928

.908

PCS

.403

.725

CHM

.861

.729

Pit-free CHM

.917

.892

Sample plots 1-4 are broadleaf forest plots. Due

to the uncertainty and complexity of the canopy

morphology of broadleaf tree, the highest overall

accuracy was only 80.5%. According to the F-score

results from different segmentation methods, layer

stacking can achieve around 80% accuracy even

when facing the challenges of varied morphology,

multiple branches, and numerous vertices of

broadleaf tree species. This method provides the best

overall segmentation performance, followed by pit-

free CHM, PCS, and CHM.

Sample plots 5-6 are dense coniferous forest

samples on the southeast side of the campus.

Compared to broadleaf plots, the morphological

differences in coniferous tree species are smaller,

allowing for a maximum overall accuracy of up to

90.8%. Based on the F-score results from different

segmentation methods, both layer stacking and pit-

free CHM provided the best segmentation

performance, each achieving over 90% accuracy.

However, in the densely populated coniferous forest

areas of the campus, the PCS algorithm performed the

poorest with an accuracy of only 37.4%. This is

because the distance threshold =1.5, which is

relatively more suitable for broadleaf plots, failed to

segment the closely spaced coniferous trees, resulting

in very poor segmentation results.

Therefore, in the tree segmentation task for urban

trees, the layer stacking algorithm should be

prioritized in areas with diverse and unstable tree

morphology, such as broadleaf areas or mixed

broadleaf-coniferous areas. In areas with stable tree

morphologies, such as coniferous areas, the faster pit-

free CHM segmentation method should be preferred.

3.2 Number of Trees Segmented and

Shrub Volume in Each Zone

Since the campus is dominated by broadleaf trees,

layer stacking method was chosen for tree

segmentation. The results of the number of trees and

shrub volume obtained in each area of the campus are

shown in Table 3.

Table 3: Number of tree segmented and shrub

volume in each zone (Picture credit: Original)

Zone ID Segment Trees Shrub Volume(m

)

1 741 2861.840

2 1921 2866.460

3 1283 6910.606

4 1092 6602.009

5 1336 6539.478

6 711 4881.820

7 748 4355.723

8 600 2953.506

3.3 Carbon Stock Calculation and

Analysis

After substituting the shrub volume and the

morphological parameters of each tree into the carbon

stock equation, the carbon stock results for each area

can be calculated and shown in Table 4.

Table 4: Summary of carbon stock (Picture credit:

Original)

Zone

Total carbon

stock(kg)

Tree carbon

stock(kg)

Shrub

carbon

t k(k )

1 256138.422 256130.744 7.678

2 83378.314 83370.632 7.682

3 446909.511 446893.057 16.454

4 377898.048 377877.747 20.301

5 735757.340 735746.870 10.470

IAMPA 2024 - International Conference on Innovations in Applied Mathematics, Physics and Astronomy

206

6 239094.774 239085.395 9.379

7 259546.127 259537.141 8.986

8 278720.130 278712.361 7.769

Total 2677442.666 2677353.950 88.719

To analyze the spatial distribution of carbon stock

within the campus, the study drew a carbon stock map

under the 50m×50m grid (Figure 8(a)) and the map of

carbon stock density in different zones (Figure 8(b)).

There are significant differences in the size and

density of carbon storage across various campus areas.

Generally, the carbon stock is smaller in areas with

dense buildings and open areas (e.g. playgrounds),

and the larger carbon stock is mainly in areas where

trees are concentrated (e.g. both sides of the main

road and the green spaces).

Figure 8: (a) Carbon stock map under 50m×50m

Grid, (b) Carbon stock density in different zones

Picture credit: Original

4 CONCLUSION

This study establishes a comprehensive and reliable

technical framework for the fine estimation of urban

vegetation carbon stock by utilizing multi-source

LiDAR data. This framework includes following

steps: This framework includes: LiDAR data

preprocessing, shrub extraction and volume

calculation, tree segmentation, and carbon stock

calculation. Specifically, after data preprocessing, the

study first uses a random forest model to extract

shrubs from the point cloud and employs a grid

method to calculate their volume. Subsequently, by

comparing four different tree segmentation

algorithms across six sample plots, the layer stacking

algorithm, which demonstrates superior accuracy and

stability in both coniferous and broad-leaved forests,

is selected for tree segmentation in the study region.

After obtaining the morphological parameters of

individual trees, the study builds biomass models

suitable for the vegetation in the study area using the

average biomass method, and calculates the final

carbon storage to be 2,677,442.666 kg.

The technical framework proposed in this study is

universally applicable to the accurate estimation of

urban vegetation carbon stock. Additionally, due to

the rich semantic information contained in LiDAR

data, the research data (such as the morphological

parameters of individual trees) can be widely applied

to other forestry applications. This provides technical

and data support for helping achieve dual carbon

goals and formulate related policies.

However, this study also has certain limitations.

The formulae used to calculate carbon stocks for

different species of trees may vary, and the study's

lack of species differentiation may have contributed

to some degree of error in the carbon stock conclusion.

Future research could consider incorporating street

view images or high-resolution remote sensing

images for tree species identification, thus building

biomass models for different species and further

refining the precision of carbon stock calculations.

REFERENCES

Ayrey, E., Fraver, S., Kershaw Jr, J. A., Kenefic, L. S.,

Hayes, D., Weiskittel, A. R., & Roth, B. E. (2017).

Layer stacking: A novel algorithm for individual forest

tree segmentation from LiDAR point clouds. Canadian

Journal of Remote Sensing, 43(1), 16-27.

Chen, Q. , Baldocchi, D. , Gong, P. , & Kelly, M. (2006).

Isolating individual trees in a savanna woodland using

small footprint lidar data. Photogrammetric

Engineering and Remote Sensing, 72(8), 923-932.

Creutzig, F., Agoston, P., Minx, J. C., Canadell, J. G.,

Andrew, R. M., Le Quéré, C., Peters, G. P., Sharifi, A.,

Yamagata, Y., & Dhakal, S. (2016). Urban

infrastructure choices structure climate solutions.

Nature Climate Change, 6(12), 1054-1056.

Fang, Y. H. (2013). Carbon sequestration and its

relationship with leaf functional traits: a study of 25

greening shrubs in Shanghai. Master’s thesis, East

China Normal University.

Kaartinen, H., Hyyppä, J., Yu, X. W., Vastaranta, M.,

Hyyppä, H., Kukko, A., Holopainen, M., Heipke, C.,

Hirschmugl, M., Morsdorf, F., Næsset, E., Pitkänen, J.,

Popescu, S., Solberg, S., Wolf, B. M., & Wu, J. C.

(2012). An International Comparison of Individual Tree

Detection and Extraction Using Airborne Laser

Scanning. Remote Sensing, 4(4), 950-974.

Khosravipour, A., Skidmore, A. K., Isenburg, M., Wang, T.,

& Hussin, Y. A. (2014). Generating pit-free canopy

height models from airborne lidar. Photogrammetric

Engineering and Remote Sensing, 80(9), 863-872.

Koch, B., Heyder, U., & Weinacker, H. (2006). Detection

of individual tree crowns in airborne lidar data.

Precise Estimation of Urban Vegetation Carbon Stock Using Multi-Source LiDAR: A Case Study of East China Normal University

207

Photogrammetric Engineering and Remote Sensing,

72(4), 357-363.

Hyyppä, J., Kelle, O., Lehikoinen, M., & Inkinen, M.

(2001). A segmentation-based method to retrieve stem

volume estimates from 3-D tree height models

produced by laser scanners. IEEE TRANSACTIONS ON

GEOSCIENCE AND REMOTE SENSING, 39(5), 969-

975.

Li, W., Guo, Q., Jakubowski, M.K., & Kelly, M. (2012). A

New Method for Segmenting Individual Trees from the

Lidar Point Cloud. Photogrammetric Engineering and

Remote Sensing, 78, 75-84.

Lin, Y., Ji, H. W., & Ye, Q. (2017). Research on method of

extracting single tree characteristics from LiDAR point.

Computer Measurement & Control, 25(06), 142-147.

Lu, X. C., Guo, Q. H., Li, W. K., & Flanagan, J. (2014). A

bottom-up approach to segment individual deciduous

trees using leaf-off lidar point cloud data. ISPRS

Journal of Photogrammetry and Remote Sensing, 94, 1-

12.

Mei, C., & Durrieu, S. (2004). Tree crown delineation from

digital elevation models and high resolution imagery.

International Archives of Photogrammetry, Remote

Sensing and Spatial Information Sciences, 36.

Morsdorf, F., Meier, E., Kötz, B., Itten, K. I., Dobbertin, M.,

& Allgöwer, B. (2004). LIDAR-based geometric

reconstruction of boreal type forest stands at single tree

level for forest and wildland fire management. Remote

Sensing of Environment, 92(3), 353-362.

Paris, C., Valduga, D., & Bruzzone, L. (2016). A

Hierarchical Approach to Three-Dimensional

Segmentation of LiDAR Data at Single-Tree Level in a

Multilayered Forest. IEEE TRANSACTIONS ON

GEOSCIENCE AND REMOTE SENSING, 54(7), 4190-

4203.

Zhang, C. Y., Zhou, Y. H., & Qiu, F. (2015). Individual

Tree Segmentation from LiDAR Point Clouds for

Urban Forest Inventory. Remote Sensing, 7(6), 7892-

7913.

Zhong, Q. C., Fu, Y.,& Zhang, G. L. (2019). Biomass

estimation and a dynamic analysis of forests in

Shanghai. Journal of Zhejiang A & F University, 36(03),

524-532.

IAMPA 2024 - International Conference on Innovations in Applied Mathematics, Physics and Astronomy

208