Optimizing Genetic Algorithms Using the Binomial Distribution

Vincent A. Cicirello

Computer Science, School of Business, Stockton University, 101 Vera King Farris Dr, Galloway, NJ, U.S.A.

Keywords:

Bernoulli Trials, Binomial Random Variable, Genetic Algorithm, Mutation, Uniform Crossover.

Abstract:

Evolutionary algorithms rely very heavily on randomized behavior. Execution speed, therefore, depends

strongly on how we implement randomness, such as our choice of pseudorandom number generator, or the

algorithms used to map pseudorandom values to speciﬁc intervals or distributions. In this paper, we observe

that the standard bit-ﬂip mutation of a genetic algorithm (GA), uniform crossover, and the GA control loop

that determines which pairs of parents to cross are all in essence binomial experiments. We then show how

to optimize each of these by utilizing a binomial distribution and sampling algorithms to dramatically speed

the runtime of a GA relative to the common implementation. We implement our approach in the open-source

Java library Chips-n-Salsa. Our experiments validate that the approach is orders of magnitude faster than the

common GA implementation, yet produces solutions that are statistically equivalent in solution quality.

1 INTRODUCTION

The simulated evolutionary processes of genetic algo-

rithms (GA), and other evolutionary algorithms (EA),

are stochastic and rely heavily on randomized behav-

ior. Mutation in a GA involves randomly ﬂipping bits.

Cross points in single-point, two-point, and k-point

crossover are chosen randomly. Uniform crossover

uses a process similar to mutation to randomly choose

which bits to exchange between parents. The decision

of whether to cross a pair of parents during a genera-

tion is random. Selection operators usually randomize

the selection of the population members that survive.

Random behavior pervades the EA. Thus, how

randomness is implemented signiﬁcantly impacts per-

formance. Many have explored the effects of the

pseudorandom number generator (PRNG) on solution

quality (Krömer et al., 2018; Rajashekharan and Ve-

layutham, 2016; Krömer et al., 2013; Tirronen et al.,

2011; Reese, 2009; Wiese et al., 2005a; Wiese et al.,

2005b; Cantú-Paz, 2002), and others the effects of

PRNG on execution times (Cicirello, 2018; Nesmach-

now et al., 2015). Choice of PRNG isn’t the only

way to optimize an EA’s random behavior. Our open

source Java library Chips-n-Salsa (Cicirello, 2020)

optimizes randomness of its EAs and metaheuristics

beyond the PRNG, such as in the choice of algorithms

for Gaussian random numbers and random integers in

an interval. Section 2 further discusses related work.

https://orcid.org/0000-0003-1072-8559

This paper focuses on optimizing the randomness

of bit-ﬂip mutation, uniform crossover, and the deter-

mination of which pairs of parents to cross. Formally,

all three of these are binomial experiments, with the

relevant GA control parameters serving as the success

probabilities for a sequence of Bernoulli trials. This

leads to our approach (Section 3) to each that replaces

explicit iteration over bits or the population with a bi-

nomial distributed random variable and an efﬁcient

sampling algorithm.

Others, such as Ye et al, previously observed that

the number of bits mutated by the standard bit-ﬂip

mutation follows a binomial distribution (Ye et al.,

2019). However, examining the source code of their

implementation (Ye, 2023) reveals that they gener-

ate binomial random variates by explicitly iterating

n times for a bit-vector of length n, generating a total

of n uniform variates in the process. Their approach

refactored where the explicit iteration occurs, but did

not eliminate it. Ye et al were not trying to optimize

the runtime of the traditional GA. Rather, their reason

for abstracting the mutated bit count was to enable ex-

ploring alternative mutation operators, such as their

normalized bit mutation (Ye et al., 2019) in which the

number of mutated bits follows a normal distribution

rather than a binomial.

In our approach, presented in detail in Section 3,

we eliminate the O(n) uniform random values gen-

erated during explicit iteration over bits. Instead,

we use an efﬁcient algorithm for generating binomial

Cicirello, V.

Optimizing Genetic Algorithms Using the Binomial Distribution.

DOI: 10.5220/0013038300003837

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 159-169

ISBN: 978-989-758-721-4; ISSN: 2184-3236

159

random variates (Kachitvichyanukul and Schmeiser,

1988) that requires only O(1) random numbers on av-

erage. Additionally, we use a more efﬁcient sampling

algorithm for choosing which bits to mutate. Ours is

the ﬁrst approach to use the binomial distribution in

this way to optimize the runtime of bit-ﬂip mutation.

Furthermore, we also apply the technique to optimize

uniform crossover as well as the process of selecting

which pairs of parents to cross.

Our experiments (Section 4) demonstrate the mas-

sive gains in execution speed that result from this ap-

proach. We will see that the optimized bit-ﬂip mu-

tation uses 70%-99% less time than the common im-

plementation. The optimized uniform crossover uses

61%-99% less time than the common implementa-

tion. A GA using the optimized decision of which

parents to cross, as well as the optimized operators,

uses 78%-97% less time than the common implemen-

tation. We implemented the approach in the open

source library Chips-n-Salsa (Cicirello, 2020) and re-

leased the code of the experiments as open source to

enable easily replicating the results. We wrap up with

a discussion in Section 5.

2 RELATED WORK

Several have shown that higher quality PRNGs that

pass more rigorous randomness tests do not lead to

better ﬁtness, and that solution quality is insensitive

to PRNG (Rajashekharan and Velayutham, 2016; Tir-

ronen et al., 2011; Wiese et al., 2005a; Wiese et al.,

2005b; Cantú-Paz, 2002). For example, the ablation

study of Cantú-Paz shows that the PRNG used for se-

lection, crossover, and mutation does not affect ﬁt-

ness, and that even using true random numbers does

not improve ﬁtness (Cantú-Paz, 2002). Thus, choice

of PRNG has little, if any, impact on solution ﬁtness.

Fewer have studied the impact of the PRNG on

execution times, but the research that exists shows po-

tential for massive efﬁciency gains. Nesmachnow et

al analyzed the effects of several implementation fac-

tors on the runtime of EAs implemented in C (Nes-

machnow et al., 2015). They showed 50%-60% im-

provement in execution times by using state-of-the-art

PRNGs such as R250 (Kirkpatrick and Stoll, 1981) or

Mersenne Twister (Matsumoto and Nishimura, 1998)

rather than the C library’s rand() function. Cicirello

showed that an adaptive permutation EA is 25%

faster (Cicirello, 2018) when using the PRNG Split-

Mix (Steele et al., 2014) rather than the classic lin-

ear congruential (Knuth, 1998), and by implementing

Gaussian mutation (Hinterding, 1995) with the zig-

gurat algorithm (Marsaglia and Tsang, 2000; Leong

Table 1: Notation shared across algorithm pseudocode.

B(n, p) binomial distributed random integer

FlipBit(v, i) ﬂips bit i of vector v

Length(v) simple accessor for length of v

Rand(a, b) random real in [a,b)

Rand(a) random integer in [0,a)

Sample(n, k) sample k distinct integers from

{0,1, ...,n −1}

⊕,∧,∨,¬ bitwise XOR, AND, OR, and NOT

et al., 2005) rather than the polar method (Knuth,

1998). There are also studies on the impact of PRNG

and related algorithmic components on the runtime

performance of randomized systems other than EAs,

such as Metropolis algorithms (Macias-Medri et al.,

2023). Others explored the effects of programming

language choice on GA runtime (Merelo-Guervós

et al., 2017; Merelo-Guervós et al., 2016).

The EAs of Chips-n-Salsa (Cicirello, 2020) op-

timize randomness in ways beyond the choice of

PRNG. For example, Chips-n-Salsa uses the algo-

rithm of Lemire for random integers in an inter-

val (Lemire, 2019) as implemented in the open source

library ρµ (Cicirello, 2022b), which is more than

twice as fast as Java’s built-in method due to a sig-

niﬁcantly faster approach to rejection sampling. Such

bounded random integers are used by EAs in a vari-

ety of ways, such as the random cross sites for single-

point, two-point, and k-point crossover.

3 APPROACH

We now present the details of our approach. In Sec-

tion 3.1, we formalize the relationship between differ-

ent processes within a GA and binomial experiments.

In Section 3.2, we describe our approach to random

sampling. We derive our optimizations of random bit-

mask generation, mutation, and uniform crossover in

Sections 3.3, 3.4, and 3.5, respectively. We show how

to optimize the process of determining which pairs of

parents to cross, as well as putting all of the optimiza-

tions together in Section 3.6.

Table 1 summarizes the notation and functions

shared by the pseudocode of the algorithms through-

out this section. We assume that indexes into bit-

vectors begin at 0. The runtime of FlipBit(v, i),

Length(v), and Rand(a, b) is O(1). The runtime of

the bitwise operators is O(n) for vectors of length n.

Our bit-vector implementation utilizes an array of 32-

bit integers, enabling exploiting implicit parallelism,

such as for bitwise operations (e.g., a bitwise opera-

tion on two bit-vectors of length n requires

bitwise

operations on 32-bit integers).

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

160

3.1 Binomial Variates and the GA

A Bernoulli trial is an experiment with two possi-

ble outcomes, usually success and failure, and speci-

ﬁed by success probability p. A binomial experiment

is a sequence of n independent Bernoulli trials with

identical p (Larson, 1982). The binomial distribution

B(n, p) is the discrete probability distribution of the

number of successes in an n-trial binomial experiment

with parameter p.

Our approach observes that GA mutation of a bit

vector of length n is a binomial experiment with n tri-

als, but the possible outcomes of each trial are “ﬂip-

bit” and “keep-bit” instead of success and failure. The

number of bits ﬂipped while mutating a bit vector of

length n must therefore follow binomial distribution

B(n, p

), where p

is the mutation rate. Uniform

crossover of a pair of bit vectors of length n is also

a binomial experiment with n trials, with the num-

ber of bits exchanged between parents following bino-

mial distribution B(n, p

), where p

is the probability

of exchanging a bit between the parents. Choosing

which pairs of parents to cross is likewise a binomial

experiment with n/2 trials for population size n, and

the number of crosses during a generation follows bi-

nomial distribution B(n/2, p

) for crossover rate p

We generate binomial random variates B(n, p)

with the BTPE algorithm (Kachitvichyanukul and

Schmeiser, 1988), whose runtime is O(1) (Cicirello,

2024b). This algorithm choice is critical to later anal-

ysis, as many alternatives do not have a constant run-

time (Kuhl, 2017; Knuth, 1998).

3.2 Sampling

To sample k distinct integers from the set

{0,1, ...,n − 1}, we implement Sample(n, k)

using a combination of reservoir sampling (Vitter,

1985), pool sampling (Goodman and Hedetniemi,

1977), and insertion sampling (Cicirello, 2022a),

choosing the most efﬁcient based on k relative to n.

1 function Sample(n, k)

2 if k ≥

then

3 return ReservoirSample(n, k)

4 end

5 if k ≥

√

n then

6 return PoolSample(n, k)

7 end

8 return InsertionSample(n, k)

9 end

Algorithm 1: Random sampling.

Algorithms 1 and 2 provide pseudocode of the

details. See the original publications of the three sam-

1 function ReservoirSample(n, k)

2 s ← an array of length k

3 for i = 0 to k −1 do

4 s[i] ← i

5 end

6 for i = k to n −1 do

7 j ← Rand(i + 1)

8 if j < k then

9 s[ j] ← i

10 end

11 end

12 return s

13 end

15 function PoolSample(n, k)

16 s ← an array of length k

17 t ← an array of length n

18 for i = 0 to n −1 do

19 t[i] ← i

20 end

21 m ← n

22 for i = 0 to k −1 do

23 j ← Rand(m)

24 s[i] ←t[ j]

25 m ← m −1

26 t[ j] ← t[m]

27 end

28 return s

29 end

31 function InsertionSample(n, k)

32 s ← an array of length k

33 for i = 0 to k −1 do

34 v ← Rand(n −i)

35 j ← k −i

36 while j < k and v ≥s[ j] do

37 v ← v + 1

38 s[ j −1] ← s[ j]

39 j ← j + 1

40 end

41 s[ j −1] ← v

42 end

43 return s

44 end

Algorithm 2: Random sampling component algorithms.

pling algorithms for explanations for why each works.

Our composition (Algorithm 1) chooses from among

the three sampling algorithms (Algorithm 2) the one

that requires the least random number generation for

the given n and k. The runtime of reservoir sampling

and pool sampling is O(n), while the runtime of in-

sertion sampling is O(k

). Pool sampling and inser-

tion sampling each generate k random integers, while

Optimizing Genetic Algorithms Using the Binomial Distribution

161

reservoir sampling requires (n −k) random integers.

The runtime of the composite of these algorithms is

O(min(n,k

)), and requires min(k,n −k) random in-

tegers (Cicirello, 2022a). Minimizing random num-

ber generation is perhaps even more important than

runtime complexity, because although it is a constant

time operation, random number generation is costly.

3.3 Optimizing Random Bitmasks

Our algorithms for mutation and crossover rely on

random bitmasks of length n for probability p that

a bit is a 1. Algorithm 3 compares pseudocode

for the simple approach and the optimized binomial

approach. The runtime (worst, average, and best

cases) of the simple approach, SimpleBitmask(n,

p), is O(n). The runtime of the optimized version,

OptimizedBitmask(n, p), is likewise O(n), but the

only O(n) step initializes an all zero bit-vector in

line 12. Most of the cost savings is due to requiring

only O(n ·min(p,1 − p)) random numbers on aver-

age (the call to Sample() on line 14), compared to

SimpleBitmask(n, p), which always requires n ran-

dom numbers. When p is small, such as for mutation

where p is the mutation rate p

, the cost savings from

minimizing random number generation is especially

advantageous as we will see in the experiments.

1 function SimpleBitmask(n, p)

2 v ← an all 0 bit-vector of length n

3 for i = 0 to n −1 do

4 if Rand(0.0, 1.0) < p then

5 FlipBit(v, i)

6 end

7 end

8 return v

9 end

11 function OptimizedBitmask(n, p)

12 v ← an all 0 bit-vector of length n

13 k ←B(n, p)

14 indexes ← Sample(n, k)

15 for i ∈indexes do

16 FlipBit(v, i)

17 end

18 return v

19 end

Algorithm 3: Simple vs optimized bitmask creation.

Not shown in Algorithm 3 for presentation clar-

ity, our implementation of OptimizedBitmask(n, p)

treats p = 0.5 as a special case by generating 32 ran-

dom bits at a time with uniformly distributed random

32-bit integers. The OptimizedBitmask(n, p), as

presented in Algorithm 3, requires

random bounded

integers when p = 0.5, while this special case treat-

ment reduces this to

random integers.

3.4 Optimizing Mutation

Algorithm 4 compares the common approach to muta-

tion and our optimized approach. The p

is mutation

rate. Since the simple approach, SimpleMutation(v,

), iterates over all n bits, generating one random

number for each, its runtime is O(n). The runtime of

OptimizedMutation(v, p

) is likewise O(n) due to

the ⊕ of vectors of length n, and the initialization of

an all zero vector of length n. It is possible to elimi-

nate these O(n) steps with explicit iteration over only

the mutated bits instead of using a bitmask. However,

these steps are relatively inexpensive given the im-

plicit parallelism associated with utilizing 32-bit in-

tegers (e.g., bit operations on 32 bits at a time). The

real time savings comes from reducing random num-

ber generation, where OptimizedMutation(v, p

)

requires only O(n ·min(p

,1 − p

)) random num-

bers on average via the call to OptimizedBitmask(n,

) in line 12, while SimpleMutation(v, p

) re-

quires n. Since the mutation rate p

is generally

quite small, OptimizedMutation(v, p

) eliminates

nearly all random number generation.

1 function SimpleMutation(v, p

)

2 n ← Length(v) ;

3 for i = 0 to n −1 do

4 if Rand(0.0, 1.0) < p

then

5 FlipBit(v, i)

6 end

7 end

8 end

9 ;

10 function OptimizedMutation(v, p

)

11 n ← Length(v) ;

12 bitmask ← OptimizedBitmask(n, p

) ;

13 v ← v ⊕bitmask

14 end

Algorithm 4: Simple vs optimized mutation.

3.5 Optimizing Uniform Crossover

Algorithm 5 compares the simple uniform crossover,

determining the bits to exchange with iteration, ver-

sus our optimized version using our binomial trick.

The p

is uniform crossover’s parameter for the

per-bit probability of bit exchange. Both versions

are identical aside from how they generate a ran-

dom bitmask. The runtime of both is O(n) due

to the bitwise operations. The time savings for

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

162

OptimizedCrossover(v

, v

, p

) derives from op-

timizing bitmask creation in line 11, leading the opti-

mized uniform crossover to require O(n ·min(p

,1 −

)) random numbers, rather than the O(n) random

numbers required by the simple approach. For ex-

ample, if p

= 0.33 or p

= 0.67, then the optimiza-

tion requires only a third of the random numbers that

would be needed if explicit bit iteration was used.

1 function SimpleCrossover(v

, v

, p

)

2 n ← Length(v

)

3 bitmask ← SimpleBitmask(n, p

)

4 temp ← (v

∧bitmask) ∨(v

∧¬bitmask)

5 v

← (v

∧bitmask) ∨(v

∧¬bitmask)

6 v

← temp

7 end

9 function OptimizedCrossover(v

, v

, p

)

10 n ← Length(v

)

11 bitmask ← OptimizedBitmask(n, p

)

12 temp ← (v

∧bitmask) ∨(v

∧¬bitmask)

13 v

← (v

∧bitmask) ∨(v

∧¬bitmask)

14 v

← temp

15 end

Algorithm 5: Simple vs optimized uniform crossover

3.6 Optimizing a Generation

Algorithm 6 compares a simple implementation

of a generation with an optimized version. The

SimpleGeneration() explicitly iterates over the

pairs of possible parents (lines 4–9), gener-

ating a uniform random variate for each to de-

termine which parents produce offspring. The

OptimizedGeneration() generates a single bino-

mial random variate from B(⌊

⌋, p

), where p

is the

crossover rate, to determine the number of crossover

applications (line 18), and then iterates without need

for additional random numbers (lines 19–21).

Although the BTPE algorithm (Ka-

chitvichyanukul and Schmeiser, 1988) that we

use to generate binomial random variates utilizes re-

jection sampling (Flury, 1990), the average number of

rejection sampling iterations is constant, and thus the

average number of uniform variates needed by BTPE

to generate a binomial is also constant (Cicirello,

2024b). While SimpleGeneration() requires O(

)

uniform random variates, OptimizedGeneration()

requires only O(1) random numbers.

The OptimizedMutation() leads to additional

speed advantage. The pseudocode uses a generic

Crossover() operation rather than assuming any

speciﬁc operator. In the experiments, we consider

both uniform crossover, which we optimize, as well

as single-point and two-point crossover, which don’t

1 function SimpleGeneration(pop, p

, p

)

2 n ← Length(pop)

3 pop ← Selection(pop)

/* assume new population pop in

random order */

4 pairs ← ⌊

⌋

5 for i = 0 to pairs −1 do

6 if Rand(0.0, 1.0) < p

then

7 Crossover(pop

, pop

i+pairs

)

8 end

9 end

10 for i = 0 to n −1 do

11 SimpleMutation(pop

, p

)

12 end

13 end

15 function OptimizedGeneration(pop, p

)

16 n ← Length(pop)

17 pop ← Selection(pop)

/* assume new population pop in

random order */

18 pairs ← B(⌊

⌋, p

)

19 for i = 0 to pairs −1 do

20 Crossover(pop

, pop

i+pairs

)

21 end

22 for i = 0 to n −1 do

23 OptimizedMutation(pop

, p

)

24 end

25 end

Algorithm 6: Simple vs optimized generation.

have corresponding binomial optimizations. The

cross points of our single-point and two-point

crossover operators are selected using a more efﬁ-

cient algorithm for bounded random integers (Lemire,

2019) than Java’s built-in method; and the pair of in-

dexes for two-point crossover are sampled using a

specially designed algorithm for small random sam-

ples (Cicirello, 2024a) that is signiﬁcantly faster than

general purpose sampling algorithms such as those

utilized earlier in Section 3.2. However, the experi-

ments in this paper that use single-point and two-point

crossover use these same optimizations for both the

simple and optimized experimental conditions.

4 EXPERIMENTS

We run the experiments on a Windows 10 PC with

an AMD A10-5700, 3.4 GHz processor and 8GB

memory, and we use OpenJDK 64-Bit Server VM

version 17.0.2. We implemented the optimized bit-

ﬂip mutation, uniform crossover, and generation loop

Optimizing Genetic Algorithms Using the Binomial Distribution

163

Table 2: URLs for Chips-n-Salsa and experiments.

Chips-n-Salsa library

Source https://github.com/cicirello/Chips-n-Salsa

Website https://chips-n-salsa.cicirello.org/

Maven https://central.sonatype.com/artifact/org.

cicirello/chips-n-salsa

Experiments

Source https://github.com/cicirello/

optimize-ga-operators

Table 3: CPU time for 10

mutations for n = 1024.

CPU time (seconds) % less t-test

simple optimized time p-value

1/1024 0.856 0.00906 98.9% ∼ 0.0

1/512 0.857 0.0119 98.6% ∼ 0.0

1/256 0.860 0.0173 98.0% ∼ 0.0

1/128 0.866 0.0300 96.5% < 10

−291

1/64 0.877 0.0642 92.7% ∼ 0.0

1/32 0.899 0.140 84.5% < 10

−285

1/16 0.946 0.192 79.7% < 10

−321

1/8 1.05 0.255 75.7% < 10

−193

1/4 1.25 0.363 71.0% ∼ 0.0

within the open source library Chips-n-Salsa (Ci-

cirello, 2020), and use version 7.0.0 in the exper-

iments. All experiment source code is also open

source. Table 2 provides the relevant URLs.

The remainder of this section is organized as fol-

lows. Sections 4.1 and 4.2 present our experiments

with mutation and uniform crossover, respectively.

Then, in Section 4.3, we provide experiments com-

paring a fully optimized GA that optimizes the choice

of which pairs of parents to cross in addition to the

mutation and uniform crossover optimizations.

4.1 Mutation Experiments

In our mutation experiments, we consider bit-vector

length n ∈ {16,32,64, 128,256, 512,1024}, and mu-

tation rate p

∈ {

,. ..,

}. For each combination

(n, p

), we measure the CPU time to perform 100,000

mutations, averaged across 100 trials. We test the sig-

niﬁcance of the differences between the simple and

optimized versions using Welch’s unequal variances

t-test (Welch, 1947; Derrick and White, 2016).

Figure 1 visualizes n ∈ {16, 64,256, 1024}. Ta-

ble 3 summarizes results for n = 1024. Data for all

other cases is found in the GitHub repository, and is

similar to the cases presented here.

The optimized mutation leads to massive perfor-

mance gains. For bit-vector length n = 1024, the opti-

mized mutation uses 71% less time for high mutation

rates. For typical low mutation rates, the optimized

Table 4: CPU time for 10

uniform crosses for n = 1024.

CPU time (seconds) % less t-test

simple optimized time p-value

0.1 0.962 0.245 74.6% ∼ 0.0

0.2 1.13 0.355 68.5% ∼ 0.0

0.3 1.31 0.471 64.0% < 10

−308

0.4 1.50 0.577 61.6% < 10

−312

0.5 1.62 0.0142 99.1% ∼ 0.0

mutation uses 96%–99% less time than the simple im-

plementation. All results are extremely statistically

signiﬁcant with t-test p-values very near zero.

4.2 Uniform Crossover Experiments

We use the same bit-vector lengths n for the crossover

experiments as we did for the mutation experiments;

and we consider p

∈ {0.1, 0.2,0.3, 0.4,0.5} for the

per-bit probability of an exchange between parents.

We do not consider p

> 0.5 because any such p

has

an equivalent counterpart p

< 0.5 (e.g., exchanging

75% of the bits between the parents leads to the same

children as if we instead exchanged the other 25% of

the bits). For each combination (n, p

), we measure

the CPU time to perform 100,000 uniform crossovers,

averaged across 100 trials, and again test signiﬁcance

with Welch’s unequal variances t-test.

Figure 2 visualizes n ∈ {16, 64,256, 1024}. Ta-

ble 4 summarizes results for n = 1024. The data for

all other cases is found in the GitHub repository, and

is similar to the cases presented here.

The optimized uniform crossover leads to similar

performance gains as seen with mutation. Speciﬁ-

cally, for bit-vector length n = 1024, the optimized

uniform crossover uses approximately 60% to 75%

less time than the simple implementation, except for

the case of p

= 0.5 where the optimized version uses

99% less time. The performance of p

= 0.5 is espe-

cially strong due to our special case treatment when

generating random bitmasks (see earlier discussion in

Section 3). All results are extremely statistically sig-

niﬁcant with t-test p-values very near zero.

4.3 GA Experiments

Unlike mutation and crossover, it is not feasible to

isolate the generation control logic of Algorithm 6

from the GA as it depends upon the genetic opera-

tors. Instead we experiment with a GA with simple

vs optimized operators. We use the OneMax prob-

lem (Ackley, 1985) for its simplicity since our focus

is on runtime performance of alternative implemen-

tations of operators, and use vector length n = 1024

bits. All experimental conditions use population size

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

164

−4

−3

−2

mutation rate p

(log scale)

0.010

0.015

0.020

CPU time (seconds)

simple

optimized

(a)

−6

−5

−4

−3

−2

mutation rate p

(log scale)

0.025

0.050

0.075

CPU time (seconds)

simple

optimized

(b)

−7

−5

−3

mutation rate p

(log scale)

0.0

0.1

0.2

0.3

CPU time (seconds)

simple

optimized

(c)

−9

−7

−5

−3

mutation rate p

(log scale)

0.0

0.5

1.0

CPU time (seconds)

simple

optimized

(d)

Figure 1: CPU time for 10

mutations vs mutation rate p

for lengths: (a) 16 bits, (b) 64 bits, (c) 256 bits, (d) 1024 bits.

0.1 0.2 0.3 0.4 0.5

uniform crossover bit-rate p

0.01

0.02

CPU time (seconds)

simple

optimized

(a)

0.1 0.2 0.3 0.4 0.5

uniform crossover bit-rate p

0.00

0.05

0.10

CPU time (seconds)

simple

optimized

(b)

0.1 0.2 0.3 0.4 0.5

uniform crossover bit-rate p

0.0

0.2

0.4

CPU time (seconds)

simple

optimized

(c)

0.1 0.2 0.3 0.4 0.5

uniform crossover bit-rate p

0.0

0.5

1.0

1.5

CPU time (seconds)

simple

optimized

(d)

Figure 2: CPU time for 10

uniform crosses vs uniform rate p

for lengths: (a) 16 bits, (b) 64 bits, (c) 256 bits, (d) 1024 bits.

100, stochastic universal sampling (Baker, 1987) for

selection, and mutation rate p

1024

, which leads

to an expected one mutated bit per population mem-

ber per generation. We consider crossover rates p

∈

{0.05,0.15,...,0.95}. Each GA run is 1000 genera-

tions, and we average results over 100 trials. We test

signiﬁcance with Welch’s unequal variances t-test.

We consider four cases. Case (a) compares the

simple versions of the generation logic, mutation, and

uniform crossover (p

= 0.33) versus the optimized

versions of these. Case (b) is similar, but with uniform

crossover parameter p

= 0.49. We decided not to

use p

= 0.5 to avoid the extra strong performance

of our optimized bitmask generation for that special

case. Cases (c) and (d) are as the others, but with

single-point and two-point crossover, respectively.

Table 5 shows the results for case (a) uniform

crossover (p

= 0.33). The optimized approach

Optimizing Genetic Algorithms Using the Binomial Distribution

165

Table 5: CPU time and average solution of 1024-bit OneMax using 1000 generations with uniform crossover (p

= 0.33).

CPU time (seconds) % less t-test average solution t-test

simple optimized time p-value simple optimized p-value

0.05 0.869 0.0423 95.1% ∼ 0.0 687.33 686.57 0.541

0.15 0.942 0.0698 92.6% < 10

−279

709.20 709.88 0.611

0.25 1.01 0.0950 90.6% < 10

−259

715.94 714.62 0.328

0.35 1.07 0.121 88.7% ∼ 0.0 719.01 719.64 0.639

0.45 1.14 0.148 87.0% < 10

−314

720.77 721.57 0.512

0.55 1.21 0.174 85.6% ∼ 0.0 721.54 722.01 0.718

0.65 1.27 0.200 84.3% ∼ 0.0 722.97 724.94 0.158

0.75 1.34 0.224 83.3% ∼ 0.0 723.89 722.16 0.163

0.85 1.41 0.252 82.1% ∼ 0.0 725.60 726.18 0.655

0.95 1.47 0.277 81.2% ∼ 0.0 724.62 724.73 0.929

Table 6: CPU time and average solution of 1024-bit OneMax using 1000 generations with uniform crossover (p

= 0.49).

CPU time (seconds) % less t-test average solution t-test

simple optimized time p-value simple optimized p-value

0.05 0.875 0.0467 94.7% ∼ 0.0 690.05 689.17 0.454

0.15 0.956 0.0803 91.6% < 10

−312

711.34 712.19 0.572

0.25 1.03 0.114 88.9% ∼ 0.0 717.99 717.08 0.439

0.35 1.11 0.148 86.7% ∼ 0.0 720.71 722.44 0.162

0.45 1.19 0.182 84.8% ∼ 0.0 722.24 720.16 0.102

0.55 1.27 0.216 83.0% ∼ 0.0 723.10 723.38 0.826

0.65 1.35 0.250 81.5% ∼ 0.0 723.67 724.12 0.707

0.75 1.43 0.283 80.2% ∼ 0.0 725.33 724.64 0.582

0.85 1.51 0.318 79.0% ∼ 0.0 725.65 724.22 0.272

0.95 1.59 0.352 77.9% ∼ 0.0 724.85 724.44 0.761

Table 7: CPU time and average solution of 1024-bit OneMax using 1000 generations with single-point crossover.

CPU time (seconds) % less t-test average solution t-test

simple optimized time p-value simple optimized p-value

0.05 0.836 0.0283 96.6% ∼ 0.0 659.20 659.51 0.798

0.15 0.838 0.0286 96.6% ∼ 0.0 683.32 684.49 0.342

0.25 0.839 0.0306 96.4% < 10

−260

693.77 694.79 0.413

0.35 0.840 0.0308 96.3% ∼ 0.0 701.48 703.06 0.230

0.45 0.839 0.0325 96.1% < 10

−321

706.65 705.55 0.334

0.55 0.842 0.0323 96.2% ∼ 0.0 709.60 708.17 0.265

0.65 0.843 0.0342 95.9% ∼ 0.0 711.61 710.39 0.321

0.75 0.843 0.0355 95.8% < 10

−310

713.20 713.91 0.571

0.85 0.843 0.0366 95.7% < 10

−269

715.36 716.18 0.503

0.95 0.850 0.0373 95.6% < 10

−223

716.60 716.36 0.854

uses from approximately 81% less time for a high

crossover rate (p

= 0.95) to 95% less time for a

low crossover rate (p

= 0.05). The runtime differ-

ences are extremely statistically signiﬁcant with t-test

p-values near 0.0.

Table 6 provides detailed results for case (b) uni-

form crossover (p

= 0.49). The results follow the

same trend as the previous case. The approach opti-

mized using the binomial distribution uses from ap-

proximately 78% less time for a high crossover rate

= 0.95) to 95% less time for a low crossover rate

= 0.05). The runtime differences are extremely

statistically signiﬁcant with t-test p-values near 0.0.

Table 7 summarizes the results for case (c) single-

point crossover. Unlike uniform crossover, the speed

difference does not vary by crossover rate. Instead,

the optimized approach uses approximately 95% to

97% less time than the simple GA implementation

for all crossover rates. All runtime differences are ex-

tremely statistically signiﬁcant with all t-test p-values

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

166

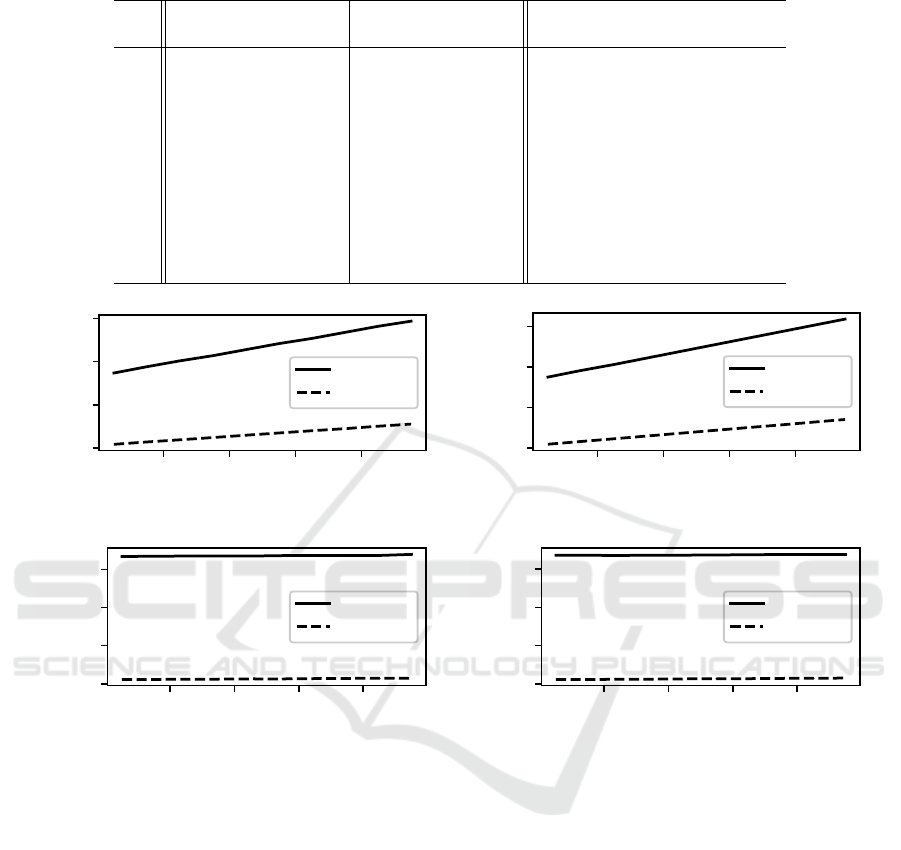
Table 8: CPU time and average solution of 1024-bit OneMax using 1000 generations with two-point crossover.

CPU time (seconds) % less t-test average solution t-test

simple optimized time p-value simple optimized p-value

0.05 0.840 0.0291 96.5% < 10

−316

666.82 666.08 0.526

0.15 0.840 0.0292 96.5% ∼ 0.0 692.26 692.32 0.959

0.25 0.839 0.0306 96.4% < 10

−296

702.23 703.29 0.394

0.35 0.841 0.0313 96.3% ∼ 0.0 708.16 709.99 0.124

0.45 0.841 0.0333 96.0% < 10

−301

712.22 712.39 0.897

0.55 0.842 0.0338 96.0% ∼ 0.0 714.05 713.80 0.845

0.65 0.844 0.0347 95.9% < 10

−311

718.86 715.63 0.00829

0.75 0.845 0.0364 95.7% ∼ 0.0 718.60 717.78 0.504

0.85 0.845 0.0377 95.5% < 10

−318

719.54 718.86 0.611

0.95 0.846 0.0383 95.5% ∼ 0.0 720.30 721.55 0.320

0.2 0.4 0.6 0.8

crossover rate p

0.0

0.5

1.0

1.5

CPU time (seconds)

simple

optimized

(a)

0.2 0.4 0.6 0.8

crossover rate p

0.0

0.5

1.0

1.5

CPU time (seconds)

simple

optimized

(b)

0.2 0.4 0.6 0.8

crossover rate p

0.00

0.25

0.50

0.75

CPU time (seconds)

simple

optimized

(c)

0.2 0.4 0.6 0.8

crossover rate p

0.00

0.25

0.50

0.75

CPU time (seconds)

simple

optimized

(d)

Figure 3: CPU time for 1024-bit OneMax using 1000 generations with population size 100 vs crossover rate p

for crossover

operators: (a) uniform (p

= 0.33), (b) uniform (p

= 0.49), (c) single-point, (d) two-point.

very near 0.0.

Table 8 summarizes the results for case (d) two-

point crossover. The trend is the same as in the case

of single-point crossover. The binomially optimized

approach uses approximately 95% to 97% less time

than the basic implementation, and does not vary by

crossover rate. All runtime differences are extremely

statistically signiﬁcant with all t-test p-values very

near 0.0.

Tables 5, 6, 7, and 8 also show average OneMax

solutions (i.e., number of 1-bits) to demonstrate that

the optimized approach does not statistically alter GA

problem-solving behavior. For any given crossover

operator and crossover rate p

, there is no statistical

signiﬁcance in solution quality between the optimized

and simple approach (i.e., high p-values).

Figure 3 visualizes the results for all four cases.

When uniform crossover is used, runtime increases

with crossover rate. The graphs appear to show con-

stant runtime when either single-point (Figure 3c) or

two-point crossover (Figure 3d) is used. However,

runtime is increasing in these cases, just very slowly

as seen in the detailed results from Tables 7 and 8.

The performance differential between the simple and

optimized approaches doesn’t vary by crossover rate

when single-point (Figure 3c) or two-point crossover

(Figure 3d) are used, with the optimized approach

consistently using 95% less time; while the perfor-

mance differential between the optimized and simple

approaches does vary with crossover rate when uni-

form crossover is used (Figures 3a and 3b).

Optimizing Genetic Algorithms Using the Binomial Distribution

167

5 CONCLUSION

In this paper, we demonstrated how we can signiﬁ-

cantly speed up the runtime of some GA operators,

including the common bit-ﬂip mutation and uniform

crossover, by observing that such operators deﬁne bi-

nomial experiments (i.e., sequence of Bernoulli tri-

als). This enables replacing explicit iteration that gen-

erates a random ﬂoating-point value for each bit to

determine whether to ﬂip (for mutation) or exchange

(for crossover), with the generation of a single bino-

mial random variate to determine the number of bits

k, and an efﬁcient sampling algorithm to choose the k

bits to mutate or cross. As a consequence, costly ran-

dom number generation is signiﬁcantly reduced. A

similar approach is also seen for the generation logic

that determines the number of parents to cross.

The technique is not limited to these opera-

tors, and is applicable for any operator that is con-

trolled by some probability p of including an ele-

ment in the mutation or cross. For example, sev-

eral evolutionary operators for permutations (Ci-

cirello, 2023) operate in this way, including uni-

form order based crossover (Syswerda, 1991), order

crossover 2 (Syswerda, 1991; Starkweather et al.,

1991), uniform partially matched crossover (Cicirello

and Smith, 2000), uniform scramble mutation (Ci-

cirello, 2023), and uniform precedence preservative

crossover (Bierwirth et al., 1996). We adapt this ap-

proach in our implementations of all of these evolu-

tionary permutation operators in the open source li-

brary Chips-n-Salsa (Cicirello, 2020).

REFERENCES

Ackley, D. H. (1985). A connectionist algorithm for genetic

search. In ICGA, pages 121–135.

Baker, J. (1987). Reducing bias and inefﬁciency in the se-

lection algorithm. In ICGA, pages 14–21.

Bierwirth, C., Mattfeld, D. C., and Kopfer, H. (1996). On

permutation representations for scheduling problems.

In PPSN, pages 310–318.

Cantú-Paz, E. (2002). On random numbers and the per-

formance of genetic algorithms. In GECCO, pages

311–318.

Cicirello, V. A. (2018). Impact of random number genera-

tion on parallel genetic algorithms. In Proceedings of

the Thirty-First International Florida Artiﬁcial Intelli-

gence Research Society Conference, pages 2–7. AAAI

Press.

Cicirello, V. A. (2020). Chips-n-Salsa: A java li-

brary of customizable, hybridizable, iterative, parallel,

stochastic, and self-adaptive local search algorithms.

Journal of Open Source Software, 5(52):2448.

Cicirello, V. A. (2022a). Cycle mutation: Evolving per-

mutations via cycle induction. Applied Sciences,

12(11):5506.

Cicirello, V. A. (2022b). ρµ: A java library of randomiza-

tion enhancements and other math utilities. Journal of

Open Source Software, 7(76):4663.

Cicirello, V. A. (2023). A survey and analysis of evo-

lutionary operators for permutations. In 15th Inter-

national Joint Conference on Computational Intelli-

gence, pages 288–299.

Cicirello, V. A. (2024a). Algorithms for generating small

random samples. Software: Practice and Experience,

pages 1–9.

Cicirello, V. A. (2024b). On the average runtime of an open

source binomial random variate generation algorithm.

arXiv preprint arXiv:2403.11018 [cs.DS].

Cicirello, V. A. and Smith, S. F. (2000). Modeling ga per-

formance for control parameter optimization. In Pro-

ceedings of the Genetic and Evolutionary Computa-

tion Conference (GECCO-2000), pages 235–242.

Derrick, B. and White, P. (2016). Why welch’s test is type

I error robust. Quantitative Methods for Psychology,

12(1):30–38.

Flury, B. D. (1990). Acceptance–rejection sampling made

easy. SIAM Review, 32(3):474–476.

Goodman, S. E. and Hedetniemi, S. T. (1977). Introduction

to the Design and Analysis of Algorithms, chapter 6.3

Probabilistic Algorithms, pages 298–316. McGraw-

Hill, New York, NY, USA.

Hinterding, R. (1995). Gaussian mutation and self-adaption

for numeric genetic algorithms. In IEEE CEC, pages

384–389.

Kachitvichyanukul, V. and Schmeiser, B. W. (1988). Bino-

mial random variate generation. CACM, 31(2):216–

222.

Kirkpatrick, S. and Stoll, E. P. (1981). A very fast shift-

of Computational Physics, 40(2):517–526.

Knuth, D. E. (1998). The Art of Computer Program-

ming, Volume 2, Seminumerical Algorithms. Addison-

Wesley, 3rd edition.

Krömer, P., Platoš, J., and Snášel, V. (2018). Evaluation

of pseudorandom number generators based on residue

arithmetic in differential evolution. In Intelligent Net-

working and Collaborative Systems, pages 336–348.

Krömer, P., Snášel, V., and Zelinka, I. (2013). On the use

of chaos in nature-inspired optimization methods. In

IEEE SMC, pages 1684–1689.

Kuhl, M. E. (2017). History of random variate generation.

In Winter Simulation Conference, pages 231–242.

Larson, H. J. (1982). Introduction to Probability Theory

and Statistical Inference. Wiley, 3rd edition.

Lemire, D. (2019). Fast random integer generation in an in-

terval. ACM Transactions on Modeling and Computer

Simulation, 29(1):3.

Leong, P. H. W., Zhang, G., Lee, D.-U., Luk, W., and Vil-

lasenor, J. (2005). A comment on the implementation

of the ziggurat method. Journal of Statistical Soft-

ware, 12(7):1–4.

ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications

168

Macias-Medri, A., Viswanathan, G., Fiore, C., Koehler, M.,

and da Luz, M. (2023). Speedup of the metropolis pro-

tocol via algorithmic optimization. Journal of Compu-

tational Science, 66:101910.

Marsaglia, G. and Tsang, W. W. (2000). The ziggurat

method for generating random variables. Journal of

Statistical Software, 5(8):1–7.

Matsumoto, M. and Nishimura, T. (1998). Mersenne

twister: A 623-dimensionally equidistributed uniform

pseudo-random number generator. ACM Transactions

on Modeling and Computer Simulation, 8(1):3–30.

Merelo-Guervós, J.-J., Blancas-Álvarez, I., Castillo, P. A.,

Romero, G., García-Sánchez, P., Rivas, V. M., García-

Valdez, M., Hernández-Águila, A., and Román, M.

(2017). Ranking programming languages for evolu-

tionary algorithm operations. In Applications of Evo-

lutionary Computation, pages 689–704.

Merelo-Guervós, J.-J., Blancas-Álvarez, I., Castillo, P. A.,

Romero, G., Rivas, V. M., García-Valdez, M.,

Hernández-Águila, A., and Romáin, M. (2016). A

comparison of implementations of basic evolutionary

algorithm operations in different languages. In IEEE

CEC, pages 1602–1609.

Nesmachnow, S., Luna, F., and Alba, E. (2015). An em-

pirical time analysis of evolutionary algorithms as

c programs. Software: Practice and Experience,

45(1):111–142.

Rajashekharan, L. and Velayutham, C. S. (2016). Is dif-

ferential evolution sensitive to pseudo random number

generator quality?–an investigation. In Intelligent Sys-

tems Technologies and Applications, pages 305–313.

Reese, A. (2009). Random number generators in genetic al-

gorithms for unconstrained and constrained optimiza-

tion. Nonlinear Analysis: Theory, Methods & Appli-

cations, 71(12):e679–e692.

Starkweather, T., McDaniel, S., Mathias, K., Whitley, D.,

and Whitley, C. (1991). A comparison of genetic se-

quencing operators. In ICGA, pages 69–76.

Steele, G. L., Lea, D., and Flood, C. H. (2014). Fast split-

table pseudorandom number generators. In OOPSLA,

pages 453–472.

Syswerda, G. (1991). Schedule optimization using genetic

algorithms. In Handbook of Genetic Algorithms. Van

Nostrand Reinhold.

Tirronen, V., Äyrämö, S., and Weber, M. (2011). Study on

the effects of pseudorandom generation quality on the

performance of differential evolution. In Adaptive and

Natural Computing Algorithms, pages 361–370.

Vitter, J. S. (1985). Random sampling with a reservoir.

ACM Trans on Mathematical Software, 11(1):37–57.

Welch, B. L. (1947). The generalization of student’s prob-

lem when several different population varlances are

involved. Biometrika, 34(1-2):28–35.

Wiese, K., Hendriks, A., Deschenes, A., and Youssef, B.

(2005a). Signiﬁcance of randomness in p-rnapredict:

a parallel evolutionary algorithm for rna folding. In

IEEE CEC, pages 467–474.

Wiese, K. C., Hendriks, A., Deschênes, A., and Youssef,

B. B. (2005b). The impact of pseudorandom number

quality on p-rnapredict, a parallel genetic algorithm

for rna secondary structure prediction. In GECCO,

pages 479–480.

Ye, F. (2023). IOHalgorithm. https://github.com/

IOHproﬁler/IOHalgorithm (accessed Sept 30, 2024).

Ye, F., Doerr, C., and Bäck, T. (2019). Interpolating local

and global search by controlling the variance of stan-

dard bit mutation. In IEEE CEC, pages 2292–2299.

Optimizing Genetic Algorithms Using the Binomial Distribution

169